 図形と方程式
図形と方程式
 図形と方程式
図形と方程式
福田の数学〜東京理科大学2022年理工学部第1問(3)〜2つの円の位置関係

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(3)座標平面上の3点(2,3),(-5,10),(-2,1)を通る円をC_1とする。この
とき、C_1の中心は$(-\boxed{ナ}, \boxed{ニ})$、半径は$\boxed{ヌ}$である。
$C_1$と点(2,3)で外接し、x軸とも接している円を$C_2$とする。このとき、
$C_2$の中心は$(\frac{\boxed{ネ}}{\boxed{ノ}},\frac{\boxed{ハヒ}}{\boxed{フ}})、半径は\frac{\boxed{ヘホ}}{\boxed{マ}}$である。
2022東京理科大学理工学部過去問
この動画を見る
(3)座標平面上の3点(2,3),(-5,10),(-2,1)を通る円をC_1とする。この
とき、C_1の中心は$(-\boxed{ナ}, \boxed{ニ})$、半径は$\boxed{ヌ}$である。
$C_1$と点(2,3)で外接し、x軸とも接している円を$C_2$とする。このとき、
$C_2$の中心は$(\frac{\boxed{ネ}}{\boxed{ノ}},\frac{\boxed{ハヒ}}{\boxed{フ}})、半径は\frac{\boxed{ヘホ}}{\boxed{マ}}$である。
2022東京理科大学理工学部過去問
福田の数学〜東京理科大学2022年理工学部第1問(2)〜三角方程式

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#円と方程式#加法定理とその応用#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(2)角θに関する方程式
$\cos 4θ=\cos θ(0\leqq θ\leqq \pi)$
について考える。①を満たすθは小さい方から順に
$θ=0,\frac{\boxed{キ}}{\boxed{ク}}\pi,\frac{\boxed{ケ}}{\boxed{コ}}\pi,\frac{\boxed{サ}}{\boxed{シ}}\pi$
の4つである。一方、θが①を満たすとき、$t=\cos θ$とおくとtは
$\boxed{ス}t^4 - \boxed{セ}t^2+\boxed{ソ}=t$
を満たす。$t=1,\cos \frac{\boxed{ケ}}{\boxed{コ}}\pi$は②の解なので、2次方程式
$\boxed{タ}t^2+\boxed{チ}t-1=0$
は$\cos \frac{\boxed{キ}}{\boxed{ク}}\pi,\cos \frac{\boxed{サ}}{\boxed{シ}}\pi$を解にもつ。これより、
$\cos \frac{\boxed{キ}}{\boxed{ク}}\pi=\frac{\sqrt{\boxed{ツ}}-\boxed{テ}}{\boxed{ト}},\cos \frac{\boxed{サ}}{\boxed{シ}}\pi=-\frac{\sqrt{\boxed{ツ}}+\boxed{テ}}{\boxed{ト}}$であることが分かる。
この動画を見る
(2)角θに関する方程式
$\cos 4θ=\cos θ(0\leqq θ\leqq \pi)$
について考える。①を満たすθは小さい方から順に
$θ=0,\frac{\boxed{キ}}{\boxed{ク}}\pi,\frac{\boxed{ケ}}{\boxed{コ}}\pi,\frac{\boxed{サ}}{\boxed{シ}}\pi$
の4つである。一方、θが①を満たすとき、$t=\cos θ$とおくとtは
$\boxed{ス}t^4 - \boxed{セ}t^2+\boxed{ソ}=t$
を満たす。$t=1,\cos \frac{\boxed{ケ}}{\boxed{コ}}\pi$は②の解なので、2次方程式
$\boxed{タ}t^2+\boxed{チ}t-1=0$
は$\cos \frac{\boxed{キ}}{\boxed{ク}}\pi,\cos \frac{\boxed{サ}}{\boxed{シ}}\pi$を解にもつ。これより、
$\cos \frac{\boxed{キ}}{\boxed{ク}}\pi=\frac{\sqrt{\boxed{ツ}}-\boxed{テ}}{\boxed{ト}},\cos \frac{\boxed{サ}}{\boxed{シ}}\pi=-\frac{\sqrt{\boxed{ツ}}+\boxed{テ}}{\boxed{ト}}$であることが分かる。
福田の数学〜杏林大学2022年医学部第3問〜空間図形と球面の方程式

単元:
#数Ⅱ#大学入試過去問(数学)#空間ベクトル#図形と方程式#円と方程式#軌跡と領域#空間ベクトル#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学#数C
指導講師:
福田次郎
問題文全文(内容文):
(1)座標平面上の3点A(-1,0),B(1,0),Cを頂点とする三角形について考える。
点Cのy座標は正であり、原点をOとして、以下の問いに答えよ。
$(\textrm{a})\angle BAC \lt \angle ABC$を満たす場合、点Cは第$\boxed{ア}$象限に存在する。
$(\textrm{b})\angle ABC \lt \angle ACB$を満たす場合、点Cは$\boxed{イ}$の$\boxed{ウ}$に存在する。
$(\textrm{c})\angle ACB \lt \frac{\pi}{2}$を満たす場合、点Cは$\boxed{エ}$の$\boxed{オ}$に存在する。
$(\textrm{d})\angle BAC \leqq \angle ABC \leqq ACB \leqq \frac{\pi}{2}$を満たす点Cが存在する領域(境界を含む)
の面積は$\frac{\boxed{カ}}{\boxed{キク }}\pi-\frac{\sqrt{\boxed{ケ }}}{\boxed{コ }}$である。
$\boxed{イ},\boxed{エ}$の解答群
①点Aを中心とし点Bを通る円
②点Bを中心とし点Aを通る円
③線分ABを直径とする円
④離心率が0.5で2点O,Aを焦点とする楕円
⑤離心率が0.5で2点O,Bを焦点とする楕円
⑥離心率が0.5で2点A,Bを焦点とする楕円
⑦線分ABを一辺にもち、重心のy座標が正である正三角形
⑧線分ABを一辺にもち、重心のy座標が正である正方形
$\boxed{ウ},\boxed{オ}$の解答群
①内部 ②周上 ③外部 ④重心
(2)座標空間内の4点$A(-1,0,0),B(1,0,0),C(s,t,0),D$を原点とし、
$\angle BAC \lt \angle ABC \lt \angle ACB$
を満たす四面体を考える。$t \gt 0$であり、点Dのz座標は正であるとする。
$(\textrm{a})\angle ADC=\frac{\pi}{2}$を満たす場合、点Dは$\boxed{サ }$に存在する。
$(\textrm{b})\angle ADC=\angle BDC=\frac{\pi}{2}$を満たす場合、
点Dのx座標はsであり、点Dは$(s,\boxed{シ},0)$を中心とする
半径$\boxed{ス}$の円周上にある。
$(\textrm{c})$以下では$t=\frac{4}{3}$とする。設問(1)の結果から、点Cのx座標sは
$\boxed{セ} \lt s \lt -\boxed{ソ}+\frac{\boxed{タ}\sqrt{\boxed{チ}}}{\boxed{ツ}}$の範囲をとりうる。この範囲でsが変化
するとき、$\angle ADB=\angle ADC =\angle BDC=\frac{\pi}{2}$を満たす四面体ABCDの体積は
$s=\frac{\boxed{テ}}{\boxed{エ}}$のとき最大値$\frac{\boxed{ナ}}{\boxed{二ヌ }}$をとる。
2022杏林大学医学部過去問
この動画を見る
(1)座標平面上の3点A(-1,0),B(1,0),Cを頂点とする三角形について考える。
点Cのy座標は正であり、原点をOとして、以下の問いに答えよ。
$(\textrm{a})\angle BAC \lt \angle ABC$を満たす場合、点Cは第$\boxed{ア}$象限に存在する。
$(\textrm{b})\angle ABC \lt \angle ACB$を満たす場合、点Cは$\boxed{イ}$の$\boxed{ウ}$に存在する。
$(\textrm{c})\angle ACB \lt \frac{\pi}{2}$を満たす場合、点Cは$\boxed{エ}$の$\boxed{オ}$に存在する。
$(\textrm{d})\angle BAC \leqq \angle ABC \leqq ACB \leqq \frac{\pi}{2}$を満たす点Cが存在する領域(境界を含む)
の面積は$\frac{\boxed{カ}}{\boxed{キク }}\pi-\frac{\sqrt{\boxed{ケ }}}{\boxed{コ }}$である。
$\boxed{イ},\boxed{エ}$の解答群
①点Aを中心とし点Bを通る円
②点Bを中心とし点Aを通る円
③線分ABを直径とする円
④離心率が0.5で2点O,Aを焦点とする楕円
⑤離心率が0.5で2点O,Bを焦点とする楕円
⑥離心率が0.5で2点A,Bを焦点とする楕円
⑦線分ABを一辺にもち、重心のy座標が正である正三角形
⑧線分ABを一辺にもち、重心のy座標が正である正方形
$\boxed{ウ},\boxed{オ}$の解答群
①内部 ②周上 ③外部 ④重心
(2)座標空間内の4点$A(-1,0,0),B(1,0,0),C(s,t,0),D$を原点とし、
$\angle BAC \lt \angle ABC \lt \angle ACB$
を満たす四面体を考える。$t \gt 0$であり、点Dのz座標は正であるとする。
$(\textrm{a})\angle ADC=\frac{\pi}{2}$を満たす場合、点Dは$\boxed{サ }$に存在する。
$(\textrm{b})\angle ADC=\angle BDC=\frac{\pi}{2}$を満たす場合、
点Dのx座標はsであり、点Dは$(s,\boxed{シ},0)$を中心とする
半径$\boxed{ス}$の円周上にある。
$(\textrm{c})$以下では$t=\frac{4}{3}$とする。設問(1)の結果から、点Cのx座標sは
$\boxed{セ} \lt s \lt -\boxed{ソ}+\frac{\boxed{タ}\sqrt{\boxed{チ}}}{\boxed{ツ}}$の範囲をとりうる。この範囲でsが変化
するとき、$\angle ADB=\angle ADC =\angle BDC=\frac{\pi}{2}$を満たす四面体ABCDの体積は
$s=\frac{\boxed{テ}}{\boxed{エ}}$のとき最大値$\frac{\boxed{ナ}}{\boxed{二ヌ }}$をとる。
2022杏林大学医学部過去問
福田の数学〜上智大学2022年理工学部第4問〜線分の中点の軌跡と直線の通過範囲

単元:
#数Ⅱ#大学入試過去問(数学)#平面上の曲線#図形と方程式#軌跡と領域#2次曲線#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
座標平面上に円C$:x^2+y^2=4$と点$P(6,\ 0)$がある。円C上を点$A(2a,\ 2b)$が
動くとき、線分APの中点をMとし、線分APの垂直二等分線をlとする。
(1)点Mの軌跡の方程式を求め、その軌跡を図示せよ。
(2)直線lの方程式をa,\ bを用いて表せ。
(3)直線lが通過する領域を表す不等式を求め、その領域を図示せよ。
2022上智大理工学部過去問
この動画を見る
座標平面上に円C$:x^2+y^2=4$と点$P(6,\ 0)$がある。円C上を点$A(2a,\ 2b)$が
動くとき、線分APの中点をMとし、線分APの垂直二等分線をlとする。
(1)点Mの軌跡の方程式を求め、その軌跡を図示せよ。
(2)直線lの方程式をa,\ bを用いて表せ。
(3)直線lが通過する領域を表す不等式を求め、その領域を図示せよ。
2022上智大理工学部過去問
福田の数学〜上智大学2022年TEAP理系型第2問〜空間ベクトルと軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#空間ベクトル#図形と方程式#軌跡と領域#空間ベクトル#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
一辺の長さが1である立方体QACB-CFGEを考える。
$\overrightarrow{ OA } = \overrightarrow{ a },\ \overrightarrow{ OB } $
$= \overrightarrow{ b },\ \overrightarrow{ OC } = \overrightarrow{ c },$ とおき、実数s,tに対し
点P,Qを
$\overrightarrow{ OP } =(1-s)\overrightarrow{ a } +s\ \overrightarrow{ b }+$
$s\ \overrightarrow{ c },\ \ \overrightarrow{ OQ } =\overrightarrow{ a } +t\ \overrightarrow{ b }+(1-t)\ \overrightarrow{ c }$
を満たす点とする。
(1)点Pは直線$\boxed{あ}$上にあり、点Qは直線$\boxed{い}$上にある。
(2)直線$\boxed{あ}$と直線$\boxed{い}$とは$\boxed{う }$
$\boxed{う}$の選択肢
$(\textrm{a})$一致する $(\textrm{b})$平行である $(\textrm{c})$直交する $(\textrm{d})$交わるが直交しない。
$(\textrm{e})$ねじれの位置にあって垂直である $(\textrm{f})$ねじれの位置にあって垂直でない。
(3)線分PQの長さは、$s=\boxed{え},\ t=\boxed{お}$のとき最小値をとり、
このとき$PQ^2=\boxed{か}$である。
$\boxed{え}\ \boxed{お}\ \boxed{か}$の選択肢
$(\textrm{a})0\ \ \ (\textrm{b})\frac{1}{6}\ \ \ (\textrm{c})\frac{1}{4}\ \ \ (\textrm{d})\frac{1}{3}$
$(\textrm{e})\frac{1}{2}\ \ \ (\textrm{f})\frac{2}{3}\ \ \ (\textrm{g})\frac{3}{4}\ \ \ (\textrm{h})1$
$(\textrm{i})\frac{4}{3}\ \ \ (\textrm{j})\frac{3}{2}\ \ \ (\textrm{k})2\ \ \ (\textrm{l})3$
(4)$s,t$が$0 \leqq s \leqq 1,\ 0 \leqq t \leqq 1$の範囲を動くとき、線分PQの中点Mの動く領域は
$\boxed{き}$であり、その面積は$\frac{\sqrt{\boxed{オ}}}{\boxed{カ}}$である。
$\boxed{き}$の選択肢
$(\textrm{a})$正三角形 $(\textrm{b})$直角二等辺三角形 $(\textrm{c})$直角二等辺三角形でない直角三角形
$(\textrm{d})$直角二等辺三角形でない直角三角形でもない三角形 $(\textrm{e})$正方形 $(\textrm{f})$正方形でない長方形
$(\textrm{g})$長方形でない平行四辺形 $(\textrm{h})$並行四辺形でない四角形$(\textrm{i})$五角形$(\textrm{i})$六角形
(5)$s,t$が$0 \leqq s \leqq 1,\ 0 \leqq t \leqq 1$の範囲を動くとき、線分PQが通過する領域の体積は
$\frac{\boxed{キ}}{\boxed{ク}}$である。
2022上智大学理系過去問
この動画を見る
一辺の長さが1である立方体QACB-CFGEを考える。
$\overrightarrow{ OA } = \overrightarrow{ a },\ \overrightarrow{ OB } $
$= \overrightarrow{ b },\ \overrightarrow{ OC } = \overrightarrow{ c },$ とおき、実数s,tに対し
点P,Qを
$\overrightarrow{ OP } =(1-s)\overrightarrow{ a } +s\ \overrightarrow{ b }+$
$s\ \overrightarrow{ c },\ \ \overrightarrow{ OQ } =\overrightarrow{ a } +t\ \overrightarrow{ b }+(1-t)\ \overrightarrow{ c }$
を満たす点とする。
(1)点Pは直線$\boxed{あ}$上にあり、点Qは直線$\boxed{い}$上にある。
(2)直線$\boxed{あ}$と直線$\boxed{い}$とは$\boxed{う }$
$\boxed{う}$の選択肢
$(\textrm{a})$一致する $(\textrm{b})$平行である $(\textrm{c})$直交する $(\textrm{d})$交わるが直交しない。
$(\textrm{e})$ねじれの位置にあって垂直である $(\textrm{f})$ねじれの位置にあって垂直でない。
(3)線分PQの長さは、$s=\boxed{え},\ t=\boxed{お}$のとき最小値をとり、
このとき$PQ^2=\boxed{か}$である。
$\boxed{え}\ \boxed{お}\ \boxed{か}$の選択肢
$(\textrm{a})0\ \ \ (\textrm{b})\frac{1}{6}\ \ \ (\textrm{c})\frac{1}{4}\ \ \ (\textrm{d})\frac{1}{3}$
$(\textrm{e})\frac{1}{2}\ \ \ (\textrm{f})\frac{2}{3}\ \ \ (\textrm{g})\frac{3}{4}\ \ \ (\textrm{h})1$
$(\textrm{i})\frac{4}{3}\ \ \ (\textrm{j})\frac{3}{2}\ \ \ (\textrm{k})2\ \ \ (\textrm{l})3$
(4)$s,t$が$0 \leqq s \leqq 1,\ 0 \leqq t \leqq 1$の範囲を動くとき、線分PQの中点Mの動く領域は
$\boxed{き}$であり、その面積は$\frac{\sqrt{\boxed{オ}}}{\boxed{カ}}$である。
$\boxed{き}$の選択肢
$(\textrm{a})$正三角形 $(\textrm{b})$直角二等辺三角形 $(\textrm{c})$直角二等辺三角形でない直角三角形
$(\textrm{d})$直角二等辺三角形でない直角三角形でもない三角形 $(\textrm{e})$正方形 $(\textrm{f})$正方形でない長方形
$(\textrm{g})$長方形でない平行四辺形 $(\textrm{h})$並行四辺形でない四角形$(\textrm{i})$五角形$(\textrm{i})$六角形
(5)$s,t$が$0 \leqq s \leqq 1,\ 0 \leqq t \leqq 1$の範囲を動くとき、線分PQが通過する領域の体積は
$\frac{\boxed{キ}}{\boxed{ク}}$である。
2022上智大学理系過去問
福田の数学〜上智大学2022年TEAP文系型第4問(3)〜指数不等式と領域における最小

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#指数関数と対数関数#軌跡と領域#指数関数#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
(3)正の数の組$(x,\ y)$が
$\begin{array}{1}
x \geqq 1\\
y \geqq 1\\
x^5y^4 \geqq 100\\
x^2y^9 \geqq 100\\
\end{array}$
を満たすとき$z=xy$は$(x,\ y)=(a,\ b)$で最小値をとる。ここで、
$\log_{10}a=\frac{\boxed{ヤ}}{\boxed{ユ}},\ \log_{10}b=\frac{\boxed{ヨ}}{\boxed{ワ}}$
である。
2022上智大学文系過去問
この動画を見る
(3)正の数の組$(x,\ y)$が
$\begin{array}{1}
x \geqq 1\\
y \geqq 1\\
x^5y^4 \geqq 100\\
x^2y^9 \geqq 100\\
\end{array}$
を満たすとき$z=xy$は$(x,\ y)=(a,\ b)$で最小値をとる。ここで、
$\log_{10}a=\frac{\boxed{ヤ}}{\boxed{ユ}},\ \log_{10}b=\frac{\boxed{ヨ}}{\boxed{ワ}}$
である。
2022上智大学文系過去問
福田の数学〜上智大学2022年TEAP文系型第4問(2)〜円が直線から切り取る線分の長さ

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(2)$t \gt 0$とし、xy平面上の直線
$l:y=-x+t$
と領域
$B:x^2+(y-2)^2 \leqq \frac{1}{4}t^2$
を考える。Bとlが2点以上で交わるとき、交わりとして得られる線分の長さは
$t=\boxed{ム}$のときに最大値$\boxed{メ}\sqrt{\boxed{モ}}$をとる。
2022上智大学文系過去問
この動画を見る
(2)$t \gt 0$とし、xy平面上の直線
$l:y=-x+t$
と領域
$B:x^2+(y-2)^2 \leqq \frac{1}{4}t^2$
を考える。Bとlが2点以上で交わるとき、交わりとして得られる線分の長さは
$t=\boxed{ム}$のときに最大値$\boxed{メ}\sqrt{\boxed{モ}}$をとる。
2022上智大学文系過去問
福田の数学〜上智大学2022年TEAP文系型第1問(3)〜サイコロの目による円と直線の位置関係の確率

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#確率#図形と方程式#点と直線#円と方程式#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
1個のさいころを投げる試行を2回繰り返し、
1回目に出た目をa,2回目に出た目をbとする。xy平面上で直線
$l:\frac{x}{a}+\frac{y}{b}=1$
を考える。lとx軸の交点をP、lとy軸の交点をQ、原点をOとし、
三角形OPQの周および内部をD、三角形OPQの面積をSとする。
(3)円$(x-3)^2+(y-3)^2=5$とlが共有点を持たない確率は$\frac{\boxed{サ}}{\boxed{シ}}$である。
2022上智大学文系過去問
この動画を見る
1個のさいころを投げる試行を2回繰り返し、
1回目に出た目をa,2回目に出た目をbとする。xy平面上で直線
$l:\frac{x}{a}+\frac{y}{b}=1$
を考える。lとx軸の交点をP、lとy軸の交点をQ、原点をOとし、
三角形OPQの周および内部をD、三角形OPQの面積をSとする。
(3)円$(x-3)^2+(y-3)^2=5$とlが共有点を持たない確率は$\frac{\boxed{サ}}{\boxed{シ}}$である。
2022上智大学文系過去問
福田の数学〜上智大学2022年TEAP文系型第1問(2)〜領域に属する確率

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#整数の性質#確率#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
1個のさいころを投げる試行を2回繰り返し、
1回目に出た目をa,2回目に出た目をbとする。xy平面上で直線
$l:\frac{x}{a}+\frac{y}{b}=1$
を考える。lとx軸の交点をP、lとy軸の交点をQ、原点をOとし、
三角形OPQの周および内部をD、三角形OPQの面積をSとする。
(2)点(2,\ 4)がDに含まれる確率は
$\frac{\boxed{キ}}{\boxed{ク}}$
点(2,\ 3)がDに含まれる確率は$\frac{\boxed{ケ}}{\boxed{コ}}$である。
2022上智大学文系過去問
この動画を見る
1個のさいころを投げる試行を2回繰り返し、
1回目に出た目をa,2回目に出た目をbとする。xy平面上で直線
$l:\frac{x}{a}+\frac{y}{b}=1$
を考える。lとx軸の交点をP、lとy軸の交点をQ、原点をOとし、
三角形OPQの周および内部をD、三角形OPQの面積をSとする。
(2)点(2,\ 4)がDに含まれる確率は
$\frac{\boxed{キ}}{\boxed{ク}}$
点(2,\ 3)がDに含まれる確率は$\frac{\boxed{ケ}}{\boxed{コ}}$である。
2022上智大学文系過去問
福田の数学〜青山学院大学2022年理工学部第5問〜切り取られる弦の中点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
xy平面上に、円$C:(x-5)^2+y^2=5$と直線$l:y=mx$がある。
(1)Cとlが共有点を持つようなmの値の範囲を求めよ。
mの値が(1)で求めた範囲にあるとき、Cとlの2つの共有点をP,Qとし、
線分PQの中点をMとする。ただし、lがCに接するときはP=Q=Mとする。
(2)点Mの座標をmを用いて表せ。
(3)mが(1)で求めた範囲を動くときの点Mの軌跡を求め、図示せよ。
(4)原点からCに引いた2本の接線と(3)で求めた点Mの軌跡で囲まれた図形を
Dとする。図形Dをx軸の周りに1回転してできる回転体の体積Vを求めよ。
2022青山学院大学理工学部過去問
この動画を見る
xy平面上に、円$C:(x-5)^2+y^2=5$と直線$l:y=mx$がある。
(1)Cとlが共有点を持つようなmの値の範囲を求めよ。
mの値が(1)で求めた範囲にあるとき、Cとlの2つの共有点をP,Qとし、
線分PQの中点をMとする。ただし、lがCに接するときはP=Q=Mとする。
(2)点Mの座標をmを用いて表せ。
(3)mが(1)で求めた範囲を動くときの点Mの軌跡を求め、図示せよ。
(4)原点からCに引いた2本の接線と(3)で求めた点Mの軌跡で囲まれた図形を
Dとする。図形Dをx軸の周りに1回転してできる回転体の体積Vを求めよ。
2022青山学院大学理工学部過去問
福田の数学〜立教大学2022年経済学部第3問〜放物線と円と直線で囲まれた面積

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#微分法と積分法#円と方程式#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
Oを原点とする座標平面上の放物線$C:y=x^2$とC上の点P$(\frac{\sqrt3}{2}, \ \frac{3}{4})$がある。
PにおけるCの接線をlとし、また、Pを通りlと直交する直線をmとする。
さらに、mとx軸の交点をQとする。このとき、次の問いに答えよ。
(1)mの方程式を$y=px+q$とするとき、定数p,qの値を求めよ。
(2)Qの座標を$(a,\ 0)$とするとき、aの値を求めよ。
(3)Qを中心とする半径rの円Dがlとただ1つの共有点を持つとき、rの値を求めよ。
(4)(1)で定めたp,qの値に対して、次の連立不等式の表す領域の面積S_1を求めよ。
$x \geqq 0,\ \ \ y \geqq 0,\ \ \ y \leqq px+q,\ \ \ y \leqq x^2$
(5)(2)で定めたaの値と(3)で定めたrの値に対して、次の連立不等式の表す領域
の面積S_2を求めよ。
$0 \leqq x \leqq \frac{\sqrt3}{2},\ \ \ y \geqq 0,\ \ \ y \leqq x^2,\ \ \ (x-a)^2+y^2 \geqq r^2$
2022立教学部経済学部過去問
この動画を見る
Oを原点とする座標平面上の放物線$C:y=x^2$とC上の点P$(\frac{\sqrt3}{2}, \ \frac{3}{4})$がある。
PにおけるCの接線をlとし、また、Pを通りlと直交する直線をmとする。
さらに、mとx軸の交点をQとする。このとき、次の問いに答えよ。
(1)mの方程式を$y=px+q$とするとき、定数p,qの値を求めよ。
(2)Qの座標を$(a,\ 0)$とするとき、aの値を求めよ。
(3)Qを中心とする半径rの円Dがlとただ1つの共有点を持つとき、rの値を求めよ。
(4)(1)で定めたp,qの値に対して、次の連立不等式の表す領域の面積S_1を求めよ。
$x \geqq 0,\ \ \ y \geqq 0,\ \ \ y \leqq px+q,\ \ \ y \leqq x^2$
(5)(2)で定めたaの値と(3)で定めたrの値に対して、次の連立不等式の表す領域
の面積S_2を求めよ。
$0 \leqq x \leqq \frac{\sqrt3}{2},\ \ \ y \geqq 0,\ \ \ y \leqq x^2,\ \ \ (x-a)^2+y^2 \geqq r^2$
2022立教学部経済学部過去問
福田の数学〜立教大学2022年理学部第3問〜接線法線と囲まれた部分の面積

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#円と方程式#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$t$を正の実数とする。座標平面上に放物線$C_1:y=x^2$とその上の点$P(t,\ t^2)$がある。
Pにおける$C_1$の接線を$l$とし、法線を$m$とする。$l$とx軸との交点をQとする。
Pにおいて$l$に接し、さらにx軸にも接する円で、中心のx座標がt以下であるものを$C_2$
とする。$C_2$の中心をAとし、$C_2$とx軸の接点をBとする。
(1)lの方程式を求めよ。
(2)mの方程式を求めよ。
(3)$\angle BAP=\frac{\pi}{3}$であるとき、tの値を求めよ。
(4)(3)のとき、Aの座標を求めよ。
(5)(3)のとき、四角形ABQPの面積を求めよ。
2022立教大学理学部過去問
この動画を見る
$t$を正の実数とする。座標平面上に放物線$C_1:y=x^2$とその上の点$P(t,\ t^2)$がある。
Pにおける$C_1$の接線を$l$とし、法線を$m$とする。$l$とx軸との交点をQとする。
Pにおいて$l$に接し、さらにx軸にも接する円で、中心のx座標がt以下であるものを$C_2$
とする。$C_2$の中心をAとし、$C_2$とx軸の接点をBとする。
(1)lの方程式を求めよ。
(2)mの方程式を求めよ。
(3)$\angle BAP=\frac{\pi}{3}$であるとき、tの値を求めよ。
(4)(3)のとき、Aの座標を求めよ。
(5)(3)のとき、四角形ABQPの面積を求めよ。
2022立教大学理学部過去問
0.5分で要点が分かる!「二次関数と直線」の動画!~全国入試問題解法 #shorts #数学 #入試問題
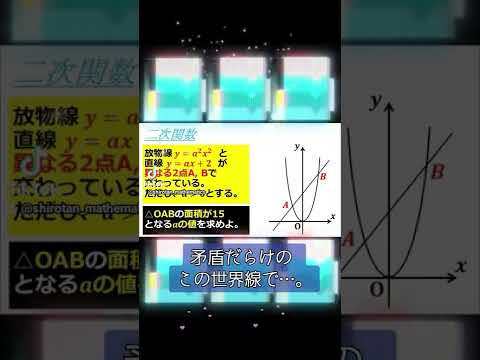
単元:
#数学(中学生)#中3数学#2次関数#図形と方程式#点と直線#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
放物線$y=a^2x^2$と直線$y=ax+2$が異なる2点$A,B$で交わっている.
ただし,$a \gt b$とする.
$\triangle OAB$の面積が15となる$a$の値を求めよ.
ノートルダム女学院高校過去問
この動画を見る
放物線$y=a^2x^2$と直線$y=ax+2$が異なる2点$A,B$で交わっている.
ただし,$a \gt b$とする.
$\triangle OAB$の面積が15となる$a$の値を求めよ.
ノートルダム女学院高校過去問
福田の数学〜早稲田大学2022年商学部第3問〜空間図形の計量

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#図形と方程式#三角関数#円と方程式#加法定理とその応用#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
座標空間において、2つの円$C_1,\ C_2$を
$C_1=\left\{(x,y,0)\ | \ x^2+y^2=1\right\},\ C_2=\left\{(0,y,z)\ | \ (y-1)^2+z^2=1\right\}$
とする。次の設問に答えよ。
(1)$C_1$上の2点と$C_2$上の点(0,1,1)を頂点とする正三角形を考える。
このような正三角形の一辺の長さをすべて求めよ。
(2)すべての頂点がC_1∪C_2上にある正四面体を考える。
このような正四面体の一辺の長さをすべて求めよ。
2022早稲田大学商学部過去問
この動画を見る
座標空間において、2つの円$C_1,\ C_2$を
$C_1=\left\{(x,y,0)\ | \ x^2+y^2=1\right\},\ C_2=\left\{(0,y,z)\ | \ (y-1)^2+z^2=1\right\}$
とする。次の設問に答えよ。
(1)$C_1$上の2点と$C_2$上の点(0,1,1)を頂点とする正三角形を考える。
このような正三角形の一辺の長さをすべて求めよ。
(2)すべての頂点がC_1∪C_2上にある正四面体を考える。
このような正四面体の一辺の長さをすべて求めよ。
2022早稲田大学商学部過去問
【実はカンタン!】媒介変数表示を3分で解説!〔数学、高校数学〕

単元:
#数Ⅱ#平面上の曲線#図形と方程式#媒介変数表示と極座標#数学(高校生)#数Ⅲ
指導講師:
3rd School
問題文全文(内容文):
$t$を実数とするとき、
$x=2t+1$
$y=4t^2+2t+1$
で表される点$(x,y)$の描く軌跡を求めよ。
この動画を見る
$t$を実数とするとき、
$x=2t+1$
$y=4t^2+2t+1$
で表される点$(x,y)$の描く軌跡を求めよ。
福田の数学〜早稲田大学2022年商学部第1問(2)〜対称式と最大値

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(2)実数$x,y$が$x^2+y^2\leqq 3$を満たしているとき、
$x-y-xy$の最大値は$\boxed{\ \ イ\ \ }$である。
2022早稲田大学商学部過去問
この動画を見る
${\large\boxed{1}}$(2)実数$x,y$が$x^2+y^2\leqq 3$を満たしているとき、
$x-y-xy$の最大値は$\boxed{\ \ イ\ \ }$である。
2022早稲田大学商学部過去問
福田の数学〜早稲田大学2022年教育学部第3問〜円の外接円の半径と円周上の点と原点の距離の最大最小

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#図形と方程式#点と直線#円と方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{3}}\ O(0,0),\ A(0,1),\ B(p,q)$を座標平面上の点とし、pは0でないとする。
AとBを通る直線をlとおく。Oを中心としlに接する円の面積を$D_1$で表す。
また、3点O,A,Bを通る円周で囲まれる円の面積を$D_2$とおく。次の問いに答えよ。
(1)$D_1$を$p,q$を使って表せ。
(2)点$(2,2\sqrt3)$を中心とする半径1の円周をCとする。点BがC上を動くときの
$D_1$と$D_2$の積$D_1D_2$の最小値と最大値を求めよ。
2022早稲田大学教育学部過去問
この動画を見る
${\large\boxed{3}}\ O(0,0),\ A(0,1),\ B(p,q)$を座標平面上の点とし、pは0でないとする。
AとBを通る直線をlとおく。Oを中心としlに接する円の面積を$D_1$で表す。
また、3点O,A,Bを通る円周で囲まれる円の面積を$D_2$とおく。次の問いに答えよ。
(1)$D_1$を$p,q$を使って表せ。
(2)点$(2,2\sqrt3)$を中心とする半径1の円周をCとする。点BがC上を動くときの
$D_1$と$D_2$の積$D_1D_2$の最小値と最大値を求めよ。
2022早稲田大学教育学部過去問
【ニガテな人が多い】通過領域の攻略法を6分で比較・解説!〔数学、高校数学〕

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$a$がすべての実数をとるとき、
$y=(a-1)x+a^2$
の通過する領域を求めよ。
この動画を見る
$a$がすべての実数をとるとき、
$y=(a-1)x+a^2$
の通過する領域を求めよ。
福田の数学〜早稲田大学2022年教育学部第1問(3)〜四面体と四面体の共通部分の切り口の面積

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#図形と方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(3)座標空間内の4点$(2,0,0),\ (-1,\sqrt3,0),\ (-1,-\sqrt3,0),\ (0,0,2)$を頂点と
する四面体をP、4点$(-2,0,1),\ (1,-\sqrt3,1),\ (1,\sqrt3,1),\ (0,0,-1)$を頂点
とする四面体をQとする。RをPとQの共通部分とする。Rを平面$z=\frac{1}{3}$で
切ったときの切り口の面積を求めよ。
2022早稲田大学教育学部過去問
この動画を見る
${\large\boxed{1}}$(3)座標空間内の4点$(2,0,0),\ (-1,\sqrt3,0),\ (-1,-\sqrt3,0),\ (0,0,2)$を頂点と
する四面体をP、4点$(-2,0,1),\ (1,-\sqrt3,1),\ (1,\sqrt3,1),\ (0,0,-1)$を頂点
とする四面体をQとする。RをPとQの共通部分とする。Rを平面$z=\frac{1}{3}$で
切ったときの切り口の面積を求めよ。
2022早稲田大学教育学部過去問
福田の数学〜早稲田大学2022年教育学部第1問(1)〜空間ベクトルと球面の方程式

単元:
#数Ⅱ#大学入試過去問(数学)#空間ベクトル#図形と方程式#円と方程式#空間ベクトル#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}$(1)座標空間内に3点A$(2,0,0),\ B(0,4,0),\ C(0,0,8)$をとる。
2つのベクトル$\overrightarrow{ AP }$と$\overrightarrow{ BP }+\overrightarrow{ CP }$の内積が0となるような点$P(x,y,z)$
のうち、$|\overrightarrow{ AP }$|が最大となる点Pの座標を求めよ。
2022早稲田大学教育学部過去問
この動画を見る
${\large\boxed{1}}$(1)座標空間内に3点A$(2,0,0),\ B(0,4,0),\ C(0,0,8)$をとる。
2つのベクトル$\overrightarrow{ AP }$と$\overrightarrow{ BP }+\overrightarrow{ CP }$の内積が0となるような点$P(x,y,z)$
のうち、$|\overrightarrow{ AP }$|が最大となる点Pの座標を求めよ。
2022早稲田大学教育学部過去問
福田の数学〜早稲田大学2022年人間科学部第7問〜複素数平面上の点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#円と方程式#軌跡と領域#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{7}}\ i$を虚数単位とする。$\alpha=-1+i$とし、zは次の条件をともに満たす複素数とする。
条件1.$\frac{z-\alpha}{z-\bar{\alpha}}$の実部は0である。
条件2.zの虚部は0以上である。
このとき、複素数平面上でzがとりうる値全体の集合を表す図形Cと、実軸で
囲まれる部分の面積は$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}\pi$である。
また、$w=\frac{iz}{z+1}$で表される点wがとりうる値全体の集合を表す図形と、
図形Cで囲まれる部分の面積は$\frac{\boxed{\ \ ウ\ \ }\ \pi+\boxed{\ \ エ\ \ }}{\boxed{\ \ オ\ \ }}$である。
2022早稲田大学人間科学部過去問
この動画を見る
${\large\boxed{7}}\ i$を虚数単位とする。$\alpha=-1+i$とし、zは次の条件をともに満たす複素数とする。
条件1.$\frac{z-\alpha}{z-\bar{\alpha}}$の実部は0である。
条件2.zの虚部は0以上である。
このとき、複素数平面上でzがとりうる値全体の集合を表す図形Cと、実軸で
囲まれる部分の面積は$\frac{\boxed{\ \ ア\ \ }}{\boxed{\ \ イ\ \ }}\pi$である。
また、$w=\frac{iz}{z+1}$で表される点wがとりうる値全体の集合を表す図形と、
図形Cで囲まれる部分の面積は$\frac{\boxed{\ \ ウ\ \ }\ \pi+\boxed{\ \ エ\ \ }}{\boxed{\ \ オ\ \ }}$である。
2022早稲田大学人間科学部過去問
【できない人多数!】直線の通過領域について4分で解説!〔数学、高校数学〕

単元:
#数Ⅱ#図形と方程式#点と直線#軌跡と領域#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$t$が全ての実数をとるとき、
直線:$y=tx+t^2$
が通過する領域を図示せよ。
この動画を見る
$t$が全ての実数をとるとき、
直線:$y=tx+t^2$
が通過する領域を図示せよ。
【意外とできない人が多い】アポロニウスの円について3分で解説!〔数学、高校数学〕

単元:
#数Ⅱ#図形と方程式#点と直線#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
アポロニウスの円について解説します。
2点A(-2,0)と点B(4,0)からの距離の比が2:1であるような点軌跡を求めよ。
この動画を見る
アポロニウスの円について解説します。
2点A(-2,0)と点B(4,0)からの距離の比が2:1であるような点軌跡を求めよ。
【数学】中高一貫校用問題集:図形と式:軌跡と方程式:2直線の交点の軌跡(直交する場合)

単元:
#数Ⅰ#数Ⅱ#図形と計量#図形と方程式#数学(高校生)
教材:
#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
mが実数全体を取って動くとき、$x+my-1=0,mx-y+2m=0$の交点Pの軌跡を求めよ
この動画を見る
mが実数全体を取って動くとき、$x+my-1=0,mx-y+2m=0$の交点Pの軌跡を求めよ
【数Ⅱ】中高一貫校問題集3(数式・関数編)394:図形と式:軌跡と方程式:2直線の交点の軌跡(直交する場合)

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
教材:
#TK数学#TK数学問題集3(数式・関数編)#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
mが実数全体を取って動くとき、x+my-1=0,mx-y+2m=0の交点Pの軌跡を求めよ
この動画を見る
mが実数全体を取って動くとき、x+my-1=0,mx-y+2m=0の交点Pの軌跡を求めよ
【テスト頻出】軌跡の求め方を3stepで解説!〔数学、高校数学〕

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
$a$を$0$以上の実数とするとき、
$y=-x^2+ax+4a$
の頂点をPとする。
このとき、点Pの描く軌跡を求めよ。
この動画を見る
$a$を$0$以上の実数とするとき、
$y=-x^2+ax+4a$
の頂点をPとする。
このとき、点Pの描く軌跡を求めよ。
福田の数学〜慶應義塾大学2022年看護医療学部第2問(1)〜円が直線から切り取る弦の長さ

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{2}}$(1)円$x^2+y^2-2x+6y=0$をCとするとき、
円Cの中心の座標は$\boxed{\ \ ア\ \ }$であり、
半径は$\boxed{\ \ イ\ \ }$である。また、円Cと直線$y=3x-1$の2つの共有点をA,Bとする
とき、線分ABの長さは$\boxed{\ \ ウ\ \ }$であり、線分ABの垂直二等分線の方程式は
$y=\boxed{\ \ エ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
この動画を見る
${\large\boxed{2}}$(1)円$x^2+y^2-2x+6y=0$をCとするとき、
円Cの中心の座標は$\boxed{\ \ ア\ \ }$であり、
半径は$\boxed{\ \ イ\ \ }$である。また、円Cと直線$y=3x-1$の2つの共有点をA,Bとする
とき、線分ABの長さは$\boxed{\ \ ウ\ \ }$であり、線分ABの垂直二等分線の方程式は
$y=\boxed{\ \ エ\ \ }$である。
2022慶應義塾大学看護医療学科過去問
福田の数学〜慶應義塾大学2022年環境情報学部第6問〜新型ウィルス感染拡大による大学の授業形態の決定

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#確率#図形と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{6}}$ある大学で来学期の授業の形式をどうするかを検討している。
授業形式の選択としては、通常の対面形式(授業形式uと呼ぶことにする)、
$\textrm{Web}$上で試料を閲覧できたり課題を行ったりできるオンデマンド形式(授業形式vと呼ぶことにする)
$\textrm{Web}$会議システムを使用するオンライン配信形式(授業形式wと呼ぶことにする)
の3つがあるとする。
また、来学期の新型ウイルスの感染状況については、
急激に拡大している状況(感染状況xと呼ぶことにする)、
ピークは過ぎたが十分な収束にはいたっていない状況(感染状況yとよぶことにする)、
ある程度収束した状況(感染状況zとよぶことにする)の3つが考えられるとする。
いま、この大学は授業形式と新型ウイルスの感染状況の組み合わせについて、
次の表(※動画参照)に示す評論値(値が高いほど評価も高い)を定めているものとする。
来学期の感染状況について、感染状況xである確率を$p_x$、
感染状況yである確率をp_y、感染状況zである確率を$p_z$とすると、
xyz空間において点$p=(p_x,p_y,p_z)は(1,0,0),(0,1,0),(0,0,1)$を頂点とする正三角形上の
点としてあらわすことができる。この正三角形上において、点pから各辺に垂線を下ろしたとき、
(1,0,0)と向かいの辺に下ろした垂線の長さをl_x、(0,1,0)と向かいの辺に下した垂線の長さを$l_y$、
(0,0,1)と向かいの辺に下した垂線の長さを$l_z$とする。
(1)このとき$p_x=\frac{\sqrt{\boxed{\ \ アイ\ \ }}}{\boxed{\ \ ウエ\ \ }}\ l_x,\ \ \ \,$
$p_y=\frac{\sqrt{\boxed{\ \ オカ\ \ }}}{\boxed{\ \ キク\ \ }}\ l_y,\ \ \ \ p_z=\frac{\sqrt{\boxed{\ \ ケコ\ \ }}}{\boxed{\ \ サシ\ \ }}\ l_z$が成り立つ。
いま、正三角形上の点$p=(p_x,p_y,p_z)$に対して、上記の評価の期待値を最大にする
授業形式のラベルをつけることにする。ただし、pによっては評価値を最大にする選択が
複数ある場合もあり、その場合にはpに複数のラベルをつけることにする。
さらに、原点と(0,1,0),(0,0,1)を原点とするyz平面上の直角二等辺三角形の頂点、辺、内部
からなるすべての点にxという感染状況のラベルをつけ、
原点と(1,0,0),(0,0,1)を原点とするxz平面上の直角二等辺三角形の頂点、辺、内部
からなるすべての点にyという感染状況のラベルをつけ、
原点と(1,0,0),(0,1,0)を原点とするxy平面上の直角二等辺三角形の頂点、辺、内部
からなるすべての点にzという感染状況のラベルをつけることにする。
すると、正三角形と3つの直角二等辺三角形からなる四面体の面上(頂点、辺も含む)
のそれぞれの点には、1つもしくは複数のラベルがつくことになる。例えば、
原点には$\left\{x,y,z\right\}$の3つのラベルがつく。
(2)このとき、正三角形の面上(頂点、辺も含む)の各点pにつけられるラベルの
可能性を列挙すると、以下の通りとなる。ただし、複数のラベルがつけられる場合には、
それぞれの中括弧内では、アルファベット順に書くものとする。空欄に入る
ラベルについて下記の選択肢から選びなさい。
単一のラベルがつく場合:$\left\{\boxed{\ \ ス\ \ }\right\},\left\{w\right\}$
2つのラベルがつく場合:$\left\{\boxed{\ \ セ\ \ },w\right\},\left\{u,\boxed{\ \ ソ\ \ }\right\},$
$\left\{\boxed{\ \ タ\ \ },y\right\},\left\{w,y\right\},\left\{\boxed{\ \ チ\ \ },z\right\}$
3つのラベルがつく場合:$\left\{\boxed{\ \ ツ\ \ },w,\boxed{\ \ テ\ \ }\right\},\left\{\boxed{\ \ ト\ \ },\boxed{\ \ ナ\ \ },\boxed{\ \ ニ\ \ }\right\}$
4つのラベルがつく場合:$\left\{u,\boxed{\ \ ヌ\ \ },\boxed{\ \ ネ\ \ },\boxed{\ \ ノ\ \ }\right\},\left\{\boxed{\ \ ハ\ \ },\boxed{\ \ ヒ\ \ },\boxed{\ \ フ\ \ },\boxed{\ \ ヘ\ \ }\right\}$
選択肢:$(1)\ \ \ u\ \ \ (2)\ \ \ v\ \ \ (3)\ \ \ w\ \ \ (4)\ \ \ x\ \ \ (5)\ \ \ y\ \ \ (6)\ \ \ z$
2022慶應義塾大学環境情報学部過去問
この動画を見る
${\large\boxed{6}}$ある大学で来学期の授業の形式をどうするかを検討している。
授業形式の選択としては、通常の対面形式(授業形式uと呼ぶことにする)、
$\textrm{Web}$上で試料を閲覧できたり課題を行ったりできるオンデマンド形式(授業形式vと呼ぶことにする)
$\textrm{Web}$会議システムを使用するオンライン配信形式(授業形式wと呼ぶことにする)
の3つがあるとする。
また、来学期の新型ウイルスの感染状況については、
急激に拡大している状況(感染状況xと呼ぶことにする)、
ピークは過ぎたが十分な収束にはいたっていない状況(感染状況yとよぶことにする)、
ある程度収束した状況(感染状況zとよぶことにする)の3つが考えられるとする。
いま、この大学は授業形式と新型ウイルスの感染状況の組み合わせについて、
次の表(※動画参照)に示す評論値(値が高いほど評価も高い)を定めているものとする。
来学期の感染状況について、感染状況xである確率を$p_x$、
感染状況yである確率をp_y、感染状況zである確率を$p_z$とすると、
xyz空間において点$p=(p_x,p_y,p_z)は(1,0,0),(0,1,0),(0,0,1)$を頂点とする正三角形上の
点としてあらわすことができる。この正三角形上において、点pから各辺に垂線を下ろしたとき、
(1,0,0)と向かいの辺に下ろした垂線の長さをl_x、(0,1,0)と向かいの辺に下した垂線の長さを$l_y$、
(0,0,1)と向かいの辺に下した垂線の長さを$l_z$とする。
(1)このとき$p_x=\frac{\sqrt{\boxed{\ \ アイ\ \ }}}{\boxed{\ \ ウエ\ \ }}\ l_x,\ \ \ \,$
$p_y=\frac{\sqrt{\boxed{\ \ オカ\ \ }}}{\boxed{\ \ キク\ \ }}\ l_y,\ \ \ \ p_z=\frac{\sqrt{\boxed{\ \ ケコ\ \ }}}{\boxed{\ \ サシ\ \ }}\ l_z$が成り立つ。
いま、正三角形上の点$p=(p_x,p_y,p_z)$に対して、上記の評価の期待値を最大にする
授業形式のラベルをつけることにする。ただし、pによっては評価値を最大にする選択が
複数ある場合もあり、その場合にはpに複数のラベルをつけることにする。
さらに、原点と(0,1,0),(0,0,1)を原点とするyz平面上の直角二等辺三角形の頂点、辺、内部
からなるすべての点にxという感染状況のラベルをつけ、
原点と(1,0,0),(0,0,1)を原点とするxz平面上の直角二等辺三角形の頂点、辺、内部
からなるすべての点にyという感染状況のラベルをつけ、
原点と(1,0,0),(0,1,0)を原点とするxy平面上の直角二等辺三角形の頂点、辺、内部
からなるすべての点にzという感染状況のラベルをつけることにする。
すると、正三角形と3つの直角二等辺三角形からなる四面体の面上(頂点、辺も含む)
のそれぞれの点には、1つもしくは複数のラベルがつくことになる。例えば、
原点には$\left\{x,y,z\right\}$の3つのラベルがつく。
(2)このとき、正三角形の面上(頂点、辺も含む)の各点pにつけられるラベルの
可能性を列挙すると、以下の通りとなる。ただし、複数のラベルがつけられる場合には、
それぞれの中括弧内では、アルファベット順に書くものとする。空欄に入る
ラベルについて下記の選択肢から選びなさい。
単一のラベルがつく場合:$\left\{\boxed{\ \ ス\ \ }\right\},\left\{w\right\}$
2つのラベルがつく場合:$\left\{\boxed{\ \ セ\ \ },w\right\},\left\{u,\boxed{\ \ ソ\ \ }\right\},$
$\left\{\boxed{\ \ タ\ \ },y\right\},\left\{w,y\right\},\left\{\boxed{\ \ チ\ \ },z\right\}$
3つのラベルがつく場合:$\left\{\boxed{\ \ ツ\ \ },w,\boxed{\ \ テ\ \ }\right\},\left\{\boxed{\ \ ト\ \ },\boxed{\ \ ナ\ \ },\boxed{\ \ ニ\ \ }\right\}$
4つのラベルがつく場合:$\left\{u,\boxed{\ \ ヌ\ \ },\boxed{\ \ ネ\ \ },\boxed{\ \ ノ\ \ }\right\},\left\{\boxed{\ \ ハ\ \ },\boxed{\ \ ヒ\ \ },\boxed{\ \ フ\ \ },\boxed{\ \ ヘ\ \ }\right\}$
選択肢:$(1)\ \ \ u\ \ \ (2)\ \ \ v\ \ \ (3)\ \ \ w\ \ \ (4)\ \ \ x\ \ \ (5)\ \ \ y\ \ \ (6)\ \ \ z$
2022慶應義塾大学環境情報学部過去問
【9分でマスター!!】とても重要な加法定理を解説!〔現役塾講師解説、数学〕

単元:
#数Ⅱ#図形と方程式#三角関数#加法定理とその応用#数学(高校生)
指導講師:
3rd School
問題文全文(内容文):
数学2B
加法定理について解説します。
①$\cos15$℃
②$\sin75$℃
$\alpha$は第1象限の角で$\sin\alpha=\frac{5}{13}$、$\beta$は第3象限の角で$\cos\beta=-\frac{3}{5}$とする。
$\sin(\alpha+\beta)$、$\cos(\alpha+\beta)$の値は?
この動画を見る
数学2B
加法定理について解説します。
①$\cos15$℃
②$\sin75$℃
$\alpha$は第1象限の角で$\sin\alpha=\frac{5}{13}$、$\beta$は第3象限の角で$\cos\beta=-\frac{3}{5}$とする。
$\sin(\alpha+\beta)$、$\cos(\alpha+\beta)$の値は?
福田の入試問題解説〜慶應義塾大学2022年医学部第3問〜内サイクロイドと極方程式

単元:
#数Ⅱ#大学入試過去問(数学)#平面上の曲線#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
(1)座標平面上の点P(x,y)を、点T(s,t)を中心として半時計周りに角$\alpha$だけ
回転させるときに、点Pが点P'(x',y')に移るとする。x'とy'を$x,y,s,t,\alpha$
の式で表すと$x'=\boxed{\ \ ア\ \ }, y'=\boxed{\ \ イ\ \ }$となる。
(2)aを正の実数とする。原点O(0,0)とする半径aの円Cに、半径$\frac{a}{2}$で原点O
を通る円Kを点A(a,0)において内接させる。この円Kを円Cに沿って
滑らないように転がす。ただし、KとCの接点がC上を半時計回りに動くようにする。
そして、接点の座標がはじめて$(a\cos\beta,a\sin\beta)(0 \leqq \beta \leqq 2\pi)$となるようにする。
円Kに対するこの操作は次の2段階の操作を続けて行うことと同等である。
$(\textrm{i})$点B$(\frac{a}{2},0)$を中心として、円Kを$\boxed{\ \ ウ\ \ }$に角$\boxed{\ \ エ\ \ }$だけ回転させる。
$(\textrm{ii})$原点Oを中心として、円Kを$\boxed{\ \ オ\ \ }$に角$\boxed{\ \ カ\ \ }$だけ回転させる。
$\boxed{\ \ ウ\ \ },\boxed{\ \ エ\ \ },\boxed{\ \ オ\ \ },\boxed{\ \ カ\ \ }$の選択肢
時計回り,反時計回り,$\beta,2\beta,\frac{1}{2}\beta$
(3)円Kが点Aにおいて円Cに内接しているとき、Kの内部に固定された点Q(b,0)
(ただし、$0 \lt b \lt a$)をとる。円Kを、Cとの接点がC上を一周するまで(2)に述べた
やり方でCに沿って転がすとき、点Qが動いてできる曲線を$S_1$とする。$S_1$上の
点の座標を(x,y)として、$S_1$の方程式をx,yを用いて書くと$\boxed{\ \ キ\ \ }$となる。
(4)円Kが点Aにおいて円Cに内接しているとき、円Cに固定された点R(0,a)をとる。
今度は円Kを固定して、円Cの方をKに接した状態で滑らないようにKに沿って転がす。
2つの円の接点が円Kを$\boxed{\ \ ク\ \ }$回転したとき、点Rははじめてもとの位置
(0,a)に戻る。Rが描く曲線を$S_2$とする。原点Oを極とし、x軸の正の部分を
始線とする極座標#$(r,\theta)$による$S_2$の極方程式は$r=\boxed{\ \ ケ\ \ }$である。
ただし$r,\theta$はそれぞれ$S_2$上の点の原点からの距離、および偏角である。
2022慶應義塾大学医学部過去問
この動画を見る
(1)座標平面上の点P(x,y)を、点T(s,t)を中心として半時計周りに角$\alpha$だけ
回転させるときに、点Pが点P'(x',y')に移るとする。x'とy'を$x,y,s,t,\alpha$
の式で表すと$x'=\boxed{\ \ ア\ \ }, y'=\boxed{\ \ イ\ \ }$となる。
(2)aを正の実数とする。原点O(0,0)とする半径aの円Cに、半径$\frac{a}{2}$で原点O
を通る円Kを点A(a,0)において内接させる。この円Kを円Cに沿って
滑らないように転がす。ただし、KとCの接点がC上を半時計回りに動くようにする。
そして、接点の座標がはじめて$(a\cos\beta,a\sin\beta)(0 \leqq \beta \leqq 2\pi)$となるようにする。
円Kに対するこの操作は次の2段階の操作を続けて行うことと同等である。
$(\textrm{i})$点B$(\frac{a}{2},0)$を中心として、円Kを$\boxed{\ \ ウ\ \ }$に角$\boxed{\ \ エ\ \ }$だけ回転させる。
$(\textrm{ii})$原点Oを中心として、円Kを$\boxed{\ \ オ\ \ }$に角$\boxed{\ \ カ\ \ }$だけ回転させる。
$\boxed{\ \ ウ\ \ },\boxed{\ \ エ\ \ },\boxed{\ \ オ\ \ },\boxed{\ \ カ\ \ }$の選択肢
時計回り,反時計回り,$\beta,2\beta,\frac{1}{2}\beta$
(3)円Kが点Aにおいて円Cに内接しているとき、Kの内部に固定された点Q(b,0)
(ただし、$0 \lt b \lt a$)をとる。円Kを、Cとの接点がC上を一周するまで(2)に述べた
やり方でCに沿って転がすとき、点Qが動いてできる曲線を$S_1$とする。$S_1$上の
点の座標を(x,y)として、$S_1$の方程式をx,yを用いて書くと$\boxed{\ \ キ\ \ }$となる。
(4)円Kが点Aにおいて円Cに内接しているとき、円Cに固定された点R(0,a)をとる。
今度は円Kを固定して、円Cの方をKに接した状態で滑らないようにKに沿って転がす。
2つの円の接点が円Kを$\boxed{\ \ ク\ \ }$回転したとき、点Rははじめてもとの位置
(0,a)に戻る。Rが描く曲線を$S_2$とする。原点Oを極とし、x軸の正の部分を
始線とする極座標#$(r,\theta)$による$S_2$の極方程式は$r=\boxed{\ \ ケ\ \ }$である。
ただし$r,\theta$はそれぞれ$S_2$上の点の原点からの距離、および偏角である。
2022慶應義塾大学医学部過去問
