微分法と積分法
微分法と積分法
福田の数学〜上智大学2025TEAP利用型文系第1問〜放物線と円の位置関係と面積
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
座標平面上の放物線$C_1:y=x^2$と
円$C_2:x^2+(y-b)^2=a^2$を考える。
ただし、$a,b$は正の実数とする。
(1)$C_1$と$C_2$が共有点をちょうど$3$つもつための
必要十分条件は
$b=\boxed{ア}a$かつ$a\gt \dfrac{\boxed{イ}}{\boxed{ウ}}$である。
(2)$C_1$と$C_2$が異なる$2$点で接するための
必要十分条件は
$b=\boxed{エ}a^2+\dfrac{\boxed{オ}}{\boxed{カ}}$かつ$a\gt \dfrac{\boxed{キ}}{\boxed{ク}}$である。
(ただし、$C_1$と$C_2$が共有点$P$で接するとは、
$P$における$C_1$の接線と$C_"$の接線が等しいことをいう)
また、このとき$2$つの接点のうち$x$座標が
正のものを$A(\alpha,\beta)$とすると、
$\beta=\boxed{ケ}a^2+\dfrac{\boxed{コ}}{\boxed{サ}}$である。
$A$における共通の接線の傾きが$\sqrt3$であるとき、
直線$y=\beta$の下側で、
$C_1$と$C_2$に囲まれた部分の面積は
$\dfrac{\boxed{シ}}{\boxed{ス}}\sqrt{\boxed{セ}}-\dfrac{\pi}{\boxed{ソ}}$である。
$2025$年上智大学TEAP利用型文系過去問題
この動画を見る
$\boxed{1}$
座標平面上の放物線$C_1:y=x^2$と
円$C_2:x^2+(y-b)^2=a^2$を考える。
ただし、$a,b$は正の実数とする。
(1)$C_1$と$C_2$が共有点をちょうど$3$つもつための
必要十分条件は
$b=\boxed{ア}a$かつ$a\gt \dfrac{\boxed{イ}}{\boxed{ウ}}$である。
(2)$C_1$と$C_2$が異なる$2$点で接するための
必要十分条件は
$b=\boxed{エ}a^2+\dfrac{\boxed{オ}}{\boxed{カ}}$かつ$a\gt \dfrac{\boxed{キ}}{\boxed{ク}}$である。
(ただし、$C_1$と$C_2$が共有点$P$で接するとは、
$P$における$C_1$の接線と$C_"$の接線が等しいことをいう)
また、このとき$2$つの接点のうち$x$座標が
正のものを$A(\alpha,\beta)$とすると、
$\beta=\boxed{ケ}a^2+\dfrac{\boxed{コ}}{\boxed{サ}}$である。
$A$における共通の接線の傾きが$\sqrt3$であるとき、
直線$y=\beta$の下側で、
$C_1$と$C_2$に囲まれた部分の面積は
$\dfrac{\boxed{シ}}{\boxed{ス}}\sqrt{\boxed{セ}}-\dfrac{\pi}{\boxed{ソ}}$である。
$2025$年上智大学TEAP利用型文系過去問題
福田の数学〜青山学院大学2025理工学部第4問〜折れ線の長さの和が4となる点の軌跡と面積
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#学校別大学入試過去問解説(数学)#数学(高校生)#青山学院大学
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
$xy$平面上に$2$つの定点$A(-1,0),B(1,0)$がある。
線分$AB$上の点$P$に対して、
$xy$平面上の点$Q$は以下の条件$(a),(b)$を
満たすとする。
$(a)$$P$と$Q$の$x$座標は等しく、
$Q$の$y$座標は正である。
$(b)$$AP+PQ+QB=4$
このとき、以下の問いに答えよ。
ただし、線分は両方の端点を含むものとする。
(1)$P$の座標を$(s,0)$とするとき、
$Q$の座標を$s$を用いて表せ。
(2)$P$が線分$AB$上を$A$から$B$まで動くとき、
$Q$の軌跡を$xy$平面上に図示せよ。
(3)$P$が線分$AB$上を$A$から$B$まで動くとき、
線分$PQ$が通過する範囲の面積を求めよ。
$2025$年青山学院大学理工学部過去問題
この動画を見る
$\boxed{4}$
$xy$平面上に$2$つの定点$A(-1,0),B(1,0)$がある。
線分$AB$上の点$P$に対して、
$xy$平面上の点$Q$は以下の条件$(a),(b)$を
満たすとする。
$(a)$$P$と$Q$の$x$座標は等しく、
$Q$の$y$座標は正である。
$(b)$$AP+PQ+QB=4$
このとき、以下の問いに答えよ。
ただし、線分は両方の端点を含むものとする。
(1)$P$の座標を$(s,0)$とするとき、
$Q$の座標を$s$を用いて表せ。
(2)$P$が線分$AB$上を$A$から$B$まで動くとき、
$Q$の軌跡を$xy$平面上に図示せよ。
(3)$P$が線分$AB$上を$A$から$B$まで動くとき、
線分$PQ$が通過する範囲の面積を求めよ。
$2025$年青山学院大学理工学部過去問題
福田の数学〜早稲田大学2025商学部第1問(3)〜定積分で表された関数方程式
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(3)$m,n$を正の整数とする。
$n$次関数$f(x)$が次の等式を満たしているとき、
$f(x)=\boxed{ウ}$である。
$\displaystyle \int_{0}^{x} {f(t)}^{m-1} dt=(2x)^m f(x)$
$2025$年早稲田大学商学部過去問題
この動画を見る
$\boxed{1}$
(3)$m,n$を正の整数とする。
$n$次関数$f(x)$が次の等式を満たしているとき、
$f(x)=\boxed{ウ}$である。
$\displaystyle \int_{0}^{x} {f(t)}^{m-1} dt=(2x)^m f(x)$
$2025$年早稲田大学商学部過去問題
福田の数学〜早稲田大学2025商学部第1問(1)〜方程式の実数解の個数
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(1)正の実数$a$に対して、円$x^2+(y-a)^2=a^2$と
曲線$y=x^3$がちょうど$2$つの共有点をもつとき、
$a=\boxed{ア}$である。
$2025$年早稲田大学商学部過去問
この動画を見る
$\boxed{1}$
(1)正の実数$a$に対して、円$x^2+(y-a)^2=a^2$と
曲線$y=x^3$がちょうど$2$つの共有点をもつとき、
$a=\boxed{ア}$である。
$2025$年早稲田大学商学部過去問
福田の数学〜早稲田大学2025教育学部第4問〜共有点の個数と面積計算
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
$k$は実数とする。
曲線$C:y=(x^3-x+2)e^{-x}$と直線$y=k$との
共有点の偶数を$f(k)$で表す。次の問いに答えよ。
ただし、必要ならば自然数$n$に対し
$\displaystyle \lim_{x\to\infty} x^n e^{-x}=0$が成り立つことは
説明なしに用いてもよい。
(1)$k$が実数全体を動くとき、
$f(k)$の最大値の最小値を求めよ。
(2)$f(k)=2$を満たす$k$の値の範囲を求めよ。
(3)$\alpha$を正の実数とする。
曲線$C,x$軸,$y$軸,および直線$x=\alpha$で囲まれる
部分の面積を$\alpha$を用いて表せ。
$2025$年早稲田大学教育学部過去問題
この動画を見る
$\boxed{4}$
$k$は実数とする。
曲線$C:y=(x^3-x+2)e^{-x}$と直線$y=k$との
共有点の偶数を$f(k)$で表す。次の問いに答えよ。
ただし、必要ならば自然数$n$に対し
$\displaystyle \lim_{x\to\infty} x^n e^{-x}=0$が成り立つことは
説明なしに用いてもよい。
(1)$k$が実数全体を動くとき、
$f(k)$の最大値の最小値を求めよ。
(2)$f(k)=2$を満たす$k$の値の範囲を求めよ。
(3)$\alpha$を正の実数とする。
曲線$C,x$軸,$y$軸,および直線$x=\alpha$で囲まれる
部分の面積を$\alpha$を用いて表せ。
$2025$年早稲田大学教育学部過去問題
福田の数学〜早稲田大学2025教育学部第3問〜楕円と接線
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
座標平面上で、
点$H(0,2\sqrt2)$から楕円$C:x^2+2y^2=8$へ引いた
$2$つの接線を$L_1,L_2$とし、$L_1,L_2$と$C$との
共有点をそれぞれ$P_1,P_2$とする。
ただし、$P_1$の$x$座標は正であるとする。
次の問いに答えよ。
(1)直線$L_1$と$L_2$それぞれの傾きを求めよ。
(2)$2$点$P_1,P_2$を通る直線を$L_3$とする。
直線$L_3$と楕円$C$で囲まれた$2$つの部分のうち、
直線$L_3$の上側にある方の面積を求めよ。
$2025$年早稲田大学教育学部過去問題
この動画を見る
$\boxed{3}$
座標平面上で、
点$H(0,2\sqrt2)$から楕円$C:x^2+2y^2=8$へ引いた
$2$つの接線を$L_1,L_2$とし、$L_1,L_2$と$C$との
共有点をそれぞれ$P_1,P_2$とする。
ただし、$P_1$の$x$座標は正であるとする。
次の問いに答えよ。
(1)直線$L_1$と$L_2$それぞれの傾きを求めよ。
(2)$2$点$P_1,P_2$を通る直線を$L_3$とする。
直線$L_3$と楕円$C$で囲まれた$2$つの部分のうち、
直線$L_3$の上側にある方の面積を求めよ。
$2025$年早稲田大学教育学部過去問題
福田の数学〜早稲田大学2025教育学部第1問(4)〜2変数関数の最大
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(4)$4$つの辺$AB,BC,CD,DA$の長さが$1$である
四面体$ABCD$を考える。
そのような四面体の体積の最大値を求めよ。
$2025$年早稲田大学教育学部過去問題
この動画を見る
$\boxed{1}$
(4)$4$つの辺$AB,BC,CD,DA$の長さが$1$である
四面体$ABCD$を考える。
そのような四面体の体積の最大値を求めよ。
$2025$年早稲田大学教育学部過去問題
数学IIIのこの問題、解けるかな？
単元：
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文)：
以下を満たすf(x)は？
f(x)=8x+2∫f(t)dt
この動画を見る
以下を満たすf(x)は？
f(x)=8x+2∫f(t)dt
定積分を含む関数f(x)を求める問題、解けてくれーー
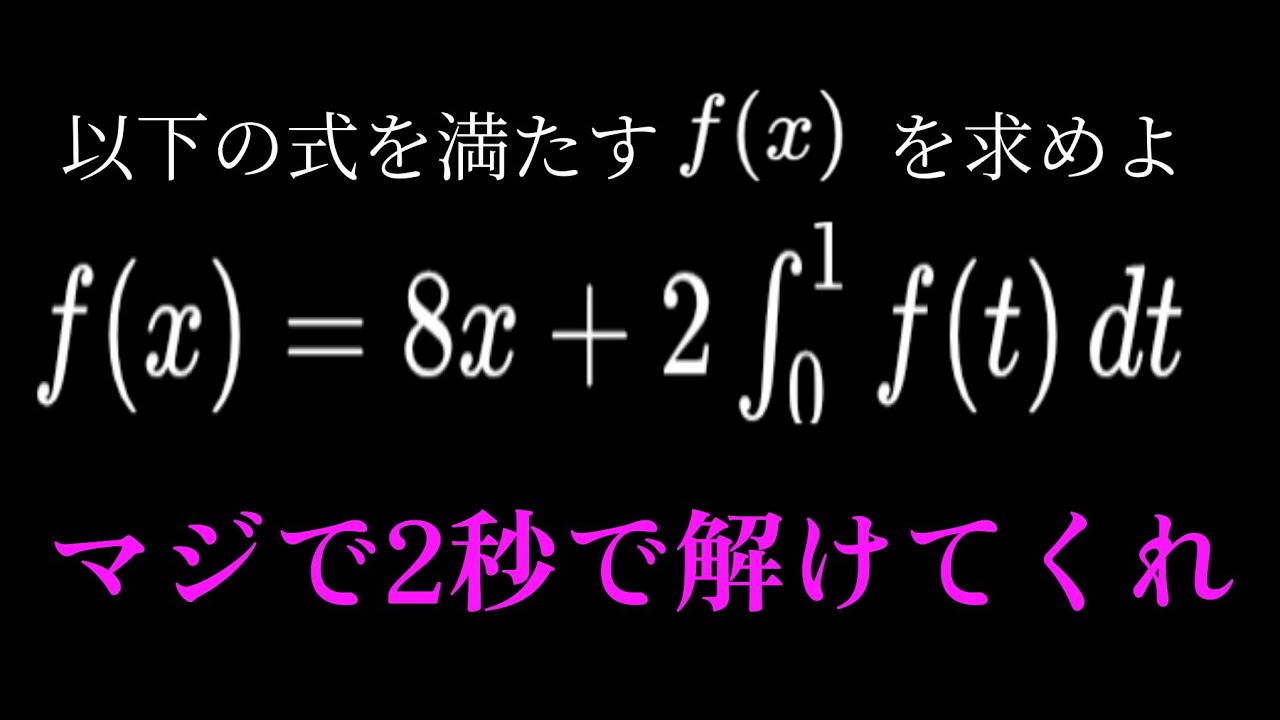
単元：
#数Ⅱ#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学(高校生)#数Ⅲ
指導講師：
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文)：
以下を満たすf(x)は？
f(x)=8x+2∫f(t)dt
この動画を見る
以下を満たすf(x)は？
f(x)=8x+2∫f(t)dt
福田の数学〜東京慈恵会医科大学2025医学部第2問〜定積分と不等式の証明
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#東京慈恵会医科大学
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
次の問いに答えよ。ただし、対数は自然対数とする。
(1)$3$以上の自然数$n$について、
次の不等式が成り立つことを示せ。
$\dfrac{1}{2\log(n+1)}\leqq \displaystyle \int_{0}^{1} \dfrac{x}{\log(x+n)} dx \leqq \dfrac{1}{2\log n}$
(2)不定積分$\displaystyle \int \dfrac{1}{x(log x)^2} dx$ を求めよ。
(3)$m \geqq n$をみたす$3$以上の自然数$m,n$について、
次の不等式が成り立つことを示せ。
$\dfrac{1}{\log n}-\dfrac{1}{\log(m+1)}\leqq \displaystyle \sum_{k=n}^{m} \dfrac{2}{k \log k} \displaystyle \int_{0}^{1} \dfrac{1}{\log(x+k)} dx \leqq \dfrac{1}{\log(n-1)} -\dfrac{1}{\log m}$
$2025$年東京慈恵会医科大学医学部過去問題
この動画を見る
$\boxed{2}$
次の問いに答えよ。ただし、対数は自然対数とする。
(1)$3$以上の自然数$n$について、
次の不等式が成り立つことを示せ。
$\dfrac{1}{2\log(n+1)}\leqq \displaystyle \int_{0}^{1} \dfrac{x}{\log(x+n)} dx \leqq \dfrac{1}{2\log n}$
(2)不定積分$\displaystyle \int \dfrac{1}{x(log x)^2} dx$ を求めよ。
(3)$m \geqq n$をみたす$3$以上の自然数$m,n$について、
次の不等式が成り立つことを示せ。
$\dfrac{1}{\log n}-\dfrac{1}{\log(m+1)}\leqq \displaystyle \sum_{k=n}^{m} \dfrac{2}{k \log k} \displaystyle \int_{0}^{1} \dfrac{1}{\log(x+k)} dx \leqq \dfrac{1}{\log(n-1)} -\dfrac{1}{\log m}$
$2025$年東京慈恵会医科大学医学部過去問題
福田の数学〜九州大学2025文系第1問〜共通接線
単元：
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
$2$つの曲線
$y=x^3+x^2-x-1,y=x^2$
の両方に接するすべての直線の
方程式を求めよ。
$2025$年九州大学文系過去問題
この動画を見る
$\boxed{1}$
$2$つの曲線
$y=x^3+x^2-x-1,y=x^2$
の両方に接するすべての直線の
方程式を求めよ。
$2025$年九州大学文系過去問題
福田のおもしろ数学544〜1分チャレンジ！微分の計算
単元：
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$y=\sqrt[3]{x+\sqrt{x^2+1}}+\sqrt[3]{x-\sqrt{x^2+1}}$
に対して、
導関数$y'$を$y$で表して下さい。
この動画を見る
$y=\sqrt[3]{x+\sqrt{x^2+1}}+\sqrt[3]{x-\sqrt{x^2+1}}$
に対して、
導関数$y'$を$y$で表して下さい。
福田のおもしろ数学542〜定積分の値の評価
単元：
#数Ⅱ#微分法と積分法#不定積分・定積分#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\dfrac{1}{3}\lt \displaystyle \int_{0}^{1}x^{(\sin x+\cos x)^2}dx \lt \dfrac{1}{2}$
を証明して下さい。
この動画を見る
$\dfrac{1}{3}\lt \displaystyle \int_{0}^{1}x^{(\sin x+\cos x)^2}dx \lt \dfrac{1}{2}$
を証明して下さい。
福田の数学〜九州大学2025理系第2問〜定積分の計算
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
以下の問いに答えよ。
(1)$y=\tan x$とするとき、
$\dfrac{dy}{dx}$を$y$の整式で表せ。
(2)次の定積分を求めよ。
$\displaystyle \int_{0}^{\frac{\pi}{4}}\dfrac{\tan^4x-\tan^2 x-2}{\tan^2x-4}dx$
$2025$年九州大学理系過去問題
この動画を見る
$\boxed{2}$
以下の問いに答えよ。
(1)$y=\tan x$とするとき、
$\dfrac{dy}{dx}$を$y$の整式で表せ。
(2)次の定積分を求めよ。
$\displaystyle \int_{0}^{\frac{\pi}{4}}\dfrac{\tan^4x-\tan^2 x-2}{\tan^2x-4}dx$
$2025$年九州大学理系過去問題
福田の数学〜神戸大学2025文系第1問〜3次方程式が異なる3個の実数解をもつ条件
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
$a$を実数とする。
$f(x)=2x^3+ax^2-1$とおくとき、以下の問いに答えよ。
(1)方程式$f(x)=0$は$x=-1$に解にもつとする。
このとき、$a$の値を求め、
方程式$f(x)=0$の解をすべて求めよ。
(2)$a$の値を(1)で求めたものとする。
関数$f(x)$の極限を求めよ。
(3)方程式$f(x)=0$が異なる$3$つの実数解を
もつような$a$の値の範囲を求めよ。
$2025$年神戸大学文系過去問題
この動画を見る
$\boxed{1}$
$a$を実数とする。
$f(x)=2x^3+ax^2-1$とおくとき、以下の問いに答えよ。
(1)方程式$f(x)=0$は$x=-1$に解にもつとする。
このとき、$a$の値を求め、
方程式$f(x)=0$の解をすべて求めよ。
(2)$a$の値を(1)で求めたものとする。
関数$f(x)$の極限を求めよ。
(3)方程式$f(x)=0$が異なる$3$つの実数解を
もつような$a$の値の範囲を求めよ。
$2025$年神戸大学文系過去問題
福田のおもしろ数学537〜2変数関数の極限
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$xy-x^3\tan \dfrac{1}{x}+y^2=0$のとき、
$\displaystyle \lim_{x\to\infty}\dfrac{y}{x}$を求めよ。
この動画を見る
$xy-x^3\tan \dfrac{1}{x}+y^2=0$のとき、
$\displaystyle \lim_{x\to\infty}\dfrac{y}{x}$を求めよ。
福田の数学〜神戸大学2025理系第5問〜連続と微分可能と曲線の長さ
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{5}$
連続関数$f(x)$は$x \geqq 0$で$f(x) \geqq 0$を満たし、
$x \gt 0$で微分可能であり、その導関数$f'(x)$は
連続であるとする。
$t \geqq 1$を満たす$t$に対して、
$y=f(x) \ (1\leqq x \leqq t)$で表される曲線の長さを
$h(t)$とし、$t=1$のときは$h(1)=0$とする。
以下の問いに答えよ。
(1)$t\gt 1$とする。
開区間$(1,t)$で常に$f(x)-xf'(x)=0$が成り立つならば、
閉区間$[1,t]$で$\dfrac{f(x)}{x}$は定数であることを示せ。
(2)$t\geqq 1$を満たす任意の$t$に対して、
$g(t)=h(t)+2$が成り立つとする。
このとき、$f(1)$の値を求めよ。
また、$t\geqq 1$のとき$f(t)$を$t$を用いて表せ。
$2025$年神戸大学理系過去問題
この動画を見る
$\boxed{5}$
連続関数$f(x)$は$x \geqq 0$で$f(x) \geqq 0$を満たし、
$x \gt 0$で微分可能であり、その導関数$f'(x)$は
連続であるとする。
$t \geqq 1$を満たす$t$に対して、
$y=f(x) \ (1\leqq x \leqq t)$で表される曲線の長さを
$h(t)$とし、$t=1$のときは$h(1)=0$とする。
以下の問いに答えよ。
(1)$t\gt 1$とする。
開区間$(1,t)$で常に$f(x)-xf'(x)=0$が成り立つならば、
閉区間$[1,t]$で$\dfrac{f(x)}{x}$は定数であることを示せ。
(2)$t\geqq 1$を満たす任意の$t$に対して、
$g(t)=h(t)+2$が成り立つとする。
このとき、$f(1)$の値を求めよ。
また、$t\geqq 1$のとき$f(t)$を$t$を用いて表せ。
$2025$年神戸大学理系過去問題
福田の数学〜神戸大学2025理系第3問〜媒介変数表示で表された曲線
単元：
#数Ⅱ#大学入試過去問(数学)#平面上の曲線#微分法と積分法#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#神戸大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
媒介変数$\theta$を用いて
$x=\sin\theta,y=\cos\theta + \vert \sin\theta \vert \quad (0\leqq \theta \leqq 2\pi)$
で表される曲線を$C$とする。以下の問いに答えよ。
(1)曲線$C$の概形をかけ。
(2)曲線$C$で囲まれた部分の面積を求めよ。
$2025$年神戸大学理系過去問題
この動画を見る
$\boxed{3}$
媒介変数$\theta$を用いて
$x=\sin\theta,y=\cos\theta + \vert \sin\theta \vert \quad (0\leqq \theta \leqq 2\pi)$
で表される曲線を$C$とする。以下の問いに答えよ。
(1)曲線$C$の概形をかけ。
(2)曲線$C$で囲まれた部分の面積を求めよ。
$2025$年神戸大学理系過去問題
福田の数学〜神戸大学2025理系第1問〜曲線と直線の共有点の個数
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
$k$を実数とする。
$f(x)$と$g(x)$を
$f(x) = \vert x^3-x \vert,\quad g(x)=k(x+1)$
とおき、曲線$y=f(x)$を$C$、
直線$y=g(x)$を$\ell$とする。以下の問いに答えよ。
(1)曲線$C$の概形をかけ。
ただし、関数$f(x)$の極大値を調べる必要はない。
(2)曲線$C$と直線$\ell$がちょうど$4$つの
共有点をもつような$k$の値を求めよ。
$2025$年神戸大学理系過去問題
この動画を見る
$\boxed{1}$
$k$を実数とする。
$f(x)$と$g(x)$を
$f(x) = \vert x^3-x \vert,\quad g(x)=k(x+1)$
とおき、曲線$y=f(x)$を$C$、
直線$y=g(x)$を$\ell$とする。以下の問いに答えよ。
(1)曲線$C$の概形をかけ。
ただし、関数$f(x)$の極大値を調べる必要はない。
(2)曲線$C$と直線$\ell$がちょうど$4$つの
共有点をもつような$k$の値を求めよ。
$2025$年神戸大学理系過去問題
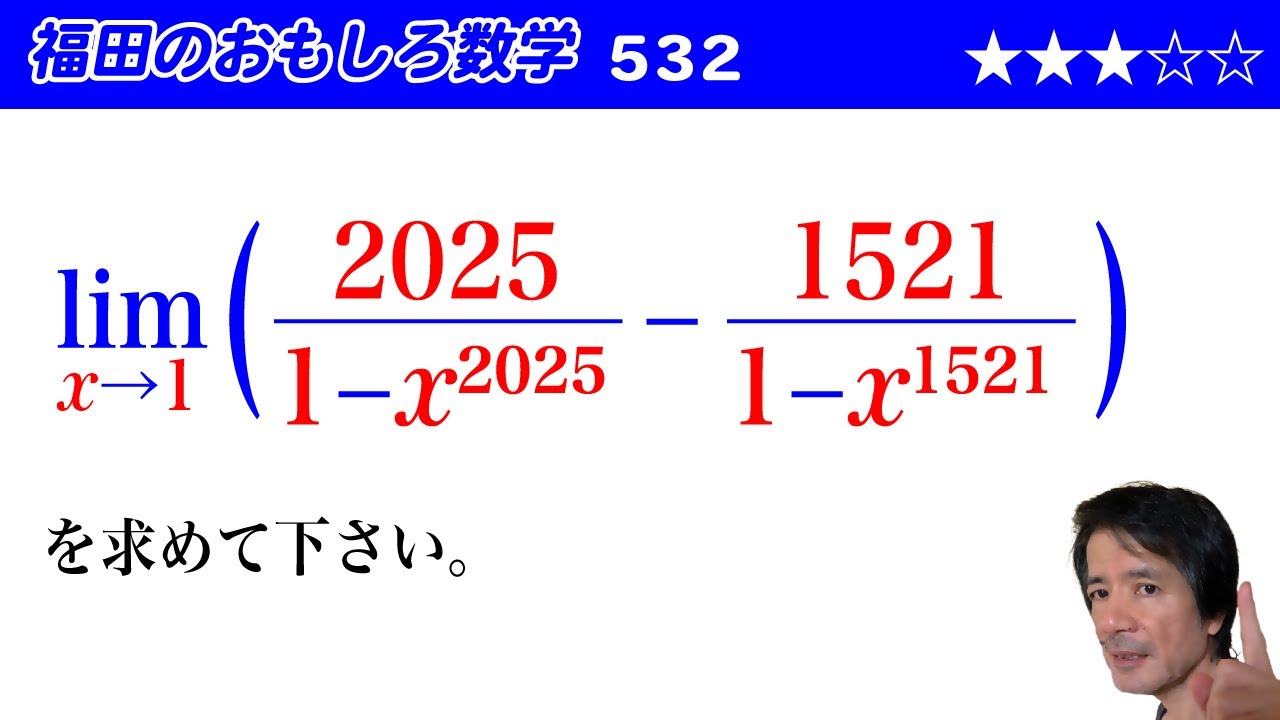
福田のおもしろ数学532〜「∞ー∞」型の極限
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\displaystyle \lim_{x\to 1} \left(\dfrac{2025}{1-x^{2025}}-\dfrac{1521}{1-x^{1521}}\right)$
を求めて下さい。
この動画を見る
$\displaystyle \lim_{x\to 1} \left(\dfrac{2025}{1-x^{2025}}-\dfrac{1521}{1-x^{1521}}\right)$
を求めて下さい。
福田の数学〜大阪大学2025文系第3問〜放物線と接線が作る面積の最大値
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
座標平面において、$y=x^2-1$で表される放物線を
$C$とする。
$C$上の点$P$における$C$の接線を$\ell$とする。
ただし、点$P$は$y$軸上にはないものとする。
$O$を原点とし、放物線$C$と線分$OP$をよび
$y$軸で囲まれた図形の面積を$S$、
放物線$C$と接線$\ell$および$y$軸で囲まれた図形の
面積を$T$とする。
$S-T$の最大値を求めよ。
$2025$年大阪大学文系過去問題
この動画を見る
$\boxed{3}$
座標平面において、$y=x^2-1$で表される放物線を
$C$とする。
$C$上の点$P$における$C$の接線を$\ell$とする。
ただし、点$P$は$y$軸上にはないものとする。
$O$を原点とし、放物線$C$と線分$OP$をよび
$y$軸で囲まれた図形の面積を$S$、
放物線$C$と接線$\ell$および$y$軸で囲まれた図形の
面積を$T$とする。
$S-T$の最大値を求めよ。
$2025$年大阪大学文系過去問題
福田の数学〜大阪大学2025理系第3問〜空間図形と最大最小の軌跡
単元：
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#微分法と積分法#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
座標空間に$3$点$O(0,0,0),A(0,1,1),B(x,y,0)$がある。
$\angle OAP=30°$かつ$y\geqq 0$を満たすように
点$P$が動くとき、
$(x+1)(y+1)$の最大値と最小値を求めよ。
$2025$年大阪大学理系過去問題
この動画を見る
$\boxed{3}$
座標空間に$3$点$O(0,0,0),A(0,1,1),B(x,y,0)$がある。
$\angle OAP=30°$かつ$y\geqq 0$を満たすように
点$P$が動くとき、
$(x+1)(y+1)$の最大値と最小値を求めよ。
$2025$年大阪大学理系過去問題
福田の数学〜大阪大学2025理系第2問〜3次関数の極値と変曲点の軌跡
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
$p$と$m$を実数とし、
関数$f(x)=x^3+3px^2+3mx$は
$x=\alpha$で極大値をとり、
$x=\beta$で極小値をとるとする。
(1)$f(\alpha)-f(\beta)$を$p$と$m$を用いて表せ。
(2)$p$と$m$が$f(\alpha)-f(\beta)=4$を
満たしながら動くとき、
曲線$y=f(x)$の変曲点の軌跡を求めよ。
$2025$年大阪大学理系過去問題
この動画を見る
$\boxed{2}$
$p$と$m$を実数とし、
関数$f(x)=x^3+3px^2+3mx$は
$x=\alpha$で極大値をとり、
$x=\beta$で極小値をとるとする。
(1)$f(\alpha)-f(\beta)$を$p$と$m$を用いて表せ。
(2)$p$と$m$が$f(\alpha)-f(\beta)=4$を
満たしながら動くとき、
曲線$y=f(x)$の変曲点の軌跡を求めよ。
$2025$年大阪大学理系過去問題
福田のおもしろ数学524〜無限級数の和
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\displaystyle \sum_{k=1}^{\infty} \dfrac{k^2}{3^k}$を求めて下さい。
この動画を見る
$\displaystyle \sum_{k=1}^{\infty} \dfrac{k^2}{3^k}$を求めて下さい。
福田のおもしろ数学518〜積分で表された関数の導関数
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#不定積分・定積分#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\displaystyle \int_{0}^{1} f(x-t)dt$
の導関数を求めよ。
この動画を見る
$\displaystyle \int_{0}^{1} f(x-t)dt$
の導関数を求めよ。
福田の数学〜立教大学2025経済学部第3問〜3次関数のグラフと直線の共有点の個数
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
$k$を実数とする。
$3$次関数$f(x)=x^3-x^2+1$に対して、
座標平面上の曲線$C$を$C:y=f(x)$とする。
また、$C$上の点$P(1,1)$を通り、
傾きが$k$である直線を$\ell$とする。
このとき、次の問いに答えよ。
(1)$\ell$の方程式を$k$を用いて表せ。
(2)$f(x)$の導関数$f'(x)$を求めよ。
(3)$f(x)$の極値を求めよ。
また、そのときの$x$の値を求めよ。
(4)$\ell$と$C$がちょうど$2$個の共有点を
もつような$k$の値を求めよ。
(5)$\ell$と$C$が異なる$3$個の共有点をもつような
$k$の値の範囲を求めよ。
(6)(5)のとき、異なる$3$個の共有点の$y$座標を
小さい方から順に$y_1,y_2,y_3$とする。
このとき、
比の等式$(y_2-y_1):(y_3-y_2)=1:2$を
満たすような$k$の値を求めよ。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{3}$
$k$を実数とする。
$3$次関数$f(x)=x^3-x^2+1$に対して、
座標平面上の曲線$C$を$C:y=f(x)$とする。
また、$C$上の点$P(1,1)$を通り、
傾きが$k$である直線を$\ell$とする。
このとき、次の問いに答えよ。
(1)$\ell$の方程式を$k$を用いて表せ。
(2)$f(x)$の導関数$f'(x)$を求めよ。
(3)$f(x)$の極値を求めよ。
また、そのときの$x$の値を求めよ。
(4)$\ell$と$C$がちょうど$2$個の共有点を
もつような$k$の値を求めよ。
(5)$\ell$と$C$が異なる$3$個の共有点をもつような
$k$の値の範囲を求めよ。
(6)(5)のとき、異なる$3$個の共有点の$y$座標を
小さい方から順に$y_1,y_2,y_3$とする。
このとき、
比の等式$(y_2-y_1):(y_3-y_2)=1:2$を
満たすような$k$の値を求めよ。
$2025$年立教大学経済学部過去問題
福田の数学〜立教大学2025経済学部第1問(5)〜絶対値の付いた関数の定積分の計算
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#立教大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(5)定積分$\displaystyle \int_{0}^{2} (x+1)\vert x-1 \vert dx$
の値は$\boxed{キ}$である。
$2025$年立教大学経済学部過去問題
この動画を見る
$\boxed{1}$
(5)定積分$\displaystyle \int_{0}^{2} (x+1)\vert x-1 \vert dx$
の値は$\boxed{キ}$である。
$2025$年立教大学経済学部過去問題
福田の数学〜慶應義塾大学2025経済学部第6問〜放物線と直線で囲まれた図形の面積
単元：
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{6}$
$C$を$y=3x^2$で定まる曲線とし、
$C$上に異なる$2$点$A(a,3a^2)$
$B(b,3b^2)$をとる。ただし、$a\lt b$とする。
(1)$C$と直線$AB$で囲まれた図形の面積$S$を、
$a$と$b$を用いて表せ。
ただし、積分を用いて計算し、
積分の計算過程も書くこと。
(2)$2$点$A,B$間の距離が$3$のとき、
(1)で求めた面積$S$の取りうる値の最大値$T$を
求めよ。
(3)$2$点$A,B$間の距離が$3$のとき、
直線$AB$は点$(0,7)$を通らないことを示せ。
$2025$年慶應義塾大学経済学部過去問題
この動画を見る
$\boxed{6}$
$C$を$y=3x^2$で定まる曲線とし、
$C$上に異なる$2$点$A(a,3a^2)$
$B(b,3b^2)$をとる。ただし、$a\lt b$とする。
(1)$C$と直線$AB$で囲まれた図形の面積$S$を、
$a$と$b$を用いて表せ。
ただし、積分を用いて計算し、
積分の計算過程も書くこと。
(2)$2$点$A,B$間の距離が$3$のとき、
(1)で求めた面積$S$の取りうる値の最大値$T$を
求めよ。
(3)$2$点$A,B$間の距離が$3$のとき、
直線$AB$は点$(0,7)$を通らないことを示せ。
$2025$年慶應義塾大学経済学部過去問題
福田の数学〜慶應義塾大学2025経済学部第4問〜指数不等式と対数
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#微分法と積分法#指数関数#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{4}$
$p$を正の実数、$m$を自然数とし、
曲線$y=-x^2$上の点$(-p,-p^2)$における
接線と直線$y=2m$の交点を$P_m$とする。
$P_m$の$x$座標が$1$以下となる$m$の最大値を
$N$とする。
(1)$P_m$の$x$座標を、$p$と$m$を用いて表せ。
(2)$N=40$が成り立つ$p$の範囲を求めよ。
以下、$n$を自然数とし、
$a=3n\log_3 6-\log_2+n$とする。
(3)$3^a$は$2$以上の自然数である。
$3^a$の素因数分解を、$n$を用いて書け。
(4)$p=3^a$のとき、$N\lt 2^{1000}$となる
自然数$n$の最大値を求めよ。
なお、必要があれば$1.58 \lt \log_2 3 \lt 1.50$を用いよ。
$2025$年慶應義塾大学経済学部過去問題
この動画を見る
$\boxed{4}$
$p$を正の実数、$m$を自然数とし、
曲線$y=-x^2$上の点$(-p,-p^2)$における
接線と直線$y=2m$の交点を$P_m$とする。
$P_m$の$x$座標が$1$以下となる$m$の最大値を
$N$とする。
(1)$P_m$の$x$座標を、$p$と$m$を用いて表せ。
(2)$N=40$が成り立つ$p$の範囲を求めよ。
以下、$n$を自然数とし、
$a=3n\log_3 6-\log_2+n$とする。
(3)$3^a$は$2$以上の自然数である。
$3^a$の素因数分解を、$n$を用いて書け。
(4)$p=3^a$のとき、$N\lt 2^{1000}$となる
自然数$n$の最大値を求めよ。
なお、必要があれば$1.58 \lt \log_2 3 \lt 1.50$を用いよ。
$2025$年慶應義塾大学経済学部過去問題
福田のおもしろ数学506〜相加平均と相乗平均の商の極限
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
自然数$n+1,n+2,\cdots,n+n$の
相加平均を$A_n$、相乗平均を$B_n$とするとき
$\displaystyle \lim_{n\to\infty}\dfrac{A_n}{B_n}$
を求めて下さい。
この動画を見る
自然数$n+1,n+2,\cdots,n+n$の
相加平均を$A_n$、相乗平均を$B_n$とするとき
$\displaystyle \lim_{n\to\infty}\dfrac{A_n}{B_n}$
を求めて下さい。