接線と増減表・最大値・最小値
接線と増減表・最大値・最小値
【短時間でポイントチェック!!】3次方程式の解の個数〔現役講師解説、数学〕
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
3rd School
問題文全文(内容文)：
$2x^3-3x^2-12x+1=0$の異なる実数解の個数は？
この動画を見る
$2x^3-3x^2-12x+1=0$の異なる実数解の個数は？
【短時間でポイントチェック!!】3次関数の最大・最小〔現役講師解説、数学〕
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
3rd School
問題文全文(内容文)：
【短時間でポイントチェック!!】
3次関数の最大・最小を解説します！
この動画を見る
【短時間でポイントチェック!!】
3次関数の最大・最小を解説します！
【短時間でポイントチェック!!】3次関数の増減〔現役講師解説、数学〕
微分の基本問題（落とし穴注意）
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$
f(x)=x^4-8x^3+18kx^2
$
が極大値をもたないkの範囲
この動画を見る
$
f(x)=x^4-8x^3+18kx^2
$
が極大値をもたないkの範囲
【演習！】微分で解く文字が含まれる関数について解説しました！【数学III】
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
3rd School
問題文全文(内容文)：
問 次の関数が$x=1$で極大値$4$をとるとき$a,b$の値と極小値を求めよ
$y=x^3-6x^2+ax+b$
この動画を見る
問 次の関数が$x=1$で極大値$4$をとるとき$a,b$の値と極小値を求めよ
$y=x^3-6x^2+ax+b$
数学どうにかしたい人へ
単元：
#数Ⅰ#数A#数Ⅱ#数と式#２次関数#場合の数と確率#図形の性質#式と証明#複素数と方程式#平面上のベクトル#空間ベクトル#平面上の曲線#複素数平面#図形と計量#データの分析#式の計算（整式・展開・因数分解）#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#一次不等式（不等式・絶対値のある方程式・不等式）#集合と命題（集合・命題と条件・背理法）#2次方程式と2次不等式#2次関数とグラフ#三角比（三角比・拡張・相互関係・単位円）#三角比への応用（正弦・余弦・面積）#データの分析#整数の性質#場合の数#確率#三角形の辺の比（内分・外分・二等分線）#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と２つの円の関係#約数・倍数・整数の割り算と余り・合同式#ユークリッド互除法と不定方程式・Ｎ進法#図形と方程式#三角関数#指数関数と対数関数#微分法と積分法#整式の除法・分数式・二項定理#恒等式・等式・不等式の証明#複素数#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#円と方程式#軌跡と領域#三角関数とグラフ#加法定理とその応用#指数関数#対数関数#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数列#確率分布と統計的な推測#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#数列とその和（等差・等比・階差・Σ）#漸化式#数学的帰納法#確率分布#統計的な推測#関数と極限#微分とその応用#積分とその応用#2次曲線#複素数平面#図形への応用#関数（分数関数・無理関数・逆関数と合成関数）#数列の極限#関数の極限#微分法#色々な関数の導関数#接線と法線・平均値の定理#関数の変化（グラフ・最大最小・方程式・不等式）#不定積分#定積分#面積・体積・長さ・速度#空間における垂直と平行と多面体（オイラーの法則）#不定積分・定積分#面積、体積#媒介変数表示と極座標#速度と近似式#数学(高校生)#数B#数C#数Ⅲ
指導講師：
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文)：
数学が共通テストのみの人の勉強法紹介動画です
この動画を見る
数学が共通テストのみの人の勉強法紹介動画です
【数Ⅱ】微分法と積分法：接線と増減表・最大値・最小値：4次関数の極値とグラフ PRIMEⅡ 485(3)
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
教材：
#PRIME数学#PRIME数学Ⅱ・B#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の関数の極値を求めよ。また，そのグラフをかけ。
$y＝\frac{1}{4}x^4－x^3$
4次関数の極値とグラフの書き方をはじめからていねいに！解説の解説！
この動画を見る
次の関数の極値を求めよ。また，そのグラフをかけ。
$y＝\frac{1}{4}x^4－x^3$
4次関数の極値とグラフの書き方をはじめからていねいに！解説の解説！
福井大 微分積分いい気分
単元：
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#面積、体積#数学(高校生)#福井大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
2016福井大学過去問題
$f(x)=x^3,g(x)=x^3-4$
①f(x),g(x)の両方と接する直線l
②g(x)とlとで囲まれる面積
この動画を見る
2016福井大学過去問題
$f(x)=x^3,g(x)=x^3-4$
①f(x),g(x)の両方と接する直線l
②g(x)とlとで囲まれる面積
【微分て何？】微分を始める前に用語のイメージをつけましょう！【数学III】
単元：
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#接線と増減表・最大値・最小値#数学(高校生)
指導講師：
3rd School
問題文全文(内容文)：
数学Ⅲ
微分について解説します。
微分の導入
この動画を見る
数学Ⅲ
微分について解説します。
微分の導入
福田の数学〜筑波大学2023年理系第1問〜３次関数の接線と三角形の面積
単元：
#大学入試過去問(数学)#図形と方程式#微分法と積分法#点と直線#平均変化率・極限・導関数#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#筑波大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ 曲線C：$y$=$x$-$x^3$上の点A(1, 0)における接線を$l$とし、Cと$l$の共有点のうちAとは異なる点をBとする。また、-2＜$t$＜1とし、C上の点P($t$, $t$-$t^3$)をとる。さらに、三角形ABPの面積を$S(t)$とする。
(1)点Bの座標を求めよ。
(2)$S(t)$を求めよ。
(3)$t$が-2＜$t$＜1の範囲を動くとき、$S(t)$の最大値を求めよ。
2023筑波大学理系過去問
この動画を見る
$\Large\boxed{1}$ 曲線C：$y$=$x$-$x^3$上の点A(1, 0)における接線を$l$とし、Cと$l$の共有点のうちAとは異なる点をBとする。また、-2＜$t$＜1とし、C上の点P($t$, $t$-$t^3$)をとる。さらに、三角形ABPの面積を$S(t)$とする。
(1)点Bの座標を求めよ。
(2)$S(t)$を求めよ。
(3)$t$が-2＜$t$＜1の範囲を動くとき、$S(t)$の最大値を求めよ。
2023筑波大学理系過去問
同志社大 三次方程式の基本問題
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#同志社大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
同志社大学過去問題
3次方程式
$2x^3+3x^2-12x-6m=0$
は相異なる3つの実数解
$\alpha,\beta,γ(\alpha\lt\beta\lt γ)$をもつ
①$m$の範囲
②$γ$の範囲
この動画を見る
同志社大学過去問題
3次方程式
$2x^3+3x^2-12x-6m=0$
は相異なる3つの実数解
$\alpha,\beta,γ(\alpha\lt\beta\lt γ)$をもつ
①$m$の範囲
②$γ$の範囲
福田の数学〜九州大学2023年文系第2問〜2直線のなす角と外接円の半径
単元：
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ xy平面上の曲線C：$y$=$x^3$-$x$ を考える。変数$t$＞0に対して、曲線C上の点A($t$, $t^3$-$t$)における接線を$l$とする。直線$l$と直線$y$=-$x$の交点をB、三角形OABの外接円の中心をPとする。以下の問いに答えよ。
(1)点Bの座標を$t$を用いて表せ。
(2)θ=$\angle$OBAとする。$\sin^2\theta$を$t$を用いて表せ。
(3)$f(t)$=$\frac{OP}{OA}$とする。$t$＞0のとき、$f(t)$を最小にする$t$の値と$f(t)$の最小値を求めよ。
2023九州大学文系過去問
この動画を見る
$\Large\boxed{2}$ xy平面上の曲線C：$y$=$x^3$-$x$ を考える。変数$t$＞0に対して、曲線C上の点A($t$, $t^3$-$t$)における接線を$l$とする。直線$l$と直線$y$=-$x$の交点をB、三角形OABの外接円の中心をPとする。以下の問いに答えよ。
(1)点Bの座標を$t$を用いて表せ。
(2)θ=$\angle$OBAとする。$\sin^2\theta$を$t$を用いて表せ。
(3)$f(t)$=$\frac{OP}{OA}$とする。$t$＞0のとき、$f(t)$を最小にする$t$の値と$f(t)$の最小値を求めよ。
2023九州大学文系過去問
青山学院大 微分の基礎
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#青山学院大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
青山学院大学過去問題
$C:y=x^2$
A(-1,1),B(4,16)
放物線C上にx座標が
$t(-1<t<4)$である点P
直線AB上にx座標がtである点Qととる。
△APQの面積の最大値とそのときのtの値
この動画を見る
青山学院大学過去問題
$C:y=x^2$
A(-1,1),B(4,16)
放物線C上にx座標が
$t(-1<t<4)$である点P
直線AB上にx座標がtである点Qととる。
△APQの面積の最大値とそのときのtの値
福田の数学〜一橋大学2023年文系第２問〜共通接線が存在する条件
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ aを正の実数とする。2つの曲線$C_1$：y=$x^3$+2$ax^2$ および$C_2$：y=3$ax^2$$-\displaystyle\frac{3}{a}$ の両方に接する直線が存在するようなaの範囲を求めよ。
2023一橋大学文系過去問
この動画を見る
$\Large\boxed{2}$ aを正の実数とする。2つの曲線$C_1$：y=$x^3$+2$ax^2$ および$C_2$：y=3$ax^2$$-\displaystyle\frac{3}{a}$ の両方に接する直線が存在するようなaの範囲を求めよ。
2023一橋大学文系過去問
福田の数学〜慶應義塾大学2023年医学部第３問〜接線が作る三角形
単元：
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#三角形の辺の比（内分・外分・二等分線）#図形と方程式#微分法と積分法#軌跡と領域#接線と増減表・最大値・最小値#関数と極限#微分とその応用#積分とその応用#数列の極限#微分法#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{3}$ 座標平面上の曲線y=$\frac{1}{x^2}$ (x $\ne$ 0)をCとする。$a_1$を正の実数とし、点$A_1$$\left(a_1, \frac{1}{a_1^2}\right)$におけるCの接線を$l_1$とする。$l_1$とCの交点で$A_1$と異なるものを$A_2$$\left(a_2, \frac{1}{a_2^2}\right)$とする。次に点$A_2$におけるCの接線を$l_2$とCの交点で$A_2$と異なるものを$A_3$$\left(a_3, \frac{1}{a_3^2}\right)$とする。以下、同様にしてn=3,4,5,...に対して、$A_n$$\left(a_n, \frac{1}{a_n^2}\right)$におけるCの接線を$l_n$とし、$l_n$とCの交点で$A_n$と異なるものを$A_{n+1}$$\left(a_{n+1}, \frac{1}{a_{n+1}^2}\right)$とする。
(1)$\frac{a_2}{a_1}$=$\boxed{\ \ あ\ \ }$であり、$\frac{a_3}{a_1}$=$\boxed{\ \ い\ \ }$である。
(2)$a_n$を$a_1$で表すと$a_n$=$\boxed{\ \ う\ \ }$である。無限級数$\displaystyle\sum_{n=1}^{\infty}a_n$の和をTを$a_1$を用いて表すとT=$\boxed{\ \ え\ \ }$である。
(3)$a_1$を正の実数すべてにわたって動かすとき、三角形$A_1A_2A_3$の重心が描く軌跡の方程式をy=f(x)の形で求めるとf(x)=$\boxed{\ \ お\ \ }$となる。
(4)三角形$A_1A_2A_3$が鋭角三角形になるための条件は$\boxed{\ \ か\ \ }$＜$a_1$＜$\boxed{\ \ き\ \ }$である。
(5)x軸上に2点$A'_1$($a_1$, 0), $A'_2$($a_2$, 0)をとり、台形$A_1A_2A'_2A'_1$の面積を$S_1$とする。また、点$A_1$から点$A_3$にいたる曲線Cの部分、および線分$A_3A_2$と$A_2A_1$で囲まれた図形の面積を$S_2$とする。このとき、$S_1$：$S_2$=$\boxed{\ \ く\ \ }$：$\boxed{\ \ け\ \ }$である。ただし、$\boxed{\ \ く\ \ }$と$\boxed{\ \ け\ \ }$は互いに素な自然数である。
2023慶應義塾大学医学部過去問
この動画を見る
$\Large\boxed{3}$ 座標平面上の曲線y=$\frac{1}{x^2}$ (x $\ne$ 0)をCとする。$a_1$を正の実数とし、点$A_1$$\left(a_1, \frac{1}{a_1^2}\right)$におけるCの接線を$l_1$とする。$l_1$とCの交点で$A_1$と異なるものを$A_2$$\left(a_2, \frac{1}{a_2^2}\right)$とする。次に点$A_2$におけるCの接線を$l_2$とCの交点で$A_2$と異なるものを$A_3$$\left(a_3, \frac{1}{a_3^2}\right)$とする。以下、同様にしてn=3,4,5,...に対して、$A_n$$\left(a_n, \frac{1}{a_n^2}\right)$におけるCの接線を$l_n$とし、$l_n$とCの交点で$A_n$と異なるものを$A_{n+1}$$\left(a_{n+1}, \frac{1}{a_{n+1}^2}\right)$とする。
(1)$\frac{a_2}{a_1}$=$\boxed{\ \ あ\ \ }$であり、$\frac{a_3}{a_1}$=$\boxed{\ \ い\ \ }$である。
(2)$a_n$を$a_1$で表すと$a_n$=$\boxed{\ \ う\ \ }$である。無限級数$\displaystyle\sum_{n=1}^{\infty}a_n$の和をTを$a_1$を用いて表すとT=$\boxed{\ \ え\ \ }$である。
(3)$a_1$を正の実数すべてにわたって動かすとき、三角形$A_1A_2A_3$の重心が描く軌跡の方程式をy=f(x)の形で求めるとf(x)=$\boxed{\ \ お\ \ }$となる。
(4)三角形$A_1A_2A_3$が鋭角三角形になるための条件は$\boxed{\ \ か\ \ }$＜$a_1$＜$\boxed{\ \ き\ \ }$である。
(5)x軸上に2点$A'_1$($a_1$, 0), $A'_2$($a_2$, 0)をとり、台形$A_1A_2A'_2A'_1$の面積を$S_1$とする。また、点$A_1$から点$A_3$にいたる曲線Cの部分、および線分$A_3A_2$と$A_2A_1$で囲まれた図形の面積を$S_2$とする。このとき、$S_1$：$S_2$=$\boxed{\ \ く\ \ }$：$\boxed{\ \ け\ \ }$である。ただし、$\boxed{\ \ く\ \ }$と$\boxed{\ \ け\ \ }$は互いに素な自然数である。
2023慶應義塾大学医学部過去問
大学入試問題#509「あえて三角関数」 自治医科大学(2023) #曲線
単元：
#数Ⅱ#大学入試過去問(数学)#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#自治医科大学
指導講師：
ますただ
問題文全文(内容文)：
$x,\ 0 \leqq y$：実数
$\displaystyle \frac{x^2}{4}+\displaystyle \frac{y^2}{9}=1$を満たすとき
$5x+2y$の最大値を$M$、最小値を$m$とするとき$\sqrt{ M^2-m^2 }$を求めよ
出典：2023年自治医科大学 入試問題
この動画を見る
$x,\ 0 \leqq y$：実数
$\displaystyle \frac{x^2}{4}+\displaystyle \frac{y^2}{9}=1$を満たすとき
$5x+2y$の最大値を$M$、最小値を$m$とするとき$\sqrt{ M^2-m^2 }$を求めよ
出典：2023年自治医科大学 入試問題
福田の数学〜北海道大学2023年文系第４問〜円と放物線の共通接線と囲まれる面積
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#北海道大学
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{4}$ qを実数とする。座標平面上に円C：$x^2$+$y^2$=1と放物線P：y=$x^2$+q がある。
(1)CとPに同じ点で接する傾き正の直線が存在するとき、qの値およびその接点の座標を求めよ。
(2)(1)で求めたqの値を$q_1$、接点のy座標を$y_1$とするとき、連立不等式
$\left\{\begin{array}{1}
x^2+y^2≧1\\
y≧x^2+q_1\\
y≦y_1\\
\end{array}\right.$
の表す領域の面積を求めよ。
2023北海道大学文系過去問
この動画を見る
$\Large\boxed{4}$ qを実数とする。座標平面上に円C：$x^2$+$y^2$=1と放物線P：y=$x^2$+q がある。
(1)CとPに同じ点で接する傾き正の直線が存在するとき、qの値およびその接点の座標を求めよ。
(2)(1)で求めたqの値を$q_1$、接点のy座標を$y_1$とするとき、連立不等式
$\left\{\begin{array}{1}
x^2+y^2≧1\\
y≧x^2+q_1\\
y≦y_1\\
\end{array}\right.$
の表す領域の面積を求めよ。
2023北海道大学文系過去問
福田の数学〜東京大学2023年文系第２問〜定積分で表された関数と最大最小
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#点と直線#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#不定積分・定積分#東京大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ 座標平面上の放物線y=3$x^2$-4xをCとおき、直線y=2xをlとおく。実数tに対し、C上の点P(t, $3t^2-4t$)とlの距離をf(t)とする。
(1)-1≦a≦2の範囲の実数aに対し、定積分
g(a)=$\displaystyle\int_{-1}^af(t)dt$
を求めよ。
(2)aが0≦a≦2の範囲を動くとき、g(a)-f(a)の最大値および最小値を求めよ。
2023東京大学文系過去問
この動画を見る
$\Large\boxed{2}$ 座標平面上の放物線y=3$x^2$-4xをCとおき、直線y=2xをlとおく。実数tに対し、C上の点P(t, $3t^2-4t$)とlの距離をf(t)とする。
(1)-1≦a≦2の範囲の実数aに対し、定積分
g(a)=$\displaystyle\int_{-1}^af(t)dt$
を求めよ。
(2)aが0≦a≦2の範囲を動くとき、g(a)-f(a)の最大値および最小値を求めよ。
2023東京大学文系過去問
福田の数学〜東京大学2023年理系第３問〜円と放物線と切り取られる弦の長さ
単元：
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#円と方程式#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{3}$ aを実数とし、座標平面上の点(0,a)を中心とする半径1の円の周をCとする。
(1)Cが不等式$y＞x^2$の表す領域に含まれるようなaの範囲を求めよ。
(2)aは(1)で求めた範囲にあるとする。Cのうちx≧0かつy＜aを満たす部分をSとする。S上の点Pに対し、点PでのCの接線が放物線$y=x^2$によって切り取られてできる線分の長さを$L_P$とする。$L_Q$=$L_R$となるS上の相異なる2点Q, Rが存在するようなaの範囲を求めよ。
2023東京大学理系過去問
この動画を見る
$\Large\boxed{3}$ aを実数とし、座標平面上の点(0,a)を中心とする半径1の円の周をCとする。
(1)Cが不等式$y＞x^2$の表す領域に含まれるようなaの範囲を求めよ。
(2)aは(1)で求めた範囲にあるとする。Cのうちx≧0かつy＜aを満たす部分をSとする。S上の点Pに対し、点PでのCの接線が放物線$y=x^2$によって切り取られてできる線分の長さを$L_P$とする。$L_Q$=$L_R$となるS上の相異なる2点Q, Rが存在するようなaの範囲を求めよ。
2023東京大学理系過去問
福田の数学〜東京大学2023年文系数学第１問〜解と係数の関係と最小値
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#解と判別式・解と係数の関係#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ kを正の実数とし、2次方程式$x^2+x-k$=0 の2つの実数解をα,βとする。
kがk＞2の範囲を動くとき、
$\displaystyle\frac{\alpha^3}{1-\beta}$+$\displaystyle\frac{\beta^3}{1-\alpha}$
の最小値を求めよ。
2023東京大学文系過去問
この動画を見る
$\Large\boxed{1}$ kを正の実数とし、2次方程式$x^2+x-k$=0 の2つの実数解をα,βとする。
kがk＞2の範囲を動くとき、
$\displaystyle\frac{\alpha^3}{1-\beta}$+$\displaystyle\frac{\beta^3}{1-\alpha}$
の最小値を求めよ。
2023東京大学文系過去問
明治大 三次不等式
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$ x^3-2ax^2-x<0$
これを解け.
明治大過去問
この動画を見る
$ x^3-2ax^2-x<0$
これを解け.
明治大過去問
福田の1.5倍速演習〜合格する重要問題056〜神戸大学2017年度文系第１問〜３次関数の最大最小
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#接線と増減表・最大値・最小値#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\Large{\boxed{1}}$ tを正の実数とする。$f(x)=x^3+3x^2-3(t^2-1)x+2t^3-3t^2+1$とおく。
以下の問いに答えよ。
(1)2t^3-3t^2+1 を因数分解せよ。
(2)$f(x)$が極小値0をもつことを示せ。
(3)$-1 \leqq x \leqq 2$における$f(x)$の最小値$m$と最大値$M$をtの式で表せ。
2017神戸大学文系過去問
この動画を見る
$\Large{\boxed{1}}$ tを正の実数とする。$f(x)=x^3+3x^2-3(t^2-1)x+2t^3-3t^2+1$とおく。
以下の問いに答えよ。
(1)2t^3-3t^2+1 を因数分解せよ。
(2)$f(x)$が極小値0をもつことを示せ。
(3)$-1 \leqq x \leqq 2$における$f(x)$の最小値$m$と最大値$M$をtの式で表せ。
2017神戸大学文系過去問
福田の1.5倍速演習〜合格する重要問題049〜早稲田大学2019年度商学部第２問〜折れ線の長さの最小値問題
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#２次関数#2次関数とグラフ#図形と方程式#微分法と積分法#点と直線#円と方程式#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
座標平面上において、放物線$y=x^2$上の点をP、円$(x-3)^2+(y-1)^2=1$上の
点をQ、直線$y=x-4$上の点をRとする。次の設問に答えよ。
(1)QR の最小値を求めよ。
(2)PR+QR の最小値を求めよ。
2019早稲田大学商学部過去問
この動画を見る
座標平面上において、放物線$y=x^2$上の点をP、円$(x-3)^2+(y-1)^2=1$上の
点をQ、直線$y=x-4$上の点をRとする。次の設問に答えよ。
(1)QR の最小値を求めよ。
(2)PR+QR の最小値を求めよ。
2019早稲田大学商学部過去問
工夫が大事！3次関数の決定【一橋大学】【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
以下の4つの条件を満たす3次関数$f(x)$を求めよ。
( i )$f(0)=0,f(2)=1$
( ii )$0.2<f(1)<0.3$
( iii )$f(x)は極限値0をもつ$
(iv)$f(x)=0の解はすべて整数$
この動画を見る
以下の4つの条件を満たす3次関数$f(x)$を求めよ。
( i )$f(0)=0,f(2)=1$
( ii )$0.2<f(1)<0.3$
( iii )$f(x)は極限値0をもつ$
(iv)$f(x)=0の解はすべて整数$
福田の1.5倍速演習〜合格する重要問題021〜一橋大学2016年度文系数学第４問〜絶対値の付いた3次関数の最大
単元：
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#接線と増減表・最大値・最小値#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
aを実数とし、$f(x)=x^3-3ax$とする。区間$-1 \leqq x \leqq 1$における
$|f(x)|$の最大値をMとする。Mの最小値とそのときのaの値を求めよ。
2016一橋大学文系過去問
この動画を見る
aを実数とし、$f(x)=x^3-3ax$とする。区間$-1 \leqq x \leqq 1$における
$|f(x)|$の最大値をMとする。Mの最小値とそのときのaの値を求めよ。
2016一橋大学文系過去問
【数検2級】数学検定2級2次：問題7
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#接線と増減表・最大値・最小値#数学検定#数学検定2級#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$y=x^3-2x$ で表されるxy平面上の曲線をＣとします。このとき、次の問いに答えなさい。
(1) Ｃ上の点($t,t^3-2t$)における接線の方程式をtを用いて表しなさい。
(2) 点(0,-2)からＣへ引いた接線の方程式を求めなさい。
この動画を見る
$y=x^3-2x$ で表されるxy平面上の曲線をＣとします。このとき、次の問いに答えなさい。
(1) Ｃ上の点($t,t^3-2t$)における接線の方程式をtを用いて表しなさい。
(2) 点(0,-2)からＣへ引いた接線の方程式を求めなさい。
福田の数学〜東京理科大学2022年理工学部第３問〜接線と法線と囲まれる面積
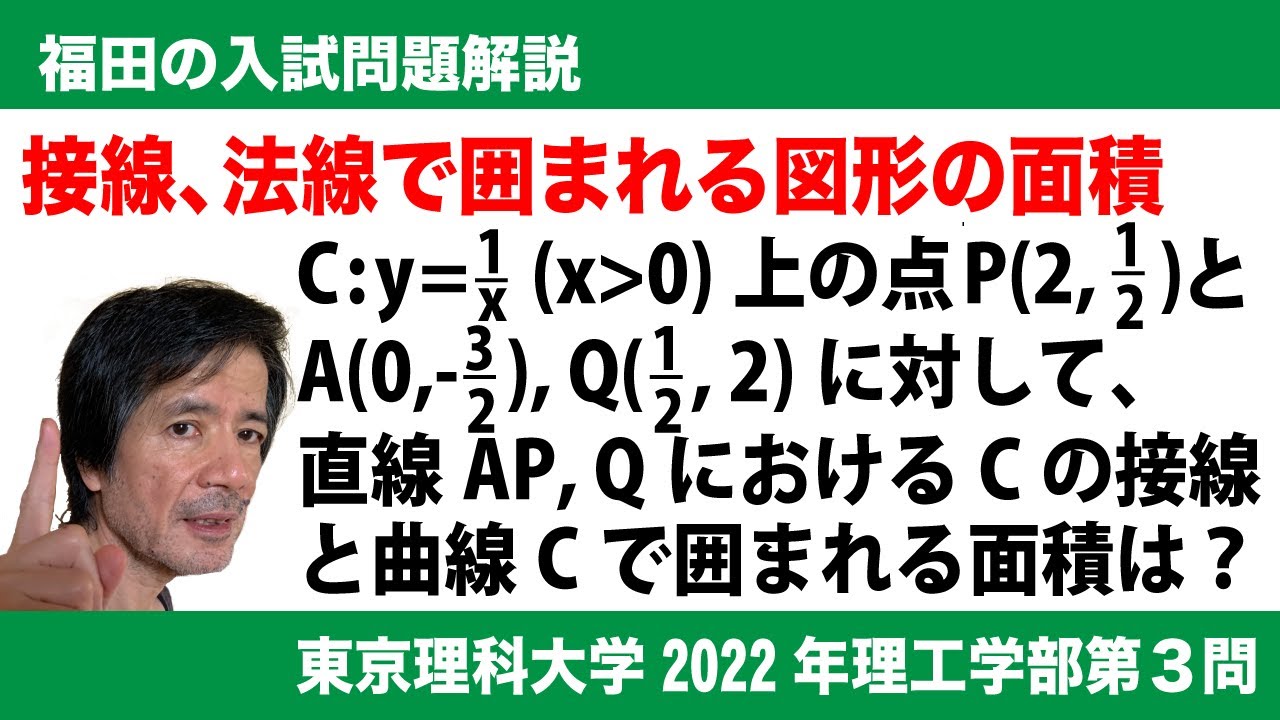
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
関数f(x)を次で定める。
$f(x)=\frac{1}{x}\ \ (x \gt 0)$
座標平面上の曲線y=f(x)をCとする。C上の点$P(2,\ \frac{1}{2})$と、正の定数tに対して
y軸上の点$A(0,\ -t)$をとる。点Aと点Pを通る直線を$l_1$とする。
(1)直線$l_1$を表す方程式を、tを用いて表せ。
(2)C上の点PにおけるCの法線とy軸の交点を$(0,\ -t_0)$とおく。$t_o$を求めよ。
上の(2)で求めたt_0に対してt \lt t_0とする。点Pを通り、直線$l_1$に垂直な直線を
$l_2$とする。$l_2$とCの交点のうち、点Pと異なる点をQとおく。
(3)点Qの座標を、tを用いて表せ。
最後に$t=\frac{3}{2}$の時を考える。
(4)点Qを通るCの接線を$l_3$とする。このとき、2つの直線$l_1,l_3$および曲線Cで
囲まれた部分の面積を求めよ。
2022東京理科大学理工学部過去問
この動画を見る
関数f(x)を次で定める。
$f(x)=\frac{1}{x}\ \ (x \gt 0)$
座標平面上の曲線y=f(x)をCとする。C上の点$P(2,\ \frac{1}{2})$と、正の定数tに対して
y軸上の点$A(0,\ -t)$をとる。点Aと点Pを通る直線を$l_1$とする。
(1)直線$l_1$を表す方程式を、tを用いて表せ。
(2)C上の点PにおけるCの法線とy軸の交点を$(0,\ -t_0)$とおく。$t_o$を求めよ。
上の(2)で求めたt_0に対してt \lt t_0とする。点Pを通り、直線$l_1$に垂直な直線を
$l_2$とする。$l_2$とCの交点のうち、点Pと異なる点をQとおく。
(3)点Qの座標を、tを用いて表せ。
最後に$t=\frac{3}{2}$の時を考える。
(4)点Qを通るCの接線を$l_3$とする。このとき、2つの直線$l_1,l_3$および曲線Cで
囲まれた部分の面積を求めよ。
2022東京理科大学理工学部過去問
福田の数学〜東京理科大学2022年理工学部第１問(1)〜解と係数の関係と３次関数の最大最小
単元：
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#指数関数と対数関数#解と判別式・解と係数の関係#指数関数#接線と増減表・最大値・最小値#微分とその応用#関数の変化（グラフ・最大最小・方程式・不等式）#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
(1)mを実数とする。xについての2次方程式$x^2-(m+3)x+m^2-9=0$の
二つの解を$α,β$とする。$α,β$が実数であるための必要十分条件は$- \boxed{ア} \leqq m \leqq \boxed{イ}$である。
mが$- \boxed{ア} \leqq m \leqq \boxed{イ}$の範囲を動くときの
$α^3+β^3$の最小値は$\boxed{ウ}$、最大値は$\boxed{エオカ}$である。
この動画を見る
(1)mを実数とする。xについての2次方程式$x^2-(m+3)x+m^2-9=0$の
二つの解を$α,β$とする。$α,β$が実数であるための必要十分条件は$- \boxed{ア} \leqq m \leqq \boxed{イ}$である。
mが$- \boxed{ア} \leqq m \leqq \boxed{イ}$の範囲を動くときの
$α^3+β^3$の最小値は$\boxed{ウ}$、最大値は$\boxed{エオカ}$である。
福田の数学〜杏林大学2022年医学部第１問〜三角関数の最大最小と極値
単元：
#数Ⅱ#大学入試過去問(数学)#三角関数#微分法と積分法#加法定理とその応用#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学
指導講師：
福田次郎
問題文全文(内容文)：
(1)三角関数について、次の等式が成り立つ。
$\cos2θ=\boxed{アイ}\sin^2θ+\boxed{ウ}$
$\sin3θ=\boxed{エオ}\sin^3θ+\boxed{カ}\sinθ$
(2)$0 \leqq θ \lt 2\pi$のとき、関数
$y=-\frac{1}{12}\sin3θ+\frac{3}{8}\cos2θ-\frac{3}{4}\sinθ$
は$θ=\frac{\boxed{キ}}{\boxed{ク}}\pi$で最小値$\frac{\boxed{ケコサ}}{\boxed{シス}}$をとり、
$\sinθ=\frac{\boxed{セソ}}{\boxed{タ}}$のとき最大値$\frac{\boxed{チツ}}{\boxed{テト}}$
をとる。また、yの極致を与えるθの個数は$\boxed{ナ}$である。
2022杏林大学医学部過去問
この動画を見る
(1)三角関数について、次の等式が成り立つ。
$\cos2θ=\boxed{アイ}\sin^2θ+\boxed{ウ}$
$\sin3θ=\boxed{エオ}\sin^3θ+\boxed{カ}\sinθ$
(2)$0 \leqq θ \lt 2\pi$のとき、関数
$y=-\frac{1}{12}\sin3θ+\frac{3}{8}\cos2θ-\frac{3}{4}\sinθ$
は$θ=\frac{\boxed{キ}}{\boxed{ク}}\pi$で最小値$\frac{\boxed{ケコサ}}{\boxed{シス}}$をとり、
$\sinθ=\frac{\boxed{セソ}}{\boxed{タ}}$のとき最大値$\frac{\boxed{チツ}}{\boxed{テト}}$
をとる。また、yの極致を与えるθの個数は$\boxed{ナ}$である。
2022杏林大学医学部過去問
数Ⅱ微分の良問です【大阪大学】【数学 入試問題】
単元：
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
$点(0,1)を通り曲線$y=x^3-ax^2$に接する直線がちょうど2本存在するとき,実数$a$の値と2本の接線の方程式を求めよ。
大阪大過去問
この動画を見る
$点(0,1)を通り曲線$y=x^3-ax^2$に接する直線がちょうど2本存在するとき,実数$a$の値と2本の接線の方程式を求めよ。
大阪大過去問