 微分法と積分法
微分法と積分法
 微分法と積分法
微分法と積分法
名古屋大学 3次方程式 正の実数解をもつ条件 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^3-5ax^2+3a^2x+a=0$が正の実数解をもつための$a$の範囲
出典:2001年名古屋大学 過去問
この動画を見る
$x^3-5ax^2+3a^2x+a=0$が正の実数解をもつための$a$の範囲
出典:2001年名古屋大学 過去問
【高校数学】微分3.5~例題・接線の求め方・基礎~ 6-7【数学Ⅱ】

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1)曲線y=-x²+2x+4上の点(-1,1)における接線の方程式を求めよ。
(2)曲線y=x²+4に点(1,1)から引いた接線の方程式と、接点の座標を求めよ。
この動画を見る
(1)曲線y=-x²+2x+4上の点(-1,1)における接線の方程式を求めよ。
(2)曲線y=x²+4に点(1,1)から引いた接線の方程式と、接点の座標を求めよ。
長崎大 微分・積分 接線 面積 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#長崎大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=-x^4+8x^3-18x^2+11$
(1)
グラフの概形
(2)
$f(x)$と異なる2点で接する直線の方程式
(3)
(2)の直線と$f(x)$とで囲まれた面積
出典:2009年長崎大学 過去問
この動画を見る
$f(x)=-x^4+8x^3-18x^2+11$
(1)
グラフの概形
(2)
$f(x)$と異なる2点で接する直線の方程式
(3)
(2)の直線と$f(x)$とで囲まれた面積
出典:2009年長崎大学 過去問
【高校数学】微分③~接線の方程式~ 6-6【数学Ⅱ】

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
微分 接線の方程式についての説明動画です
この動画を見る
微分 接線の方程式についての説明動画です
大分大(医) 面積 積分計算の工夫 高校数学 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#微分とその応用#微分法#学校別大学入試過去問解説(数学)#不定積分・定積分#大分大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=(x-a)(x-4)(x-b)$
$a \lt 4 \lt b$
(1)
$f(x)$と$x$軸とで囲まれる2つの部分の面積が等しいとき、$a+b$の値は?
(2)
$a \gt o,f(x),x$軸$,y$軸とで囲まれる3つの部分の面積が等しいとき、$a,b$の値は?
出典:2006年大分大学 過去問
この動画を見る
$f(x)=(x-a)(x-4)(x-b)$
$a \lt 4 \lt b$
(1)
$f(x)$と$x$軸とで囲まれる2つの部分の面積が等しいとき、$a+b$の値は?
(2)
$a \gt o,f(x),x$軸$,y$軸とで囲まれる3つの部分の面積が等しいとき、$a,b$の値は?
出典:2006年大分大学 過去問
数検準1級 極限値 高校数学
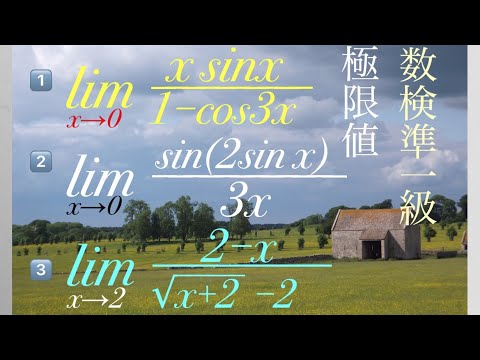
単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#平均変化率・極限・導関数#数学検定#数学検定準1級#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{x \sin x}{1-\cos 3x}$
(2)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{\sin (2\sin x)}{3x}$
(3)
$\displaystyle \lim_{ x \to 2 }\displaystyle \frac{2-x}{\sqrt{ x+2 }-2}$
出典:数学検定準1級 過去問
この動画を見る
(1)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{x \sin x}{1-\cos 3x}$
(2)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{\sin (2\sin x)}{3x}$
(3)
$\displaystyle \lim_{ x \to 2 }\displaystyle \frac{2-x}{\sqrt{ x+2 }-2}$
出典:数学検定準1級 過去問
東工大 積分 放物線と直線 面積最小値 高校数学 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分法と積分法#点と直線#学校別大学入試過去問解説(数学)#不定積分・定積分#東京工業大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$y=-2x^2+x+1$上の1点における接線と$y=x^2$とによって囲まれる部分の面積の最小値を求めよ。
出典:1967年 東京工業大学 過去問
この動画を見る
$y=-2x^2+x+1$上の1点における接線と$y=x^2$とによって囲まれる部分の面積の最小値を求めよ。
出典:1967年 東京工業大学 過去問
【高校数学】微分2.5~例題・微分の活用・応用~ 6-5【数学Ⅱ】

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1)次の条件をすべて満たす2次関数f(x)を求めよ。
f(0)=2、f'(0)=-3、f'(1)=1
(2)半径rの球の表面積Sと体積Vをそれぞれrの関数と考え、
SとVをrで微分せよ。
この動画を見る
(1)次の条件をすべて満たす2次関数f(x)を求めよ。
f(0)=2、f'(0)=-3、f'(1)=1
(2)半径rの球の表面積Sと体積Vをそれぞれrの関数と考え、
SとVをrで微分せよ。
【高校数学】微分2.5~例題・微分の仕方・基礎~ 6-4【数学Ⅱ】

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1)関数y=x³+x²の導関数を求めよ。
(2)関数y=(2x-1)(3x+5)を微分せよ。
(☆) f(x)=x²のx=2における微分係数を求めよ。
この動画を見る
(1)関数y=x³+x²の導関数を求めよ。
(2)関数y=(2x-1)(3x+5)を微分せよ。
(☆) f(x)=x²のx=2における微分係数を求めよ。
【高校数学】微分②~導関数~ 6-3【数学Ⅱ】

【高校数学】微分1.5~例題・微分係数と極限~ 6-2【数学Ⅱ】

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1) $f(x)=x^2$の$x=2$における微分係数を求めよ。
(2) $\displaystyle \lim_{ x \to 3 }$$(x^2-2x+4)$
(3) $\displaystyle \lim_{ x \to -3 }$$\frac{x^2-9}{x+3}$
(4) $\displaystyle \lim_{ x \to 3 }$$\frac{2x}{x-5}$
(5) $\displaystyle \lim_{ x \to 0 }$$\frac{1}{x}$$(\frac{1}{x-1}+1)$
この動画を見る
(1) $f(x)=x^2$の$x=2$における微分係数を求めよ。
(2) $\displaystyle \lim_{ x \to 3 }$$(x^2-2x+4)$
(3) $\displaystyle \lim_{ x \to -3 }$$\frac{x^2-9}{x+3}$
(4) $\displaystyle \lim_{ x \to 3 }$$\frac{2x}{x-5}$
(5) $\displaystyle \lim_{ x \to 0 }$$\frac{1}{x}$$(\frac{1}{x-1}+1)$
山口大 3次方程式の解の個数 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#数学(高校生)#山口大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
05年 山口大学
次の方程式 $x^3-kx+2=0$において$k$ が実数であるときの実数解の個数を求めよ。
この動画を見る
05年 山口大学
次の方程式 $x^3-kx+2=0$において$k$ が実数であるときの実数解の個数を求めよ。
佐賀大 三次関数 最大値・最小値 高校数学 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#佐賀大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
09年 佐賀大学
$0\lt p\lt1$の範囲のとき、$f(x)=x^3-(3p+2)x^2+8px$の $0\leqq x\leqq1$における最大値、最小値を求めよ
この動画を見る
09年 佐賀大学
$0\lt p\lt1$の範囲のとき、$f(x)=x^3-(3p+2)x^2+8px$の $0\leqq x\leqq1$における最大値、最小値を求めよ
【高校数学】微分①~平均変化率と微分係数~ 6-1【数学Ⅱ】

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
微分 平均変化率と微分係数についての説明動画です
この動画を見る
微分 平均変化率と微分係数についての説明動画です
和歌山大 4次関数と接線 高校数学 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#面積、体積#数学(高校生)#岡山大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
94年 和歌山大学過去問
$f(x)=x^4+ax^3+bx^2+cx+d$と$y=mx$は2点P、Qで接している。
P、Qの$x$座標はそれぞれ、-1、2で$f(x)$は$x=1$で極大値をとる。
(1)$f(x)$と$y=mx$で囲まれる面積を求めよ
(2)$m$の値と極大値を求めよ
この動画を見る
94年 和歌山大学過去問
$f(x)=x^4+ax^3+bx^2+cx+d$と$y=mx$は2点P、Qで接している。
P、Qの$x$座標はそれぞれ、-1、2で$f(x)$は$x=1$で極大値をとる。
(1)$f(x)$と$y=mx$で囲まれる面積を求めよ
(2)$m$の値と極大値を求めよ
香川大 4次関数と接線 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#香川大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
1994年 国立大学法人香川大学
$f(x)=x^4-2x^2$
$(a,f(a))$における接線と$f(x)$との共有点の個数
この動画を見る
1994年 国立大学法人香川大学
$f(x)=x^4-2x^2$
$(a,f(a))$における接線と$f(x)$との共有点の個数
京都大 式の値域 Mathematics Japanese university entrance exam Kyoto University

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2012年 学校法人京都大学
実数$x,y$が$x^2+xy+y^2=6$を満たす
$x^2y+xy^2-x^2-2xy-y^2+x+y$のとりうる値の範囲
この動画を見る
2012年 学校法人京都大学
実数$x,y$が$x^2+xy+y^2=6$を満たす
$x^2y+xy^2-x^2-2xy-y^2+x+y$のとりうる値の範囲
東海大 4次方程式 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
東海大学
$x^4-2x^3+bx^2-2x+1=0$
$(1)$実数解をもつ$b$の値の範囲
$(2)$ちょうど$3$個の実数解をもつ$b$の値と実数解
この動画を見る
東海大学
$x^4-2x^3+bx^2-2x+1=0$
$(1)$実数解をもつ$b$の値の範囲
$(2)$ちょうど$3$個の実数解をもつ$b$の値と実数解
数学の魔術師ヨビノリのたくみさん5度目の登場 東大入試問題 Mathematics Japanese university entrance examTokyo University

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
国立大学法人東京大学
$y=x^2$上に$P,Q$がある
線分$PQ$の中点の$y$座標を$h$
$(1)PQ$の長さ$L$と傾き$m$で$h$を表せ
$(2)L$を固定したときの$h$の最小値
この動画を見る
国立大学法人東京大学
$y=x^2$上に$P,Q$がある
線分$PQ$の中点の$y$座標を$h$
$(1)PQ$の長さ$L$と傾き$m$で$h$を表せ
$(2)L$を固定したときの$h$の最小値
京都大 微分 合成関数 Mathematics Japanese university entrance exam Kyoto University

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#関数(分数関数・無理関数・逆関数と合成関数)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
1993年 国立大学法人京都大学
$f(x)=x^3-3ax$
$(1)f(x)=t$が相違3実根をもつ$a,t$の条件
$(2)g(x)=f(f(x)),g(x)=0$
が相違9実根をもつ$a$の範囲
この動画を見る
1993年 国立大学法人京都大学
$f(x)=x^3-3ax$
$(1)f(x)=t$が相違3実根をもつ$a,t$の条件
$(2)g(x)=f(f(x)),g(x)=0$
が相違9実根をもつ$a$の範囲
新潟大 微分・積分 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#数学(高校生)#新潟大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
国立大学法人新潟大学
$C:$$f(x)=2x^3-12x$
$(1,-2)$を通る接線$C$の接線を$l$
$(1)l$の方程式
$(2)C$と$l$で囲まれる面積
この動画を見る
国立大学法人新潟大学
$C:$$f(x)=2x^3-12x$
$(1,-2)$を通る接線$C$の接線を$l$
$(1)l$の方程式
$(2)C$と$l$で囲まれる面積
新潟大 微分・積分 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#微分法と積分法#面積、体積#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
新潟大学過去問題
$C:f(x)=2x^3-12x$
(1,-2)を通るCの接線をl
(1)lの方程式
(2)Cとlで囲まれる面積
この動画を見る
新潟大学過去問題
$C:f(x)=2x^3-12x$
(1,-2)を通るCの接線をl
(1)lの方程式
(2)Cとlで囲まれる面積
弘前大 積分 面積公式導出 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#不定積分・定積分#面積、体積#数学(高校生)#弘前大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
'90弘前大学過去問題
$C:y=x^3-(a+3)x^2+3ax+5$
$L:y=3x-4$
CとLの共有点が2点のとき、CとLで囲まれる面積
この動画を見る
'90弘前大学過去問題
$C:y=x^3-(a+3)x^2+3ax+5$
$L:y=3x-4$
CとLの共有点が2点のとき、CとLで囲まれる面積
東大 不等式 たくみさん4度目の登場 Mathematics Japanese university entrance exam Tokyo University

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#微分法と積分法#対数関数#微分とその応用#微分法#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
'09東京大学過去問題
実数$x,-1<x<1,x \neq 0$
(1)示せ
$(1-x)^{1-\frac{1}{x}} < (1+x)^{\frac{1}{x}} $
(2)示せ
$0.9999^{101} < 0.99 < 0.9999^{100} $
この動画を見る
'09東京大学過去問題
実数$x,-1<x<1,x \neq 0$
(1)示せ
$(1-x)^{1-\frac{1}{x}} < (1+x)^{\frac{1}{x}} $
(2)示せ
$0.9999^{101} < 0.99 < 0.9999^{100} $
大阪教育大 微分 3次関数 最大値 高校数学 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#大阪教育大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
'08大阪教育大学過去問題
$f(x)=-x^3-3x^2+3kx+3k+2$の$-1 \leqq x \leqq 1 $における最大値
この動画を見る
'08大阪教育大学過去問題
$f(x)=-x^3-3x^2+3kx+3k+2$の$-1 \leqq x \leqq 1 $における最大値
関西学院大 微分 3次関数の最大値 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#複素数と方程式#微分法と積分法#剰余の定理・因数定理・組み立て除法と高次方程式#接線と増減表・最大値・最小値#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
'03関西学院大学
0<k<1
$f(x)=x(x-3k)^2$の$0 \leqq x \leqq 1$における最大値。
また最大値が$\frac{1}{2}$のときkの値
この動画を見る
'03関西学院大学
0<k<1
$f(x)=x(x-3k)^2$の$0 \leqq x \leqq 1$における最大値。
また最大値が$\frac{1}{2}$のときkの値
大阪教育大 指数関数の最小値 解の個数 高校数学 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#指数関数と対数関数#微分法と積分法#恒等式・等式・不等式の証明#指数関数#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#大阪教育大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
'03大阪教育大学過去問題
x,a実数
$f(x)=4^x-6・2^x-6・2^{-x}+4^{-x}$
(1)f(x)の最小値
(2)f(x)=aとなるようなxの個数
この動画を見る
'03大阪教育大学過去問題
x,a実数
$f(x)=4^x-6・2^x-6・2^{-x}+4^{-x}$
(1)f(x)の最小値
(2)f(x)=aとなるようなxの個数
北海道大 積分 高校数学 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#北海道大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
'02北海道大学過去問題
a,b,cは定数
$f(x)=x^2+ax+b,g(x)=x+c$
(1)$\int_0^1f(x)dx = \int_0^1g(x)dx$となるためのa,b,cの条件
(2)(1)の条件のもとで、$0 \leqq x \leqq 1$における2つの関数f(x)とg(x)の共有点の個数
この動画を見る
'02北海道大学過去問題
a,b,cは定数
$f(x)=x^2+ax+b,g(x)=x+c$
(1)$\int_0^1f(x)dx = \int_0^1g(x)dx$となるためのa,b,cの条件
(2)(1)の条件のもとで、$0 \leqq x \leqq 1$における2つの関数f(x)とg(x)の共有点の個数
群馬大・津田塾大 数列の和・積分 高校数学 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#群馬大学#数B#津田塾大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
群馬大学過去問題
$a_k= \frac{(3k+1)(3k+2)}{3k(k+1)}$ (k自然数)
$\displaystyle\sum_{k=1}^n a_k$をnの式で
津田塾大学過去問題
$C:y=x^2-x-4|x-1|$と直線lは2点で接する。
Cとlで囲まれた面積
この動画を見る
群馬大学過去問題
$a_k= \frac{(3k+1)(3k+2)}{3k(k+1)}$ (k自然数)
$\displaystyle\sum_{k=1}^n a_k$をnの式で
津田塾大学過去問題
$C:y=x^2-x-4|x-1|$と直線lは2点で接する。
Cとlで囲まれた面積
富山大 積分 6分の1公式 高校数学 Mathematics Japanese university entrance exam

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#富山大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
富山大学過去問題
$y=x^2-2x+1$と$y=mx+2$とで囲まれる面積の最小値
この動画を見る
富山大学過去問題
$y=x^2-2x+1$と$y=mx+2$とで囲まれる面積の最小値
