 漸化式
漸化式
 漸化式
漸化式
室蘭工業大 漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=2,b_1=1$
$a_{n+1}=\dfrac{7}{3}a_n+\dfrac{4}{3}b_n+n$
$b_{n+1}=\dfrac{2}{3}a_n+\dfrac{5}{3}b_n-n$
2021室蘭工大過去問
この動画を見る
$a_1=2,b_1=1$
$a_{n+1}=\dfrac{7}{3}a_n+\dfrac{4}{3}b_n+n$
$b_{n+1}=\dfrac{2}{3}a_n+\dfrac{5}{3}b_n-n$
2021室蘭工大過去問
福田の数学〜慶應義塾大学2021年総合政策学部第5問〜人形を並べる方法と漸化式
単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{5}}$(1)同じ人形$n$体(nは正の整数)を、1体または2体ずつ前方を向かせて列に並べる。
例えば$n=10$のとき、下図(※動画参照)のような並べ方がある。
ここで、$n$体の人形の並べ方の総数を$a_n$とすると
$a_1=1,\ a_2=2,\ a_3=3,\ldots,\ a_{12}=\boxed{\ \ アイウ\ \ },\ a_{13}=\boxed{\ \ エオカ\ \ },\ a_{14}=\boxed{\ \ キクケ\ \ }$
となる。ただし、列の先頭の人形の前には門があり、その門の方向を前方とする。
(2)同じ人形n体(nは2以上の整数)を、2体または3体ずつ前方を向かせて列に並べる。
その並べ方の総数を$b_n$とすると
$b_2=1,\ b_3=1,\ b_4=1,\ldots,\ b_{12}=\boxed{\ \ コサシ\ \ },\ b_{13}=\boxed{\ \ スセソ\ \ },\ b_{14}=\boxed{\ \ タチツ\ \ }$
となる。ただし、列の先頭の人形の前には門があり、その門の方向を前方とする。
2021慶應義塾大学整合政策学部過去問
この動画を見る
${\Large\boxed{5}}$(1)同じ人形$n$体(nは正の整数)を、1体または2体ずつ前方を向かせて列に並べる。
例えば$n=10$のとき、下図(※動画参照)のような並べ方がある。
ここで、$n$体の人形の並べ方の総数を$a_n$とすると
$a_1=1,\ a_2=2,\ a_3=3,\ldots,\ a_{12}=\boxed{\ \ アイウ\ \ },\ a_{13}=\boxed{\ \ エオカ\ \ },\ a_{14}=\boxed{\ \ キクケ\ \ }$
となる。ただし、列の先頭の人形の前には門があり、その門の方向を前方とする。
(2)同じ人形n体(nは2以上の整数)を、2体または3体ずつ前方を向かせて列に並べる。
その並べ方の総数を$b_n$とすると
$b_2=1,\ b_3=1,\ b_4=1,\ldots,\ b_{12}=\boxed{\ \ コサシ\ \ },\ b_{13}=\boxed{\ \ スセソ\ \ },\ b_{14}=\boxed{\ \ タチツ\ \ }$
となる。ただし、列の先頭の人形の前には門があり、その門の方向を前方とする。
2021慶應義塾大学整合政策学部過去問
名古屋市立大(医)漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n$を自然数とする.
$a_1=2$
$\dfrac{a_{n+1}}{a_n}=\dfrac{n}{n+2}$
$\displaystyle \sum_{n=1}^{\infty}a_n$を求めよ.
名古屋市立(医)過去問
この動画を見る
$n$を自然数とする.
$a_1=2$
$\dfrac{a_{n+1}}{a_n}=\dfrac{n}{n+2}$
$\displaystyle \sum_{n=1}^{\infty}a_n$を求めよ.
名古屋市立(医)過去問
数学「大学入試良問集」【17−4 漸化式と等比数列・極限】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数Ⅲ#東京農工大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次のように定義された数列を$\{a_n\}$とする。
$a_1=r^2,a_2=1,2a_n=(r+3)a_{n-1}-(r+1)a_{n-2}(n \geqq 3)$
このとき、次の各問いに答えよ。
(1)$b_n=a_{n+1}-a_n$とおくとき、$b_n$を$n$と$r$を用いて表せ。
(2)$a_n$を求めよ。
(3)数列$\{a_n\}$が収束するような$r$の範囲およびそのときの極限値を求めよ。
この動画を見る
次のように定義された数列を$\{a_n\}$とする。
$a_1=r^2,a_2=1,2a_n=(r+3)a_{n-1}-(r+1)a_{n-2}(n \geqq 3)$
このとき、次の各問いに答えよ。
(1)$b_n=a_{n+1}-a_n$とおくとき、$b_n$を$n$と$r$を用いて表せ。
(2)$a_n$を求めよ。
(3)数列$\{a_n\}$が収束するような$r$の範囲およびそのときの極限値を求めよ。
福田の数学〜早稲田大学2021年人間科学部第5問〜漸化式の作成と値の評価

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{5}}$ 半径$r_1=2$の円$O_1$に接する平行でない$2$つの直線がある。接点を$A,B$とし、$2$つの直線の交点を$P$とし、$\angle APB=\frac{\pi}{3}$とする。$O_1$より半径が小さく、$O_1$の中心を通り、直線$AP$と直線$BP$に接する円を$O_2$とする。同様に自然数$n$に対して、$O_n$より半径が小さく、$O_n$の中心を通り、直線$AP$と直線$BP$に接する円を$O_{n+1}$とする。$O_n$の半径を$r_n$とするとき、$\frac{r_n}{r_{n+1}}=\frac{\boxed{\ \ ノ\ \ }}{\boxed{\ \ ハ\ \ }}$ となる。次に、$n$個の円$O_1,O_2,\ldots,O_n$の面積の和を$S_n$とするとき、$S_{10}$の整数部分は$\boxed{\ \ ヒ\ \ }$である。
2021早稲田大学人間科学部過去問
この動画を見る
${\Large\boxed{5}}$ 半径$r_1=2$の円$O_1$に接する平行でない$2$つの直線がある。接点を$A,B$とし、$2$つの直線の交点を$P$とし、$\angle APB=\frac{\pi}{3}$とする。$O_1$より半径が小さく、$O_1$の中心を通り、直線$AP$と直線$BP$に接する円を$O_2$とする。同様に自然数$n$に対して、$O_n$より半径が小さく、$O_n$の中心を通り、直線$AP$と直線$BP$に接する円を$O_{n+1}$とする。$O_n$の半径を$r_n$とするとき、$\frac{r_n}{r_{n+1}}=\frac{\boxed{\ \ ノ\ \ }}{\boxed{\ \ ハ\ \ }}$ となる。次に、$n$個の円$O_1,O_2,\ldots,O_n$の面積の和を$S_n$とするとき、$S_{10}$の整数部分は$\boxed{\ \ ヒ\ \ }$である。
2021早稲田大学人間科学部過去問
数学「大学入試良問集」【13−14 確率漸化式の基本】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数B
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
袋の中に$1~9$までの異なる数字を1つずつ書いた9枚のカードが入っている。
この中から1枚を取り出し、数字を調べて袋に戻す。
この試行を$n$回繰り返したとき、調べた$n$枚のカードの数字の和が偶数になる確率を$P_n$とする。
このとき、次の各問いに答えよ。
(1)$P_2,P_3$の値を求めよ。
(2)$P_{n+1}$を$P_n$を用いて表せ。
(3)$P_n$を$n$を用いて表せ。
この動画を見る
袋の中に$1~9$までの異なる数字を1つずつ書いた9枚のカードが入っている。
この中から1枚を取り出し、数字を調べて袋に戻す。
この試行を$n$回繰り返したとき、調べた$n$枚のカードの数字の和が偶数になる確率を$P_n$とする。
このとき、次の各問いに答えよ。
(1)$P_2,P_3$の値を求めよ。
(2)$P_{n+1}$を$P_n$を用いて表せ。
(3)$P_n$を$n$を用いて表せ。
数学「大学入試良問集」【13−6 連立漸化式】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の条件によって定められる数列$\{x_n\},\{y_n\}$を考える。
$x_1=1,y_1=5$ $x_{n+1}=x_n+y_n$ $y_{n+1}=5x_n+y_n(n=1,2,・・・)$
次の問いに答えよ。
(1)
$a_n=x_n+cy_n$とおいたとき、数列$\{a_n\}$が等比数列となるように定数$c$の値を定め、$a_n$を$n$の式で表せ。
(2)
$x_n$および$y_n$を$n$の式で表せ。
この動画を見る
次の条件によって定められる数列$\{x_n\},\{y_n\}$を考える。
$x_1=1,y_1=5$ $x_{n+1}=x_n+y_n$ $y_{n+1}=5x_n+y_n(n=1,2,・・・)$
次の問いに答えよ。
(1)
$a_n=x_n+cy_n$とおいたとき、数列$\{a_n\}$が等比数列となるように定数$c$の値を定め、$a_n$を$n$の式で表せ。
(2)
$x_n$および$y_n$を$n$の式で表せ。
数学「大学入試良問集」【13−5② 漸化式(デザイン型】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#滋賀大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$a_1=2,a_{n+1=2a_n-2a_n-2n+1(n=1,2,・・・)}$によって定められる数列$\{a_n\}$について、次の問いに答えよ。
(1)
$b_n=a_n-(\alpha+\beta)$とおいて、数列$\{b_n\}$が等比数列になるように定数$\alpha,\beta$の値を定めよ。
(2)
一般項$a_n$を求めよ。
(3)
初項から第$n$項までの和$S_n=\displaystyle \sum_{k=1}^n a_k$を求めよ。
この動画を見る
$a_1=2,a_{n+1=2a_n-2a_n-2n+1(n=1,2,・・・)}$によって定められる数列$\{a_n\}$について、次の問いに答えよ。
(1)
$b_n=a_n-(\alpha+\beta)$とおいて、数列$\{b_n\}$が等比数列になるように定数$\alpha,\beta$の値を定めよ。
(2)
一般項$a_n$を求めよ。
(3)
初項から第$n$項までの和$S_n=\displaystyle \sum_{k=1}^n a_k$を求めよ。
数学「大学入試良問集」【13−5 漸化式(割り算型)】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数B
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
数列$\{a_n\}$は
$a_1=9,a_{n+1}=4a_n+5^n(n=1,2,・・・)$をみたす。このとき、次の問いに答えよ。
(1)$b_n=a_n-5^n$とおく。$b_{n+1}$を$b_n$で表せ。
(2)数列$\{a_n\}$の一般項を求めよ。
この動画を見る
数列$\{a_n\}$は
$a_1=9,a_{n+1}=4a_n+5^n(n=1,2,・・・)$をみたす。このとき、次の問いに答えよ。
(1)$b_n=a_n-5^n$とおく。$b_{n+1}$を$b_n$で表せ。
(2)数列$\{a_n\}$の一般項を求めよ。
数学「大学入試良問集」【13−4 漸化式(逆数型)】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#群馬大学#数B
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$a_1=1,a_{n+1}=\displaystyle \frac{a_n}{4a_n+1}(n=1,2,・・・)$で定まる数列$\{a_n\}$に関して、次の各問に答えよ。
(1)
$\displaystyle \frac{1}{a_n}$を$n$の式で表せ。
(2)
$\displaystyle \sum_{k=1}^n\left[ \dfrac{ 12 }{ a_k-a_{k+1} }+9 \right]$を$n$の式で表せ。
この動画を見る
$a_1=1,a_{n+1}=\displaystyle \frac{a_n}{4a_n+1}(n=1,2,・・・)$で定まる数列$\{a_n\}$に関して、次の各問に答えよ。
(1)
$\displaystyle \frac{1}{a_n}$を$n$の式で表せ。
(2)
$\displaystyle \sum_{k=1}^n\left[ \dfrac{ 12 }{ a_k-a_{k+1} }+9 \right]$を$n$の式で表せ。
数学「大学入試良問集」【13−1 Snとanの取り扱い】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#数B#明星大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
数列$\{a_n\}$の初項から第$n$項までの和を$S_n$とする。
$S_n=-2a_n+3n$が成り立つとき、次の問いに答えよ。
(1)$a_1$と$a_2$を求めよ。
(2)$a_{n+1}$を$a_n$を用いて表せ。
(3)$a_n$を$n$を用いて表せ。
この動画を見る
数列$\{a_n\}$の初項から第$n$項までの和を$S_n$とする。
$S_n=-2a_n+3n$が成り立つとき、次の問いに答えよ。
(1)$a_1$と$a_2$を求めよ。
(2)$a_{n+1}$を$a_n$を用いて表せ。
(3)$a_n$を$n$を用いて表せ。
福田のわかった数学〜高校3年生理系010〜極限(10)解けない漸化式の極限

単元:
#数列#漸化式#関数と極限#数列の極限#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 極限(10)
$a_1=2, a_{n+1}=\sqrt{a_n+30}$ のとき、
$\lim_{n \to \infty}a_n$ を調べよ。
この動画を見る
数学$\textrm{III}$ 極限(10)
$a_1=2, a_{n+1}=\sqrt{a_n+30}$ のとき、
$\lim_{n \to \infty}a_n$ を調べよ。
大分大 漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
一般項$a_n$を求めよ.
$S_n=(n+3)(\dfrac{1}{3}a_n-2)$
2020大分大過去問
この動画を見る
一般項$a_n$を求めよ.
$S_n=(n+3)(\dfrac{1}{3}a_n-2)$
2020大分大過去問
【数B】漸化式:東大1995年 タイルの敷き詰め

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
2辺の長さが1と2の長方形と1辺の長さが2の正方形の2種類のタイルがある。縦2,横nの長方形の部屋をこれらのタイルで過不足なく敷き詰めることを考える。その並べ方の総数をA[n]で表す。ただし,nは正の整数である。たとえば$ A_1=1, A_2=3, A_3=5$ である。このとき,以下の問いに答えよう。
(1)$n≧3$のとき,$A_n$を$A_{n-1},A_{n-2}$を用いて表そう。
(2)$A_n$をnで表そう。
この動画を見る
2辺の長さが1と2の長方形と1辺の長さが2の正方形の2種類のタイルがある。縦2,横nの長方形の部屋をこれらのタイルで過不足なく敷き詰めることを考える。その並べ方の総数をA[n]で表す。ただし,nは正の整数である。たとえば$ A_1=1, A_2=3, A_3=5$ である。このとき,以下の問いに答えよう。
(1)$n≧3$のとき,$A_n$を$A_{n-1},A_{n-2}$を用いて表そう。
(2)$A_n$をnで表そう。
【数B・Ⅲ】漸化式と極限:連立漸化式:数列{x[n]},{y[n]}をx[1]=y[1]=1, x[n+1]=(2/3)x[n]+(1/6)y[n], y[n+1]=(1/3)x[n]+(5/6)y…

単元:
#数列#漸化式#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
数列{$x_n$},{$y_n$}を$x_1=y_1=1, x_{n+1}=\dfrac{2}{3}x_n+\dfrac{1}{6}y_n, y_{n+1}=\dfrac{1}{3}x_n+\dfrac{5}{6}y_n$で定めるとき、
(1)$x_{n+1}+αy_{n+1}=\beta(x_n+αy_n)$を満たす$\alpha,\beta$の組を2組求めよう。
(2)数列{$x_n$},{$y_n$}の一般項を求めよう。
(3)数列{$x_n$},{$y_n$}の極限を求めよう。
この動画を見る
数列{$x_n$},{$y_n$}を$x_1=y_1=1, x_{n+1}=\dfrac{2}{3}x_n+\dfrac{1}{6}y_n, y_{n+1}=\dfrac{1}{3}x_n+\dfrac{5}{6}y_n$で定めるとき、
(1)$x_{n+1}+αy_{n+1}=\beta(x_n+αy_n)$を満たす$\alpha,\beta$の組を2組求めよう。
(2)数列{$x_n$},{$y_n$}の一般項を求めよう。
(3)数列{$x_n$},{$y_n$}の極限を求めよう。
2つの解法レピュニット数の和

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
和を求めよ.
$1+11+111+・・・・\underbrace{111・・・・1}_{n桁}$
この動画を見る
和を求めよ.
$1+11+111+・・・・\underbrace{111・・・・1}_{n桁}$
岩手大 漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$n=1,2,3・・・・$
$a_1=31$
$a_{n+1}=\dfrac{(n+3)a_n-28}{n+2}$
一般項を求めよ.
2020岩手大過去問
この動画を見る
$n=1,2,3・・・・$
$a_1=31$
$a_{n+1}=\dfrac{(n+3)a_n-28}{n+2}$
一般項を求めよ.
2020岩手大過去問
旭川医科大2021 確率漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
コイン2枚 表表+2,表裏+1,裏裏0であり,0からスタートする.
$n$回の合計が
(1)$a_1,b_1,c_1,a_2,b_2,c_2$のとき,求めよ.
(2)$a_{n+1},b_{n+1},c_{n+1}$を,$a_n,b_n,c_n$で求めよ.
(3)$x_{n+1}=\dfrac{1}{4}x_n;\dfrac{1}{4}$を$x_1$を用いて表せ.
(4)$a_n$を求めよ.
2021旭川医大過去問
この動画を見る
コイン2枚 表表+2,表裏+1,裏裏0であり,0からスタートする.
$n$回の合計が
(1)$a_1,b_1,c_1,a_2,b_2,c_2$のとき,求めよ.
(2)$a_{n+1},b_{n+1},c_{n+1}$を,$a_n,b_n,c_n$で求めよ.
(3)$x_{n+1}=\dfrac{1}{4}x_n;\dfrac{1}{4}$を$x_1$を用いて表せ.
(4)$a_n$を求めよ.
2021旭川医大過去問
【数B】数列:特性方程式はなぜ解けるのか

【数B】数列:漸化式の基本を解説シリーズその5 分数型

単元:
#数列#漸化式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$a_1=1,a_{n+1}=\dfrac{a_{n}}{3a_n+2}$で定められる数列{$a_n$}の一般項を求めよ。
この動画を見る
$a_1=1,a_{n+1}=\dfrac{a_{n}}{3a_n+2}$で定められる数列{$a_n$}の一般項を求めよ。
【数B】数列:漸化式の基本を解説シリーズその4 特殊解型

単元:
#数列#漸化式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$a_1=2,a_{n+1}+2a_{n}=1$で定められる数列{$a_n$}の一般項を求めよ。
この動画を見る
$a_1=2,a_{n+1}+2a_{n}=1$で定められる数列{$a_n$}の一般項を求めよ。
【数B】数列:漸化式の基本を解説シリーズその3 階差型

単元:
#数列#漸化式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$a_1=3,a_{n+1}=a_n+2^n$ で定められる数列{$a_n$}の一般項を求めよ。
この動画を見る
$a_1=3,a_{n+1}=a_n+2^n$ で定められる数列{$a_n$}の一般項を求めよ。
【数B】数列:漸化式の基本を解説シリーズその1 等差型

単元:
#数列#漸化式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$a_1=2,a_{n+1}=a_n+1$で定められる数列{$a_n$}の一般項を求めよ。
この動画を見る
$a_1=2,a_{n+1}=a_n+1$で定められる数列{$a_n$}の一般項を求めよ。
富山大 積分のフリしたただの漸化式
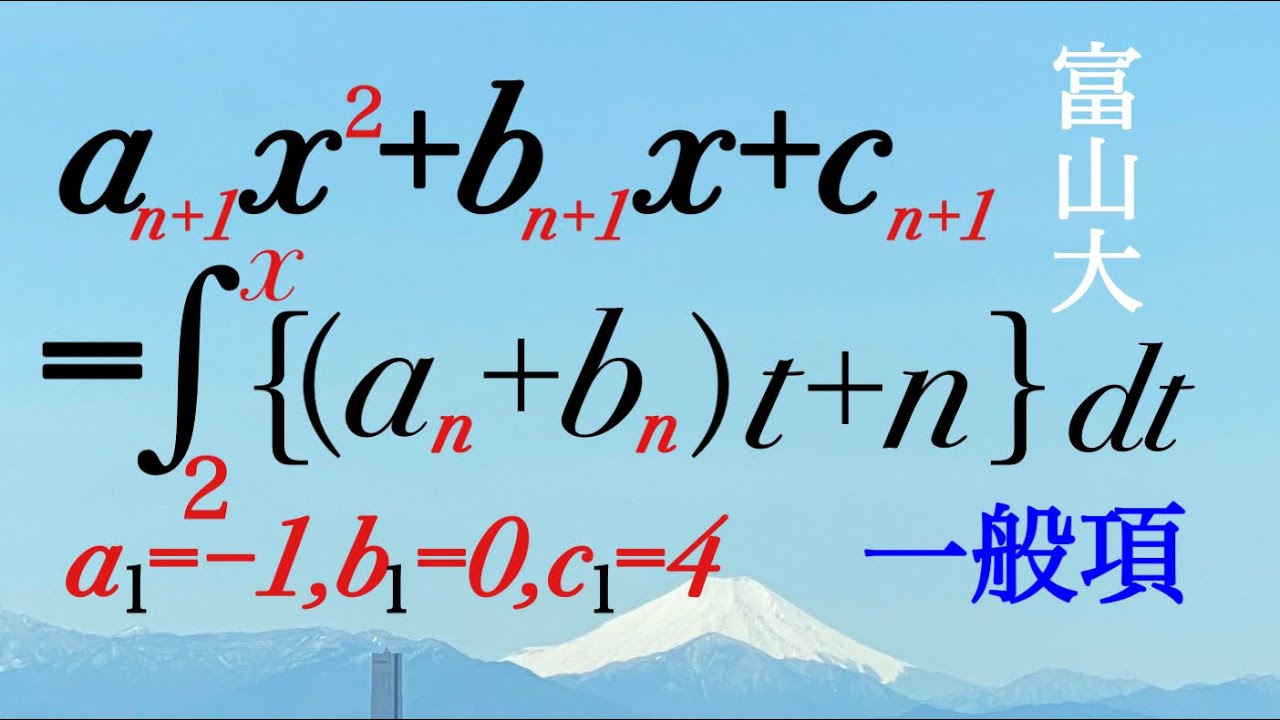
単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=-1,b=0,c_1=4$
$a_{n+4}x^2+b_{n+1}x+c_{n+1}=\displaystyle \int_{2}^{x}{(a_n+b_n)t+n}at$
$a_n,b_n,c_n$の一般項を求めよ.
2021富山大過去問
この動画を見る
$a_1=-1,b=0,c_1=4$
$a_{n+4}x^2+b_{n+1}x+c_{n+1}=\displaystyle \int_{2}^{x}{(a_n+b_n)t+n}at$
$a_n,b_n,c_n$の一般項を求めよ.
2021富山大過去問
2021北海道大 連立漸化式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$a_1=2,b_1=1$
$c_n=a_nb_n$
$a_{n+1}=2a_n+3b_n$
$b_{n+1}=a_n+2b_n$
①$c_2$
②$c_n$は偶数
③$n$が偶数なら$c_n$は28の倍数であることを示せ.
2021北海道大過去問
この動画を見る
$a_1=2,b_1=1$
$c_n=a_nb_n$
$a_{n+1}=2a_n+3b_n$
$b_{n+1}=a_n+2b_n$
①$c_2$
②$c_n$は偶数
③$n$が偶数なら$c_n$は28の倍数であることを示せ.
2021北海道大過去問
【数B】数列:漸化式の基本を解説シリーズその2 等比型
共通テスト2021年数学詳しい解説〜共通テスト2021年2B第4問〜数列

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#漸化式#センター試験・共通テスト関連#共通テスト#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
${\large第4問}$
初項3、交差$p$の等差数列を$\left\{a_n\right\}$とし、初項3、公比$r$の等比数列を$\left\{b_n\right\}$と
する。ただし、$p \ne 0$かつ$r \ne 0$とする。さらに、これらの数列が次を満たすとする。
$a_nb_{n+1}-2a_{n+1}b_n+3b_{n+1}=0$ $(n=1,2,3,\ldots)\cdots$①
(1)$p$と$r$の値を求めよう。自然数$n$について、$a_n,a_{n+1},b_n$はそれぞれ
$a_n=\boxed{\ \ ア\ \ }+(n-1)p$ $\cdots$②
$a_{n+1}=\boxed{\ \ ア\ \ }+np$ $\cdots$③
$b_n=\boxed{\ \ イ\ \ }r^{n-1}$
と表される。$r \ne 0$により、すべての自然数$n$について、$b_n \ne 0$となる。
$\displaystyle \frac{b_{n+1}}{b_n}=r$であることから、①の両辺を$b_n$で割ることにより
$\boxed{\ \ ウ\ \ }a_{n+1}=r\left(a_n+\boxed{\ \ エ\ \ }\right)$ $\cdots$④
が成り立つことが分かる。④に②と③を代入すると
$\left(r-\boxed{\ \ オ\ \ }\right)pn=r\left(p-\boxed{\ \ カ\ \ }\right)$$+\boxed{\ \ キ\ \ }$ $\cdots$⑤
となる。⑤が全ての$n$で成り立つことおよび$p \ne 0$により、$r=\boxed{\ \ オ\ \ }$を得る。
さらに、このことから、$p=\boxed{\ \ ク\ \ }$を得る。
以上から、すべての自然数$n$について、$a_n$と$b_n$が正であることもわかる。
(2)$p=\boxed{\ \ ク\ \ },$ $r=\boxed{\ \ オ\ \ }$であるから、$\left\{a_n\right\},$ $\left\{b_n\right\}$の初項から第$n$項
までの和は、それぞれ次の式で与えられる。
$\sum_{k=1}^na_k=\displaystyle \frac{\boxed{\ \ ケ\ \ }}{\boxed{\ \ コ\ \ }}n\left(n+\boxed{\ \ サ\ \ }\right)$
$\sum_{k=1}^nb_k$$=\boxed{\ \ シ\ \ }\left(\boxed{\ \ オ\ \ }^n-\boxed{\ \ ス\ \ }\right)$
(3)数列$\left\{a_n\right\}$に対して、初項3の数列$\left\{c_n\right\}$が次を満たすとする。
$a_nc_{n+1}-4a_{n+1}c_n+3c_{n+1}=0$ $(n=1,2,3,\ldots)\cdots$⑥
$a_n$が正であることから、⑥を変形して、$c_{n+1}=\displaystyle \frac{\boxed{\ \ セ\ \ }a_{n+1}}{a_n+\boxed{\ \ ソ\ \ }}c_n$を得る。
さらに、$p=\boxed{\ \ ク\ \ }$であることから、数列$\left\{c_n\right\}$は$\boxed{\boxed{\ \ タ\ \ }}$ことがわかる。
$\boxed{\boxed{\ \ タ\ \ }}$の解答群
⓪すべての項が同じ値をとる数列である
①公差が0でない等差数列である
②公比が1より大きい等比数列である
③公比が1より小さい等比数列である
④等差数列でも等比数列でもない
(4)$q,u$は定数で$q \ne 0$とする。数列$\left\{b_n\right\}$に対して、初項3の数列$\left\{d_n\right\}$が
次を満たすとする。
$d_nb_{n+1}-qd_{n+1}b_n+ub_{n+1}=0$ $(n=1,2,3,\ldots)\cdots$⑦
$r=\boxed{\ \ オ\ \ }$であることから、⑦を変形して、$d_{n+1}=\displaystyle \frac{\boxed{\ \ チ\ \ }}{q}(d_n+u)$
を得る。したがって、数列$\left\{d_n\right\}$が、公比が0より大きく1より小さい
等比数列となるための必要十分条件は、$q \gt \boxed{\ \ ツ\ \ }$かつ$u=\boxed{\ \ テ\ \ }$
である。
2021共通テスト過去問
この動画を見る
${\large第4問}$
初項3、交差$p$の等差数列を$\left\{a_n\right\}$とし、初項3、公比$r$の等比数列を$\left\{b_n\right\}$と
する。ただし、$p \ne 0$かつ$r \ne 0$とする。さらに、これらの数列が次を満たすとする。
$a_nb_{n+1}-2a_{n+1}b_n+3b_{n+1}=0$ $(n=1,2,3,\ldots)\cdots$①
(1)$p$と$r$の値を求めよう。自然数$n$について、$a_n,a_{n+1},b_n$はそれぞれ
$a_n=\boxed{\ \ ア\ \ }+(n-1)p$ $\cdots$②
$a_{n+1}=\boxed{\ \ ア\ \ }+np$ $\cdots$③
$b_n=\boxed{\ \ イ\ \ }r^{n-1}$
と表される。$r \ne 0$により、すべての自然数$n$について、$b_n \ne 0$となる。
$\displaystyle \frac{b_{n+1}}{b_n}=r$であることから、①の両辺を$b_n$で割ることにより
$\boxed{\ \ ウ\ \ }a_{n+1}=r\left(a_n+\boxed{\ \ エ\ \ }\right)$ $\cdots$④
が成り立つことが分かる。④に②と③を代入すると
$\left(r-\boxed{\ \ オ\ \ }\right)pn=r\left(p-\boxed{\ \ カ\ \ }\right)$$+\boxed{\ \ キ\ \ }$ $\cdots$⑤
となる。⑤が全ての$n$で成り立つことおよび$p \ne 0$により、$r=\boxed{\ \ オ\ \ }$を得る。
さらに、このことから、$p=\boxed{\ \ ク\ \ }$を得る。
以上から、すべての自然数$n$について、$a_n$と$b_n$が正であることもわかる。
(2)$p=\boxed{\ \ ク\ \ },$ $r=\boxed{\ \ オ\ \ }$であるから、$\left\{a_n\right\},$ $\left\{b_n\right\}$の初項から第$n$項
までの和は、それぞれ次の式で与えられる。
$\sum_{k=1}^na_k=\displaystyle \frac{\boxed{\ \ ケ\ \ }}{\boxed{\ \ コ\ \ }}n\left(n+\boxed{\ \ サ\ \ }\right)$
$\sum_{k=1}^nb_k$$=\boxed{\ \ シ\ \ }\left(\boxed{\ \ オ\ \ }^n-\boxed{\ \ ス\ \ }\right)$
(3)数列$\left\{a_n\right\}$に対して、初項3の数列$\left\{c_n\right\}$が次を満たすとする。
$a_nc_{n+1}-4a_{n+1}c_n+3c_{n+1}=0$ $(n=1,2,3,\ldots)\cdots$⑥
$a_n$が正であることから、⑥を変形して、$c_{n+1}=\displaystyle \frac{\boxed{\ \ セ\ \ }a_{n+1}}{a_n+\boxed{\ \ ソ\ \ }}c_n$を得る。
さらに、$p=\boxed{\ \ ク\ \ }$であることから、数列$\left\{c_n\right\}$は$\boxed{\boxed{\ \ タ\ \ }}$ことがわかる。
$\boxed{\boxed{\ \ タ\ \ }}$の解答群
⓪すべての項が同じ値をとる数列である
①公差が0でない等差数列である
②公比が1より大きい等比数列である
③公比が1より小さい等比数列である
④等差数列でも等比数列でもない
(4)$q,u$は定数で$q \ne 0$とする。数列$\left\{b_n\right\}$に対して、初項3の数列$\left\{d_n\right\}$が
次を満たすとする。
$d_nb_{n+1}-qd_{n+1}b_n+ub_{n+1}=0$ $(n=1,2,3,\ldots)\cdots$⑦
$r=\boxed{\ \ オ\ \ }$であることから、⑦を変形して、$d_{n+1}=\displaystyle \frac{\boxed{\ \ チ\ \ }}{q}(d_n+u)$
を得る。したがって、数列$\left\{d_n\right\}$が、公比が0より大きく1より小さい
等比数列となるための必要十分条件は、$q \gt \boxed{\ \ ツ\ \ }$かつ$u=\boxed{\ \ テ\ \ }$
である。
2021共通テスト過去問
【数B】数列:2020年駿台,高2,第2回全国模試 第6問(数列)の解説

単元:
#大学入試過去問(数学)#数列#漸化式#数学(高校生)#駿台模試
指導講師:
理数個別チャンネル
問題文全文(内容文):
2020年駿台,高2,第2回全国模試 第6問
数列{$a_n$},{$b_n$},{$c_n$}を次のように定める。$a_1=1, a_{n+1}=2a_n+1, b_1=1, b_{n+1}=2b_n+a_n, c_1=1, c_{n+1}=3c_n+b_n (n=1,2,3,...)$。次の問いに答えよう。
(1){$a_n$}の一般項を求めよう。
(2)$d_n=\dfrac{b_n}{2^(n-1)}$とおくとき、
(i)$d_{n+1}$を$d_n$を用いて表そう。 (ii){$d_n$}の一般項を求めよう。
(3){$c_n$}の一般項を求めよう。
この動画を見る
2020年駿台,高2,第2回全国模試 第6問
数列{$a_n$},{$b_n$},{$c_n$}を次のように定める。$a_1=1, a_{n+1}=2a_n+1, b_1=1, b_{n+1}=2b_n+a_n, c_1=1, c_{n+1}=3c_n+b_n (n=1,2,3,...)$。次の問いに答えよう。
(1){$a_n$}の一般項を求めよう。
(2)$d_n=\dfrac{b_n}{2^(n-1)}$とおくとき、
(i)$d_{n+1}$を$d_n$を用いて表そう。 (ii){$d_n$}の一般項を求めよう。
(3){$c_n$}の一般項を求めよう。
ガウス記号・漸化式・合同式

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$[(7+\sqrt{41}^{2021}]$を$2^{2021}$で割った余りを求めよ.
この動画を見る
$[(7+\sqrt{41}^{2021}]$を$2^{2021}$で割った余りを求めよ.
ヨビノリたくみ 東大 非典型的な漸化式
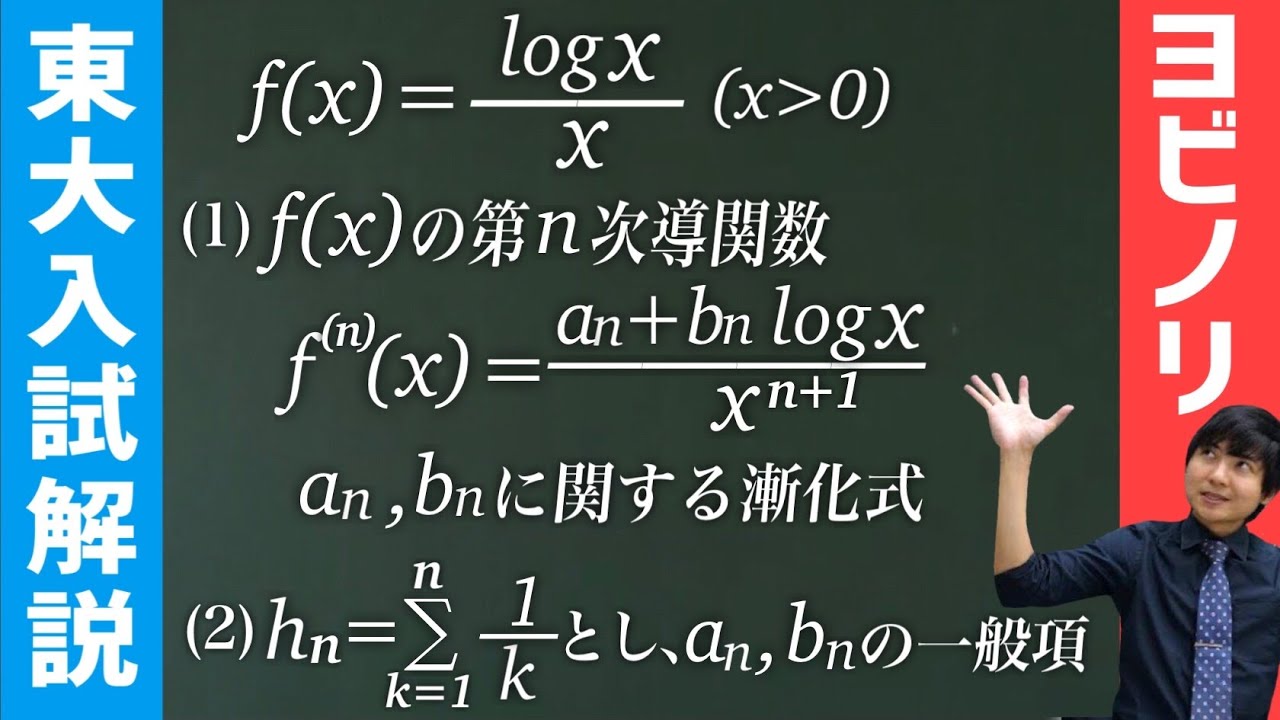
単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=\dfrac{\log_x}{x}(x \gt 0)$である.
(1)$f^{(n)}(x)=\dfrac{a_n+b_n\log x}{x^{n+1}}$と表される事を示し,漸化式を求めよ.
(2)$h_n=\displaystyle \sum_{\beta=1}^n \dfrac{1}{k}$を用いて,$a_n,b_n$の一般項を求めよ.
2005東大過去問
この動画を見る
$f(x)=\dfrac{\log_x}{x}(x \gt 0)$である.
(1)$f^{(n)}(x)=\dfrac{a_n+b_n\log x}{x^{n+1}}$と表される事を示し,漸化式を求めよ.
(2)$h_n=\displaystyle \sum_{\beta=1}^n \dfrac{1}{k}$を用いて,$a_n,b_n$の一般項を求めよ.
2005東大過去問
