 数列
数列
 数列
数列
福田のおもしろ数学127〜こんな漸化式解けるの?〜難しい漸化式の解き方

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$a_1$=$\displaystyle\frac{1}{2}$, $a_{n+1}$=$\sqrt{\displaystyle\frac{a_n+1}{2}}$ を満たす数列$\left\{a_n\right\}$の一般項$a_n$を求めよ。
この動画を見る
$a_1$=$\displaystyle\frac{1}{2}$, $a_{n+1}$=$\sqrt{\displaystyle\frac{a_n+1}{2}}$ を満たす数列$\left\{a_n\right\}$の一般項$a_n$を求めよ。
福田の数学〜一橋大学2024年文系第1問〜シグマが2024になるような2変数の値

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ $\displaystyle\sum_{k=1}^mk(n-2k)$=2024 を満たす正の整数の組($m$, $n$)を求めよ。
この動画を見る
$\Large\boxed{1}$ $\displaystyle\sum_{k=1}^mk(n-2k)$=2024 を満たす正の整数の組($m$, $n$)を求めよ。
福田の数学〜東北大学2024年文系第4問〜連立漸化式と不定方程式の整数解

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ $n$を正の整数とする。2つの整数$a_n$, $b_n$を条件
$(1+\sqrt 2)^n$=$a_n$+$b_n\sqrt 2$
により定める。ここで$\sqrt 2$は無理数なので、このような整数の組($a_n$, $b_n$)はただ1つに定まる。
(1)$a_{n+1}$, $b_{n+1}$を$a_n$, $b_n$を用いてそれぞれ表せ。さらに$b_4$, $b_5$, $b_6$の値をそれぞれ求めよ。
(2)等式$(1-\sqrt 2)^n$=$a_n$-$b_n\sqrt 2$ が成り立つことを数学的帰納法を用いて示せ。
(3)$n$≧2 のとき、$b_{n+1}b_{n-1}$-$b_n^2$ を求めよ。
(4)$pb_6$-$qb_5$=1, 0≦$p$≦100, 0≦$q$≦100 をすべて満たす整数$p$, $q$の組($p$, $q$)を1組求めよ。
この動画を見る
$\Large\boxed{4}$ $n$を正の整数とする。2つの整数$a_n$, $b_n$を条件
$(1+\sqrt 2)^n$=$a_n$+$b_n\sqrt 2$
により定める。ここで$\sqrt 2$は無理数なので、このような整数の組($a_n$, $b_n$)はただ1つに定まる。
(1)$a_{n+1}$, $b_{n+1}$を$a_n$, $b_n$を用いてそれぞれ表せ。さらに$b_4$, $b_5$, $b_6$の値をそれぞれ求めよ。
(2)等式$(1-\sqrt 2)^n$=$a_n$-$b_n\sqrt 2$ が成り立つことを数学的帰納法を用いて示せ。
(3)$n$≧2 のとき、$b_{n+1}b_{n-1}$-$b_n^2$ を求めよ。
(4)$pb_6$-$qb_5$=1, 0≦$p$≦100, 0≦$q$≦100 をすべて満たす整数$p$, $q$の組($p$, $q$)を1組求めよ。
福田の数学〜北海道大学2024年文系第2問〜漸化式を解く

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ 次の条件によって定められる数列$\left\{a_n\right\}$について考える。
$a_1$=3, $a_{n+1}$=$3a_n$-$\displaystyle\frac{3^{n+1}}{n(n+1)}$
(1)$b_n$=$\frac{a_n}{3^n}$ とおくとき、$b_{n+1}$を$b_n$と$n$の式で表せ。
(2)数列$\left\{a_n\right\}$ の一般項を求めよ。
この動画を見る
$\Large{\boxed{2}}$ 次の条件によって定められる数列$\left\{a_n\right\}$について考える。
$a_1$=3, $a_{n+1}$=$3a_n$-$\displaystyle\frac{3^{n+1}}{n(n+1)}$
(1)$b_n$=$\frac{a_n}{3^n}$ とおくとき、$b_{n+1}$を$b_n$と$n$の式で表せ。
(2)数列$\left\{a_n\right\}$ の一般項を求めよ。
福田の数学〜慶應義塾大学2024年看護医療学部第3問〜群数列

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 数列 $\frac{0}{1}$, $\frac{1}{1}$, $\frac{0}{2}$, $\frac{1}{2}$, $\frac{2}{2}$, $\frac{0}{3}$, $\frac{1}{3}$, $\frac{2}{3}$, $\frac{3}{3}$, $\frac{0}{4}$, $\frac{1}{4}$, $\frac{2}{4}$, $\frac{3}{4}$, $\frac{4}{4}$, $\frac{0}{5}$, ...
の第$n$項を$a_n$とする。
(1)約分することで$a_n$=1 を満たす自然数$n$のうち、$k$番目に小さいものを$N_k$で表す。例えば、$N_1$=2, $N_2$=5 である。また、自然数$k$に対して、$N_k$を$k$を用いて表すと$N_k$=$\boxed{\ \ セ\ \ }$である。また、自然数$k$に対して、数列$\left\{a_n\right\}$の初項から第$N_k$項までの和を$k$を用いて表すと$\boxed{\ \ ソ\ \ }$である。
(2)約分することで$a_n$=$\frac{1}{4}$ を満たす自然数$n$のうち、$k$番目に小さいものを$M_k$で表す。例えば$M_1$=11, $M_2$=$\boxed{\ \ タ\ \ }$である。このとき、自然数$k$に対して、$M_k$を$k$を用いて表すと$M_k$=$\boxed{\ \ チ\ \ }$である。
(3)$a_{200}$を約分した形で表すと$a_{200}$=$\boxed{\ \ ツ\ \ }$である。また数列$\left\{a_n\right\}$の初項から第200項までの和は$\boxed{\ \ テ\ \ }$である。
この動画を見る
$\Large\boxed{3}$ 数列 $\frac{0}{1}$, $\frac{1}{1}$, $\frac{0}{2}$, $\frac{1}{2}$, $\frac{2}{2}$, $\frac{0}{3}$, $\frac{1}{3}$, $\frac{2}{3}$, $\frac{3}{3}$, $\frac{0}{4}$, $\frac{1}{4}$, $\frac{2}{4}$, $\frac{3}{4}$, $\frac{4}{4}$, $\frac{0}{5}$, ...
の第$n$項を$a_n$とする。
(1)約分することで$a_n$=1 を満たす自然数$n$のうち、$k$番目に小さいものを$N_k$で表す。例えば、$N_1$=2, $N_2$=5 である。また、自然数$k$に対して、$N_k$を$k$を用いて表すと$N_k$=$\boxed{\ \ セ\ \ }$である。また、自然数$k$に対して、数列$\left\{a_n\right\}$の初項から第$N_k$項までの和を$k$を用いて表すと$\boxed{\ \ ソ\ \ }$である。
(2)約分することで$a_n$=$\frac{1}{4}$ を満たす自然数$n$のうち、$k$番目に小さいものを$M_k$で表す。例えば$M_1$=11, $M_2$=$\boxed{\ \ タ\ \ }$である。このとき、自然数$k$に対して、$M_k$を$k$を用いて表すと$M_k$=$\boxed{\ \ チ\ \ }$である。
(3)$a_{200}$を約分した形で表すと$a_{200}$=$\boxed{\ \ ツ\ \ }$である。また数列$\left\{a_n\right\}$の初項から第200項までの和は$\boxed{\ \ テ\ \ }$である。
福田のおもしろ数学100〜帰納的に考える方法〜階段の登り方

福田のおもしろ数学095〜素数が並ぶ数列

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
次の数列は全ての項が素数であるかどうか調べよ。
17, 19, 23, 29, 37, 47, 59, 73, 89, ...
この動画を見る
次の数列は全ての項が素数であるかどうか調べよ。
17, 19, 23, 29, 37, 47, 59, 73, 89, ...
福田の数学〜慶應義塾大学2024年薬学部第1問(1)〜等差数列と等比中項

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (1)$n$を自然数とする。数列$\left\{a_n\right\}$は初項が25, 公差が0でない等差数列であり、3つの項$a_8$, $a_9$, $a_{10}$を
$a_9$, $a_{10}$, $a_8$
の順に並べると等比数列になる。この数列の初項から第$n$項までの和を$S_n$とする。
(i)一般項$a_n$を$n$の式で表すと$a_n$=$\boxed{\ \ ア\ \ }$である。
(ii)不等式$S_n$<0 を満たす最小の$n$の値は$\boxed{\ \ イ\ \ }$である。
この動画を見る
$\Large\boxed{1}$ (1)$n$を自然数とする。数列$\left\{a_n\right\}$は初項が25, 公差が0でない等差数列であり、3つの項$a_8$, $a_9$, $a_{10}$を
$a_9$, $a_{10}$, $a_8$
の順に並べると等比数列になる。この数列の初項から第$n$項までの和を$S_n$とする。
(i)一般項$a_n$を$n$の式で表すと$a_n$=$\boxed{\ \ ア\ \ }$である。
(ii)不等式$S_n$<0 を満たす最小の$n$の値は$\boxed{\ \ イ\ \ }$である。
福田の数学〜東京工業大学2024年理系第3問〜点列と漸化式の極限

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ $xy$平面上に、点A($a$,0), B(0,$b$), C($-a$,0)(ただし0<$a$<$b$)をとる。点A,Bを通る直線を$l$とし、点Cを通り線分BCに垂直な直線を$k$とする。さらに、点Aを通り$y$軸に平行な直線と直線$k$との交点を$C_1$とし、点$C_1$を通り、$x$軸に平行な直線と直線$l$との交点を$A_1$とする。以下、$n$=1,2,3,...に対して、点$A_n$を通り$y$軸に平行な直線と直線$k$との交点を$C_{n+1}$、点$C_{n+1}$を通り$x$軸に平行な直線と直線$l$との交点を$A_{n+1}$とする。
(1)点$A_n$, $C_n$の座標を求めよ。
(2)△$CBA_n$の面積$S_n$を求めよ。
(3)$\displaystyle\lim_{n \to \infty}\frac{BA_n}{BC}$を求めよ。
この動画を見る
$\Large\boxed{3}$ $xy$平面上に、点A($a$,0), B(0,$b$), C($-a$,0)(ただし0<$a$<$b$)をとる。点A,Bを通る直線を$l$とし、点Cを通り線分BCに垂直な直線を$k$とする。さらに、点Aを通り$y$軸に平行な直線と直線$k$との交点を$C_1$とし、点$C_1$を通り、$x$軸に平行な直線と直線$l$との交点を$A_1$とする。以下、$n$=1,2,3,...に対して、点$A_n$を通り$y$軸に平行な直線と直線$k$との交点を$C_{n+1}$、点$C_{n+1}$を通り$x$軸に平行な直線と直線$l$との交点を$A_{n+1}$とする。
(1)点$A_n$, $C_n$の座標を求めよ。
(2)△$CBA_n$の面積$S_n$を求めよ。
(3)$\displaystyle\lim_{n \to \infty}\frac{BA_n}{BC}$を求めよ。
難解な数列の問題 By 英語orドイツ語シはBかHか さん

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$a_0=b_0=1$
$a_{n+1}=\displaystyle \frac{a_n}{a_n^2+b_n^2}$
$b_{n+1}=2-\displaystyle \frac{b_n}{a_n^2+b_n^2}$
一般項$a_n,b_n$を求めよ。
この動画を見る
$a_0=b_0=1$
$a_{n+1}=\displaystyle \frac{a_n}{a_n^2+b_n^2}$
$b_{n+1}=2-\displaystyle \frac{b_n}{a_n^2+b_n^2}$
一般項$a_n,b_n$を求めよ。
福田の数学〜慶應義塾大学2024年理工学部第1問(2)〜漸化式とはさみうちの原理

単元:
#大学入試過去問(数学)#漸化式#関数と極限#数列の極限#関数の極限#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
関数f(x)は実数全体で定義されており、$x\leqq 2$において
$\dfrac{2}{3}-\dfrac{1}{3}x\leqq f(x)\leqq 2-x$
を満たしているものとする。数列{$a_{ n }$}は漸化式
$a_{ n+1 }=a_{ n }+f(a_{ n })$
を満たしているものとする。
(i)$a_{ 1 } \leqq 2$ならば、すべての自然数nに対して、$a_{ 1 } \leqq a_{ n }\leqq2$となる事を証明しなさい。
(ii)$a_{ 1 } \leqq 2$ならば、$a_{ 1 }$の値によらず$\displaystyle \lim_{ n \to \infty } a_n = 2$となる事を証明しなさい。
この動画を見る
関数f(x)は実数全体で定義されており、$x\leqq 2$において
$\dfrac{2}{3}-\dfrac{1}{3}x\leqq f(x)\leqq 2-x$
を満たしているものとする。数列{$a_{ n }$}は漸化式
$a_{ n+1 }=a_{ n }+f(a_{ n })$
を満たしているものとする。
(i)$a_{ 1 } \leqq 2$ならば、すべての自然数nに対して、$a_{ 1 } \leqq a_{ n }\leqq2$となる事を証明しなさい。
(ii)$a_{ 1 } \leqq 2$ならば、$a_{ 1 }$の値によらず$\displaystyle \lim_{ n \to \infty } a_n = 2$となる事を証明しなさい。
福田のおもしろ数学051〜10秒チャレンジ!〜階乗の付いた分数の計算

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\displaystyle \frac{1}{2!}+\displaystyle \frac{2}{3!}+\displaystyle \frac{3}{4!}+\displaystyle \frac{4}{5!}+\displaystyle \frac{5}{6!}$を計算してください。
この動画を見る
$\displaystyle \frac{1}{2!}+\displaystyle \frac{2}{3!}+\displaystyle \frac{3}{4!}+\displaystyle \frac{4}{5!}+\displaystyle \frac{5}{6!}$を計算してください。
福田の数学〜東京大学2018年理系第2問〜数列の増減とユークリッドの互除法

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#数列#漸化式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$a_{ 1 },a_{ 2 }・・・$を
$a_{ n }=\dfrac{2_{ n }+{}_1 \mathrm{ C }_n}{n!}$(n=1,2,・・・)
で定める
(1)$n \geqq 2$とする。$\dfrac{a_{n}}{a_{n-1}}$を規約分数$\dfrac{q_{n}}{p_{n}}$として表したときの分母$p_{n} \geqq 1$と分子$q_{n}$を求めよ。
(2)$a_{n}$が整数となる$n\geqq1$をすべて求めよ。
2018東京大学理過去問
この動画を見る
$a_{ 1 },a_{ 2 }・・・$を
$a_{ n }=\dfrac{2_{ n }+{}_1 \mathrm{ C }_n}{n!}$(n=1,2,・・・)
で定める
(1)$n \geqq 2$とする。$\dfrac{a_{n}}{a_{n-1}}$を規約分数$\dfrac{q_{n}}{p_{n}}$として表したときの分母$p_{n} \geqq 1$と分子$q_{n}$を求めよ。
(2)$a_{n}$が整数となる$n\geqq1$をすべて求めよ。
2018東京大学理過去問
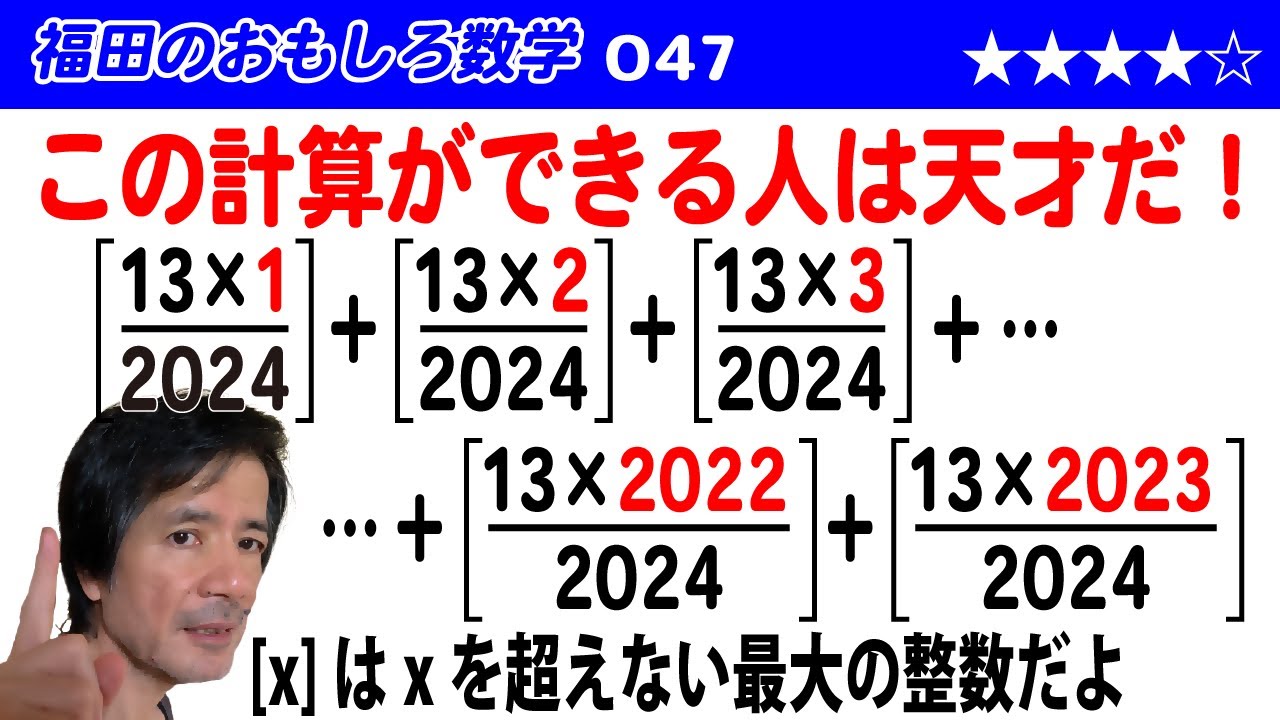
福田のおもしろ数学047〜これができたら天才〜ガウス記号のついた数の和
単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\left[\dfrac{13×1}{2024}\right]+\left[\dfrac{13×2}{2024}\right]+\left[\dfrac{13×3}{2024}\right]+・・・+\left[\dfrac{13×2023}{2024}\right]$を計算してください。
ただし、$[x]$は$x$を超えない最大の整数を表します。
この動画を見る
$\left[\dfrac{13×1}{2024}\right]+\left[\dfrac{13×2}{2024}\right]+\left[\dfrac{13×3}{2024}\right]+・・・+\left[\dfrac{13×2023}{2024}\right]$を計算してください。
ただし、$[x]$は$x$を超えない最大の整数を表します。
数列 by ハルハルさん すげー解答: 英語orドイツ語さん #Shorts

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$a_1=0$
$a_{n+1}=(a_n+4)(a_n+10)$
この動画を見る
$a_1=0$
$a_{n+1}=(a_n+4)(a_n+10)$
2024年共通テスト徹底解説〜数学ⅡB第4問数列〜福田の入試問題解説

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト#数B
指導講師:
福田次郎
問題文全文(内容文):
共通テスト2024の数学ⅡB第4問数列を徹底解説します
2024共通テスト過去問
この動画を見る
共通テスト2024の数学ⅡB第4問数列を徹底解説します
2024共通テスト過去問
数列 難易度高め by Picmin3daisukiさん #Shorts

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$a_1=\sqrt{ 3 }$
$a_{n+1}=\displaystyle \frac{-1+\sqrt{ 1+a_n^2 }}{a_n}$を満たす一般項$a_n$を求めよ。
この動画を見る
$a_1=\sqrt{ 3 }$
$a_{n+1}=\displaystyle \frac{-1+\sqrt{ 1+a_n^2 }}{a_n}$を満たす一般項$a_n$を求めよ。
数列 By Picmin3daisukiさん

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$a_1=\sin^22$
$a_{n+1}=4a_n(1-a_n)$を満たす一般項$a_n$を求めよ。
この動画を見る
$a_1=\sin^22$
$a_{n+1}=4a_n(1-a_n)$を満たす一般項$a_n$を求めよ。
Picmin3daisukiさんの数列(オリジナル)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$a_1=\sqrt{ 3 }$
$\displaystyle \frac{a_{n+1}}{a_n}=a_{n+1}\ a_n+2$のとき一般項$a_n$を求めよ
この動画を見る
$a_1=\sqrt{ 3 }$
$\displaystyle \frac{a_{n+1}}{a_n}=a_{n+1}\ a_n+2$のとき一般項$a_n$を求めよ
福田のおもしろ数学020〜わんちゃんの男の子と女の子の比率は〜Google入社試験の類題

単元:
#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#数列の極限#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
わんちゃんの国があります。この国ではどの家庭も男の子が産まれるまで子供を作り続けます。この国の男の子と女の子の比率はどうなりますか.
google入社試験過去問
この動画を見る
わんちゃんの国があります。この国ではどの家庭も男の子が産まれるまで子供を作り続けます。この国の男の子と女の子の比率はどうなりますか.
google入社試験過去問
等差数列の和 視聴者さんからいただいた問題

福田の数学〜0と1の間に整数は存在しないなんて当たり前〜東京大学2018年文系第2問〜数列の増減と整数となる条件

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
数列$a_{ 1},a_{ 2 }$,・・・を$a_{ n }=\displaystyle \frac{{}_2n \mathrm{ C }_n}{n!}$(n=1,2,・・・)で定める。
(1)$a_{ 7 }$と1の大小を調べよ。
(2)$n \geqq 2$とする。$\displaystyle \frac{a_{ n }}{a_{ n-1}}<1$を満たすnの範囲を求めよ。
(3)$a_{ n }$が整数となる$n \geqq 1$を全て求めよ。
2018東京大学文過去問
この動画を見る
数列$a_{ 1},a_{ 2 }$,・・・を$a_{ n }=\displaystyle \frac{{}_2n \mathrm{ C }_n}{n!}$(n=1,2,・・・)で定める。
(1)$a_{ 7 }$と1の大小を調べよ。
(2)$n \geqq 2$とする。$\displaystyle \frac{a_{ n }}{a_{ n-1}}<1$を満たすnの範囲を求めよ。
(3)$a_{ n }$が整数となる$n \geqq 1$を全て求めよ。
2018東京大学文過去問
福田のおもしろ数学011〜あけましておめでとうございます〜2024の階乗は末尾に0が何個並ぶか

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
2024 !の末尾に並ぶ 0 の個数を求めよ。
この動画を見る
2024 !の末尾に並ぶ 0 の個数を求めよ。
福田のおもしろ数学010〜10秒で解けるキミは天才〜階乗の和の1の位

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
1 !十 2 !十 3 !十・・・十 2023 !十 2024 !の 1 の位を求めよ。
この動画を見る
1 !十 2 !十 3 !十・・・十 2023 !十 2024 !の 1 の位を求めよ。
福田の数学〜ポリアの壺とは逆の試行における確率の極限〜杏林大学2023年医学部第1問後編〜確率漸化式と極限

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
複数の玉が人った袋から玉を 1 個取り出して袋に戻す事象を考える。どの玉も同じ確率で取り出されるものとし、nを自然数として、以下の間いに答えよ。
(1) 袋の中に赤玉 1 個と黒玉 2 個が入っている。この袋の中から玉を 1 個取り出し、取り出した玉と同じ色の玉をひとつ加え、合計 2 個の玉を袋に戻すという試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、$p_{ 2 }=\dfrac{\fbox{ア}}{\fbox{イ}}, p_{ 3 }=\dfrac{\fbox{ウ}}{\fbox{エ}}$
( 2 )袋の中に赤玉 3 個と黒玉 2 個が人っている。この袋の中から玉を 1 個取り出し、赤玉と黒玉を 1 個ずつ、合計 2 個の球を袋に戻す試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、次式が成り立つ。
$p_{ 2 }=\dfrac{\fbox{オカ}}{\fbox{キク}}, p_{ 3 }=\dfrac{\fbox{ケコ}}{\fbox{サシ}}$
n回目の試行開始時点で袋に人っている玉の個数$M_{ n } はM_{ n }=n+\fbox{ス}$であり、この時点で袋に入っていると期待される赤玉の個数$R_{ n }はR_{ n }=M_{ n }×P_{ n }$と表される。n回目の試行において、黒玉が取り出された場合にのみ、試行後の赤玉の個数が施行前と比べて$\fbox{セ}$個増えるため、n+ 1 回目の試行開始時点で袋に入っていると期待される赤玉の個数は$R_{ n+1 }=R_{ n }+(1-P_{ n })×\fbox{セ}$となる。したがって、
$P_{ n+1 }=\dfrac{n+\fbox{ソ}}{n+\fbox{タ}}×P_{ n }+\dfrac{1}{n+\fbox{チ}}$
が成り立つ。このことから、$(n+3)×(n+\fbox{ツ})×(P_{n}-\dfrac{\fbox{テ}}{\fbox{ト}})$がnに依らず一定となる事が分かり、$\displaystyle \lim_{ n \to \infty } P_n =\dfrac{\fbox{ナ}}{\fbox{ニ}}$と求められる。
2023杏林大学医過去問
この動画を見る
複数の玉が人った袋から玉を 1 個取り出して袋に戻す事象を考える。どの玉も同じ確率で取り出されるものとし、nを自然数として、以下の間いに答えよ。
(1) 袋の中に赤玉 1 個と黒玉 2 個が入っている。この袋の中から玉を 1 個取り出し、取り出した玉と同じ色の玉をひとつ加え、合計 2 個の玉を袋に戻すという試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、$p_{ 2 }=\dfrac{\fbox{ア}}{\fbox{イ}}, p_{ 3 }=\dfrac{\fbox{ウ}}{\fbox{エ}}$
( 2 )袋の中に赤玉 3 個と黒玉 2 個が人っている。この袋の中から玉を 1 個取り出し、赤玉と黒玉を 1 個ずつ、合計 2 個の球を袋に戻す試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、次式が成り立つ。
$p_{ 2 }=\dfrac{\fbox{オカ}}{\fbox{キク}}, p_{ 3 }=\dfrac{\fbox{ケコ}}{\fbox{サシ}}$
n回目の試行開始時点で袋に人っている玉の個数$M_{ n } はM_{ n }=n+\fbox{ス}$であり、この時点で袋に入っていると期待される赤玉の個数$R_{ n }はR_{ n }=M_{ n }×P_{ n }$と表される。n回目の試行において、黒玉が取り出された場合にのみ、試行後の赤玉の個数が施行前と比べて$\fbox{セ}$個増えるため、n+ 1 回目の試行開始時点で袋に入っていると期待される赤玉の個数は$R_{ n+1 }=R_{ n }+(1-P_{ n })×\fbox{セ}$となる。したがって、
$P_{ n+1 }=\dfrac{n+\fbox{ソ}}{n+\fbox{タ}}×P_{ n }+\dfrac{1}{n+\fbox{チ}}$
が成り立つ。このことから、$(n+3)×(n+\fbox{ツ})×(P_{n}-\dfrac{\fbox{テ}}{\fbox{ト}})$がnに依らず一定となる事が分かり、$\displaystyle \lim_{ n \to \infty } P_n =\dfrac{\fbox{ナ}}{\fbox{ニ}}$と求められる。
2023杏林大学医過去問
【共テ数学IIB】知らなきゃ損な裏技集__これで解答時間をキュッと短縮します(指数・対数、微分積分、数列、ベクトル)

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#指数関数と対数関数#微分法と積分法#指数関数#対数関数#数列#数列とその和(等差・等比・階差・Σ)#センター試験・共通テスト関連#共通テスト#数学(高校生)#数B#数C
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【共テ数学IIB】解答時間短縮裏技集 紹介動画です(指数・対数、微分積分、数列、ベクトル)
この動画を見る
【共テ数学IIB】解答時間短縮裏技集 紹介動画です(指数・対数、微分積分、数列、ベクトル)
福田の数学〜ポリアの壺は証明を覚えよう〜杏林大学2023年医学部第1問前編〜ポリアの壺

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
複数の玉が人った袋から玉を 1 個取り出して袋に戻す事象を考える。どの玉も同じ確率で取り出されるものとし、nを自然数として、以下の間いに答えよ。
(1) 袋の中に赤玉 1 個と黒玉 2 個が入っている。この袋の中から玉を 1 個取り出し、取り出した玉と同じ色の玉をひとつ加え、合計 2 個の玉を袋に戻すという試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、$p_{ 2 }=\dfrac{\fbox{ア}}{\fbox{イ}}, p_{ 3 }=\dfrac{\fbox{ウ}}{\fbox{エ}}$
( 2 )袋の中に赤玉 3 個と黒玉 2 個が人っている。この袋の中から玉を 1 個取り出し、赤玉と黒玉を 1 個ずつ、合計 2 個の球を袋に戻す試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、次式が成り立つ。
$p_{ 2 }=\dfrac{\fbox{オカ}}{\fbox{キク}}, p_{ 3 }=\dfrac{\fbox{ケコ}}{\fbox{サシ}}$
n回目の試行開始時点で袋に人っている玉の個数$M_{ n } はM_{ n }=n+\fbox{ス}$であり、この時点で袋に入っていると期待される赤玉の個数$R_{ n }はR_{ n }=M_{ n }×P_{ n }$と表される。n回目の試行において、黒玉が取り出された場合にのみ、試行後の赤玉の個数が施行前と比べて$\fbox{セ}$個増えるため、n+ 1 回目の試行開始時点で袋に入っていると期待される赤玉の個数は$R_{ n+1 }=R_{ n }+(1-P_{ n })×\fbox{セ}$となる。したがって、
$P_{ n+1 }=\dfrac{n+\fbox{ソ}}{n+\fbox{タ}}×P_{ n }+\dfrac{1}{n+\fbox{チ}}$
が成り立つ。このことから、$(n+3)×(n+\fbox{ツ})×(P_{n}-\dfrac{\fbox{テ}}{\fbox{ト}})$がnに依らず一定となる事が分かり、$\displaystyle \lim_{ n \to \infty } P_n =\dfrac{\fbox{ナ}}{\fbox{ニ}}$と求められる。
2023杏林大学医過去問
この動画を見る
複数の玉が人った袋から玉を 1 個取り出して袋に戻す事象を考える。どの玉も同じ確率で取り出されるものとし、nを自然数として、以下の間いに答えよ。
(1) 袋の中に赤玉 1 個と黒玉 2 個が入っている。この袋の中から玉を 1 個取り出し、取り出した玉と同じ色の玉をひとつ加え、合計 2 個の玉を袋に戻すという試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、$p_{ 2 }=\dfrac{\fbox{ア}}{\fbox{イ}}, p_{ 3 }=\dfrac{\fbox{ウ}}{\fbox{エ}}$
( 2 )袋の中に赤玉 3 個と黒玉 2 個が人っている。この袋の中から玉を 1 個取り出し、赤玉と黒玉を 1 個ずつ、合計 2 個の球を袋に戻す試行を繰り返す。n回目の試行において赤玉が取り出される確率を$p_{ n }$とすると、次式が成り立つ。
$p_{ 2 }=\dfrac{\fbox{オカ}}{\fbox{キク}}, p_{ 3 }=\dfrac{\fbox{ケコ}}{\fbox{サシ}}$
n回目の試行開始時点で袋に人っている玉の個数$M_{ n } はM_{ n }=n+\fbox{ス}$であり、この時点で袋に入っていると期待される赤玉の個数$R_{ n }はR_{ n }=M_{ n }×P_{ n }$と表される。n回目の試行において、黒玉が取り出された場合にのみ、試行後の赤玉の個数が施行前と比べて$\fbox{セ}$個増えるため、n+ 1 回目の試行開始時点で袋に入っていると期待される赤玉の個数は$R_{ n+1 }=R_{ n }+(1-P_{ n })×\fbox{セ}$となる。したがって、
$P_{ n+1 }=\dfrac{n+\fbox{ソ}}{n+\fbox{タ}}×P_{ n }+\dfrac{1}{n+\fbox{チ}}$
が成り立つ。このことから、$(n+3)×(n+\fbox{ツ})×(P_{n}-\dfrac{\fbox{テ}}{\fbox{ト}})$がnに依らず一定となる事が分かり、$\displaystyle \lim_{ n \to \infty } P_n =\dfrac{\fbox{ナ}}{\fbox{ニ}}$と求められる。
2023杏林大学医過去問
【共テ数学IIB】知らなきゃ損な裏技集__これで解答時間をキュッと短縮します(指数・対数、微分積分、数列、ベクトル)

単元:
#数Ⅱ#大学入試過去問(数学)#平面上のベクトル#指数関数と対数関数#微分法と積分法#指数関数#対数関数#数列#センター試験・共通テスト関連#共通テスト#数学(高校生)#数B#数C
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【共テ数学IIB】解答時間短縮、裏技集説明動画です。(指数・対数、微分積分、数列、ベクトル)
この動画を見る
【共テ数学IIB】解答時間短縮、裏技集説明動画です。(指数・対数、微分積分、数列、ベクトル)
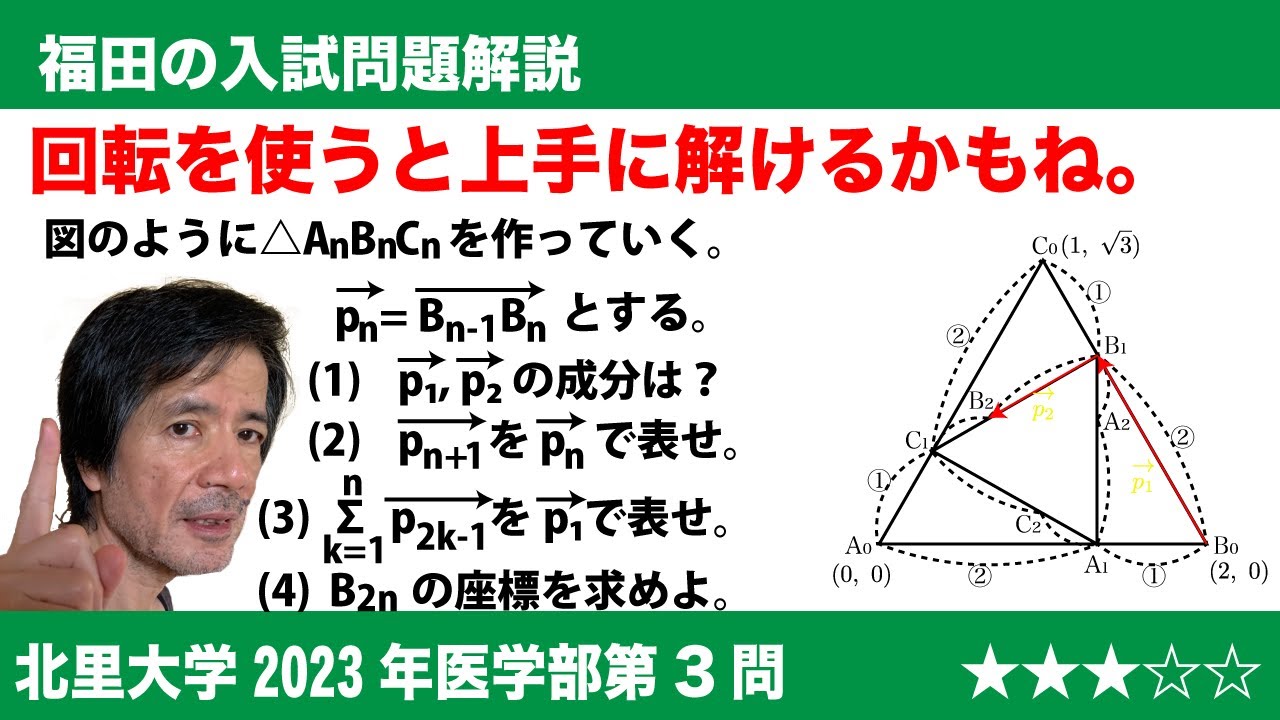
福田の数学〜回転の概念を使って考えるよ〜北里大学2023年医学部第3問〜ベクトルの漸化式と点列
単元:
#大学入試過去問(数学)#平面上のベクトル#数列#ベクトルと平面図形、ベクトル方程式#漸化式#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数B#数C
指導講師:
福田次郎
問題文全文(内容文):
座標平面上に 3 点 $A_{0} ( 0 , 0 ), B_{0} ( 2 , 0 ), C_{0}( 1 ,\sqrt{ 3 })$があり、線分$A_{0}B_{0},B_{0}C_{0},C_{0}A_{0}$をそれぞれ 2 : 1 に内分する点 $A_{1} ,B_{1} ,C_{1}$をとる。以下同様にして、正の整数nに対し、線分$A_{n}B_{n},B_{n}C_{n},C_{n}A_{n}$をそれぞれ 2 : 1 に内分する点$A_{n+1},B_{n+1},C_{n+1}$をとる。また、$\overrightarrow{ P_{n} }=\overrightarrow{ B_{n-1}B_{n} }(n=1,2,3,・・・)$とおく。
(1)$\overrightarrow{ p_{1} },\overrightarrow{ p_{2} }$をそれぞれ成分表示せよ。
(2)$\overrightarrow{ p_{n+2} }を\overrightarrow{ p_{n} }$を用いて表せ。
(3)$\displaystyle \sum_{k=1}^n \overrightarrow{ p_{2k-1}}$を$\overrightarrow{ p-1}$を用いて表せ。
(4)点B_{2n}の座標を求めよ。
2023北里大学医過去問
この動画を見る
座標平面上に 3 点 $A_{0} ( 0 , 0 ), B_{0} ( 2 , 0 ), C_{0}( 1 ,\sqrt{ 3 })$があり、線分$A_{0}B_{0},B_{0}C_{0},C_{0}A_{0}$をそれぞれ 2 : 1 に内分する点 $A_{1} ,B_{1} ,C_{1}$をとる。以下同様にして、正の整数nに対し、線分$A_{n}B_{n},B_{n}C_{n},C_{n}A_{n}$をそれぞれ 2 : 1 に内分する点$A_{n+1},B_{n+1},C_{n+1}$をとる。また、$\overrightarrow{ P_{n} }=\overrightarrow{ B_{n-1}B_{n} }(n=1,2,3,・・・)$とおく。
(1)$\overrightarrow{ p_{1} },\overrightarrow{ p_{2} }$をそれぞれ成分表示せよ。
(2)$\overrightarrow{ p_{n+2} }を\overrightarrow{ p_{n} }$を用いて表せ。
(3)$\displaystyle \sum_{k=1}^n \overrightarrow{ p_{2k-1}}$を$\overrightarrow{ p-1}$を用いて表せ。
(4)点B_{2n}の座標を求めよ。
2023北里大学医過去問
福田の数学〜整数部分の評価が難しい問題〜北里大学2023年医学部第1問(3)〜漸化式と整数部分の評価

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$a=3+\sqrt{10},b=3-\sqrt{10}$とし、正の整数nに対して$A_n=a^n+b^n$とおく。
このとき、$A_{2} ,A_{3}$の値はそれぞれ$A_{2}=\fbox{ク},A_{3}=\fbox{ケ}$であり、
$A_{n+2}$を$A_{n+1},A_{n}$を用いて表すと$A_{n+2}=\boxed{コ}$である。
また、$a^{111}$の整数部分を$k$とするとき、kを10で割ると$\boxed{サ}$余る。
2023北里大学医過去問
この動画を見る
$a=3+\sqrt{10},b=3-\sqrt{10}$とし、正の整数nに対して$A_n=a^n+b^n$とおく。
このとき、$A_{2} ,A_{3}$の値はそれぞれ$A_{2}=\fbox{ク},A_{3}=\fbox{ケ}$であり、
$A_{n+2}$を$A_{n+1},A_{n}$を用いて表すと$A_{n+2}=\boxed{コ}$である。
また、$a^{111}$の整数部分を$k$とするとき、kを10で割ると$\boxed{サ}$余る。
2023北里大学医過去問
