 数B
数B
 数B
数B
福田の数学〜東京工業大学2023年理系第3問〜複素数の絶対値と偏角に関する確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#複素数平面#確率#漸化式#複素数平面#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数B#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 実数が書かれた3枚のカード$\boxed{0}$,$\boxed{1}$,$\boxed{\sqrt 3}$から無作為に2枚のカードを順に選び、出た実数を順に実部と虚部にもつ複素数を得る操作を考える。正の整数nに対して、この操作をn回繰り返して得られるn個の複素数の積を$z_n$で表す。
(1)|$z_n$|<5となる確率$P_n$を求めよ。
(2)$z_n^2$が実数となる確率$Q_n$を求めよ。
2023東京工業大学理系過去問
この動画を見る
$\Large\boxed{3}$ 実数が書かれた3枚のカード$\boxed{0}$,$\boxed{1}$,$\boxed{\sqrt 3}$から無作為に2枚のカードを順に選び、出た実数を順に実部と虚部にもつ複素数を得る操作を考える。正の整数nに対して、この操作をn回繰り返して得られるn個の複素数の積を$z_n$で表す。
(1)|$z_n$|<5となる確率$P_n$を求めよ。
(2)$z_n^2$が実数となる確率$Q_n$を求めよ。
2023東京工業大学理系過去問
【数B】数列:等比数列の和 公比が4、第10項が4096である等比数列の初項を求めよ。

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
理数個別チャンネル
問題文全文(内容文):
第1項から第10項までの和が4、第1項から第20項までの和が24のとき、第1項から第40項までの和を求めよ。
この動画を見る
第1項から第10項までの和が4、第1項から第20項までの和が24のとき、第1項から第40項までの和を求めよ。
【数B】数列・等比数列の和 公比が4、第10項が4096である等比数列の初項を求めよ。

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
第1項から第10項までの和が4、第1項から第20項までの和が24のとき、第1項から第40項までの和を求めよ。
この動画を見る
第1項から第10項までの和が4、第1項から第20項までの和が24のとき、第1項から第40項までの和を求めよ。
大学入試問題#463「ええ問題や~~」 信州大学 理・医 (2016) #積分の応用

単元:
#大学入試過去問(数学)#数学的帰納法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} (1-x^2)^n dx$
$=\displaystyle \frac{4^n(n!)^2}{(2n+1)!}$を示せ
出典:2016年信州大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} (1-x^2)^n dx$
$=\displaystyle \frac{4^n(n!)^2}{(2n+1)!}$を示せ
出典:2016年信州大学医学部 入試問題
福田の数学〜東京大学2023年理系第1問〜定積分と不等式

単元:
#大学入試過去問(数学)#漸化式#微分とその応用#積分とその応用#微分法#定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ [1]正の整数kに対し、$A_k=\displaystyle\int_{\sqrt{k\pi}}^{\sqrt{(k+1)\pi}}|\sin(x^2)|dx$ とおく。次の不等式が成り立つことを示せ。
$\displaystyle\frac{1}{\sqrt{(k+1)\pi}}$≦$A_k$≦$\displaystyle\frac{1}{\sqrt{k\pi}}$
[2]正の整数nに対し、$B_n$=$\displaystyle\frac{1}{\sqrt n}\int_{\sqrt{n\pi}}^{\sqrt{2n\pi}}|\sin(x^2)|dx$ とおく。
極限$\displaystyle\lim_{n \to \infty}B_n$ を求めよ。
2023東京大学理系過去問
この動画を見る
$\Large\boxed{1}$ [1]正の整数kに対し、$A_k=\displaystyle\int_{\sqrt{k\pi}}^{\sqrt{(k+1)\pi}}|\sin(x^2)|dx$ とおく。次の不等式が成り立つことを示せ。
$\displaystyle\frac{1}{\sqrt{(k+1)\pi}}$≦$A_k$≦$\displaystyle\frac{1}{\sqrt{k\pi}}$
[2]正の整数nに対し、$B_n$=$\displaystyle\frac{1}{\sqrt n}\int_{\sqrt{n\pi}}^{\sqrt{2n\pi}}|\sin(x^2)|dx$ とおく。
極限$\displaystyle\lim_{n \to \infty}B_n$ を求めよ。
2023東京大学理系過去問
福田の1.5倍速演習〜合格する重要問題090〜名古屋大学2018年度理系第1問〜定積分と不等式と極限

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#微分とその応用#積分とその応用#数列の極限#微分法#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ 自然数nに対し、定積分$I_n$=$\displaystyle\int_0^1\frac{x^n}{x^2+1}dx$を考える。このとき、次の問いに答えよ。
(1)$I_n$+$I_{n+2}$=$\frac{1}{n+1}$を示せ。
(2)0≦$I_{n+1}$≦$I_n$≦$\frac{1}{n+1}$を示せ。
(3)$\displaystyle\lim_{n \to \infty}nI_n$ を求めよ。
(4)$S_n$=$\displaystyle\sum_{k=1}^n\frac{(-1)^{k-1}}{2k}$ とする。このとき(1), (2)を用いて$\displaystyle\lim_{n \to \infty}S_n$ を求めよ。
2018名古屋大学理系過去問
この動画を見る
$\Large\boxed{1}$ 自然数nに対し、定積分$I_n$=$\displaystyle\int_0^1\frac{x^n}{x^2+1}dx$を考える。このとき、次の問いに答えよ。
(1)$I_n$+$I_{n+2}$=$\frac{1}{n+1}$を示せ。
(2)0≦$I_{n+1}$≦$I_n$≦$\frac{1}{n+1}$を示せ。
(3)$\displaystyle\lim_{n \to \infty}nI_n$ を求めよ。
(4)$S_n$=$\displaystyle\sum_{k=1}^n\frac{(-1)^{k-1}}{2k}$ とする。このとき(1), (2)を用いて$\displaystyle\lim_{n \to \infty}S_n$ を求めよ。
2018名古屋大学理系過去問
【数学】新課程「統計」が20分で分かる動画【全国1位の勉強法】

福田の数学〜2023年共通テスト速報〜数学IIB第3問確率分布〜正規分布と二項分布

単元:
#大学入試過去問(数学)#確率分布と統計的な推測#確率分布#センター試験・共通テスト関連#共通テスト#数学(高校生)#大学入試解答速報#数学#共通テスト#数B
指導講師:
福田次郎
問題文全文(内容文):
第3問
以下の問題を解答するにあたっては、必要に応じて43ページの正規分布表を用いてもよい。
(1)ある生産地で生産されるピーマン全体を母集団とし、この母集団におけるピーマン1個の重さ(単位はg)を表す確率変数をXとする。mとσを正の実数とし、Xは正規分布N(m, $\sigma^2$)に従うとする。
(i)この母集団から1個のピーマンを無作為に抽出したとき、重さがm g以上である確率P(X≧m)は
P(X≧m)=P$\left(\frac{X-m}{\sigma}\geqq \boxed{\ \ ア\ \ }\right)$=$\frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }}$
である。
(ii)母集団から無作為に抽出された大きさnの標本$X_1$, $X_2$, ..., $X_n$の標本平均を$\bar{X}$とする。$\bar{X}$の平均(期待値)と標準偏差はそれぞれ
E($\bar{X}$)=$\boxed{\boxed{\ \ エ\ \ }}$, σ($\bar{X}$)=$\boxed{\boxed{\ \ オ\ \ }}$
となる。
n=400, 標本平均が30.0g, 標本の標準偏差が3.6gのとき、mの信頼度90%の信頼区間を次の方針で求めよう。
方針:Zを標準正規分布N(0,1)に従う確率変数として、P($-z_0 \leqq Z \leqq z_0$)=0.901 となる$z_0$を正規分布表から求める。この$z_0$を用いるとmの信頼度90.1%の信頼区間が求められるが、これを信頼度90%の信頼区間とみなして考える。
方針において、$z_0$=$\boxed{\ \ カ\ \ }$.$\boxed{\ \ キク\ \ }$である。
一般に、標本の大きさnが大きいときには、母標準偏差の代わりに、標本の標準偏差を用いてよいことが知られている。n=400は十分に大きいので、方針に基づくと、mの信頼度90%の信頼区間は$\boxed{\boxed{\ \ ケ\ \ }}$となる。
$\boxed{\boxed{\ \ エ\ \ }}, \boxed{\boxed{\ \ オ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪σ ①$\sigma^2$ ②$\frac{\sigma}{\sqrt n}$ ③$\frac{\sigma^2}{n}$
④m ⑤2m ⑥$m^2$ ⑦$\sqrt m$
⑧$\frac{\sigma}{n}$ ⑨$n\sigma $ⓐ$nm$ ⓑ$\frac{m}{n}$
$\boxed{\boxed{\ \ ケ\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
⓪28.6≦m≦31.4 ①28.7≦m≦31.3 ②28.9≦m≦31.1
③29.6≦m≦30.4 ④29.7≦m≦30.3 ⑤29.9≦m≦30.1
(2)(1)の確率変数Xにおいて、m=30.0, σ=3.6とした母集団から無作為にピーマンを1個ずつ抽出し、ピーマン2個を1組にしたものを袋に入れていく。このようにしてピーマン2個を1組にしたものを25袋作る。その際、1袋ずつの重さの分数を小さくするために、次のピーマン分類法を考える。
ピーマン分類法:無作為に抽出したいくつかのピーマンについて、重さが30.0g以下のときをSサイズ、30.0gを超えるときはLサイズと分類する。そして、分類されたピーマンからSサイズとLサイズのピーマンを一つずつ選び、ピーマン2個を1組とした袋を作る。
(i)ピーマンを無作為に50個抽出した時、ピーマン分類法で25袋作ることができる確率$p_0$を考えよう。無作為に1個抽出したピーマンがSサイズである確率は$\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$である。ピーマンを無作為に50個抽出したときのSサイズのピーマンの個数を表す確率変数を$U_0$とすると、$U_0$は二項分布$B\left(50, \frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)$に従うので
$p_0$=${}_{50}C_{\boxed{シス}}×\left(\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)^{\boxed{シス}}×\left(1-\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)^{50-\boxed{シス}}$
となる。
$p_0$を計算すると、$p_0$=0.1122...となることから、ピーマンを無作為に50個抽出したとき、25袋作ることができる確率は0.11程度とわかる。
(ii)ピーマン分類法で25袋作ることができる確率が0.95以上となるようなピーマンの個数を考えよう。
kを自然数とし、ピーマンを無作為に(50+k)個抽出したとき、Sサイズのピーマンの個数を表す確率変数を$U_k$とすると、$U_k$は二項分布$B\left(50+k, \frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)$に従う。
(50+k)は十分に大きいので、$U_k$は近似的に正規分布$N\left(\boxed{\boxed{\ \ セ\ \ }}, \boxed{\boxed{\ \ ソ\ \ }}\right)$に従い、$Y=\frac{U_k-\boxed{\boxed{\ \ セ\ \ }}}{\sqrt{\boxed{\boxed{\ \ ソ\ \ }}}}$とすると、Yは近似的に標準正規分布N(0,1)に従う。
よって、ピーマン分類法で、25袋作ることができる確率を$p_k$とすると
$p_k$=$P(25 \leqq U_k \leqq 25+k)$=$P\left(-\frac{\boxed{\boxed{\ \ タ\ \ }}}{\sqrt{50+k}} \leqq Y \leqq \frac{\boxed{\boxed{\ \ タ\ \ }}}{\sqrt{50+k}}\right)$
となる。
$\boxed{\boxed{\ \ タ\ \ }}$=a, $\sqrt{50+k}$=$\beta$とおく。
$p_k$≧0.95になるような$\frac{\alpha}{\beta}$について、正規分布表から$\frac{\alpha}{\beta}$≧1.96を満たせばよいことが分かる。ここでは
$\frac{\alpha}{\beta}$≧2 ...①
を満たす自然数kを考えることとする。①の両辺は正であるから、$\alpha^2$≧4$\beta^2$を満たす最小のkを$k_0$とすると、$k_0$=$\boxed{\ \ チツ\ \ }$であることがわかる。ただし、$\boxed{\ \ チツ\ \ }$の計算においては、$\sqrt{51}=7.14$を用いてもよい。
したがって、少なくとも(50+$\boxed{\ \ チツ\ \ }$)個のピーマンを抽出しておけば、ピーマン分類法で25袋作ることができる確率は0.95以上となる。
$\boxed{\boxed{\ \ セ\ \ }}$~$\boxed{\boxed{\ \ タ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪k ①2k ②3k ③$\frac{50+k}{2}$
④$\frac{25+k}{2}$ ⑤25+k ⑥$\frac{\sqrt{50+k}}{2}$ ⑦$\frac{50+k}{4}$
2023共通テスト過去問
この動画を見る
第3問
以下の問題を解答するにあたっては、必要に応じて43ページの正規分布表を用いてもよい。
(1)ある生産地で生産されるピーマン全体を母集団とし、この母集団におけるピーマン1個の重さ(単位はg)を表す確率変数をXとする。mとσを正の実数とし、Xは正規分布N(m, $\sigma^2$)に従うとする。
(i)この母集団から1個のピーマンを無作為に抽出したとき、重さがm g以上である確率P(X≧m)は
P(X≧m)=P$\left(\frac{X-m}{\sigma}\geqq \boxed{\ \ ア\ \ }\right)$=$\frac{\boxed{\ \ イ\ \ }}{\boxed{\ \ ウ\ \ }}$
である。
(ii)母集団から無作為に抽出された大きさnの標本$X_1$, $X_2$, ..., $X_n$の標本平均を$\bar{X}$とする。$\bar{X}$の平均(期待値)と標準偏差はそれぞれ
E($\bar{X}$)=$\boxed{\boxed{\ \ エ\ \ }}$, σ($\bar{X}$)=$\boxed{\boxed{\ \ オ\ \ }}$
となる。
n=400, 標本平均が30.0g, 標本の標準偏差が3.6gのとき、mの信頼度90%の信頼区間を次の方針で求めよう。
方針:Zを標準正規分布N(0,1)に従う確率変数として、P($-z_0 \leqq Z \leqq z_0$)=0.901 となる$z_0$を正規分布表から求める。この$z_0$を用いるとmの信頼度90.1%の信頼区間が求められるが、これを信頼度90%の信頼区間とみなして考える。
方針において、$z_0$=$\boxed{\ \ カ\ \ }$.$\boxed{\ \ キク\ \ }$である。
一般に、標本の大きさnが大きいときには、母標準偏差の代わりに、標本の標準偏差を用いてよいことが知られている。n=400は十分に大きいので、方針に基づくと、mの信頼度90%の信頼区間は$\boxed{\boxed{\ \ ケ\ \ }}$となる。
$\boxed{\boxed{\ \ エ\ \ }}, \boxed{\boxed{\ \ オ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪σ ①$\sigma^2$ ②$\frac{\sigma}{\sqrt n}$ ③$\frac{\sigma^2}{n}$
④m ⑤2m ⑥$m^2$ ⑦$\sqrt m$
⑧$\frac{\sigma}{n}$ ⑨$n\sigma $ⓐ$nm$ ⓑ$\frac{m}{n}$
$\boxed{\boxed{\ \ ケ\ \ }}$については、最も適当なものを、次の⓪~⑤のうちから一つ選べ。
⓪28.6≦m≦31.4 ①28.7≦m≦31.3 ②28.9≦m≦31.1
③29.6≦m≦30.4 ④29.7≦m≦30.3 ⑤29.9≦m≦30.1
(2)(1)の確率変数Xにおいて、m=30.0, σ=3.6とした母集団から無作為にピーマンを1個ずつ抽出し、ピーマン2個を1組にしたものを袋に入れていく。このようにしてピーマン2個を1組にしたものを25袋作る。その際、1袋ずつの重さの分数を小さくするために、次のピーマン分類法を考える。
ピーマン分類法:無作為に抽出したいくつかのピーマンについて、重さが30.0g以下のときをSサイズ、30.0gを超えるときはLサイズと分類する。そして、分類されたピーマンからSサイズとLサイズのピーマンを一つずつ選び、ピーマン2個を1組とした袋を作る。
(i)ピーマンを無作為に50個抽出した時、ピーマン分類法で25袋作ることができる確率$p_0$を考えよう。無作為に1個抽出したピーマンがSサイズである確率は$\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}$である。ピーマンを無作為に50個抽出したときのSサイズのピーマンの個数を表す確率変数を$U_0$とすると、$U_0$は二項分布$B\left(50, \frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)$に従うので
$p_0$=${}_{50}C_{\boxed{シス}}×\left(\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)^{\boxed{シス}}×\left(1-\frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)^{50-\boxed{シス}}$
となる。
$p_0$を計算すると、$p_0$=0.1122...となることから、ピーマンを無作為に50個抽出したとき、25袋作ることができる確率は0.11程度とわかる。
(ii)ピーマン分類法で25袋作ることができる確率が0.95以上となるようなピーマンの個数を考えよう。
kを自然数とし、ピーマンを無作為に(50+k)個抽出したとき、Sサイズのピーマンの個数を表す確率変数を$U_k$とすると、$U_k$は二項分布$B\left(50+k, \frac{\boxed{\ \ コ\ \ }}{\boxed{\ \ サ\ \ }}\right)$に従う。
(50+k)は十分に大きいので、$U_k$は近似的に正規分布$N\left(\boxed{\boxed{\ \ セ\ \ }}, \boxed{\boxed{\ \ ソ\ \ }}\right)$に従い、$Y=\frac{U_k-\boxed{\boxed{\ \ セ\ \ }}}{\sqrt{\boxed{\boxed{\ \ ソ\ \ }}}}$とすると、Yは近似的に標準正規分布N(0,1)に従う。
よって、ピーマン分類法で、25袋作ることができる確率を$p_k$とすると
$p_k$=$P(25 \leqq U_k \leqq 25+k)$=$P\left(-\frac{\boxed{\boxed{\ \ タ\ \ }}}{\sqrt{50+k}} \leqq Y \leqq \frac{\boxed{\boxed{\ \ タ\ \ }}}{\sqrt{50+k}}\right)$
となる。
$\boxed{\boxed{\ \ タ\ \ }}$=a, $\sqrt{50+k}$=$\beta$とおく。
$p_k$≧0.95になるような$\frac{\alpha}{\beta}$について、正規分布表から$\frac{\alpha}{\beta}$≧1.96を満たせばよいことが分かる。ここでは
$\frac{\alpha}{\beta}$≧2 ...①
を満たす自然数kを考えることとする。①の両辺は正であるから、$\alpha^2$≧4$\beta^2$を満たす最小のkを$k_0$とすると、$k_0$=$\boxed{\ \ チツ\ \ }$であることがわかる。ただし、$\boxed{\ \ チツ\ \ }$の計算においては、$\sqrt{51}=7.14$を用いてもよい。
したがって、少なくとも(50+$\boxed{\ \ チツ\ \ }$)個のピーマンを抽出しておけば、ピーマン分類法で25袋作ることができる確率は0.95以上となる。
$\boxed{\boxed{\ \ セ\ \ }}$~$\boxed{\boxed{\ \ タ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪k ①2k ②3k ③$\frac{50+k}{2}$
④$\frac{25+k}{2}$ ⑤25+k ⑥$\frac{\sqrt{50+k}}{2}$ ⑦$\frac{50+k}{4}$
2023共通テスト過去問
【2分でOK!まずはここから!】統計:明治学院高等学校~全国入試問題解法

単元:
#数学(中学生)#確率分布と統計的な推測#統計的な推測#高校入試過去問(数学)#数B
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の6つのデータの平均値は60であり,$ x:y=1:2 $である.
$ 75, 80, 60, x, 40, y$
このときの中央値を求めよ.
明治学院高校過去問
この動画を見る
次の6つのデータの平均値は60であり,$ x:y=1:2 $である.
$ 75, 80, 60, x, 40, y$
このときの中央値を求めよ.
明治学院高校過去問
福田の1.5倍速演習〜合格する重要問題076〜東京大学2018年度理系第2問〜数列の項の大小とユークリッドの互除法

単元:
#数A#大学入試過去問(数学)#整数の性質#ユークリッド互除法と不定方程式・N進法#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
第2問
数列$a_1$, $a_2$, $\cdots$を
$a_n$=$\displaystyle\frac{{}_{2n+1}C_n}{n!}$ ($n$=1,2,...)
で定める。
(1)n≧2とする。$\frac{a_n}{a_{n-1}}$を既約分数$\frac{q_n}{p_n}$として表したときの分母$p_n$≧1と分子$q_n$を求めよ。
(2)$a_n$が整数となるn≧1をすべて求めよ。
2018東京大学理系過去問
この動画を見る
第2問
数列$a_1$, $a_2$, $\cdots$を
$a_n$=$\displaystyle\frac{{}_{2n+1}C_n}{n!}$ ($n$=1,2,...)
で定める。
(1)n≧2とする。$\frac{a_n}{a_{n-1}}$を既約分数$\frac{q_n}{p_n}$として表したときの分母$p_n$≧1と分子$q_n$を求めよ。
(2)$a_n$が整数となるn≧1をすべて求めよ。
2018東京大学理系過去問
福田の数学〜2023年共通テスト速報〜数学IIB第4問数列〜複利計算

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式#数学(高校生)#大学入試解答速報#数学#共通テスト#数B
指導講師:
福田次郎
問題文全文(内容文):
第4問
花子さんは、毎年の初めに預金口座に一定額の入金をすることにした。この入金を始める前における花子さんの預金は10万円である。ここで、預金とは預金口座にあるお金の額のことである。預金には年利1%で利息がつき、ある年の初めの預金がx万円であれば、その年の終わりには預金は1.01x万円となる。次の年の初めには1.01x万円に入金額を加えたものが預金となる。
毎年の初めの入金額をp万円とし、n年目の初めの預金を$a_n$万円とおく。ただし、p>0とし、nは自然数とする。
例えば、$a_1=10+p, a_2=1.01(10+p)+p$である。
(1)$a_n$を求めるために二つの方針で考える。
方針1
n年目の初めの預金と(n+1)年目の初めの預金との関係に着目して考える。
3年目の初めの預金$a_3$万円について、$a_3=\boxed{\boxed{\ \ ア\ \ }}$である。全ての自然数nについて
$a_{n+1}=\boxed{\boxed{\ \ イ\ \ }}a_n+\boxed{\boxed{\ \ ウ\ \ }}$
が成り立つ。これは
$a_{n+1}+\boxed{\boxed{\ \ エ\ \ }}=\boxed{\boxed{\ \ オ\ \ }}(a_n+\boxed{\boxed{\ \ エ\ \ }})$
と変形でき、$a_n$を求めることができる。
$\boxed{\boxed{\ \ ア\ \ }}$の解答群
⓪1.01{1.01(10+p)+p} ①1.01{1.01(10+p)+1.01p}
②1.01{1.01(10+p)+p}+p ③1.01{1.01(10+p)+p}+1.01p
④1.01(10+p)+1.01p ⑤1.01(10+1.01p)+1.01p
$\boxed{\boxed{\ \ イ\ \ }}$~$\boxed{\boxed{\ \ オ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪1.01 ①$1.01^{n-1}$ ②$1.01^n$
③p ④100p ⑤np
⑥100np ⑦$1.01^{n-1}$×100p ⑧$1.01^n$×100p
方針2
もともと預金口座にあった10万円と毎年の初めに入金したp万円について、n年目の初めにそれぞれがいくらになるかに着目して考える。
もともと預金口座にあった10万円は、2年目の初めには10×1.01万円になり、3年目の初めには10×$1.01^2$万円になる。同様に考えるとn年目の初めには10×$1.01^{n-1}$万円になる。
・1年目の初めに入金したp万円は、n年目の初めにはp×$1.01^{\boxed{\boxed{カ}}}$万円になる。
・2年目の初めに入金したp万円は、n年目の初めにはp×$1.01^{\boxed{\boxed{キ}}}$万円になる。
・n年目の初めに入金したp万円は、n年目の初めにはp万円のままである。
これより
$a_n$=10×$1.01^{n-1}$+p×$1.01^{\boxed{\boxed{カ}}}$+p×$1.01^{\boxed{\boxed{キ}}}$+...+p
=10×$1.01^{n-1}$+p$\displaystyle\sum_{k=1}^n1.01^{\boxed{\boxed{ク}}}$
となることがわかる。ここで、$\displaystyle\sum_{k=1}^n1.01^{\boxed{\boxed{ク}}}$=$\boxed{\boxed{ \ \ ケ\ \ }}$となるので、$a_n$を求めることができる。
$\boxed{\boxed{ \ \ ケ\ \ }}$, $\boxed{\boxed{ \ \ キ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪n+1 ①n ②n-1 ③n-2
$\boxed{\boxed{ \ \ ク\ \ }}$の解答群
⓪k+1 ①k ②k-1 ③k-2
$\boxed{\boxed{ \ \ ケ\ \ }}$の解答群
⓪100×$1.01^n$ ①100($1.01^n$-1)
②100($1.01^{n-1}-1$) ③n+$1.01^{n-1}$-1
④0.01(101n-1) ⑤$\frac{n×1.01^{n-1}}{2}$
(2)花子さんは、10年目の終わりの預金が30万円以上になるための入金額について考えた。
10年目の終わりの預金が30万円以上であることを不等式を用いて表すと
$\boxed{\boxed{\ \ コ\ \ }}$≧30となる。この不等式をpについて解くと
p≧$\frac{\boxed{\ \ サシ\ \ }-\boxed{\ \ スセ\ \ }×1.01^{10}}{101(1.01^{10}-1)}$
となる。したがって、毎年の初めの入金額が例えば18000円であれば、10年目の終わりの預金が30万円以上になることがわかる。
$\boxed{\boxed{\ \ コ\ \ }}$の解答群
⓪$a_{10}$ ①$a_{10}$+p ②$a_{10}$-p
③1.01$a_{10}$ ④1.01$a_{10}$+p ⑤1.01$a_{10}$-p
(3)1年目の入金を始める前における花子さんの預金が10万円ではなく、13万円の場合を考える。すべての自然数nに対して、この場合のn年目の初めの預金は$a_n$万円よりも$\boxed{\boxed{\ \ ソ\ \ }}$万円多い。なお、年利は1%であり、毎年の初めの入金額はp万円のままである。
$\boxed{\boxed{\ \ ソ\ \ }}$の解答群
⓪3 ①13 ②3(n-1)
③3n ④13(n-1) ⑤13n
⑥$3^n$ ⑦3+1.01(n-1) ⑧3×$1.01^{n-1}$
⑨3×$1.01^n$ ⓐ13×$1.01^{n-1}$ ⓑ13×$1.01^n$
2023共通テスト過去問
この動画を見る
第4問
花子さんは、毎年の初めに預金口座に一定額の入金をすることにした。この入金を始める前における花子さんの預金は10万円である。ここで、預金とは預金口座にあるお金の額のことである。預金には年利1%で利息がつき、ある年の初めの預金がx万円であれば、その年の終わりには預金は1.01x万円となる。次の年の初めには1.01x万円に入金額を加えたものが預金となる。
毎年の初めの入金額をp万円とし、n年目の初めの預金を$a_n$万円とおく。ただし、p>0とし、nは自然数とする。
例えば、$a_1=10+p, a_2=1.01(10+p)+p$である。
(1)$a_n$を求めるために二つの方針で考える。
方針1
n年目の初めの預金と(n+1)年目の初めの預金との関係に着目して考える。
3年目の初めの預金$a_3$万円について、$a_3=\boxed{\boxed{\ \ ア\ \ }}$である。全ての自然数nについて
$a_{n+1}=\boxed{\boxed{\ \ イ\ \ }}a_n+\boxed{\boxed{\ \ ウ\ \ }}$
が成り立つ。これは
$a_{n+1}+\boxed{\boxed{\ \ エ\ \ }}=\boxed{\boxed{\ \ オ\ \ }}(a_n+\boxed{\boxed{\ \ エ\ \ }})$
と変形でき、$a_n$を求めることができる。
$\boxed{\boxed{\ \ ア\ \ }}$の解答群
⓪1.01{1.01(10+p)+p} ①1.01{1.01(10+p)+1.01p}
②1.01{1.01(10+p)+p}+p ③1.01{1.01(10+p)+p}+1.01p
④1.01(10+p)+1.01p ⑤1.01(10+1.01p)+1.01p
$\boxed{\boxed{\ \ イ\ \ }}$~$\boxed{\boxed{\ \ オ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪1.01 ①$1.01^{n-1}$ ②$1.01^n$
③p ④100p ⑤np
⑥100np ⑦$1.01^{n-1}$×100p ⑧$1.01^n$×100p
方針2
もともと預金口座にあった10万円と毎年の初めに入金したp万円について、n年目の初めにそれぞれがいくらになるかに着目して考える。
もともと預金口座にあった10万円は、2年目の初めには10×1.01万円になり、3年目の初めには10×$1.01^2$万円になる。同様に考えるとn年目の初めには10×$1.01^{n-1}$万円になる。
・1年目の初めに入金したp万円は、n年目の初めにはp×$1.01^{\boxed{\boxed{カ}}}$万円になる。
・2年目の初めに入金したp万円は、n年目の初めにはp×$1.01^{\boxed{\boxed{キ}}}$万円になる。
・n年目の初めに入金したp万円は、n年目の初めにはp万円のままである。
これより
$a_n$=10×$1.01^{n-1}$+p×$1.01^{\boxed{\boxed{カ}}}$+p×$1.01^{\boxed{\boxed{キ}}}$+...+p
=10×$1.01^{n-1}$+p$\displaystyle\sum_{k=1}^n1.01^{\boxed{\boxed{ク}}}$
となることがわかる。ここで、$\displaystyle\sum_{k=1}^n1.01^{\boxed{\boxed{ク}}}$=$\boxed{\boxed{ \ \ ケ\ \ }}$となるので、$a_n$を求めることができる。
$\boxed{\boxed{ \ \ ケ\ \ }}$, $\boxed{\boxed{ \ \ キ\ \ }}$の解答群(同じものを繰り返し選んでもよい。)
⓪n+1 ①n ②n-1 ③n-2
$\boxed{\boxed{ \ \ ク\ \ }}$の解答群
⓪k+1 ①k ②k-1 ③k-2
$\boxed{\boxed{ \ \ ケ\ \ }}$の解答群
⓪100×$1.01^n$ ①100($1.01^n$-1)
②100($1.01^{n-1}-1$) ③n+$1.01^{n-1}$-1
④0.01(101n-1) ⑤$\frac{n×1.01^{n-1}}{2}$
(2)花子さんは、10年目の終わりの預金が30万円以上になるための入金額について考えた。
10年目の終わりの預金が30万円以上であることを不等式を用いて表すと
$\boxed{\boxed{\ \ コ\ \ }}$≧30となる。この不等式をpについて解くと
p≧$\frac{\boxed{\ \ サシ\ \ }-\boxed{\ \ スセ\ \ }×1.01^{10}}{101(1.01^{10}-1)}$
となる。したがって、毎年の初めの入金額が例えば18000円であれば、10年目の終わりの預金が30万円以上になることがわかる。
$\boxed{\boxed{\ \ コ\ \ }}$の解答群
⓪$a_{10}$ ①$a_{10}$+p ②$a_{10}$-p
③1.01$a_{10}$ ④1.01$a_{10}$+p ⑤1.01$a_{10}$-p
(3)1年目の入金を始める前における花子さんの預金が10万円ではなく、13万円の場合を考える。すべての自然数nに対して、この場合のn年目の初めの預金は$a_n$万円よりも$\boxed{\boxed{\ \ ソ\ \ }}$万円多い。なお、年利は1%であり、毎年の初めの入金額はp万円のままである。
$\boxed{\boxed{\ \ ソ\ \ }}$の解答群
⓪3 ①13 ②3(n-1)
③3n ④13(n-1) ⑤13n
⑥$3^n$ ⑦3+1.01(n-1) ⑧3×$1.01^{n-1}$
⑨3×$1.01^n$ ⓐ13×$1.01^{n-1}$ ⓑ13×$1.01^n$
2023共通テスト過去問
東大 レピュニット数

単元:
#数A#大学入試過去問(数学)#整数の性質#数列#数学的帰納法#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\overbrace{ 1111 + \cdots +11}^{3^n桁}$は$3^n$で割り切れるが
$3^{n+1}$では割り切れないことを示せ.
東大過去問
この動画を見る
$\overbrace{ 1111 + \cdots +11}^{3^n桁}$は$3^n$で割り切れるが
$3^{n+1}$では割り切れないことを示せ.
東大過去問
近畿大(医)やっぱり出た2023年問題

単元:
#数A#大学入試過去問(数学)#整数の性質#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#近畿大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a,n$は整数$(n \geqq2)a$から始まる連続n個の整数の和が2023となる$(a,n)$の組は,
(1)全部で何通りか?
(2)a,nともに奇数は何通りか?
近畿大(医)過去問
この動画を見る
$ a,n$は整数$(n \geqq2)a$から始まる連続n個の整数の和が2023となる$(a,n)$の組は,
(1)全部で何通りか?
(2)a,nともに奇数は何通りか?
近畿大(医)過去問
階乗に関する方程式
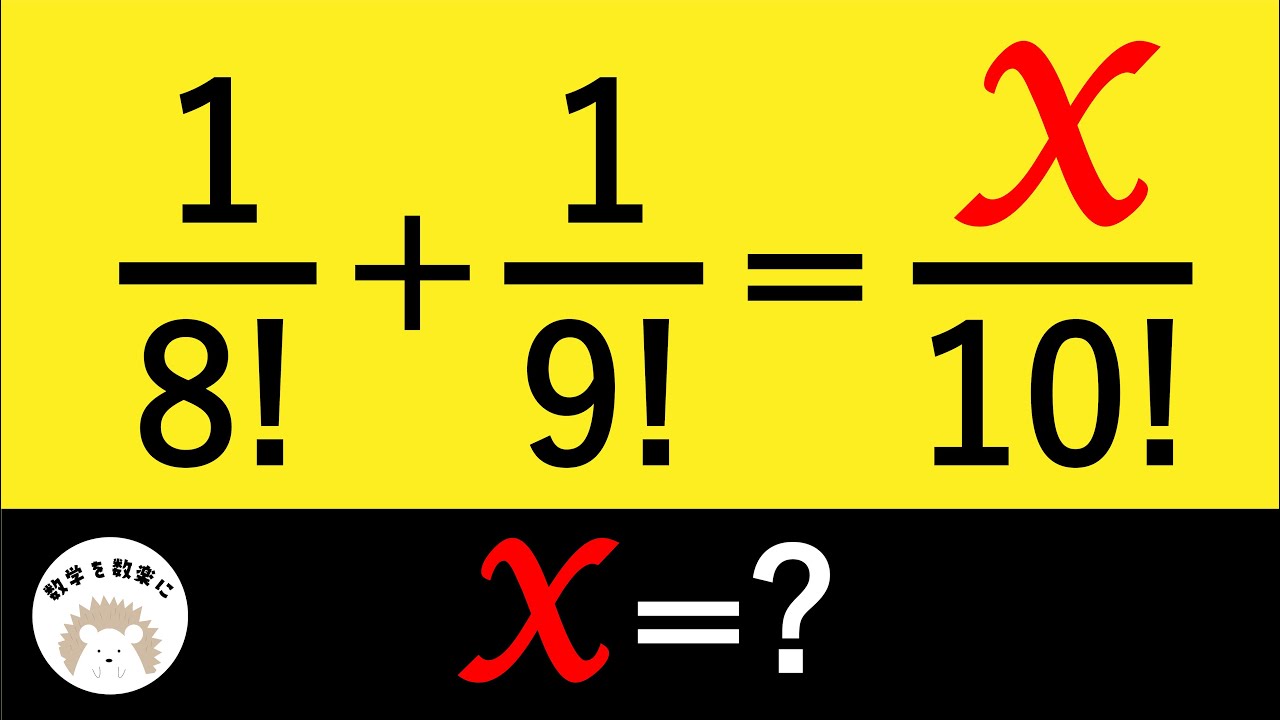
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{8!} + \frac{1}{9!} = \frac{x}{10!}$
x=?
この動画を見る
$\frac{1}{8!} + \frac{1}{9!} = \frac{x}{10!}$
x=?
福田の1.5倍速演習〜合格する重要問題072〜上智大学2019年度理工学部第3問〜ガウス記号で定義された数列

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#対数関数#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ $\alpha=\log_23$とし、自然数nに対して
$a_n=[n\alpha]$, $b_n=\left[\displaystyle\frac{n\alpha}{\alpha-1}\right]$
とする。ただし、実数xに対して[x]はxを超えない最大の整数を表す。
(1)$a_5=\boxed{\ \ ス\ \ }$である。
(2)$b_3=k$とおくと、不等式$\displaystyle\frac{3^{k+c}}{2^k} \leqq 1 \lt \frac{3^{k+1+c}}{2^{k+1}}$が整数$c=\boxed{\ \ セ\ \ }$で成り立ち、
$b_3=\boxed{\ \ ソ\ \ }$であることがわかる。
(3)$a_n \leqq$ 10を満たす自然数nの個数は$\boxed{\ \ タ\ \ }$である。
(4)$b_n \leqq$ 10を満たす自然数nの個数は$\boxed{\ \ チ\ \ }$である。
(5)$a_n \leqq$ 50を満たす自然数nの個数をsとし、$b_n \leqq$ 50を満たす自然数nの個数をtとする。このとき、s+t=$\boxed{\ \ ツ\ \ }$である。
2019上智大学理工学部過去問
この動画を見る
$\Large{\boxed{3}}$ $\alpha=\log_23$とし、自然数nに対して
$a_n=[n\alpha]$, $b_n=\left[\displaystyle\frac{n\alpha}{\alpha-1}\right]$
とする。ただし、実数xに対して[x]はxを超えない最大の整数を表す。
(1)$a_5=\boxed{\ \ ス\ \ }$である。
(2)$b_3=k$とおくと、不等式$\displaystyle\frac{3^{k+c}}{2^k} \leqq 1 \lt \frac{3^{k+1+c}}{2^{k+1}}$が整数$c=\boxed{\ \ セ\ \ }$で成り立ち、
$b_3=\boxed{\ \ ソ\ \ }$であることがわかる。
(3)$a_n \leqq$ 10を満たす自然数nの個数は$\boxed{\ \ タ\ \ }$である。
(4)$b_n \leqq$ 10を満たす自然数nの個数は$\boxed{\ \ チ\ \ }$である。
(5)$a_n \leqq$ 50を満たす自然数nの個数をsとし、$b_n \leqq$ 50を満たす自然数nの個数をtとする。このとき、s+t=$\boxed{\ \ ツ\ \ }$である。
2019上智大学理工学部過去問
福田の1.5倍速演習〜合格する重要問題070〜筑波大学2017年度理系第5問〜格子点の個数とガウス記号と区分求積

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#積分とその応用#関数(分数関数・無理関数・逆関数と合成関数)#関数の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{5}}$ xy平面において、x座標とy座標がともに整数である点を格子点という。また、実数aに対して、a以下の最大の整数を[a]で表す。記号[ ]をガウス記号という。
以下の問いではNを自然数とする。
(1) nを0 $\leqq$ n $\leqq$ Nを満たす整数とする。点(n, 0)と点(n, N$\sin\left(\displaystyle\frac{\pi x}{2N}\right)$)を結ぶ線分上にある格子点の個数をガウス記号を用いて表せ。
(2) 直線y=xと、x軸、および直線x=Nで囲まれた領域(境界を含む)にある格子点の個数をA(N)とおく。このときA(N)を求めよ。
(3) 曲線y=N$\sin\left(\displaystyle\frac{\pi x}{2N}\right)$(0 $\leqq$ x $\leqq$ N)と、x軸、および直線x=Nで囲まれた領域(境界を含む)にある格子点の個数をB(N)とおく。(2)のA(N)に対して$\displaystyle\lim_{N \to \infty}\frac{B(N)}{A(N)}$を求めよ。
2017筑波大学理系過去問
この動画を見る
$\Large{\boxed{5}}$ xy平面において、x座標とy座標がともに整数である点を格子点という。また、実数aに対して、a以下の最大の整数を[a]で表す。記号[ ]をガウス記号という。
以下の問いではNを自然数とする。
(1) nを0 $\leqq$ n $\leqq$ Nを満たす整数とする。点(n, 0)と点(n, N$\sin\left(\displaystyle\frac{\pi x}{2N}\right)$)を結ぶ線分上にある格子点の個数をガウス記号を用いて表せ。
(2) 直線y=xと、x軸、および直線x=Nで囲まれた領域(境界を含む)にある格子点の個数をA(N)とおく。このときA(N)を求めよ。
(3) 曲線y=N$\sin\left(\displaystyle\frac{\pi x}{2N}\right)$(0 $\leqq$ x $\leqq$ N)と、x軸、および直線x=Nで囲まれた領域(境界を含む)にある格子点の個数をB(N)とおく。(2)のA(N)に対して$\displaystyle\lim_{N \to \infty}\frac{B(N)}{A(N)}$を求めよ。
2017筑波大学理系過去問
【数列】超基本的な問題です!解けますか?【甲南大学】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
9を分母とする正の既約分数で,100より小さいものの総和を求めよ。
甲南大過去問
この動画を見る
9を分母とする正の既約分数で,100より小さいものの総和を求めよ。
甲南大過去問
福田の1.5倍速演習〜合格する重要問題068〜千葉大学2017年度理系第11問〜部分和で定義された数列の極限

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#数列の極限#千葉大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{11}}$ 数列$\left\{a_n\right\}$を次の条件によって定める。
$a_1=2$, $a_{n+1}=1+\frac{1}{\displaystyle1-\sum_{k=1}^n\frac{1}{a_k}}$ (n=1,2,3,$\cdots$)
(1) $a_5$を求めよ。
(2) $a_{n+1}$を$a_n$の式で表せ。
(3) 無限級数$\displaystyle\sum_{k=1}^{\infty}\frac{1}{a_k}$が収束することを示し、その和を求めよ。
2017千葉大学理系過去問
この動画を見る
$\Large{\boxed{11}}$ 数列$\left\{a_n\right\}$を次の条件によって定める。
$a_1=2$, $a_{n+1}=1+\frac{1}{\displaystyle1-\sum_{k=1}^n\frac{1}{a_k}}$ (n=1,2,3,$\cdots$)
(1) $a_5$を求めよ。
(2) $a_{n+1}$を$a_n$の式で表せ。
(3) 無限級数$\displaystyle\sum_{k=1}^{\infty}\frac{1}{a_k}$が収束することを示し、その和を求めよ。
2017千葉大学理系過去問
福田の1.5倍速演習〜合格する重要問題066〜九州大学2017年度理系第3問〜等差数列の7の倍数になる項の個数

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ 初項$a_1=1$, 公差4の等差数列$\left\{a_n\right\}$を考える。以下の問いに答えよ。
(1) $\left\{a_n\right\}$の初項から第600項のうち、7の倍数である項の個数を求めよ。
(2) $\left\{a_n\right\}$の初項から第600項のうち、$7^2$の倍数である項の個数を求めよ。
(3) 初項から第n項までの積$a_1a_2\cdots a_n$が$7^{45}$の倍数となる最小の自然数nを求めよ。
2017九州大学理系過去問
この動画を見る
$\Large{\boxed{3}}$ 初項$a_1=1$, 公差4の等差数列$\left\{a_n\right\}$を考える。以下の問いに答えよ。
(1) $\left\{a_n\right\}$の初項から第600項のうち、7の倍数である項の個数を求めよ。
(2) $\left\{a_n\right\}$の初項から第600項のうち、$7^2$の倍数である項の個数を求めよ。
(3) 初項から第n項までの積$a_1a_2\cdots a_n$が$7^{45}$の倍数となる最小の自然数nを求めよ。
2017九州大学理系過去問
はじめしゃちょーの宝くじ710万円購入210万円当選を数学的に考える

単元:
#確率分布と統計的な推測#確率分布#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
はじめしゃちょーの宝くじ710万円購入210万円当選を数学的に考えていきます.
この動画を見る
はじめしゃちょーの宝くじ710万円購入210万円当選を数学的に考えていきます.
福田の1.5倍速演習〜合格する重要問題065〜中央大学2019年度理工学部第3問〜反復試行と確率漸化式

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#数列とその和(等差・等比・階差・Σ)#漸化式#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{3}$ Oを原点とする平面上の動点Rが$R_0$(1, 0)から出発して、単位円の周上を1秒ごとに反時計周りに移動する。移動するときの動径ORの回転角は、確率$\frac{1}{2}$で$\frac{\pi}{6}$、確率$\frac{1}{2}$で$\frac{\pi}{3}$である。n秒後のRの位置を$R_n$とする。以下の問いに答えよ。
(1)$R_5$が(-1, 0)である確率を求めよ。
(2)$R_9$がx軸上にある確率を求めよ。
次に、$R_n$がx軸上またはy軸上にある確率を$p_n$(n≧1)とする。
(3)$p_{n+1}$を$p_n$を用いて表せ。
(4)$p_n$を求めよ。
2019中央大学理工学部過去問
この動画を見る
$\boxed{3}$ Oを原点とする平面上の動点Rが$R_0$(1, 0)から出発して、単位円の周上を1秒ごとに反時計周りに移動する。移動するときの動径ORの回転角は、確率$\frac{1}{2}$で$\frac{\pi}{6}$、確率$\frac{1}{2}$で$\frac{\pi}{3}$である。n秒後のRの位置を$R_n$とする。以下の問いに答えよ。
(1)$R_5$が(-1, 0)である確率を求めよ。
(2)$R_9$がx軸上にある確率を求めよ。
次に、$R_n$がx軸上またはy軸上にある確率を$p_n$(n≧1)とする。
(3)$p_{n+1}$を$p_n$を用いて表せ。
(4)$p_n$を求めよ。
2019中央大学理工学部過去問
ヒカキンさん何円当たるのか?

【ヒカキンTV】宝くじ1万枚買ったら何円当たるのか計算しまし

無限等比級数

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{2} + \frac{1}{4} + \frac{1}{8} +\frac{1}{16} +\frac{1}{32} + \cdots =?$
この動画を見る
$\frac{1}{2} + \frac{1}{4} + \frac{1}{8} +\frac{1}{16} +\frac{1}{32} + \cdots =?$
福田の数学〜北里大学2021年医学部第2問〜条件が複雑な重複順列

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ $n$ を正の整数とし、1,2,3,4,5,6の6個の数字から同じ数字を繰り返し用いることを許して$n$桁の整数をつくる。このような整数のうち、1が奇数個用いられるものの総数を$A_n$、それ以外のものの総数を$B_n$とする。
また、1か6がいずれも奇数個用いられるものの総数を$C_n$とする。次の問いに答えよ。
(1)$A_4$を求めよ。
(2)正の整数$n$に対して、$A_{n+1}$を$A_n$と$B_n$を用いて表せ。
(3)正の整数$n$に対して、$A_n$と$B_n$を求めよ。
(4)$p$を定数とする。$X_1=p$,$X_{n+1}=2X_n+6^n$($n$=1,2,3,...)で定められる
数列を$\left\{X_n\right\}$とする。正の整数$n$に対して、$X_n$を$n$と$p$を用いて表せ。
(5)正の整数$n$に対して、$C_n$を求めよ。
2021北里大学医学部過去問
この動画を見る
$\Large{\boxed{2}}$ $n$ を正の整数とし、1,2,3,4,5,6の6個の数字から同じ数字を繰り返し用いることを許して$n$桁の整数をつくる。このような整数のうち、1が奇数個用いられるものの総数を$A_n$、それ以外のものの総数を$B_n$とする。
また、1か6がいずれも奇数個用いられるものの総数を$C_n$とする。次の問いに答えよ。
(1)$A_4$を求めよ。
(2)正の整数$n$に対して、$A_{n+1}$を$A_n$と$B_n$を用いて表せ。
(3)正の整数$n$に対して、$A_n$と$B_n$を求めよ。
(4)$p$を定数とする。$X_1=p$,$X_{n+1}=2X_n+6^n$($n$=1,2,3,...)で定められる
数列を$\left\{X_n\right\}$とする。正の整数$n$に対して、$X_n$を$n$と$p$を用いて表せ。
(5)正の整数$n$に対して、$C_n$を求めよ。
2021北里大学医学部過去問
福田の1.5倍速演習〜合格する重要問題043〜北海道大学2017年度文系第3問〜確率漸化式の定番問題

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#漸化式#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数B
指導講師:
福田次郎
問題文全文(内容文):
正四面体ABCDの頂点を移動する点Pがある。点Pは、1秒ごとに、
隣の3頂点のいずれかに等しい確率$\frac{a}{3}$で移るか、もとの頂点に確率1-aで
留まる。初め頂点Aにいた点Pが、n秒後に頂点Aにいる確率を$p_n$とする。
ただし、$0 \lt a \lt 1$とし、nは自然数とする。
(1)数列$\left\{p_n\right\}$の漸化式を求めよ。
(2)確率$p_n$を求めよ。
2017北海道大学文系過去問
この動画を見る
正四面体ABCDの頂点を移動する点Pがある。点Pは、1秒ごとに、
隣の3頂点のいずれかに等しい確率$\frac{a}{3}$で移るか、もとの頂点に確率1-aで
留まる。初め頂点Aにいた点Pが、n秒後に頂点Aにいる確率を$p_n$とする。
ただし、$0 \lt a \lt 1$とし、nは自然数とする。
(1)数列$\left\{p_n\right\}$の漸化式を求めよ。
(2)確率$p_n$を求めよ。
2017北海道大学文系過去問
福田の1.5倍速演習〜合格する重要問題039〜早稲田大学2019年度理工学部第2問〜正n角形の周の長さと極限

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
nは3以上の自然数とする。面積1の正n角形$P_n$を考え、その周の
長さを$L_n$とする。次の問いに答えよ。
(1)$(L_n)^2$を求めよ。
(2)$\lim_{n \to \infty}L_n$を求めよ。
(3)$n \lt k$ならば$(L_n)^2 \gt (L_k)^2$となることを示せ。
2019早稲田大学理工学部過去問
この動画を見る
nは3以上の自然数とする。面積1の正n角形$P_n$を考え、その周の
長さを$L_n$とする。次の問いに答えよ。
(1)$(L_n)^2$を求めよ。
(2)$\lim_{n \to \infty}L_n$を求めよ。
(3)$n \lt k$ならば$(L_n)^2 \gt (L_k)^2$となることを示せ。
2019早稲田大学理工学部過去問
福田の1.5倍速演習〜合格する重要問題035〜東京大学2017年度理系第4問〜数列の帰納的定義と最大公約数

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#数学的帰納法#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$p=2+\sqrt5$とおき、自然数$n=1,2,3,\cdots$対して
$a_n=p^n+\left(-\frac{1}{p}\right)^n$
と定める。以下の問いに答えよ。(1)は結論のみを書けばよい。
(1)$a_1,a_2$の値を求めよ。
(2)$n \geqq 2$とする。積$a_1a_n$を、$a_{n+1}$と$a_{n-1}$を用いて表せ。
(3)$a_n$は自然数であることを示せ。
(4)$a_{n+1}$と$a_n$の最大公約数を求めよ。
2017東京大学理系過去問
この動画を見る
$p=2+\sqrt5$とおき、自然数$n=1,2,3,\cdots$対して
$a_n=p^n+\left(-\frac{1}{p}\right)^n$
と定める。以下の問いに答えよ。(1)は結論のみを書けばよい。
(1)$a_1,a_2$の値を求めよ。
(2)$n \geqq 2$とする。積$a_1a_n$を、$a_{n+1}$と$a_{n-1}$を用いて表せ。
(3)$a_n$は自然数であることを示せ。
(4)$a_{n+1}$と$a_n$の最大公約数を求めよ。
2017東京大学理系過去問
2023にしたかったのだけど‥‥

【高校数学】数列の和と一般項の例題 3-11【数学B】

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
初項から第n項までの和SnがSn = n² + 3nで表される数列{a_n}の一般項を求めよ。
この動画を見る
初項から第n項までの和SnがSn = n² + 3nで表される数列{a_n}の一般項を求めよ。
