関数（分数関数・無理関数・逆関数と合成関数）
関数（分数関数・無理関数・逆関数と合成関数）
【数Ⅲ】【関数】次の関数のグラフをかけ。(1) y=√(4-x²)(2) y=-2/3 √(9-x² )(3) y=3/2 √(x²+4)
単元：
#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数学(高校生)#数Ⅲ
教材：
#4S数学#4S数学ⅢのB問題解説#中高教材#関数
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の関数のグラフをかけ。
(1) $y=\sqrt{4-x^2}$
(2) $y=-\dfrac23\sqrt{9-x^2}$
(3) $y=\dfrac32\sqrt{x^2+4}$
この動画を見る
次の関数のグラフをかけ。
(1) $y=\sqrt{4-x^2}$
(2) $y=-\dfrac23\sqrt{9-x^2}$
(3) $y=\dfrac32\sqrt{x^2+4}$
【数Ⅲ】【関数】2つの関数 y=√(x+1), y= x+ kのグラフの共有点の個数を調べよ。
単元：
#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数学(高校生)#数Ⅲ
教材：
#4S数学#4S数学ⅢのB問題解説#中高教材#関数
指導講師：
理数個別チャンネル
問題文全文(内容文)：
2つの関数
$y=\sqrt{x+1}$
$y=x+k$
のグラフの共有点の個数を調べよ。
この動画を見る
2つの関数
$y=\sqrt{x+1}$
$y=x+k$
のグラフの共有点の個数を調べよ。
【数Ⅲ】【関数】次の不等式を解け。(1) (x-4)/(x²+x-6) ＞0 (2) 2/(x-1) - 2/x ≧1
単元：
#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数学(高校生)#数Ⅲ
教材：
#4S数学#4S数学ⅢのB問題解説#中高教材#関数
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の不等式を解け。
(1) $\dfrac{x-4}{x^2+x-6}>0$
(2) $\dfrac2{x-1}-\dfrac2x\geqq1$
この動画を見る
次の不等式を解け。
(1) $\dfrac{x-4}{x^2+x-6}>0$
(2) $\dfrac2{x-1}-\dfrac2x\geqq1$
福田のおもしろ数学549〜無理関数の不定積分その2
単元：
#関数と極限#積分とその応用#関数（分数関数・無理関数・逆関数と合成関数）#不定積分#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
不定積分
$I=\displaystyle \int \sqrt{x^2-1}dx \ (x\gt 1)$を
$x=\sqrt{x^2-1}=t$
と置き換えて求めて下さい。
この動画を見る
不定積分
$I=\displaystyle \int \sqrt{x^2-1}dx \ (x\gt 1)$を
$x=\sqrt{x^2-1}=t$
と置き換えて求めて下さい。
福田のおもしろ数学548〜無理関数の不定積分
単元：
#関数と極限#積分とその応用#関数（分数関数・無理関数・逆関数と合成関数）#不定積分#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
不定積分$I=\displaystyle \int \sqrt{x^2-1}dx \ (x\gt 1)$を
$x=\dfrac{1}{\cos\theta}$と
置き換えて求めて下さい。
この動画を見る
不定積分$I=\displaystyle \int \sqrt{x^2-1}dx \ (x\gt 1)$を
$x=\dfrac{1}{\cos\theta}$と
置き換えて求めて下さい。
福田のおもしろ数学522〜連続関数の性質
単元：
#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
すべての実数で定義された連続関数$f(x)$に対し、
$\dfrac{f(x)}{x} \ (x\neq 0)$
が常に正であるとき、
$f(0)$の値を求めて下さい。
この動画を見る
すべての実数で定義された連続関数$f(x)$に対し、
$\dfrac{f(x)}{x} \ (x\neq 0)$
が常に正であるとき、
$f(0)$の値を求めて下さい。
福田の数学〜東京科学大学(旧・東京工業大学)2025理系第5問〜分数関数のグラフと解の存在範囲
単元：
#大学入試過去問(数学)#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{5}$
(1)関数
$f(t)=\dfrac{t^2-1}{t^3} (t\neq 0)$
の増減を調べ、グラフの概形をかけ。
(2)実数$x,y,z$が、条件
$\begin{eqnarray}
\left\{
\begin{array}{l}
x \lt y \lt z \\
xyz \neq 0 \\\
x^3y^2-x^3=x^2y^3-y^3 \\\
y^3z^2-y^3=y^2z^3-z^3
\end{array}
\right.
\end{eqnarray}$
を満たしながら動くとき、
$x$が取り得る値の範囲を求めよ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
この動画を見る
$\boxed{5}$
(1)関数
$f(t)=\dfrac{t^2-1}{t^3} (t\neq 0)$
の増減を調べ、グラフの概形をかけ。
(2)実数$x,y,z$が、条件
$\begin{eqnarray}
\left\{
\begin{array}{l}
x \lt y \lt z \\
xyz \neq 0 \\\
x^3y^2-x^3=x^2y^3-y^3 \\\
y^3z^2-y^3=y^2z^3-z^3
\end{array}
\right.
\end{eqnarray}$
を満たしながら動くとき、
$x$が取り得る値の範囲を求めよ。
$2025$年東京科学大学(旧・東京工業大学)
理系過去問題
福田の数学〜早稲田大学理工学部2025第5問〜無理関数のグラフ上に無数の有理点が存在する証明
単元：
#大学入試過去問(数学)#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{5}$
$xy$平面上の曲線$C:y=\sqrt[3]{x^2+2}$と考え、
$C$上の$(0,\sqrt[3]{2})$以外の点$P(a,b)$における接線を
$\ell : y = kx +c$と表す。$C$と$\ell$の方程式から
$x$を消去して得られる$y$についての$3$次方程式
$f(y)=0$は$b$を重解としてもつので、もう$1$つの解を
$b'$とする。
ただし、$b'$が$3$重解のときは$b'=b$とみなす。
次の問いに答えよ。
(1)$2b+b'$を$k$のみの分数式で表せ。
(2)$b'$を$b$のみの分数式で表せ。
(3)$C$と$\ell$の共有点で、その$y$座標が$b'$であるものを
$P'(a',b')$とする。
$a$と$b$が有理数ならば、$a'$と$b'$も有理数であることを
示せ。
(4)$b$が奇数$p,q$と負でない整数$r$を用いて
$b=\dfrac{p}{2^r q}$で与えられるとする。
有理数$b'$を奇数$p',q'$と整数$s$を用いて$b'=\dfrac{p'}{2^s q'}$と
表すとき、$s$を$r$の式で表せ。
(5)$P(5,3)$が曲線$C$上の点であることを利用して、
$C$上に$x$座標と$y$座標がともに有理数であるような点が
無数に存在することを示せ。
$2025$年早稲田大学理工学部過去問題
この動画を見る
$\boxed{5}$
$xy$平面上の曲線$C:y=\sqrt[3]{x^2+2}$と考え、
$C$上の$(0,\sqrt[3]{2})$以外の点$P(a,b)$における接線を
$\ell : y = kx +c$と表す。$C$と$\ell$の方程式から
$x$を消去して得られる$y$についての$3$次方程式
$f(y)=0$は$b$を重解としてもつので、もう$1$つの解を
$b'$とする。
ただし、$b'$が$3$重解のときは$b'=b$とみなす。
次の問いに答えよ。
(1)$2b+b'$を$k$のみの分数式で表せ。
(2)$b'$を$b$のみの分数式で表せ。
(3)$C$と$\ell$の共有点で、その$y$座標が$b'$であるものを
$P'(a',b')$とする。
$a$と$b$が有理数ならば、$a'$と$b'$も有理数であることを
示せ。
(4)$b$が奇数$p,q$と負でない整数$r$を用いて
$b=\dfrac{p}{2^r q}$で与えられるとする。
有理数$b'$を奇数$p',q'$と整数$s$を用いて$b'=\dfrac{p'}{2^s q'}$と
表すとき、$s$を$r$の式で表せ。
(5)$P(5,3)$が曲線$C$上の点であることを利用して、
$C$上に$x$座標と$y$座標がともに有理数であるような点が
無数に存在することを示せ。
$2025$年早稲田大学理工学部過去問題
福田の数学〜慶應義塾大学理工学部2025第2問〜分数関数の接線とベクトル計算
単元：
#大学入試過去問(数学)#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{2}$
座標平面上の点$P(1,1)$と点$Q(1,-1)$および
曲線$C:y=\dfrac{1}{x-4}(x\gt 4)$を考える。
(1)曲線$C$の接線で点$Q$を通るものは存在しないことを
証明しなさい。
(2)曲線$C$の接線で点$P$を通るものを$l$とし、
$C$と$l$の接点を$A$とする。
このとき、$l$の方程式は$y=\boxed{キ}$であり、
点$A$の座標は$\boxed{ク}$である。
また、曲線$C$上の点の点$B$が
$\overrightarrow{PB}･\overrightarrow{PA}+\overrightarrow{PA}･\overrightarrow{AQ}+\overrightarrow{AB}･\overrightarrow{AQ}=-\dfrac{2}{3}$
を満たすとき、点$B$の座標は$\boxed{ケ}$である。
(3)$A,B$を(2)で定めた点とする。
正の数$t$に対し、曲線$C$上の点$R\left(t+4,\dfrac{1}{t}\right)$は
点$A$と異なるものとする。
線分$AR$を$2:1$に内分する点を$S$とし、
線分$BS$を$3:2$に内分する点を$T(u,v)$とするとき、
$u$を$t$の式で表すと$u=\boxed{コ}$である。
また、$uv$の値は$t-\boxed{サ}$のとき最小となる。
$2025$年慶應義塾大学理工学部過去問題
この動画を見る
$\boxed{2}$
座標平面上の点$P(1,1)$と点$Q(1,-1)$および
曲線$C:y=\dfrac{1}{x-4}(x\gt 4)$を考える。
(1)曲線$C$の接線で点$Q$を通るものは存在しないことを
証明しなさい。
(2)曲線$C$の接線で点$P$を通るものを$l$とし、
$C$と$l$の接点を$A$とする。
このとき、$l$の方程式は$y=\boxed{キ}$であり、
点$A$の座標は$\boxed{ク}$である。
また、曲線$C$上の点の点$B$が
$\overrightarrow{PB}･\overrightarrow{PA}+\overrightarrow{PA}･\overrightarrow{AQ}+\overrightarrow{AB}･\overrightarrow{AQ}=-\dfrac{2}{3}$
を満たすとき、点$B$の座標は$\boxed{ケ}$である。
(3)$A,B$を(2)で定めた点とする。
正の数$t$に対し、曲線$C$上の点$R\left(t+4,\dfrac{1}{t}\right)$は
点$A$と異なるものとする。
線分$AR$を$2:1$に内分する点を$S$とし、
線分$BS$を$3:2$に内分する点を$T(u,v)$とするとき、
$u$を$t$の式で表すと$u=\boxed{コ}$である。
また、$uv$の値は$t-\boxed{サ}$のとき最小となる。
$2025$年慶應義塾大学理工学部過去問題
福田の数学〜慶應義塾大学理工学部2025第1問(3)〜逆関数の微分
単元：
#大学入試過去問(数学)#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$
(3)$f(x)$を微分可能な関数とし、
$g(x)=x^3+x$とする。
関数$g(x)$は微分可能な逆関数$g^{-1}(x)$をもつ。
定数$t$に対して、関数$t^2x^2-f(g^{-1}(x))$は
$x=t^3+t$で極値をとるとする。
このとき、$f'(t)$を$t$の多項式で表すと$f'(t)=\boxed{オ}$となる。
次に、任意の定数$t$に対して、関数$t^2x^2-f(g^{-1}(x))$は
$x=t^3+t$で極値をとるとする。
このとき、$f(0)=-2$ならば$f(1)=\boxed{カ}$である。
$2025$年慶應義塾大学理工学部過去問題
この動画を見る
$\boxed{1}$
(3)$f(x)$を微分可能な関数とし、
$g(x)=x^3+x$とする。
関数$g(x)$は微分可能な逆関数$g^{-1}(x)$をもつ。
定数$t$に対して、関数$t^2x^2-f(g^{-1}(x))$は
$x=t^3+t$で極値をとるとする。
このとき、$f'(t)$を$t$の多項式で表すと$f'(t)=\boxed{オ}$となる。
次に、任意の定数$t$に対して、関数$t^2x^2-f(g^{-1}(x))$は
$x=t^3+t$で極値をとるとする。
このとき、$f(0)=-2$ならば$f(1)=\boxed{カ}$である。
$2025$年慶應義塾大学理工学部過去問題
福田の数学〜慶應義塾大学薬学部2025第3問〜逆関数と定積分
単元：
#大学入試過去問(数学)#関数と極限#積分とその応用#関数（分数関数・無理関数・逆関数と合成関数）#定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{3}$
実数$x$に対して、関数
$f(x)=\dfrac{1}{3}x+\sqrt{\dfrac{1}{9}x^2+8}$
がある。ただし、定義域は$x\geqq 0$である。
$y=f(x)$の逆関数を$y=g(x)$とする。
(1)$g(x)$を求めると、$g(x)=\boxed{ナ}$であり、
$g(x)$定義域は$\boxed{ニ}$である。
(2)$\displaystyle \int_{2\sqrt2}^{4}g(x)dx$を求めると$\boxed{ヌ}$である。
(3)$\displaystyle \int_{0}^{3} f(x) dx$を求めると$\boxed{ネ}$である。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{3}$
実数$x$に対して、関数
$f(x)=\dfrac{1}{3}x+\sqrt{\dfrac{1}{9}x^2+8}$
がある。ただし、定義域は$x\geqq 0$である。
$y=f(x)$の逆関数を$y=g(x)$とする。
(1)$g(x)$を求めると、$g(x)=\boxed{ナ}$であり、
$g(x)$定義域は$\boxed{ニ}$である。
(2)$\displaystyle \int_{2\sqrt2}^{4}g(x)dx$を求めると$\boxed{ヌ}$である。
(3)$\displaystyle \int_{0}^{3} f(x) dx$を求めると$\boxed{ネ}$である。
$2025$年慶應義塾大学薬学部過去問題
福田のおもしろ数学429〜複雑な無理関数の最大値
単元：
#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$xy+x\sqrt{1-y^2}+y\sqrt{1-x^2}$
$\qquad -\sqrt{(1-x^2)(1-y^2)}$
の最大値を求めよ。
この動画を見る
$xy+x\sqrt{1-y^2}+y\sqrt{1-x^2}$
$\qquad -\sqrt{(1-x^2)(1-y^2)}$
の最大値を求めよ。
福田の数学〜旧・東京工業大学、東京科学大学2025理系第1問〜逆関数の定積分
単元：
#大学入試過去問(数学)#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\boxed{1}$$\quad$関数$f(x)$を$x\geqq 0$に対して
$f(x)=x\log(1+x)$と定める。
(1)不定積分$\displaystyle \int x\log(1+x)dx$を求めよ。
(2)$y=f(x) \quad (x\geqq 0)$の逆関数を
$y=g(x) \quad (x\geqq 0)$とする。
また、$a,b$を$g(a)=1,g(b)=2$となる
実数となる。
このとき定積分$I=\displaystyle \int_{a}{b} g(x)dx$の値を求めよ。
(3)関数$P(x)$を$x\geqq 0$に対して
$P(x)=\displaystyle \int_{0}^{x}\sqrt{1+f(t)dt}$と定める。
このとき、$y=P(x)$について、
定義域を$x\geqq 0$とする逆関数
$y=Q(x)$が微分可能であることは
説明なしに認めてよい。
関数$R(x)$を$x\geqq 0$に対して
$R(x)=\displaystyle int_{0}^{P(x)}\dfrac{1}{Q'(\upsilon)}$と定めるとき、
$R(x)$を求めよ。
図は動画内参照
$2025$年東京科学大学(旧・東京工業大学)理系過去問題
この動画を見る
$\boxed{1}$$\quad$関数$f(x)$を$x\geqq 0$に対して
$f(x)=x\log(1+x)$と定める。
(1)不定積分$\displaystyle \int x\log(1+x)dx$を求めよ。
(2)$y=f(x) \quad (x\geqq 0)$の逆関数を
$y=g(x) \quad (x\geqq 0)$とする。
また、$a,b$を$g(a)=1,g(b)=2$となる
実数となる。
このとき定積分$I=\displaystyle \int_{a}{b} g(x)dx$の値を求めよ。
(3)関数$P(x)$を$x\geqq 0$に対して
$P(x)=\displaystyle \int_{0}^{x}\sqrt{1+f(t)dt}$と定める。
このとき、$y=P(x)$について、
定義域を$x\geqq 0$とする逆関数
$y=Q(x)$が微分可能であることは
説明なしに認めてよい。
関数$R(x)$を$x\geqq 0$に対して
$R(x)=\displaystyle int_{0}^{P(x)}\dfrac{1}{Q'(\upsilon)}$と定めるとき、
$R(x)$を求めよ。
図は動画内参照
$2025$年東京科学大学(旧・東京工業大学)理系過去問題
福田の数学〜過去の入試問題(期間限定)〜東京慈恵会医科大学医学部2020第2問〜関数列の極限
単元：
#大学入試過去問(数学)#微分法と積分法#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京慈恵会医科大学#東京慈恵会医科大学
指導講師：
福田次郎
問題文全文(内容文)：
$p$を$2$以上の自然数の定数とする。$n$=$2$, $3$, $4$...に対して、関数 $f_n(x) $$(n\gt0)$を
$f_n(x) = (1 + \dfrac{x}{n})(1 + \dfrac{x}{n+1}) \cdot\cdot \cdot(1 + \dfrac{x}{pn})
$
で定める。例えば$p$ = $2$のとき
$
f_2(x) = (1 + \dfrac{x}{2})(1 + \dfrac{x}{3})(1 + \dfrac{x}{4})
$
$
f_3(x) = (1 + \dfrac{x}{3})(1 + \dfrac{x}{4})(1 + \dfrac{x}{5})(1 + \dfrac{x}{6})
$
である。$f(x)=\displaystyle \lim_{ n \to \infty }f_n(x)$ $(n\gt0)$とおくとき、次の問に答えよ。
$(1)$$t$$\geqq$$0$のとき、不等式$\dfrac{t}{1+t}$$\leqq$$\log(1+t)$$\leqq$$t$ が成り立つことを示せ。ただし、対数は自然対数とする。
$(2)$ $f(x)$を求めよ。
この動画を見る
$p$を$2$以上の自然数の定数とする。$n$=$2$, $3$, $4$...に対して、関数 $f_n(x) $$(n\gt0)$を
$f_n(x) = (1 + \dfrac{x}{n})(1 + \dfrac{x}{n+1}) \cdot\cdot \cdot(1 + \dfrac{x}{pn})
$
で定める。例えば$p$ = $2$のとき
$
f_2(x) = (1 + \dfrac{x}{2})(1 + \dfrac{x}{3})(1 + \dfrac{x}{4})
$
$
f_3(x) = (1 + \dfrac{x}{3})(1 + \dfrac{x}{4})(1 + \dfrac{x}{5})(1 + \dfrac{x}{6})
$
である。$f(x)=\displaystyle \lim_{ n \to \infty }f_n(x)$ $(n\gt0)$とおくとき、次の問に答えよ。
$(1)$$t$$\geqq$$0$のとき、不等式$\dfrac{t}{1+t}$$\leqq$$\log(1+t)$$\leqq$$t$ が成り立つことを示せ。ただし、対数は自然対数とする。
$(2)$ $f(x)$を求めよ。
福田のおもしろ数学341〜関数方程式を解く
単元：
#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
実数から実数への関数$f(x)$が$f(x+y)=f(x)f(y)f(xy)$を満たしている。このような$f(x)$をすべて求めて下さい。
この動画を見る
実数から実数への関数$f(x)$が$f(x+y)=f(x)f(y)f(xy)$を満たしている。このような$f(x)$をすべて求めて下さい。
福田のおもしろ数学318〜合成関数と関数方程式
単元：
#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
実数から実数への関数$f(x)$がすべての実数$x$で
$f(f(x)f(1-x))=f(x)$
かつ$f(f(x))=1-f(x)$を満たす。
このような$f(x)$をすべて求めて下さい。
この動画を見る
実数から実数への関数$f(x)$がすべての実数$x$で
$f(f(x)f(1-x))=f(x)$
かつ$f(f(x))=1-f(x)$を満たす。
このような$f(x)$をすべて求めて下さい。
福田のおもしろ数学259〜複雑な無理不等式の解
単元：
#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\displaystyle \frac{4x^2}{(1-\sqrt{2x+1})^2} \lt 2x+9$ を解け。
この動画を見る
$\displaystyle \frac{4x^2}{(1-\sqrt{2x+1})^2} \lt 2x+9$ を解け。
福田のおもしろ数学247〜複雑な無理方程式の解を1つ見つける
単元：
#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$
5(\sqrt{1-x}+\sqrt{1+x})=6x+8\sqrt{1-x^2}
$の解を1つ求めて下さい。
この動画を見る
$
5(\sqrt{1-x}+\sqrt{1+x})=6x+8\sqrt{1-x^2}
$の解を1つ求めて下さい。
福田のおもしろ数学228〜合成関数の定義からf(0)を求める
単元：
#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$f(f(x))=x^2-x+1$のとき、$f(0)$を求めよ。
この動画を見る
$f(f(x))=x^2-x+1$のとき、$f(0)$を求めよ。
福田のおもしろ数学223〜合成関数でできた方程式の解と不動点
単元：
#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$f(x)=|x-1|$のとき、$f(f(x))=f(f(f(x)))$を満たす$x$をすべて求めよ。
この動画を見る
$f(x)=|x-1|$のとき、$f(f(x))=f(f(f(x)))$を満たす$x$をすべて求めよ。
福田のおもしろ数学218〜不動点と合成関数の作る方程式の解
単元：
#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$f(x)=x^2+1$のとき、方程式$f(f(x))=x$を満たす$x$をすべて求めよ。
この動画を見る
$f(x)=x^2+1$のとき、方程式$f(f(x))=x$を満たす$x$をすべて求めよ。
福田のおもしろ数学209〜無理不等式の解き方
単元：
#関数と極限#微分とその応用#関数（分数関数・無理関数・逆関数と合成関数）#関数の変化（グラフ・最大最小・方程式・不等式）#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\sqrt{x}+sqrt{x-2} < 3$を解いて下さい。
この動画を見る
$\sqrt{x}+sqrt{x-2} < 3$を解いて下さい。
【高校数学】数Ⅲ：関数：逆関数と合成関数：逆関数の求め方とグラフの書き方【NI・SHI・NOがていねいに解説】
単元：
#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数学(高校生)#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の関数の逆関数を求め，そのグラフをかけ。
$y＝log_{\frac{1}{3}}x$
この動画を見る
次の関数の逆関数を求め，そのグラフをかけ。
$y＝log_{\frac{1}{3}}x$
【高校数学】数Ⅲ：関数：逆関数と合成関数：逆関数の求め方【NI・SHI・NOがていねいに解説】
単元：
#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数学(高校生)#数Ⅲ
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の関数の逆関数を求めよ。
$\displaystyle y＝\frac{x-2}{3x+1}$
この動画を見る
次の関数の逆関数を求めよ。
$\displaystyle y＝\frac{x-2}{3x+1}$
福田のおもしろ数学158〜無理不等式と同値変形
単元：
#関数（分数関数・無理関数・逆関数と合成関数）#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
不等式$\sqrt{2x+1}$≧$x$－1 ...(＊)を
(1)同値変形することで解け。 (2)グラフを利用して解け。
この動画を見る
不等式$\sqrt{2x+1}$≧$x$－1 ...(＊)を
(1)同値変形することで解け。 (2)グラフを利用して解け。
福田の数学〜神戸大学2024年理系第1問〜無理関数を利用して定義された数列の一般項
単元：
#数列#数列とその和（等差・等比・階差・Σ）#漸化式#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#神戸大学#数学(高校生)#数B#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{1}$ $c$を正の実数とする。各項が正である数列$\left\{a_n\right\}$を次のように定める。$a_1$は関数
$y$=$x$+$\sqrt{c-x^2}$ (0≦$x$≦$\sqrt c$)
が最大値をとるときの$x$の値とする。$a_{n+1}$は関数
$y$=$x$+$\sqrt{a_n-x^2}$ (0≦$x$≦$\sqrt{a_n}$)
が最大値をとるときの$x$の値とする。数列$\left\{b_n\right\}$を$b_n$=$\log_2a_n$ で定める。以下の問いに答えよ。
(1)$a_1$を$c$を用いて表せ。
(2)$b_{n+1}$を$b_n$を用いて表せ。
(3)数列$\left\{b_n\right\}$の一般項を$n$と$c$を用いて表せ。
この動画を見る
$\Large\boxed{1}$ $c$を正の実数とする。各項が正である数列$\left\{a_n\right\}$を次のように定める。$a_1$は関数
$y$=$x$+$\sqrt{c-x^2}$ (0≦$x$≦$\sqrt c$)
が最大値をとるときの$x$の値とする。$a_{n+1}$は関数
$y$=$x$+$\sqrt{a_n-x^2}$ (0≦$x$≦$\sqrt{a_n}$)
が最大値をとるときの$x$の値とする。数列$\left\{b_n\right\}$を$b_n$=$\log_2a_n$ で定める。以下の問いに答えよ。
(1)$a_1$を$c$を用いて表せ。
(2)$b_{n+1}$を$b_n$を用いて表せ。
(3)数列$\left\{b_n\right\}$の一般項を$n$と$c$を用いて表せ。
福田のおもしろ数学132〜合成関数のグラフ
単元：
#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$f(x)$=$\left\{\begin{array}{1}
2x (0≦x≦\frac{1}{2})\\
2-2x (\frac{1}{2}≦x≦1)\\
\end{array}\right.$
$y$=$f(f(x))$ のグラフをかけ。
この動画を見る
$f(x)$=$\left\{\begin{array}{1}
2x (0≦x≦\frac{1}{2})\\
2-2x (\frac{1}{2}≦x≦1)\\
\end{array}\right.$
$y$=$f(f(x))$ のグラフをかけ。
福田のおもしろ数学130〜合成関数の性質
単元：
#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
$f(x)$=$ax$+$b$, $g(x)$=$cx$+$d$ ($a$≠0, $c$≠0)とする。このとき次の条件を満たす関数$h(x)$, $k(x)$を求めよ。
(1)$g(h(x))$=$f(x)$ (2)$k(g(x))$=$f(x)$
この動画を見る
$f(x)$=$ax$+$b$, $g(x)$=$cx$+$d$ ($a$≠0, $c$≠0)とする。このとき次の条件を満たす関数$h(x)$, $k(x)$を求めよ。
(1)$g(h(x))$=$f(x)$ (2)$k(g(x))$=$f(x)$
約束記号 四天王寺
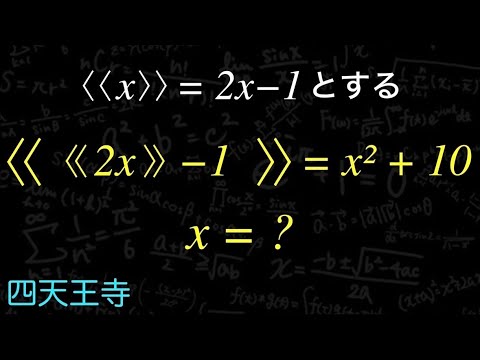
単元：
#大学入試過去問(数学)#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師：
数学を数楽に
問題文全文(内容文)：
$\langle\langle x \rangle\rangle=2x-1$とする
$\langle\langle \quad \langle\langle 2x \rangle\rangle -1 \rangle\rangle=x^2+10$
$x=?$
四天王寺高等学校
この動画を見る
$\langle\langle x \rangle\rangle=2x-1$とする
$\langle\langle \quad \langle\langle 2x \rangle\rangle -1 \rangle\rangle=x^2+10$
$x=?$
四天王寺高等学校
福田のおもしろ数学112〜多変数の式の最大最小
単元：
#数Ⅱ#図形と方程式#関数と極限#関数（分数関数・無理関数・逆関数と合成関数）#数学(高校生)#数Ⅲ
指導講師：
福田次郎
問題文全文(内容文)：
実数$x$,$y$,$z$が0≦$x$≦1, 0≦$y$≦1, 2≦$z$≦3 を満たして変わるとき、$\displaystyle\frac{z-y}{z-x}$ の最大値、最小値を求めよ。
この動画を見る
実数$x$,$y$,$z$が0≦$x$≦1, 0≦$y$≦1, 2≦$z$≦3 を満たして変わるとき、$\displaystyle\frac{z-y}{z-x}$ の最大値、最小値を求めよ。