 関数と極限
関数と極限
 関数と極限
関数と極限
#65数検1級1次過去問「ミスれない戦い」 #極限

単元:
#関数と極限#数列の極限#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{\sqrt[ n ]{ n! }}{n}$
出典:数検1級1次過去問
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{\sqrt[ n ]{ n! }}{n}$
出典:数検1級1次過去問
#筑波大学(2020) #極限 #Shorts
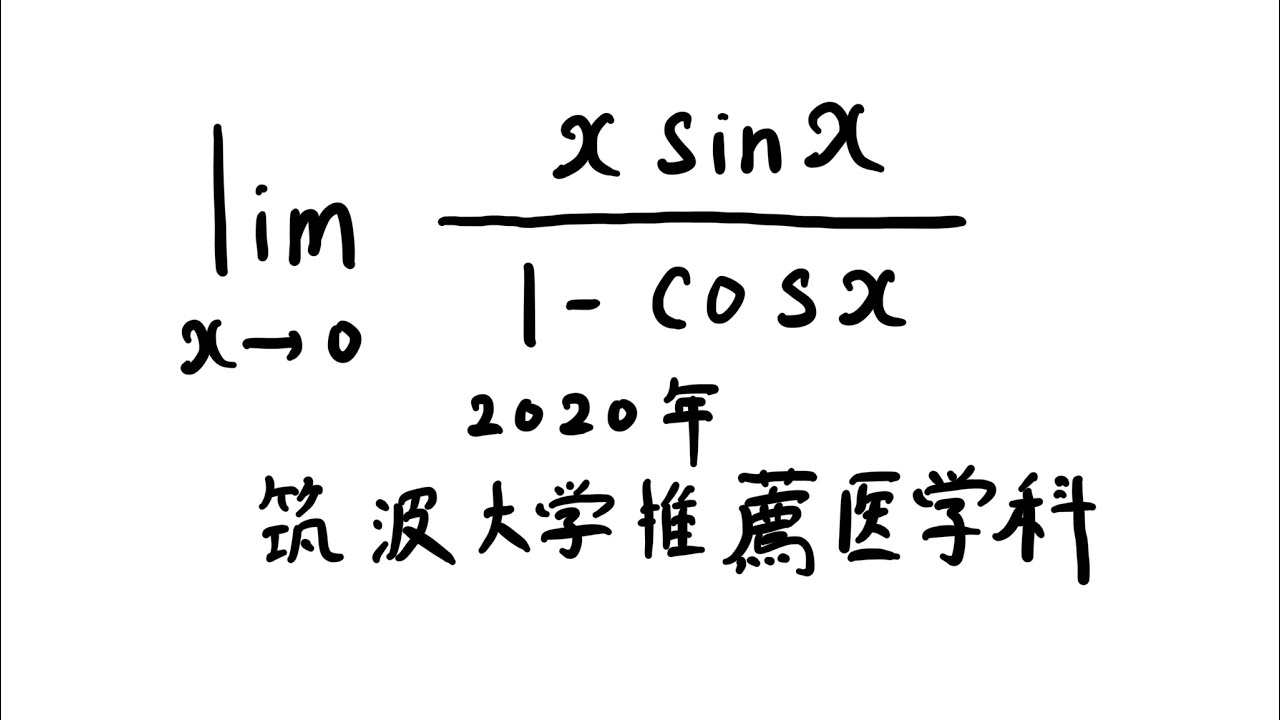
単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{x\ \sin\ x}{1-\cos\ x}$
出典:2020年筑波大学推薦医学科
この動画を見る
$\displaystyle \lim_{ x \to 0 } \displaystyle \frac{x\ \sin\ x}{1-\cos\ x}$
出典:2020年筑波大学推薦医学科
福田のおもしろ数学132〜合成関数のグラフ

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$f(x)$=$\left\{\begin{array}{1}
2x (0≦x≦\frac{1}{2})\\
2-2x (\frac{1}{2}≦x≦1)\\
\end{array}\right.$
$y$=$f(f(x))$ のグラフをかけ。
この動画を見る
$f(x)$=$\left\{\begin{array}{1}
2x (0≦x≦\frac{1}{2})\\
2-2x (\frac{1}{2}≦x≦1)\\
\end{array}\right.$
$y$=$f(f(x))$ のグラフをかけ。
福田のおもしろ数学130〜合成関数の性質

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$f(x)$=$ax$+$b$, $g(x)$=$cx$+$d$ ($a$≠0, $c$≠0)とする。このとき次の条件を満たす関数$h(x)$, $k(x)$を求めよ。
(1)$g(h(x))$=$f(x)$ (2)$k(g(x))$=$f(x)$
この動画を見る
$f(x)$=$ax$+$b$, $g(x)$=$cx$+$d$ ($a$≠0, $c$≠0)とする。このとき次の条件を満たす関数$h(x)$, $k(x)$を求めよ。
(1)$g(h(x))$=$f(x)$ (2)$k(g(x))$=$f(x)$
大学入試問題#801「1番は、みるからに1だけど」 #明治大学(2011) #極限

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
1.$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{log(n+5)}{log(n+2)}$
2.数列$\{a_n\},\{b_n\}$をそれぞれ$a_n=(n+5)^{-2n+1},b_n=\displaystyle \frac{1}{n\ log(n+2)}$で定める。
このとき、$\displaystyle \lim_{ n \to \infty } (a_n)^b_n$を求めよ。
出典:2011年明治大学 入試問題
この動画を見る
1.$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{log(n+5)}{log(n+2)}$
2.数列$\{a_n\},\{b_n\}$をそれぞれ$a_n=(n+5)^{-2n+1},b_n=\displaystyle \frac{1}{n\ log(n+2)}$で定める。
このとき、$\displaystyle \lim_{ n \to \infty } (a_n)^b_n$を求めよ。
出典:2011年明治大学 入試問題
約束記号 四天王寺
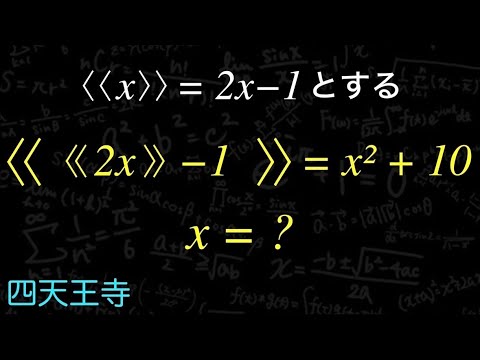
単元:
#大学入試過去問(数学)#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
数学を数楽に
問題文全文(内容文):
$\langle\langle x \rangle\rangle=2x-1$とする
$\langle\langle \quad \langle\langle 2x \rangle\rangle -1 \rangle\rangle=x^2+10$
$x=?$
四天王寺高等学校
この動画を見る
$\langle\langle x \rangle\rangle=2x-1$とする
$\langle\langle \quad \langle\langle 2x \rangle\rangle -1 \rangle\rangle=x^2+10$
$x=?$
四天王寺高等学校
大学入試問題#800「コメントが難しい」 #兵庫県立大学中期(2012) #極限

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#兵庫県立大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
実数$x$に対して
$f(x)=\displaystyle \lim_{ x \to \infty } n\{\sin(\displaystyle \frac{1+n}{n}x)+\sin(\displaystyle \frac{1-n}{n}x)\}$とおく。
次の問いに答えよ。
1.$f(x)$を求めよ。
2.定積分$\displaystyle \int_{0}^{\pi} f(x) dx$を求めよ。
出典:2012年兵庫県立大学中期 入試問題
この動画を見る
実数$x$に対して
$f(x)=\displaystyle \lim_{ x \to \infty } n\{\sin(\displaystyle \frac{1+n}{n}x)+\sin(\displaystyle \frac{1-n}{n}x)\}$とおく。
次の問いに答えよ。
1.$f(x)$を求めよ。
2.定積分$\displaystyle \int_{0}^{\pi} f(x) dx$を求めよ。
出典:2012年兵庫県立大学中期 入試問題
福田のおもしろ数学112〜多変数の式の最大最小

単元:
#数Ⅱ#図形と方程式#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
実数$x$,$y$,$z$が0≦$x$≦1, 0≦$y$≦1, 2≦$z$≦3 を満たして変わるとき、$\displaystyle\frac{z-y}{z-x}$ の最大値、最小値を求めよ。
この動画を見る
実数$x$,$y$,$z$が0≦$x$≦1, 0≦$y$≦1, 2≦$z$≦3 を満たして変わるとき、$\displaystyle\frac{z-y}{z-x}$ の最大値、最小値を求めよ。
「安定の良問」 by にっし~Diaryさん #極限

単元:
#数Ⅱ#微分法と積分法#平均変化率・極限・導関数#関数と極限#数列の極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{x\{\sin(\displaystyle \frac{1}{x})-\sin(\sin(\displaystyle \frac{1}{x}))\}}{1-x\ \sin(\displaystyle \frac{1}{x})}$
この動画を見る
$\displaystyle \lim_{ x \to \infty } \displaystyle \frac{x\{\sin(\displaystyle \frac{1}{x})-\sin(\sin(\displaystyle \frac{1}{x}))\}}{1-x\ \sin(\displaystyle \frac{1}{x})}$
福田の数学〜東京工業大学2024年理系第4問〜表の出る確率が異なるコインを投げたときの表が奇数枚出る確率と極限

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#関数と極限#数列の極限#関数の極限#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ $n$を正の整数とし、$C_1$,...,$C_n$を$n$枚の硬貨とする。各$k$=1,...,$n$に対し、硬貨$C_k$を投げて表が出る確率を$p_k$、裏が出る確率を1-$p_k$とする。この$n$枚の硬貨を同時に投げ、表が出た硬貨の枚数が奇数であれば成功、というゲームを考える。
(1)$p_k$=$\frac{1}{3}$ ($k$=1,...,$n$)のとき、このゲームで成功する確率$X_n$を求めよ。
(2)$p_k$=$\frac{1}{2(k+1)}$ ($k$=1,...,$n$)のとき、このゲームで成功する確率$Y_n$を求めよ。
(3)$n$=$3m$($m$は正の定数)で$k$=1,...,$3m$に対して
$p_k$=$\left\{\begin{array}{1}
\frac{1}{3m} (k=1,...,m) \\
\frac{2}{3m} (k=m+1,...,2m)\\
\frac{1}{m} (k=2m+1,...,3m)\\
\end{array}\right.$
とする。このゲームで成功する確率を$Z_{3m}$とするとき、$\displaystyle\lim_{m \to \infty}Z_{3m}$ を求めよ。
この動画を見る
$\Large\boxed{4}$ $n$を正の整数とし、$C_1$,...,$C_n$を$n$枚の硬貨とする。各$k$=1,...,$n$に対し、硬貨$C_k$を投げて表が出る確率を$p_k$、裏が出る確率を1-$p_k$とする。この$n$枚の硬貨を同時に投げ、表が出た硬貨の枚数が奇数であれば成功、というゲームを考える。
(1)$p_k$=$\frac{1}{3}$ ($k$=1,...,$n$)のとき、このゲームで成功する確率$X_n$を求めよ。
(2)$p_k$=$\frac{1}{2(k+1)}$ ($k$=1,...,$n$)のとき、このゲームで成功する確率$Y_n$を求めよ。
(3)$n$=$3m$($m$は正の定数)で$k$=1,...,$3m$に対して
$p_k$=$\left\{\begin{array}{1}
\frac{1}{3m} (k=1,...,m) \\
\frac{2}{3m} (k=m+1,...,2m)\\
\frac{1}{m} (k=2m+1,...,3m)\\
\end{array}\right.$
とする。このゲームで成功する確率を$Z_{3m}$とするとき、$\displaystyle\lim_{m \to \infty}Z_{3m}$ を求めよ。
福田の数学〜東京工業大学2024年理系第3問〜点列と漸化式の極限

単元:
#大学入試過去問(数学)#数列#漸化式#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ $xy$平面上に、点A($a$,0), B(0,$b$), C($-a$,0)(ただし0<$a$<$b$)をとる。点A,Bを通る直線を$l$とし、点Cを通り線分BCに垂直な直線を$k$とする。さらに、点Aを通り$y$軸に平行な直線と直線$k$との交点を$C_1$とし、点$C_1$を通り、$x$軸に平行な直線と直線$l$との交点を$A_1$とする。以下、$n$=1,2,3,...に対して、点$A_n$を通り$y$軸に平行な直線と直線$k$との交点を$C_{n+1}$、点$C_{n+1}$を通り$x$軸に平行な直線と直線$l$との交点を$A_{n+1}$とする。
(1)点$A_n$, $C_n$の座標を求めよ。
(2)△$CBA_n$の面積$S_n$を求めよ。
(3)$\displaystyle\lim_{n \to \infty}\frac{BA_n}{BC}$を求めよ。
この動画を見る
$\Large\boxed{3}$ $xy$平面上に、点A($a$,0), B(0,$b$), C($-a$,0)(ただし0<$a$<$b$)をとる。点A,Bを通る直線を$l$とし、点Cを通り線分BCに垂直な直線を$k$とする。さらに、点Aを通り$y$軸に平行な直線と直線$k$との交点を$C_1$とし、点$C_1$を通り、$x$軸に平行な直線と直線$l$との交点を$A_1$とする。以下、$n$=1,2,3,...に対して、点$A_n$を通り$y$軸に平行な直線と直線$k$との交点を$C_{n+1}$、点$C_{n+1}$を通り$x$軸に平行な直線と直線$l$との交点を$A_{n+1}$とする。
(1)点$A_n$, $C_n$の座標を求めよ。
(2)△$CBA_n$の面積$S_n$を求めよ。
(3)$\displaystyle\lim_{n \to \infty}\frac{BA_n}{BC}$を求めよ。
福田の数学〜慶應義塾大学2024年理工学部第1問(2)〜漸化式とはさみうちの原理

単元:
#大学入試過去問(数学)#漸化式#関数と極限#数列の極限#関数の極限#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
関数f(x)は実数全体で定義されており、$x\leqq 2$において
$\dfrac{2}{3}-\dfrac{1}{3}x\leqq f(x)\leqq 2-x$
を満たしているものとする。数列{$a_{ n }$}は漸化式
$a_{ n+1 }=a_{ n }+f(a_{ n })$
を満たしているものとする。
(i)$a_{ 1 } \leqq 2$ならば、すべての自然数nに対して、$a_{ 1 } \leqq a_{ n }\leqq2$となる事を証明しなさい。
(ii)$a_{ 1 } \leqq 2$ならば、$a_{ 1 }$の値によらず$\displaystyle \lim_{ n \to \infty } a_n = 2$となる事を証明しなさい。
この動画を見る
関数f(x)は実数全体で定義されており、$x\leqq 2$において
$\dfrac{2}{3}-\dfrac{1}{3}x\leqq f(x)\leqq 2-x$
を満たしているものとする。数列{$a_{ n }$}は漸化式
$a_{ n+1 }=a_{ n }+f(a_{ n })$
を満たしているものとする。
(i)$a_{ 1 } \leqq 2$ならば、すべての自然数nに対して、$a_{ 1 } \leqq a_{ n }\leqq2$となる事を証明しなさい。
(ii)$a_{ 1 } \leqq 2$ならば、$a_{ 1 }$の値によらず$\displaystyle \lim_{ n \to \infty } a_n = 2$となる事を証明しなさい。
【高校数学】無理関数のグラフの裏ワザ!例題もあるよ!

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の無理関数のグラフをかけ。
(1)$y=\sqrt{x+2}$
(2)$y=\sqrt{-3x-6}$
(3)$y=-\sqrt{7-4x}$
(4)$y=-\sqrt{\dfrac{1}{2}x-3}$
この動画を見る
次の無理関数のグラフをかけ。
(1)$y=\sqrt{x+2}$
(2)$y=\sqrt{-3x-6}$
(3)$y=-\sqrt{7-4x}$
(4)$y=-\sqrt{\dfrac{1}{2}x-3}$
【高校数学】無理関数のグラフの裏ワザ!例題もあるよ!

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の無理関数のグラフをかけ。
(1)$ y=\sqrt{x+2}$
(2)$ y=\sqrt{ー3x-6}$
(3)$ y=-\sqrt{7-4x}$
(4)$ y=-\sqrt{\frac{1}{2}x-3}$
この動画を見る
次の無理関数のグラフをかけ。
(1)$ y=\sqrt{x+2}$
(2)$ y=\sqrt{ー3x-6}$
(3)$ y=-\sqrt{7-4x}$
(4)$ y=-\sqrt{\frac{1}{2}x-3}$
福田の数学〜東京大学2018年理系第3問〜軌跡と領域そして極限

単元:
#大学入試過去問(数学)#平面上のベクトル#図形と方程式#軌跡と領域#ベクトルと平面図形、ベクトル方程式#関数と極限#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
放物線$y=x^2$のうち$-1 \leqq x \leqq 1$を満たす部分をCとする。座標平面上の原点Oと点A(1,0)を考える。K>0を実数とする。点PがCの上を動き、天Qが線分OA上を動くとき$\overrightarrow{ OR }=\displaystyle \frac{1}{k}\overrightarrow{ OP }+k\overrightarrow{ OQ }$を満たす点Rが動く領域の面積をS(k)とする。
S(k)および$\displaystyle \lim_{ k \to +0 } S(k) ,\displaystyle \lim_{ k \to \infty }S(k)$を求めよ。
2018東京大学理系過去問
この動画を見る
放物線$y=x^2$のうち$-1 \leqq x \leqq 1$を満たす部分をCとする。座標平面上の原点Oと点A(1,0)を考える。K>0を実数とする。点PがCの上を動き、天Qが線分OA上を動くとき$\overrightarrow{ OR }=\displaystyle \frac{1}{k}\overrightarrow{ OP }+k\overrightarrow{ OQ }$を満たす点Rが動く領域の面積をS(k)とする。
S(k)および$\displaystyle \lim_{ k \to +0 } S(k) ,\displaystyle \lim_{ k \to \infty }S(k)$を求めよ。
2018東京大学理系過去問
大学入試問題#732「まあ面白い良問!」 早稲田大学人間科学部(2022) 級数

単元:
#関数と極限#数列の極限#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
自然数$n$に対して、
$S_n=\displaystyle \int_{e^{n-1}}^{e^n} \displaystyle \frac{\sin(\pi\ log\ x)}{x^2} dx$とする。
さらに $T=\displaystyle \sum_{n=1}^\infty S_n$とする。
以下の問いに答えよ。
(1)$S_1$を求めよ。
(2)$\displaystyle \frac{S_{n+1}}{S_n}$を求めよ。
(3)$T$を求めよ。
出典:2022年早稲田大学人間科学部 入試問題
この動画を見る
自然数$n$に対して、
$S_n=\displaystyle \int_{e^{n-1}}^{e^n} \displaystyle \frac{\sin(\pi\ log\ x)}{x^2} dx$とする。
さらに $T=\displaystyle \sum_{n=1}^\infty S_n$とする。
以下の問いに答えよ。
(1)$S_1$を求めよ。
(2)$\displaystyle \frac{S_{n+1}}{S_n}$を求めよ。
(3)$T$を求めよ。
出典:2022年早稲田大学人間科学部 入試問題
高校数学:数学検定準1級1次:問題6,7 双曲線の焦点、関数の極限

単元:
#数学検定・数学甲子園・数学オリンピック等#平面上の曲線#関数と極限#2次曲線#関数の極限#数学検定#数学検定準1級#数学(高校生)#数C#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
xy平面上の双曲線
$\frac{x^2}{36}-\frac{y^2}{64}=-1$
の焦点の座標を求めなさい。
次の極限値を求めなさい。
$\displaystyle \lim_{ x \to 1 }\displaystyle \frac{x^2+2x-3}{\sqrt[ 3 ]{ x }-1}$
この動画を見る
xy平面上の双曲線
$\frac{x^2}{36}-\frac{y^2}{64}=-1$
の焦点の座標を求めなさい。
次の極限値を求めなさい。
$\displaystyle \lim_{ x \to 1 }\displaystyle \frac{x^2+2x-3}{\sqrt[ 3 ]{ x }-1}$
福田の数学〜東京大学2018年理系第1問〜関数の増減と極限の計算

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#色々な関数の導関数#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$f(x)=\dfrac{x}{\sin x}+\cos x (0 \lt x \lt \pi)$のぞうげんひょうを作り、$x→+0,x→\pi-0$のときの極限を調べよ。
2018東京大学理過去問
この動画を見る
$f(x)=\dfrac{x}{\sin x}+\cos x (0 \lt x \lt \pi)$のぞうげんひょうを作り、$x→+0,x→\pi-0$のときの極限を調べよ。
2018東京大学理過去問
【高校数学】分数関数と一次関数の不等式をグラフを使わない裏ワザ!②

単元:
#関数と極限#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の不等式を解け。
$\displaystyle\frac{2x}{x+1}≧x+6$
この動画を見る
次の不等式を解け。
$\displaystyle\frac{2x}{x+1}≧x+6$
【高校数学】分数関数と一次関数の不等式をグラフを使わない裏ワザ!②

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の不等式を解け。
$\dfrac{2x}{x+1}\geqq x+6$
この動画を見る
次の不等式を解け。
$\dfrac{2x}{x+1}\geqq x+6$
【高校数学】分数関数と一次関数の不等式をグラフを使わない裏ワザ!

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の不等式を解け。
$\dfrac{3x-4}{2x-3}\lt x$
この動画を見る
次の不等式を解け。
$\dfrac{3x-4}{2x-3}\lt x$
【高校数学】分数関数と一次関数の不等式をグラフを使わない裏ワザ!

単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の不等式を解け。
$\displaystyle\frac{3x-4}{2x-3} < x$
この動画を見る
次の不等式を解け。
$\displaystyle\frac{3x-4}{2x-3} < x$
【高校数学】分数関数の漸近線とグラフの簡単な求め方!
単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
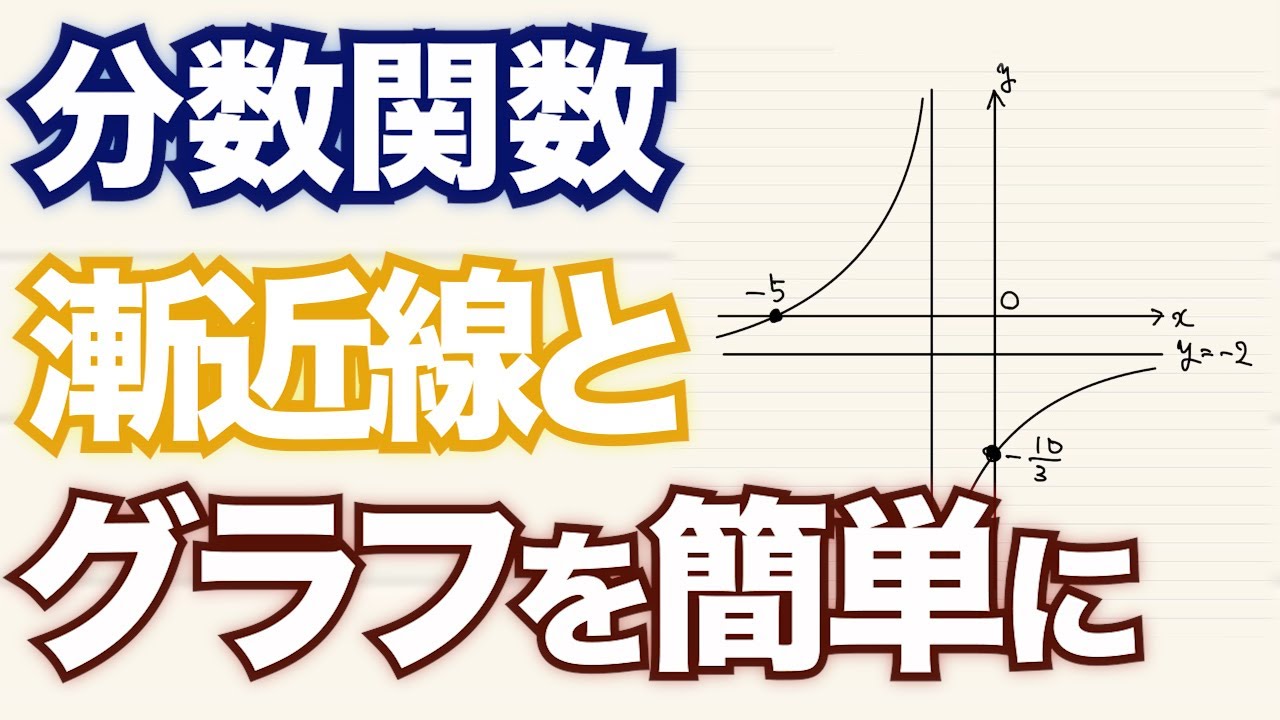
次の関数のグラフをかけ。また,その漸近線を求めよ。
$y=\dfrac{-2x–10}{x+3}$
この動画を見る
次の関数のグラフをかけ。また,その漸近線を求めよ。
$y=\dfrac{-2x–10}{x+3}$
【高校数学】分数関数の漸近線とグラフの簡単な求め方!
単元:
#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
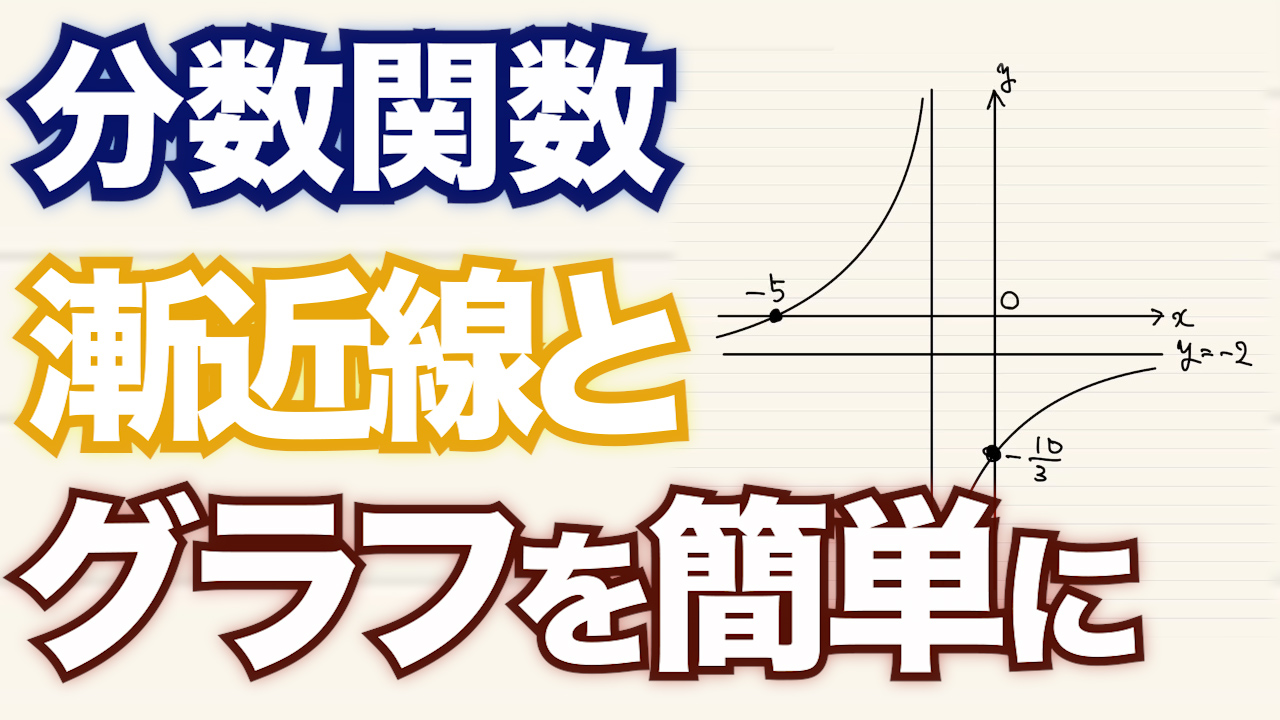
次の関数のグラフをかけ。また,その漸近線を求めよ。
$y=\frac{–2x–10}{x+3}$
この動画を見る
次の関数のグラフをかけ。また,その漸近線を求めよ。
$y=\frac{–2x–10}{x+3}$
中学からの極限(応用編)~全国入試問題解法 #shorts #数学 #高校入試 #頭の体操

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \displaystyle \lim_{x \to 1}\dfrac{x^2+2x-3}{x^2+x-2}$を求めよ.
この動画を見る
$ \displaystyle \lim_{x \to 1}\dfrac{x^2+2x-3}{x^2+x-2}$を求めよ.
中学からの極限(発展編)~全国入試問題解法 #shorts #数学 #極限 #頭の体操

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \displaystyle \lim_{x \to 1}\dfrac{ax-1}{x-a}$を求めよ.
この動画を見る
$ \displaystyle \lim_{x \to 1}\dfrac{ax-1}{x-a}$を求めよ.
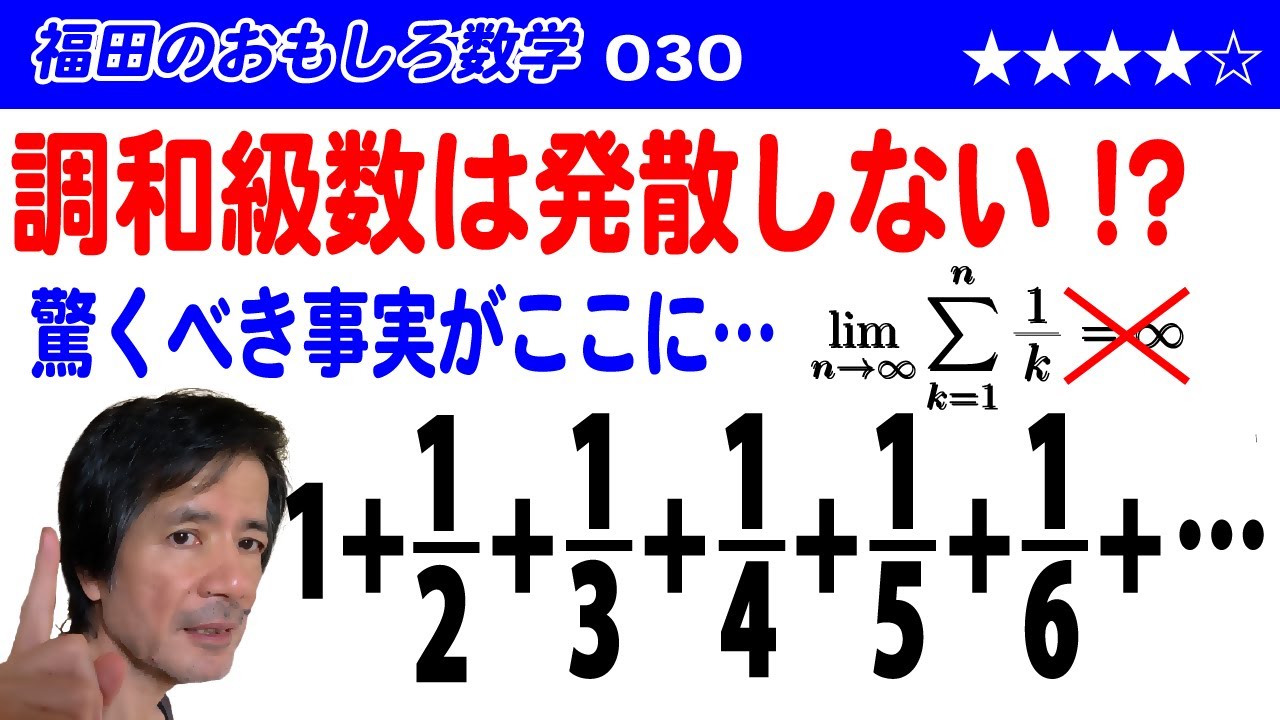
福田のおもしろ数学030〜調和級数は発散しない?〜驚くべき事実がここに
単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
調和級数
$1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}…$
について解説します
この動画を見る
調和級数
$1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}…$
について解説します
中学からの極限(基礎編)!~全国入試問題解法 #数学 #極限 #微分積分 #頭の体操

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \displaystyle \lim_{x \to \infty}\dfrac{5x^2+x+4}{x^2+2x+3}$を求めよ.
この動画を見る
$ \displaystyle \lim_{x \to \infty}\dfrac{5x^2+x+4}{x^2+2x+3}$を求めよ.
福田のおもしろ数学020〜わんちゃんの男の子と女の子の比率は〜Google入社試験の類題

単元:
#数列#数列とその和(等差・等比・階差・Σ)#関数と極限#数列の極限#数学(高校生)#数B#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
わんちゃんの国があります。この国ではどの家庭も男の子が産まれるまで子供を作り続けます。この国の男の子と女の子の比率はどうなりますか.
google入社試験過去問
この動画を見る
わんちゃんの国があります。この国ではどの家庭も男の子が産まれるまで子供を作り続けます。この国の男の子と女の子の比率はどうなりますか.
google入社試験過去問
中学からの極限(徹底編)~全国入試問題解法 #shorts #数学 #高校入試 #動体視力

単元:
#関数と極限#関数の極限#数学(高校生)#数Ⅲ
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \displaystyle \lim_{(x,y)\to (0,0)}\dfrac{x^2-y^2}{x^2+y^2}$
次の関数の極限を調べよ.
この動画を見る
$ \displaystyle \lim_{(x,y)\to (0,0)}\dfrac{x^2-y^2}{x^2+y^2}$
次の関数の極限を調べよ.
