 定積分
定積分
 定積分
定積分
【超良問】大学入試問題#337 弘前大学(2010) #定積分 #ウォリス積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\{x(1-x)\}^{\frac{3}{2}}dx$
出典:2010年弘前大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\{x(1-x)\}^{\frac{3}{2}}dx$
出典:2010年弘前大学 入試問題
大学入試問題#338 数学トークさん #定積分 #キングプロパティ
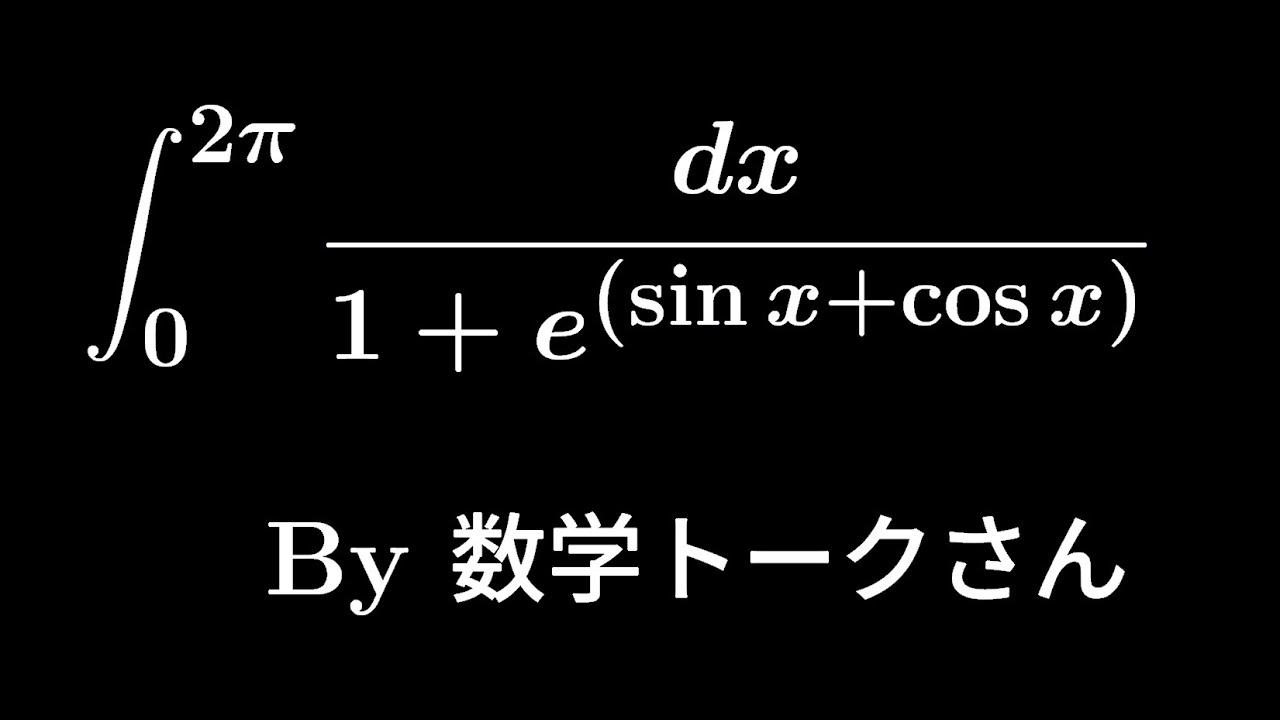
単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2\pi}\displaystyle \frac{dx}{1+e^{(\sin\ x+\cos\ x)}}$
この動画を見る
$\displaystyle \int_{0}^{2\pi}\displaystyle \frac{dx}{1+e^{(\sin\ x+\cos\ x)}}$
福田の数学〜上智大学2022年TEAP理系型第4問〜媒介変数で表された極方程式

単元:
#大学入試過去問(数学)#平面上の曲線#微分とその応用#積分とその応用#微分法#定積分#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#上智大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
座標平面において、原点を極とし、x軸の正の部分を始線とする極座標を考え
る。平面上を運動する点Pの極座標$(r,\ θ)$が、時刻$t \geqq 0$の関数として、
$r=1+t,\ \ \ θ=\log(1+t)$
で与えられるとする。時刻$t=0$にPが出発してから初めてy軸上に到着するまで
にPが描く軌跡をCとする。
(1)$\ t \gt 0$において、Pが初めてy軸上に到着するときのtの値を求めよ。
(2)C上の点のx座標の最大値を求めよ。
(3)Cの長さを求めよ。
(4)Cを座標平面上に図示せよ。
(5)Cとx軸とy軸で囲まれた部分の面積を求めよ。
2022上智大学理系過去問
この動画を見る
座標平面において、原点を極とし、x軸の正の部分を始線とする極座標を考え
る。平面上を運動する点Pの極座標$(r,\ θ)$が、時刻$t \geqq 0$の関数として、
$r=1+t,\ \ \ θ=\log(1+t)$
で与えられるとする。時刻$t=0$にPが出発してから初めてy軸上に到着するまで
にPが描く軌跡をCとする。
(1)$\ t \gt 0$において、Pが初めてy軸上に到着するときのtの値を求めよ。
(2)C上の点のx座標の最大値を求めよ。
(3)Cの長さを求めよ。
(4)Cを座標平面上に図示せよ。
(5)Cとx軸とy軸で囲まれた部分の面積を求めよ。
2022上智大学理系過去問
大学入試問題#336 横浜国立大学2013 #定積分
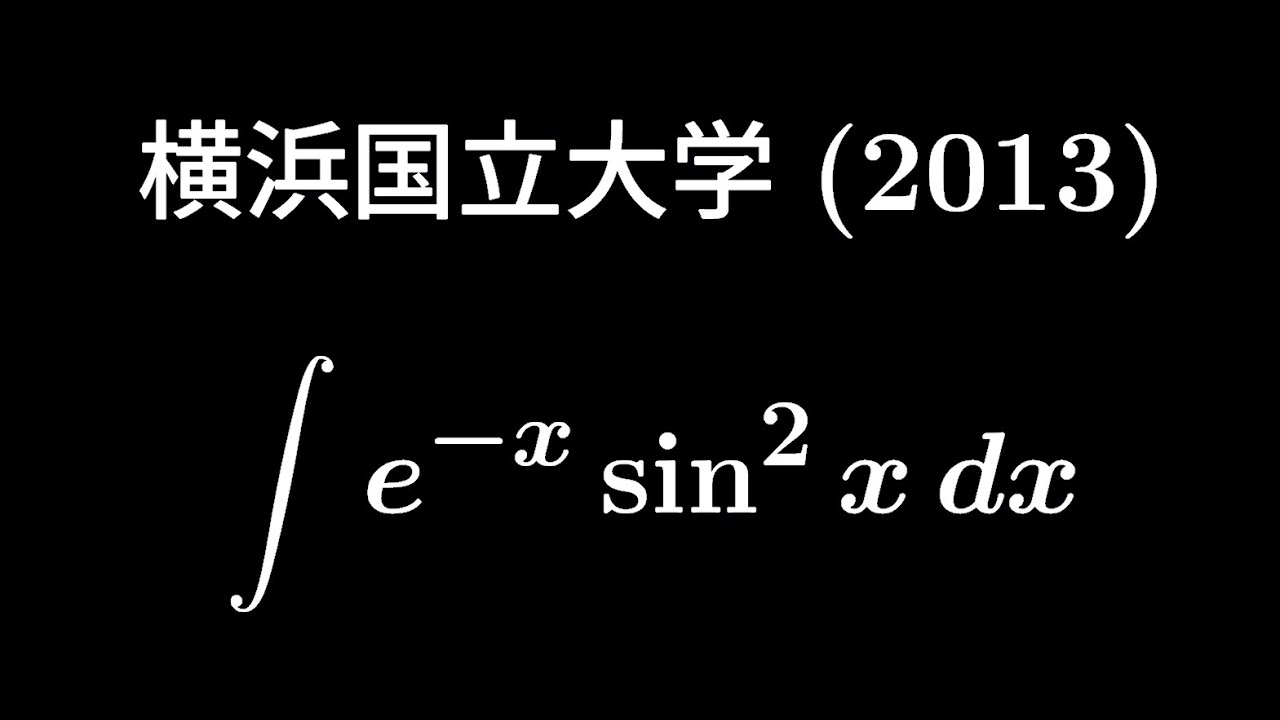
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int e^{-x}\sin^2x\ dx$
出典:2013年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int e^{-x}\sin^2x\ dx$
出典:2013年横浜国立大学 入試問題
大学入試問題#335 防衛医科大学(2010) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#防衛医科大学
指導講師:
ますただ
問題文全文(内容文):
$0 \lt a \lt 1$
$\displaystyle \int_{a}^{1}x\sqrt{ 1-x }\ dx$
出典:2010年防衛医科大学 入試問題
この動画を見る
$0 \lt a \lt 1$
$\displaystyle \int_{a}^{1}x\sqrt{ 1-x }\ dx$
出典:2010年防衛医科大学 入試問題
大学入試問題#333 青山学院大学(2013) #定積分 #極限

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ a \to \infty }\displaystyle \int_{0}^{log\ a}\displaystyle \frac{e^x}{e^x+a}dx$
出典:2013年青山学院大学 入試問題
この動画を見る
$\displaystyle \lim_{ a \to \infty }\displaystyle \int_{0}^{log\ a}\displaystyle \frac{e^x}{e^x+a}dx$
出典:2013年青山学院大学 入試問題
大学入試問題#331 高校教員が作成した問題 #定積分
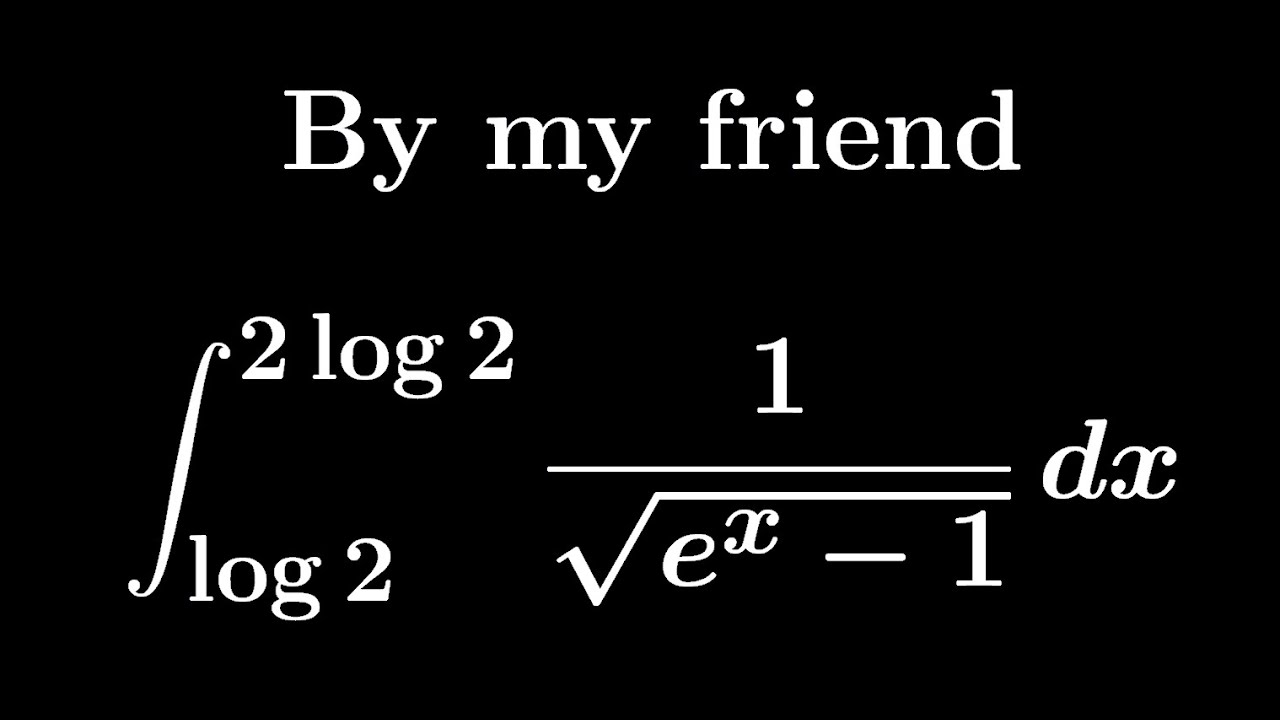
単元:
#積分とその応用#定積分#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{log2}^{2log2}\displaystyle \frac{dx}{\sqrt{ e^x-1 }}$
この動画を見る
$\displaystyle \int_{log2}^{2log2}\displaystyle \frac{dx}{\sqrt{ e^x-1 }}$
大学入試問題#330 横浜国立大学(2013) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\sqrt{ 1+2\sqrt{ x } }\ dx$
出典:2013年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\sqrt{ 1+2\sqrt{ x } }\ dx$
出典:2013年横浜国立大学 入試問題
大学入試問題#329 熊本大学(2013) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#熊本大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\displaystyle \frac{\sin\displaystyle \frac{\theta}{2}}{1+\sin\displaystyle \frac{\theta}{2}}d\theta$
出典:2013年熊本大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\displaystyle \frac{\sin\displaystyle \frac{\theta}{2}}{1+\sin\displaystyle \frac{\theta}{2}}d\theta$
出典:2013年熊本大学 入試問題
大学入試問題#328 金沢大学(2013) #定積分
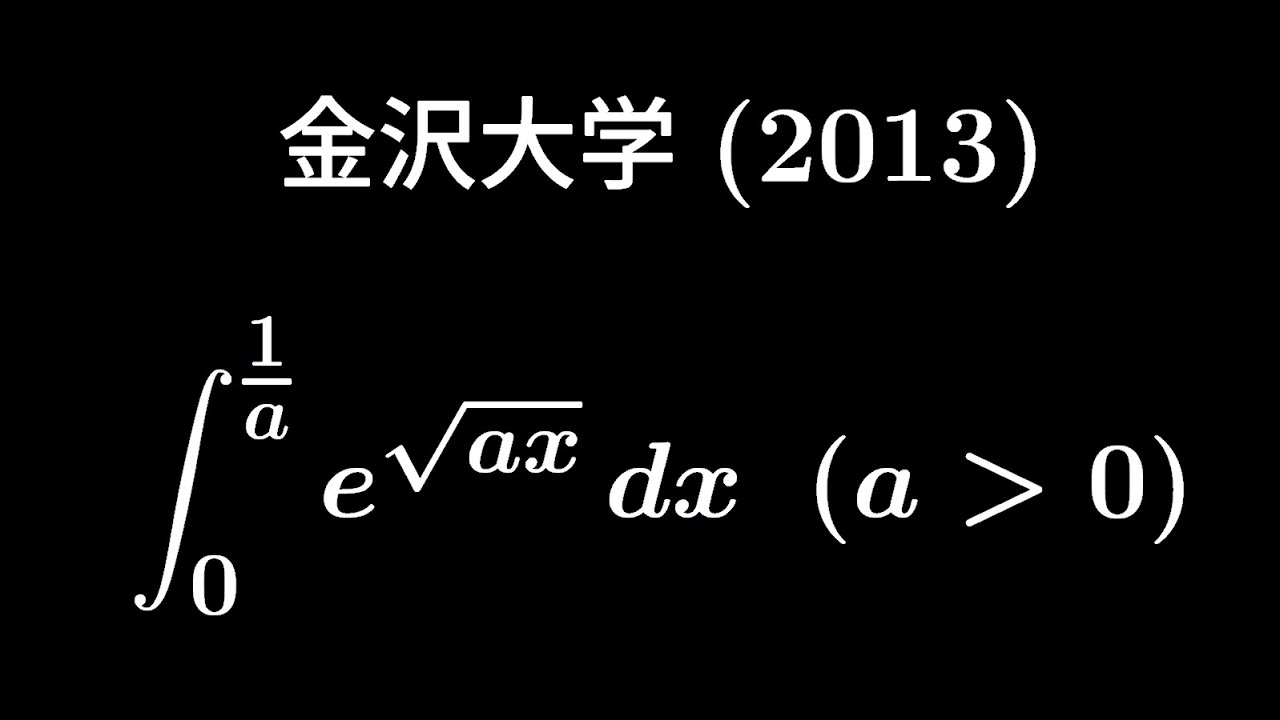
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#金沢大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a \gt 0$
$\displaystyle \int_{0}^{\frac{1}{a}}e^{\sqrt{ ax }}dx$
出典:2013年金沢大学 入試問題
この動画を見る
$a \gt 0$
$\displaystyle \int_{0}^{\frac{1}{a}}e^{\sqrt{ ax }}dx$
出典:2013年金沢大学 入試問題
大学入試問題#327 埼玉大学(2010) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\sin\ x}{9+16\sin^2x}dx$
出典:2010年埼玉大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\sin\ x}{9+16\sin^2x}dx$
出典:2010年埼玉大学 入試問題
大学入試問題#325 宮崎大学(2013) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\pi}^{\pi}|e^{\cos\ x}\sin\ x|dx$
出典:2013年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{-\pi}^{\pi}|e^{\cos\ x}\sin\ x|dx$
出典:2013年宮崎大学 入試問題
AkiyaMathさんと学ぶ積分問題 #King_property
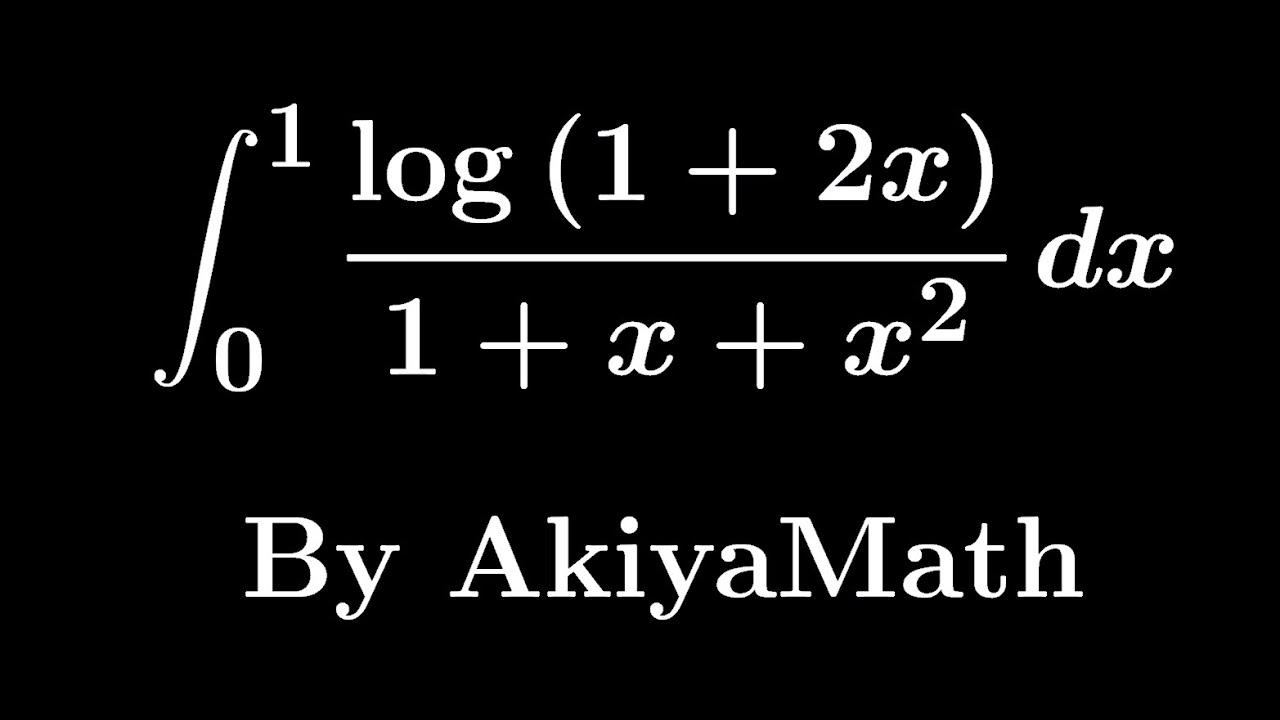
単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{log(1+2x)}{1+x+x^2}dx$
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{log(1+2x)}{1+x+x^2}dx$
大学入試問題#324 宮崎大学(2013) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}x^3log(x^2+1)dx$
出典:2013年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}x^3log(x^2+1)dx$
出典:2013年宮崎大学 入試問題
福田の数学〜青山学院大学2022年理工学部第4問〜部分積分と定積分で表された関数

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$ x \gt 0$を定義域とする関数f(x)が次の等式
$f(x)=\int_1^e\log(xt) f(t)dt+x$
を満たすとき、以下の問いに答えよ。
(1)$\int_1^e\log x dx$を求めよ。
(2)$\int_1^e(\log x)^2 dx$ を求めよ。
(3)$\int_1^ex\log x dx$を求めよ。
(4)$f(x)$を求めよ。
2022青山学院大学理工学部過去問
この動画を見る
$ x \gt 0$を定義域とする関数f(x)が次の等式
$f(x)=\int_1^e\log(xt) f(t)dt+x$
を満たすとき、以下の問いに答えよ。
(1)$\int_1^e\log x dx$を求めよ。
(2)$\int_1^e(\log x)^2 dx$ を求めよ。
(3)$\int_1^ex\log x dx$を求めよ。
(4)$f(x)$を求めよ。
2022青山学院大学理工学部過去問
大学入試問題#321 甲南大学(2021) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#甲南大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^2(1-x)^2}{1+x^2}dx$
出典:2021年甲南大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^2(1-x)^2}{1+x^2}dx$
出典:2021年甲南大学 入試問題
大学入試問題#320 宮崎大学 改 (2010) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{log\ \pi}^{log\ 2\pi}e^{2x}\sin(e^x)dx$
出典:2010年宮崎大学 入試問題
この動画を見る
$\displaystyle \int_{log\ \pi}^{log\ 2\pi}e^{2x}\sin(e^x)dx$
出典:2010年宮崎大学 入試問題
大学入試問題#319 電気通信大学(2010) #定積分 #極限

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#不定積分#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ a \to \infty }\displaystyle \int_{0}^{a}\displaystyle \frac{1}{1+e^x}dx$
出典:2010年電気通信大学 入試問題
この動画を見る
$\displaystyle \lim_{ a \to \infty }\displaystyle \int_{0}^{a}\displaystyle \frac{1}{1+e^x}dx$
出典:2010年電気通信大学 入試問題
大学入試問題#318 立教大学 改 (2021) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e}\displaystyle \frac{(log\ x)^4}{x^2}dx$
出典:2021年立教大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e}\displaystyle \frac{(log\ x)^4}{x^2}dx$
出典:2021年立教大学 入試問題
大学入試問題#317 鳥取大学(2010) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#鳥取大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e}(log\ x)^4dx$
出典:2010年鳥取大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e}(log\ x)^4dx$
出典:2010年鳥取大学 入試問題
大学入試問題#315 富山県立大学(2010) #定積分
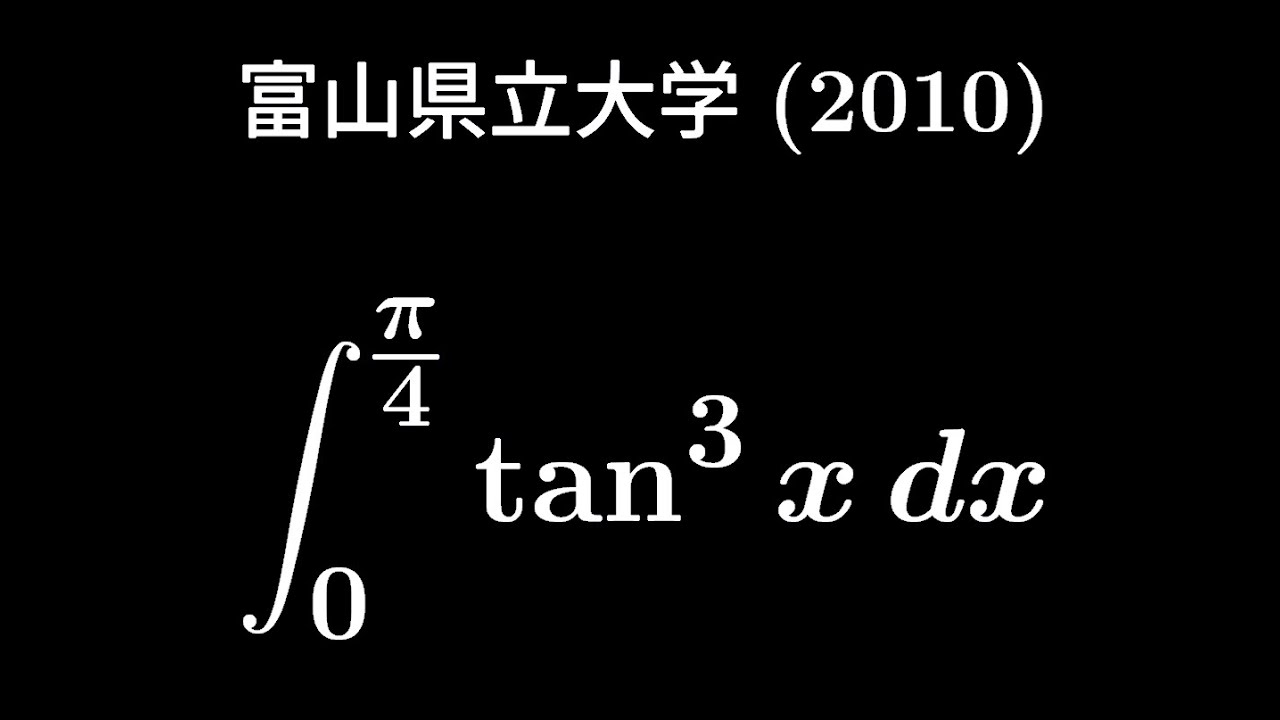
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#富山県立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}}\tan^3x\ dx$
出典:2010年富山県立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}\tan^3x\ dx$
出典:2010年富山県立大学 入試問題
大学入試問題#314 弘前大学(2010) #定積分
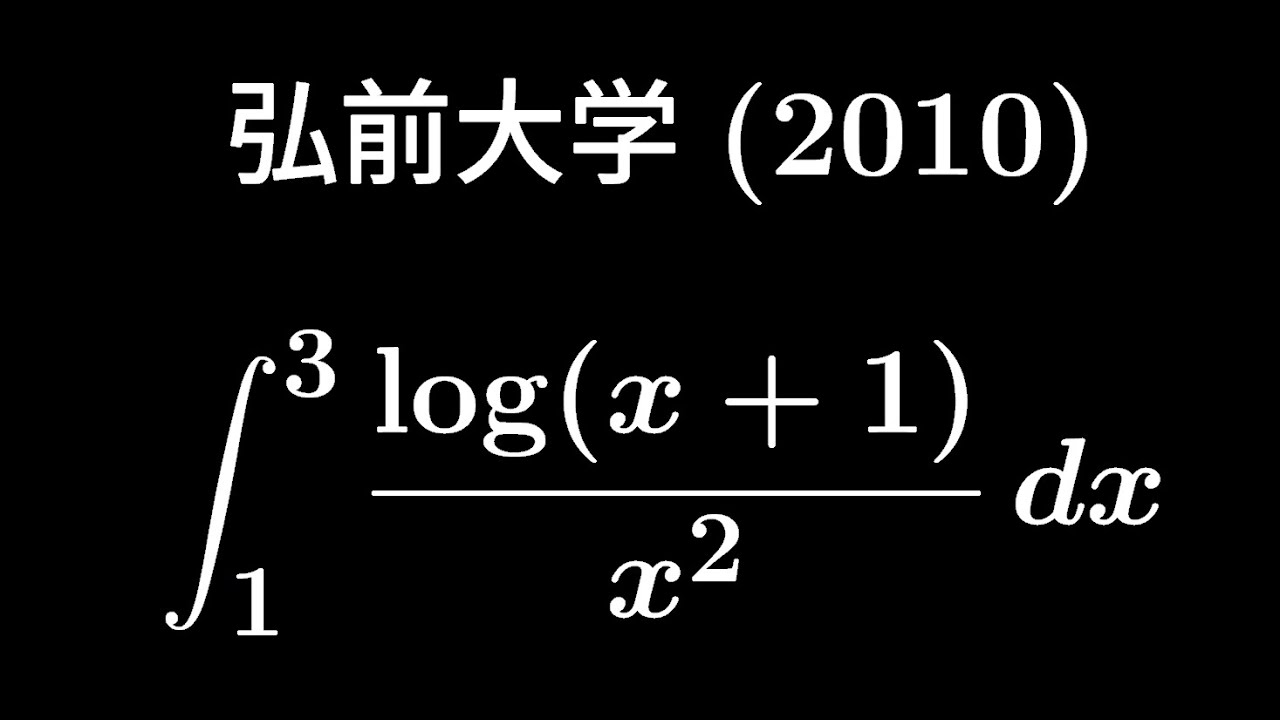
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{3}\displaystyle \frac{log(x+1)}{x^2}dx$
出典:2010年広前大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{3}\displaystyle \frac{log(x+1)}{x^2}dx$
出典:2010年広前大学 入試問題
大学入試問題#313 自治医科大学(2021) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#自治医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\cos\ x(1+\sin\ x)}{2+\sin\ x}dx$
出典:2021年自治医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\cos\ x(1+\sin\ x)}{2+\sin\ x}dx$
出典:2021年自治医科大学 入試問題
数学コンテスト(米国、加奈陀) 2005年 #定積分 #King_property
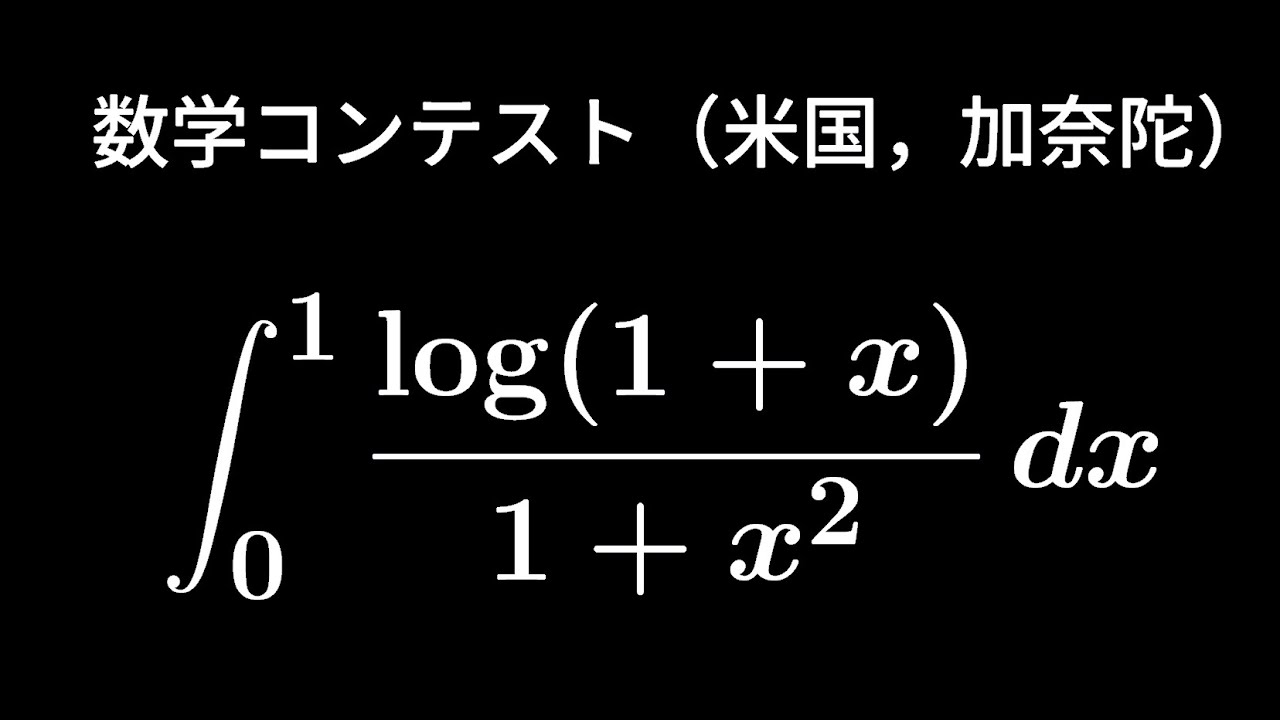
単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{log(1+x)}{1+x^2}dx$
出典:数学コンテスト
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{log(1+x)}{1+x^2}dx$
出典:数学コンテスト
#55数検準1級1次 過去問 2022年6月 #定積分

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^3}{1+x^2}dx$
出典:2022年6月数検準一級一次
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^3}{1+x^2}dx$
出典:2022年6月数検準一級一次
福田の数学〜明治大学2022年全学部統一入試理系第3問〜2次曲線の極方程式と置換積分

単元:
#大学入試過去問(数学)#平面上の曲線#微分とその応用#積分とその応用#2次曲線#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#明治大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$a,\ h$を正の実数とする。座標平面において、原点Oからの距離が
直線$x=h$からの距離の$a$倍であるような点$P$の軌跡を考える。点$P$の座標を$(x,\ y)$とする
と、$x,\ y$は次の方程式を満たす。
$(1-\boxed{ア})\ x^2+2\ \boxed{イ}\ x+y^2=\boxed{ウ}...(1)$
$\boxed{ア},\ \boxed{イ},\ \boxed{ウ}$の解答群
$⓪a^2 ①h^2 ②a^3 ③a^2h ④ah^2$
$⑤h^3 ⑥b^4 ⑦a^2h^2 ⑧ah^3 ⑨h^4$
次に、座標平面の原点$O$を極、$x$軸の正の部分を始線とする極座標を考える。
点$P$の極座標を$(r\ \theta)$とする。$r \leqq h$を満たすとき、
点$P$の直交座標$(x,\ y)$を$a,\ h,\ θ$を用いて表すと
$(x,\ y)=(\frac{\boxed{エ}}{\boxed{オ}}\ \cos θ,\ \frac{\boxed{エ}}{\boxed{オ}}\ \sin θ)...(2) $
$\boxed{エ},\ \boxed{オ}$の解答群
$⓪h①ah②h^2③ah^2④1+a\cos θ$
$⑤1+a\sin θ ⑥a\cos θ-1⑦a\sin θ-1⑧1-a\cos θ ⑨1-a\sin θ$
(1)から、$a=\boxed{カ}$のとき、点$P$の軌跡は放物線$x=\boxed{キ}\ y^2+\boxed{ク}$となる。
この放物線とy軸で囲まれた図形の面積$S$は
$S=2\int_0^{\boxed{ケ}}xdy=2\int_0^{\boxed{ケ}}(\boxed{キ}\ y^2+\boxed{ク})dy=$
$\frac{\boxed{コ}}{\boxed{サ}}\ h^2$
である。したがって、(2)を利用すれば、置換積分法により次の等式が成り立つことが分かる。
$\int_0^{\frac{\pi}{2}}\frac{\cos θ}{(1+\cos θ)^2}dθ=\frac{\boxed{シ}}{\boxed{ス}}$
$\boxed{キ},\ \boxed{ク},\ \boxed{ケ}$の解答群
$⓪h ①2h ②\frac{h}{2} ③-\frac{h}{2} ④\frac{1}{h}$
$⑤-\frac{1}{h} ⑥\frac{1}{2h} ⑦-\frac{1}{2h} ⑧h^2 ⑨-h^2$
2022明治大学全統理系過去問
この動画を見る
$a,\ h$を正の実数とする。座標平面において、原点Oからの距離が
直線$x=h$からの距離の$a$倍であるような点$P$の軌跡を考える。点$P$の座標を$(x,\ y)$とする
と、$x,\ y$は次の方程式を満たす。
$(1-\boxed{ア})\ x^2+2\ \boxed{イ}\ x+y^2=\boxed{ウ}...(1)$
$\boxed{ア},\ \boxed{イ},\ \boxed{ウ}$の解答群
$⓪a^2 ①h^2 ②a^3 ③a^2h ④ah^2$
$⑤h^3 ⑥b^4 ⑦a^2h^2 ⑧ah^3 ⑨h^4$
次に、座標平面の原点$O$を極、$x$軸の正の部分を始線とする極座標を考える。
点$P$の極座標を$(r\ \theta)$とする。$r \leqq h$を満たすとき、
点$P$の直交座標$(x,\ y)$を$a,\ h,\ θ$を用いて表すと
$(x,\ y)=(\frac{\boxed{エ}}{\boxed{オ}}\ \cos θ,\ \frac{\boxed{エ}}{\boxed{オ}}\ \sin θ)...(2) $
$\boxed{エ},\ \boxed{オ}$の解答群
$⓪h①ah②h^2③ah^2④1+a\cos θ$
$⑤1+a\sin θ ⑥a\cos θ-1⑦a\sin θ-1⑧1-a\cos θ ⑨1-a\sin θ$
(1)から、$a=\boxed{カ}$のとき、点$P$の軌跡は放物線$x=\boxed{キ}\ y^2+\boxed{ク}$となる。
この放物線とy軸で囲まれた図形の面積$S$は
$S=2\int_0^{\boxed{ケ}}xdy=2\int_0^{\boxed{ケ}}(\boxed{キ}\ y^2+\boxed{ク})dy=$
$\frac{\boxed{コ}}{\boxed{サ}}\ h^2$
である。したがって、(2)を利用すれば、置換積分法により次の等式が成り立つことが分かる。
$\int_0^{\frac{\pi}{2}}\frac{\cos θ}{(1+\cos θ)^2}dθ=\frac{\boxed{シ}}{\boxed{ス}}$
$\boxed{キ},\ \boxed{ク},\ \boxed{ケ}$の解答群
$⓪h ①2h ②\frac{h}{2} ③-\frac{h}{2} ④\frac{1}{h}$
$⑤-\frac{1}{h} ⑥\frac{1}{2h} ⑦-\frac{1}{2h} ⑧h^2 ⑨-h^2$
2022明治大学全統理系過去問
福田の数学〜明治大学2022年全学部統一入試理系第1問(2)〜定積分と極限

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
(2)$\log$を自然対数とするとき、次の等式が成り立つ。
$\lim_{h \to 0}\int_{\frac{\pi}{3}}^{\frac{\pi}{3}+h}\log(|\sin t|^{\frac{1}{h}})dt=$
$\frac{1}{\boxed{ウ}}\log\frac{\boxed{エ}}{\boxed{オ}}$
2022明治大学全統理系過去問
この動画を見る
(2)$\log$を自然対数とするとき、次の等式が成り立つ。
$\lim_{h \to 0}\int_{\frac{\pi}{3}}^{\frac{\pi}{3}+h}\log(|\sin t|^{\frac{1}{h}})dt=$
$\frac{1}{\boxed{ウ}}\log\frac{\boxed{エ}}{\boxed{オ}}$
2022明治大学全統理系過去問
福田の数学〜明治大学2022年全学部統一入試理系第1問(1)〜面積計算

単元:
#大学入試過去問(数学)#積分とその応用#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
(1)曲線$y=1+\sin^2 x$と$x$軸、$y$軸、
および直線$x=\pi$で囲まれた図形の面積は
$\frac{\boxed{ア}}{\boxed{イ}}\ \pi$となる。
2022明治大学全統理系過去問
この動画を見る
(1)曲線$y=1+\sin^2 x$と$x$軸、$y$軸、
および直線$x=\pi$で囲まれた図形の面積は
$\frac{\boxed{ア}}{\boxed{イ}}\ \pi$となる。
2022明治大学全統理系過去問
AkiyaMathさんと学ぶ積分計算Level 3
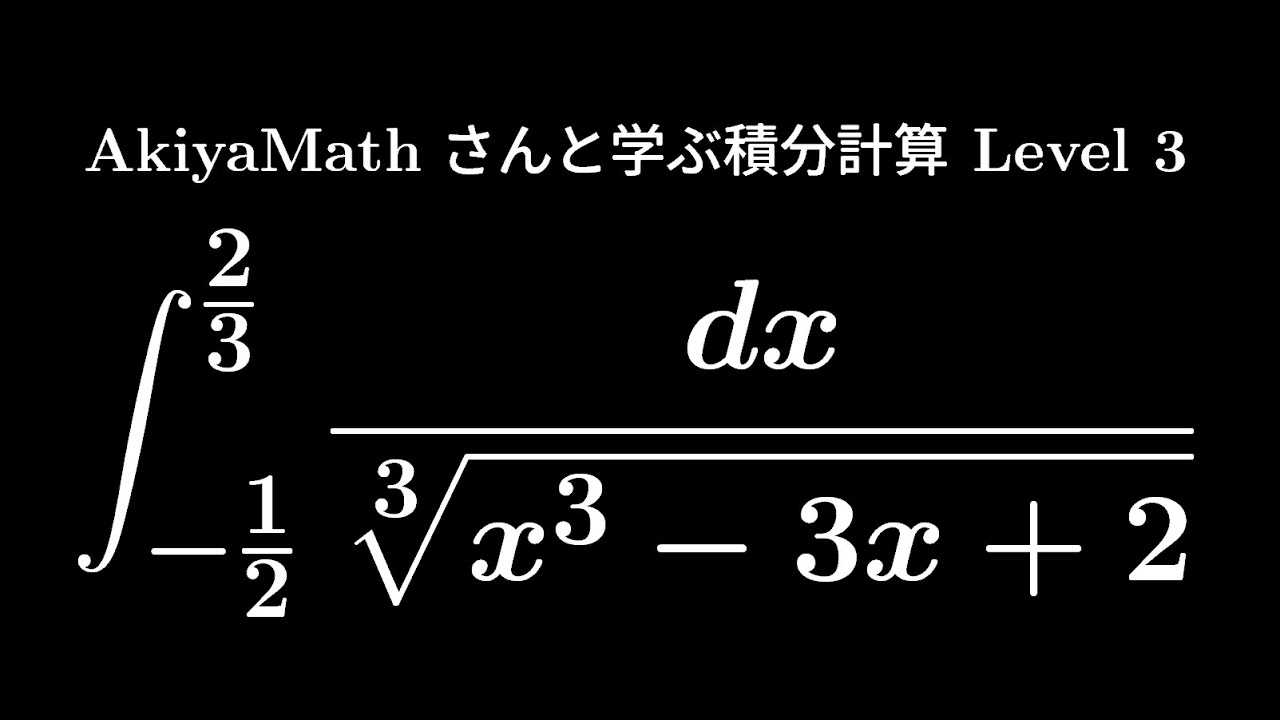
単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{1}{2}}^{\frac{2}{3}}\displaystyle \frac{dx}{\sqrt[ 3 ]{ x^3-3x+2 }}$
この動画を見る
$\displaystyle \int_{-\frac{1}{2}}^{\frac{2}{3}}\displaystyle \frac{dx}{\sqrt[ 3 ]{ x^3-3x+2 }}$
福田の数学〜早稲田大学2022年教育学部第1問(2)〜定積分で表された関数

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}\ (2)t \geqq 0$に対して
$f(t)=2\pi\int_0^{2t}|x-t|\cos(2\pi x)dx-t\sin(4\pi t)$
と定義する。このとき、
$f(t)=0$
を満たすtのうち、閉区間[0,1]に属する相異なるものはいくつあるか
早稲田大学教育学部過去問
この動画を見る
${\large\boxed{1}}\ (2)t \geqq 0$に対して
$f(t)=2\pi\int_0^{2t}|x-t|\cos(2\pi x)dx-t\sin(4\pi t)$
と定義する。このとき、
$f(t)=0$
を満たすtのうち、閉区間[0,1]に属する相異なるものはいくつあるか
早稲田大学教育学部過去問
