 積分とその応用
積分とその応用
 積分とその応用
積分とその応用
大学入試問題#385「もはや日曜日の朝食のメニュー」 信州大学(2009) #定積分

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a \gt 0$
$\displaystyle \int_{-a}^{a} \displaystyle \frac{x^2\cos\ x+e^x}{e^x+1} dx$
出典:2009年信州大学 入試問題
この動画を見る
$a \gt 0$
$\displaystyle \int_{-a}^{a} \displaystyle \frac{x^2\cos\ x+e^x}{e^x+1} dx$
出典:2009年信州大学 入試問題
福田の1.5倍速演習〜合格する重要問題017〜東北大学2016年度理系数学第6問〜定積分で表された関数

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
関数
$f(x)=\int_0^{\pi}|\sin(t-x)-\sin2t|dt$
の区間$\ 0 \leqq x \leqq \pi\ $における最大値と最小値を求めよ。
2016東北大学理系過去問
この動画を見る
関数
$f(x)=\int_0^{\pi}|\sin(t-x)-\sin2t|dt$
の区間$\ 0 \leqq x \leqq \pi\ $における最大値と最小値を求めよ。
2016東北大学理系過去問
大学入試問題#383「もう、この手法は擦りすぎか」 東洋大学2011 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東洋大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \displaystyle \frac{\cos^2x}{2^x+1} dx$
出典:2011年東洋大学 入試問題
この動画を見る
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \displaystyle \frac{\cos^2x}{2^x+1} dx$
出典:2011年東洋大学 入試問題
大学入試問題#382「初手が重要かと」 千葉大学 改 2009 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{3\sqrt{ 3 }} \displaystyle \frac{1}{1+\sqrt[ 3 ]{ x^2 }} dx$
出典:2009年千葉大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{3\sqrt{ 3 }} \displaystyle \frac{1}{1+\sqrt[ 3 ]{ x^2 }} dx$
出典:2009年千葉大学 入試問題
大学入試問題#381「ストック0でPC破損との闘い」 愛知工業大学2011 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#愛知工業大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2} \displaystyle \frac{x^3+3x}{x^2+1} dx$
出典:2011年愛知工業大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{2} \displaystyle \frac{x^3+3x}{x^2+1} dx$
出典:2011年愛知工業大学 入試問題
#大学への数学 学力コンテスト(3)「どこで技をかけにいくか・・・」 #定積分
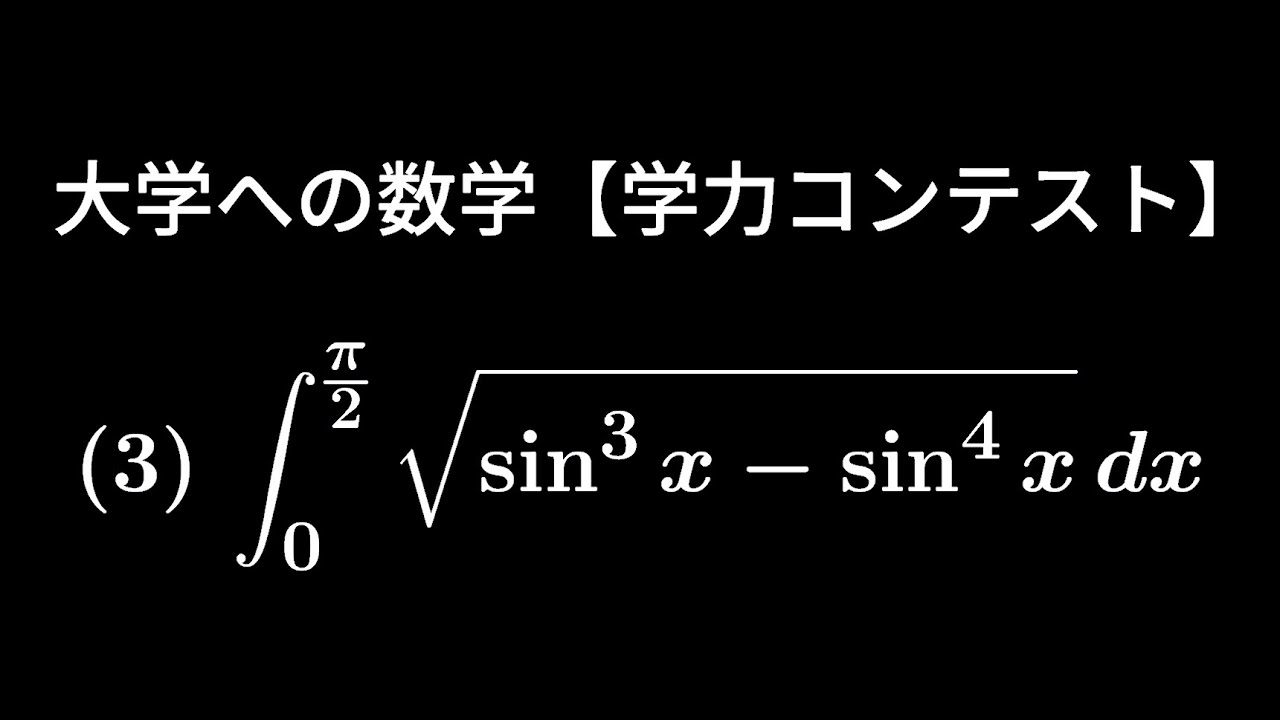
単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\sqrt{ \displaystyle \frac{x}{1+x} }(0 \leqq x \leqq 1)$
(1)
$f'(x)$を求めよ。
(2)
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{ \sin\ x-\sin^2x }\ dx$
(3)
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{ \sin^3x-\sin^4x }\ dx$
この動画を見る
$f(x)=\sqrt{ \displaystyle \frac{x}{1+x} }(0 \leqq x \leqq 1)$
(1)
$f'(x)$を求めよ。
(2)
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{ \sin\ x-\sin^2x }\ dx$
(3)
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{ \sin^3x-\sin^4x }\ dx$
#大学への数学「大学受験で、たまに使う技」 学力コンテスト (1)(2) #定積分
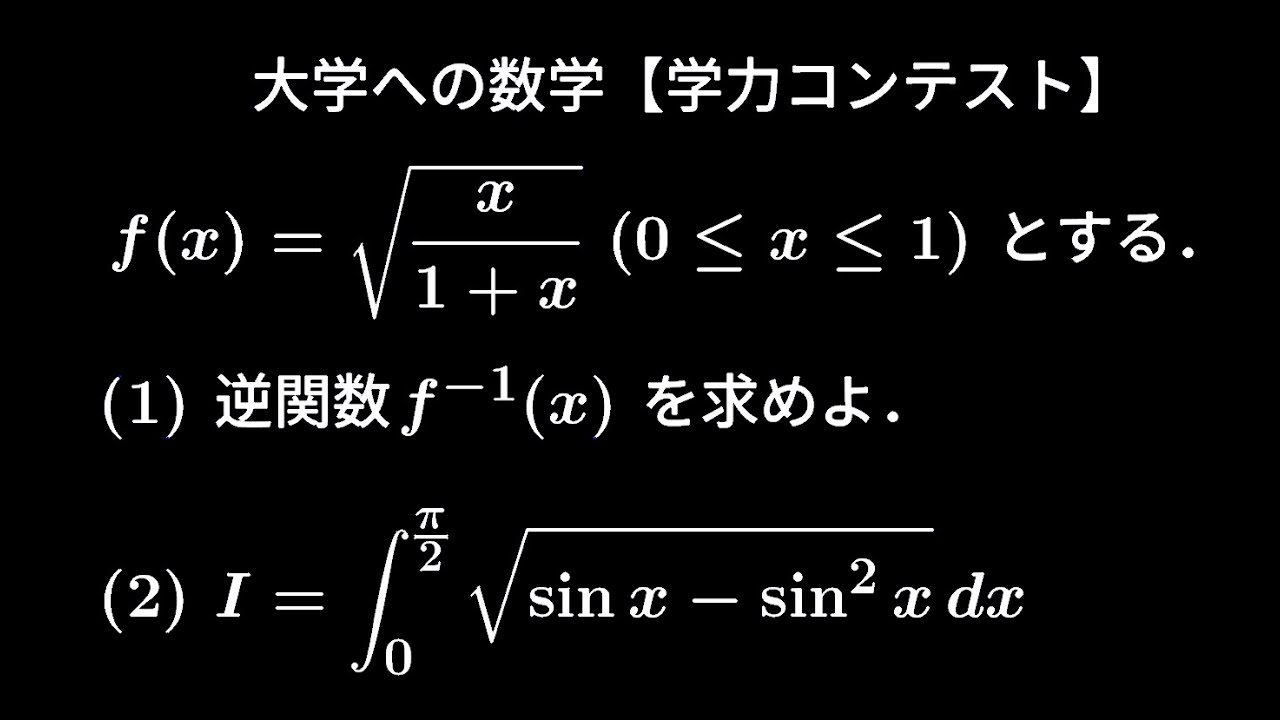
単元:
#微分とその応用#積分とその応用#微分法#色々な関数の導関数#定積分#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\sqrt{ \displaystyle \frac{x}{1+x} }(0 \leqq x \leqq 1)$
(1)
逆関数$f^{-1}(x)$を求めよ。
(2)
$I=\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{ \sin\ x-\sin^2x }\ dx$
(3)
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{ \sin^3x-\sin^4x }\ dx$
この動画を見る
$f(x)=\sqrt{ \displaystyle \frac{x}{1+x} }(0 \leqq x \leqq 1)$
(1)
逆関数$f^{-1}(x)$を求めよ。
(2)
$I=\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{ \sin\ x-\sin^2x }\ dx$
(3)
$\displaystyle \int_{0}^{\frac{\pi}{2}} \sqrt{ \sin^3x-\sin^4x }\ dx$
福田の1.5倍速演習〜合格する重要問題009〜九州大学2015年度理系数学第2問〜関数の増減と区分求積

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
以下の問いに答えよ。
(1)関数$\ y=\frac{1}{x(\log x)^2}$は$x \gt 1$において単調に減少することを示せ。
(2)不定積分$\ \int\frac{1}{x(\log x)^2}dx$ を求めよ。
(3)nを3以上の整数とするとき、不等式
$\sum_{k=3}^n\frac{1}{k(\log k)^2} \lt \frac{1}{\log 2}$
が成り立つことを示せ。
2015九州大学理系過去問
この動画を見る
以下の問いに答えよ。
(1)関数$\ y=\frac{1}{x(\log x)^2}$は$x \gt 1$において単調に減少することを示せ。
(2)不定積分$\ \int\frac{1}{x(\log x)^2}dx$ を求めよ。
(3)nを3以上の整数とするとき、不等式
$\sum_{k=3}^n\frac{1}{k(\log k)^2} \lt \frac{1}{\log 2}$
が成り立つことを示せ。
2015九州大学理系過去問
大学入試問題#377「基本的な手筋」 琉球大学(2015) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#琉球大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{1}|x|\sqrt{ 1-x^2 }\ dx$
出典:2015年琉球大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{1}|x|\sqrt{ 1-x^2 }\ dx$
出典:2015年琉球大学 入試問題
大学入試問題#376「平均点の調整問題?」 奈良県立医科大学(2015) #積分の応用

単元:
#大学入試過去問(数学)#積分とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#奈良県立医科大学
指導講師:
ますただ
問題文全文(内容文):
$f(x)=5+2\displaystyle \int_{0}^{1}e^{t-x}f(t)dt$をみたす$f(x)$を求めよ。
出典:2015年奈良県立医科大学 入試問題
この動画を見る
$f(x)=5+2\displaystyle \int_{0}^{1}e^{t-x}f(t)dt$をみたす$f(x)$を求めよ。
出典:2015年奈良県立医科大学 入試問題
大学入試問題#375「定跡どおり」 広島市立大学2015 #定積分
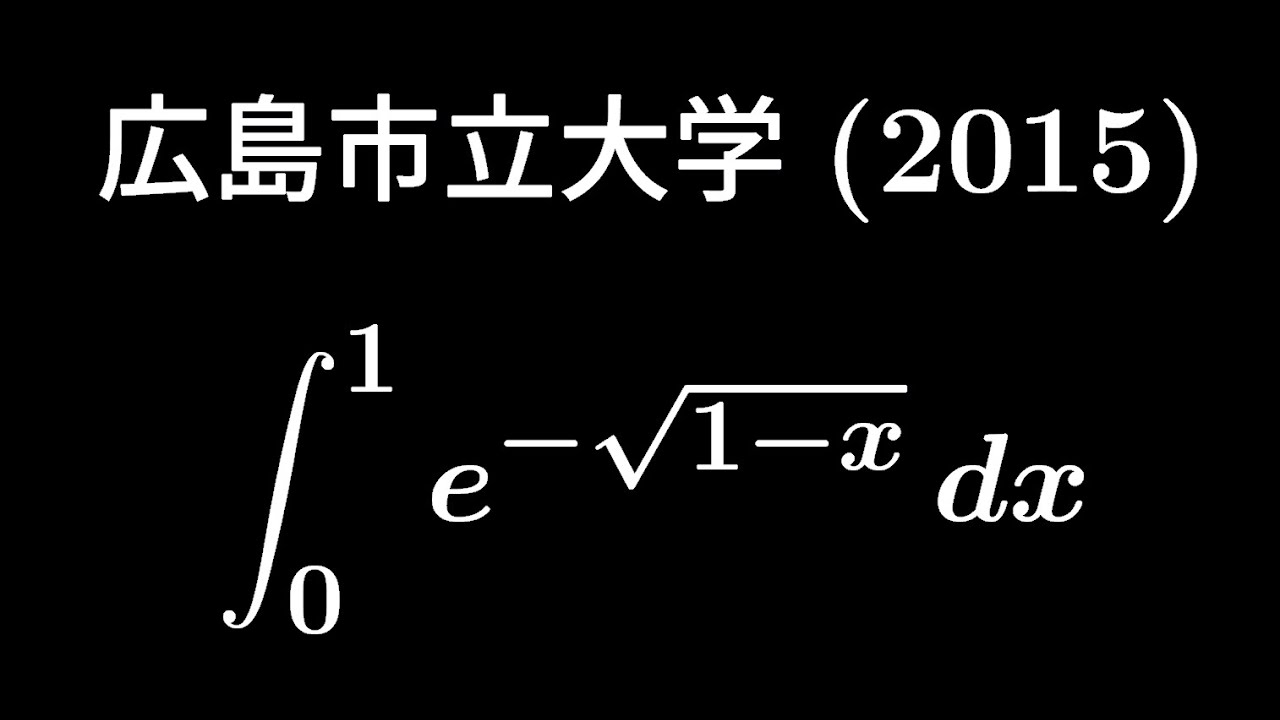
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}e^{-\sqrt{ 1-x }}dx$
出典:2015年広島市立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}e^{-\sqrt{ 1-x }}dx$
出典:2015年広島市立大学 入試問題
大学入試問題#374「技をかける前の味付け」 富山県立大学(2015) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#富山県立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\displaystyle \frac{\sin\ x}{3+4\cos^2x}dx$
出典:2015年富山県立大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\displaystyle \frac{\sin\ x}{3+4\cos^2x}dx$
出典:2015年富山県立大学 入試問題
大学入試問題#373「結局いつもの唐揚げ定食」 横浜国立大学2012 #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a \gt 0$
$\displaystyle \int x^2\cos(a\ log\ x)dx$
出典:2012年横浜国立大学 入試問題
この動画を見る
$a \gt 0$
$\displaystyle \int x^2\cos(a\ log\ x)dx$
出典:2012年横浜国立大学 入試問題
大学入試問題#372「初手が命」 兵庫県立大学2015 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#兵庫県立大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{3}}\displaystyle \frac{dx}{\cos^4x}$
出典:2015年兵庫県立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{3}}\displaystyle \frac{dx}{\cos^4x}$
出典:2015年兵庫県立大学 入試問題
大学入試問題#371「少し変わった置換積分」 京都大学 改 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{2}{\sqrt{ 3 }}}^{2}\displaystyle \frac{dx}{x\sqrt{ x^2-1 }}$
出典:京都大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{2}{\sqrt{ 3 }}}^{2}\displaystyle \frac{dx}{x\sqrt{ x^2-1 }}$
出典:京都大学 入試問題
福田の1.5倍速演習〜合格する重要問題002〜京都大学2015年理系数学第1問〜回転体の体積

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
2つの関数$y = \sin(x+\frac{\pi}{8})$と$y=\sin2x$のグラフの$0\leqq x\leqq \frac{\pi}{2}$の部分で囲まれ
る領域を、x軸のまわりに1回転させてできる立体の体積を求めよ。
ただし、$x=0$と$x=\frac{\pi}{2}$は領域を囲む線とは考えない。
2015京都大学理系過去問
この動画を見る
2つの関数$y = \sin(x+\frac{\pi}{8})$と$y=\sin2x$のグラフの$0\leqq x\leqq \frac{\pi}{2}$の部分で囲まれ
る領域を、x軸のまわりに1回転させてできる立体の体積を求めよ。
ただし、$x=0$と$x=\frac{\pi}{2}$は領域を囲む線とは考えない。
2015京都大学理系過去問
大学入試問題#370「初手は好み」 滋賀医科大学2012 #定積分
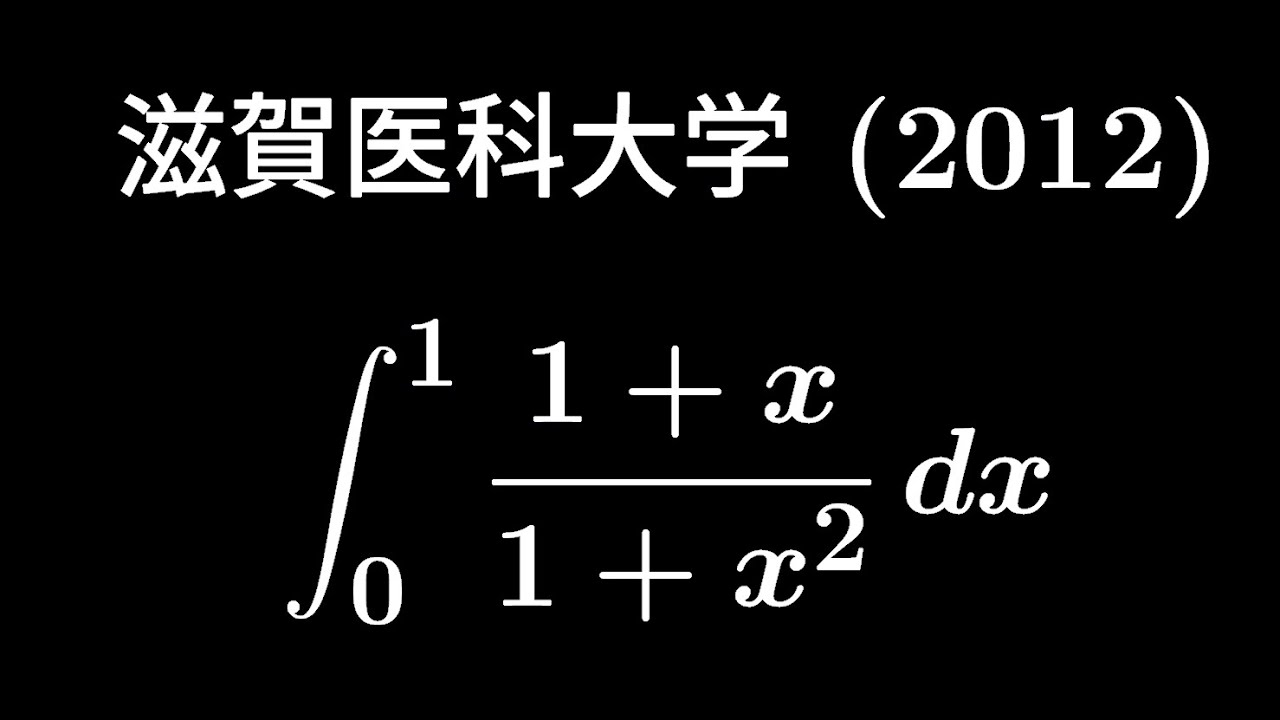
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#滋賀医科大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{1+x}{1+x^2}dx$
出典:2012年滋賀医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{1+x}{1+x^2}dx$
出典:2012年滋賀医科大学 入試問題
大学入試問題#369「2種類準備しました」 広島市立大学2014 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#広島市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{\cos\ x}{\cos^2x+2\sin\ x-2}dx$
出典:2014年広島市立大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{\cos\ x}{\cos^2x+2\sin\ x-2}dx$
出典:2014年広島市立大学 入試問題
大学入試問題#368「よくみる積分」 防衛医科大学校2014 #不定積分
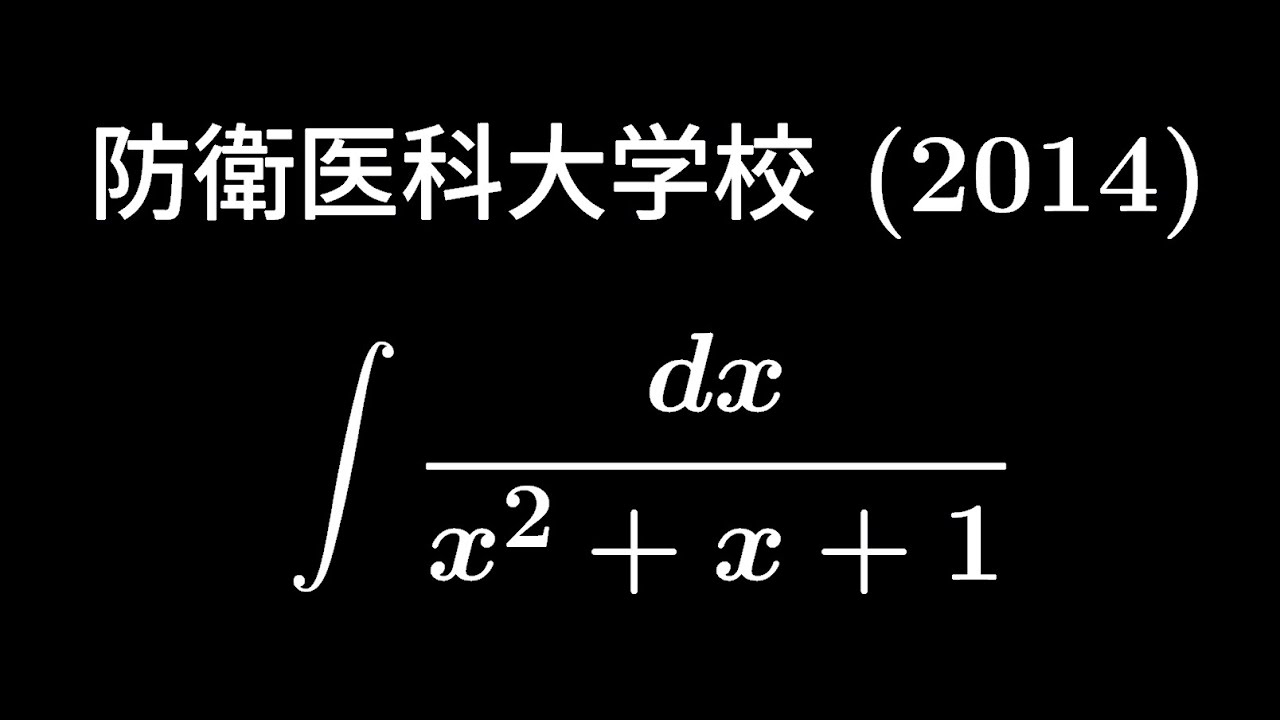
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#防衛医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{dx}{x^2+x+1}$
出典:2014年防衛医科大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{dx}{x^2+x+1}$
出典:2014年防衛医科大学 入試問題
大学入試問題#367「これは、たぶん一撃で倒せる」 横浜国立大学2012 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\displaystyle \frac{2+\sin\ x}{1+\cos\ x}dx$
出典:2012年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{3}}^{\frac{\pi}{2}}\displaystyle \frac{2+\sin\ x}{1+\cos\ x}dx$
出典:2012年横浜国立大学 入試問題
大学入試問題#366「これは有名問題」 静岡大学2014 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#静岡大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\cos^3x}{\cos\ x+\sin\ x}dx$
出典:2014年静岡大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\cos^3x}{\cos\ x+\sin\ x}dx$
出典:2014年静岡大学 入試問題
大学入試問題#365「さすがに小問」 旭川医科大学(2014) #定積分
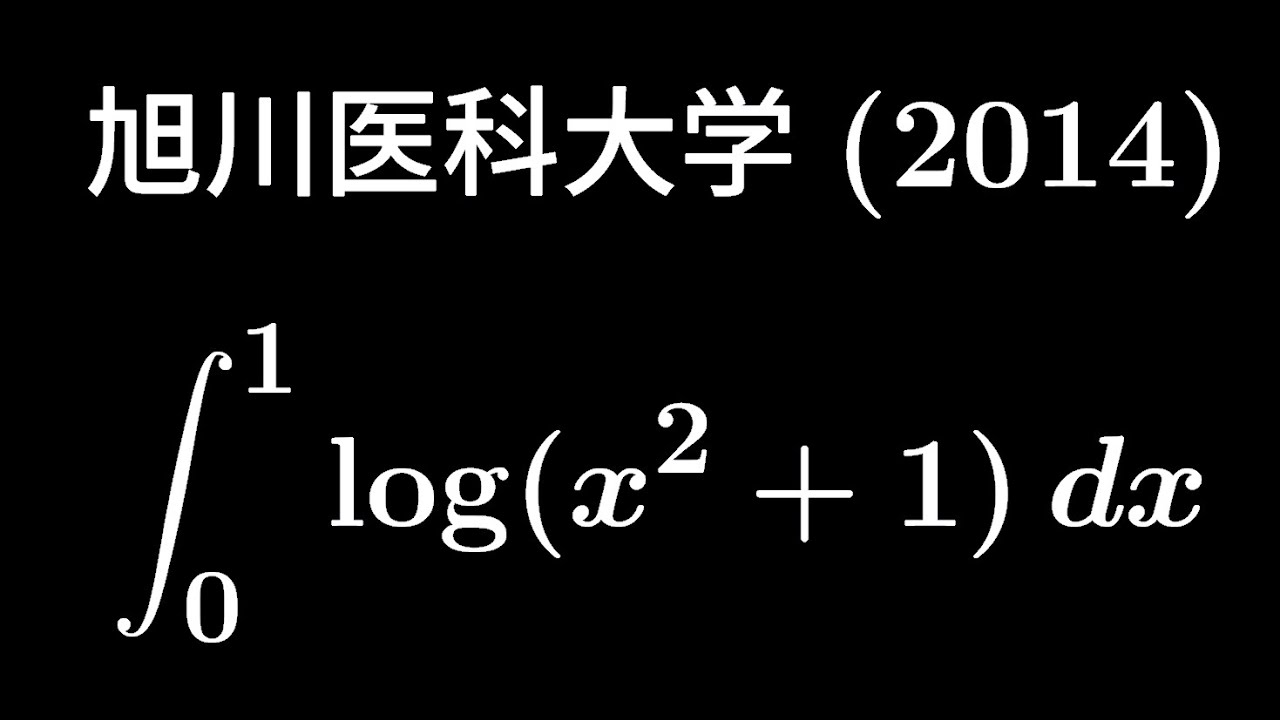
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#旭川医科大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}log(x^2+1)dx$
出典:2014年旭川医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}log(x^2+1)dx$
出典:2014年旭川医科大学 入試問題
大学入試問題#364「計算が大変でした」 岩手大学2014 #不定積分
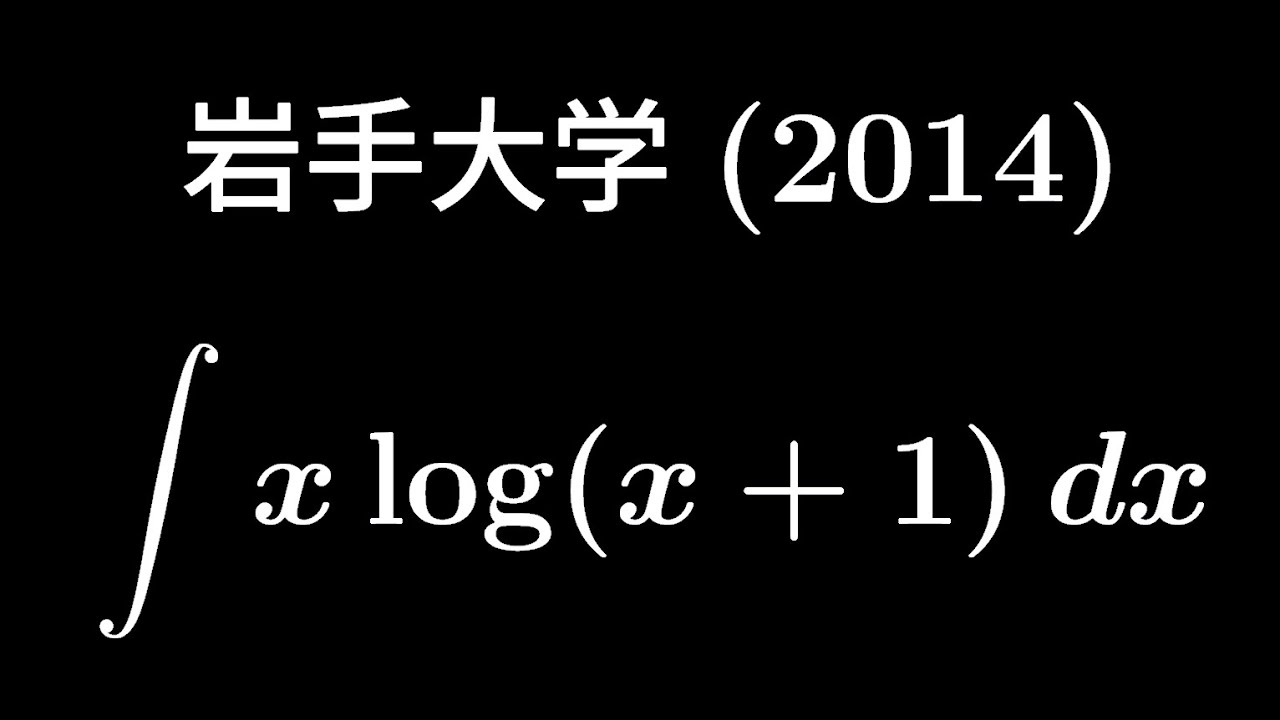
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#岩手大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int x\ log(x+1)dx$
出典:2014年岩手大学 入試問題
この動画を見る
$\displaystyle \int x\ log(x+1)dx$
出典:2014年岩手大学 入試問題
大学入試問題#363「置換からの部分積分?」 横浜国立大学(2014) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\sqrt{ \frac{\pi}{2} }}x^3\cos(x^2)dx$
出典:2014年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\sqrt{ \frac{\pi}{2} }}x^3\cos(x^2)dx$
出典:2014年横浜国立大学 入試問題
大学入試問題#362「頻出問題ではないでしょうか?」 福島大学 改 2014 #定積分 #極限

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ a \to \infty } \displaystyle \int_{-a}^{a}\displaystyle \frac{dx}{(e^x+e^{-x})^2}$
出典:2014年福島大学 入試問題
この動画を見る
$\displaystyle \lim_{ a \to \infty } \displaystyle \int_{-a}^{a}\displaystyle \frac{dx}{(e^x+e^{-x})^2}$
出典:2014年福島大学 入試問題
大学入試問題#361「作成時間がありませんでした。」 横浜国立大学(2014) #定積分
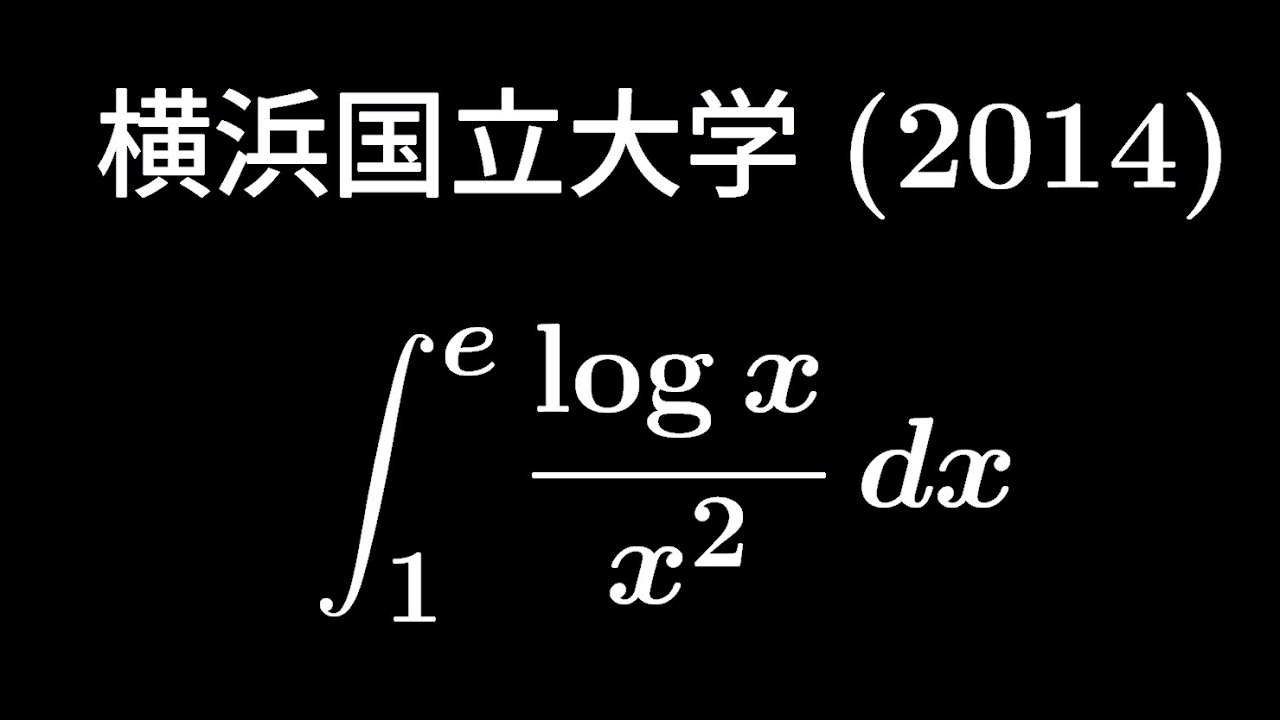
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e}\displaystyle \frac{log\ x}{x^2}dx$
出典:2014年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e}\displaystyle \frac{log\ x}{x^2}dx$
出典:2014年横浜国立大学 入試問題
大学入試問題#360「もっとスマートな解答がありそう・・・」 宮崎大学2014 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#宮崎大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^3+3x^2}{x^2+3x+2}dx$
出典:2014年宮崎大学
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{x^3+3x^2}{x^2+3x+2}dx$
出典:2014年宮崎大学
大学入試問題#359「読みの入った部分積分で解いてみた」 神戸大学(2014) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{6}}\displaystyle \frac{2x\ sin\ x}{\cos^2x}dx$
出典:2014年神戸大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{6}}\displaystyle \frac{2x\ sin\ x}{\cos^2x}dx$
出典:2014年神戸大学 入試問題
大学入試問題#358「チャートの例題に載ってもいいのかな?」 青山学院大学(2010) #定積分 #極限

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#青山学院大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ a \to \infty } \displaystyle \int_{1}^{0}(\displaystyle \frac{x+1}{\sqrt{ x^2+2x }}-1)dx$
出典:2010年青山学院大学 入試問題
この動画を見る
$\displaystyle \lim_{ a \to \infty } \displaystyle \int_{1}^{0}(\displaystyle \frac{x+1}{\sqrt{ x^2+2x }}-1)dx$
出典:2010年青山学院大学 入試問題
【誘導あり:概要欄】大学入試問題#357「この大問は落とせないかな~~」 横浜国立大学2010 #定積分 #積分の応用

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)
$0 \lt x \lt \pi$のとき
$\sin\ x-x\cos\ x \gt 0$を示せ
(2)
$0 \lt a \lt 1$
$I=\displaystyle \int_{0}^{\pi} |\sin\ x-ax| dx$を最小にする$a$の値を求めよ。
出典:2010年横浜国立大学 入試問題
この動画を見る
(1)
$0 \lt x \lt \pi$のとき
$\sin\ x-x\cos\ x \gt 0$を示せ
(2)
$0 \lt a \lt 1$
$I=\displaystyle \int_{0}^{\pi} |\sin\ x-ax| dx$を最小にする$a$の値を求めよ。
出典:2010年横浜国立大学 入試問題
