 積分とその応用
積分とその応用
 積分とその応用
積分とその応用
大学入試問題#356「初手迷う」 関東学院大学(2019) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{2} \displaystyle \frac{5x^2+2}{x(x^2+1)} dx$
出典:2019年関東学院大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{2} \displaystyle \frac{5x^2+2}{x(x^2+1)} dx$
出典:2019年関東学院大学 入試問題
大学入試問題#355「定番の定食」 山梨大学2019 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#山梨大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \sqrt{ 4-3x^2 }\ dx$
出典:2019年山梨大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1} \sqrt{ 4-3x^2 }\ dx$
出典:2019年山梨大学 入試問題
福田の数学〜杏林大学2022年医学部第2問〜定積分と関数の増減

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#杏林大学#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
(1)Cを積分定数として、指数関数とたんっ公式の席の不定積分について、次式が成り立つ。
$\int xe^{-3x}dx = -(\frac{\boxed{ア}\ x+\boxed{イ}}{\boxed{ウ}})\ e^{-3x}+C$
$\int x^2e^{-3x}dx = -(\frac{\boxed{エ}\ x^2+\boxed{オ}\ x+\boxed{カ}}{\boxed{キク}})\ e^{-3x}+C$
また、定積分について、
$\int_0^1|(9x^2-1)e^{-3x}|dx=\frac{1}{\boxed{ケ}}(-1+\boxed{コ}\ e^{\boxed{サシ}}-\boxed{スセ}\ e^{-3})$
が成り立つ。
(2)p,q,rを実数の定数とする。関数$f(x)=(px^2+qx+r)e^{-3x}$が$x=0$で極大、
$x=1$で極小となるための必要十分条件は
$p=\boxed{ソタ}\ r,\ \ \ q=\boxed{チ}\ r,\ \ \ \boxed{ツ}$
である。さらに、$f(x)$の極小値が-1であるとすると、$f(x)$の極大値は$\frac{e^{\boxed{テ}}}{\boxed{ト }}$となる.
このとき、$\int_0^1f(x)dx=\frac{\boxed{ナ}}{\boxed{二}}$である。
$\boxed{ツ}$の解答群
$①\ r\gt 0\ \ \ \ ②\ r=0\ \ \ \ ③\ r \lt 0\ \ \ \ ④\ r \gt 1\ \ \ \ ⑤\ r=1$
$⑥\ r \lt 1\ \ \ \ ⑦\ r \gt \frac{1}{3}\ \ \ \ ⑧\ r =\frac{1}{3}\ \ \ \ ⑨r \lt \frac{1}{3}$
2022杏林大学医学部過去問
この動画を見る
(1)Cを積分定数として、指数関数とたんっ公式の席の不定積分について、次式が成り立つ。
$\int xe^{-3x}dx = -(\frac{\boxed{ア}\ x+\boxed{イ}}{\boxed{ウ}})\ e^{-3x}+C$
$\int x^2e^{-3x}dx = -(\frac{\boxed{エ}\ x^2+\boxed{オ}\ x+\boxed{カ}}{\boxed{キク}})\ e^{-3x}+C$
また、定積分について、
$\int_0^1|(9x^2-1)e^{-3x}|dx=\frac{1}{\boxed{ケ}}(-1+\boxed{コ}\ e^{\boxed{サシ}}-\boxed{スセ}\ e^{-3})$
が成り立つ。
(2)p,q,rを実数の定数とする。関数$f(x)=(px^2+qx+r)e^{-3x}$が$x=0$で極大、
$x=1$で極小となるための必要十分条件は
$p=\boxed{ソタ}\ r,\ \ \ q=\boxed{チ}\ r,\ \ \ \boxed{ツ}$
である。さらに、$f(x)$の極小値が-1であるとすると、$f(x)$の極大値は$\frac{e^{\boxed{テ}}}{\boxed{ト }}$となる.
このとき、$\int_0^1f(x)dx=\frac{\boxed{ナ}}{\boxed{二}}$である。
$\boxed{ツ}$の解答群
$①\ r\gt 0\ \ \ \ ②\ r=0\ \ \ \ ③\ r \lt 0\ \ \ \ ④\ r \gt 1\ \ \ \ ⑤\ r=1$
$⑥\ r \lt 1\ \ \ \ ⑦\ r \gt \frac{1}{3}\ \ \ \ ⑧\ r =\frac{1}{3}\ \ \ \ ⑨r \lt \frac{1}{3}$
2022杏林大学医学部過去問
大学入試問題#354「思った以上に大変でした・・・」 弘前大学 改 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{log\ x} \displaystyle \frac{(e^x-1)(e^x-2)}{e^x+1} dx$
出典:広前大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{log\ x} \displaystyle \frac{(e^x-1)(e^x-2)}{e^x+1} dx$
出典:広前大学 入試問題
絶対に落としたくない問題です【自治医科大学】【数学 入試問題】

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
関数$f(x)$は,等式$f(x)=3x^2 \displaystyle \int_{-1}^{1} f(t) dt+x+\displaystyle \int_{0}^{1} [{f(t)}]^{2} dt+$
$\displaystyle \int_{0}^{1} f(t) dt$を満たす。
$\displaystyle \int_{0}^{1} f(t) dt \neq 0$とするとき,$f(0)$の値を求めよ。
自治医科大過去問
この動画を見る
関数$f(x)$は,等式$f(x)=3x^2 \displaystyle \int_{-1}^{1} f(t) dt+x+\displaystyle \int_{0}^{1} [{f(t)}]^{2} dt+$
$\displaystyle \int_{0}^{1} f(t) dt$を満たす。
$\displaystyle \int_{0}^{1} f(t) dt \neq 0$とするとき,$f(0)$の値を求めよ。
自治医科大過去問
大学入試問題#353「依頼により誘導通りに解いてみた」 埼玉大学2013 #定積分 #キングプロパティ

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)
$f(x)$連続
$\displaystyle \int_{0}^{\pi} x\ f(\sin\ x)dx=\displaystyle \frac{\pi}{2}\displaystyle \int_{0}^{\pi} f(\sin\ x) dx$
(2)
$\displaystyle \int_{0}^{\pi} \displaystyle \frac{x(a^2-4\cos^2\ x)\sin\ x}{a^2-\cos^2x} dx$
出典:2013年埼玉大学 入試問題
この動画を見る
(1)
$f(x)$連続
$\displaystyle \int_{0}^{\pi} x\ f(\sin\ x)dx=\displaystyle \frac{\pi}{2}\displaystyle \int_{0}^{\pi} f(\sin\ x) dx$
(2)
$\displaystyle \int_{0}^{\pi} \displaystyle \frac{x(a^2-4\cos^2\ x)\sin\ x}{a^2-\cos^2x} dx$
出典:2013年埼玉大学 入試問題
大学入試問題#352「よく出題されそうな綺麗な問題」 京都工芸繊維大学(2011) #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int (\displaystyle \frac{log\ x}{x})^2 dx$
出典:2011年京都工芸繊維大学 入試問題
この動画を見る
$\displaystyle \int (\displaystyle \frac{log\ x}{x})^2 dx$
出典:2011年京都工芸繊維大学 入試問題
福田の数学〜北里大学2022年医学部第2問〜定積分と不等式

単元:
#大学入試過去問(数学)#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#学校別大学入試過去問解説(数学)#北里大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
次の各問いに答えよ。
(1)定積分\int^1_0\frac{1}{1+x^2}dxを求めよ。
(2)$x≠0$を満たすすべての実数xに対して、$e^x \gt 1+x$と$e^{-x^2} \lt \frac{1}{1+x^2}$が
成り立つことを証明せよ。
(3)$\frac{2}{3} \lt \int^1_0e^{-x^2}dx \lt \frac{\pi}{4}$が成り立つことを証明せよ。
2022北里大学医学部過去問
この動画を見る
次の各問いに答えよ。
(1)定積分\int^1_0\frac{1}{1+x^2}dxを求めよ。
(2)$x≠0$を満たすすべての実数xに対して、$e^x \gt 1+x$と$e^{-x^2} \lt \frac{1}{1+x^2}$が
成り立つことを証明せよ。
(3)$\frac{2}{3} \lt \int^1_0e^{-x^2}dx \lt \frac{\pi}{4}$が成り立つことを証明せよ。
2022北里大学医学部過去問
大学入試問題#351「積分できて満足できない問題」 電気通信大学(2013) #定積分 #極限

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n}\displaystyle \int_{-n}^{n} (\displaystyle \frac{e^x}{e^x+e^{-x}})^2 dx$
出典:2013年電気通信大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \frac{1}{n}\displaystyle \int_{-n}^{n} (\displaystyle \frac{e^x}{e^x+e^{-x}})^2 dx$
出典:2013年電気通信大学 入試問題
こういう問題に苦手意識ある人は必見です【甲南大学】【数学 入試問題】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
次の2つの等式を満たす多項式$(x),g(x)$及び定数$a$を求めよ。
$\displaystyle \int_{1}^{x} f(t) dt=2xg(x)-3x+a $
$g(x)=x^2+x \displaystyle \int_{0}^{1} f(t)dx+1$
甲南大過去問
この動画を見る
次の2つの等式を満たす多項式$(x),g(x)$及び定数$a$を求めよ。
$\displaystyle \int_{1}^{x} f(t) dt=2xg(x)-3x+a $
$g(x)=x^2+x \displaystyle \int_{0}^{1} f(t)dx+1$
甲南大過去問
大学入試問題#350「見た目とのギャップ」 岩手医科大学2019 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\sqrt{ 3 }}{2}} \displaystyle \frac{dx}{(1-x^2)^2}$
出典:2019年岩手医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\sqrt{ 3 }}{2}} \displaystyle \frac{dx}{(1-x^2)^2}$
出典:2019年岩手医科大学 入試問題
大学入試問題#349「定跡どおりの超良問」 獨協医科大学2019 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\sqrt{ 5 }}^{2\sqrt{ 3 }} \sqrt{ 1+(\displaystyle \frac{2}{x})^2 }\ dx$
出典:2019年獨協医科大学 入試問題
この動画を見る
$\displaystyle \int_{\sqrt{ 5 }}^{2\sqrt{ 3 }} \sqrt{ 1+(\displaystyle \frac{2}{x})^2 }\ dx$
出典:2019年獨協医科大学 入試問題
大学入試問題#348「もはや、あれで置換」 横浜国立大学 #定積分

単元:
#大学入試過去問(数学)#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{1}{2}} x^2\sqrt{ 1-x^2 }\ dx$
出典:横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{1}{2}} x^2\sqrt{ 1-x^2 }\ dx$
出典:横浜国立大学 入試問題
大学入試問題#347 東京電機大学 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京電機大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{3}} (x\ \tan\ x-log(\cos\ x)) dx$
出典:東京電機大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{3}} (x\ \tan\ x-log(\cos\ x)) dx$
出典:東京電機大学 入試問題
大学入試問題#346「2種類の解法の紹介」 電気通信大学(2013) #定積分 #キングプロパティ

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#電気通信大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{1} \displaystyle \frac{e^x}{e^x+e^{-x}} dx$
出典:2013年電気通信大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{1} \displaystyle \frac{e^x}{e^x+e^{-x}} dx$
出典:2013年電気通信大学 入試問題
福田の数学〜中央大学2022年理工学部第3問〜指数関数の接線と囲まれる部分の面積

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#指数関数#微分とその応用#積分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#定積分#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
関数 $f(x) = -xe^x$ を考える。曲線$C: y = f(x)$の点(a, f(a)) における接線を$l_a$と
し、接線$l_a$とy軸の交点を $(0, g(a))$ とおく。以下の問いに答えよ。
(1) 接線$l_a$の方程式と$g (a)$を求めよ。
以下、aの関数$g (a)$ が極大値をとるときのaの値をbとおく。
(2) bを求め、点$(b, f(b))$ は曲線Cの変曲点であることを示せ。
(3) 曲線Cの点 $(b, f(b))$ における接線$l_b$と x軸の交点のx座標cを求めよ。さらに、
$c\leqq x\leqq 0$の範囲で曲線Cの概形と接線l_bをxy 平面上に図示せよ。
(4)曲線C、接線$l_b$およびy軸で囲まれた部分の面積Sを求めよ。
2022中央大学理工学部過去問
この動画を見る
関数 $f(x) = -xe^x$ を考える。曲線$C: y = f(x)$の点(a, f(a)) における接線を$l_a$と
し、接線$l_a$とy軸の交点を $(0, g(a))$ とおく。以下の問いに答えよ。
(1) 接線$l_a$の方程式と$g (a)$を求めよ。
以下、aの関数$g (a)$ が極大値をとるときのaの値をbとおく。
(2) bを求め、点$(b, f(b))$ は曲線Cの変曲点であることを示せ。
(3) 曲線Cの点 $(b, f(b))$ における接線$l_b$と x軸の交点のx座標cを求めよ。さらに、
$c\leqq x\leqq 0$の範囲で曲線Cの概形と接線l_bをxy 平面上に図示せよ。
(4)曲線C、接線$l_b$およびy軸で囲まれた部分の面積Sを求めよ。
2022中央大学理工学部過去問
大学入試問題#345「とりあえず第一感は置換積分っぽい」 大阪大学 改 2010 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{1} (\displaystyle \frac{e^x}{1+e^x})^2 dx$
出典:2010年大阪大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{1} (\displaystyle \frac{e^x}{1+e^x})^2 dx$
出典:2010年大阪大学 入試問題
大学入試問題#344「みるからにあの性質・・・」 富山大学 #定積分 #キングプロパティ

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#富山大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \displaystyle \frac{x\ sin\ x}{1+e^{-x}}dx$
出典:富山大学 入試問題
この動画を見る
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \displaystyle \frac{x\ sin\ x}{1+e^{-x}}dx$
出典:富山大学 入試問題
福田の数学〜中央大学2022年理工学部第1問〜定積分で表された関数

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
関数f(x)が
$f(x)=\int_0^{\pi}tf(t)\cos(x+t)dt+\frac{1}{4}$
を満たしている。このとき,
$A= \int_0^{\pi}tf(t)\cos tdt$,
$B=\int_0^{\pi}tf(t)\sin tdt... ①$
とおいて$f(x)$をAとBで表すと、
$f(x)=A×(\ \ \ \boxed{ア}\ \ \ )+B×(\ \ \ \boxed{イ}\ \ \ )+\frac{1}{4}... ②$
となる。ここで、
$\int_0^{\pi}t\cos tdt=-2,\ \ \ \int_0^{\pi}t\cos^2 tdt=\boxed{ウ},\ \ \ \int_0^{\pi}t\sin tdt=\pi$
$\int_0^{\pi}t\sin^2 tdt=\boxed{エ},\ \ \ \int_0^{\pi}t\cos t\sin tdt=\boxed{オ}$
を用い、①に②を代入して整理すると、AとBの満たす連立方程式
$\left\{
\begin{array}{1}
(\ \ \ \boxed{\ \ カ\ \ }\ \ \ )A-\pi B+2=0\\
\pi A +(\ \ \ \boxed{\ \ キ\ \ }\ \ \ )B-\pi = 0\\
\end{array}
\right.$
が得られる。この連立方程式を解くと
$A=\frac{\boxed{ク}}{\pi^4-\pi^2-16},\ \ \ B=\frac{\pi (\ \ \ \boxed{ケ}\ \ \ )}{\pi^4-\pi^2-16}$
が得られ、したがって
$f(x)= \frac{\boxed{ク}}{\pi^4-\pi^2-16}×(\ \ \ \boxed{ア}\ \ \ )+$
$\frac{\pi (\ \ \ \boxed{ケ}\ \ \ )}{\pi^4-\pi^2-16}×(\ \ \ \boxed{イ}\ \ \ )+\frac{1}{4}$
となる。
$\boxed{ア},\boxed{イ}$の解答群
$ⓐ\sin x\ \ \ ⓑ-\sin x\ \ \ ⓒ\cos x\ \ \ ⓓ-\cos x$
$ⓔ\tan x\ \ \ ⓕ-\tan x$
$\boxed{ウ},\boxed{エ},\boxed{オ}$の解答群
$ⓐ\pi \ \ \ ⓑ\frac{\pi}{2}\ \ \ ⓒ\frac{\pi}{4}\ \ \ ⓓ\frac{\pi}{8}\ \ \ ⓔ-\pi $
$ⓕ-\frac{\pi}{2}\ \ \ ⓖ-\frac{\pi}{4}\ \ \ ⓗ-\frac{\pi}{8}\ \ \ ⓘ\pi^2 \ \ \ ⓙ\frac{\pi^2}{2}$
$ⓚ\frac{\pi^2}{4}\ \ \ ⓛ\frac{\pi^2}{8}\ \ \ ⓜ-\pi^2 \ \ \ ⓝ-\frac{\pi^2}{2}\ \ \ ⓞ-\frac{\pi^2}{4}$
$ⓟ-\frac{\pi^2}{8}\ \ \ ⓠ\frac{\pi^2+4}{16}\ \ \ ⓡ\frac{\pi^2-4}{16}\ \ \ ⓢ\frac{-\pi^2+4}{16}\ \ \ ⓣ-\frac{\pi^2+4}{16}$
$\boxed{カ},\boxed{キ},\boxed{ク},\boxed{ケ}$の解答群
$ⓐ\pi^2+2\ \ \ ⓑ\pi^2-2\ \ \ ⓒ-\pi^2+2\ \ \ ⓓ-\pi^2-2$
$ⓔ\pi^2+4\ \ \ ⓕ\pi^2-4\ \ \ ⓖ-\pi^2+4\ \ \ ⓗ-\pi^2-4$
$ⓘ\pi^2+6\ \ \ ⓙ\pi^2-6\ \ \ ⓚ-\pi^2+6\ \ \ ⓛ-\pi^2-6$
$ⓜ\pi^2+8\ \ \ ⓝ\pi^2-8\ \ \ ⓞ-\pi^2+8\ \ \ ⓟ-\pi^2-8$
2022中央大学理工学部過去問
この動画を見る
関数f(x)が
$f(x)=\int_0^{\pi}tf(t)\cos(x+t)dt+\frac{1}{4}$
を満たしている。このとき,
$A= \int_0^{\pi}tf(t)\cos tdt$,
$B=\int_0^{\pi}tf(t)\sin tdt... ①$
とおいて$f(x)$をAとBで表すと、
$f(x)=A×(\ \ \ \boxed{ア}\ \ \ )+B×(\ \ \ \boxed{イ}\ \ \ )+\frac{1}{4}... ②$
となる。ここで、
$\int_0^{\pi}t\cos tdt=-2,\ \ \ \int_0^{\pi}t\cos^2 tdt=\boxed{ウ},\ \ \ \int_0^{\pi}t\sin tdt=\pi$
$\int_0^{\pi}t\sin^2 tdt=\boxed{エ},\ \ \ \int_0^{\pi}t\cos t\sin tdt=\boxed{オ}$
を用い、①に②を代入して整理すると、AとBの満たす連立方程式
$\left\{
\begin{array}{1}
(\ \ \ \boxed{\ \ カ\ \ }\ \ \ )A-\pi B+2=0\\
\pi A +(\ \ \ \boxed{\ \ キ\ \ }\ \ \ )B-\pi = 0\\
\end{array}
\right.$
が得られる。この連立方程式を解くと
$A=\frac{\boxed{ク}}{\pi^4-\pi^2-16},\ \ \ B=\frac{\pi (\ \ \ \boxed{ケ}\ \ \ )}{\pi^4-\pi^2-16}$
が得られ、したがって
$f(x)= \frac{\boxed{ク}}{\pi^4-\pi^2-16}×(\ \ \ \boxed{ア}\ \ \ )+$
$\frac{\pi (\ \ \ \boxed{ケ}\ \ \ )}{\pi^4-\pi^2-16}×(\ \ \ \boxed{イ}\ \ \ )+\frac{1}{4}$
となる。
$\boxed{ア},\boxed{イ}$の解答群
$ⓐ\sin x\ \ \ ⓑ-\sin x\ \ \ ⓒ\cos x\ \ \ ⓓ-\cos x$
$ⓔ\tan x\ \ \ ⓕ-\tan x$
$\boxed{ウ},\boxed{エ},\boxed{オ}$の解答群
$ⓐ\pi \ \ \ ⓑ\frac{\pi}{2}\ \ \ ⓒ\frac{\pi}{4}\ \ \ ⓓ\frac{\pi}{8}\ \ \ ⓔ-\pi $
$ⓕ-\frac{\pi}{2}\ \ \ ⓖ-\frac{\pi}{4}\ \ \ ⓗ-\frac{\pi}{8}\ \ \ ⓘ\pi^2 \ \ \ ⓙ\frac{\pi^2}{2}$
$ⓚ\frac{\pi^2}{4}\ \ \ ⓛ\frac{\pi^2}{8}\ \ \ ⓜ-\pi^2 \ \ \ ⓝ-\frac{\pi^2}{2}\ \ \ ⓞ-\frac{\pi^2}{4}$
$ⓟ-\frac{\pi^2}{8}\ \ \ ⓠ\frac{\pi^2+4}{16}\ \ \ ⓡ\frac{\pi^2-4}{16}\ \ \ ⓢ\frac{-\pi^2+4}{16}\ \ \ ⓣ-\frac{\pi^2+4}{16}$
$\boxed{カ},\boxed{キ},\boxed{ク},\boxed{ケ}$の解答群
$ⓐ\pi^2+2\ \ \ ⓑ\pi^2-2\ \ \ ⓒ-\pi^2+2\ \ \ ⓓ-\pi^2-2$
$ⓔ\pi^2+4\ \ \ ⓕ\pi^2-4\ \ \ ⓖ-\pi^2+4\ \ \ ⓗ-\pi^2-4$
$ⓘ\pi^2+6\ \ \ ⓙ\pi^2-6\ \ \ ⓚ-\pi^2+6\ \ \ ⓛ-\pi^2-6$
$ⓜ\pi^2+8\ \ \ ⓝ\pi^2-8\ \ \ ⓞ-\pi^2+8\ \ \ ⓟ-\pi^2-8$
2022中央大学理工学部過去問
大学入試問題#343「計算のクセが強すぎる」 防衛大学校2013 #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#防衛大学校#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
${}^{ \forall } t \in \Bbb R,$
$\sin\ 3t=f(\sin\ t)$
$\displaystyle \int_{0}^{1} \{f(x)\}^2\sqrt{ 1-x^2 }\ dx$
出典:2013年防衛大学校 入試問題
この動画を見る
${}^{ \forall } t \in \Bbb R,$
$\sin\ 3t=f(\sin\ t)$
$\displaystyle \int_{0}^{1} \{f(x)\}^2\sqrt{ 1-x^2 }\ dx$
出典:2013年防衛大学校 入試問題
大学入試問題#342「深夜24時ストック0の選択」 岡山県立大学(2013) #定積分
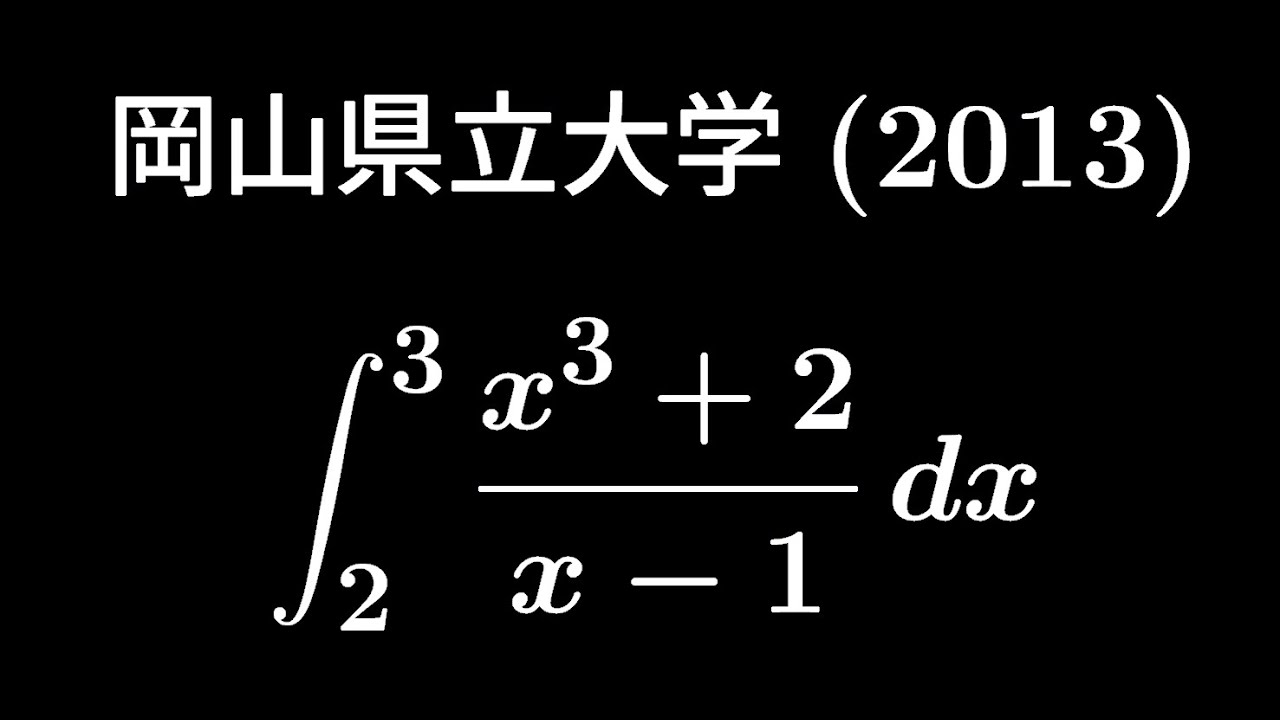
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#岡山県立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{2}^{3} \displaystyle \frac{x^3+2}{x-1} dx$
出典2013年岡山県立大学 入試問題
この動画を見る
$\displaystyle \int_{2}^{3} \displaystyle \frac{x^3+2}{x-1} dx$
出典2013年岡山県立大学 入試問題
大学入試問題#341「部分積分の心を・・・」 立教大学 #不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int (\sin\ x+x\ \cos\ x)log\ x\ dx$
出典:立教大学 入試問題
この動画を見る
$\displaystyle \int (\sin\ x+x\ \cos\ x)log\ x\ dx$
出典:立教大学 入試問題
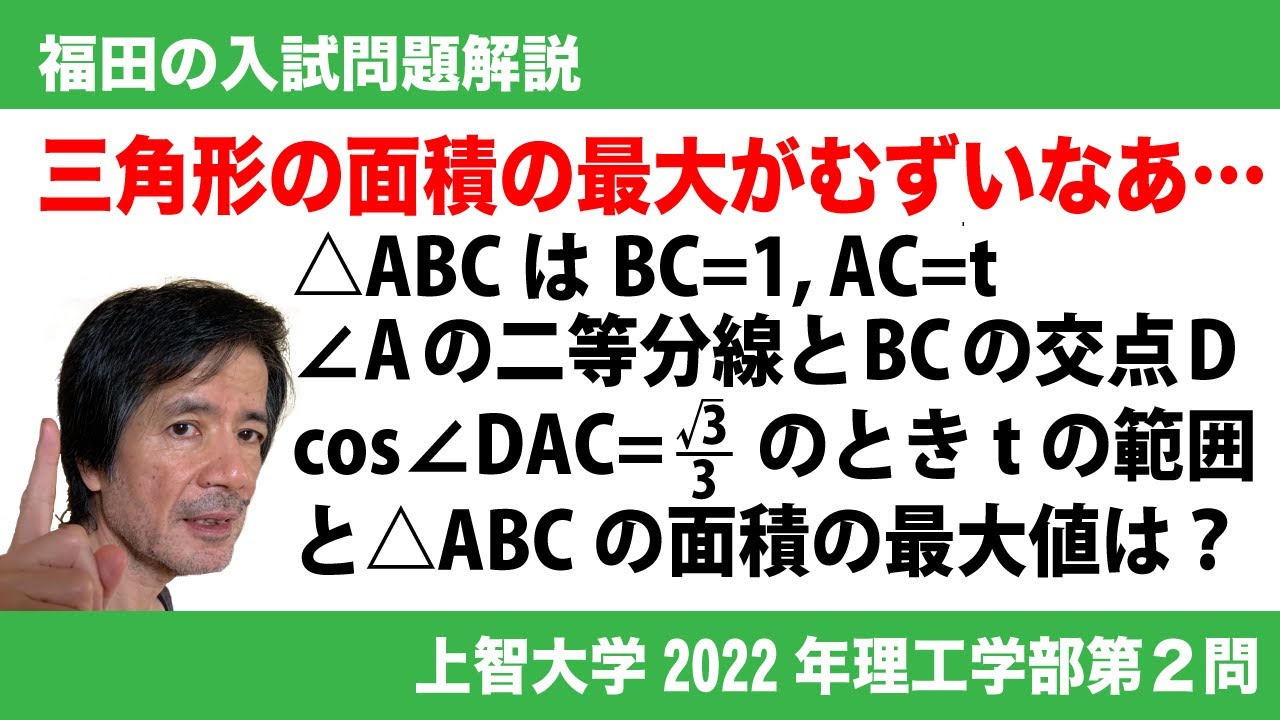
福田の数学〜上智大学2022年理工学部第2問〜三角比と通過領域の体積
単元:
#数Ⅰ#大学入試過去問(数学)#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
tを実数とする。次の条件(★)を満たす$\triangle ABC$を考える。
(★)$AC=t,\ BC=1$を満たし、$\angle BAC$の2等分線と辺BCの交点をDとおくと、
$\cos\angle DAC=\frac{\sqrt3}{3}$である。
(1)$\cos\angle DAC=\frac{\boxed{カ}}{\boxed{キ}}$である。
(2)tの取りうる範囲を$t_1\lt t \lt t_2$とするとき、$t_1=\boxed{あ},t_2=\boxed{い}$である。
$\boxed{あ},\ \boxed{い}$の選択肢
$(\textrm{a})0\ \ \ (\textrm{b})\frac{1}{3}\ \ \ (\textrm{c})\frac{1}{2}\ \ \ (\textrm{d})\frac{\sqrt3}{3}\ \ \ (\textrm{e})\frac{2}{3}$
$ (\textrm{f})1\ \ \ (\textrm{g})\frac{2\sqrt3}{2}\ \ \ (\textrm{h})\sqrt3\ \ \ (\textrm{i})2\ \ \ (\textrm{j})3$
(3)辺ABの長さをtの式で表すと$AB=\frac{\boxed{ク}}{\boxed{ケ}}t+$
$\sqrt{1+\frac{\boxed{コ}}{\boxed{サ}}t^2}$である。
(4)$\triangle ABC$の面積は$t=\frac{\sqrt{\boxed{シ}}}{\boxed{ス}}$
で最大値$\frac{\sqrt{\boxed{セ}}}{\boxed{ソ}}$をとる。
(5)$t_1,t_2$を(2)で定めた値とする。
$t_1 \lt t \lt t_2$の範囲で、xyz-座標空間内の平面z=t上に、条件(★)を満たす
$\triangle ABC$が、$B(0,0,t),C(0,1,t)$を満たし、Aのx座標が正であるように
おかれている。まgた、$B_1(0,0,t_1),C_1(0,1,t_1),B_2(0,0,t_2),C_2(0,1,t_2)$と
おく。
$\triangle ABC$を$t_1 \lt t \lt t_2$の範囲で動かしたときに通過してできる図形に線分$B_1C_1$、
線分$B_2C_2$を付け加えた立体の体積は$\frac{\sqrt{\boxed{タ}}}{\boxed{チ}}$である。
この動画を見る
tを実数とする。次の条件(★)を満たす$\triangle ABC$を考える。
(★)$AC=t,\ BC=1$を満たし、$\angle BAC$の2等分線と辺BCの交点をDとおくと、
$\cos\angle DAC=\frac{\sqrt3}{3}$である。
(1)$\cos\angle DAC=\frac{\boxed{カ}}{\boxed{キ}}$である。
(2)tの取りうる範囲を$t_1\lt t \lt t_2$とするとき、$t_1=\boxed{あ},t_2=\boxed{い}$である。
$\boxed{あ},\ \boxed{い}$の選択肢
$(\textrm{a})0\ \ \ (\textrm{b})\frac{1}{3}\ \ \ (\textrm{c})\frac{1}{2}\ \ \ (\textrm{d})\frac{\sqrt3}{3}\ \ \ (\textrm{e})\frac{2}{3}$
$ (\textrm{f})1\ \ \ (\textrm{g})\frac{2\sqrt3}{2}\ \ \ (\textrm{h})\sqrt3\ \ \ (\textrm{i})2\ \ \ (\textrm{j})3$
(3)辺ABの長さをtの式で表すと$AB=\frac{\boxed{ク}}{\boxed{ケ}}t+$
$\sqrt{1+\frac{\boxed{コ}}{\boxed{サ}}t^2}$である。
(4)$\triangle ABC$の面積は$t=\frac{\sqrt{\boxed{シ}}}{\boxed{ス}}$
で最大値$\frac{\sqrt{\boxed{セ}}}{\boxed{ソ}}$をとる。
(5)$t_1,t_2$を(2)で定めた値とする。
$t_1 \lt t \lt t_2$の範囲で、xyz-座標空間内の平面z=t上に、条件(★)を満たす
$\triangle ABC$が、$B(0,0,t),C(0,1,t)$を満たし、Aのx座標が正であるように
おかれている。まgた、$B_1(0,0,t_1),C_1(0,1,t_1),B_2(0,0,t_2),C_2(0,1,t_2)$と
おく。
$\triangle ABC$を$t_1 \lt t \lt t_2$の範囲で動かしたときに通過してできる図形に線分$B_1C_1$、
線分$B_2C_2$を付け加えた立体の体積は$\frac{\sqrt{\boxed{タ}}}{\boxed{チ}}$である。
大学入試問題#340「とりあえず絶対値はずそ」 日本大学医学部(2010) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#日本大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{4}{3}\pi} |\sqrt{ 3 }\cos\ x-\sin\ x| dx$
出典:2010年日本大学医学部 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{4}{3}\pi} |\sqrt{ 3 }\cos\ x-\sin\ x| dx$
出典:2010年日本大学医学部 入試問題
福田の数学〜上智大学2022年理工学部第1問(3)〜定積分の計算

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\large\boxed{1}}\ (3)\int_0^{\frac{2}{3}\pi}x\sin2xdx=\frac{\pi}{\boxed{イ}}+$
$\frac{\boxed{ウ}}{\boxed{エ}}\sqrt{\boxed{オ}}$である。
2022上智大理工学部過去問
この動画を見る
${\large\boxed{1}}\ (3)\int_0^{\frac{2}{3}\pi}x\sin2xdx=\frac{\pi}{\boxed{イ}}+$
$\frac{\boxed{ウ}}{\boxed{エ}}\sqrt{\boxed{オ}}$である。
2022上智大理工学部過去問
大学入試問題#339「とりま部分積分じゃろ~~」 岡山県立大学(2013) #定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#岡山県立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{log(\cos\ x)}{\cos^2x} dx$
出典:2013年岡山県立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{log(\cos\ x)}{\cos^2x} dx$
出典:2013年岡山県立大学 入試問題
【超良問】大学入試問題#337 弘前大学(2010) #定積分 #ウォリス積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\{x(1-x)\}^{\frac{3}{2}}dx$
出典:2010年弘前大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\{x(1-x)\}^{\frac{3}{2}}dx$
出典:2010年弘前大学 入試問題
大学入試問題#338 数学トークさん #定積分 #キングプロパティ
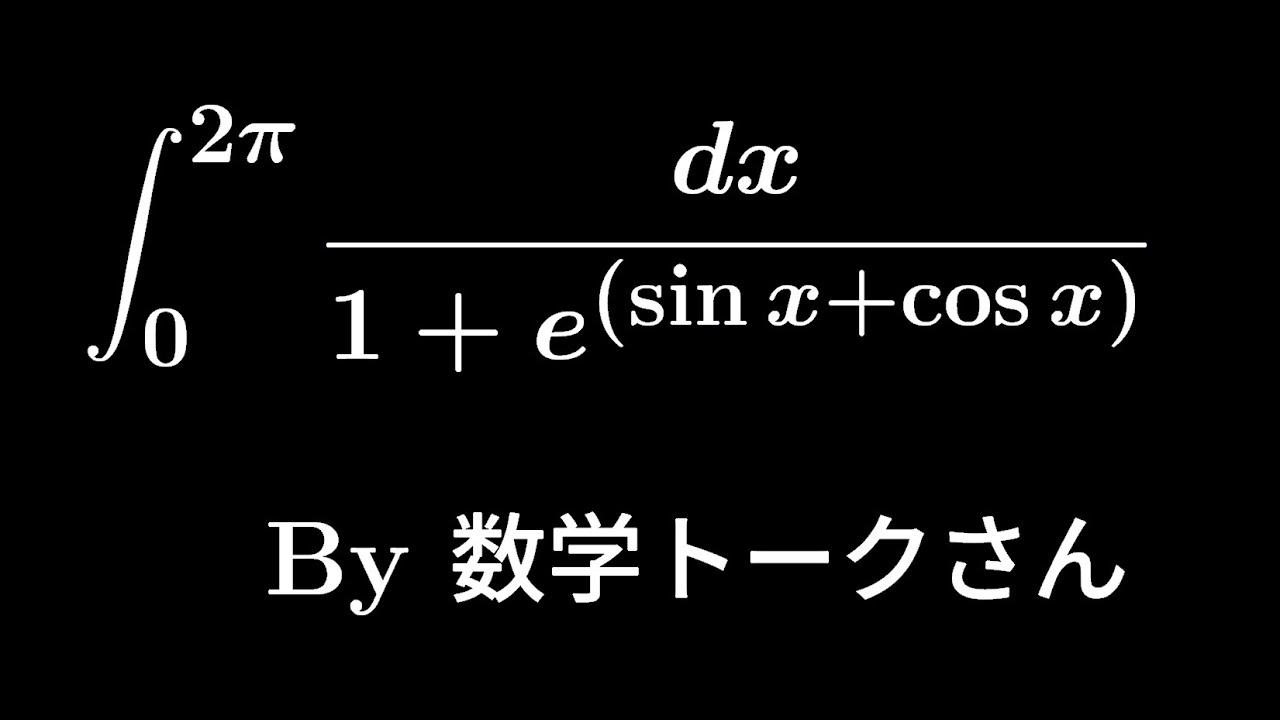
単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{2\pi}\displaystyle \frac{dx}{1+e^{(\sin\ x+\cos\ x)}}$
この動画を見る
$\displaystyle \int_{0}^{2\pi}\displaystyle \frac{dx}{1+e^{(\sin\ x+\cos\ x)}}$
福田の数学〜上智大学2022年TEAP理系型第4問〜媒介変数で表された極方程式

単元:
#大学入試過去問(数学)#平面上の曲線#微分とその応用#積分とその応用#微分法#定積分#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#上智大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
座標平面において、原点を極とし、x軸の正の部分を始線とする極座標を考え
る。平面上を運動する点Pの極座標$(r,\ θ)$が、時刻$t \geqq 0$の関数として、
$r=1+t,\ \ \ θ=\log(1+t)$
で与えられるとする。時刻$t=0$にPが出発してから初めてy軸上に到着するまで
にPが描く軌跡をCとする。
(1)$\ t \gt 0$において、Pが初めてy軸上に到着するときのtの値を求めよ。
(2)C上の点のx座標の最大値を求めよ。
(3)Cの長さを求めよ。
(4)Cを座標平面上に図示せよ。
(5)Cとx軸とy軸で囲まれた部分の面積を求めよ。
2022上智大学理系過去問
この動画を見る
座標平面において、原点を極とし、x軸の正の部分を始線とする極座標を考え
る。平面上を運動する点Pの極座標$(r,\ θ)$が、時刻$t \geqq 0$の関数として、
$r=1+t,\ \ \ θ=\log(1+t)$
で与えられるとする。時刻$t=0$にPが出発してから初めてy軸上に到着するまで
にPが描く軌跡をCとする。
(1)$\ t \gt 0$において、Pが初めてy軸上に到着するときのtの値を求めよ。
(2)C上の点のx座標の最大値を求めよ。
(3)Cの長さを求めよ。
(4)Cを座標平面上に図示せよ。
(5)Cとx軸とy軸で囲まれた部分の面積を求めよ。
2022上智大学理系過去問
大学入試問題#336 横浜国立大学2013 #定積分
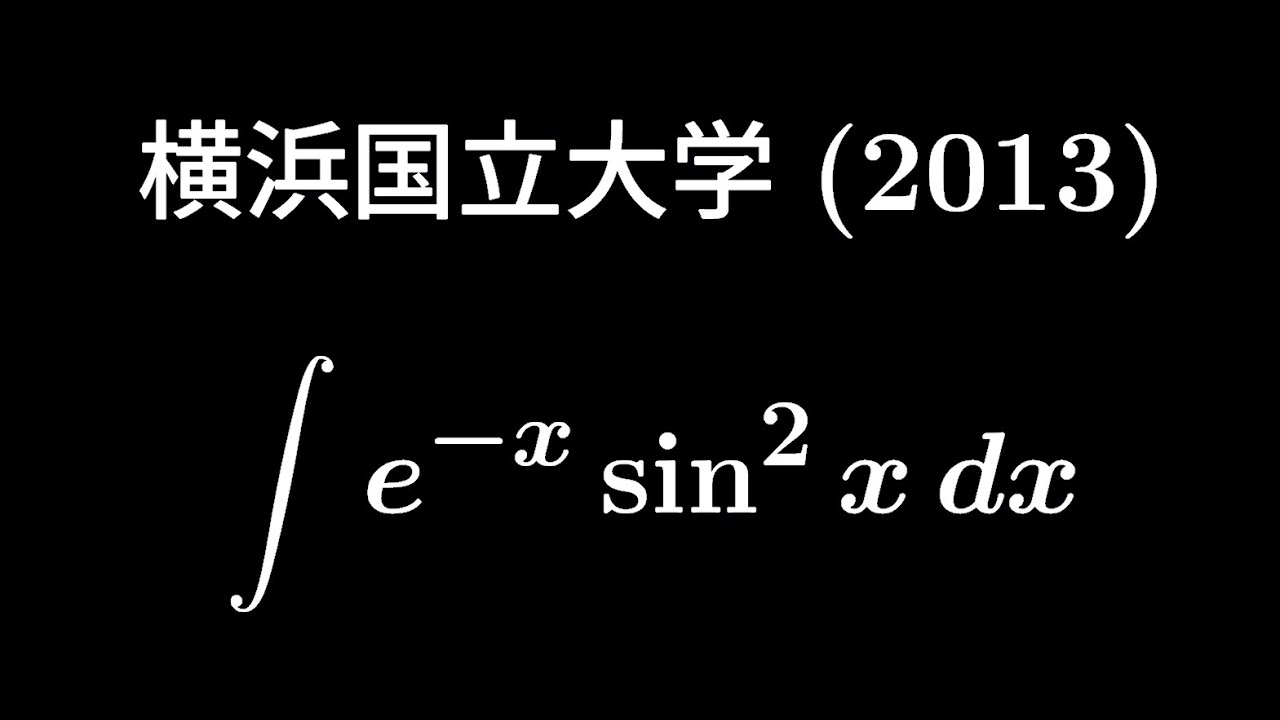
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int e^{-x}\sin^2x\ dx$
出典:2013年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int e^{-x}\sin^2x\ dx$
出典:2013年横浜国立大学 入試問題
