 積分とその応用
積分とその応用
 積分とその応用
積分とその応用
大学入試問題#130 東海大学医学部(2016) 定積分
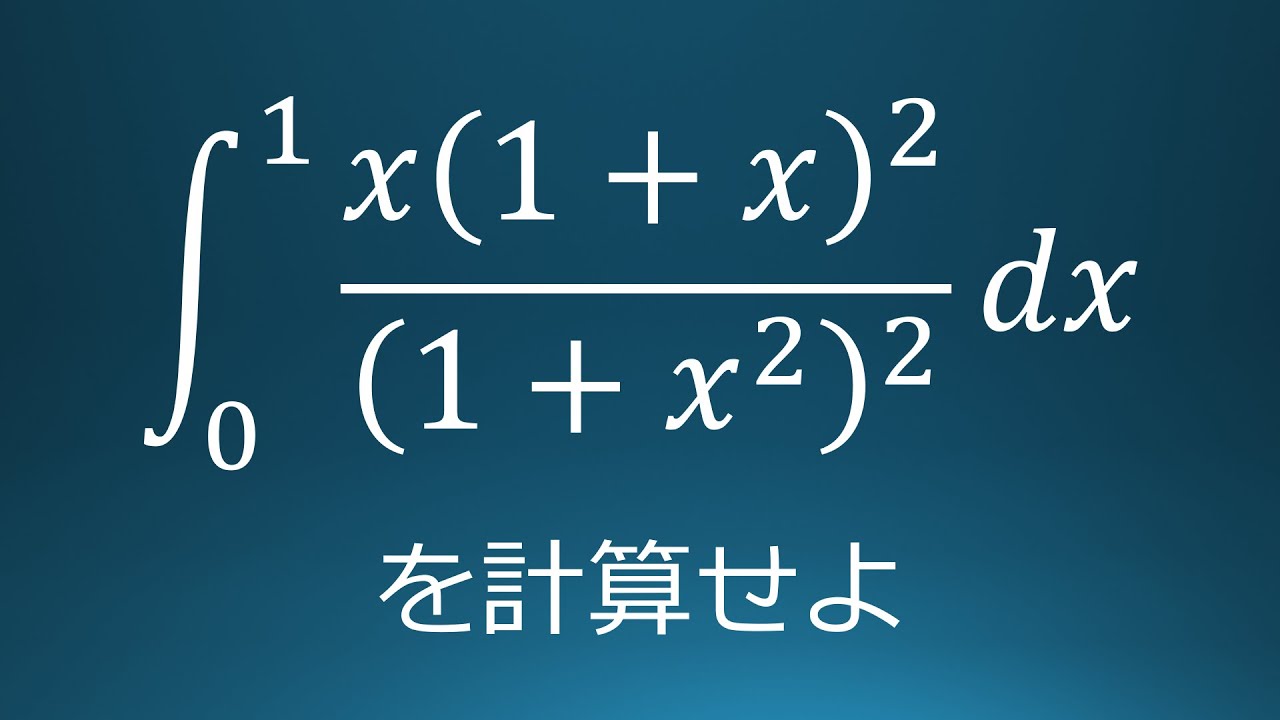
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東海大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{x(1+x)^2}{(1+x^2)^2}\ dx$を計算せよ。
出典:2016年東海大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{x(1+x)^2}{(1+x^2)^2}\ dx$を計算せよ。
出典:2016年東海大学医学部 入試問題
【数Ⅲ】微分法・積分法:<公式忘れても大丈夫!>三角関数の微積分 ~ぐるぐる回そう~

単元:
#微分とその応用#積分とその応用#色々な関数の導関数#不定積分#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形の重心における、頂点→重心:重心→中点の線分の比を導出する動画になります。
この動画を見る
三角形の重心における、頂点→重心:重心→中点の線分の比を導出する動画になります。
福田の入試問題解説〜東京大学2022年理系第1問〜最小値の存在と定積分の計算

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
次の関数f(x)を考える。
$f(x)=(\cos x)\log(\cos x)-\cos x+\int_0^x(\cos t)\log(\cos t)dt (0 \leqq x \lt \frac{\pi}{2})$
(1)f(x)は区間$0 \leqq x \lt \frac{\pi}{2}$において最小値を持つことを示せ。
(2)f(x)は区間$0 \leqq x \lt \frac{\pi}{2}$における最小値を求めよ。
2022東京大学理系過去問
この動画を見る
次の関数f(x)を考える。
$f(x)=(\cos x)\log(\cos x)-\cos x+\int_0^x(\cos t)\log(\cos t)dt (0 \leqq x \lt \frac{\pi}{2})$
(1)f(x)は区間$0 \leqq x \lt \frac{\pi}{2}$において最小値を持つことを示せ。
(2)f(x)は区間$0 \leqq x \lt \frac{\pi}{2}$における最小値を求めよ。
2022東京大学理系過去問
大学入試問題#126 慶應大学医学部(2005) 不定積分
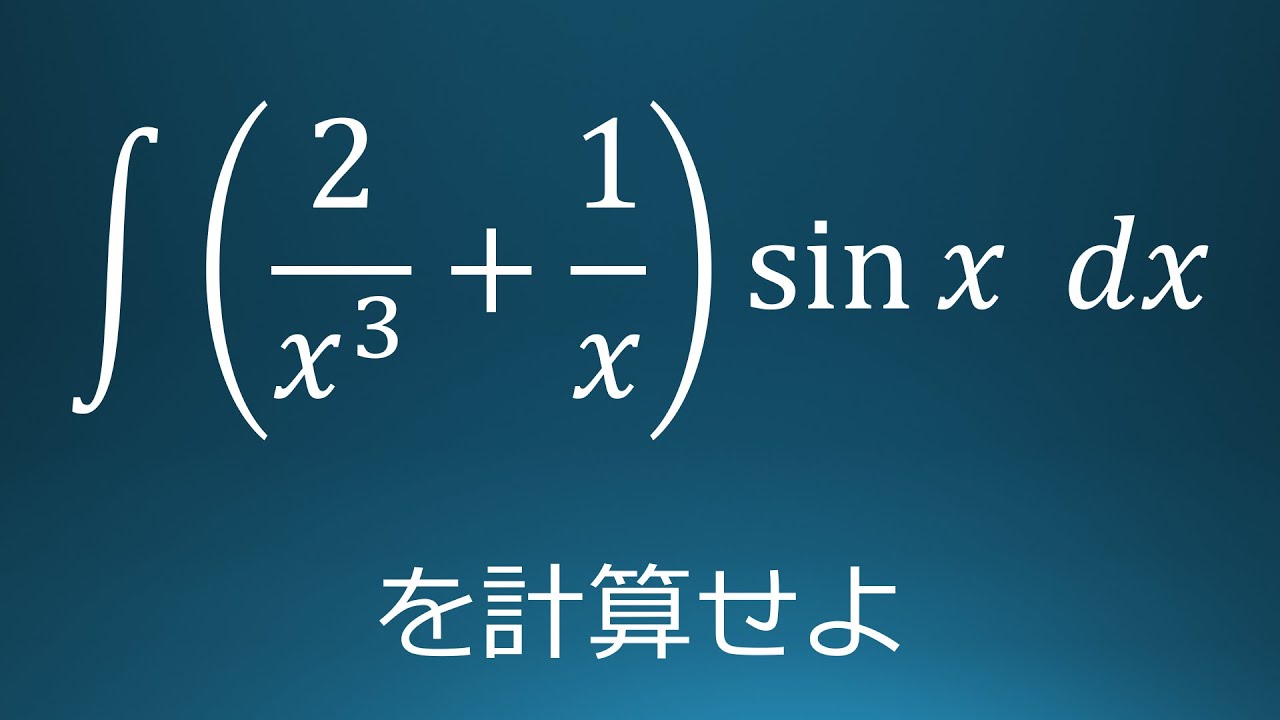
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int (\displaystyle \frac{2}{x^3}+\displaystyle \frac{1}{x})\sin\ x\ dx$を計算せよ。
出典:2005年慶應義塾大学 入試問題
この動画を見る
$\displaystyle \int (\displaystyle \frac{2}{x^3}+\displaystyle \frac{1}{x})\sin\ x\ dx$を計算せよ。
出典:2005年慶應義塾大学 入試問題
福田の数学〜東京慈恵会医科大学2022年医学部第2問〜微分可能性と最大値と体積

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#微分とその応用#積分とその応用#微分法#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
実数aは正の定数とする。実数全体で定義された関数$f(x)=\frac{|x+a|}{\sqrt{x^2+1}}$について、
次の問いに答えよ。
(1)$f(x)$が$x=-a$で微分可能であるかどうか調べよ。
(2)$f(x)$の最大値が$\sqrt2$となるように、定数aの値を定めよ。
(3)定数aは(2)で定めた値とする。$y=f(x)$のグラフとx軸およびy軸で囲まれた部分
をx軸の周りに1回転させてできる立体の体積Vを求めよ。
2022東京慈恵会医科大学医学部過去問
この動画を見る
実数aは正の定数とする。実数全体で定義された関数$f(x)=\frac{|x+a|}{\sqrt{x^2+1}}$について、
次の問いに答えよ。
(1)$f(x)$が$x=-a$で微分可能であるかどうか調べよ。
(2)$f(x)$の最大値が$\sqrt2$となるように、定数aの値を定めよ。
(3)定数aは(2)で定めた値とする。$y=f(x)$のグラフとx軸およびy軸で囲まれた部分
をx軸の周りに1回転させてできる立体の体積Vを求めよ。
2022東京慈恵会医科大学医学部過去問
大学入試問題#124 高知大学(2020) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#高知大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{7}{2}}^{\frac{9}{2}}\displaystyle \frac{2^x}{2^x+\sqrt{ 2 }}\ dx$を計算せよ。
出典:2020年高知大学 入試問題
この動画を見る
$\displaystyle \int_{-\frac{7}{2}}^{\frac{9}{2}}\displaystyle \frac{2^x}{2^x+\sqrt{ 2 }}\ dx$を計算せよ。
出典:2020年高知大学 入試問題
大学入試問題#121 横浜国立大学(2004) 定積分
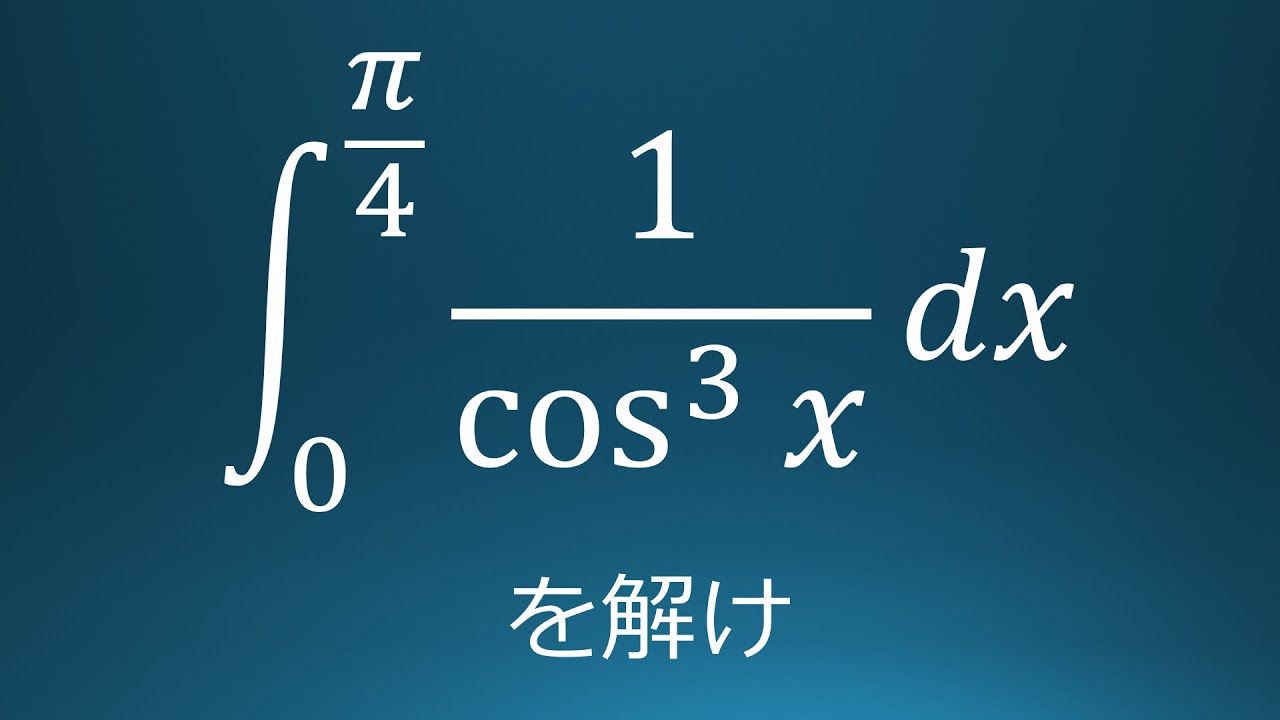
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{1}{\cos^3\ x}\ dx$を計算せよ。
出典:2004年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{1}{\cos^3\ x}\ dx$を計算せよ。
出典:2004年横浜国立大学 入試問題
大学入試問題#119 横浜国立大学(2020) 定積分
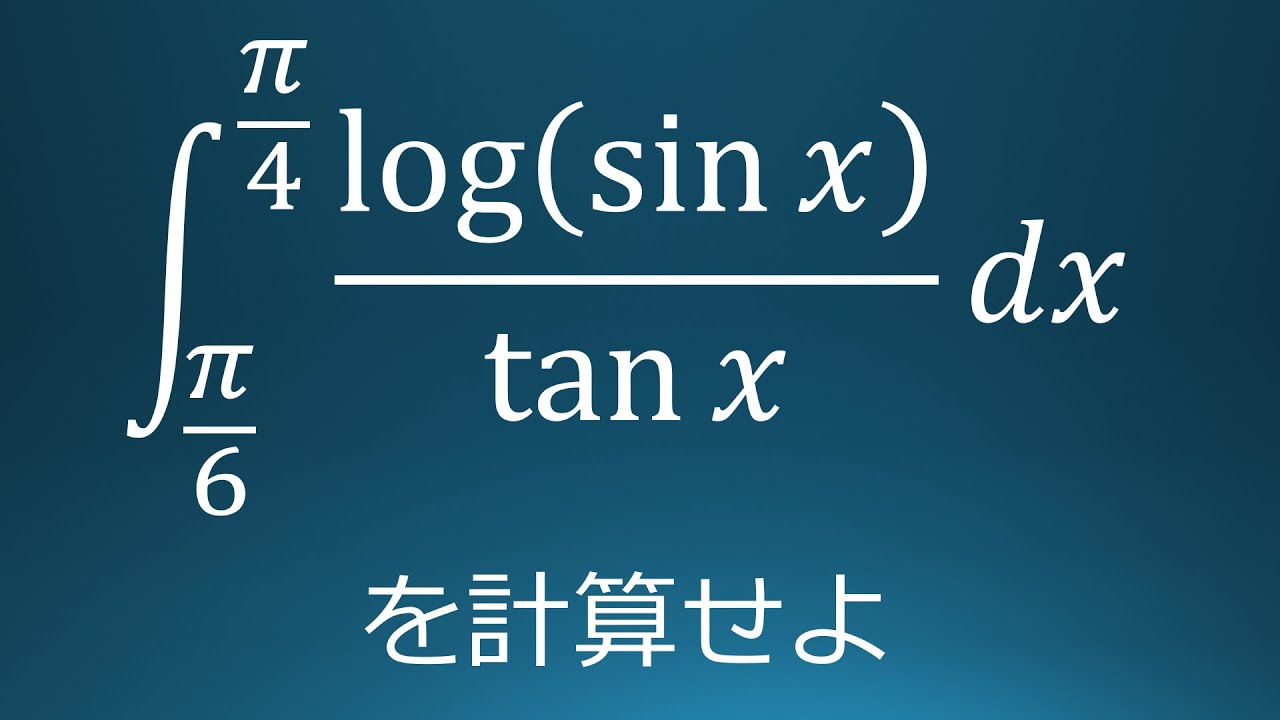
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{4}}\displaystyle \frac{log(\sin\ x)}{\tan\ x}\ dx$を計算せよ。
出典:2020年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{4}}\displaystyle \frac{log(\sin\ x)}{\tan\ x}\ dx$を計算せよ。
出典:2020年横浜国立大学 入試問題
大学入試問題#118 防衛医科大学(2012) 区分求積法

単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#防衛医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\sqrt[ n ]{ \displaystyle \frac{(4n)!}{(3n)!} }$を求めよ。
出典:2012年防衛医科大学 入試問題
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\sqrt[ n ]{ \displaystyle \frac{(4n)!}{(3n)!} }$を求めよ。
出典:2012年防衛医科大学 入試問題
大学入試問題#116 岡山県立大学(2009) 定積分②
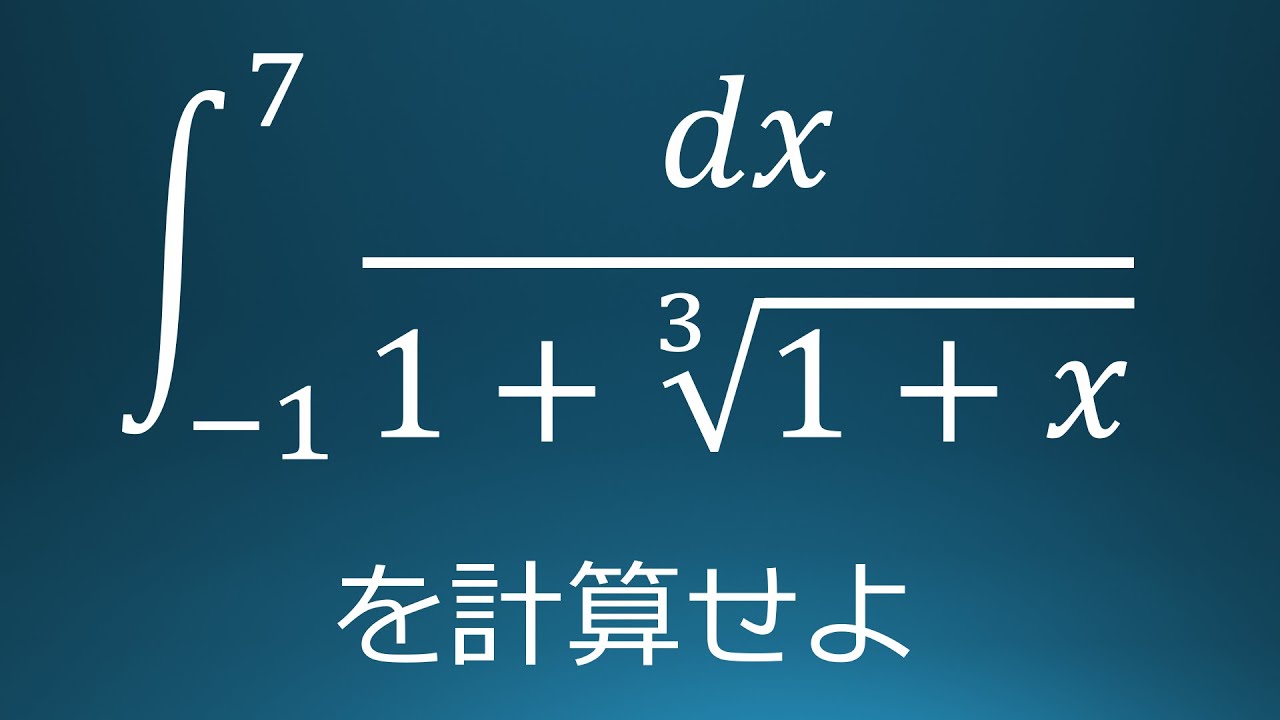
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#岡山県立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-1}^{7}\displaystyle \frac{dx}{1+\sqrt[ 3 ]{ 1+x }}$を計算せよ。
出典:2009年岡山県立大学 入試問題
この動画を見る
$\displaystyle \int_{-1}^{7}\displaystyle \frac{dx}{1+\sqrt[ 3 ]{ 1+x }}$を計算せよ。
出典:2009年岡山県立大学 入試問題
大学入試問題#114 岡山県立大学(2009) 定積分
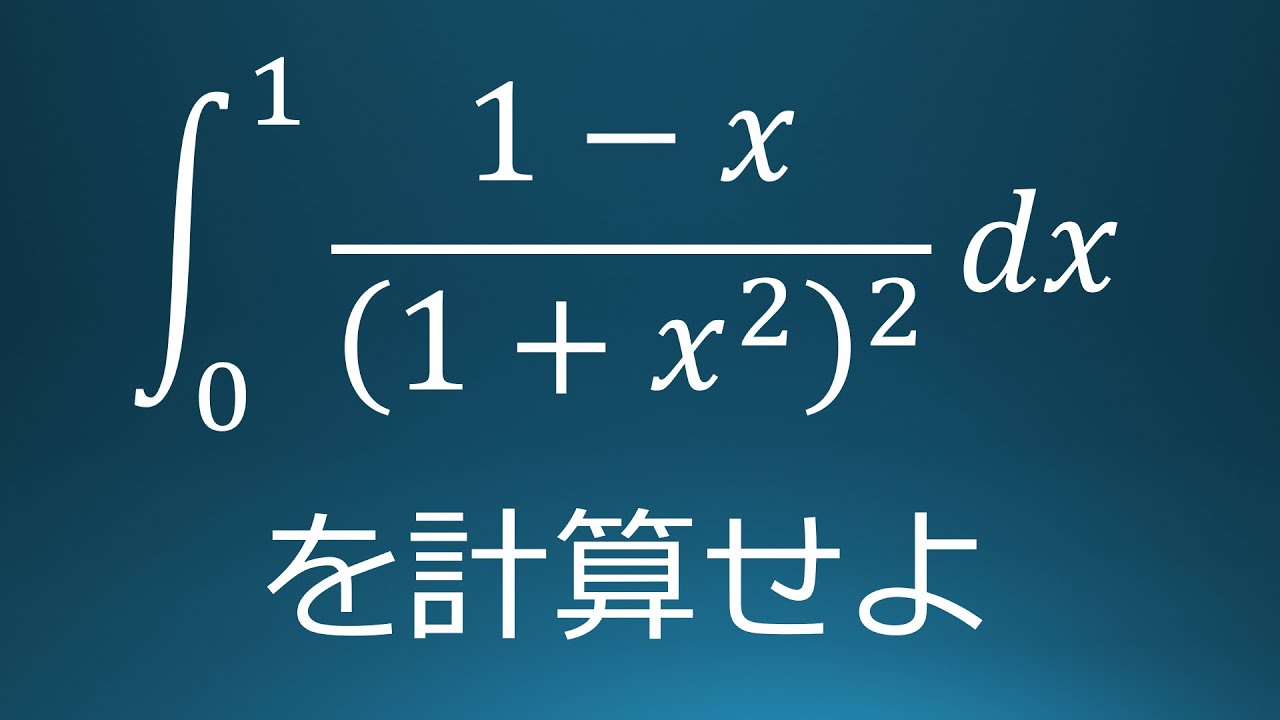
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#岡山県立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}\displaystyle \frac{1-x}{(1+x^2)^2}\ dx$を計算せよ。
出典:2009年岡山県立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}\displaystyle \frac{1-x}{(1+x^2)^2}\ dx$を計算せよ。
出典:2009年岡山県立大学 入試問題
大学入試問題#112 琉球大学(1989) 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#琉球大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$-1 \neq \alpha$:定数
$\displaystyle \int \displaystyle \frac{(log\ x)^\alpha}{x}\ log(\log\ x)dx$を計算せよ。
出典:1989年琉球大学 入試問題
この動画を見る
$-1 \neq \alpha$:定数
$\displaystyle \int \displaystyle \frac{(log\ x)^\alpha}{x}\ log(\log\ x)dx$を計算せよ。
出典:1989年琉球大学 入試問題
大学入試問題#110 産業医科大学(2019) 定積分②
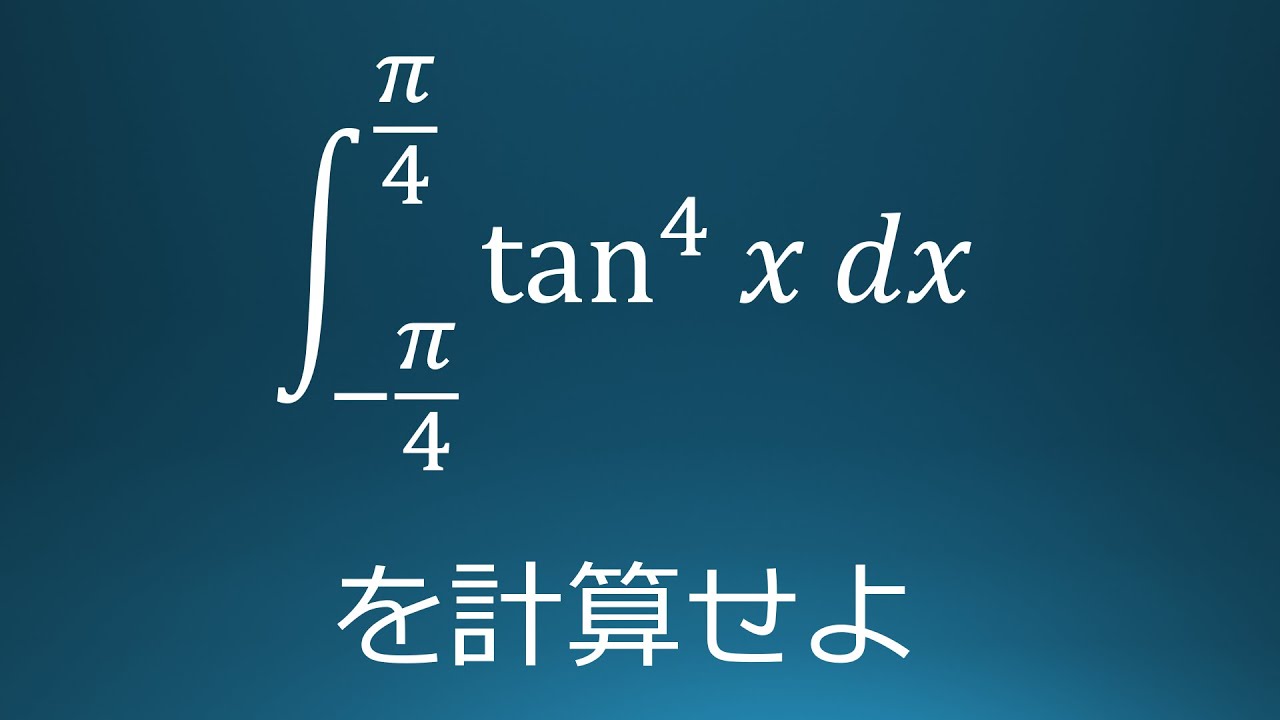
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#産業医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}}\ \tan^4x\ dx$を計算せよ。
出典:2019年産業医科大学 入試問題
この動画を見る
$\displaystyle \int_{-\frac{\pi}{4}}^{\frac{\pi}{4}}\ \tan^4x\ dx$を計算せよ。
出典:2019年産業医科大学 入試問題
大学入試問題#108 弘前大学(2018) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a \gt 0$
$\displaystyle \int_{0}^{1}\displaystyle \frac{dx}{(e^{2x}+a)(e^{-2x}+a)}\ $を計算せよ。
出典:2018年弘前大学 入試問題
この動画を見る
$a \gt 0$
$\displaystyle \int_{0}^{1}\displaystyle \frac{dx}{(e^{2x}+a)(e^{-2x}+a)}\ $を計算せよ。
出典:2018年弘前大学 入試問題
大学入試問題#107 産業医科大学(2019) 定積分①

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#産業医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{99}^{101}\sqrt{ (x-99)(101-x) }\ dx\ $を計算せよ。
出典:2019年産業医科大学 入試問題
この動画を見る
$\displaystyle \int_{99}^{101}\sqrt{ (x-99)(101-x) }\ dx\ $を計算せよ。
出典:2019年産業医科大学 入試問題
大学入試問題#101 東海大学医学部(2017) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東海大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}x^3(1-x^2)^8dx$を計算せよ。
出典:2017年東海大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}x^3(1-x^2)^8dx$を計算せよ。
出典:2017年東海大学医学部 入試問題
大学入試問題#98 千葉大学医学部(2018) 積分・極限
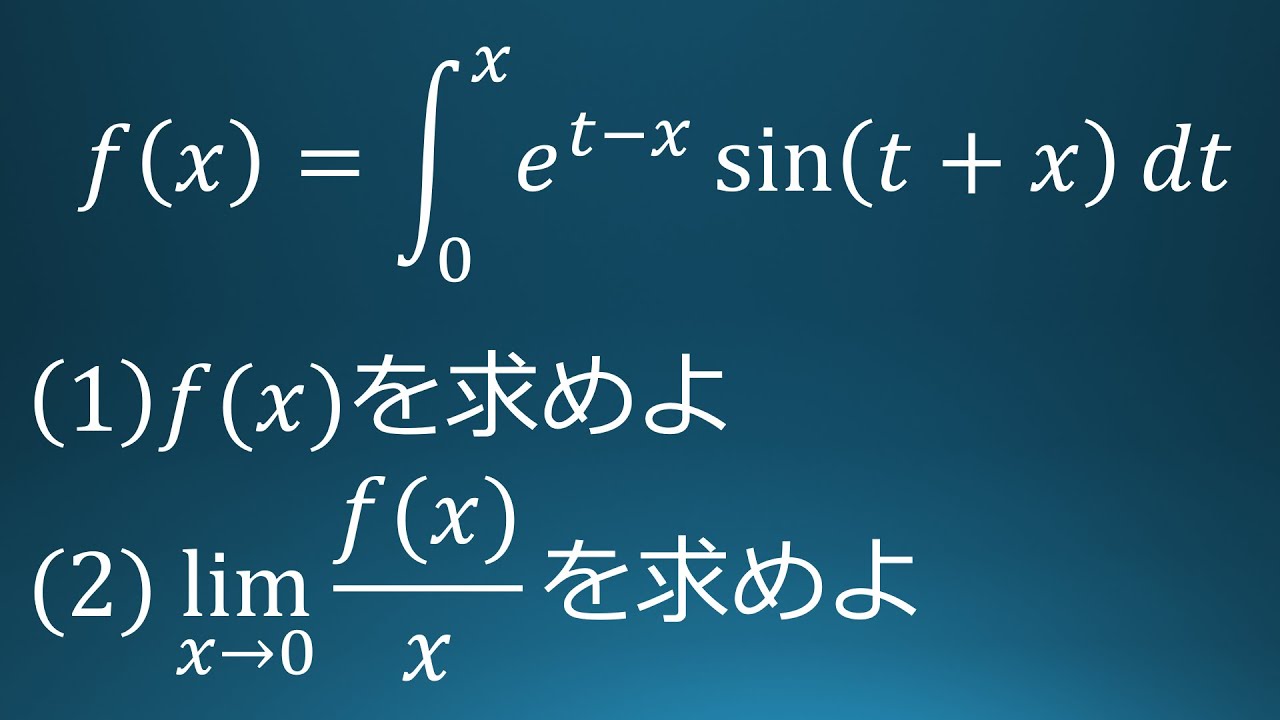
単元:
#大学入試過去問(数学)#関数と極限#積分とその応用#関数の極限#不定積分#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
(1)
$f(x)=\displaystyle \int_{0}^{x}e^{t-x}\sin(t+x)dt$を求めよ。
(2)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{f(x)}{x}$を求めよ。
出典:2018年千葉大学 入試問題
この動画を見る
(1)
$f(x)=\displaystyle \int_{0}^{x}e^{t-x}\sin(t+x)dt$を求めよ。
(2)
$\displaystyle \lim_{ x \to 0 }\displaystyle \frac{f(x)}{x}$を求めよ。
出典:2018年千葉大学 入試問題
大学入試問題#96 横浜国立大学(2015) 定積分
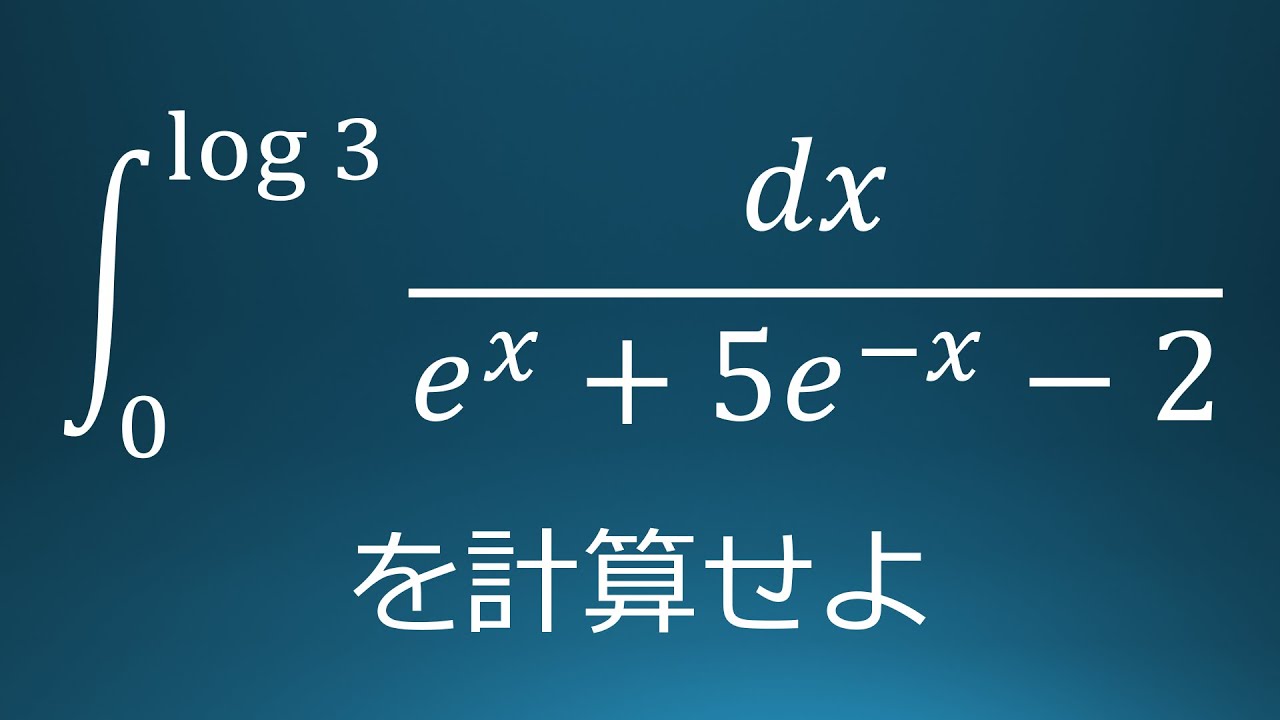
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{log\ 3}\displaystyle \frac{dx}{e^x+5e^{-x}-2}$を求めよ。
出典:2015横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{log\ 3}\displaystyle \frac{dx}{e^x+5e^{-x}-2}$を求めよ。
出典:2015横浜国立大学 入試問題
大学入試問題#95 横浜市立大学医学部(2013) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#横浜市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\sqrt{ 2 }}{\sin\ x+\cos\ x}\ dx$を求めよ。
出典:2013年横浜市立大学医学部 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\sqrt{ 2 }}{\sin\ x+\cos\ x}\ dx$を求めよ。
出典:2013年横浜市立大学医学部 入試問題
大学入試問題#94 横浜国立大学(2007) 定積分
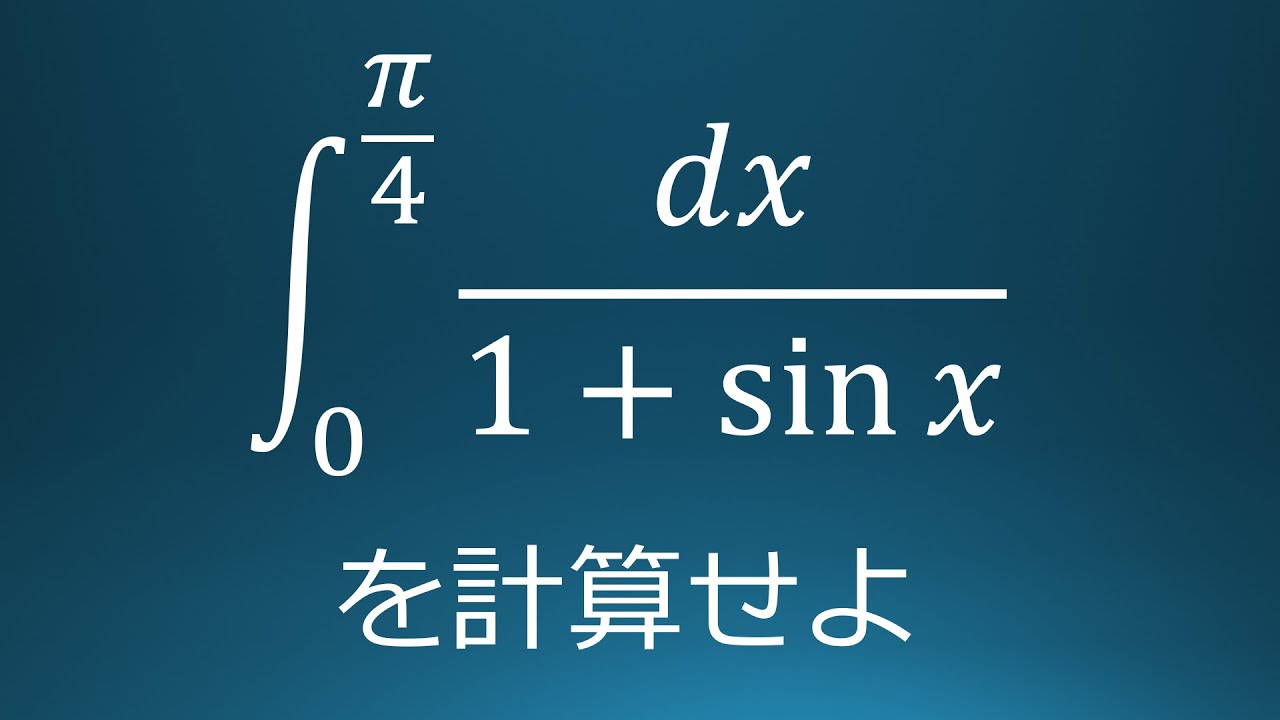
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{dx}{1+\sin\ x}$を計算せよ。
出典:2007年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{dx}{1+\sin\ x}$を計算せよ。
出典:2007年横浜国立大学 入試問題
大学入試問題#92 東京医科大学(2015) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}(x\sqrt{ 1-x^2 })^3 dx$を計算せよ。
出典:2015年東京医科大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}(x\sqrt{ 1-x^2 })^3 dx$を計算せよ。
出典:2015年東京医科大学 入試問題
大学入試問題#91 関西学院大学(2006) 不定積分
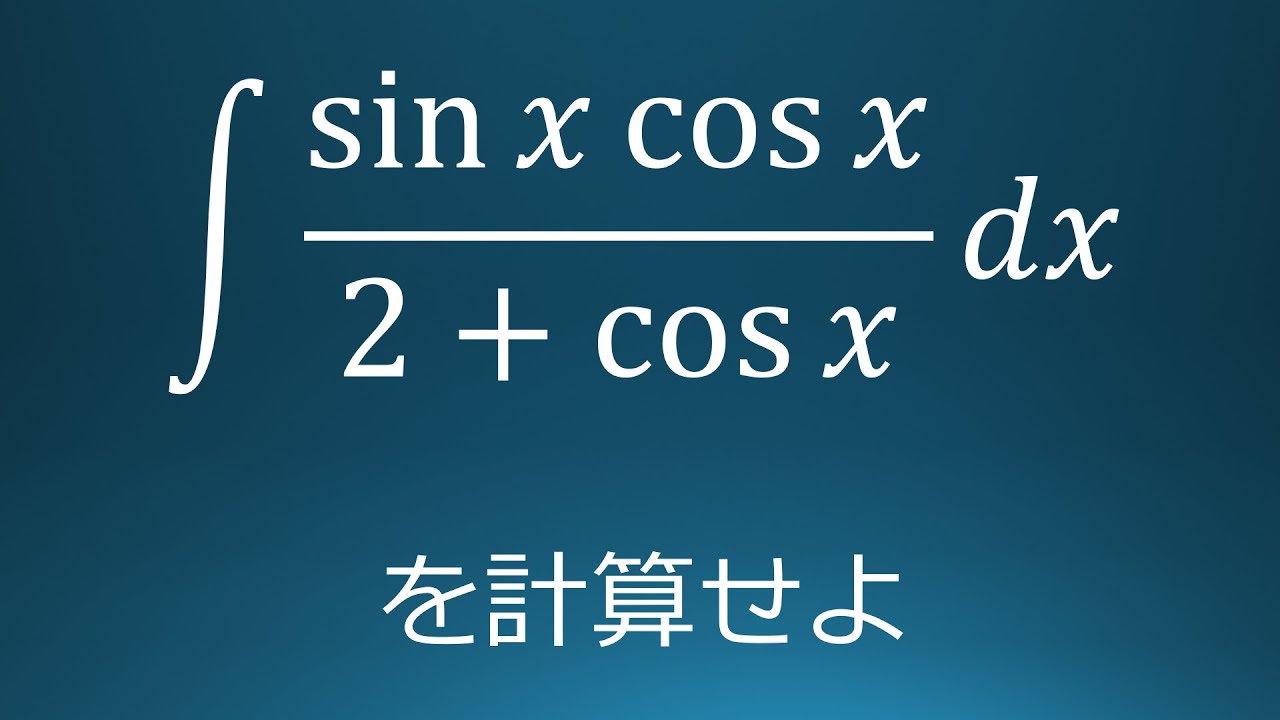
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#関西学院大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{\sin\ x\ \cos\ x}{2+\cos\ x}\ dx$を計算せよ。
出典:2006年関西学院大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{\sin\ x\ \cos\ x}{2+\cos\ x}\ dx$を計算せよ。
出典:2006年関西学院大学 入試問題
大学入試問題#89 信州大学(1988) 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int (x^2+a^2)^{-\frac{3}{2}}dx$
$a \neq 0$を計算せよ。
出典:1988年信州大学 入試問題
この動画を見る
$\displaystyle \int (x^2+a^2)^{-\frac{3}{2}}dx$
$a \neq 0$を計算せよ。
出典:1988年信州大学 入試問題
大学入試問題#85 小樽商科大学(1988) 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#小樽商科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \sin(log\ x)dx$を計算せよ。
出典:1988年小樽商科大学 入試問題
この動画を見る
$\displaystyle \int \sin(log\ x)dx$を計算せよ。
出典:1988年小樽商科大学 入試問題
大学入試問題#84 弘前大学(1986) 不定積分
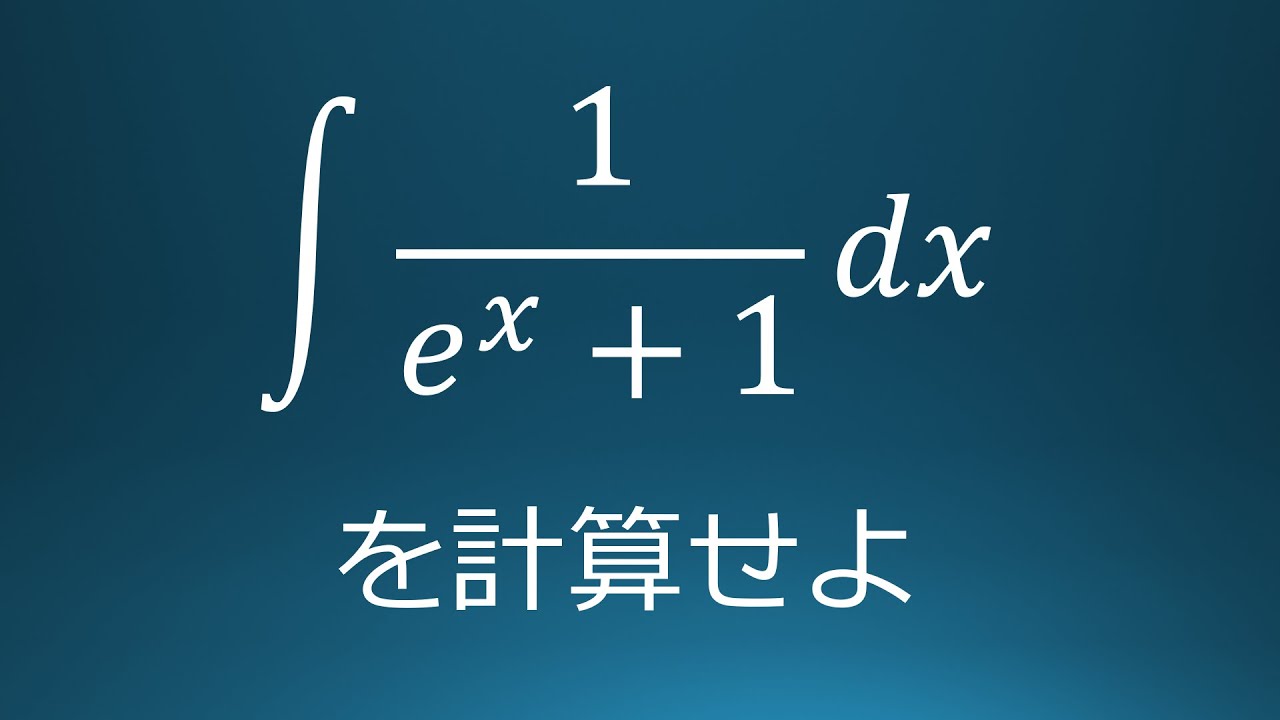
単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#弘前大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{1}{e^x+1}\ dx$を計算せよ。
出典:1986年弘前大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{1}{e^x+1}\ dx$を計算せよ。
出典:1986年弘前大学 入試問題
大学入試問題#82 神戸大学(2012) 複雑な置換積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\sin\ x-\cos\ x}{1+\cos\ x}\ dx$
出典:2012年神戸大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}\displaystyle \frac{\sin\ x-\cos\ x}{1+\cos\ x}\ dx$
出典:2012年神戸大学 入試問題
大学入試問題#80 信州大学(2001) 不定積分

単元:
#大学入試過去問(数学)#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#数学(高校生)#信州大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ x+1 }+1}\ dx$を計算せよ。
出典:2001年信州大学 入試問題
この動画を見る
$\displaystyle \int \displaystyle \frac{x}{\sqrt{ x+1 }+1}\ dx$を計算せよ。
出典:2001年信州大学 入試問題
大学入試問題#78 横浜国立大学(2006) 置換積分
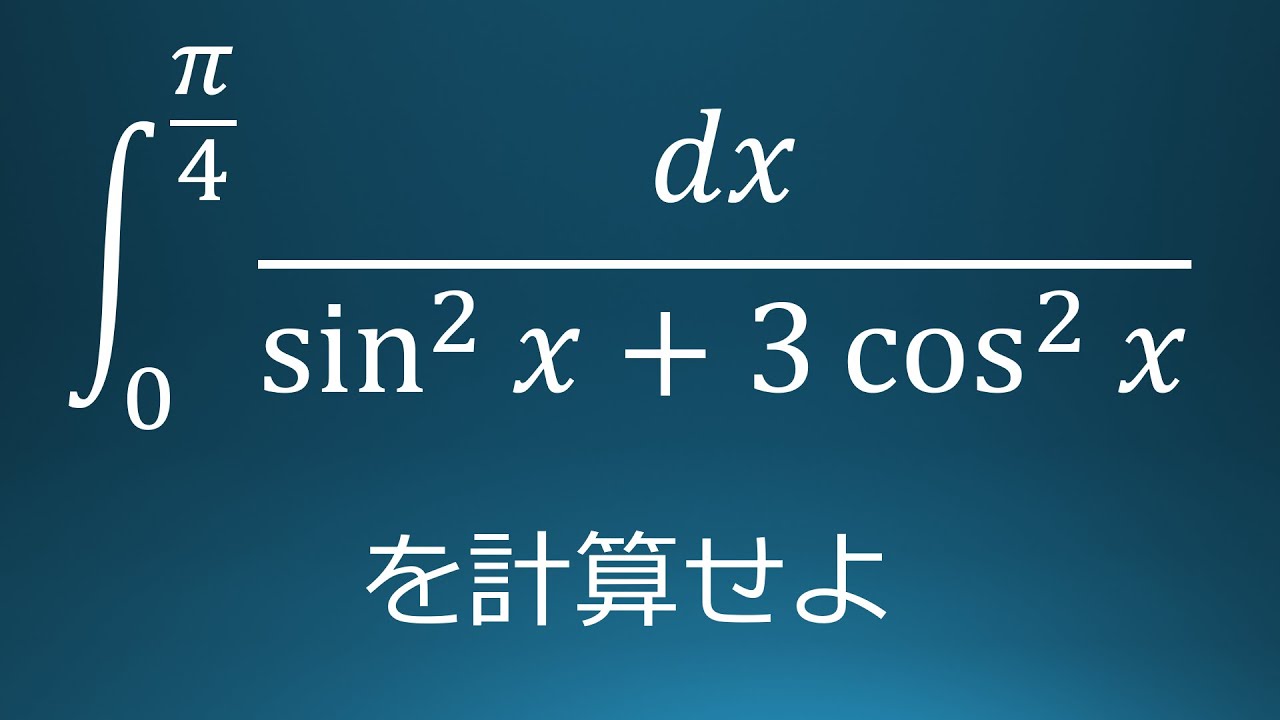
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{dx}{\sin^2x+3\cos^2x}$を計算せよ。
出典:2006年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{dx}{\sin^2x+3\cos^2x}$を計算せよ。
出典:2006年横浜国立大学 入試問題
大学入試問題#75 横浜国立大学(2006) 部分積分
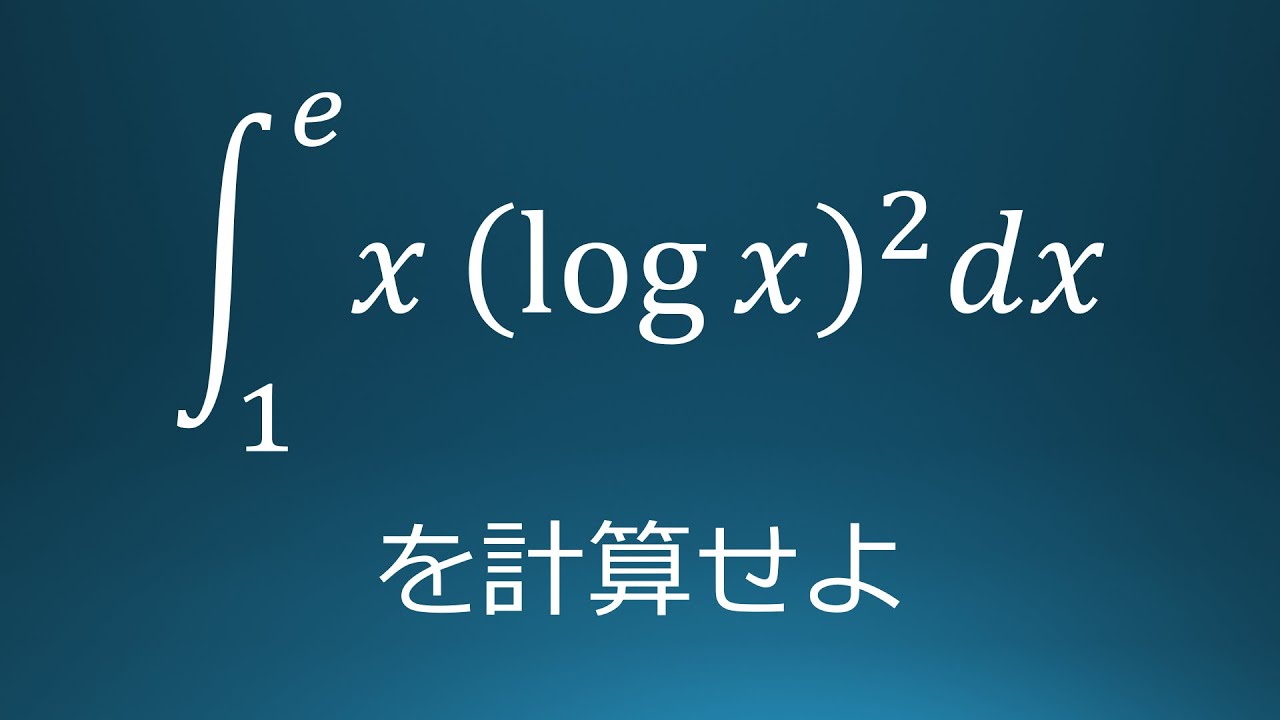
単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#横浜国立大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{e}x(log\ x)^2dx$を計算せよ。
出典:2006年横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{e}x(log\ x)^2dx$を計算せよ。
出典:2006年横浜国立大学 入試問題
大学入試問題#72 福岡教育大学(2009) 置換積分②

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{log\ 7}(\displaystyle \frac{e^x}{1+e^x})^3dx$を計算せよ。
出典:2009年福岡教育大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{log\ 7}(\displaystyle \frac{e^x}{1+e^x})^3dx$を計算せよ。
出典:2009年福岡教育大学 入試問題
