 複素数平面
複素数平面
 複素数平面
複素数平面
福田の数学〜青山学院大学2025理工学部第2問〜虚数係数の2次方程式の解と正方形の頂点
単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#青山学院大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{2}$
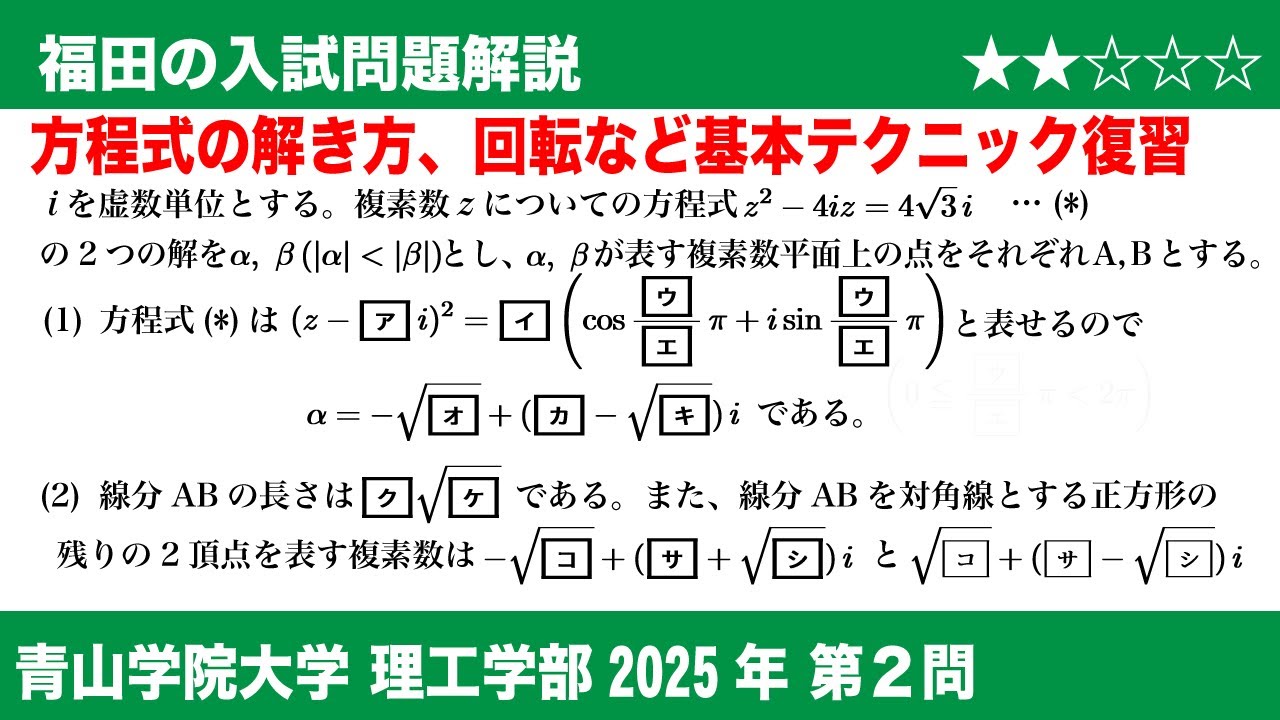
$i$を虚数単位とする。
複素数$z$についての方程式
$z^2-4iz=4\sqrt3 i \ \cdots (*)$
の$2$つの解を$\alpha,\beta(\vert \alpha \vert \lt \vert \beta \vert )$とし、
$\alpha,\beta$が表す複素数平面上の点を
それぞれ$A,B$とする。
(1)方程式$(*)$は
$(z-\boxed{ア}i)^2=\boxed{イ} \left(\cos \dfrac{\boxed{ウ}}{\boxed{エ}}\pi+i\sin\dfrac{\boxed{ウ}}{\boxed{エ}}\pi\right) \qquad \left(0\leqq \dfrac{\boxed{ウ}}{\boxed{エ}}\pi \lt 2\pi \right)$
と表せるので
$\alpha=-\sqrt{\boxed{オ}}+\left(\boxed{カ}-\sqrt{\boxed{キ}}\right)i$である。
(2)線分$AB$の長さは$\boxed{ク}\sqrt{\boxed{ケ}}$である。
また、線分$AB$を対角線とする正方形の
残りの$2$頂点を表す複素数は
$-\sqrt{\boxed{コ}}+\left(\boxed{サ}+\sqrt{\boxed{シ}}\right)i$と
$\sqrt{\boxed{コ}}-\left(\boxed{サ}+\sqrt{\boxed{シ}}\right)i$である。
$2025$年青山学院大学理工学部過去問題
この動画を見る
$\boxed{2}$
$i$を虚数単位とする。
複素数$z$についての方程式
$z^2-4iz=4\sqrt3 i \ \cdots (*)$
の$2$つの解を$\alpha,\beta(\vert \alpha \vert \lt \vert \beta \vert )$とし、
$\alpha,\beta$が表す複素数平面上の点を
それぞれ$A,B$とする。
(1)方程式$(*)$は
$(z-\boxed{ア}i)^2=\boxed{イ} \left(\cos \dfrac{\boxed{ウ}}{\boxed{エ}}\pi+i\sin\dfrac{\boxed{ウ}}{\boxed{エ}}\pi\right) \qquad \left(0\leqq \dfrac{\boxed{ウ}}{\boxed{エ}}\pi \lt 2\pi \right)$
と表せるので
$\alpha=-\sqrt{\boxed{オ}}+\left(\boxed{カ}-\sqrt{\boxed{キ}}\right)i$である。
(2)線分$AB$の長さは$\boxed{ク}\sqrt{\boxed{ケ}}$である。
また、線分$AB$を対角線とする正方形の
残りの$2$頂点を表す複素数は
$-\sqrt{\boxed{コ}}+\left(\boxed{サ}+\sqrt{\boxed{シ}}\right)i$と
$\sqrt{\boxed{コ}}-\left(\boxed{サ}+\sqrt{\boxed{シ}}\right)i$である。
$2025$年青山学院大学理工学部過去問題
福田の数学〜早稲田大学2025教育学部第1問(2)〜三角形の外心と垂心と点の回転

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(2)座標平面上の$3$点
$A(1,0),B(0,-1),C(-1,1)$を
頂点とする三角形$ABC$を考える。
三角形$ABC$をその外心を中心として反時計回りに
$\dfrac{\pi}{3}$だけ回転することで得られる三角形の
垂心の座標を求めよ。
なお、三角形の$3$頂点から対辺または
その延長に下ろした$3$本の垂線は一点で交わり、
その交点を三角形の垂心という。
$2025$年早稲田大学教育学部第1問過去問題
この動画を見る
$\boxed{1}$
(2)座標平面上の$3$点
$A(1,0),B(0,-1),C(-1,1)$を
頂点とする三角形$ABC$を考える。
三角形$ABC$をその外心を中心として反時計回りに
$\dfrac{\pi}{3}$だけ回転することで得られる三角形の
垂心の座標を求めよ。
なお、三角形の$3$頂点から対辺または
その延長に下ろした$3$本の垂線は一点で交わり、
その交点を三角形の垂心という。
$2025$年早稲田大学教育学部第1問過去問題
福田の数学〜東京慈恵会医科大学2025医学部第4問〜複素数の絶対値の取りうる値の範囲

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
$z$は実数ではない複素数で、
$z+\dfrac{1}{z-1}$が正の実数となるものとする。
このとき、
$ \left \vert \dfrac{1}{z-1}-\dfrac{z- \overline{z}}{2}+1 \right \vert $がとりうる値の
範囲を求めよ。
ただし、$\overline{z}$は$z$に共役な複素数とする。
$2025$年東京慈恵会医科大学医学部過去問題
この動画を見る
$\boxed{4}$
$z$は実数ではない複素数で、
$z+\dfrac{1}{z-1}$が正の実数となるものとする。
このとき、
$ \left \vert \dfrac{1}{z-1}-\dfrac{z- \overline{z}}{2}+1 \right \vert $がとりうる値の
範囲を求めよ。
ただし、$\overline{z}$は$z$に共役な複素数とする。
$2025$年東京慈恵会医科大学医学部過去問題
福田の数学〜立教大学2025理学部第1問(5)〜ド・モアブルの定理と複素数の計算

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(5)$i$を虚数単位とする。
実数$a,b$が等式
$\left(\dfrac{1}{\sqrt2}+\dfrac{1}{\sqrt2}i\right)^9+\left(\dfrac{1}{2}+\dfrac{\sqrt3}{2}i\right)^{11}=a+bi$
を満たすとき、$a=\boxed{ク},b=\boxed{ケ}$である。
$2025$年立教大学理学部過去問題
この動画を見る
$\boxed{1}$
(5)$i$を虚数単位とする。
実数$a,b$が等式
$\left(\dfrac{1}{\sqrt2}+\dfrac{1}{\sqrt2}i\right)^9+\left(\dfrac{1}{2}+\dfrac{\sqrt3}{2}i\right)^{11}=a+bi$
を満たすとき、$a=\boxed{ク},b=\boxed{ケ}$である。
$2025$年立教大学理学部過去問題
福田の数学〜早稲田大学理工学部2025第1問〜複素数平面上の点の軌跡と面積

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
複素数平面上で、複素数$z$が円$\vert z \vert=1$の上の点を動くとき、
$w=\left(\dfrac{1+\sqrt2}{2}\right)z+\left(\dfrac{1-\sqrt2}{2}\right)\dfrac{1}{z}$
を満たす点$w$の軌跡を$C$とする。
次の問いに答えよ。
(1)$C$はどのような図形か。複素数平面上に図示せよ。
(2)$C$と円$\left \vert z-\dfrac{2+\sqrt2}{2}\right \vert =\sqrt2$の共有点を求めよ。
(3)$C$で囲まれる領域と$\left \vert z-\dfrac{2+\sqrt2}{2}\right \vert \leqq \sqrt2$の
表す領域の共通部分の面積を求めよ。
$2025$年早稲田大学理工学部過去問題
この動画を見る
$\boxed{1}$
複素数平面上で、複素数$z$が円$\vert z \vert=1$の上の点を動くとき、
$w=\left(\dfrac{1+\sqrt2}{2}\right)z+\left(\dfrac{1-\sqrt2}{2}\right)\dfrac{1}{z}$
を満たす点$w$の軌跡を$C$とする。
次の問いに答えよ。
(1)$C$はどのような図形か。複素数平面上に図示せよ。
(2)$C$と円$\left \vert z-\dfrac{2+\sqrt2}{2}\right \vert =\sqrt2$の共有点を求めよ。
(3)$C$で囲まれる領域と$\left \vert z-\dfrac{2+\sqrt2}{2}\right \vert \leqq \sqrt2$の
表す領域の共通部分の面積を求めよ。
$2025$年早稲田大学理工学部過去問題
福田の数学〜慶應義塾大学理工学部2025第1問(1)〜複素数平面上の点の軌跡

単元:
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(1)複素数平面上で、方程式
$\vert z+i \vert = 2 \vert z-\sqrt3 \vert$
を満たす点$z$全体が表す図形は、
中心が$\boxed{ア}$,半径が$\boxed{イ}$である。
$2025$年慶應義塾大学理工学部過去問題
この動画を見る
$\boxed{1}$
(1)複素数平面上で、方程式
$\vert z+i \vert = 2 \vert z-\sqrt3 \vert$
を満たす点$z$全体が表す図形は、
中心が$\boxed{ア}$,半径が$\boxed{イ}$である。
$2025$年慶應義塾大学理工学部過去問題
福田の数学〜慶應義塾大学薬学部2025第1問(5)〜複素数平面上の正n角形の頂点に関する性質

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}$
(5)$n$は$n\geqq 3$を満たす自然数とする。
複素数$z$を$\cos\dfrac{2\pi}{n}+i\sin \dfrac{2\pi}{n}$とおき、
複素数平面において$z^k (0\leqq k \leqq n-1)$が表す点を
$P_k$とする。
ただし、$k$は整数、$i$は虚数単位とする。
(i)$n$個の点$P_0,P_1,P_2,\cdots P_{n-1}$を
頂点とする正$n$角形の面積を$S_n$とする。
$S_n$を$n$の式で表すと$S_n=\boxed{シ}$であり、
$\displaystyle \lim_{n\to\infty}S_n$を求めると$\boxed{ス}$である。
(ii)$\displaystyle \sum_{k=1}^{n-1} z^k$を求めると$\boxed{ス}$である。
(iii)$n=7$とする。
三角形$P_1P_2P_4$の重心を$A(\alpha)$、
三角形$P_3P_5P_6$の重心を$B(\beta)$とおく。
複素数$\alpha,\beta$を求めると、
$\alpha=\boxed{ソ},\beta=\boxed{タ}$である。
$2025$年慶應義塾大学薬学部過去問題
この動画を見る
$\boxed{1}$
(5)$n$は$n\geqq 3$を満たす自然数とする。
複素数$z$を$\cos\dfrac{2\pi}{n}+i\sin \dfrac{2\pi}{n}$とおき、
複素数平面において$z^k (0\leqq k \leqq n-1)$が表す点を
$P_k$とする。
ただし、$k$は整数、$i$は虚数単位とする。
(i)$n$個の点$P_0,P_1,P_2,\cdots P_{n-1}$を
頂点とする正$n$角形の面積を$S_n$とする。
$S_n$を$n$の式で表すと$S_n=\boxed{シ}$であり、
$\displaystyle \lim_{n\to\infty}S_n$を求めると$\boxed{ス}$である。
(ii)$\displaystyle \sum_{k=1}^{n-1} z^k$を求めると$\boxed{ス}$である。
(iii)$n=7$とする。
三角形$P_1P_2P_4$の重心を$A(\alpha)$、
三角形$P_3P_5P_6$の重心を$B(\beta)$とおく。
複素数$\alpha,\beta$を求めると、
$\alpha=\boxed{ソ},\beta=\boxed{タ}$である。
$2025$年慶應義塾大学薬学部過去問題
福田の数学〜北海道大学2025理系第4問〜複素数平面上の点の軌跡と2円が共有点をもつ条件

単元:
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{4}$
$a$を正の実数とする。
(1)$a$が$1$でないとき、複素数$z$についての方程式
$a \vert z-1 \vert = \vert (a-2)z +a \vert$
を考える。
この方程式を満たす$z$全体の集合を
複素数平面上に図示せよ。
$2025$年北海道大学理系過去問題
この動画を見る
$\boxed{4}$
$a$を正の実数とする。
(1)$a$が$1$でないとき、複素数$z$についての方程式
$a \vert z-1 \vert = \vert (a-2)z +a \vert$
を考える。
この方程式を満たす$z$全体の集合を
複素数平面上に図示せよ。
$2025$年北海道大学理系過去問題
【数C】【複素数平面】高次方程式3 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
方程式$z^6+z^3+1=0$の解を求めよ。ただし、解は 極形式のままでよい。
この動画を見る
方程式$z^6+z^3+1=0$の解を求めよ。ただし、解は 極形式のままでよい。
【数C】【複素数平面】高次方程式2 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
複素数$z$が、$z+\dfrac 1z=2\cos\theta$を満たすとき、次の問いに答えよ。
(1)$z$を$\theta$を用いて表せ。
(2)$n$が自然数のとき、等式、$z^n+\dfrac{1}{z^n}=2\cos n\theta$が成り立つことを示せ。
この動画を見る
複素数$z$が、$z+\dfrac 1z=2\cos\theta$を満たすとき、次の問いに答えよ。
(1)$z$を$\theta$を用いて表せ。
(2)$n$が自然数のとき、等式、$z^n+\dfrac{1}{z^n}=2\cos n\theta$が成り立つことを示せ。
【数C】【複素数平面】高次方程式1 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
$n$を自然数とし、$\displaystyle \alpha = \cos \frac{\pi}{n}+i\sin \frac{\pi}{n}$とする。次の問いに答えよ。
(1) $1+ \alpha +\alpha^2 + \cdots\cdots +\alpha^{2n-1}$の値を求めよ。
(2) $z^{2n}=1$の解は$1, \alpha, \alpha^2, \cdots\cdots, \alpha^{2n-1}$であることを示せ。
この動画を見る
$n$を自然数とし、$\displaystyle \alpha = \cos \frac{\pi}{n}+i\sin \frac{\pi}{n}$とする。次の問いに答えよ。
(1) $1+ \alpha +\alpha^2 + \cdots\cdots +\alpha^{2n-1}$の値を求めよ。
(2) $z^{2n}=1$の解は$1, \alpha, \alpha^2, \cdots\cdots, \alpha^{2n-1}$であることを示せ。
【数C】【複素数平面】ド・モアブルの定理2 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
$n$が、$ \displaystyle a_n=(\frac{\sqrt{3}+1}{2} +\frac{\sqrt{3}-1}{2})^{2n}$ が実数となる最小の自然数であるとき、$a_n$の値を求めよ。
この動画を見る
$n$が、$ \displaystyle a_n=(\frac{\sqrt{3}+1}{2} +\frac{\sqrt{3}-1}{2})^{2n}$ が実数となる最小の自然数であるとき、$a_n$の値を求めよ。
【数C】【複素数平面】ド・モアブルの定理1 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
$n$が自然数のとき、$\displaystyle (\frac{1+i}{\sqrt{2}})^n-(\frac{1-i}{\sqrt{2}})^n$ の値を求めよ。
この動画を見る
$n$が自然数のとき、$\displaystyle (\frac{1+i}{\sqrt{2}})^n-(\frac{1-i}{\sqrt{2}})^n$ の値を求めよ。
【数C】【複素数平面】複素数平面の対称移動 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
複素数平面上で$\mathrm{O}(0)、\mathrm{A}(-1+\sqrt{3}i)$とする。点$z$を直線$\mathrm{OA}$に関して対称移動した点を$w$とするとき、$w$を$z$を用いて表せ。
この動画を見る
複素数平面上で$\mathrm{O}(0)、\mathrm{A}(-1+\sqrt{3}i)$とする。点$z$を直線$\mathrm{OA}$に関して対称移動した点を$w$とするとき、$w$を$z$を用いて表せ。
【数C】【複素数平面】複素数平面の回転 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
座標平面上の点 $\mathrm{P}(x,y)$ を原点を中心として $\theta$ だけ回転した点を $\mathrm{Q}$ とするとき、 $\mathrm{Q}$ の座標を求めよ。
この動画を見る
座標平面上の点 $\mathrm{P}(x,y)$ を原点を中心として $\theta$ だけ回転した点を $\mathrm{Q}$ とするとき、 $\mathrm{Q}$ の座標を求めよ。
福田の数学〜東京大学2025理系第6問〜複素数平面上の点の軌跡と実部の最大最小

単元:
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{6}$
複素数平面上の点$\dfrac{1}{2}$を中心とする
半径$\dfrac{1}{2}$の円の周から原点を除いた曲線を
$C$とする。
(1)曲線$C$上の複素数$z$に対し、$\dfrac{1}{z}$の実部は
$1$であることを示せ。
(2)$\alpha,\beta$を曲線$C$上の相異なる複素数とするとき、
$\dfrac{1}{alpha^2}+\dfrac{1}{\beta^2}$がとりうる範囲を
複素数平面上に図示せよ。
(3)$\nu $を(2)で求めた範囲に属さない複素数とするとき、
$\dfrac{1}{\gamma}$の実部がとりうる値の
最大値と最小値を求めよ。
$2025$年東京大学理系過去問題
この動画を見る
$\boxed{6}$
複素数平面上の点$\dfrac{1}{2}$を中心とする
半径$\dfrac{1}{2}$の円の周から原点を除いた曲線を
$C$とする。
(1)曲線$C$上の複素数$z$に対し、$\dfrac{1}{z}$の実部は
$1$であることを示せ。
(2)$\alpha,\beta$を曲線$C$上の相異なる複素数とするとき、
$\dfrac{1}{alpha^2}+\dfrac{1}{\beta^2}$がとりうる範囲を
複素数平面上に図示せよ。
(3)$\nu $を(2)で求めた範囲に属さない複素数とするとき、
$\dfrac{1}{\gamma}$の実部がとりうる値の
最大値と最小値を求めよ。
$2025$年東京大学理系過去問題
【数C】【複素数平面】複素数の回転と三角形 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
複素数平面上の3点O(0),A(2-i),Bについて、次の条件を満たしているとき、
点Bを表す複素数を求めよ。
(1)△OABが正三角形となる。(2)△OABがBを直角の頂点とする二等辺三角形になる。
この動画を見る
複素数平面上の3点O(0),A(2-i),Bについて、次の条件を満たしているとき、
点Bを表す複素数を求めよ。
(1)△OABが正三角形となる。(2)△OABがBを直角の頂点とする二等辺三角形になる。
【数C】【複素数平面】 極形式から三角比の値を求める ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
$1+i$、$\sqrt{3}+i$を極形式で表すことにより、$cos \displaystyle \frac{5π}{12}$と$sin \displaystyle \frac{5π}{12}$の値を求めよ。
この動画を見る
$1+i$、$\sqrt{3}+i$を極形式で表すことにより、$cos \displaystyle \frac{5π}{12}$と$sin \displaystyle \frac{5π}{12}$の値を求めよ。
【数C】【複素数平面】 極形式で表す ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
次の複素数を 極形式で表せ。ただし、偏角θは0≦θ<2πとする。
(1)$\displaystyle \frac{4+3i}{1+7i}$
(2)$\sqrt{3}+\displaystyle \frac{1-i}{1+i}$
(3)$ー4(\cos \displaystyle \frac{π}{6} + i\sin \displaystyle \frac{π}{6})$
(4)$cos\displaystyle \frac{2π}{3}ーisin \displaystyle \frac{2π}{3}$
(5)$2(sin \displaystyle \frac{π}{3} + i cos \displaystyle \frac{π}{3})$
この動画を見る
次の複素数を 極形式で表せ。ただし、偏角θは0≦θ<2πとする。
(1)$\displaystyle \frac{4+3i}{1+7i}$
(2)$\sqrt{3}+\displaystyle \frac{1-i}{1+i}$
(3)$ー4(\cos \displaystyle \frac{π}{6} + i\sin \displaystyle \frac{π}{6})$
(4)$cos\displaystyle \frac{2π}{3}ーisin \displaystyle \frac{2π}{3}$
(5)$2(sin \displaystyle \frac{π}{3} + i cos \displaystyle \frac{π}{3})$
【数C】【複素数平面】複素数の大きさ・対称式の利用 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\alpha,\beta$は複素数とする。$|\alpha|=|\beta|=1,\alpha+\beta+1=0$のとき、$\alpha^2+\beta^2$の値を求めよ。
この動画を見る
$\alpha,\beta$は複素数とする。$|\alpha|=|\beta|=1,\alpha+\beta+1=0$のとき、$\alpha^2+\beta^2$の値を求めよ。
【数C】【複素数平面】複素数の大きさと式変形 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
$|z|=3$かつ$|z-2|=4$を満たす複素数$z$について、次の値を求めよ。
(1)$z\bar{z}$ (2) $z+\bar{z}$
この動画を見る
$|z|=3$かつ$|z-2|=4$を満たす複素数$z$について、次の値を求めよ。
(1)$z\bar{z}$ (2) $z+\bar{z}$
【数C】【複素数平面】複素数の大きさ ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
$z=2-i$のとき、$|z+\displaystyle \frac{1}{z}|^2$の値を求めよ。
この動画を見る
$z=2-i$のとき、$|z+\displaystyle \frac{1}{z}|^2$の値を求めよ。
【数C】【複素数平面】実数であることの証明 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
α、βを複素数とし、α≠0とするとき、次のことを証明せよ。
αβが実数 ⇔ β=kαとなる実数kがある
この動画を見る
α、βを複素数とし、α≠0とするとき、次のことを証明せよ。
αβが実数 ⇔ β=kαとなる実数kがある
【数C】【複素数平面】基本公式と式変形 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#複素数平面
指導講師:
理数個別チャンネル
問題文全文(内容文):
複素数$z$が$3z+\bar{z}=2-2i$を満たすとき、以下の問いに答えよ。
(1)$3\bar{z}+z$を求めよ。
(2)$z$を求めよ。
この動画を見る
複素数$z$が$3z+\bar{z}=2-2i$を満たすとき、以下の問いに答えよ。
(1)$3\bar{z}+z$を求めよ。
(2)$z$を求めよ。
福田のおもしろ数学342〜複素数に関する三角不等式と等号成立条件

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
複素数$z_1,z_2$に対して、$|z_1+z_2|\leqq |z_1|+|z_2|が成り立つことを証明してください。$
この動画を見る
複素数$z_1,z_2$に対して、$|z_1+z_2|\leqq |z_1|+|z_2|が成り立つことを証明してください。$
福田のおもしろ数学304〜複素数の実部の最大値

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
複素数 $z$ が $|z|=4$ を満たすとき $\displaystyle (75+117i) z + \frac{96 + 144i}{z}$ の実部の最大値を求めよ。
この動画を見る
複素数 $z$ が $|z|=4$ を満たすとき $\displaystyle (75+117i) z + \frac{96 + 144i}{z}$ の実部の最大値を求めよ。
福田の数学〜早稲田大学2024教育学部第2問〜複素数の集合に関する論証

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$3$つの複素数 $z_1, z_2, z_3$に関する条件$P$を次のように定める。
P: 「$z_1, z_2, z_3$はどれも0ではなく、互いに異なり、かつ$ \{{z_1}^n | n は整数\} = \{{z_2}^n | nは整数\} = \{{z_3}^n |n は整数\}$
である。」
次の問いに答えよ。
(1) $3$つの複素数 $z_1,z_2,z_3$が条件$P$を満たしているとする。このとき$ |z_1| = 1$ であることを示せ。また集合$ \{{z_1}^n | n は整数\}$の要素の個数は有限であることを示せ。
(2) 条件$P$を満たす3つの複素数 $z_1,z_2,z_3$のうち、集合$ \{{z_1}^n | n は整数\}$の要素の個数が最小となるものを考える。このとき集合$ \{{z_1}^n | n は整数\}$を求めよ。
この動画を見る
$3$つの複素数 $z_1, z_2, z_3$に関する条件$P$を次のように定める。
P: 「$z_1, z_2, z_3$はどれも0ではなく、互いに異なり、かつ$ \{{z_1}^n | n は整数\} = \{{z_2}^n | nは整数\} = \{{z_3}^n |n は整数\}$
である。」
次の問いに答えよ。
(1) $3$つの複素数 $z_1,z_2,z_3$が条件$P$を満たしているとする。このとき$ |z_1| = 1$ であることを示せ。また集合$ \{{z_1}^n | n は整数\}$の要素の個数は有限であることを示せ。
(2) 条件$P$を満たす3つの複素数 $z_1,z_2,z_3$のうち、集合$ \{{z_1}^n | n は整数\}$の要素の個数が最小となるものを考える。このとき集合$ \{{z_1}^n | n は整数\}$を求めよ。
福田の数学〜東京理科大学2024創域理工学部第1問(1)〜複素数と三角形の外接円

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#東京理科大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\boxed{1}(1)a$を正の実数とする。$x$についての方程式
$(x^2+ax+2)(x^2-ax-1)=0・・・①$
が異なる2つの実数解と異なる2つの虚数解をもつのは
$\boxed{ア} \lt a \lt \boxed{イ}\sqrt{\boxed{ウ}}・・・②$
のときである。
以下では、$a$は不等式$②$を満たす最大の整数とし、$i$は虚数単位とする。このとき、複素数平面上において、方程式$①$の異なる2つの虚数解と$3+i$を頂点とする三角形の面積は$\boxed{エ}$であり、この三角形の外接円を複素数zの方程式で表すと
$|x-\boxed{オ}|=\sqrt{\boxed{カ}}$
である。
この動画を見る
$\boxed{1}(1)a$を正の実数とする。$x$についての方程式
$(x^2+ax+2)(x^2-ax-1)=0・・・①$
が異なる2つの実数解と異なる2つの虚数解をもつのは
$\boxed{ア} \lt a \lt \boxed{イ}\sqrt{\boxed{ウ}}・・・②$
のときである。
以下では、$a$は不等式$②$を満たす最大の整数とし、$i$は虚数単位とする。このとき、複素数平面上において、方程式$①$の異なる2つの虚数解と$3+i$を頂点とする三角形の面積は$\boxed{エ}$であり、この三角形の外接円を複素数zの方程式で表すと
$|x-\boxed{オ}|=\sqrt{\boxed{カ}}$
である。
福田の数学〜上智大学2024理工学部第1問(1)〜複素数の絶対値と三角関数の計算

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
複素数 $z=(-3+2 \cos\theta )+(4+2 \sin \theta)i$ の絶対値は、$\theta = \theta_1$ のとき最小値 $\fbox{ア}$ をとる。このとき、 $\sin{\theta_1} = \frac{\fbox{イ}}{\fbox{ウ}}$ である。
この動画を見る
複素数 $z=(-3+2 \cos\theta )+(4+2 \sin \theta)i$ の絶対値は、$\theta = \theta_1$ のとき最小値 $\fbox{ア}$ をとる。このとき、 $\sin{\theta_1} = \frac{\fbox{イ}}{\fbox{ウ}}$ である。
福田の数学〜上智大学2024TEAP利用型理系第1問(2)〜複素数の極形式とド・モアブルの定理

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$
\begin{eqnarray}
\fcolorbox{#000}{ #fff }{1}(2)\
複素数(\sqrt{2}+\sqrt{6}i)^{2024}を極形式で表したときの絶対値をr、偏角をθとする。ただし、0\leqqθ<2π\
このとき、\dfrac{log_2r}{2024}=\fcolorbox{#000}{ #fff }{$あ \ \ \ $}、θ=\fcolorbox{#000}{ #fff }{$い \ \ \ $}πである。
\end{eqnarray}
$
この動画を見る
$
\begin{eqnarray}
\fcolorbox{#000}{ #fff }{1}(2)\
複素数(\sqrt{2}+\sqrt{6}i)^{2024}を極形式で表したときの絶対値をr、偏角をθとする。ただし、0\leqqθ<2π\
このとき、\dfrac{log_2r}{2024}=\fcolorbox{#000}{ #fff }{$あ \ \ \ $}、θ=\fcolorbox{#000}{ #fff }{$い \ \ \ $}πである。
\end{eqnarray}
$
