 数C
数C
 数C
数C
福田の数学〜慶應義塾大学2022年商学部第2問〜空間ベクトルと平面の方程式

単元:
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$点Oを原点とするxyz座標空間に、2点A(2,3,1),\ B(-2,1,3)をとる。
また、x座標が正の点Cを、$\overrightarrow{ OC }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$に垂直で、
$|\overrightarrow{ OC }|=8\sqrt3$となるように定める。
(1)$\triangle OAB$の面積は$\boxed{\ \ ア\ \ }\sqrt{\boxed{\ \ イ\ \ }}$である。
(2)点Cの座標は$(\boxed{\ \ ウ\ \ },\ \boxed{\ \ エオ\ \ },\ \boxed{\ \ カ\ \ })$である。
(3)四面体OABCの体積は$\boxed{\ \ キク\ \ }$である。
(4)平面ABCの方程式は$\ x+\boxed{\ \ ケ\ \ }\ y+\boxed{\ \ コ\ \ }\ z-\ \boxed{\ \ サシ\ \ }=0$である。
(5)原点Oから平面ABCに垂線OHを下ろしたとき、点Hの座標は
$(\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セソ\ \ }},\frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }},\frac{\boxed{\ \ ツテ\ \ }}{\boxed{\ \ トナ\ \ }})$
である。
2022慶應義塾大学商学部過去問
この動画を見る
${\Large\boxed{2}}$点Oを原点とするxyz座標空間に、2点A(2,3,1),\ B(-2,1,3)をとる。
また、x座標が正の点Cを、$\overrightarrow{ OC }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$に垂直で、
$|\overrightarrow{ OC }|=8\sqrt3$となるように定める。
(1)$\triangle OAB$の面積は$\boxed{\ \ ア\ \ }\sqrt{\boxed{\ \ イ\ \ }}$である。
(2)点Cの座標は$(\boxed{\ \ ウ\ \ },\ \boxed{\ \ エオ\ \ },\ \boxed{\ \ カ\ \ })$である。
(3)四面体OABCの体積は$\boxed{\ \ キク\ \ }$である。
(4)平面ABCの方程式は$\ x+\boxed{\ \ ケ\ \ }\ y+\boxed{\ \ コ\ \ }\ z-\ \boxed{\ \ サシ\ \ }=0$である。
(5)原点Oから平面ABCに垂線OHを下ろしたとき、点Hの座標は
$(\frac{\boxed{\ \ ス\ \ }}{\boxed{\ \ セソ\ \ }},\frac{\boxed{\ \ タ\ \ }}{\boxed{\ \ チ\ \ }},\frac{\boxed{\ \ ツテ\ \ }}{\boxed{\ \ トナ\ \ }})$
である。
2022慶應義塾大学商学部過去問
【数B】ベクトル:ベクトルの基本⑦内積を求めたいときの絶対値の2乗

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
$a=\sqrt3,b=5,a-b=\sqrt5$のとき、内積a・bを求めよ.
この動画を見る
$a=\sqrt3,b=5,a-b=\sqrt5$のとき、内積a・bを求めよ.
【数C】ベクトルの基本⑦内積を求めたいときの絶対値の2乗

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#チャート式#青チャートⅡ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
a=√3,b=5,a-b=√5のとき、内積a・bを求めよ
この動画を見る
a=√3,b=5,a-b=√5のとき、内積a・bを求めよ
福田の数学〜慶應義塾大学2022年経済学部第4問〜空間ベクトルと四面体の体積

単元:
#大学入試過去問(数学)#空間ベクトル#空間ベクトル#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{4}}$tを実数とする。また、Oを原点とする座標空間内に
3点$A(4,2,5),\ B(-1,1,1),\ C(2-t,4-3t,6+2t)$をとる。
(1)$\triangle OAB$の面積を求めよ。
(2)4点O,A,B,Cが同一平面上にあるとき、Cの座標を求めよ。
(3)点Cがxy平面上にあるとき、四面体OABCの体積Vを求めよ。
(4)四面体OABCの体積が(3)で求めたVの3倍となるようなtの値を
すべて求めよ。
2022慶應義塾大学経済学部過去問
この動画を見る
${\Large\boxed{4}}$tを実数とする。また、Oを原点とする座標空間内に
3点$A(4,2,5),\ B(-1,1,1),\ C(2-t,4-3t,6+2t)$をとる。
(1)$\triangle OAB$の面積を求めよ。
(2)4点O,A,B,Cが同一平面上にあるとき、Cの座標を求めよ。
(3)点Cがxy平面上にあるとき、四面体OABCの体積Vを求めよ。
(4)四面体OABCの体積が(3)で求めたVの3倍となるようなtの値を
すべて求めよ。
2022慶應義塾大学経済学部過去問
大学入試問題#235 自治医科大学(2014) 複素数

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#数C#自治医科大学
指導講師:
ますただ
問題文全文(内容文):
$\omega=\displaystyle \frac{-1+\sqrt{ 3 }i}{2}$のとき
$\omega^{20}+\omega^{19}+\omega^8+\omega^6+\omega^4+\omega^3$の値を求めよ。
出典:2012年自治医科大学 入試問題
この動画を見る
$\omega=\displaystyle \frac{-1+\sqrt{ 3 }i}{2}$のとき
$\omega^{20}+\omega^{19}+\omega^8+\omega^6+\omega^4+\omega^3$の値を求めよ。
出典:2012年自治医科大学 入試問題
【数B】ベクトル:ベクトルの基本⑥内積の基本計算2 成分を用いて計算する

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
内積の基本計算(直角三角形ABCにおける内積計算)に関して解説していきます.
この動画を見る
内積の基本計算(直角三角形ABCにおける内積計算)に関して解説していきます.
【数C】ベクトルの基本⑥内積の基本計算2 成分を用いて計算する

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#チャート式#青チャートⅡ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
内積の基本計算(直角三角形ABCにおける内積計算)
この動画を見る
内積の基本計算(直角三角形ABCにおける内積計算)
福田の入試問題解説〜慶應義塾大学2022年医学部第3問〜内サイクロイドと極方程式

単元:
#数Ⅱ#大学入試過去問(数学)#平面上の曲線#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
(1)座標平面上の点P(x,y)を、点T(s,t)を中心として半時計周りに角$\alpha$だけ
回転させるときに、点Pが点P'(x',y')に移るとする。x'とy'を$x,y,s,t,\alpha$
の式で表すと$x'=\boxed{\ \ ア\ \ }, y'=\boxed{\ \ イ\ \ }$となる。
(2)aを正の実数とする。原点O(0,0)とする半径aの円Cに、半径$\frac{a}{2}$で原点O
を通る円Kを点A(a,0)において内接させる。この円Kを円Cに沿って
滑らないように転がす。ただし、KとCの接点がC上を半時計回りに動くようにする。
そして、接点の座標がはじめて$(a\cos\beta,a\sin\beta)(0 \leqq \beta \leqq 2\pi)$となるようにする。
円Kに対するこの操作は次の2段階の操作を続けて行うことと同等である。
$(\textrm{i})$点B$(\frac{a}{2},0)$を中心として、円Kを$\boxed{\ \ ウ\ \ }$に角$\boxed{\ \ エ\ \ }$だけ回転させる。
$(\textrm{ii})$原点Oを中心として、円Kを$\boxed{\ \ オ\ \ }$に角$\boxed{\ \ カ\ \ }$だけ回転させる。
$\boxed{\ \ ウ\ \ },\boxed{\ \ エ\ \ },\boxed{\ \ オ\ \ },\boxed{\ \ カ\ \ }$の選択肢
時計回り,反時計回り,$\beta,2\beta,\frac{1}{2}\beta$
(3)円Kが点Aにおいて円Cに内接しているとき、Kの内部に固定された点Q(b,0)
(ただし、$0 \lt b \lt a$)をとる。円Kを、Cとの接点がC上を一周するまで(2)に述べた
やり方でCに沿って転がすとき、点Qが動いてできる曲線を$S_1$とする。$S_1$上の
点の座標を(x,y)として、$S_1$の方程式をx,yを用いて書くと$\boxed{\ \ キ\ \ }$となる。
(4)円Kが点Aにおいて円Cに内接しているとき、円Cに固定された点R(0,a)をとる。
今度は円Kを固定して、円Cの方をKに接した状態で滑らないようにKに沿って転がす。
2つの円の接点が円Kを$\boxed{\ \ ク\ \ }$回転したとき、点Rははじめてもとの位置
(0,a)に戻る。Rが描く曲線を$S_2$とする。原点Oを極とし、x軸の正の部分を
始線とする極座標#$(r,\theta)$による$S_2$の極方程式は$r=\boxed{\ \ ケ\ \ }$である。
ただし$r,\theta$はそれぞれ$S_2$上の点の原点からの距離、および偏角である。
2022慶應義塾大学医学部過去問
この動画を見る
(1)座標平面上の点P(x,y)を、点T(s,t)を中心として半時計周りに角$\alpha$だけ
回転させるときに、点Pが点P'(x',y')に移るとする。x'とy'を$x,y,s,t,\alpha$
の式で表すと$x'=\boxed{\ \ ア\ \ }, y'=\boxed{\ \ イ\ \ }$となる。
(2)aを正の実数とする。原点O(0,0)とする半径aの円Cに、半径$\frac{a}{2}$で原点O
を通る円Kを点A(a,0)において内接させる。この円Kを円Cに沿って
滑らないように転がす。ただし、KとCの接点がC上を半時計回りに動くようにする。
そして、接点の座標がはじめて$(a\cos\beta,a\sin\beta)(0 \leqq \beta \leqq 2\pi)$となるようにする。
円Kに対するこの操作は次の2段階の操作を続けて行うことと同等である。
$(\textrm{i})$点B$(\frac{a}{2},0)$を中心として、円Kを$\boxed{\ \ ウ\ \ }$に角$\boxed{\ \ エ\ \ }$だけ回転させる。
$(\textrm{ii})$原点Oを中心として、円Kを$\boxed{\ \ オ\ \ }$に角$\boxed{\ \ カ\ \ }$だけ回転させる。
$\boxed{\ \ ウ\ \ },\boxed{\ \ エ\ \ },\boxed{\ \ オ\ \ },\boxed{\ \ カ\ \ }$の選択肢
時計回り,反時計回り,$\beta,2\beta,\frac{1}{2}\beta$
(3)円Kが点Aにおいて円Cに内接しているとき、Kの内部に固定された点Q(b,0)
(ただし、$0 \lt b \lt a$)をとる。円Kを、Cとの接点がC上を一周するまで(2)に述べた
やり方でCに沿って転がすとき、点Qが動いてできる曲線を$S_1$とする。$S_1$上の
点の座標を(x,y)として、$S_1$の方程式をx,yを用いて書くと$\boxed{\ \ キ\ \ }$となる。
(4)円Kが点Aにおいて円Cに内接しているとき、円Cに固定された点R(0,a)をとる。
今度は円Kを固定して、円Cの方をKに接した状態で滑らないようにKに沿って転がす。
2つの円の接点が円Kを$\boxed{\ \ ク\ \ }$回転したとき、点Rははじめてもとの位置
(0,a)に戻る。Rが描く曲線を$S_2$とする。原点Oを極とし、x軸の正の部分を
始線とする極座標#$(r,\theta)$による$S_2$の極方程式は$r=\boxed{\ \ ケ\ \ }$である。
ただし$r,\theta$はそれぞれ$S_2$上の点の原点からの距離、および偏角である。
2022慶應義塾大学医学部過去問
【数B】ベクトル:ベクトルの基本⑤内積の基本計算1 始点を揃えて考える

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
内積の基本計算(直角三角形ABCにおける内積計算)に関して解説していきます.
この動画を見る
内積の基本計算(直角三角形ABCにおける内積計算)に関して解説していきます.
【数C】ベクトルの基本⑤内積の基本計算1 始点を揃えて考える

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#チャート式#青チャートⅡ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
内積の基本計算(直角三角形ABCにおける内積計算)
この動画を見る
内積の基本計算(直角三角形ABCにおける内積計算)
福田の入試問題解説〜慶應義塾大学2022年理工学部第1問(1)〜空間のベクトル方程式

単元:
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
(1)$\overrightarrow{ a }=(\sqrt3,0,1)$とする。
空間ベクトル$\overrightarrow{ b }, \overrightarrow{ c }$はともに大きさが1であり、
$\overrightarrow{ a }∟\overrightarrow{ b }, \overrightarrow{ b }∟\overrightarrow{ c }, \overrightarrow{ c }∟\overrightarrow{ a }$とする。
$(\textrm{i})p,q,r$を実数とし、$\overrightarrow{ x }=p\overrightarrow{ a }+q\overrightarrow{ b }+r\overrightarrow{ c }$とするとき、
内積$\overrightarrow{ x }・\overrightarrow{ a }$と$\overrightarrow{ x }$の大きさ$|\overrightarrow{ x }|$をp,q,rを用いて表すと、
$\overrightarrow{ x }・\overrightarrow{ a }=\boxed{\ \ ア\ \ },|\ \overrightarrow{ x } \ |=\boxed{\ \ イ\ \ }$である。
$(\textrm{ii})(5,0,z)=s\overrightarrow{ a }+(\cos\theta)\overrightarrow{ b }+(\sin\theta)\overrightarrow{ c }$を満たす実数$s,\theta$が存在するような
実数zは2個あるが、それらを全て求めると$z=\boxed{\ \ ウ\ \ }$である。
2022慶應義塾大学理工学部過去問
この動画を見る
(1)$\overrightarrow{ a }=(\sqrt3,0,1)$とする。
空間ベクトル$\overrightarrow{ b }, \overrightarrow{ c }$はともに大きさが1であり、
$\overrightarrow{ a }∟\overrightarrow{ b }, \overrightarrow{ b }∟\overrightarrow{ c }, \overrightarrow{ c }∟\overrightarrow{ a }$とする。
$(\textrm{i})p,q,r$を実数とし、$\overrightarrow{ x }=p\overrightarrow{ a }+q\overrightarrow{ b }+r\overrightarrow{ c }$とするとき、
内積$\overrightarrow{ x }・\overrightarrow{ a }$と$\overrightarrow{ x }$の大きさ$|\overrightarrow{ x }|$をp,q,rを用いて表すと、
$\overrightarrow{ x }・\overrightarrow{ a }=\boxed{\ \ ア\ \ },|\ \overrightarrow{ x } \ |=\boxed{\ \ イ\ \ }$である。
$(\textrm{ii})(5,0,z)=s\overrightarrow{ a }+(\cos\theta)\overrightarrow{ b }+(\sin\theta)\overrightarrow{ c }$を満たす実数$s,\theta$が存在するような
実数zは2個あるが、それらを全て求めると$z=\boxed{\ \ ウ\ \ }$である。
2022慶應義塾大学理工学部過去問
【数B】ベクトル:ベクトルの基本④内積の基本的な考え方

【数C】ベクトルの基本④内積の基本的な考え方

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#チャート式#青チャートⅡ・B#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
内積の基本的な考え方
直角三角形ABCにおいて内積AB・AC、BA・BC、CA・CB、AB・BCを求めよ。
この動画を見る
内積の基本的な考え方
直角三角形ABCにおいて内積AB・AC、BA・BC、CA・CB、AB・BCを求めよ。
福田の数学〜浜松医科大学2022年医学部第1問〜媒介変数表示で表された曲線の長さと接線の傾きと体積

単元:
#大学入試過去問(数学)#平面上の曲線#学校別大学入試過去問解説(数学)#媒介変数表示と極座標#浜松医科大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
媒介変数$t\ (t \geqq 0)$に対して、$x=\frac{4}{\sqrt3}t^{\frac{3}{2}},y=2t$で表される曲線C上に
点$P_1$と$P_2$がある。原点から点$P_1$までの曲線の長さは$\frac{28}{9}$であり、点$P_2$における曲線C
の接線の傾きは$\frac{1}{3}$である。以下の問いに答えよ。
(1)点$P_1$の座標$(x_1,y_1)$を求めよ。
(2)点$P_2$の座標$(x_2,y_2)$を求めよ。
(3)曲線Cとy軸、および2直線$y=y_1,y=y_2$で囲まれた図形を、y軸の周りに1回転
してできる回転体を考える。この回転体の体積を求めよ。
2022浜松医科大学医学部過去問
この動画を見る
媒介変数$t\ (t \geqq 0)$に対して、$x=\frac{4}{\sqrt3}t^{\frac{3}{2}},y=2t$で表される曲線C上に
点$P_1$と$P_2$がある。原点から点$P_1$までの曲線の長さは$\frac{28}{9}$であり、点$P_2$における曲線C
の接線の傾きは$\frac{1}{3}$である。以下の問いに答えよ。
(1)点$P_1$の座標$(x_1,y_1)$を求めよ。
(2)点$P_2$の座標$(x_2,y_2)$を求めよ。
(3)曲線Cとy軸、および2直線$y=y_1,y=y_2$で囲まれた図形を、y軸の周りに1回転
してできる回転体を考える。この回転体の体積を求めよ。
2022浜松医科大学医学部過去問
福田の数学〜筑波大学2022年理系第6問〜複素数平面上の点の軌跡と最小値

単元:
#数Ⅱ#大学入試過去問(数学)#複素数平面#図形と方程式#軌跡と領域#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数C
指導講師:
福田次郎
問題文全文(内容文):
$i$は虚数単位とする。次の条件$(\textrm{I}),(\textrm{II})$のどちらも満たす複素数z全体の集合を
Sとする。
$(\textrm{I})z$の虚部は正である。
$(\textrm{II})$複素数平面上の点$A(1),B(1-iz),C(z^2)$は一直線上にある。
このとき、以下の問いに答えよ。
(1)1でない複素数$\alpha$について、$\alpha$の虚部が正であることは、$\frac{1}{\alpha-1}$の虚部が
負であるための必要十分条件であることを示せ。
(2)集合Sを複素数平面上に図示せよ。
(3)$w=\frac{1}{z-1}$とする。zがSを動くとき、$|w+\frac{i}{\sqrt2}|$の最小値を求めよ。
2022筑波大学理系過去問
この動画を見る
$i$は虚数単位とする。次の条件$(\textrm{I}),(\textrm{II})$のどちらも満たす複素数z全体の集合を
Sとする。
$(\textrm{I})z$の虚部は正である。
$(\textrm{II})$複素数平面上の点$A(1),B(1-iz),C(z^2)$は一直線上にある。
このとき、以下の問いに答えよ。
(1)1でない複素数$\alpha$について、$\alpha$の虚部が正であることは、$\frac{1}{\alpha-1}$の虚部が
負であるための必要十分条件であることを示せ。
(2)集合Sを複素数平面上に図示せよ。
(3)$w=\frac{1}{z-1}$とする。zがSを動くとき、$|w+\frac{i}{\sqrt2}|$の最小値を求めよ。
2022筑波大学理系過去問
基本問題
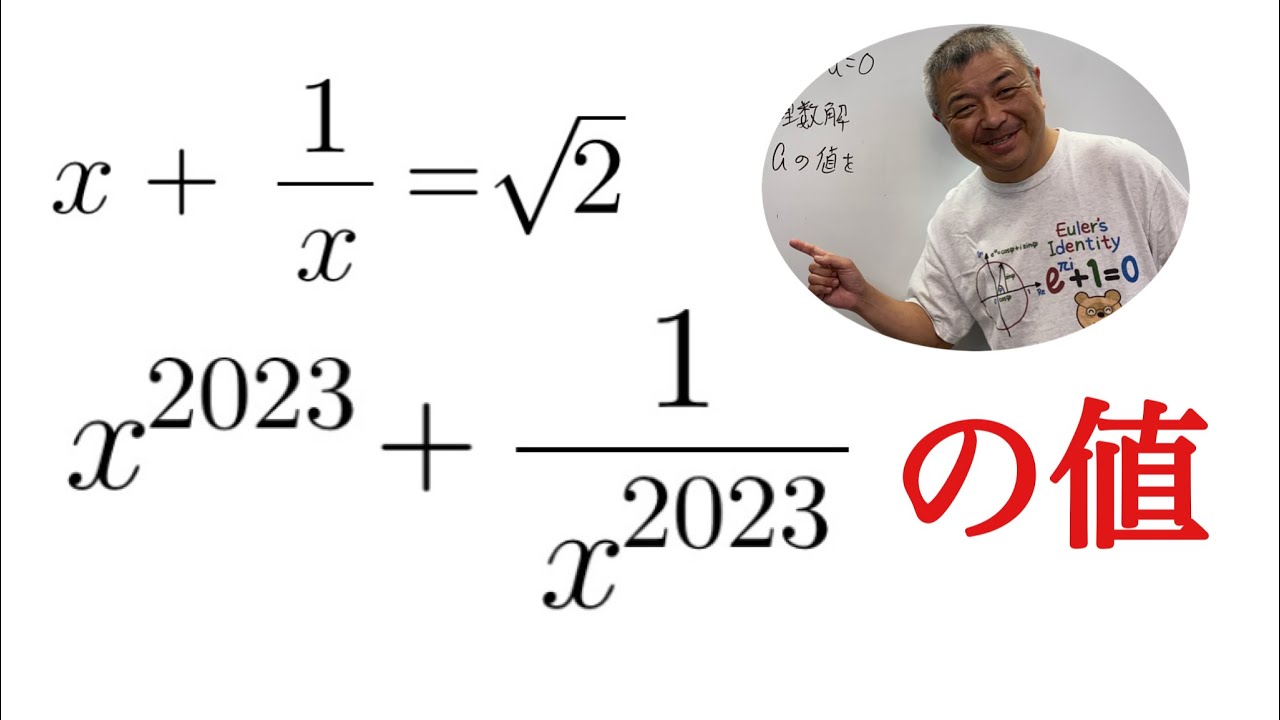
単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ x+\dfrac{1}{x}-\sqrt2$のとき,
x^{2023}+\dfrac{1}{x^{2023}}$の値を求めよ.
この動画を見る
$ x+\dfrac{1}{x}-\sqrt2$のとき,
x^{2023}+\dfrac{1}{x^{2023}}$の値を求めよ.
藤田医科大学 式の最小値
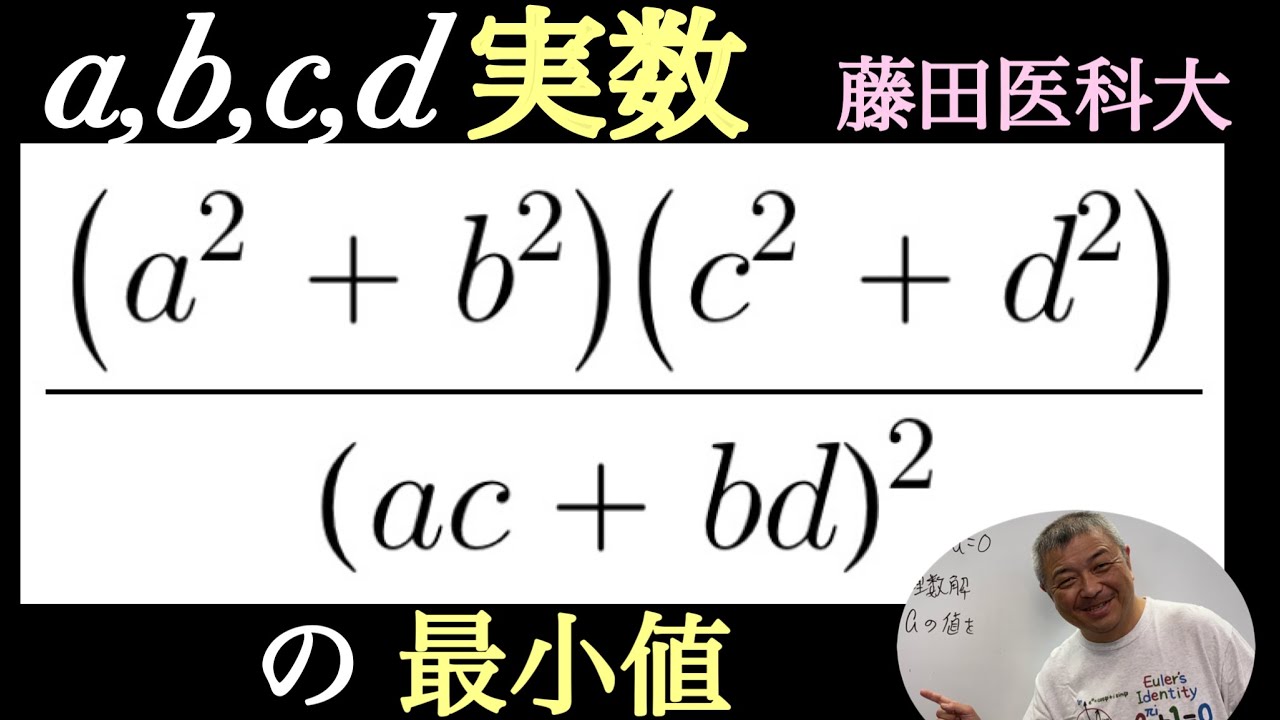
単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#複素数#複素数平面#数学(高校生)#藤田医科大学#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a,b,c,dは実数である.
$\dfrac{(a^2+b^2)(c^2+d^2)}{(ac+bd)^2}$の最小値を求めよ.
この動画を見る
$ a,b,c,dは実数である.
$\dfrac{(a^2+b^2)(c^2+d^2)}{(ac+bd)^2}$の最小値を求めよ.
【数C】ベクトル平面ベクトル:ベクトルの基本③ 絶対値の最大最小は2乗で考えよ

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
tは実数とする。
aベクトル=(2,1), bベクトル=(3,4)に対して
|a+tb|はt=□のとき最小値□を取る
この動画を見る
tは実数とする。
aベクトル=(2,1), bベクトル=(3,4)に対して
|a+tb|はt=□のとき最小値□を取る
【数B】平面ベクトル:ベクトルの基本③ 絶対値の最大最小は2乗で考えよ

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
tは実数とする。
aベクトル=(2,1), bベクトル=(3,4)に対して
$\vert a+tb\vert $は$t=□$のとき最小値$□$を取る
この動画を見る
tは実数とする。
aベクトル=(2,1), bベクトル=(3,4)に対して
$\vert a+tb\vert $は$t=□$のとき最小値$□$を取る
福田の数学〜筑波大学2022年理系第3問〜平行四辺形の中の平行四辺形

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数C
指導講師:
福田次郎
問題文全文(内容文):
$0 \lt t \lt 1$とする。平行四辺形ABCDにおいて、線分AB,BC,CD,DAを
$t:1-t$に内分する点をそれぞれ$A_1,B_1,C_1,D_1$とする。さらに$A_2,B_2,C_2,D_2$および$A_3,B_3,C_3,D_3$を次の条件を満たすように定める。
$(\ 条件\ )k=1,2$について、点$A_{k+1},B_{k+1},C_{k+1},D_{k+1}$はそれぞれ線分$A_kB_k$,
$B_kC_k,C_kD_k,D_kA_k$を$t:1-t$に内分する。
$\overrightarrow{ AB }=\overrightarrow{ a }, \overrightarrow{ AD }=\overrightarrow{ b }$とするとき、以下の問いに答えよ。
(1)$\overrightarrow{ A_1B_1 }=p\overrightarrow{ a }+q\overrightarrow{ b }, \overrightarrow{ A_1D_1 }=x\ \overrightarrow{ a }+y\ \overrightarrow{ b }$ を満たす実数p,q,x,yを
tを用いて表せ。
(2)四角形$A_1B_1C_1D_1$は平行四辺形であることを示せ。
(3)$\overrightarrow{ AD }$と$\overrightarrow{ A_3B_3 }$が平行となるようなtの値を求めよ。
2022筑波大学理系過去問
この動画を見る
$0 \lt t \lt 1$とする。平行四辺形ABCDにおいて、線分AB,BC,CD,DAを
$t:1-t$に内分する点をそれぞれ$A_1,B_1,C_1,D_1$とする。さらに$A_2,B_2,C_2,D_2$および$A_3,B_3,C_3,D_3$を次の条件を満たすように定める。
$(\ 条件\ )k=1,2$について、点$A_{k+1},B_{k+1},C_{k+1},D_{k+1}$はそれぞれ線分$A_kB_k$,
$B_kC_k,C_kD_k,D_kA_k$を$t:1-t$に内分する。
$\overrightarrow{ AB }=\overrightarrow{ a }, \overrightarrow{ AD }=\overrightarrow{ b }$とするとき、以下の問いに答えよ。
(1)$\overrightarrow{ A_1B_1 }=p\overrightarrow{ a }+q\overrightarrow{ b }, \overrightarrow{ A_1D_1 }=x\ \overrightarrow{ a }+y\ \overrightarrow{ b }$ を満たす実数p,q,x,yを
tを用いて表せ。
(2)四角形$A_1B_1C_1D_1$は平行四辺形であることを示せ。
(3)$\overrightarrow{ AD }$と$\overrightarrow{ A_3B_3 }$が平行となるようなtの値を求めよ。
2022筑波大学理系過去問
数学を数楽にの川端さん三乗
福田の数学〜東京医科歯科大学2022年理系第1問〜2つのベクトルで生成される異なる点の個数

単元:
#数A#数Ⅱ#大学入試過去問(数学)#場合の数と確率#平面上のベクトル#場合の数#三角関数#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#数学(高校生)#数C#東京医科歯科大学
指導講師:
福田次郎
問題文全文(内容文):
nを自然数とする。整数i,jに対し、xy平面上の点$P_{i,j}$の座標を
$(\cos\frac{2\pi}{n}i+\cos\frac{2\pi}{n}j, \sin\frac{2\pi}{n}i+\sin\frac{2\pi}{n}j)$
で与える。さらに、i,jを動かしたとき、$P_{i,j}$の取り得る異なる座標の
個数を$S_n$とする。このとき、以下の問いに答えよ。
(1)$n=3$のとき、$\triangle P_{0,0}P_{0,1}P_{0,2}$および$\triangle P_{1,0}P_{1,1}P_{1,2}$を同一平面上
に図示せよ。
(2)$S_4$を求めよ。
(3)平面上の異なる2点A,Bに対して、$AQ=BQ=1$であるような
同一平面上の点Qはいくつあるか。AB=dの値で場合分けして答えよ。
(4)$S_n$をnを用いて表せ。
2022東京医科歯科大学理系過去問
この動画を見る
nを自然数とする。整数i,jに対し、xy平面上の点$P_{i,j}$の座標を
$(\cos\frac{2\pi}{n}i+\cos\frac{2\pi}{n}j, \sin\frac{2\pi}{n}i+\sin\frac{2\pi}{n}j)$
で与える。さらに、i,jを動かしたとき、$P_{i,j}$の取り得る異なる座標の
個数を$S_n$とする。このとき、以下の問いに答えよ。
(1)$n=3$のとき、$\triangle P_{0,0}P_{0,1}P_{0,2}$および$\triangle P_{1,0}P_{1,1}P_{1,2}$を同一平面上
に図示せよ。
(2)$S_4$を求めよ。
(3)平面上の異なる2点A,Bに対して、$AQ=BQ=1$であるような
同一平面上の点Qはいくつあるか。AB=dの値で場合分けして答えよ。
(4)$S_n$をnを用いて表せ。
2022東京医科歯科大学理系過去問
【数C】ベクトル平面ベクトル:ベクトルの基本② ベクトルの大きさ

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
ベクトルの大きさの求め方
a=(3,4)の大きさを求めよ。
この動画を見る
ベクトルの大きさの求め方
a=(3,4)の大きさを求めよ。
【数B】平面ベクトル:ベクトルの基本② ベクトルの大きさ

【球面の方程式って?】球面の方程式の解釈と求め方を解説!〔数学、高校数学〕

福田の数学〜千葉大学2022年理系第6問〜独立に動く空間上の2点の距離の最小

単元:
#大学入試過去問(数学)#空間ベクトル#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
座標空間において、原点Oと点A(1,0,-1)と点B(0,5,0)がある。
実数$t$を用いて$t\ \overrightarrow{ OA }+\overrightarrow{ OB }$と表される点全体をlとする。また、平面xy平面上
の$y=x^2$を満たす点全体からなる曲線をCとする。
(1)曲線$C$上の点$P(a,a^2,0)$を固定する。l上の点Qを、$\overrightarrow{ OA }$と$\overrightarrow{ PQ }$
が垂直であるようにとる。このとき、点Qの座標をaを用いて表せ。
(2)曲線C上の点Rとl上の点Sのうち、$|\overrightarrow{ RS }|$を最小にする点Rと点Sの
組み合わせを全て求めよ。また、そのときの$|\overrightarrow{ RS }|$の値を求めよ。
2022千葉大学理系過去問
この動画を見る
座標空間において、原点Oと点A(1,0,-1)と点B(0,5,0)がある。
実数$t$を用いて$t\ \overrightarrow{ OA }+\overrightarrow{ OB }$と表される点全体をlとする。また、平面xy平面上
の$y=x^2$を満たす点全体からなる曲線をCとする。
(1)曲線$C$上の点$P(a,a^2,0)$を固定する。l上の点Qを、$\overrightarrow{ OA }$と$\overrightarrow{ PQ }$
が垂直であるようにとる。このとき、点Qの座標をaを用いて表せ。
(2)曲線C上の点Rとl上の点Sのうち、$|\overrightarrow{ RS }|$を最小にする点Rと点Sの
組み合わせを全て求めよ。また、そのときの$|\overrightarrow{ RS }|$の値を求めよ。
2022千葉大学理系過去問
【数C】ベクトル平面ベクトル:ベクトルの基本① 基本的な考え方「終わり-始め」

【数B】平面ベクトル:ベクトルの基本① 基本的な考え方「終わり-始め」

単元:
#平面上のベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
ベクトルの基本的な考え方、ベクトルの和、始点の変更に関して解説していきます.
この動画を見る
ベクトルの基本的な考え方、ベクトルの和、始点の変更に関して解説していきます.
【平面の方程式の求め方はこれ!】平面の方程式の求め方を2つ解説しました〔数学、高校数学〕

福田の数学〜九州大学2022年文系第2問〜点と平面の距離と対称点

単元:
#大学入試過去問(数学)#平面上のベクトル#空間ベクトル#平面上のベクトルと内積#ベクトルと平面図形、ベクトル方程式#空間ベクトル#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学#数C
指導講師:
福田次郎
問題文全文(内容文):
座標空間内の4点
$O(0,0,0),A(1,1,0),B(2,1,2),P(4,0,-1)$
を考える。3点O,A,Bを通る平面を$\alpha$とし、$\overrightarrow{ a }=\overrightarrow{ OA }$,
$\overrightarrow{ b }=\overrightarrow{ OB }$とおく。
以下の問いに答えよ。
(1)ベクトル$\overrightarrow{ a },\ \overrightarrow{ b }$の両方に垂直であり、x成分が正であるような、大きさが1
のベクトル$\overrightarrow{ n }$を求めよ。
(2)点Pから平面$\alpha$に垂線を下ろし、その交点をQとおく。
線分PQの長さを求めよ。
(3)平面$\alpha$に関して点Pと対称な点P'の座標を求めよ。
2022九州大学文系過去問
この動画を見る
座標空間内の4点
$O(0,0,0),A(1,1,0),B(2,1,2),P(4,0,-1)$
を考える。3点O,A,Bを通る平面を$\alpha$とし、$\overrightarrow{ a }=\overrightarrow{ OA }$,
$\overrightarrow{ b }=\overrightarrow{ OB }$とおく。
以下の問いに答えよ。
(1)ベクトル$\overrightarrow{ a },\ \overrightarrow{ b }$の両方に垂直であり、x成分が正であるような、大きさが1
のベクトル$\overrightarrow{ n }$を求めよ。
(2)点Pから平面$\alpha$に垂線を下ろし、その交点をQとおく。
線分PQの長さを求めよ。
(3)平面$\alpha$に関して点Pと対称な点P'の座標を求めよ。
2022九州大学文系過去問
