 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
【数Ⅰ】相反方程式の解法(偶数次数の場合)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
相反方程式という特殊な方程式の解法を説明します。こちらの動画では定義の説明と、偶数次数の場合の解法を紹介しています。
この動画を見る
相反方程式という特殊な方程式の解法を説明します。こちらの動画では定義の説明と、偶数次数の場合の解法を紹介しています。
【数学Ⅰ/高1の予習】複雑な式の因数分解
単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$a(b^2-c^2)+b(c^2-a^2)+c(a^2-b^2)$を因数分解せよ
この動画を見る
$a(b^2-c^2)+b(c^2-a^2)+c(a^2-b^2)$を因数分解せよ
素数に関する整数問題

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^3+5$が素数となる素数xは何コ?
京都教育大学附属高等学校
この動画を見る
$x^3+5$が素数となる素数xは何コ?
京都教育大学附属高等学校
福田の数学〜名古屋大学2022年理系第1問〜割り算の余りと異なる実数解の個数

単元:
#数A#数Ⅱ#大学入試過去問(数学)#複素数と方程式#整数の性質#約数・倍数・整数の割り算と余り・合同式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋大学
指導講師:
福田次郎
問題文全文(内容文):
a,bを実数とする。
(1)整式$x^3$を2次式$(x-a)^2$で割った時の余りを求めよ。
(2)実数を係数とする2次式$f(x)=x^2+\alpha x+\beta$で整式$x^3$を割った時の余りが
$3x+b$とする。bの値に応じて、このようなf(x)が何個あるかを求めよ。
2022名古屋大学理系過去問
この動画を見る
a,bを実数とする。
(1)整式$x^3$を2次式$(x-a)^2$で割った時の余りを求めよ。
(2)実数を係数とする2次式$f(x)=x^2+\alpha x+\beta$で整式$x^3$を割った時の余りが
$3x+b$とする。bの値に応じて、このようなf(x)が何個あるかを求めよ。
2022名古屋大学理系過去問
【テストに出る】複雑な式の因数分解を解説!(高校数学Ⅰ)

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
$a(b^2-c^2)+b(c^2-a^2)+c(a^2-b^2)$を因数分解せよ
この動画を見る
$a(b^2-c^2)+b(c^2-a^2)+c(a^2-b^2)$を因数分解せよ
大学入試問題#161 大阪市立大学(1999) 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#大阪市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}}(\displaystyle \frac{x\ \sin\ x}{1+\cos\ x}+\displaystyle \frac{x\ \cos\ x}{1+\sin\ x})dx$を計算せよ。
出典:1999年大阪市立大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}}(\displaystyle \frac{x\ \sin\ x}{1+\cos\ x}+\displaystyle \frac{x\ \cos\ x}{1+\sin\ x})dx$を計算せよ。
出典:1999年大阪市立大学 入試問題
整数の基本問題

【#5】【因数分解100問】基礎から応用まで!(41)〜(50)【解説付き】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(41)$2xy-x-2y+1$
(42)$ab-bc+cd-da$
(43)$16-12y+3xy-x^2$
(44)$x^3y+x^2-xyz^2-z^2$
(45)$a^2+b^2+2bc+2ca+2ab$
(46)$(x+y+5)(x+2y-3)$
(47)$(x-y-2)(x-y+1)$
(48)$(2x+y+4)(3x+y-5)$
(49)$-(a-b)(b-c)(c-a)$
(50)$(a+1)(b+1)(c+1)$
この動画を見る
(41)$2xy-x-2y+1$
(42)$ab-bc+cd-da$
(43)$16-12y+3xy-x^2$
(44)$x^3y+x^2-xyz^2-z^2$
(45)$a^2+b^2+2bc+2ca+2ab$
(46)$(x+y+5)(x+2y-3)$
(47)$(x-y-2)(x-y+1)$
(48)$(2x+y+4)(3x+y-5)$
(49)$-(a-b)(b-c)(c-a)$
(50)$(a+1)(b+1)(c+1)$
数学が、どうしても苦手な人向け。唯一の解決法~偏差値84.9の数学勉強法【篠原好】

単元:
#その他#勉強法#数学(高校生)
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
数学が、どうしても苦手な人向け。唯一の解決法~偏差値84.9の数学勉強法を紹介します。
この動画を見る
数学が、どうしても苦手な人向け。唯一の解決法~偏差値84.9の数学勉強法を紹介します。
福田の数学・入試問題解説〜東北大学2022年文系第2問〜定積分で表された関数の最小値

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#不定積分・定積分#東北大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
実数tの関数
$F(t)=\int_0^1|x^2-t^2|dx$
について考える。
(1)$0 \leqq t \leqq 1$のとき、$F(t)$をtの整式として表せ。
(2)$t \geqq 0$ のとき、F(t)を最小にするtの値TとF(T)の値を求めよ。
2022東北大学文系過去問
この動画を見る
実数tの関数
$F(t)=\int_0^1|x^2-t^2|dx$
について考える。
(1)$0 \leqq t \leqq 1$のとき、$F(t)$をtの整式として表せ。
(2)$t \geqq 0$ のとき、F(t)を最小にするtの値TとF(T)の値を求めよ。
2022東北大学文系過去問
大学入試問題#160 名古屋市立大学(2020) 三角関数

単元:
#数Ⅱ#大学入試過去問(数学)#三角関数#三角関数とグラフ#学校別大学入試過去問解説(数学)#数学(高校生)#名古屋市立大学
指導講師:
ますただ
問題文全文(内容文):
$0 \leqq \theta \leqq \pi$
$\cos4\theta=\cos2\theta$をみたす$\theta$をすべて求めよ。
出典:2020年名古屋市立大学 入試問題
この動画を見る
$0 \leqq \theta \leqq \pi$
$\cos4\theta=\cos2\theta$をみたす$\theta$をすべて求めよ。
出典:2020年名古屋市立大学 入試問題
3乗根の方程式

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$ x^3+1=2\sqrt[3]{2x-1}$
この動画を見る
実数解を求めよ.
$ x^3+1=2\sqrt[3]{2x-1}$
9つの正方形と角の和
単元:
#数学(中学生)#中2数学#数Ⅰ#数A#図形の性質#図形と計量#三角形と四角形#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
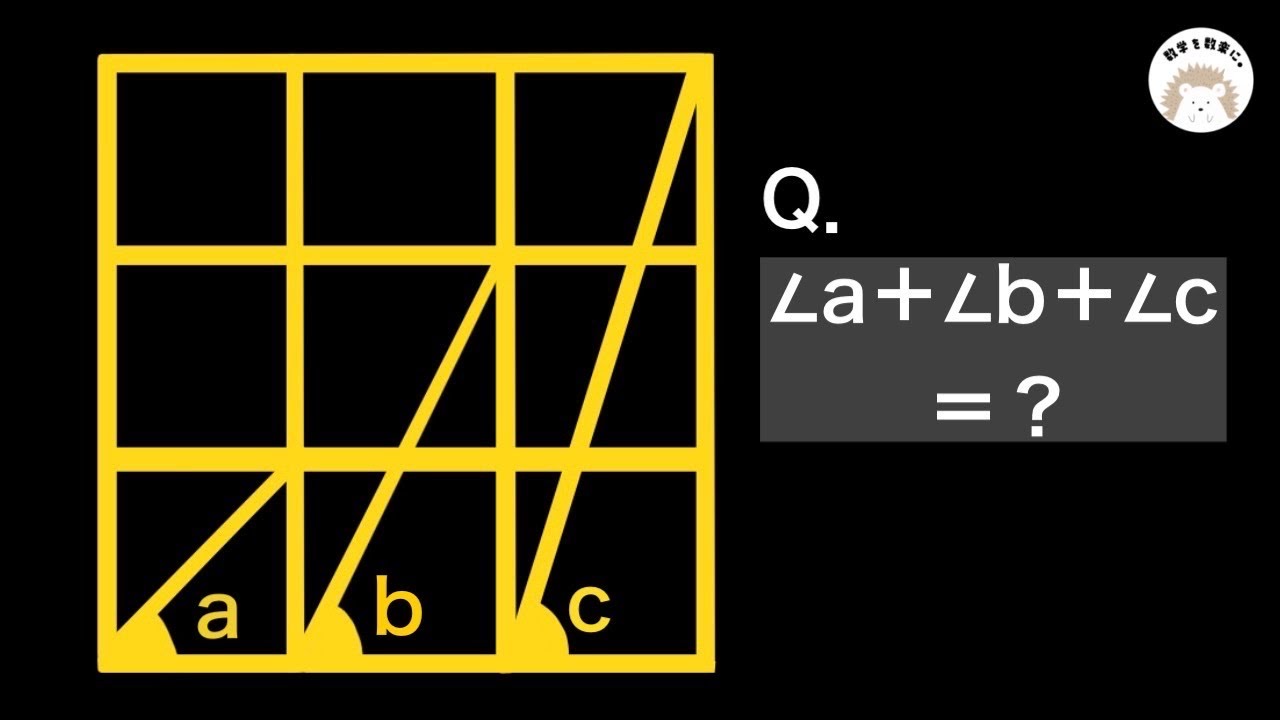
$\angle a + \angle b +\angle c=? $
*図は動画内参照
この動画を見る
$\angle a + \angle b +\angle c=? $
*図は動画内参照
【#4】【因数分解100問】基礎から応用まで!(31)〜(40)【解説付き】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(31)$(x^2+5)(x+3)(x-3)$
(32)$(x^2+1)(x+1)(x-1)$
(33)$(a+2b)(a-2b)(2a+3b)(2a-3b)$
(34)$3b^2(3a+2bc)(3a-2bc)$
(35)$\dfrac{1}{4}(2a+b-c)(2a-b+c)$
(36)$(5x+3)(25x^2-15x+9)$
(37)$(2x-3y)(4x^2+6xy+9y^2)$
(38)$(x-2)(x+1)(x-3)(x+2)$
(39)$(x+1)(x+3)(x+2)^2$
(40)$(x-1)^2(x^2-2x-4)$
この動画を見る
(31)$(x^2+5)(x+3)(x-3)$
(32)$(x^2+1)(x+1)(x-1)$
(33)$(a+2b)(a-2b)(2a+3b)(2a-3b)$
(34)$3b^2(3a+2bc)(3a-2bc)$
(35)$\dfrac{1}{4}(2a+b-c)(2a-b+c)$
(36)$(5x+3)(25x^2-15x+9)$
(37)$(2x-3y)(4x^2+6xy+9y^2)$
(38)$(x-2)(x+1)(x-3)(x+2)$
(39)$(x+1)(x+3)(x+2)^2$
(40)$(x-1)^2(x^2-2x-4)$
【数Ⅱ】三角形の重心の軌跡【除外点に注意しよう】

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
点Qが円$x^2+y^2=9$上を動くとき,
点$A(4,0)$と点Qを結ぶ線分AQの中点Pの軌跡を求めよ.
この動画を見る
点Qが円$x^2+y^2=9$上を動くとき,
点$A(4,0)$と点Qを結ぶ線分AQの中点Pの軌跡を求めよ.
【数学Ⅱ】繁分数式(分数の中に分数がある)

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理#数学(高校生)
指導講師:
【ゼロから理解できる】高校数学・物理
問題文全文(内容文):
次の式を簡単にせよ。
(1)$\displaystyle \frac{x-2-\displaystyle \frac{2}{x-1}}{x+2+\displaystyle \frac{2}{x-1}}$
(2)$1-\displaystyle \frac{1}{1-\displaystyle \frac{1}{1-x}}$
この動画を見る
次の式を簡単にせよ。
(1)$\displaystyle \frac{x-2-\displaystyle \frac{2}{x-1}}{x+2+\displaystyle \frac{2}{x-1}}$
(2)$1-\displaystyle \frac{1}{1-\displaystyle \frac{1}{1-x}}$
大学ではなく高校入試。2種類の解法

単元:
#計算と数の性質#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$2^{ 56 }$と$5^{ 24 }$どっちが大きい?
この動画を見る
$2^{ 56 }$と$5^{ 24 }$どっちが大きい?
福田の数学〜東京工業大学2022年理系第5問〜定積分と不等式と区分求積

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
aは$0 \lt a \leqq \frac{\pi}{4}$を満たす実数とし、
$f(x)=\frac{4}{3}\sin(\frac{\pi}{4}+ax)\cos(\frac{\pi}{4}-ax)$
とする。このとき、次の問いに答えよ。
(1)次の等式(*)を満たすaがただ1つ存在することを示せ。
(*) $\int_0^1f(x)dx=1$
(2)$0 \leqq b \lt c \leqq 1$を満たす実数b,cについて、不等式
$f(b)(c-b) \leqq \int_b^cf(x)dx \leqq f(c)(c-b)$
が成り立つことを示せ。
(3)次の試行を考える。\\
[試行]n個の数$1,2,\ldots\ldots,n$を出目とする、あるルーレットをk回まわす。
この試行において、各$i=1,2,\ldots\ldots,n$についてiが出た回数を$S_{n,k,i}$とし、
(**)$\lim_{k \to \infty}\frac{S_{n,k,i}}{k}=\int_{\frac{i-1}{n}}^{\frac{i}{n}}f(x)dx$
が成り立つとする。このとき、(1)の等式(*)が成り立つことを示せ。
(4)(3)の[試行]において出た数の平均値を$A_{n,k}$とし、$A_n=\lim_{k \to \infty}A_{n,k}$とする。
(**)が成り立つとき、極限$\lim_{n \to \infty}\frac{A_n}{n}$をaを用いて表せ。
2022東京工業大学理系過去問
この動画を見る
aは$0 \lt a \leqq \frac{\pi}{4}$を満たす実数とし、
$f(x)=\frac{4}{3}\sin(\frac{\pi}{4}+ax)\cos(\frac{\pi}{4}-ax)$
とする。このとき、次の問いに答えよ。
(1)次の等式(*)を満たすaがただ1つ存在することを示せ。
(*) $\int_0^1f(x)dx=1$
(2)$0 \leqq b \lt c \leqq 1$を満たす実数b,cについて、不等式
$f(b)(c-b) \leqq \int_b^cf(x)dx \leqq f(c)(c-b)$
が成り立つことを示せ。
(3)次の試行を考える。\\
[試行]n個の数$1,2,\ldots\ldots,n$を出目とする、あるルーレットをk回まわす。
この試行において、各$i=1,2,\ldots\ldots,n$についてiが出た回数を$S_{n,k,i}$とし、
(**)$\lim_{k \to \infty}\frac{S_{n,k,i}}{k}=\int_{\frac{i-1}{n}}^{\frac{i}{n}}f(x)dx$
が成り立つとする。このとき、(1)の等式(*)が成り立つことを示せ。
(4)(3)の[試行]において出た数の平均値を$A_{n,k}$とし、$A_n=\lim_{k \to \infty}A_{n,k}$とする。
(**)が成り立つとき、極限$\lim_{n \to \infty}\frac{A_n}{n}$をaを用いて表せ。
2022東京工業大学理系過去問
大学入試問題#159 横浜国立大学 定積分

単元:
#大学入試過去問(数学)#積分とその応用#定積分#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{4}\displaystyle \frac{dx}{\sqrt{ 3-\sqrt{ x } }}$を計算せよ
出典:横浜国立大学 入試問題
この動画を見る
$\displaystyle \int_{1}^{4}\displaystyle \frac{dx}{\sqrt{ 3-\sqrt{ x } }}$を計算せよ
出典:横浜国立大学 入試問題
対数の基本問題(近似値は使えません)

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)$ \log_{10}2$が無理数であることを証明せよ.
(2)$2^{104}$は何桁か求めよ.
この動画を見る
(1)$ \log_{10}2$が無理数であることを証明せよ.
(2)$2^{104}$は何桁か求めよ.
指数の計算 log使わずに解ける

【#3】【因数分解100問】基礎から応用まで!(21)〜(30)【解説付き】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(21)$x^2-4x+4-y^2$
(22)$x^2-y^2+6y-9$
(23)$4a^2-4b^2+4b-1$
(24)$x^2-2xy+y^2-4z^2$
(25)$(x+2)^2+7(x+2)+6$
(26)$(x+y)^2-x-y-12$
(27)$6(x-y)^2-5(x-y)-4$
(28)$(a+b)^2+10c(a+b)+25c^2$
(29)$(x+y+2)(x+y-3)-6$
(30)$(x+2y)(x+2y-2z)-8z^2$
この動画を見る
(21)$x^2-4x+4-y^2$
(22)$x^2-y^2+6y-9$
(23)$4a^2-4b^2+4b-1$
(24)$x^2-2xy+y^2-4z^2$
(25)$(x+2)^2+7(x+2)+6$
(26)$(x+y)^2-x-y-12$
(27)$6(x-y)^2-5(x-y)-4$
(28)$(a+b)^2+10c(a+b)+25c^2$
(29)$(x+y+2)(x+y-3)-6$
(30)$(x+2y)(x+2y-2z)-8z^2$
【足元をすくわれるな!】整数:八代白百合学園高等学校~全国入試問題解法

単元:
#数学(中学生)#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の問いに答えなさい.
$-2.7$より大きく$\dfrac{14}{3}$より小さい整数は全部で何個あるか.
八代白百合学園高等学校過去問
この動画を見る
次の問いに答えなさい.
$-2.7$より大きく$\dfrac{14}{3}$より小さい整数は全部で何個あるか.
八代白百合学園高等学校過去問
有名な高校入試解説できる?

単元:
#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#その他#その他#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$2^{ 56 }$と$5^{ 24 }$ どちらが大きい?
この動画を見る
$2^{ 56 }$と$5^{ 24 }$ どちらが大きい?
福田の入試問題解説〜北海道大学2022年文系第4問〜復元抽出と非復元抽出の確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
福田次郎
問題文全文(内容文):
箱の中に1文字ずつ書かれたカードが10枚ある。そのうち5枚にはA、
3枚にはB、2枚にはCと書かれている。箱から1枚ずつ、3回カードを
取り出す試行を考える。
(1)カードを取り出すごとに箱に戻す場合、1回目と3回目に取り出したカード
の文字が一致する確率を求めよ。
(2)取り出したカードを箱に戻さない場合、1回目と3回目に取り出したカード
の文字が一致する確率を求めよ。
(3)取り出したカードを箱に戻さない場合、2回目に取り出したカードの文字が
Cであるとき、1回目と3回目に取り出したカードの文字が一致する
条件つき確率を求めよ。
2022北海道大学文系過去問
この動画を見る
箱の中に1文字ずつ書かれたカードが10枚ある。そのうち5枚にはA、
3枚にはB、2枚にはCと書かれている。箱から1枚ずつ、3回カードを
取り出す試行を考える。
(1)カードを取り出すごとに箱に戻す場合、1回目と3回目に取り出したカード
の文字が一致する確率を求めよ。
(2)取り出したカードを箱に戻さない場合、1回目と3回目に取り出したカード
の文字が一致する確率を求めよ。
(3)取り出したカードを箱に戻さない場合、2回目に取り出したカードの文字が
Cであるとき、1回目と3回目に取り出したカードの文字が一致する
条件つき確率を求めよ。
2022北海道大学文系過去問
ハルハル様の作成問題 手筋連発

単元:
#数Ⅱ#式と証明#整数の性質#約数・倍数・整数の割り算と余り・合同式#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x$についての方程式
$x^3+x^2-x-5=0$の最小の実数解を$\alpha$とする。
$\alpha^5$の整数部分を求めよ。
この動画を見る
$x$についての方程式
$x^3+x^2-x-5=0$の最小の実数解を$\alpha$とする。
$\alpha^5$の整数部分を求めよ。
正五角形の作図と証明

2つの円
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
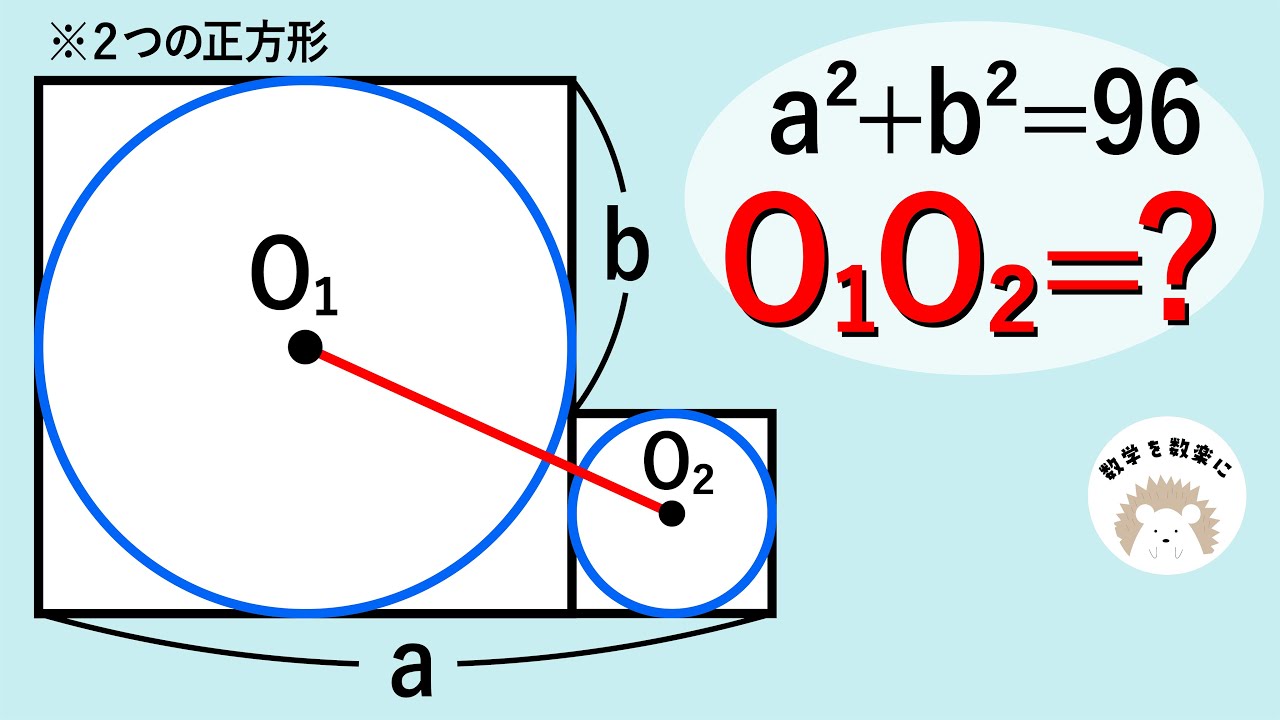
*2つの正方形
$a^2+b^2=96$
$O_1O_2=?$
*図は動画内参照
この動画を見る
*2つの正方形
$a^2+b^2=96$
$O_1O_2=?$
*図は動画内参照
【#2】【因数分解100問】基礎から応用まで!(11)〜(20)【解説付き】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
(11)$x^2+19x+48$
(12)$x^2-6x-27$
(13)$x^2+8xy-20y^2$
(14)$y^2-7xy+10x^2$
(15)$5a^2+7a+2$
(16)$2x^2-7x-15$
(17)$4a^2+23a-27$
(18)$12x^2-25x+12$
(19)$5a^2+13ab-6b^2$
(20)$6x^2-3xy-18y^2$
この動画を見る
(11)$x^2+19x+48$
(12)$x^2-6x-27$
(13)$x^2+8xy-20y^2$
(14)$y^2-7xy+10x^2$
(15)$5a^2+7a+2$
(16)$2x^2-7x-15$
(17)$4a^2+23a-27$
(18)$12x^2-25x+12$
(19)$5a^2+13ab-6b^2$
(20)$6x^2-3xy-18y^2$
福田の数学〜東京工業大学2022年理系第4問〜複素数平面上の点の軌跡と線分の通過範囲

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#東京工業大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
aを正の実数とする。複素数$z$が$|z-1|=a$かつ$z\neq \frac{1}{2}$を満たしながら
動くとき、複素数平面上の点$w=\frac{z-3}{1-2z}$が描く図形をKとする。
このとき、次の問いに答えよ。
(1)Kが円となるためのaの条件を求めよ。また、そのとき
Kの中心が表す複素数とKの半径を、それぞれaを用いて表せ。
(2)aが(1)の条件を満たしながら動くとき、虚軸に平行で円Kの直径となる
線分が通過する領域を複素数平面上に図示せよ。
2022東京工業大学理系過去問
この動画を見る
aを正の実数とする。複素数$z$が$|z-1|=a$かつ$z\neq \frac{1}{2}$を満たしながら
動くとき、複素数平面上の点$w=\frac{z-3}{1-2z}$が描く図形をKとする。
このとき、次の問いに答えよ。
(1)Kが円となるためのaの条件を求めよ。また、そのとき
Kの中心が表す複素数とKの半径を、それぞれaを用いて表せ。
(2)aが(1)の条件を満たしながら動くとき、虚軸に平行で円Kの直径となる
線分が通過する領域を複素数平面上に図示せよ。
2022東京工業大学理系過去問
