 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
福田のわかった数学〜高校3年生理系098〜不等式の証明(5)

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 不等式の証明(5)
$b(\log a-\log b) \leqq a-b (a \gt 0, b \gt 0)$を証明せよ。
この動画を見る
数学$\textrm{III}$ 不等式の証明(5)
$b(\log a-\log b) \leqq a-b (a \gt 0, b \gt 0)$を証明せよ。
大学入試問題#49 神戸大学(2021) 極値の判定

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$a$:実数
$f(x)=ax+\cos\ x+\displaystyle \frac{1}{2}\sin2x$が極値をもたないように$a$の値の範囲を求めよ。
出典:2010年神戸大学 入試問題
この動画を見る
$a$:実数
$f(x)=ax+\cos\ x+\displaystyle \frac{1}{2}\sin2x$が極値をもたないように$a$の値の範囲を求めよ。
出典:2010年神戸大学 入試問題
指数方程式 答えは1つじゃないよ

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
すべての解を求めよ.
$5^x・8^{\frac{x}{x+1}}=100$
この動画を見る
すべての解を求めよ.
$5^x・8^{\frac{x}{x+1}}=100$
1+2=❓ AKB□❗️❗️

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
1+2=
(a) 1!
(b) 2!
(c) 3!
(d) 3!!
この動画を見る
1+2=
(a) 1!
(b) 2!
(c) 3!
(d) 3!!
福田のわかった数学〜高校2年生080〜三角関数(19)2直線のなす角(3)

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 三角関数(19) なす角(3)
2点A(0,2), B(0,8)がある。点P(a,0) $(a \gt 0)$について$\angle APB$が最大となるaは?
この動画を見る
数学$\textrm{II}$ 三角関数(19) なす角(3)
2点A(0,2), B(0,8)がある。点P(a,0) $(a \gt 0)$について$\angle APB$が最大となるaは?
大学入試問題#48 神戸大学(2021) 定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#神戸大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1}x^3log(x^2+1)dx$を計算せよ。
出典:2021年神戸大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{1}x^3log(x^2+1)dx$を計算せよ。
出典:2021年神戸大学 入試問題
失敗しないたすきがけ因数分解

負の数の三乗根
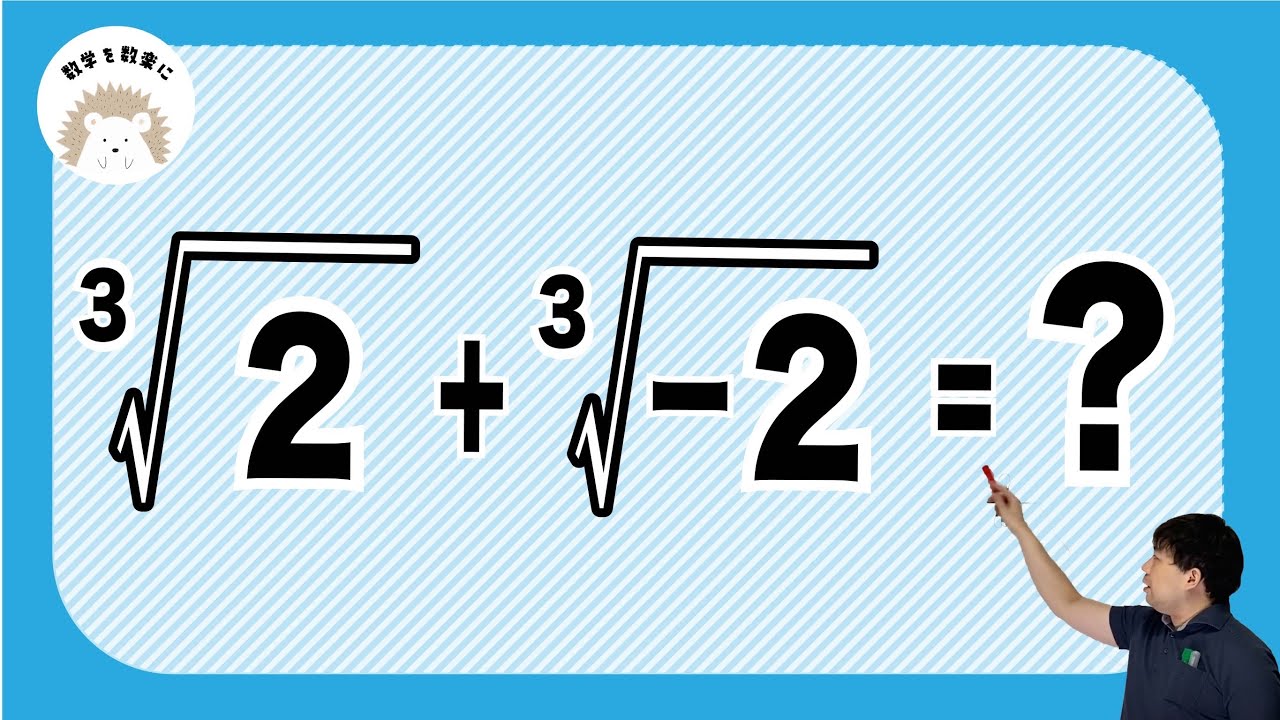
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
${}^3 \sqrt 2 + {}^3 \sqrt {-2}$
この動画を見る
${}^3 \sqrt 2 + {}^3 \sqrt {-2}$
【数Ⅱ】相加平均・相乗平均の関係を正しく使いこなそう【よくある間違え方とは】

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$ (1)x \gt 0のとき,x+\dfrac{9}{x}\geqq 6を示せ.
(2)x \gt 0のとき,x+\dfrac{9}{x}の最小値を求めよ.
(3)x \gt 0のとき,x+\dfrac{6}{x+1}の最小値を求めよ.
(4)x \gt 0のとき,\dfrac{x^2;5x+15}{x+2}の最小値を求めよ.
(5)a \gt 0,b \gt 0のとき\left(a+\frac{1}{b} \right)\left(\frac{16}{a}+b \right)の最小値
を求めよ.$
この動画を見る
$ (1)x \gt 0のとき,x+\dfrac{9}{x}\geqq 6を示せ.
(2)x \gt 0のとき,x+\dfrac{9}{x}の最小値を求めよ.
(3)x \gt 0のとき,x+\dfrac{6}{x+1}の最小値を求めよ.
(4)x \gt 0のとき,\dfrac{x^2;5x+15}{x+2}の最小値を求めよ.
(5)a \gt 0,b \gt 0のとき\left(a+\frac{1}{b} \right)\left(\frac{16}{a}+b \right)の最小値
を求めよ.$
福田のわかった数学〜高校1年生080〜場合の数(19)道順(5)

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 場合の数(17) 道順(5)
図(※動画参照)のように立方体ABCD-EFGHの各面が3×3の正方形となるような
碁盤の目状に区切られた図形がある。点Aから点Gまで辺上を通って最短経路で行く
方法は何通りあるか。
この動画を見る
数学$\textrm{I}$ 場合の数(17) 道順(5)
図(※動画参照)のように立方体ABCD-EFGHの各面が3×3の正方形となるような
碁盤の目状に区切られた図形がある。点Aから点Gまで辺上を通って最短経路で行く
方法は何通りあるか。
#40 数検1級1次 過去問 微分方程式

単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$3y\displaystyle \frac{d^2y}{dx^2}+(\displaystyle \frac{dy}{dx})^2=0$において
$x=0$のとき$y=0$
$X=1$のとき$y=1$
を満たす特殊解を求めよ。
この動画を見る
$3y\displaystyle \frac{d^2y}{dx^2}+(\displaystyle \frac{dy}{dx})^2=0$において
$x=0$のとき$y=0$
$X=1$のとき$y=1$
を満たす特殊解を求めよ。
三角関数基本

単元:
#数Ⅱ#三角関数#三角関数とグラフ#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
値を求めよ.
$\cos \dfrac{\pi}{7}・\cos \dfrac{2\pi}{7}・\cos\dfrac{3\pi}{7}$
この動画を見る
値を求めよ.
$\cos \dfrac{\pi}{7}・\cos \dfrac{2\pi}{7}・\cos\dfrac{3\pi}{7}$
1分で分かる!数学勉強法~全国模試1位の勉強法 #Shorts【篠原好】

気付けば一瞬!!の確率の問題 東奥義塾

単元:
#数学(中学生)#数A#場合の数と確率#確率#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
1⃣ 2⃣ 3⃣ 4⃣ 5⃣
の5枚のカードから3枚のカードを並べてできる3ケタの整数で
奇数となる確率は?
東奥義塾高等学校
この動画を見る
1⃣ 2⃣ 3⃣ 4⃣ 5⃣
の5枚のカードから3枚のカードを並べてできる3ケタの整数で
奇数となる確率は?
東奥義塾高等学校
福田のわかった数学〜高校3年生理系097〜不等式の証明(4)

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 不等式の証明(4)
$(x+2)\log(x+1) \geqq 2x (x \geqq 0)$を証明せよ。
この動画を見る
数学$\textrm{III}$ 不等式の証明(4)
$(x+2)\log(x+1) \geqq 2x (x \geqq 0)$を証明せよ。
方程式
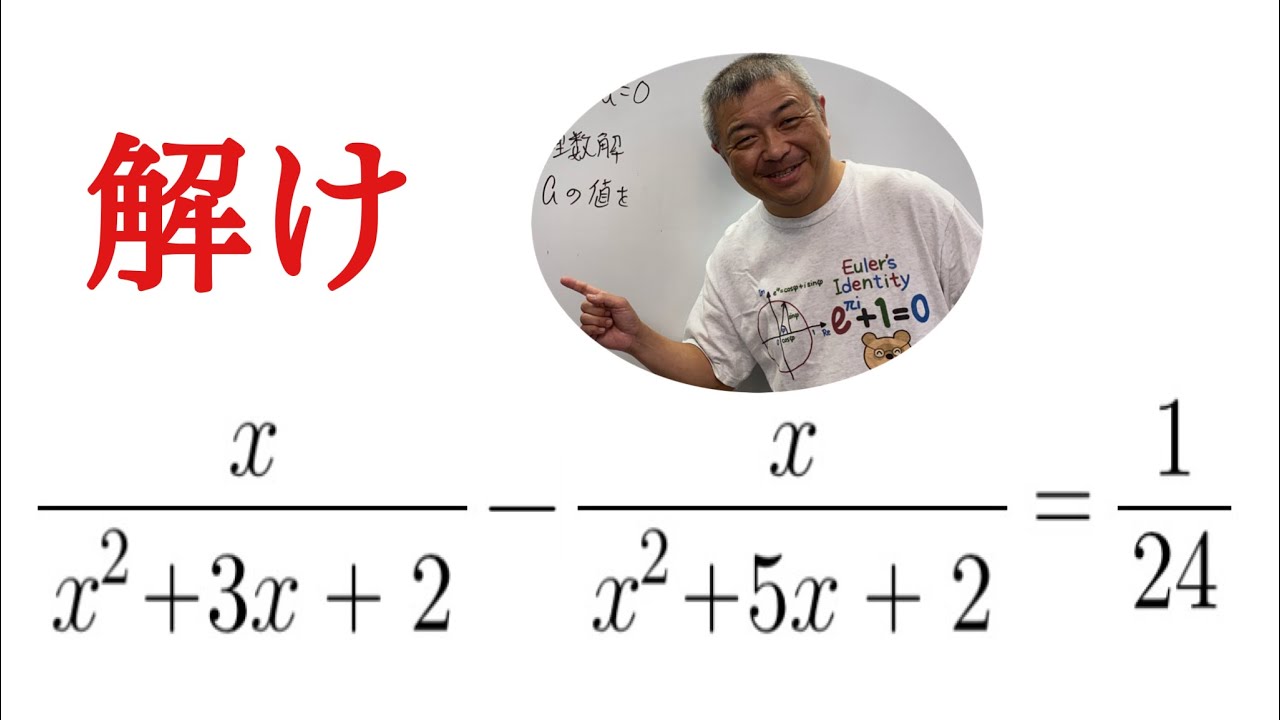
単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\dfrac{x}{x^2+3x+2}-\dfrac{x}{x^2+5x+2}=\dfrac{1}{24}$
この動画を見る
これを解け.
$\dfrac{x}{x^2+3x+2}-\dfrac{x}{x^2+5x+2}=\dfrac{1}{24}$
これできる?

単元:
#その他#その他#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
下記を成立させよ
2 2 2=6
3 3 3=6
4 4 4=6
5 5 5=6
この動画を見る
下記を成立させよ
2 2 2=6
3 3 3=6
4 4 4=6
5 5 5=6
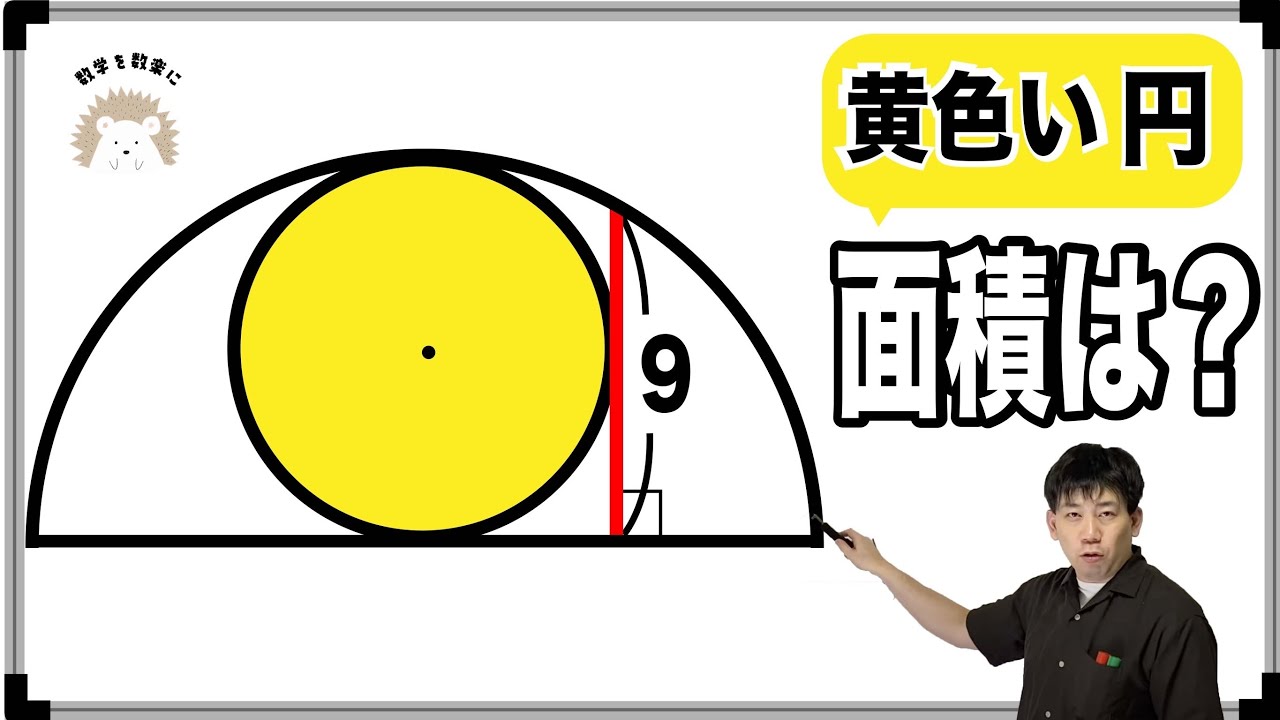
半円と円
福田のわかった数学〜高校2年生079〜三角関数(18)2直線のなす角(2)

単元:
#数Ⅱ#三角関数#加法定理とその応用#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 三角関数(18) なす角(2)
$y=3x+1$と$\frac{\pi}{6}$の角をなし、原点を通る直線の方程式を求めよ。
この動画を見る
数学$\textrm{II}$ 三角関数(18) なす角(2)
$y=3x+1$と$\frac{\pi}{6}$の角をなし、原点を通る直線の方程式を求めよ。
大学入試問題#46 岡山大学(2013) 曲面で囲まれた領域の面積

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#岡山大学
指導講師:
ますただ
問題文全文(内容文):
$x \gt 0$
曲線$y=|x-\displaystyle \frac{1}{x}|$と直線$y=2$で囲まれた領域の面積$S$を求めよ
出典:2013年岡山大学 入試問題
この動画を見る
$x \gt 0$
曲線$y=|x-\displaystyle \frac{1}{x}|$と直線$y=2$で囲まれた領域の面積$S$を求めよ
出典:2013年岡山大学 入試問題
4次方程式
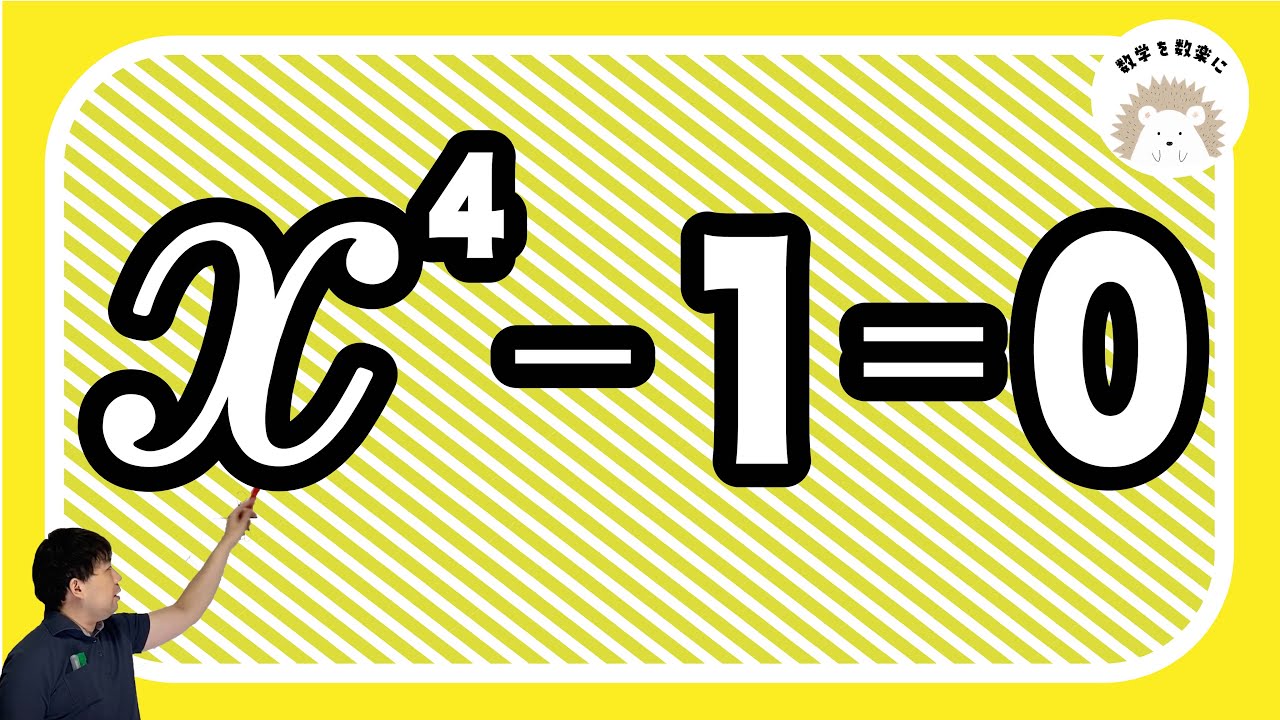
数学「大学入試良問集」【16−3 ド・モアブルの定理と累乗の取り扱い】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)#数C
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$z$を絶対値が1の複素数とする。
このとき以下の問いに答えよ。
(1)$z^3-z$の実部が$0$となるような$z$をすべて求めよ。
(2)$z^5+z$の絶対値が1となるような$z$をすべて求めよ。
(3)$n$を自然数とする。$z^n+1$の絶対値が1となるような$z$となるような$z$をすべてかけ合わせて得られる複素数を求めよ。
この動画を見る
$z$を絶対値が1の複素数とする。
このとき以下の問いに答えよ。
(1)$z^3-z$の実部が$0$となるような$z$をすべて求めよ。
(2)$z^5+z$の絶対値が1となるような$z$をすべて求めよ。
(3)$n$を自然数とする。$z^n+1$の絶対値が1となるような$z$となるような$z$をすべてかけ合わせて得られる複素数を求めよ。
福田のわかった数学〜高校1年生079〜場合の数(18)連続しない自然数の選び方

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 場合の数(18) 連続しない整数
$1,2,3,\ldots,19,20$の20個の数字から、どの2つも連続しないような8個の数字を
選ぶ方法は何通りあるか。
この動画を見る
数学$\textrm{I}$ 場合の数(18) 連続しない整数
$1,2,3,\ldots,19,20$の20個の数字から、どの2つも連続しないような8個の数字を
選ぶ方法は何通りあるか。
【数Ⅱ】不等式の証明・基本パターン【書き出しに注意!】

大学入試問題#45 岡山大学(2011) 行列

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#岡山大学
指導講師:
ますただ
問題文全文(内容文):
$t$:実数
$A=(\begin{eqnarray}
t\ t-1 \\
1-t\ 2-t
\end{eqnarray})$
$A^{2n}-tA^n$が$n$の値によらない行列になるとき、$t$の値を求めよ。
出典:2011年岡山大学 入試問題
この動画を見る
$t$:実数
$A=(\begin{eqnarray}
t\ t-1 \\
1-t\ 2-t
\end{eqnarray})$
$A^{2n}-tA^n$が$n$の値によらない行列になるとき、$t$の値を求めよ。
出典:2011年岡山大学 入試問題
未知数2で式1つの方程式

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
これの実数解を求めよ.
$x^2+y^2+15=\sqrt 6(x-3y)$
この動画を見る
これの実数解を求めよ.
$x^2+y^2+15=\sqrt 6(x-3y)$
等式を変形せよ。
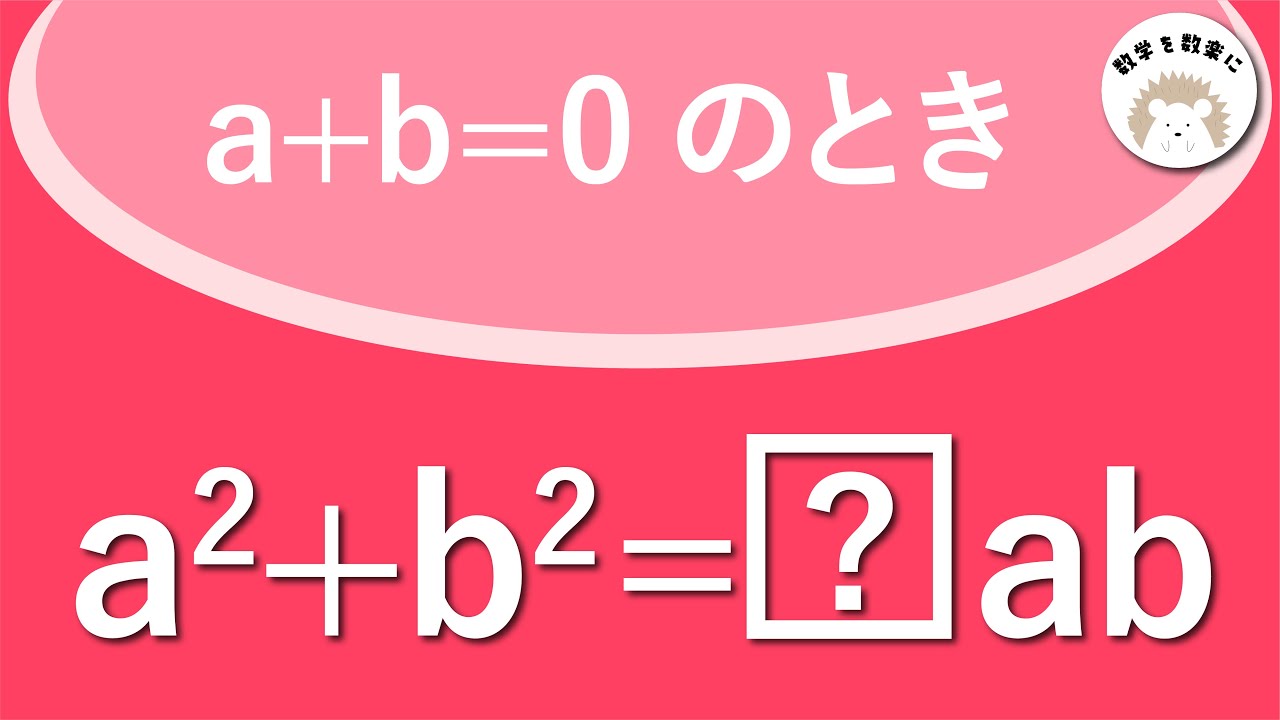
単元:
#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a+b=0$
$a^2+b^2 = ▢ab$
この動画を見る
$a+b=0$
$a^2+b^2 = ▢ab$
高校範囲だけど中3生も解けるし

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{x^2-2}{x-1} + \frac{1}{x-1}$
この動画を見る
$\frac{x^2-2}{x-1} + \frac{1}{x-1}$
福田のわかった数学〜高校3年生理系096〜不等式の証明(3)
単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
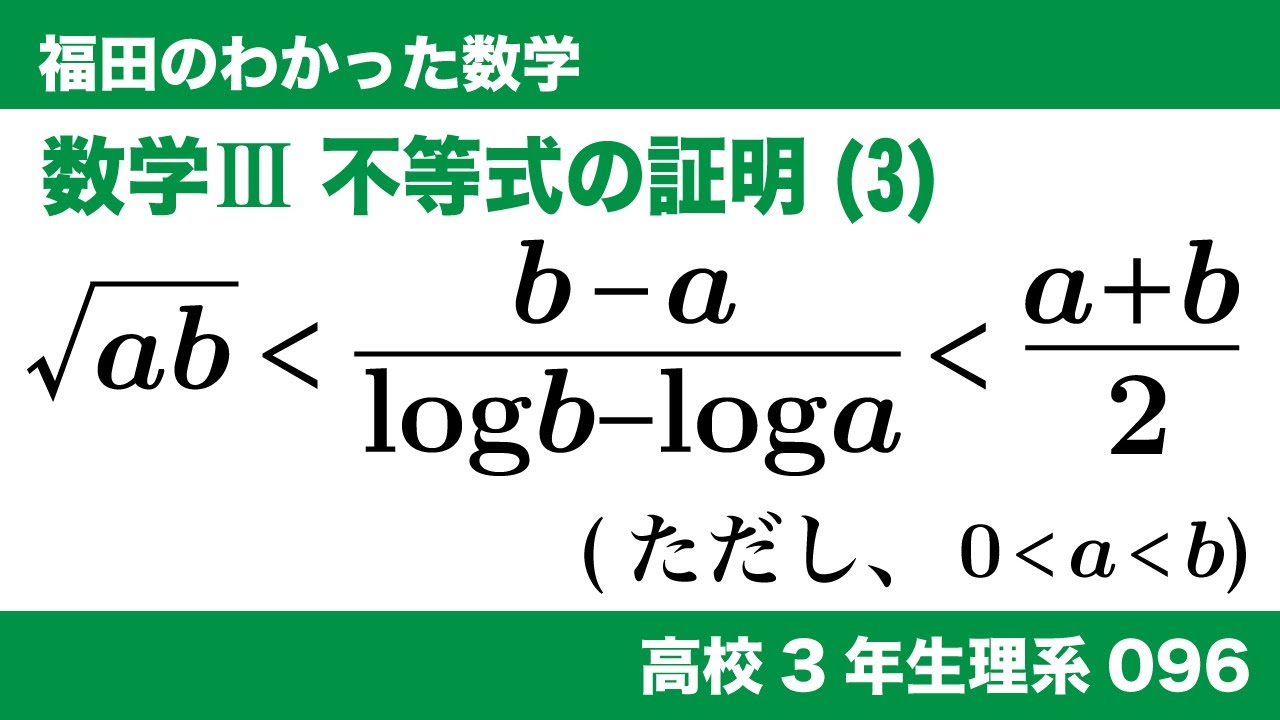
数学$\textrm{III}$ 不等式の証明(3)
$\sqrt{ab} \lt \frac{b-a}{\log b-\log a} \lt \frac{a+b}{2} (0 \lt a \lt b)$を証明せよ。
この動画を見る
数学$\textrm{III}$ 不等式の証明(3)
$\sqrt{ab} \lt \frac{b-a}{\log b-\log a} \lt \frac{a+b}{2} (0 \lt a \lt b)$を証明せよ。
#39 数検1級1次 過去問 解と係数の関係 整数問題

単元:
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$m,n:$正の整数
$x^3-mx^2+nx-n=0$のすべての解が正の整数であるような組$(m,n)$を求めよ。
この動画を見る
$m,n:$正の整数
$x^3-mx^2+nx-n=0$のすべての解が正の整数であるような組$(m,n)$を求めよ。
