 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
福田のわかった数学〜高校1年生010〜2次関数の最大最小(3)

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 2次関数の最大最小(3)
$y=(x^2-2ax)^2+4(x^2-2ax)$
の最小値が$-4$となるような定数$a$
の値の範囲を求めよ。
この動画を見る
数学$\textrm{I}$ 2次関数の最大最小(3)
$y=(x^2-2ax)^2+4(x^2-2ax)$
の最小値が$-4$となるような定数$a$
の値の範囲を求めよ。
#12数検1級1次過去問 極限(マクローリン展開)Σn^2/n!

単元:
#数学検定・数学甲子園・数学オリンピック等#関数と極限#数列の極限#関数の極限#数学検定#数学検定準1級#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6}$
$\displaystyle \sum_{n=1}^{\infty}\dfrac{n^2}{n!}$を求めよ.
この動画を見る
$\boxed{6}$
$\displaystyle \sum_{n=1}^{\infty}\dfrac{n^2}{n!}$を求めよ.
【理数個別の過去問解説】2021年度東京大学 数学 理科第2問(1)解説

単元:
#大学入試過去問(数学)#複素数平面#複素数平面#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
複素数a,b,cに対して整式$f(z)=az^2+bz+c$を考える。iを虚数単位とする。$\alpha,\beta,y$を複素数とする。
$f(0)=α,f(1)=β,f(i)=(γ)$が成り立つとき、$a,b,c$をそれぞれ$\alpha,\beta,y$で表せ。
この動画を見る
複素数a,b,cに対して整式$f(z)=az^2+bz+c$を考える。iを虚数単位とする。$\alpha,\beta,y$を複素数とする。
$f(0)=α,f(1)=β,f(i)=(γ)$が成り立つとき、$a,b,c$をそれぞれ$\alpha,\beta,y$で表せ。
ルートの計算 パズル感覚で! C
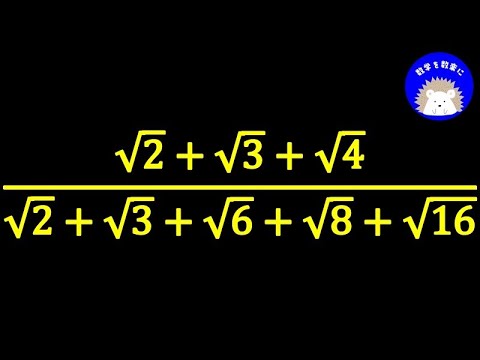
単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{\sqrt 2 + \sqrt 3 + \sqrt 4}{\sqrt 2 + \sqrt 3 + \sqrt 6 + \sqrt 8 + \sqrt {16} }=$
この動画を見る
$\frac{\sqrt 2 + \sqrt 3 + \sqrt 4}{\sqrt 2 + \sqrt 3 + \sqrt 6 + \sqrt 8 + \sqrt {16} }=$
福田のわかった数学〜高校3年生理系003〜極限(3)

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 極限(3)
$\lim_{n \to \infty}(2^n+3^n)^{\frac{1}{n}}$ を求めよ。
この動画を見る
数学$\textrm{III}$ 極限(3)
$\lim_{n \to \infty}(2^n+3^n)^{\frac{1}{n}}$ を求めよ。
福田のわかった数学〜高校2年生第9回〜高次方程式の有理数解

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 高次方程式
$a,b,c$を整数とするとき、3次方程式
$x^3+ax^2+bx+c=0$
が有理数解$s$をもつなら、$s$は整数である。
これを示せ。
この動画を見る
数学$\textrm{II}$ 高次方程式
$a,b,c$を整数とするとき、3次方程式
$x^3+ax^2+bx+c=0$
が有理数解$s$をもつなら、$s$は整数である。
これを示せ。
#11数検1級1次過去問

単元:
#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#解と判別式・解と係数の関係#剰余の定理・因数定理・組み立て除法と高次方程式#数学検定#数学検定準1級
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}$
$x^4-4x^3+x^2-3=0$を解け.
この動画を見る
$\boxed{1}$
$x^4-4x^3+x^2-3=0$を解け.
【数A】整数の性質:φ関数(φ(6)について) 問題文「1~nまでの自然数でnと互いに素な自然数の個数を求めよ」

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
1~nまでの自然数でnと互いに素な自然数の個数を求めよ
この動画を見る
1~nまでの自然数でnと互いに素な自然数の個数を求めよ
素数判定 あの定理の証明

数学「大学入試良問集」【10−6 領域図式と最大値】を宇宙一わかりやすく

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
座標平面上で不等式
$2(log_3\ x-1) \leqq log_3\ y-1 \leqq log_3\left[ \dfrac{ x }{ 3 } \right]+log_3(2-x)$
を満たす点$x(x,y)$全体をつくる領域を$D$とする。
(1)$D$を座標平面上に図示せよ。
(2)$a \lt 2$の範囲にある定数$a$に対し、$y-ax$の$D$上での最大値$M(a)$を求めよ。
この動画を見る
座標平面上で不等式
$2(log_3\ x-1) \leqq log_3\ y-1 \leqq log_3\left[ \dfrac{ x }{ 3 } \right]+log_3(2-x)$
を満たす点$x(x,y)$全体をつくる領域を$D$とする。
(1)$D$を座標平面上に図示せよ。
(2)$a \lt 2$の範囲にある定数$a$に対し、$y-ax$の$D$上での最大値$M(a)$を求めよ。
小学生解き方 中学生の解き方
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
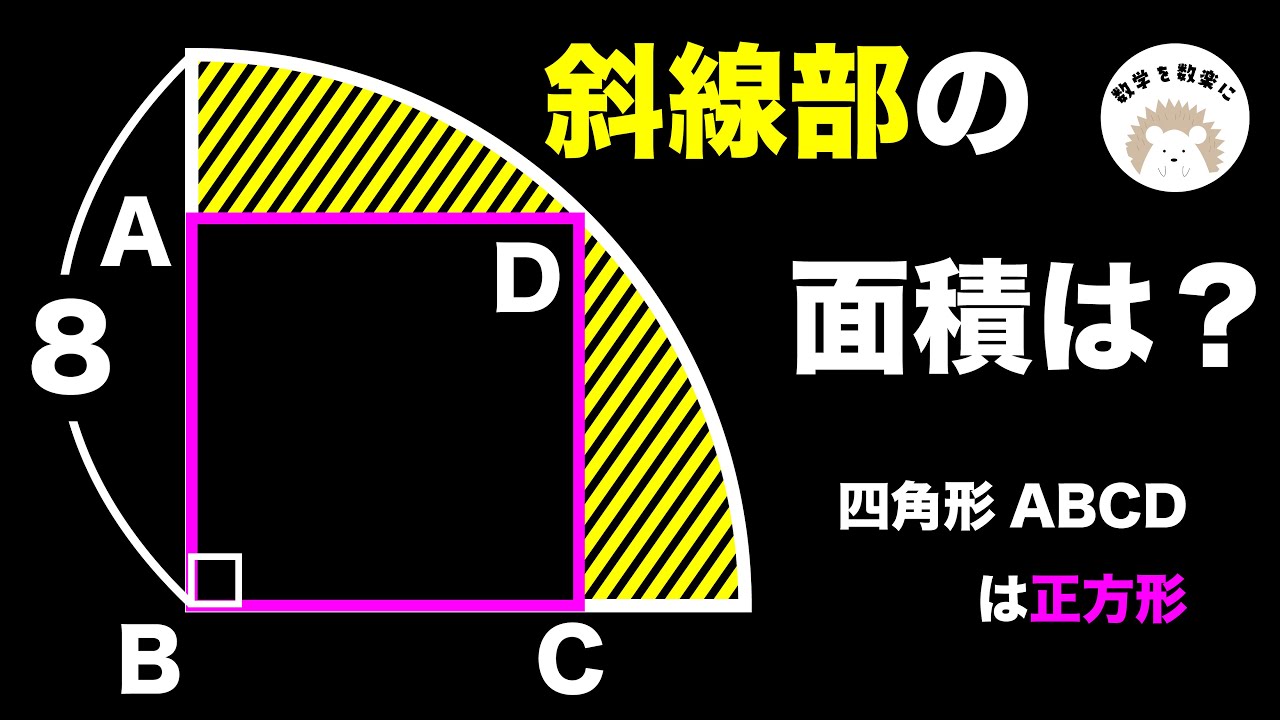
四角形ABCDは正方形
斜線部の面積=?
*図は動画内参照
この動画を見る
四角形ABCDは正方形
斜線部の面積=?
*図は動画内参照
福田のわかった数学〜高校1年生第9回〜2次関数の最大最小(2)

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 2次関数の最大最小(2)
次の関数の最小値とそのときの$x$を求めよ。
(1)$y=x^4+4x^2-3$
(2)$y=(x^2-2x)^2+4(x^2-2x)-1$
この動画を見る
数学$\textrm{I}$ 2次関数の最大最小(2)
次の関数の最小値とそのときの$x$を求めよ。
(1)$y=x^4+4x^2-3$
(2)$y=(x^2-2x)^2+4(x^2-2x)-1$
#10数検準1級1次 複素数

単元:
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数#数学検定#数学検定準1級#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{4}$
$z=-2-i$の偏角を$\theta$とする.
$\sin4\theta$の値を求めよ.
この動画を見る
$\boxed{4}$
$z=-2-i$の偏角を$\theta$とする.
$\sin4\theta$の値を求めよ.
三乗根の整数問題

単元:
#数Ⅰ#数A#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
整数$(m,n) m\gt 0$をすべて求めよ.
$\sqrt[3]{7+\sqrt m}+\sqrt[3]{7-\sqrt m}=n$
この動画を見る
整数$(m,n) m\gt 0$をすべて求めよ.
$\sqrt[3]{7+\sqrt m}+\sqrt[3]{7-\sqrt m}=n$
数学「大学入試良問集」【10−5③ 直線の通過領域】を宇宙一わかりやすく

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#数学(高校生)#関西大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
平面上の2点$P(t,0),Q(0,1)$に対して、$P$を通り、$PQ$に垂直な直線を$l$とする。
$t$が$-1 \leqq t \leqq 1$の範囲を動くとき、$l$が通る領域を求めて、平面上に図示せよ。
この動画を見る
平面上の2点$P(t,0),Q(0,1)$に対して、$P$を通り、$PQ$に垂直な直線を$l$とする。
$t$が$-1 \leqq t \leqq 1$の範囲を動くとき、$l$が通る領域を求めて、平面上に図示せよ。
大学入試の因数分解 松山大
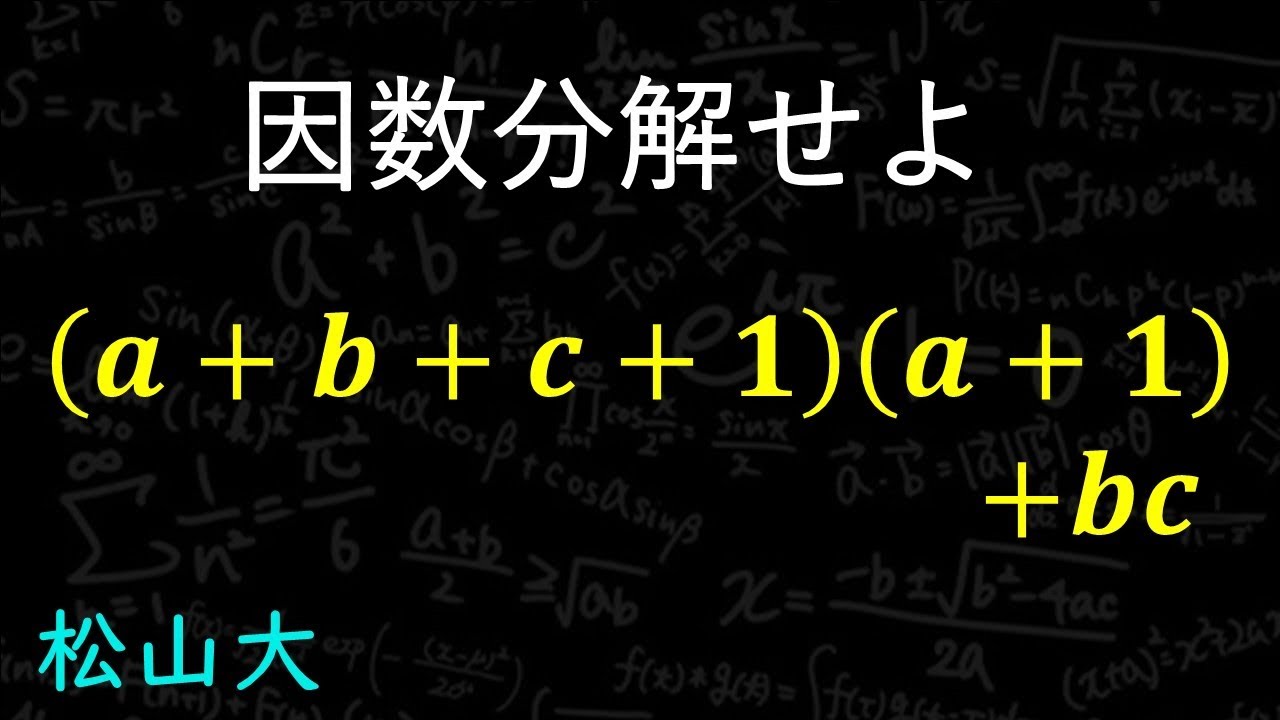
単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(a+b+c+1)(a+1)+bc$を因数分解
松山大学
この動画を見る
$(a+b+c+1)(a+1)+bc$を因数分解
松山大学
福田のわかった数学〜高校3年生理系002〜極限(2)

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{III}$ 極限(2)
次の命題で正しくないものは反例を示せ。
(1)$\displaystyle\lim_{n \to \infty}a_n=+\infty,\displaystyle\lim_{n \to \infty}b_n=+\infty $
$\to \displaystyle\lim_{n \to \infty}(a_n-b_n)=0$
(2)$\displaystyle\lim_{n \to \infty}a_n=+\infty,\displaystyle\lim_{n \to \infty}b_n=0 $
$\to \displaystyle\lim_{n \to \infty}a_nb_n=0$
(3)$0 \leqq a_n \lt 1 $
$\to \displaystyle\lim_{n \to \infty}(a_n)^n=0$
この動画を見る
数学$\textrm{III}$ 極限(2)
次の命題で正しくないものは反例を示せ。
(1)$\displaystyle\lim_{n \to \infty}a_n=+\infty,\displaystyle\lim_{n \to \infty}b_n=+\infty $
$\to \displaystyle\lim_{n \to \infty}(a_n-b_n)=0$
(2)$\displaystyle\lim_{n \to \infty}a_n=+\infty,\displaystyle\lim_{n \to \infty}b_n=0 $
$\to \displaystyle\lim_{n \to \infty}a_nb_n=0$
(3)$0 \leqq a_n \lt 1 $
$\to \displaystyle\lim_{n \to \infty}(a_n)^n=0$
福田のわかった数学〜高校2年生第8回〜相加相乗平均の関係

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 相加相乗平均の関係
$a\gt0,b\gt0,c\gt0$のとき、次の最小値を求めよ。
(1)$(a+b+c)\left(\displaystyle \frac{1}{a}+\displaystyle \frac{1}{b}+\displaystyle \frac{1}{c}\right)$
(2)$(a+2b+4c)\left(\displaystyle \frac{1}{a}+\displaystyle \frac{2}{b}+\displaystyle \frac{4}{c}\right)$
この動画を見る
数学$\textrm{II}$ 相加相乗平均の関係
$a\gt0,b\gt0,c\gt0$のとき、次の最小値を求めよ。
(1)$(a+b+c)\left(\displaystyle \frac{1}{a}+\displaystyle \frac{1}{b}+\displaystyle \frac{1}{c}\right)$
(2)$(a+2b+4c)\left(\displaystyle \frac{1}{a}+\displaystyle \frac{2}{b}+\displaystyle \frac{4}{c}\right)$
【数B】平面ベクトル:ベクトル方程式 ベクトルと軌跡:座標平面において、△ABCはBA・CA=0を満たしている。この平面上の点Pが条件AP・BP+BP・CP+CP・AP=0を満たす(続きは概要欄で)

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
座標平面において、△ABCはBA・CA=0を満たしている。この平面上の点Pが条件AP・BP+BP・CP+CP・AP=0を満たすとき、Pはどのような図形上の点であるか。
この動画を見る
座標平面において、△ABCはBA・CA=0を満たしている。この平面上の点Pが条件AP・BP+BP・CP+CP・AP=0を満たすとき、Pはどのような図形上の点であるか。
#9数検準1級1次過去問 極限

単元:
#数学検定・数学甲子園・数学オリンピック等#関数と極限#数列の極限#関数の極限#数学検定#数学検定準1級#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\boxed{7}$
$\displaystyle \lim_{x\to 1}\dfrac{x^2+2x-3}{\sqrt[3]x-1}$を求めよ.
この動画を見る
$\boxed{7}$
$\displaystyle \lim_{x\to 1}\dfrac{x^2+2x-3}{\sqrt[3]x-1}$を求めよ.
ちょっと変わった指数方程式

【数C】平面ベクトル:ベクトル方程式 ベクトルと軌跡:座標平面において、△ABCはBA・CA=0を満たしている。この平面上の点Pが条件AP・BP+BP・CP+CP・AP=0を満たす(続きは概要欄で)

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
座標平面において、△ABCはBA・CA=0を満たしている。この平面上の点Pが条件AP・BP+BP・CP+CP・AP=0を満たすとき、Pはどのような図形上の点であるか。
この動画を見る
座標平面において、△ABCはBA・CA=0を満たしている。この平面上の点Pが条件AP・BP+BP・CP+CP・AP=0を満たすとき、Pはどのような図形上の点であるか。
指数の計算 2通りで解説

単元:
#数学(中学生)#数Ⅱ#指数関数と対数関数#指数関数#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$2^{13}-2^{12} = 2^▢$
常総学院高等学校
この動画を見る
$2^{13}-2^{12} = 2^▢$
常総学院高等学校
【数Ⅰ】集合と命題:センター試験2013年

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#集合と命題(集合・命題と条件・背理法)#センター試験・共通テスト関連#センター試験#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
三角形に関する条件p,q,rを次のように定める。p:3つの内角がすべて異なる q:直角三角形でない r:45度の内角は1つもない。条件pの否定をpバーで表し、同様にq,rはそれぞれ条件qバー、rバーの否定を表すものとする。
[1]命題「r ⇒ (pまたはq)」の対偶は「(ア)⇒r」である。(ア)に当てはまるものを, 次の(0)~(3)のうちから1つ選べ。
(0)(pかつq) (1) (pかつq) (2) (pまたはq ) (3) (pまたはq)
[2] 次の(0)~(4)のうち、命題「(pまたはq) ⇒ r」に対する反例となっている三角形は(イ)と(ウ)である。(イ)と(ウ)に当てはまるものを、(0)~(4)のうちから1つずつ選べ。ただし、(イ)と(ウ)の解答の順序は問わない。
(0) 直角二等辺三角形 (1) 内角が30度,45度,105度の三角形 (2) 正三角形 (3) 3辺の長さが3,4,5の三角形 (4) 頂角が45度の二等辺三角形
[3] rは(pまたはq)であるための(エ) 。(エ)に当てはまるものを、次の(0)~(3)のうちから1つ選べ。
(0) 必要十分条件である (1) 必要条件であるが十分条件ではない (2) 十分条件であるが必要条件ではない (3) 必要条件でも十分条件でもない
この動画を見る
三角形に関する条件p,q,rを次のように定める。p:3つの内角がすべて異なる q:直角三角形でない r:45度の内角は1つもない。条件pの否定をpバーで表し、同様にq,rはそれぞれ条件qバー、rバーの否定を表すものとする。
[1]命題「r ⇒ (pまたはq)」の対偶は「(ア)⇒r」である。(ア)に当てはまるものを, 次の(0)~(3)のうちから1つ選べ。
(0)(pかつq) (1) (pかつq) (2) (pまたはq ) (3) (pまたはq)
[2] 次の(0)~(4)のうち、命題「(pまたはq) ⇒ r」に対する反例となっている三角形は(イ)と(ウ)である。(イ)と(ウ)に当てはまるものを、(0)~(4)のうちから1つずつ選べ。ただし、(イ)と(ウ)の解答の順序は問わない。
(0) 直角二等辺三角形 (1) 内角が30度,45度,105度の三角形 (2) 正三角形 (3) 3辺の長さが3,4,5の三角形 (4) 頂角が45度の二等辺三角形
[3] rは(pまたはq)であるための(エ) 。(エ)に当てはまるものを、次の(0)~(3)のうちから1つ選べ。
(0) 必要十分条件である (1) 必要条件であるが十分条件ではない (2) 十分条件であるが必要条件ではない (3) 必要条件でも十分条件でもない
数学「大学入試良問集」【10−5② 直線の通過領域の標準レベル】を宇宙一わかりやすく

単元:
#数Ⅱ#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
実数$t$が$0 \leqq t \leqq 1$をみたすときの直線$y=tx+t^2$の通過領域を求めよ。
この動画を見る
実数$t$が$0 \leqq t \leqq 1$をみたすときの直線$y=tx+t^2$の通過領域を求めよ。
【高校数学】ユークリッドの互除法の例題2題 5-7.5【数学A】

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1⃣
390と273の最大公約数を求めよ
2⃣
31$x$+22$y$=3を満たす整数$x、y$の組を1つ求めよ
この動画を見る
1⃣
390と273の最大公約数を求めよ
2⃣
31$x$+22$y$=3を満たす整数$x、y$の組を1つ求めよ
【数B】漸化式:東大1995年 タイルの敷き詰め

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
2辺の長さが1と2の長方形と1辺の長さが2の正方形の2種類のタイルがある。縦2,横nの長方形の部屋をこれらのタイルで過不足なく敷き詰めることを考える。その並べ方の総数をA[n]で表す。ただし,nは正の整数である。たとえば$ A_1=1, A_2=3, A_3=5$ である。このとき,以下の問いに答えよう。
(1)$n≧3$のとき,$A_n$を$A_{n-1},A_{n-2}$を用いて表そう。
(2)$A_n$をnで表そう。
この動画を見る
2辺の長さが1と2の長方形と1辺の長さが2の正方形の2種類のタイルがある。縦2,横nの長方形の部屋をこれらのタイルで過不足なく敷き詰めることを考える。その並べ方の総数をA[n]で表す。ただし,nは正の整数である。たとえば$ A_1=1, A_2=3, A_3=5$ である。このとき,以下の問いに答えよう。
(1)$n≧3$のとき,$A_n$を$A_{n-1},A_{n-2}$を用いて表そう。
(2)$A_n$をnで表そう。
福田のわかった数学〜高校1年生第8回〜2次関数の最大最小(1)

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 2次関数の最大最小(1)
次の関数の最大最小を調べよ。
(1) $y=\displaystyle \frac{x^2+6x+6}{x^2+x+1}$ (2)$y=x-\sqrt x$
この動画を見る
数学$\textrm{I}$ 2次関数の最大最小(1)
次の関数の最大最小を調べよ。
(1) $y=\displaystyle \frac{x^2+6x+6}{x^2+x+1}$ (2)$y=x-\sqrt x$
07愛知県教員採用試験(数学:6番 対数関数)

単元:
#数Ⅱ#指数関数と対数関数#対数関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{6}$
$f(x)=\log_2 (x+2)+\log_4 (4-x)$の
最大値を求めよ.
この動画を見る
$\boxed{6}$
$f(x)=\log_2 (x+2)+\log_4 (4-x)$の
最大値を求めよ.
【数I】集合と命題:条件の否定:否定は○○“じゃない”

単元:
#数Ⅰ#数と式#集合と命題(集合・命題と条件・背理法)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
かつ、または、すべて(任意)、あるの否定。
文字はすべて実数とする。次の条件の否定を述べよ。
(1)x>0かつy≦0
(2)x≧2またはx<-3
(3)a=b=c=0
この動画を見る
かつ、または、すべて(任意)、あるの否定。
文字はすべて実数とする。次の条件の否定を述べよ。
(1)x>0かつy≦0
(2)x≧2またはx<-3
(3)a=b=c=0
