 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
いろいろな方法で解こう

単元:
#数Ⅱ#指数関数と対数関数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\left(\dfrac{1}{2021}\right)$ VS $\left(\dfrac{1}{2022}\right)^{2021}$
どちらが大きいか?
この動画を見る
$\left(\dfrac{1}{2021}\right)$ VS $\left(\dfrac{1}{2022}\right)^{2021}$
どちらが大きいか?
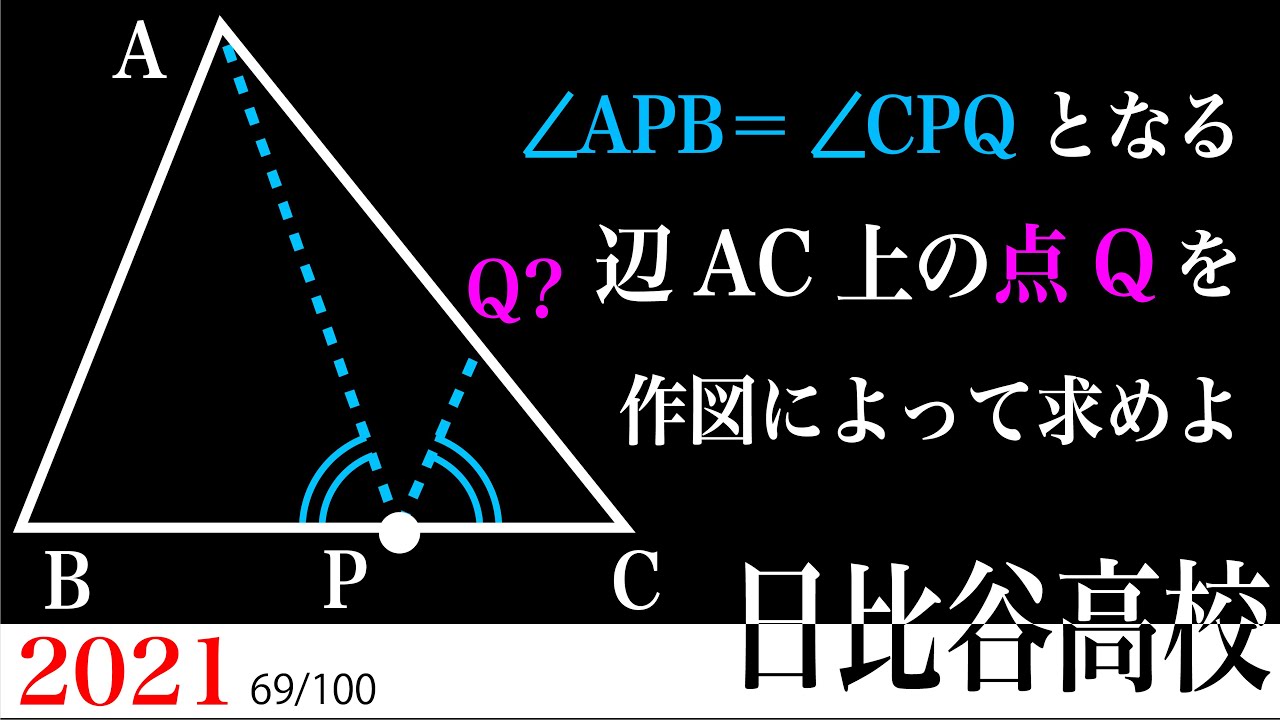
角度が等しい作図 2021 日比谷 B
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle APB = \angle CPQ$となる辺AC上の点Qを作図によって求めよ。
*図は動画内参照
2021日比谷高等学校
この動画を見る
$\angle APB = \angle CPQ$となる辺AC上の点Qを作図によって求めよ。
*図は動画内参照
2021日比谷高等学校
2021 八王子東高校最初の一問 A

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\frac{\sqrt 6 + 2}{\sqrt 2})(\frac{\sqrt 2 - \sqrt 3 }{3})$
2021八王子東高等学校
この動画を見る
$(\frac{\sqrt 6 + 2}{\sqrt 2})(\frac{\sqrt 2 - \sqrt 3 }{3})$
2021八王子東高等学校
倍数の性質の利用 2021 新宿 B

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
次の条件を満たす4ケタの自然数A=?
・Aの千の位と一の位を入れ替えた数をB
・Aの十の位と一の位を入れ替えた数をC
・Aの千の位と百の位を入れ替えた数をD
・Aは3の倍数
・Aは1の位が素数
・Bは5の倍数
・Cは10の倍数
・D-A=3600
2021都立新宿高等学校
この動画を見る
次の条件を満たす4ケタの自然数A=?
・Aの千の位と一の位を入れ替えた数をB
・Aの十の位と一の位を入れ替えた数をC
・Aの千の位と百の位を入れ替えた数をD
・Aは3の倍数
・Aは1の位が素数
・Bは5の倍数
・Cは10の倍数
・D-A=3600
2021都立新宿高等学校
○か✖️か 2021 中大横浜 B

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
正しいものをすべて選べ
(ア)$\frac{-4+2\sqrt 3}{2} = -2+2\sqrt 3$
(イ)1は素数である
(ウ)$\sqrt{1.69}$は有理数
(エ)$\frac{3}{0}=0$である
(オ)$\sqrt 9 + \sqrt{16} = \sqrt{25}$
2021中央大学附属横浜高等学校
この動画を見る
正しいものをすべて選べ
(ア)$\frac{-4+2\sqrt 3}{2} = -2+2\sqrt 3$
(イ)1は素数である
(ウ)$\sqrt{1.69}$は有理数
(エ)$\frac{3}{0}=0$である
(オ)$\sqrt 9 + \sqrt{16} = \sqrt{25}$
2021中央大学附属横浜高等学校
【高校数学】末尾の0の数の個数の例題 5-5.5【数学A】

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1) 1から100までの100個の自然数の積N=1・2・3・・・・・100について計算すると、
末尾には0が連続して何個並ぶか答えよ。
(2) 200!は一の位からいくつ0が連続する整数か答えよ。
この動画を見る
(1) 1から100までの100個の自然数の積N=1・2・3・・・・・100について計算すると、
末尾には0が連続して何個並ぶか答えよ。
(2) 200!は一の位からいくつ0が連続する整数か答えよ。
07大阪府教員採用試験(数学:1番 三角関数と極限)

単元:
#数Ⅱ#三角関数#微分法と積分法#平均変化率・極限・導関数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\boxed{1}$
$x-2\sin\theta-\cos2\theta$
$y=\displaystyle \sum_{n=1}^{\infty} \left(\dfrac{x}{6}\right)^n$のとりうる値の範囲を求めよ.
この動画を見る
$\boxed{1}$
$x-2\sin\theta-\cos2\theta$
$y=\displaystyle \sum_{n=1}^{\infty} \left(\dfrac{x}{6}\right)^n$のとりうる値の範囲を求めよ.
2021同志社大 4次方程式4つの虚数解

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$c$は実数であり,定数である.
$x^4+cx^3+cx^2+cx+1=0$の$4$つの解がすべて虚数となる.$c$の必要十分条件である.
$4$つの虚数解が複素平面上で正方形になる$c$の値を求めよ.
2021同志社過去問
この動画を見る
$c$は実数であり,定数である.
$x^4+cx^3+cx^2+cx+1=0$の$4$つの解がすべて虚数となる.$c$の必要十分条件である.
$4$つの虚数解が複素平面上で正方形になる$c$の値を求めよ.
2021同志社過去問
四面体の体積(垂線はどこに落ちる??)慶應義塾 2021 C

単元:
#数学(中学生)#数A#図形の性質#空間における垂直と平行と多面体(オイラーの法則)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
体積=?
*図は動画内参照
2021慶應義塾高等学校
この動画を見る
体積=?
*図は動画内参照
2021慶應義塾高等学校
複素関数論⑧ 逆関数 高専数学 *25(1)-(4), *26
単元:
#数Ⅱ#複素数と方程式#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
複素関数論⑧ 逆関数に関して解説します.
この動画を見る
複素関数論⑧ 逆関数に関して解説します.
慶応高校 一言言いたいだけの動画

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
因数分解せよ.
$(a^2-2a-6)(a^2-2a-17)+18$
2021慶應義塾高過去問
この動画を見る
因数分解せよ.
$(a^2-2a-6)(a^2-2a-17)+18$
2021慶應義塾高過去問
福田の数学〜慶應義塾大学2021年理工学部第2問〜複素数と多項式の商と余り

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#複素数平面#複素数#複素数平面#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$ (1)複素数$\alpha$は$\alpha^2+3\alpha+3=0$ を満たすとする。このとき、$(\alpha+1)^2(\alpha+2)^5=\boxed{\ \ キ\ \ }$
である。また、$(\alpha+2)^s(\alpha+3)^t=3$となる整数$s,t$の組を全て求めよ。
(2)多項式$(x+1)^3(x+2)^2$を$x^2+3x+3$で割った時の商は$\boxed{\ \ ク\ \ }$、余りは$\boxed{\ \ ケ\ \ }$である。
また、$(x+1)^{2021}$を$x^2+3x+3$で割った時の余りは$\boxed{\ \ コ\ \ }$である。
2021慶應義塾大学理工学部過去問
この動画を見る
${\Large\boxed{2}}$ (1)複素数$\alpha$は$\alpha^2+3\alpha+3=0$ を満たすとする。このとき、$(\alpha+1)^2(\alpha+2)^5=\boxed{\ \ キ\ \ }$
である。また、$(\alpha+2)^s(\alpha+3)^t=3$となる整数$s,t$の組を全て求めよ。
(2)多項式$(x+1)^3(x+2)^2$を$x^2+3x+3$で割った時の商は$\boxed{\ \ ク\ \ }$、余りは$\boxed{\ \ ケ\ \ }$である。
また、$(x+1)^{2021}$を$x^2+3x+3$で割った時の余りは$\boxed{\ \ コ\ \ }$である。
2021慶應義塾大学理工学部過去問
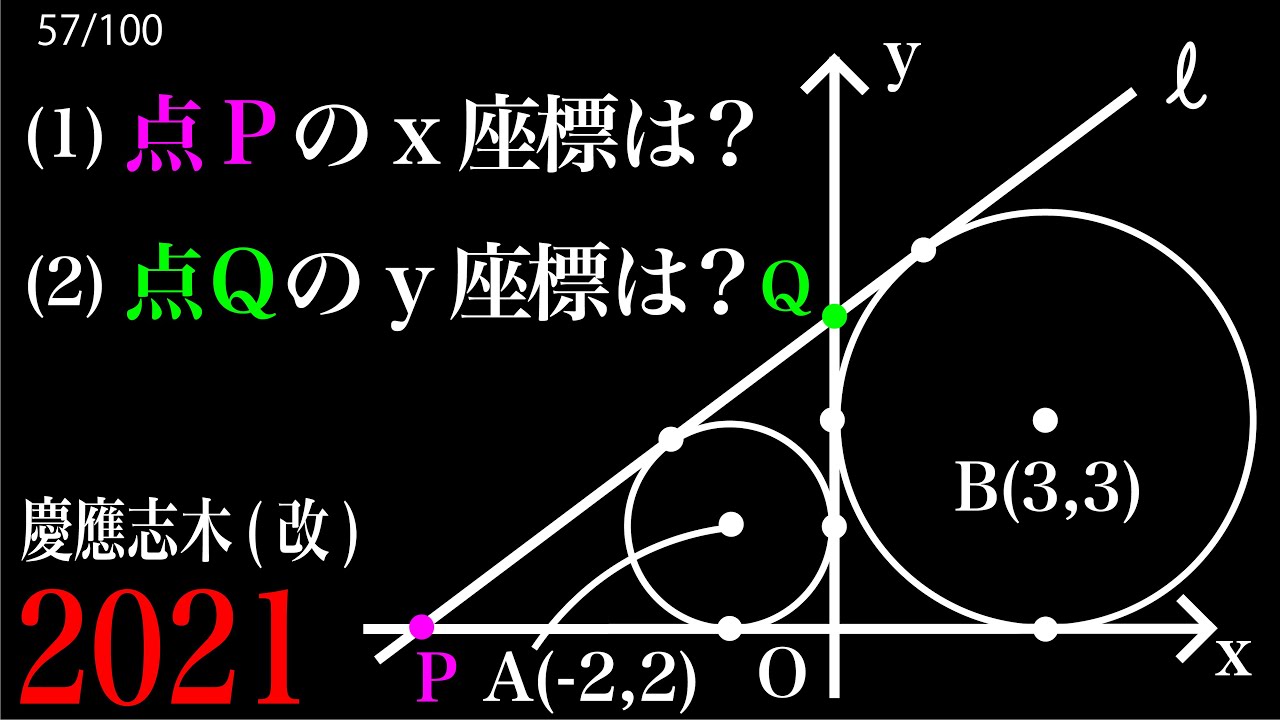
内接円 傍接円 関数 B 慶應志木2021
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
(1)点Pのx座標は?
(2)点Qのy座標は?
*図は動画内参照
2021慶應義塾志木高等学校
この動画を見る
(1)点Pのx座標は?
(2)点Qのy座標は?
*図は動画内参照
2021慶應義塾志木高等学校
17岡山県教員採用試験(数学:5番 積分)

単元:
#積分とその応用#その他#数学(高校生)#数Ⅲ#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{5}$
$n$を自然数とする.
$f(x)=e^{-x}\ \sin x,(n-1)\pi \leqq x\leqq n\pi$と
$x$軸で囲まれた部分の面積を$S_n$とする.
$\displaystyle \sum_{n=1}^{\infty} S_n$を求めよ.
この動画を見る
$\boxed{5}$
$n$を自然数とする.
$f(x)=e^{-x}\ \sin x,(n-1)\pi \leqq x\leqq n\pi$と
$x$軸で囲まれた部分の面積を$S_n$とする.
$\displaystyle \sum_{n=1}^{\infty} S_n$を求めよ.
2021早稲田 4次方程式の解

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^4+5x^3-3x^2+4x+2=0$は$\dfrac{1+\sqrt3 i}{2}$を解にもつ.
実数解を求めよ.
2021早稲田(教)
この動画を見る
$x^4+5x^3-3x^2+4x+2=0$は$\dfrac{1+\sqrt3 i}{2}$を解にもつ.
実数解を求めよ.
2021早稲田(教)
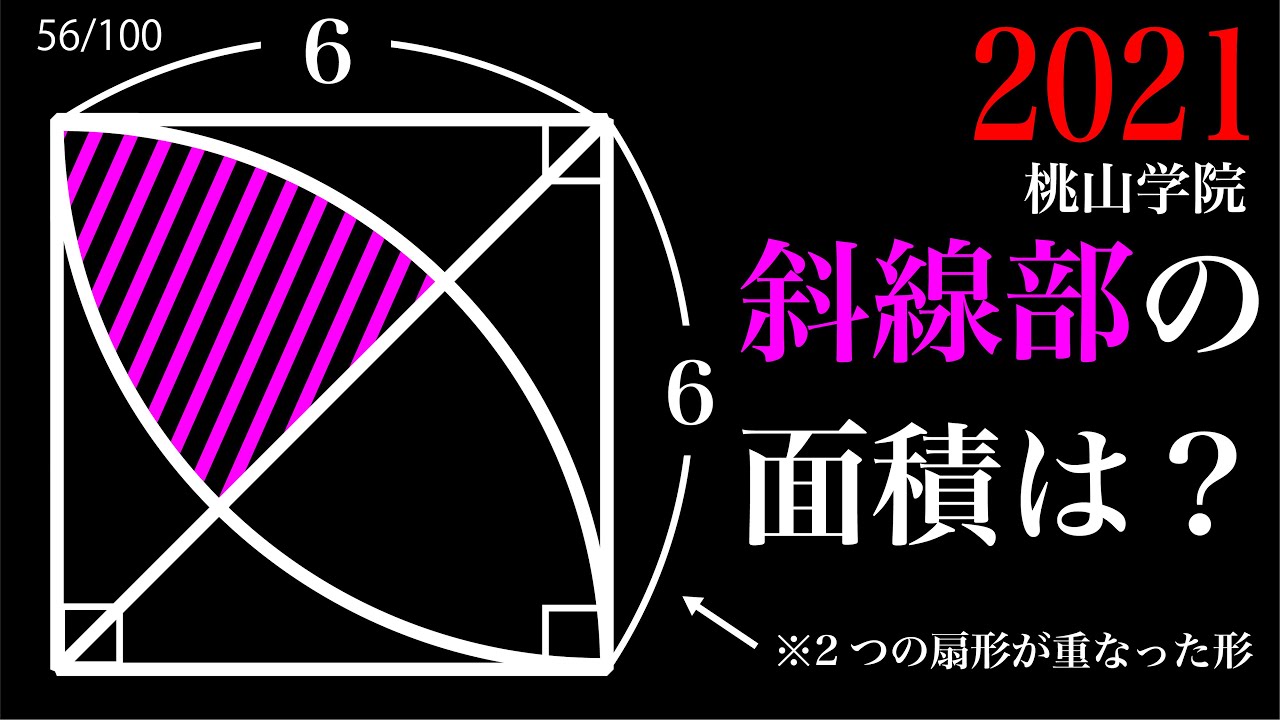
葉っぱの半分 桃山学院 A
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
斜線部の面積=?
*図は動画内参照
2021桃山学院高等学校
この動画を見る
斜線部の面積=?
*図は動画内参照
2021桃山学院高等学校
【高校数学】合同式の基本事項~modの使い方・考え方~ 5-6【数学A】

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
合同式の基本事項 modの使い方・考え方についての説明動画です
この動画を見る
合同式の基本事項 modの使い方・考え方についての説明動画です
17愛知県教員採用試験(数学:2番 三角関数)

単元:
#数Ⅱ#三角関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{2}$
$y=\cos2\theta+4k\ \sin\theta+3k-3$
任意の定数$theta$に対して$y\leqq 0$となる.
$k$の範囲を求めよ.
この動画を見る
$\boxed{2}$
$y=\cos2\theta+4k\ \sin\theta+3k-3$
任意の定数$theta$に対して$y\leqq 0$となる.
$k$の範囲を求めよ.
2021早稲田大 整式の剰余

単元:
#数Ⅱ#大学入試過去問(数学)#式と証明#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^4-x^2+1$
①$x^6$を$f(x)$で割った余りを求めよ.
②$x^{2021}$を$f(x)$で割った余りを求めよ.
③$(x^2-1)^{3k}-1$は$f(x)$で割り切れることを示せ.$k$は自然数である.
2021早稲田(理)
この動画を見る
$f(x)=x^4-x^2+1$
①$x^6$を$f(x)$で割った余りを求めよ.
②$x^{2021}$を$f(x)$で割った余りを求めよ.
③$(x^2-1)^{3k}-1$は$f(x)$で割り切れることを示せ.$k$は自然数である.
2021早稲田(理)
福田の数学〜慶應義塾大学2021年理工学部第1問〜直線群と通過範囲

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#微分とその応用#微分法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$ $t$を実数とし、座標平面上の直線$l:(2t^2-4t+2)x$$-(t^2+2)y+4t+2=0$
を考える。
(1)直線$l$は$t$の値によらず、定点を通る。その定点の座標は$\boxed{\ \ ア\ \ }$である。
(2)直線$l$の傾きを$f(t)$とする。$f(t)$の値が最小となるのは$t=\boxed{\ \ イ\ \ }$
のときであり、最大となるのは$t=\boxed{\ \ ウ\ \ }$のときである。また、
$a$を実数とするとき、$t$に関する方程式$f(t)=a$がちょうど1個の
実数解をもつような$a$の値を全て求めると、$a=\boxed{\ \ エ\ \ }$である。
(3)$t$が実数全体を動くとき、直線$l$が通過する領域を$S$とする。また$k$を
実数とする。放物線$y=\displaystyle \frac{1}{2}(x-k)^2+\displaystyle \frac{1}{2}(k-1)^2$が領域$S$と共有点
を持つような$k$の値の範囲は$\boxed{\ \ オ\ \ } \leqq k \leqq \boxed{\ \ カ\ \ }$である。
2021慶應義塾大学理工学部過去問
この動画を見る
${\Large\boxed{1}}$ $t$を実数とし、座標平面上の直線$l:(2t^2-4t+2)x$$-(t^2+2)y+4t+2=0$
を考える。
(1)直線$l$は$t$の値によらず、定点を通る。その定点の座標は$\boxed{\ \ ア\ \ }$である。
(2)直線$l$の傾きを$f(t)$とする。$f(t)$の値が最小となるのは$t=\boxed{\ \ イ\ \ }$
のときであり、最大となるのは$t=\boxed{\ \ ウ\ \ }$のときである。また、
$a$を実数とするとき、$t$に関する方程式$f(t)=a$がちょうど1個の
実数解をもつような$a$の値を全て求めると、$a=\boxed{\ \ エ\ \ }$である。
(3)$t$が実数全体を動くとき、直線$l$が通過する領域を$S$とする。また$k$を
実数とする。放物線$y=\displaystyle \frac{1}{2}(x-k)^2+\displaystyle \frac{1}{2}(k-1)^2$が領域$S$と共有点
を持つような$k$の値の範囲は$\boxed{\ \ オ\ \ } \leqq k \leqq \boxed{\ \ カ\ \ }$である。
2021慶應義塾大学理工学部過去問
各辺の垂直二等分線の交点が一致することの証明 慶応志木 2021 C

単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
下の図において点Pから辺BCに下した垂線と辺BCとの交点をQとするとき
点Qは辺BCの中点であることを示せ。
(各辺の垂直二等分線の交点一致の証明)
*図は動画内参照
2021慶應義塾志木高等学校
この動画を見る
下の図において点Pから辺BCに下した垂線と辺BCとの交点をQとするとき
点Qは辺BCの中点であることを示せ。
(各辺の垂直二等分線の交点一致の証明)
*図は動画内参照
2021慶應義塾志木高等学校
複素関数論⑦(逆関数)高専数学*24(1)-(3)

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
次の値を求めよ.
(1)$\sqrt i$
(2)$\sqrt{1+i}$
(3)$\sqrt{-4}$
この動画を見る
次の値を求めよ.
(1)$\sqrt i$
(2)$\sqrt{1+i}$
(3)$\sqrt{-4}$
18愛知県教員採用試験(数学:7番 三角関数)

単元:
#数Ⅱ#三角関数#その他#数学(高校生)#教員採用試験
指導講師:
ますただ
問題文全文(内容文):
$\boxed{7}$
$0\leqq \theta \leqq \dfrac{\pi}{2}$
$y=6\ \sin\theta\ \cos\theta+8\cos^2\theta-4$
の最大値,最小値を求めよ.
この動画を見る
$\boxed{7}$
$0\leqq \theta \leqq \dfrac{\pi}{2}$
$y=6\ \sin\theta\ \cos\theta+8\cos^2\theta-4$
の最大値,最小値を求めよ.
2021慶應義塾大 整式の剰余

単元:
#数Ⅱ#式と証明#整式の除法・分数式・二項定理
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha^2+3\alpha+3=0$のとき,
(1)$(\alpha+1)^2(\alpha+2)^5=\Box$
$(\alpha+2)^s(\alpha+3)^t=3$となる整数$s,t$の組をすべて求めよ.
(2)$(x+1)^3(x+2)^2$を$x^2+3x+3$で割った商と余りを求めよ.
$(x+1)^{2021}$を$x^2+3x+3$で割った余りを求めよ.
2021慶應(理)
この動画を見る
$\alpha^2+3\alpha+3=0$のとき,
(1)$(\alpha+1)^2(\alpha+2)^5=\Box$
$(\alpha+2)^s(\alpha+3)^t=3$となる整数$s,t$の組をすべて求めよ.
(2)$(x+1)^3(x+2)^2$を$x^2+3x+3$で割った商と余りを求めよ.
$(x+1)^{2021}$を$x^2+3x+3$で割った余りを求めよ.
2021慶應(理)
複素関数論⑥(指数関数e^zの微分)
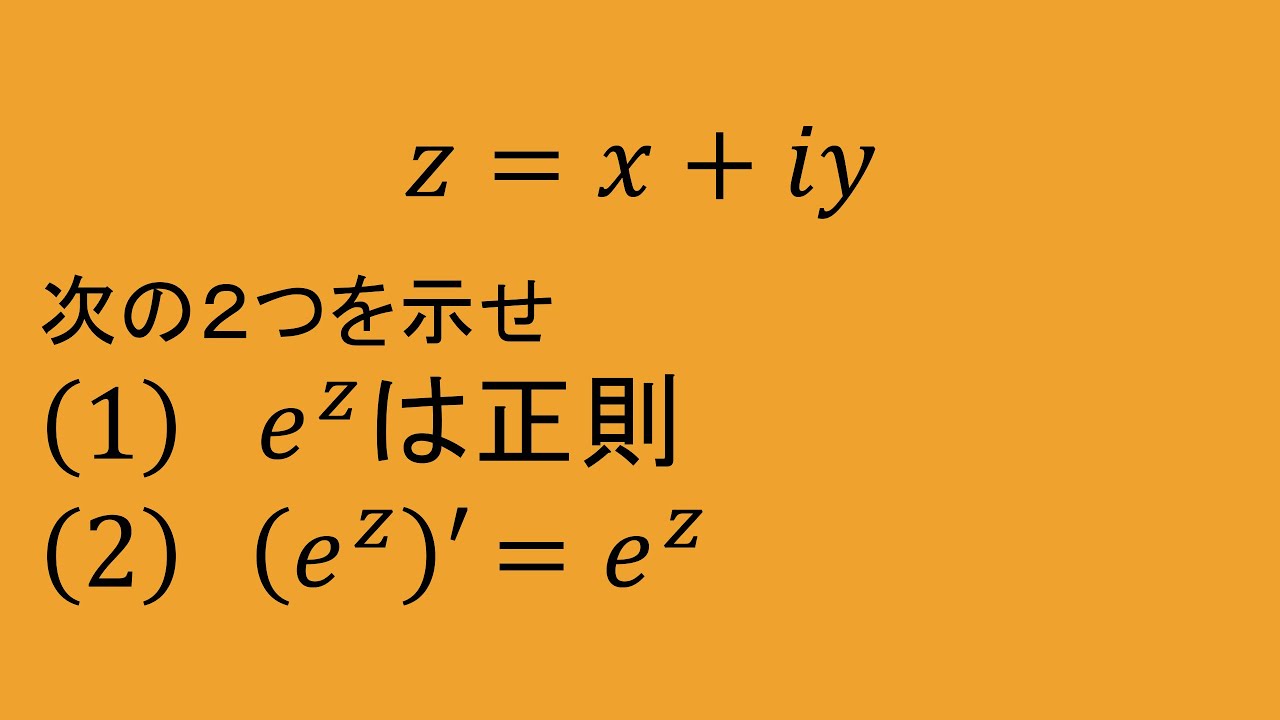
練習問題16 教採用の練習問題(格子点の数 数列)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$n:$自然数とする.
$1\leqq x \leqq 3^{n+1},0\leqq y \leqq \log_3 x$を
みたす整数の組$(x,y)$の個数を求めよ.
この動画を見る
$n:$自然数とする.
$1\leqq x \leqq 3^{n+1},0\leqq y \leqq \log_3 x$を
みたす整数の組$(x,y)$の個数を求めよ.
2021慶應義塾大(理工) 式の値

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\alpha^2+3\alpha+3=0$のとき,$(\alpha+1)^2(\alpha+2)^5=\Box$
$(\alpha+2)^s(\alpha+3)^t=3$となる整数$s,t$の組をすべて求めよ.
2021慶應(理)
この動画を見る
$\alpha^2+3\alpha+3=0$のとき,$(\alpha+1)^2(\alpha+2)^5=\Box$
$(\alpha+2)^s(\alpha+3)^t=3$となる整数$s,t$の組をすべて求めよ.
2021慶應(理)
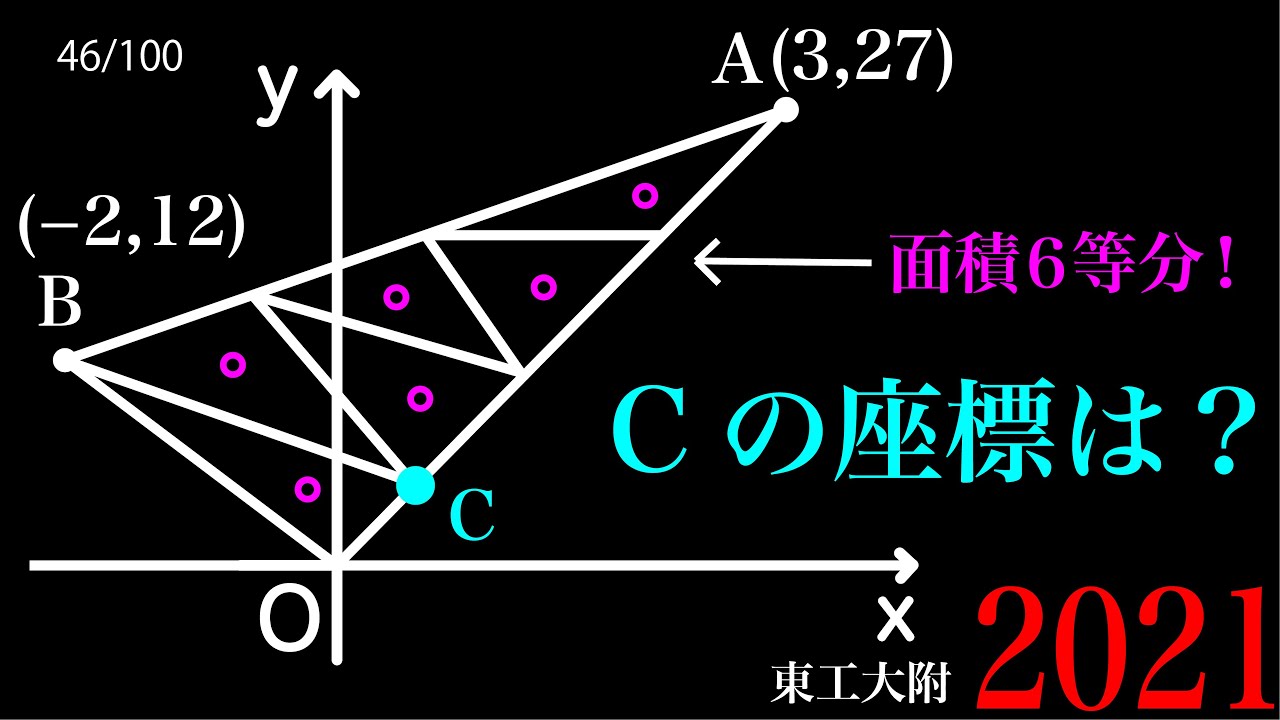
関数と図形 東工大附属(改) B
単元:
#数学(中学生)#数Ⅰ#数A#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
面積6等分
Cの座標は?
*図は動画内参照
2021東京工業大学附属科学技術高等学校
この動画を見る
面積6等分
Cの座標は?
*図は動画内参照
2021東京工業大学附属科学技術高等学校
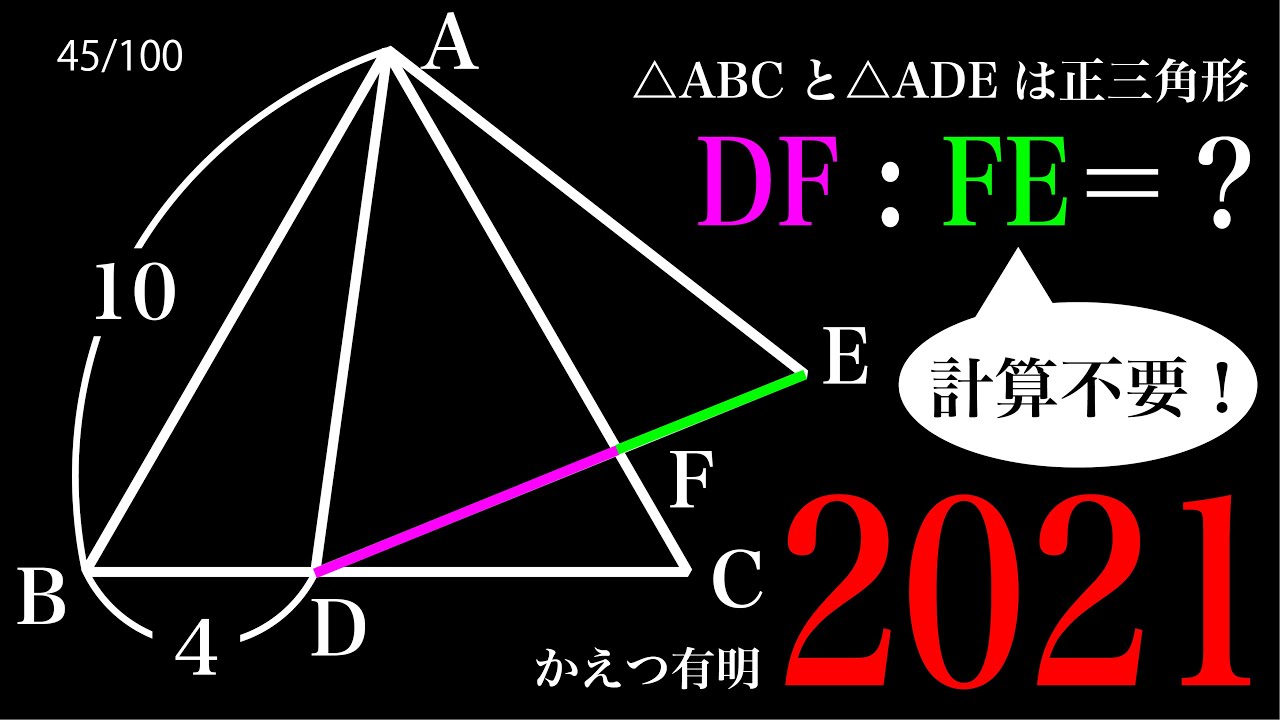
計算不要 正三角形2こ 2021かえつ有明 C
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABC、△ADEは正三角形
DF:FE=?
*図は動画内参照
2021かえつ有明高等学校
この動画を見る
△ABC、△ADEは正三角形
DF:FE=?
*図は動画内参照
2021かえつ有明高等学校
2021灘高 不思議な誘導付き整数問題

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ab^2+(3a+4)b+2a+6=0・・・①$を満たす.
(1)$P=2ab+3a+4$とする.$P^2$を$a$のみを用いて表せ.
(2)①を満たす整数$a,b$を求めよ.$a \neq 0,b \neq 0$
2021灘高過去問
この動画を見る
$ab^2+(3a+4)b+2a+6=0・・・①$を満たす.
(1)$P=2ab+3a+4$とする.$P^2$を$a$のみを用いて表せ.
(2)①を満たす整数$a,b$を求めよ.$a \neq 0,b \neq 0$
2021灘高過去問
