 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
共通テストを終えて_全部難しかったよ

単元:
#大学入試過去問(数学)#物理#化学#生物#情報Ⅰ(高校生)#センター試験・共通テスト関連#共通テスト#大学入試過去問(物理)#大学入試過去問(化学)#英語(高校生)#国語(高校生)#社会(高校生)#日本史#世界史#大学入試過去問(英語)#大学入試過去問(国語)#共通テスト#共通テスト(現代文)#大学入試過去問(生物)#共通テスト・センター試験#共通テスト(古文)#共通テスト#大学入試過去問・共通テスト・模試関連#大学入試過去問・共通テスト・模試関連#数学(高校生)#理科(高校生)#共通テスト#模試解説・過去問解説#【河合塾】全統共通テスト模試
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
この動画を見る
福田の数学〜過去の入試問題(期間限定)〜東京慈恵会医科大学医学部2020第2問〜関数列の極限

単元:
#大学入試過去問(数学)#微分法と積分法#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京慈恵会医科大学#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$p$を$2$以上の自然数の定数とする。$n$=$2$, $3$, $4$...に対して、関数 $f_n(x) $$(n\gt0)$を
$f_n(x) = (1 + \dfrac{x}{n})(1 + \dfrac{x}{n+1}) \cdot\cdot \cdot(1 + \dfrac{x}{pn})
$
で定める。例えば$p$ = $2$のとき
$
f_2(x) = (1 + \dfrac{x}{2})(1 + \dfrac{x}{3})(1 + \dfrac{x}{4})
$
$
f_3(x) = (1 + \dfrac{x}{3})(1 + \dfrac{x}{4})(1 + \dfrac{x}{5})(1 + \dfrac{x}{6})
$
である。$f(x)=\displaystyle \lim_{ n \to \infty }f_n(x)$ $(n\gt0)$とおくとき、次の問に答えよ。
$(1)$$t$$\geqq$$0$のとき、不等式$\dfrac{t}{1+t}$$\leqq$$\log(1+t)$$\leqq$$t$ が成り立つことを示せ。ただし、対数は自然対数とする。
$(2)$ $f(x)$を求めよ。
この動画を見る
$p$を$2$以上の自然数の定数とする。$n$=$2$, $3$, $4$...に対して、関数 $f_n(x) $$(n\gt0)$を
$f_n(x) = (1 + \dfrac{x}{n})(1 + \dfrac{x}{n+1}) \cdot\cdot \cdot(1 + \dfrac{x}{pn})
$
で定める。例えば$p$ = $2$のとき
$
f_2(x) = (1 + \dfrac{x}{2})(1 + \dfrac{x}{3})(1 + \dfrac{x}{4})
$
$
f_3(x) = (1 + \dfrac{x}{3})(1 + \dfrac{x}{4})(1 + \dfrac{x}{5})(1 + \dfrac{x}{6})
$
である。$f(x)=\displaystyle \lim_{ n \to \infty }f_n(x)$ $(n\gt0)$とおくとき、次の問に答えよ。
$(1)$$t$$\geqq$$0$のとき、不等式$\dfrac{t}{1+t}$$\leqq$$\log(1+t)$$\leqq$$t$ が成り立つことを示せ。ただし、対数は自然対数とする。
$(2)$ $f(x)$を求めよ。
福田のおもしろ数学383〜関数方程式

単元:
#数列#数学的帰納法#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$0$以上の整数の集合を$\mathbb{N}$$_0$とする。
$f:$$\mathbb{N}$$_0$→$\mathbb{N}$$_0$が任意の$x≧y\in $$\mathbb{N}$$_0$で$f(x^2)-f(y^2)=f(x+y)f(x-y)$を満たす。
$f(x)$を求めよ。
この動画を見る
$0$以上の整数の集合を$\mathbb{N}$$_0$とする。
$f:$$\mathbb{N}$$_0$→$\mathbb{N}$$_0$が任意の$x≧y\in $$\mathbb{N}$$_0$で$f(x^2)-f(y^2)=f(x+y)f(x-y)$を満たす。
$f(x)$を求めよ。
共通テスト2日目_ふきふき占い【午後も頑張れ】

単元:
#大学入試過去問(数学)#物理#化学#生物#情報Ⅰ(高校生)#センター試験・共通テスト関連#共通テスト#大学入試過去問(物理)#大学入試過去問(化学)#英語(高校生)#国語(高校生)#社会(高校生)#日本史#世界史#大学入試過去問(英語)#大学入試過去問(国語)#共通テスト#共通テスト(現代文)#大学入試過去問(生物)#共通テスト・センター試験#共通テスト(古文)#共通テスト#大学入試過去問・共通テスト・模試関連#大学入試過去問・共通テスト・模試関連#数学(高校生)#理科(高校生)#共通テスト#模試解説・過去問解説#【河合塾】全統共通テスト模試
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
この動画を見る
福田の数学〜過去の入試問題(期間限定)〜東京慈恵会医科大学医学部2020第2問〜関数列の極限

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\fbox{1}$ 次の$\square$にあてはまる適切な数値を解答欄に記入せよ。
袋$A$には赤玉$3$個、白玉$1$個、袋$B$には赤玉$1$個、白玉$3$個が入っている。
「袋$A$から$2$個の玉を取り出して袋$B$に入れ、次に袋$B$から$2$個の玉を取り出して袋$A$に入れる」という操作を繰り返す。$1$回の操作の後、袋$A$に白玉が$2$個以上ある確率は$\fbox{ア}$、$2$回の操作の後、袋$A$の中が白玉だけになる確率は$\fbox{イ}$である。
この動画を見る
$\fbox{1}$ 次の$\square$にあてはまる適切な数値を解答欄に記入せよ。
袋$A$には赤玉$3$個、白玉$1$個、袋$B$には赤玉$1$個、白玉$3$個が入っている。
「袋$A$から$2$個の玉を取り出して袋$B$に入れ、次に袋$B$から$2$個の玉を取り出して袋$A$に入れる」という操作を繰り返す。$1$回の操作の後、袋$A$に白玉が$2$個以上ある確率は$\fbox{ア}$、$2$回の操作の後、袋$A$の中が白玉だけになる確率は$\fbox{イ}$である。
角の二度分線

福田のおもしろ数学382〜整式が素数となる自然数nの値

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$n^8+n+1$が素数となる$n$をすべて求めて下さい。
この動画を見る
$n^8+n+1$が素数となる$n$をすべて求めて下さい。
福田の数学〜過去の入試問題(期間限定)〜東京慈恵会医科大学医学部2020第1問〜確率の基本性質

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#数学(高校生)#東京慈恵会医科大学#東京慈恵会医科大学
指導講師:
福田次郎
問題文全文(内容文):
$\fbox{1}$ 次の$\square$にあてはまる適切な数値を解答欄に記入せよ。
袋$A$には赤玉$3$個、白玉$1$個、袋$B$には赤玉$1$個、白玉$3$個が入っている。
「袋$A$から$2$個の玉を取り出して袋$B$に入れ、次に袋$B$から$2$個の玉を取り出して袋$A$に入れる」という操作を繰り返す。$1$回の操作の後、袋$A$に白玉が$2$個以上ある確率は$\fbox{(ア)}$、$2$回の操作の後、袋$A$の中が白玉だけになる確率は$\fbox{(イ)}$である。
この動画を見る
$\fbox{1}$ 次の$\square$にあてはまる適切な数値を解答欄に記入せよ。
袋$A$には赤玉$3$個、白玉$1$個、袋$B$には赤玉$1$個、白玉$3$個が入っている。
「袋$A$から$2$個の玉を取り出して袋$B$に入れ、次に袋$B$から$2$個の玉を取り出して袋$A$に入れる」という操作を繰り返す。$1$回の操作の後、袋$A$に白玉が$2$個以上ある確率は$\fbox{(ア)}$、$2$回の操作の後、袋$A$の中が白玉だけになる確率は$\fbox{(イ)}$である。
【数A】【場合の数と確率】確率の基本3 ※問題文は概要欄

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
$1$個のさいころを$3$回投げるとき, 次の確率を求めよ。
(1) 何回目かにその回の番号と同じ目が出る確率
(2) どの回にもその回の番号と同じ目が出ないで,しかも$1$の目が1回も出ない確率
ある試行における2つの事象 $A, B$について,$P(A)=0.5,P(B)=11$,
$P(A\cup B) = 0.6$ であるとき, 次の問いに答えよ。
(1)$ P(A \cap B),P(A \cap \overline{ B }), P(\overline{ A }∩B)$ を求めよ。
(2)$ A,B$のどちらか一方だけが起こる事象を,$ A, B, U, 0, \overline{ }$ を用いて表せ。また,その事象が起こる確率を求めよ。
この動画を見る
$1$個のさいころを$3$回投げるとき, 次の確率を求めよ。
(1) 何回目かにその回の番号と同じ目が出る確率
(2) どの回にもその回の番号と同じ目が出ないで,しかも$1$の目が1回も出ない確率
ある試行における2つの事象 $A, B$について,$P(A)=0.5,P(B)=11$,
$P(A\cup B) = 0.6$ であるとき, 次の問いに答えよ。
(1)$ P(A \cap B),P(A \cap \overline{ B }), P(\overline{ A }∩B)$ を求めよ。
(2)$ A,B$のどちらか一方だけが起こる事象を,$ A, B, U, 0, \overline{ }$ を用いて表せ。また,その事象が起こる確率を求めよ。
福田のおもしろ数学381〜三角形に内接する長方形と円の面積和の最大値
単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
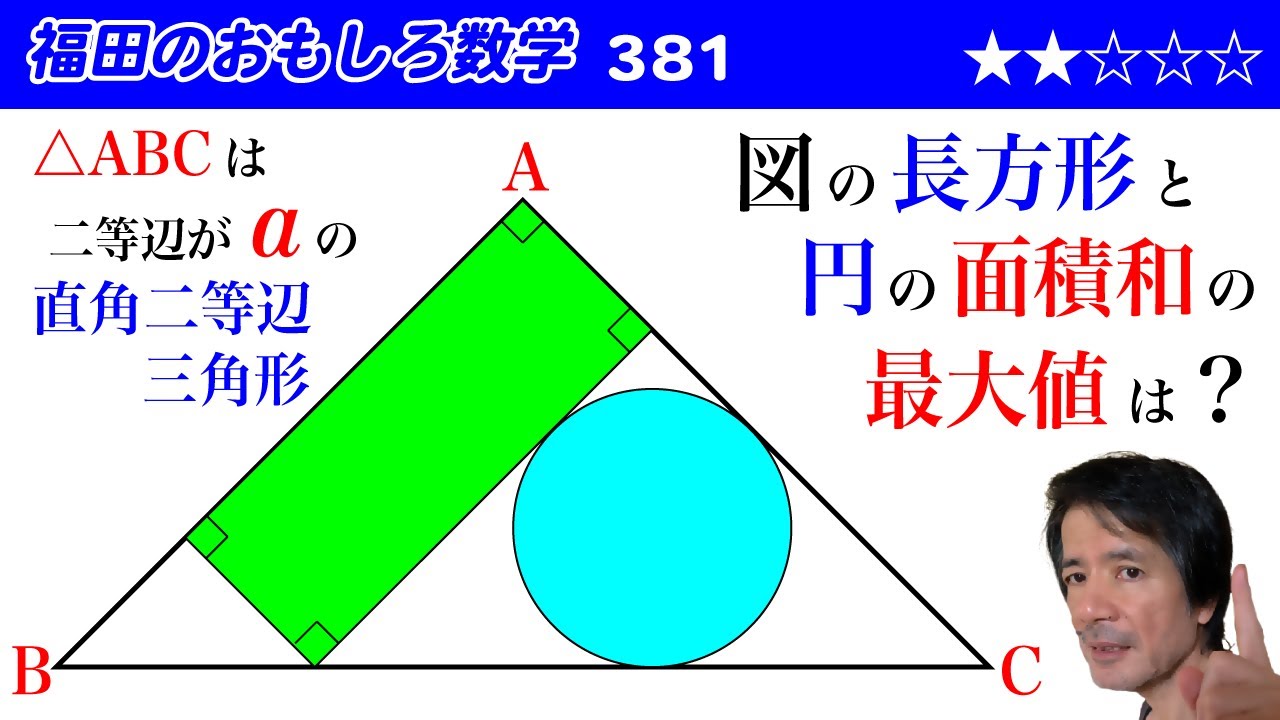
$\triangle$$ABC$は二等辺が$a$の直角二等辺三角形である。また、図のように
三角形の内部に長方形と円を配置する。
図の長方形と円の面積和の最大値は?
この動画を見る
$\triangle$$ABC$は二等辺が$a$の直角二等辺三角形である。また、図のように
三角形の内部に長方形と円を配置する。
図の長方形と円の面積和の最大値は?
福田の数学〜過去の入試問題(期間限定)〜慶應義塾大学理工学部2020第5問〜平面ベクトルと面積比

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\fbox{5}$ 平行四辺形$ABCD$において、$AB=2, BC=3$とし、対角線$AC$の長さを$4$とする。 辺$AB, BC, CD, DA$上にそれぞれ点$E, F, G, H$を$AE=BF=CG=DH=x$を満たすようにとる。ただし、$x$は$0x<2$の範囲を動くとする。さらに、対角線$AC$上に点$P$を$AP=x^2$を満たすようにとる。以下では、平行四辺形$ABCD$の面積を$S$とする。
(1) $\triangle$$AEP$の面積を$T_1$とする。$\frac{T_1}{S}$は、$x$を用いて表すと$\fbox{ テ }$となる。
(2) $\triangle$$EFP$ の面積を$T_2$とする。$\frac{T_2}{S}$は、$x=$$\fbox{ ト }$のとき最大値$\fbox{ ナ }$をとる。
(3) $\triangle$$GHP$の面積を$T_3$とする。$\frac{T_3}{S}$となるのは$x=$$\fbox{ ニ }$のときである。
(4) 点$P$が線分$EH$上にあるのは$x=$$\fbox{ ヌ }$のときである。
この動画を見る
$\fbox{5}$ 平行四辺形$ABCD$において、$AB=2, BC=3$とし、対角線$AC$の長さを$4$とする。 辺$AB, BC, CD, DA$上にそれぞれ点$E, F, G, H$を$AE=BF=CG=DH=x$を満たすようにとる。ただし、$x$は$0x<2$の範囲を動くとする。さらに、対角線$AC$上に点$P$を$AP=x^2$を満たすようにとる。以下では、平行四辺形$ABCD$の面積を$S$とする。
(1) $\triangle$$AEP$の面積を$T_1$とする。$\frac{T_1}{S}$は、$x$を用いて表すと$\fbox{ テ }$となる。
(2) $\triangle$$EFP$ の面積を$T_2$とする。$\frac{T_2}{S}$は、$x=$$\fbox{ ト }$のとき最大値$\fbox{ ナ }$をとる。
(3) $\triangle$$GHP$の面積を$T_3$とする。$\frac{T_3}{S}$となるのは$x=$$\fbox{ ニ }$のときである。
(4) 点$P$が線分$EH$上にあるのは$x=$$\fbox{ ヌ }$のときである。
福田のおもしろ数学380〜定積分の計算

【数学】2023年度 第4回 高2模試 全問解説

単元:
#大学入試過去問(数学)#全統模試(河合塾)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
大問1:小問集合
(1)AB=15, AC=7, ∠BAC=60°の△ABCがある。辺BCの長さと△ABCの内接円の半径を求めよ。
(2)aを実数の定数とする。xの2次方程式x2-ax-a-9=0が-2より小さい解と3より大きい解をもつようなの値の範囲を求めよ。
(3)方程式x3+3x2+2x-6=0を複素数の範囲で解け。
(4)座標平面上の直線y=x上の点で、直線x+2y-4=0までの距離が√5である点の座標をすべて求めよ。
(5)方程式4^(x+1)+7・2^x-2=0を解け。
(6)不等式log₂x+1≧log₂(2-x)を解け。
大問2:三角関数
aを正の定数とし、関数f(θ)をf(θ)=2sin²θ+2√3sinθcosθ+a(√3sinθ+cosθ)-6a²+1とする。
(1)√3sinθ+cosθをrsin(θ+α)の形に表せ。ただし、r>0,-π<α≦πとする。
(2)t=√3sinθ+cosθとおくとき、f(θ)をtの2次式で表せ。
(3)方程式f(θ)=0(0≦θ≦π)…(*)について考える。
(i)a=1のとき、(*)を解け。
(ii)(*)の異なる解の個数がちょうど2個となるようなaの値の範囲を求めよ。
大問3:場合の数
A,B,Cの3人を含む9人の生徒について考える。
(1)4人と5人の2つの組に分けるとき、分け方は何通りあるか。
(2)3人ずつ3つの組に分けるとき、
(i)分け方は全部で何通りあるか。
(ii)AとBが同じ組に入る分け方は何通りあるか。
(3)「9人を3人ずつ3つの班に分けて、それぞれの班で1人ずつ班長を選ぶこと」を班決めということにする。その際、AとBが同じ班に入るときAは班長になることができず、BとCが同じ班に入るときBは班長になることができないものとする。
(i)AとBが同じ班に入り、Cは別の班に入る班決めの仕方は何通りあるか。
(ii)班決めの仕方は全部で何通りあるか。
大問4:微分法
t>0とする。f(x)=x⁴-6x²とし、曲線C:y=f(x)上の点P(t,f(t))におけるCの接線をlとする。
(1)t=1のときのlの方程式を求めよ。また、このときlとCのP以外の共有点の座標を求めよ。
(2)lとCがP以外に異なる2つの共有点をもつようなtの値の範囲を求めよ。
(3)(2)のとき、lとCのP以外の2つの共有点をQ(α,f(α)), R(β,f(β))(a<β)とし、3点P, Q, RにおけるCの接線の傾きをそれぞれmP、mQ、mRとする。このとき、mP+mQ+mRのとり得る値の範囲を求めよ。
大問5:数列
数列{a[n]}(n=1,2,3,…)は公差が正の等差数列でa₁+a₂+a₃=-3. a₁a₃=-3を満たし、数列{b[n]}は
b₁=-1, b[n+1]=│b[n]│+a[n] (n=1,2,3,…)を満たしている。
(1)数列{a[n])の一般項を求めよ。
(2)b₂、b₃を求めよ。また、b≧0となるようなnの値の範囲を求めよ。
(3)n≧4のとき、数列{b[n]}の一般項を求めよ。
(4)n≧4のとき、∑[k=1~n]b[k]を求めよ。
この動画を見る
大問1:小問集合
(1)AB=15, AC=7, ∠BAC=60°の△ABCがある。辺BCの長さと△ABCの内接円の半径を求めよ。
(2)aを実数の定数とする。xの2次方程式x2-ax-a-9=0が-2より小さい解と3より大きい解をもつようなの値の範囲を求めよ。
(3)方程式x3+3x2+2x-6=0を複素数の範囲で解け。
(4)座標平面上の直線y=x上の点で、直線x+2y-4=0までの距離が√5である点の座標をすべて求めよ。
(5)方程式4^(x+1)+7・2^x-2=0を解け。
(6)不等式log₂x+1≧log₂(2-x)を解け。
大問2:三角関数
aを正の定数とし、関数f(θ)をf(θ)=2sin²θ+2√3sinθcosθ+a(√3sinθ+cosθ)-6a²+1とする。
(1)√3sinθ+cosθをrsin(θ+α)の形に表せ。ただし、r>0,-π<α≦πとする。
(2)t=√3sinθ+cosθとおくとき、f(θ)をtの2次式で表せ。
(3)方程式f(θ)=0(0≦θ≦π)…(*)について考える。
(i)a=1のとき、(*)を解け。
(ii)(*)の異なる解の個数がちょうど2個となるようなaの値の範囲を求めよ。
大問3:場合の数
A,B,Cの3人を含む9人の生徒について考える。
(1)4人と5人の2つの組に分けるとき、分け方は何通りあるか。
(2)3人ずつ3つの組に分けるとき、
(i)分け方は全部で何通りあるか。
(ii)AとBが同じ組に入る分け方は何通りあるか。
(3)「9人を3人ずつ3つの班に分けて、それぞれの班で1人ずつ班長を選ぶこと」を班決めということにする。その際、AとBが同じ班に入るときAは班長になることができず、BとCが同じ班に入るときBは班長になることができないものとする。
(i)AとBが同じ班に入り、Cは別の班に入る班決めの仕方は何通りあるか。
(ii)班決めの仕方は全部で何通りあるか。
大問4:微分法
t>0とする。f(x)=x⁴-6x²とし、曲線C:y=f(x)上の点P(t,f(t))におけるCの接線をlとする。
(1)t=1のときのlの方程式を求めよ。また、このときlとCのP以外の共有点の座標を求めよ。
(2)lとCがP以外に異なる2つの共有点をもつようなtの値の範囲を求めよ。
(3)(2)のとき、lとCのP以外の2つの共有点をQ(α,f(α)), R(β,f(β))(a<β)とし、3点P, Q, RにおけるCの接線の傾きをそれぞれmP、mQ、mRとする。このとき、mP+mQ+mRのとり得る値の範囲を求めよ。
大問5:数列
数列{a[n]}(n=1,2,3,…)は公差が正の等差数列でa₁+a₂+a₃=-3. a₁a₃=-3を満たし、数列{b[n]}は
b₁=-1, b[n+1]=│b[n]│+a[n] (n=1,2,3,…)を満たしている。
(1)数列{a[n])の一般項を求めよ。
(2)b₂、b₃を求めよ。また、b≧0となるようなnの値の範囲を求めよ。
(3)n≧4のとき、数列{b[n]}の一般項を求めよ。
(4)n≧4のとき、∑[k=1~n]b[k]を求めよ。
素数を扱う整数問題の良問!分からなければ実験あるのみ!【京都大学】【数学 入試問題】

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#京都大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
f(x)=x³+2x²+2
|f(n)|と|f(n+1)|が素数となる整数nをすべて求めよ。
この動画を見る
f(x)=x³+2x²+2
|f(n)|と|f(n+1)|が素数となる整数nをすべて求めよ。
福田のおもしろ数学379〜関数の偶奇性の判定
単元:
#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
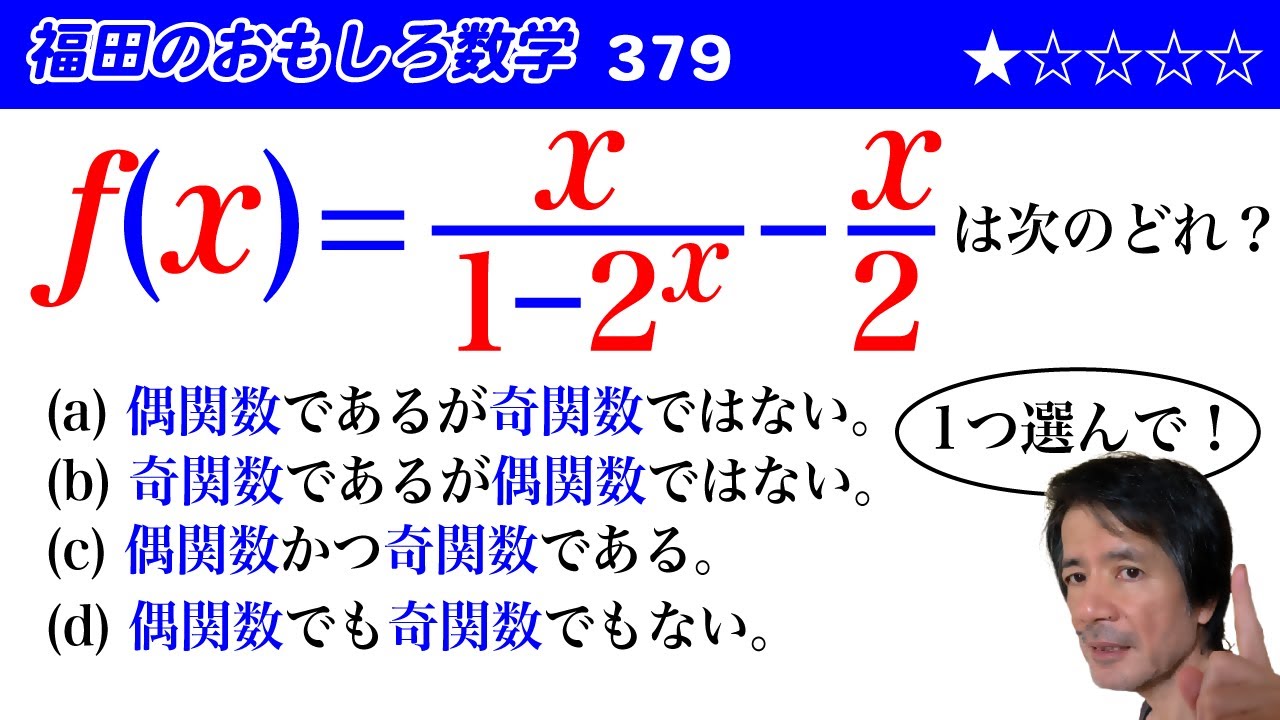
$f(x)=\frac{x}{1-2^x}-\frac{x}{2}$について正しい記述を以下から1つ選べ。
(a) 偶関数であるが奇関数ではない。
(b) 奇関数であるが偶関数ではない。
(c) 偶関数かつ奇関数である。
この動画を見る
$f(x)=\frac{x}{1-2^x}-\frac{x}{2}$について正しい記述を以下から1つ選べ。
(a) 偶関数であるが奇関数ではない。
(b) 奇関数であるが偶関数ではない。
(c) 偶関数かつ奇関数である。
福田のおもしろ数学378〜ある漸化式で定められる数列の最初の2025項が正で2026番目が初めて負になることが可能かどうかの検証

単元:
#数Ⅱ#三角関数#加法定理とその応用#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$a_{0}>0, c>0, a_{n+1}=\frac{a_{n}+c}{1-a_{n}c}$で定まる数列${a_{n}}$に対し、$a_{0}, a_{1}, \cdots ,a_{2024}$がすべて正であり、$a_{2025}<0$となることは可能か。
この動画を見る
$a_{0}>0, c>0, a_{n+1}=\frac{a_{n}+c}{1-a_{n}c}$で定まる数列${a_{n}}$に対し、$a_{0}, a_{1}, \cdots ,a_{2024}$がすべて正であり、$a_{2025}<0$となることは可能か。
【数C】【複素数平面】複素数の大きさ・対称式の利用 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\alpha,\beta$は複素数とする。$|\alpha|=|\beta|=1,\alpha+\beta+1=0$のとき、$\alpha^2+\beta^2$の値を求めよ。
この動画を見る
$\alpha,\beta$は複素数とする。$|\alpha|=|\beta|=1,\alpha+\beta+1=0$のとき、$\alpha^2+\beta^2$の値を求めよ。
福田のおもしろ数学377〜3つの素数の和と積の一方が他方の101倍になる条件

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$p, q, rを素数とする。p+q+rとpqrの一方が他方の101倍になるような素数の組(p, q, r)をすべて求めて下さい。$
この動画を見る
$p, q, rを素数とする。p+q+rとpqrの一方が他方の101倍になるような素数の組(p, q, r)をすべて求めて下さい。$
再UP【共通テスト】数学2B、2BCの誰でも簡単にできる点数アップのコツ10選

単元:
#その他#勉強法#その他#勉強法#数学(高校生)
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
再UP【共通テスト】数学2B、2BCの誰でも簡単にできる点数アップのコツ10選を解説していきます。
この動画を見る
再UP【共通テスト】数学2B、2BCの誰でも簡単にできる点数アップのコツ10選を解説していきます。
再UP【知ってるだけで+10%】数学2B・Cのコツ10選まとめ【共通テスト対策】

単元:
#その他#勉強法#その他#数学(高校生)#その他
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
数学2B・Cのコツ10選を解説していきます。【共通テスト対策】
この動画を見る
数学2B・Cのコツ10選を解説していきます。【共通テスト対策】
福田のおもしろ数学375〜関数方程式を解こう

単元:
#数Ⅱ#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$f(2025x + f(0)) = 2025x^2$が任意の実数$x$で成り立つような$f(x)$をすべて求めよ。
この動画を見る
$f(2025x + f(0)) = 2025x^2$が任意の実数$x$で成り立つような$f(x)$をすべて求めよ。
福田のおもしろ数学374〜365と366を1から365までの整数で割った余りの総和の大小比較

単元:
#数列#数列とその和(等差・等比・階差・Σ)#漸化式
指導講師:
福田次郎
問題文全文(内容文):
$360$を$1,2,3,…,365$で割った余りの総和を$A$、$366$を$1,2,3,…,365$で割った余りの総和を$B$とする。$A$と$B$の大小を比較せよ。
この動画を見る
$360$を$1,2,3,…,365$で割った余りの総和を$A$、$366$を$1,2,3,…,365$で割った余りの総和を$B$とする。$A$と$B$の大小を比較せよ。
福田のおもしろ数学373〜4変数の連立方程式と循環形式

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
\begin{eqnarray}
\left\{
\begin{array}{l}
abc+ab+bc+ca+a+b+c=2 \\
bcd+bc+cd+db+b+c+d=0 \\
cda+cd+da+ac+c+d+a=2 \\
dab+da+ab+bd+d+a+b=5
\end{array}
\right.
\end{eqnarray}
を満たす実数$a,b,c,d$を求めよ。
この動画を見る
\begin{eqnarray}
\left\{
\begin{array}{l}
abc+ab+bc+ca+a+b+c=2 \\
bcd+bc+cd+db+b+c+d=0 \\
cda+cd+da+ac+c+d+a=2 \\
dab+da+ab+bd+d+a+b=5
\end{array}
\right.
\end{eqnarray}
を満たす実数$a,b,c,d$を求めよ。
福田のおもしろ数学372〜絶対値の付いた式に関する証明

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
整数$a,b,c,d$は$|ac+bd|=|ad+bc|=1$を満たしている。このとき、次を示せ。
$|a|=|b|=1$ or $|c|=|d|=1$
この動画を見る
整数$a,b,c,d$は$|ac+bd|=|ad+bc|=1$を満たしている。このとき、次を示せ。
$|a|=|b|=1$ or $|c|=|d|=1$
高校1年生から早稲田に挑戦!三角比の難問!【早稲田大学】【数学 入試問題】

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
m,nを正の整数とする。半径1の円に内接する△ABCが
sinA=m/17,sinB=n/17,sin²C=sin²A+sin²B
を満たすとき△ABCの内接円の半径を求めよ。
この動画を見る
m,nを正の整数とする。半径1の円に内接する△ABCが
sinA=m/17,sinB=n/17,sin²C=sin²A+sin²B
を満たすとき△ABCの内接円の半径を求めよ。
福田のおもしろ数学371〜初項が素数で漸化式で定義された数列が素数でない項をもつ証明

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$a_1=p$(素数), $a_{n+1}=2a_n-1$で定まる数列には素数でない項が存在する。証明せよ。
この動画を見る
$a_1=p$(素数), $a_{n+1}=2a_n-1$で定まる数列には素数でない項が存在する。証明せよ。
function : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study #test
単元:
#数Ⅱ#軌跡と領域#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2点$A(1,7),B(6,-2)$
$y=ax+2とABが共有する点を持つようaの値の範囲を求めよ$
この動画を見る
2点$A(1,7),B(6,-2)$
$y=ax+2とABが共有する点を持つようaの値の範囲を求めよ$
【数C】【複素数平面】複素数の大きさと式変形 ※問題文は概要欄

単元:
#複素数平面#複素数平面#数学(高校生)#数C
指導講師:
理数個別チャンネル
問題文全文(内容文):
$|z|=3$かつ$|z-2|=4$を満たす複素数$z$について、次の値を求めよ。
(1)$z\bar{z}$ (2) $z+\bar{z}$
この動画を見る
$|z|=3$かつ$|z-2|=4$を満たす複素数$z$について、次の値を求めよ。
(1)$z\bar{z}$ (2) $z+\bar{z}$
福田のおもしろ数学370〜フェルマーの小定理の証明

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
フェルマーの小定理
素数$p$と整数$a$が互いに素のとき
$a^{p-1}\equiv1~~({\rm mod} ~p)$であることを証明せよ。
この動画を見る
フェルマーの小定理
素数$p$と整数$a$が互いに素のとき
$a^{p-1}\equiv1~~({\rm mod} ~p)$であることを証明せよ。
福田のおもしろ数学369〜条件付きの不等式の証明JP

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$abc=1$, $a,b,c > 0$のとき
$a^{b+c}b^{c+a}c^{a+b} \leqq1$が成り立つことを証明せよ。
この動画を見る
$abc=1$, $a,b,c > 0$のとき
$a^{b+c}b^{c+a}c^{a+b} \leqq1$が成り立つことを証明せよ。
