 数学(高校生)
数学(高校生)
 数学(高校生)
数学(高校生)
自然数の4乗の逆数の和 オイラー級数(Euler) やっぱりπが登場

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\frac{1}{1^4}$+$\frac{1}{2^4}$+$\frac{1}{3^4}$+$\frac{1}{4^4}$+$\cdots$$\frac{1}{n^4}$=$\frac{\pi^4}{90}$
この動画を見る
$\frac{1}{1^4}$+$\frac{1}{2^4}$+$\frac{1}{3^4}$+$\frac{1}{4^4}$+$\cdots$$\frac{1}{n^4}$=$\frac{\pi^4}{90}$
【高校数学】数Ⅲ-74 数列の極限⑩(無限等比級数)

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の無限級数が収束するような実数$x$の値の範囲と、
収束するときの和を求めよ。
①$1+\dfrac{x}{3}+\dfrac{x^2}{9}+\dfrac{x^3}{27}+・・・$
②$(x-4)+\dfrac{x(x-4)}{2x-4}+\dfrac{x^2(x-4)}{(2x-4)^2}+・・・ \quad (x \neq 2)$
この動画を見る
次の無限級数が収束するような実数$x$の値の範囲と、
収束するときの和を求めよ。
①$1+\dfrac{x}{3}+\dfrac{x^2}{9}+\dfrac{x^3}{27}+・・・$
②$(x-4)+\dfrac{x(x-4)}{2x-4}+\dfrac{x^2(x-4)}{(2x-4)^2}+・・・ \quad (x \neq 2)$
【高校数学】数Ⅲ-73 数列の極限⑨(無限等比級数)

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の無限級数の収束、発散を調べ、収束するときにはその和を求めよ。
①$4+2+1+\dfrac{1}{2}+・・・$
②$1-2+4-8+・・・$
③$3-3+3-3+・・・$
④$\displaystyle \sum_{n=1}^{\infty}2\left(-\dfrac{1}{3}\right)^{n-1}$
この動画を見る
次の無限級数の収束、発散を調べ、収束するときにはその和を求めよ。
①$4+2+1+\dfrac{1}{2}+・・・$
②$1-2+4-8+・・・$
③$3-3+3-3+・・・$
④$\displaystyle \sum_{n=1}^{\infty}2\left(-\dfrac{1}{3}\right)^{n-1}$
【高校数学】数Ⅲ-72 数列の極限⑧(無限級数)

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の無限級数の収束、発散を調べ、収束するときにはその和を求めよ。
①$\dfrac{1}{1・3}+\dfrac{1}{3・5}+・・・+\dfrac{1}{(2n-1)(2n+1)}+・・・$
②$\displaystyle \sum_{n=1}^{\infty}\dfrac{1}{\sqrt n+\sqrt{n+1}}$
この動画を見る
次の無限級数の収束、発散を調べ、収束するときにはその和を求めよ。
①$\dfrac{1}{1・3}+\dfrac{1}{3・5}+・・・+\dfrac{1}{(2n-1)(2n+1)}+・・・$
②$\displaystyle \sum_{n=1}^{\infty}\dfrac{1}{\sqrt n+\sqrt{n+1}}$
天才オイラーが解決した問題。奇数の平方の逆数の和にπが登場

【高校数学】数Ⅲ-71 数列の極限⑦(無限等比数列)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$a_1=1,a_{n+1}=\dfrac{1}{3}a_n+2(n=1,2,・・・)$によって
定められる数列$\{a_n\}$について、$\displaystyle \lim_{n\to\infty}a_n$を求めよ。
②$a_1=o,a_2=1,a_{n+2}=\dfrac{1}{4}(a_{n+1}+3a_n)(n=1,2,・・・)$によって
定められる数列$\{a_n\}$について、$\displaystyle \lim_{n\to\infty}a_n$を求めよ。
この動画を見る
①$a_1=1,a_{n+1}=\dfrac{1}{3}a_n+2(n=1,2,・・・)$によって
定められる数列$\{a_n\}$について、$\displaystyle \lim_{n\to\infty}a_n$を求めよ。
②$a_1=o,a_2=1,a_{n+2}=\dfrac{1}{4}(a_{n+1}+3a_n)(n=1,2,・・・)$によって
定められる数列$\{a_n\}$について、$\displaystyle \lim_{n\to\infty}a_n$を求めよ。
【高校数学】数Ⅲ-70 数列の極限⑥(無限等比数列)

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の極限を求めよ。
①$\displaystyle \lim_{n\to\infty}\dfrac{1-r^n}{1+r^n}(r \neq -1)$
②$\displaystyle \lim_{n\to\infty}\dfrac{r^{2n+1}}{1+r^{2n}}$
この動画を見る
次の極限を求めよ。
①$\displaystyle \lim_{n\to\infty}\dfrac{1-r^n}{1+r^n}(r \neq -1)$
②$\displaystyle \lim_{n\to\infty}\dfrac{r^{2n+1}}{1+r^{2n}}$
平方数でない自然数の平方根は全て無理数であることの証明

【高校数学】数Ⅲ-69 数列の極限⑤(無限等比数列)

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の極限を求めよ。
①$\displaystyle \lim_{n\to\infty}3^n$
②$\displaystyle \lim_{n\to\infty}1^n$
③$\displaystyle \lim_{n\to\infty}\left(-\dfrac{1}{3}\right)^n$
④$\displaystyle \lim_{n\to\infty}(-3)^n$
⑤$\displaystyle \lim_{n\to\infty}\dfrac{3^n+4^n}{5^n}$
⑥$\displaystyle \lim_{n\to\infty}\dfrac{2^n}{1+2^n}$
⑦$\displaystyle \lim_{n\to\infty}\dfrac{5^n+3^n}{2^n-3^n}$
⑧$\displaystyle \lim_{n\to\infty}\dfrac{2^{n+1}-4^{n+1}}{3^n-4^n}$
この動画を見る
次の極限を求めよ。
①$\displaystyle \lim_{n\to\infty}3^n$
②$\displaystyle \lim_{n\to\infty}1^n$
③$\displaystyle \lim_{n\to\infty}\left(-\dfrac{1}{3}\right)^n$
④$\displaystyle \lim_{n\to\infty}(-3)^n$
⑤$\displaystyle \lim_{n\to\infty}\dfrac{3^n+4^n}{5^n}$
⑥$\displaystyle \lim_{n\to\infty}\dfrac{2^n}{1+2^n}$
⑦$\displaystyle \lim_{n\to\infty}\dfrac{5^n+3^n}{2^n-3^n}$
⑧$\displaystyle \lim_{n\to\infty}\dfrac{2^{n+1}-4^{n+1}}{3^n-4^n}$
【高校数学】数Ⅲ-68 数列の極限④ はさみうちの原理

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の数列の極限を求めよ。
①$\displaystyle \lim_{n\to\infty}\dfrac{(-1)^n}{n+3}$
②$\displaystyle \lim_{n\to\infty}\dfrac{1}{n}\sin^2 n\theta \quad $($\theta$は定数)
この動画を見る
次の数列の極限を求めよ。
①$\displaystyle \lim_{n\to\infty}\dfrac{(-1)^n}{n+3}$
②$\displaystyle \lim_{n\to\infty}\dfrac{1}{n}\sin^2 n\theta \quad $($\theta$は定数)
【高校数学】数Ⅲ-67 数列の極限③

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の極限を求めよ。
①$\displaystyle \lim_{n\to\infty}\dfrac{n^2-n+2}{3n^2-5}$
②$\displaystyle \lim_{n\to\infty}\dfrac{5n^2-1}{4+n}$
③$\displaystyle \lim_{n\to\infty}(\sqrt{n+1}-\sqrt n)$
④$\displaystyle \lim_{n\to\infty}(\sqrt{n^2-2n}-n)$
⑤$\displaystyle \lim_{n\to\infty}\dfrac{4n}{\sqrt{n^2+n}+3n}$
⑥$\displaystyle \lim_{n\to\infty}\dfrac{5}{\sqrt{n^2+2n}-n}$
この動画を見る
次の極限を求めよ。
①$\displaystyle \lim_{n\to\infty}\dfrac{n^2-n+2}{3n^2-5}$
②$\displaystyle \lim_{n\to\infty}\dfrac{5n^2-1}{4+n}$
③$\displaystyle \lim_{n\to\infty}(\sqrt{n+1}-\sqrt n)$
④$\displaystyle \lim_{n\to\infty}(\sqrt{n^2-2n}-n)$
⑤$\displaystyle \lim_{n\to\infty}\dfrac{4n}{\sqrt{n^2+n}+3n}$
⑥$\displaystyle \lim_{n\to\infty}\dfrac{5}{\sqrt{n^2+2n}-n}$
【高校数学】数Ⅲ-66 数列の極限②

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の極限を求めよ。
①$\displaystyle \lim_{n\to\infty}(-3n+8)$
②$\displaystyle \lim_{n\to\infty}(n-1)$
③$\displaystyle \lim_{n\to\infty}\left(5+\dfrac{2}{n}\right)$
④$\displaystyle \lim_{n\to\infty}(-3)^n$
⑤$\displaystyle \lim_{n\to\infty}\dfrac{n-3}{2n+1}$
⑥$\displaystyle \lim_{n\to\infty}(4n-3n^2)$
この動画を見る
次の極限を求めよ。
①$\displaystyle \lim_{n\to\infty}(-3n+8)$
②$\displaystyle \lim_{n\to\infty}(n-1)$
③$\displaystyle \lim_{n\to\infty}\left(5+\dfrac{2}{n}\right)$
④$\displaystyle \lim_{n\to\infty}(-3)^n$
⑤$\displaystyle \lim_{n\to\infty}\dfrac{n-3}{2n+1}$
⑥$\displaystyle \lim_{n\to\infty}(4n-3n^2)$
【高校数学】数Ⅲ-65 数列の極限①

単元:
#関数と極限#数列の極限#数学(高校生)#数Ⅲ
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
次の数列の収束、発散を調べよ。
①$-3,-1,1,・・・2n-5,・・・$
②$1,\dfrac{3}{2},\dfrac{5}{3},・・・,2-\dfrac{1}{n},・・・$
③$-1,-4,-9,・・・,-n^2,・・・$
④$-4,16,-64,・・・,(-4)^n,・・・$
この動画を見る
次の数列の収束、発散を調べよ。
①$-3,-1,1,・・・2n-5,・・・$
②$1,\dfrac{3}{2},\dfrac{5}{3},・・・,2-\dfrac{1}{n},・・・$
③$-1,-4,-9,・・・,-n^2,・・・$
④$-4,16,-64,・・・,(-4)^n,・・・$
確率漸化式 特性方程式

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)正三角形ABCの頂点を1秒ごとに無作為に必ず隣の頂点に移動する虫がいる。虫がはじめ頂点Aにいる時、n秒後に頂点Aにいる確率を求めよ。
(2)2,3,5,7,9の数字が書かれたカードが各1枚入った箱がある。箱から無作為に1枚取り出し数字をメモしてカードは箱に戻す。これをn回繰り返したときにメモされた数字の合計が奇数である確率を求めよ。
この動画を見る
(1)正三角形ABCの頂点を1秒ごとに無作為に必ず隣の頂点に移動する虫がいる。虫がはじめ頂点Aにいる時、n秒後に頂点Aにいる確率を求めよ。
(2)2,3,5,7,9の数字が書かれたカードが各1枚入った箱がある。箱から無作為に1枚取り出し数字をメモしてカードは箱に戻す。これをn回繰り返したときにメモされた数字の合計が奇数である確率を求めよ。
因数分解 たすきがけ

【中学生必見】偏差値84.9の「中学数学」勉強法~なぜ中学からできなくなった?算数との違いとは?~京大模試全国一位の勉強法【篠原好】

単元:
#その他#勉強法#数学(高校生)
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
なぜ中学からできなくなった?算数との違いとは?
「中学生の数学勉強法」についてお話しています。
この動画を見る
なぜ中学からできなくなった?算数との違いとは?
「中学生の数学勉強法」についてお話しています。
球の体積、表面積 中学生にも納得のいく方法で。 積分でも出します

単元:
#数学(中学生)#中1数学#数Ⅱ#空間図形#微分法と積分法#面積、体積#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
球の表面積、体積の公式がなぜそうなるのかわかりやすく解説します!
この動画を見る
球の表面積、体積の公式がなぜそうなるのかわかりやすく解説します!
ちょっと工夫した 因数分解 9991を素因数分解(慶應女子高)

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
9991を素因数分解せよ.
慶應女子高過去問
この動画を見る
9991を素因数分解せよ.
慶應女子高過去問
確率、等比数列 巴戦は平等な優勝決定法か?(類)東大、神戸大

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
確率、等比数列 巴戦は平等な優勝決定法か?
(類)東大、神戸大
この動画を見る
確率、等比数列 巴戦は平等な優勝決定法か?
(類)東大、神戸大
努力は「見える化」せよ!数字で勉強をとらえるべき理由~やる気が出る計画的勉強法~京大模試全国一位の勉強法【篠原好】

単元:
#その他#勉強法#数学(高校生)
指導講師:
篠原好【京大模試全国一位の勉強法】
問題文全文(内容文):
数字で勉強をとらえるべき理由
「努力は”見える化”せよ!」ということについてお話しています。
この動画を見る
数字で勉強をとらえるべき理由
「努力は”見える化”せよ!」ということについてお話しています。
「素数が連続して出現しない区間はどれくらい?」の訂正動画です。

ハノイの塔 漸化式 規則性

【数学III・小技】∫esinxdxの簡単な求め方

単元:
#微分とその応用#微分法#数学(高校生)#数Ⅲ
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
【数学III・小技】∫esinxdxの簡単な求め方
この動画を見る
【数学III・小技】∫esinxdxの簡単な求め方
二項定理・多項定理を理解する

場合の数 10個のりんごを3人に分ける

単元:
#算数(中学受験)#数A#場合の数と確率#場合の数#場合の数#場合の数#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
10個のりんごを3人に分ける分け方は何通りか?
この動画を見る
10個のりんごを3人に分ける分け方は何通りか?
すいの体積はなぜ1/3か

三倍角の公式を複素数の掛け算(ド・モアブルの定理)で簡単に導く

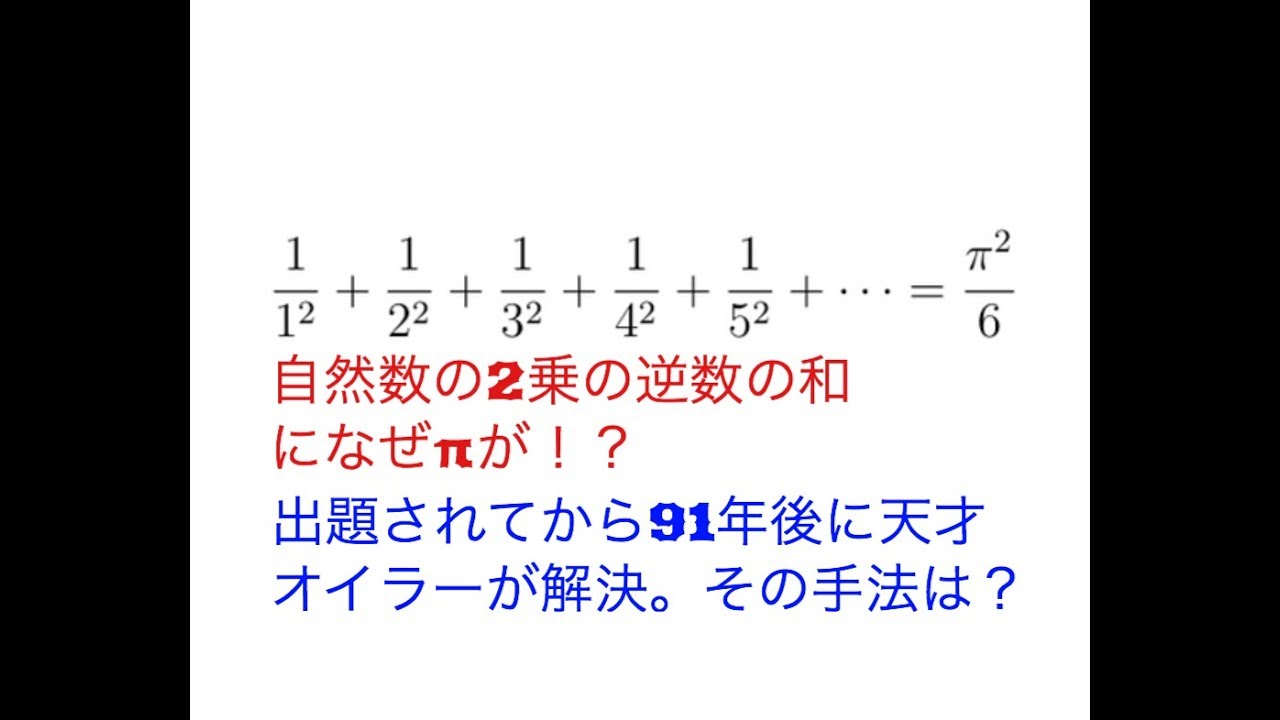
オイラー(Euler)が解決した「自然数の平方の逆数の和」。円とは無関係なのに結論にπが登場
ド・モアブルの定理を用いてオイラーの公式を導く

単元:
#複素数平面#関数と極限#複素数平面#関数の極限#数学(高校生)#数C#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
ド・モアブルの定理を用いてオイラーの公式を導く方法を解説していきます.
この動画を見る
ド・モアブルの定理を用いてオイラーの公式を導く方法を解説していきます.
ド・モアブルの定理を数学的帰納法で証明するよ。

