 高校入試過去問(数学)
高校入試過去問(数学)
 高校入試過去問(数学)
高校入試過去問(数学)
連立方程式:豊島岡女子学園高等学校~全国入試問題解法【神授業】
単元:
#数学(中学生)#中1数学#中2数学#方程式#連立方程式#高校入試過去問(数学)#豊島岡女子高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 豊島岡女子学園高等学校
ある中学校の合唱部の2017年の部員数は、女子が$x$ 人、男子が64人でした。2018年の部員数は、2017 年と比べて女子が$y$%減り、男子が$y$%増えました。 2019年の部員数は、2018年と比べて女子が40%増 え、男子が$y$%減りました。
2019年の部員数が、女子が63人、男子が60人のとき
$x$の値を求めなさい。
(ただし、$ y\gt 0$)
この動画を見る
入試問題 豊島岡女子学園高等学校
ある中学校の合唱部の2017年の部員数は、女子が$x$ 人、男子が64人でした。2018年の部員数は、2017 年と比べて女子が$y$%減り、男子が$y$%増えました。 2019年の部員数は、2018年と比べて女子が40%増 え、男子が$y$%減りました。
2019年の部員数が、女子が63人、男子が60人のとき
$x$の値を求めなさい。
(ただし、$ y\gt 0$)
【5分で完答 !?】空間図形:函館ラ・サール高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#空間図形#高校入試過去問(数学)#函館ラ・サール高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 函館ラ・サール高等学校
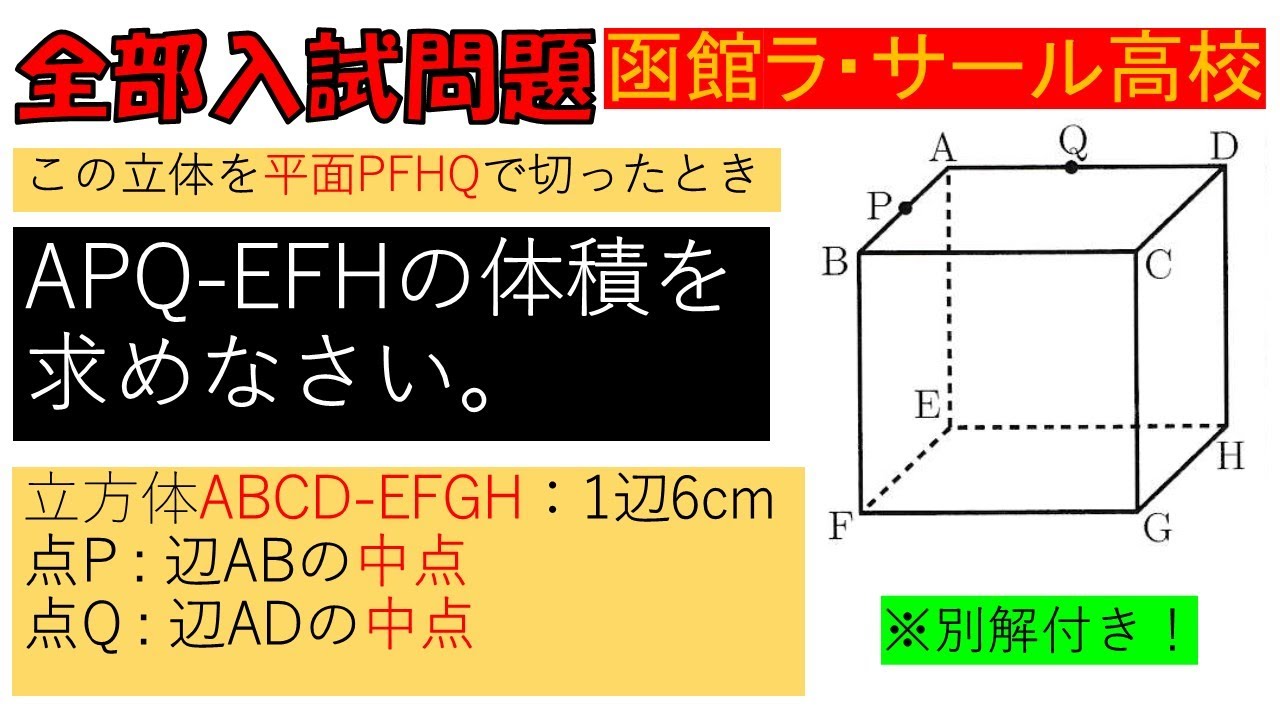
この立体を平面$PFHQ$で切ったとき
$APQ-EFH$の体積を 求めなさい。
立方体$ABCD-EFGH$:1辺6cm
点$P$:辺$AB$の中点
点$Q$:辺$AD$の中点
※図は動画内参照
この動画を見る
入試問題 函館ラ・サール高等学校
この立体を平面$PFHQ$で切ったとき
$APQ-EFH$の体積を 求めなさい。
立方体$ABCD-EFGH$:1辺6cm
点$P$:辺$AB$の中点
点$Q$:辺$AD$の中点
※図は動画内参照
計算:土浦日本大学高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#土浦日本大学高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 土浦日本大学高等学校
次の▭を埋めなさい。
$624^2-623\times 625=▭$
この動画を見る
入試問題 土浦日本大学高等学校
次の▭を埋めなさい。
$624^2-623\times 625=▭$
リーグ戦の試合数 B (長野県)
単元:
#計算と数の性質#数学(中学生)#規則性(周期算・方陣算・数列・日暦算・N進法)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
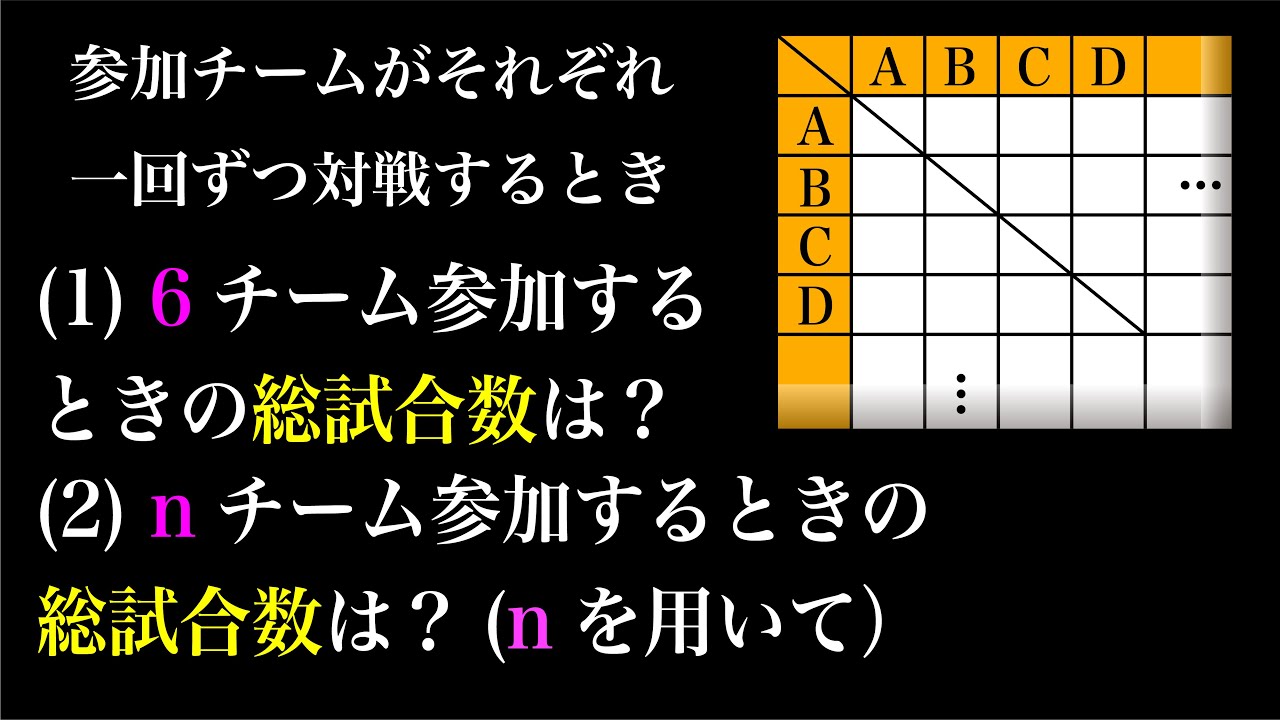
リーグ戦(総当たり戦)
1回ずつ対戦するとき
(1)6チーム参加するときの総試合数は?
(2)nチーム参加するときの総試合数は?
*図は動画内参照
この動画を見る
リーグ戦(総当たり戦)
1回ずつ対戦するとき
(1)6チーム参加するときの総試合数は?
(2)nチーム参加するときの総試合数は?
*図は動画内参照
トーナメント表の対戦の組み合わせ (勝ち上がりの対戦は考慮しません!!)B

単元:
#数学(中学生)#数A#場合の数と確率#場合の数#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
A,B,C,D,Eの5チームがトーナメント表をもとに対戦する組み合わせは何通り?
*図は動画内参照
この動画を見る
A,B,C,D,Eの5チームがトーナメント表をもとに対戦する組み合わせは何通り?
*図は動画内参照
京都女子
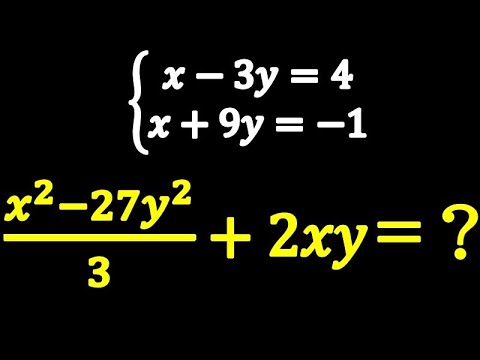
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x - 3y = 4 \\
x + 9y = -1
\end{array}
\right.
\end{eqnarray}
$
のとき
$\frac{x^2-27y^2}{3}+2xy$
京都女子高等学校
この動画を見る
$
\begin{eqnarray}
\left\{
\begin{array}{l}
x - 3y = 4 \\
x + 9y = -1
\end{array}
\right.
\end{eqnarray}
$
のとき
$\frac{x^2-27y^2}{3}+2xy$
京都女子高等学校
計算:慶応志木高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#慶應義塾志木高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 慶応志木高等学校
正の整数$m$を求めよ。
$18 \times 19 \times 20 \times 21 + 1 = m^2$
この動画を見る
入試問題 慶応志木高等学校
正の整数$m$を求めよ。
$18 \times 19 \times 20 \times 21 + 1 = m^2$
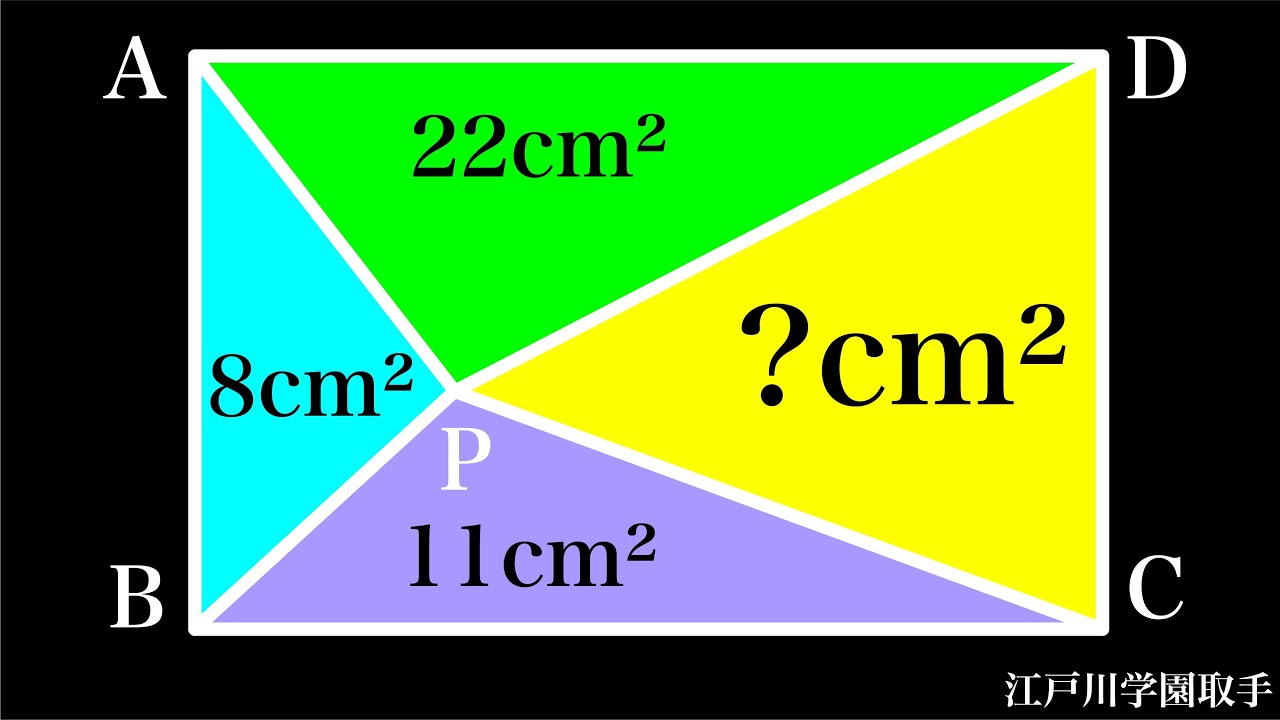
長方形の分割 江戸川学園取手
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
三角形CDPの面積=?
*図は動画内参照
この動画を見る
三角形CDPの面積=?
*図は動画内参照
良問!!整数問題
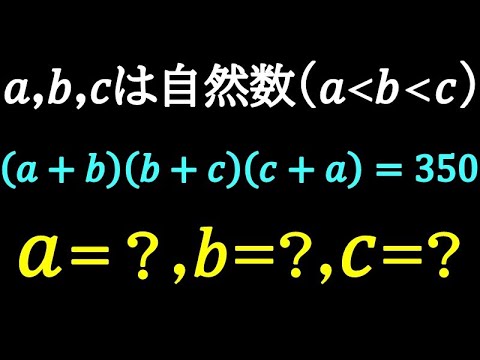
単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a=? b=? c=?
a,b,cは自然数でa<b<c
(a+b)(b+c)(c+a)=350
この動画を見る
a=? b=? c=?
a,b,cは自然数でa<b<c
(a+b)(b+c)(c+a)=350
確率:同志社高等学校~全国入試問題解法【能研!】
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)#同志社高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
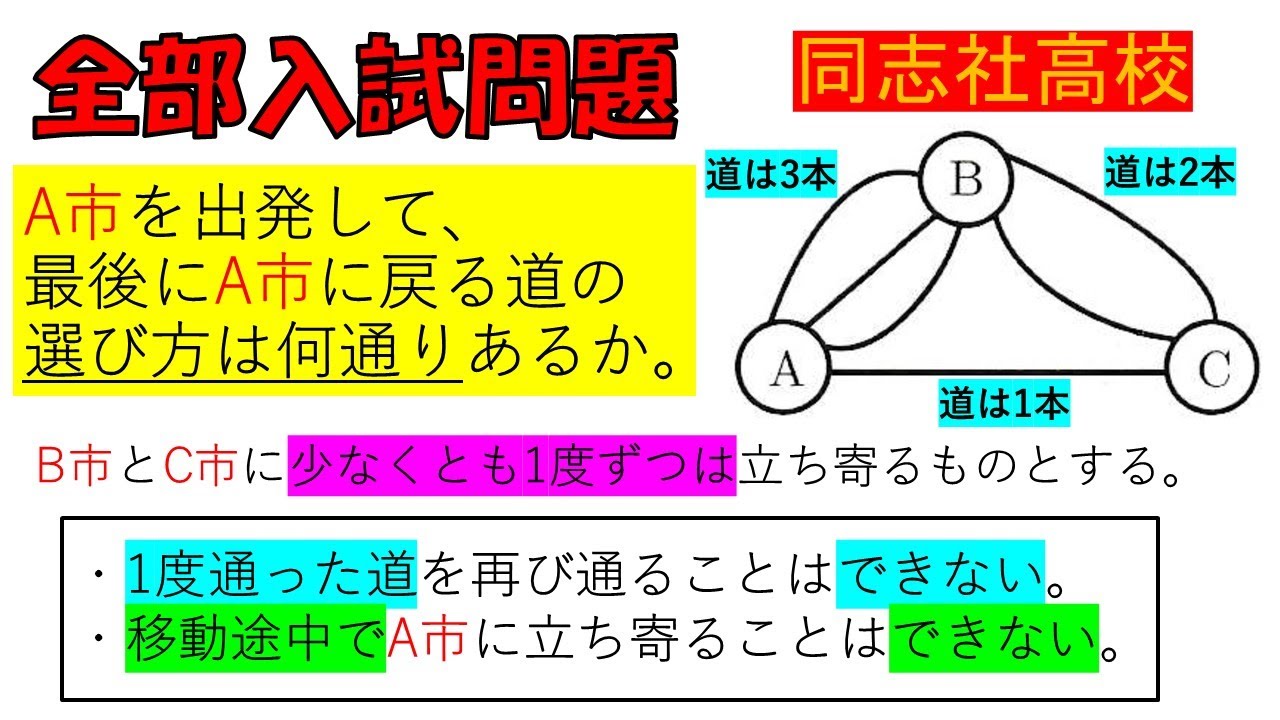
入試問題 同志社高等学校
$A$市を出発して、 最後に$A$市に戻る道の 選び方は何通りあるか求めよ。
$B$市と$C$市に少なくとも1度ずつは立ち寄るものとする。
・1度通った道を再び通ることはできない。
・移動途中で$A$市に立ち寄ることはできない。
この動画を見る
入試問題 同志社高等学校
$A$市を出発して、 最後に$A$市に戻る道の 選び方は何通りあるか求めよ。
$B$市と$C$市に少なくとも1度ずつは立ち寄るものとする。
・1度通った道を再び通ることはできない。
・移動途中で$A$市に立ち寄ることはできない。
さぁどう解く?? 徳島文理
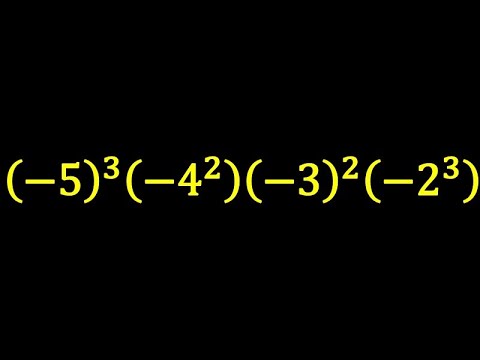
単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(-5)^3(-4^2)(-3)^2(-2^3)=$
この動画を見る
$(-5)^3(-4^2)(-3)^2(-2^3)=$
確率:岐阜県高校入試~全国入試問題解法
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)#岐阜県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 岐阜県の高校
袋の中に、「1~5までの数字」を
1つずつ書いた5枚のカードがある。
カードを1枚 取り出し
戻さずに 2枚目を取り出す。
1枚目:十の位の数字
2枚目:一の位の数字
つくった整数が偶数になる確率を求めなさい。
この動画を見る
入試問題 岐阜県の高校
袋の中に、「1~5までの数字」を
1つずつ書いた5枚のカードがある。
カードを1枚 取り出し
戻さずに 2枚目を取り出す。
1枚目:十の位の数字
2枚目:一の位の数字
つくった整数が偶数になる確率を求めなさい。
三平方の定理不要!! B

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABC=?
*図は動画内参照
鎌倉学園高等学校
この動画を見る
△ABC=?
*図は動画内参照
鎌倉学園高等学校
❓
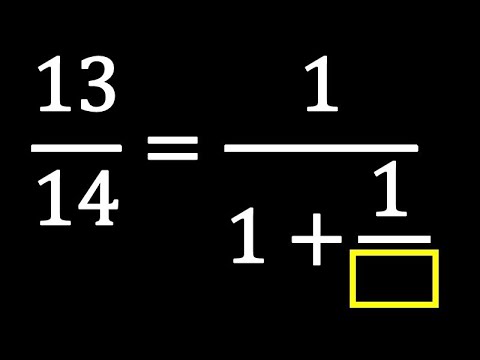
単元:
#計算と数の性質#数の性質その他#数学(中学生)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{13}{14} = \frac{1}{1+\frac{1}{▢}}$
$\frac{13}{14} =$
この動画を見る
$\frac{13}{14} = \frac{1}{1+\frac{1}{▢}}$
$\frac{13}{14} =$
3通りで解説しました (城北)
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
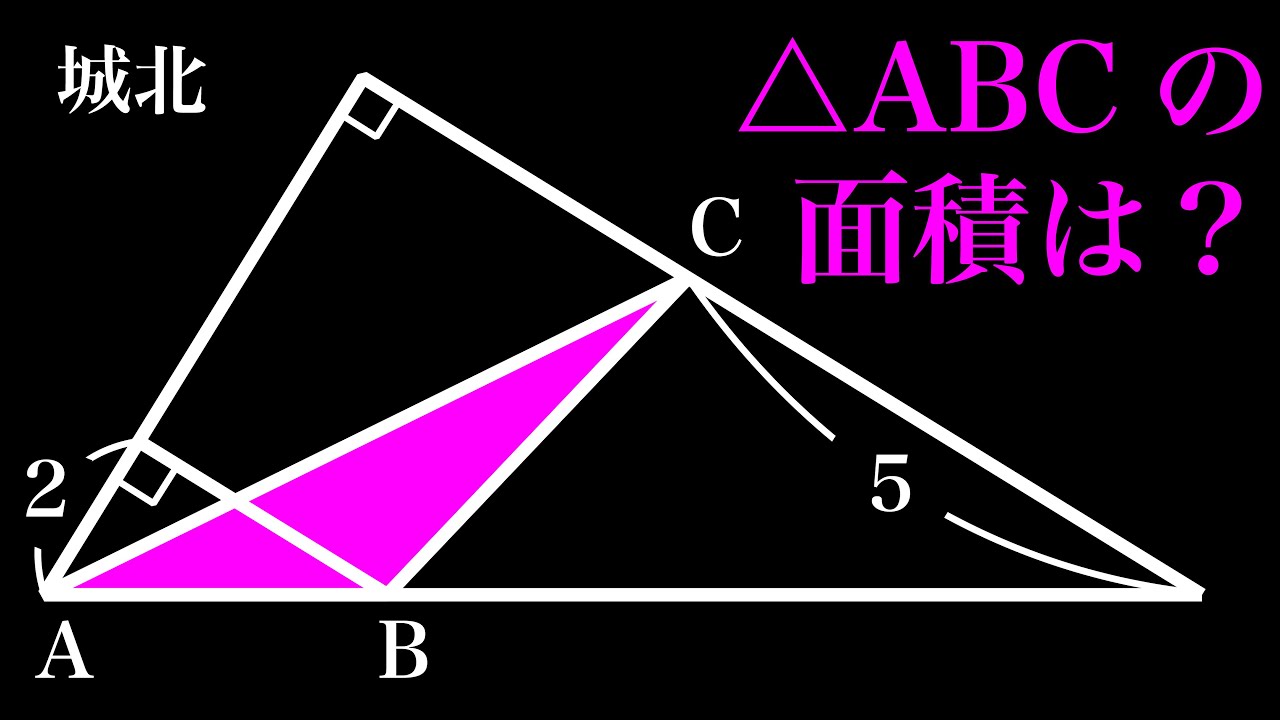
△ABCの面積=?
*図は動画内参照
城北高等学校
この動画を見る
△ABCの面積=?
*図は動画内参照
城北高等学校
分数式:埼玉工業~全国入試問題解法
単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 埼玉工業
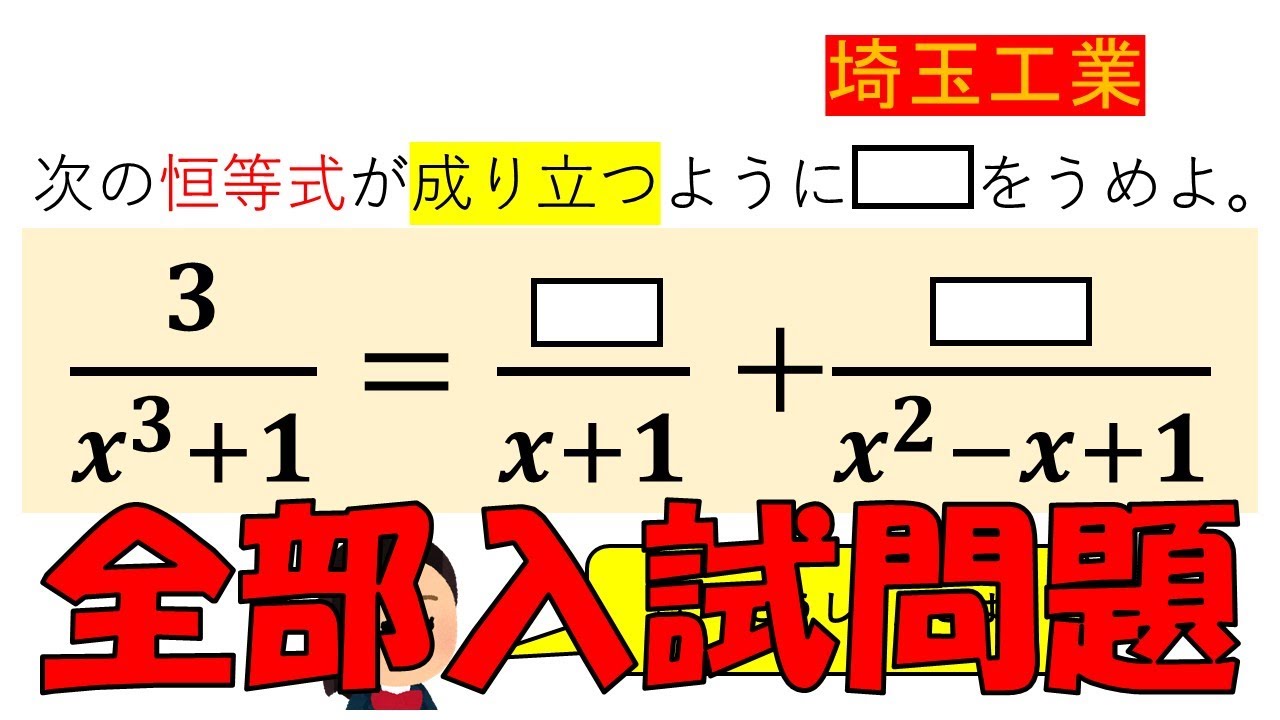
次の恒等式が成り立つようにをうめよ。
$\displaystyle \frac{3}{x^3+1}=\displaystyle \frac{▭}{x+1}+\displaystyle \frac{▭}{x^2-x+1}$
この動画を見る
入試問題 埼玉工業
次の恒等式が成り立つようにをうめよ。
$\displaystyle \frac{3}{x^3+1}=\displaystyle \frac{▭}{x+1}+\displaystyle \frac{▭}{x^2-x+1}$
【みんな大好き】因数分解:東京電機~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#文字と式#高校入試過去問(数学)#東京電機大学高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京電機
因数分解せよ。
$x^8-16$
この動画を見る
入試問題 東京電機
因数分解せよ。
$x^8-16$
三角形に内接する正方形 B
単元:
#数学(中学生)#中2数学#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#三角形と四角形#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
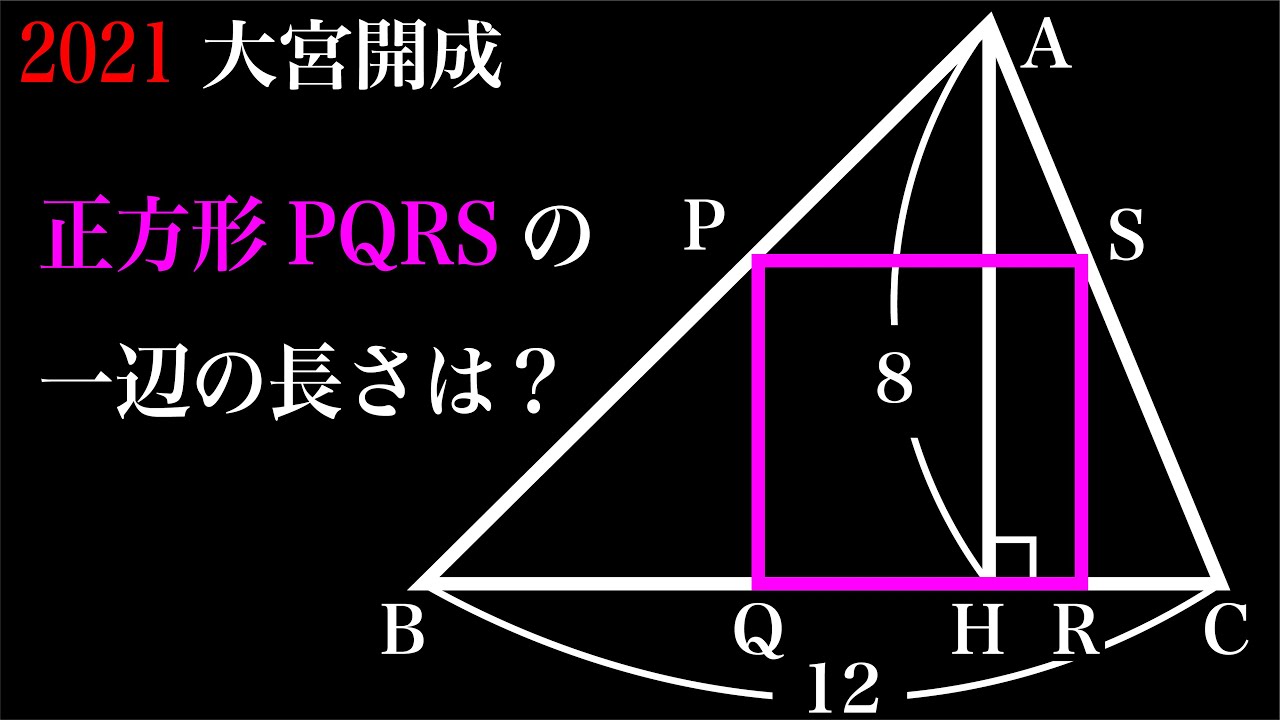
正方形PQRSの1辺の長さ=?
*図は動画内参照
2021大宮開成高等学校
この動画を見る
正方形PQRSの1辺の長さ=?
*図は動画内参照
2021大宮開成高等学校
パズル的な問題!! B
単元:
#数学(中学生)#中2数学#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#三角形と四角形#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
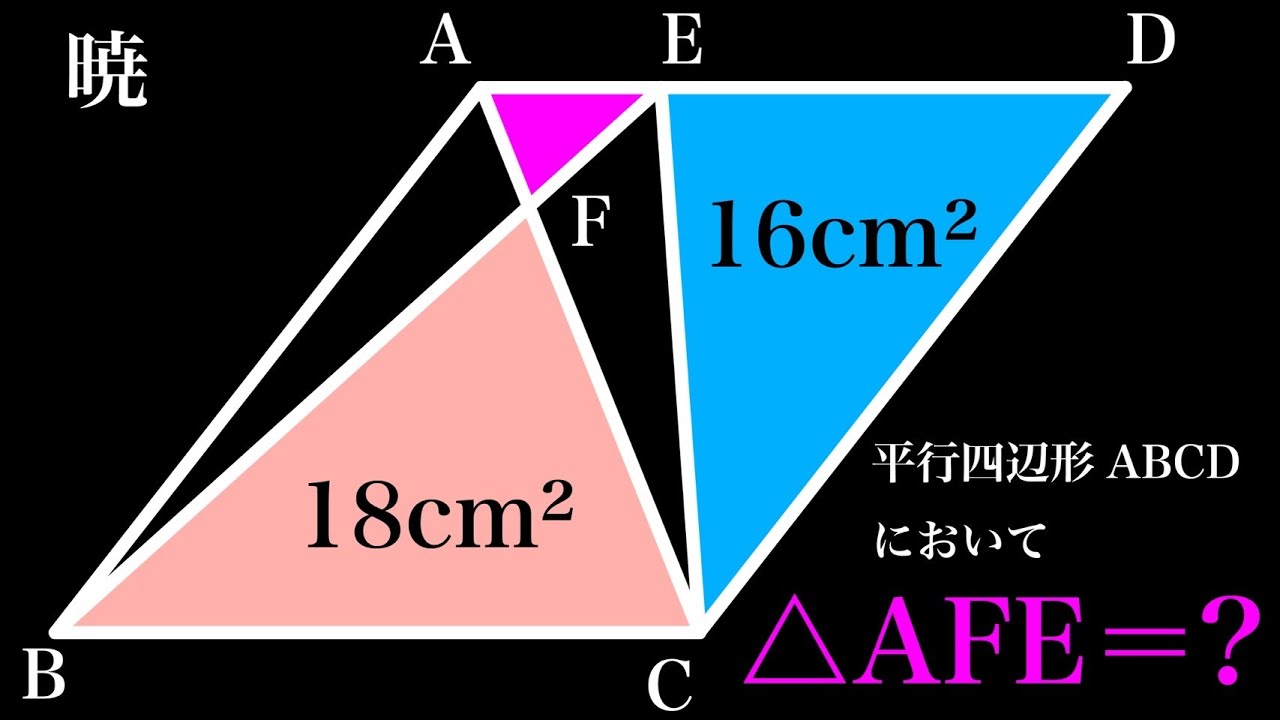
平行四辺形ABCDにおいて
△AFEの面積=?
*図は動画内参照
暁高等学校
この動画を見る
平行四辺形ABCDにおいて
△AFEの面積=?
*図は動画内参照
暁高等学校
角の三等分!!2通りで解説 B
単元:
#数学(中学生)#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
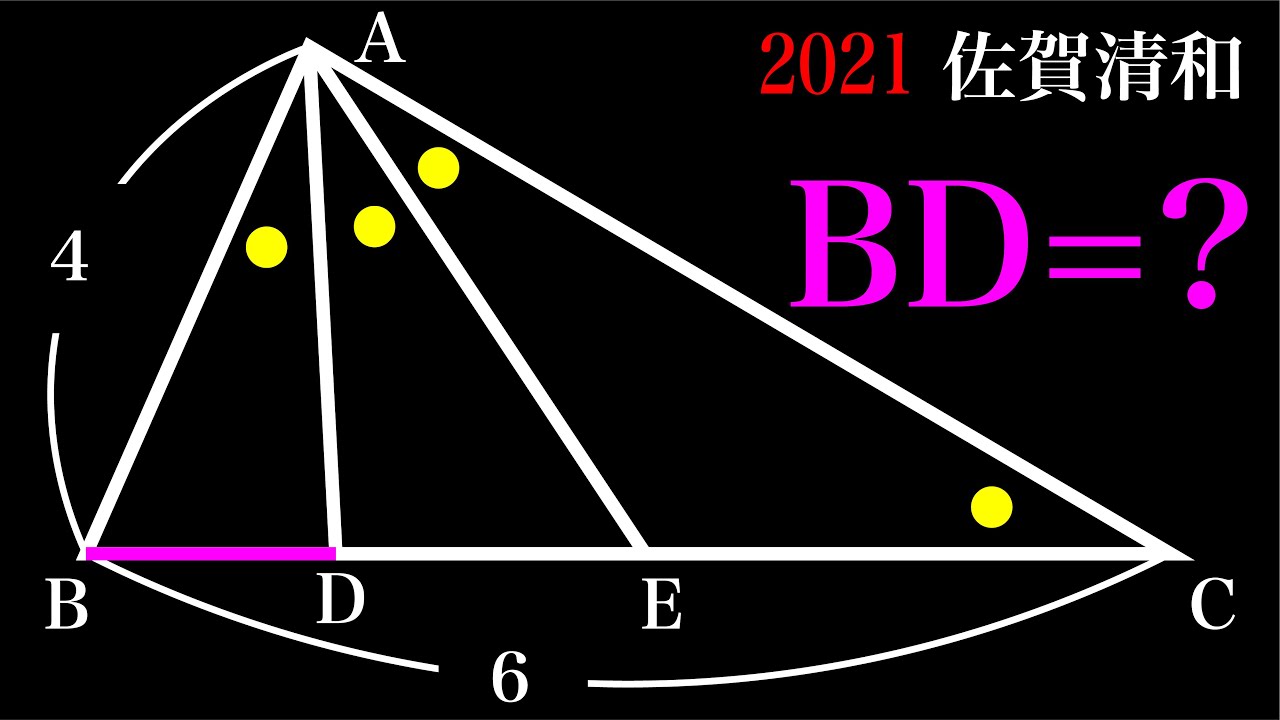
BD=?
*図は動画内参照
2021佐賀清和高等学校
この動画を見る
BD=?
*図は動画内参照
2021佐賀清和高等学校
円周の長さ 円の面積 文字式 A

単元:
#数学(中学生)#中1数学#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#文字と式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
周の長さがaの円の面積をaで表せ。
大阪教育大学附属高等学校天王寺校舎
この動画を見る
周の長さがaの円の面積をaで表せ。
大阪教育大学附属高等学校天王寺校舎
連立方程式:東京都立青山高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#東京都立青山高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立青山高等学校
連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{x-1}{3}+\displaystyle \frac{3y+1}{6}= 0 \\
0.4(x+4) + 0.5(y-3) = 0
\end{array}
\right.
\end{eqnarray}$
この動画を見る
入試問題 東京都立青山高等学校
連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{x-1}{3}+\displaystyle \frac{3y+1}{6}= 0 \\
0.4(x+4) + 0.5(y-3) = 0
\end{array}
\right.
\end{eqnarray}$
因数分解:東京都立日比谷高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#東京都立日比谷高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立日比谷高等学校
$\displaystyle \frac{(2x-6)^2}{4}-5x+15$
を因数分解せよ。
この動画を見る
入試問題 東京都立日比谷高等学校
$\displaystyle \frac{(2x-6)^2}{4}-5x+15$
を因数分解せよ。
2019 三重高校

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{2020^2 - 4040 + 1}{673^2} =$
2019三重高等学校
この動画を見る
$\frac{2020^2 - 4040 + 1}{673^2} =$
2019三重高等学校
【みんな好き好き】因数分解:大阪体育~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#大阪体育大学浪商高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 大阪体育
$(x^2-1)(y^2-1)-4xy$
因数分解せよ。
この動画を見る
入試問題 大阪体育
$(x^2-1)(y^2-1)-4xy$
因数分解せよ。
999 マークシートです B

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$999^2-1+999^2+4 \times 999 +3 = ▢ \times 10^▢$
日本大学櫻丘高等学校
この動画を見る
$999^2-1+999^2+4 \times 999 +3 = ▢ \times 10^▢$
日本大学櫻丘高等学校
入試予想問題:山形県立高等学校~全国入試問題解法

単元:
#数学(中学生)#山形県立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試予想問題 山形県立高等学校
・大問4題(総合問題)(小問集合)
・記述問題がポイント。 途中式,証明,作図。
・分量多い!!
【予想問題】
・$8a \div (-4a^2ℓ) \times aℓ^2$
・$4\sqrt{ 3 } \div \sqrt{ 2 }+\sqrt{ 54 }$
・$2x^2+4x-7=x^2-2$
・3枚の硬貨を同時に投げるとき、少なくとも1枚は表が 出る確率?
・$y=-\displaystyle \frac{12}{x}$・・・・①
(1)関数①について、 $x$の値を4倍にすると$y$の値は何倍になるか。
(2)①上の点$A$と$y$軸上の点$B$を通る直線②があり、2点$A,B$の$y$座標はそれぞれ2、-3である。
直線②の式を求めよ。
※図は動画内参照
線分$AB$を直径とする円○。 円○の周上に点$C$
$BC \lt AC$である$\triangle ABC$. $\triangle ACD$が
$AC=AD$の直角二等辺$\triangle $となる$D$.
辺$CD$と直径$AB$の交点$E$。
$D$から$AB$に垂線→交点$F$
(1) $\triangle ABC ∞ \triangle DAF$の証明。
(2) $AB=10cm, BC= 6cm, CA=8cm$ 線分施の長さを求めよ。
※図は動画内参照
この動画を見る
入試予想問題 山形県立高等学校
・大問4題(総合問題)(小問集合)
・記述問題がポイント。 途中式,証明,作図。
・分量多い!!
【予想問題】
・$8a \div (-4a^2ℓ) \times aℓ^2$
・$4\sqrt{ 3 } \div \sqrt{ 2 }+\sqrt{ 54 }$
・$2x^2+4x-7=x^2-2$
・3枚の硬貨を同時に投げるとき、少なくとも1枚は表が 出る確率?
・$y=-\displaystyle \frac{12}{x}$・・・・①
(1)関数①について、 $x$の値を4倍にすると$y$の値は何倍になるか。
(2)①上の点$A$と$y$軸上の点$B$を通る直線②があり、2点$A,B$の$y$座標はそれぞれ2、-3である。
直線②の式を求めよ。
※図は動画内参照
線分$AB$を直径とする円○。 円○の周上に点$C$
$BC \lt AC$である$\triangle ABC$. $\triangle ACD$が
$AC=AD$の直角二等辺$\triangle $となる$D$.
辺$CD$と直径$AB$の交点$E$。
$D$から$AB$に垂線→交点$F$
(1) $\triangle ABC ∞ \triangle DAF$の証明。
(2) $AB=10cm, BC= 6cm, CA=8cm$ 線分施の長さを求めよ。
※図は動画内参照
場合の数 慶應義塾2021

単元:
#数学(中学生)#数A#場合の数と確率#場合の数#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
1~20の自然数から異なる4つを選び、小さい順にa,b,c,dとする。
c=8のときa,b,dの選び方は何通り?
2021慶應義塾高等学校
この動画を見る
1~20の自然数から異なる4つを選び、小さい順にa,b,c,dとする。
c=8のときa,b,dの選び方は何通り?
2021慶應義塾高等学校
入試予想問題:岐阜県立高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#岐阜県立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試予想問題 岐阜県立高等学校
・幅広い学力に対応 (←基礎・基本)
・平面図形(←→空間図形)
・連立方程式は文章題。
・作図は必須
・$-3+15 \div 3$
・$8a^2 \div \displaystyle \frac{2}{3}a\timesℓ$
・$\sqrt{ 27 }-\sqrt{ 12 }$
・2個のさいころを同時に投げるとき、
出る目の数の差が$1$になる確率
・$y$が$x$に反比例し、$x=3$のとき$y=6$である。
$x=2$のときの$y$の値を求めなさい。
4点$ABCDは$円○の円周上の点。
点$B$を通り$CD$に平行な直線と$DA$を延長した直線の交点を$E$とする。
(1) $\triangle ABC ∞ \triangle ABED$であることの証明.
(2) $AE = 2cm, BE = 3cm, CD=5cm BC = 2AB$のとき、
(ア)$AD$の長さ?
(イ)△BCDの面積は$\triangle ABDの何倍か求めよ。
※図は動画内参照
この動画を見る
入試予想問題 岐阜県立高等学校
・幅広い学力に対応 (←基礎・基本)
・平面図形(←→空間図形)
・連立方程式は文章題。
・作図は必須
・$-3+15 \div 3$
・$8a^2 \div \displaystyle \frac{2}{3}a\timesℓ$
・$\sqrt{ 27 }-\sqrt{ 12 }$
・2個のさいころを同時に投げるとき、
出る目の数の差が$1$になる確率
・$y$が$x$に反比例し、$x=3$のとき$y=6$である。
$x=2$のときの$y$の値を求めなさい。
4点$ABCDは$円○の円周上の点。
点$B$を通り$CD$に平行な直線と$DA$を延長した直線の交点を$E$とする。
(1) $\triangle ABC ∞ \triangle ABED$であることの証明.
(2) $AE = 2cm, BE = 3cm, CD=5cm BC = 2AB$のとき、
(ア)$AD$の長さ?
(イ)△BCDの面積は$\triangle ABDの何倍か求めよ。
※図は動画内参照
2021 素因数分解

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2021を素因数分解せよ(ただし$45^2=2025$とする)
2021就実高等学校
この動画を見る
2021を素因数分解せよ(ただし$45^2=2025$とする)
2021就実高等学校
