 連立方程式
連立方程式
 連立方程式
連立方程式
【そう考えるか…!】連立方程式:東京都立国立高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#東京都立国立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
連立方程式
$\begin{equation}
\left\{ \,
\begin{aligned}
& \frac{3}{2}x-\frac{2}{3}y = 20 \\
& -\frac{2}{3}x+\frac{3}{2}y = 20
\end{aligned}
\right.
\end{equation}\;$を解け。
この動画を見る
連立方程式
$\begin{equation}
\left\{ \,
\begin{aligned}
& \frac{3}{2}x-\frac{2}{3}y = 20 \\
& -\frac{2}{3}x+\frac{3}{2}y = 20
\end{aligned}
\right.
\end{equation}\;$を解け。
【他の解き方は…!】連立方程式:洛南高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#洛南高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
連立方程式
$\begin{equation}
\left\{ \,
\begin{aligned}
& \frac{3}{x}+\frac{2}{y}=7 \\
& \frac{5}{x}-\frac{4}{y}=8
\end{aligned}
\right.
\end{equation}\;$を解きなさい。
この動画を見る
連立方程式
$\begin{equation}
\left\{ \,
\begin{aligned}
& \frac{3}{x}+\frac{2}{y}=7 \\
& \frac{5}{x}-\frac{4}{y}=8
\end{aligned}
\right.
\end{equation}\;$を解きなさい。
【少しでも上手く…!】連立方程式:慶応義塾高等学校~全国入試問題解法
単元:
#連立方程式#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$a,b$を定数とする。$x,y$の連立方程式、
\begin{eqnarray}
\left\{
\begin{array}{l}
(a+2)x - (b-1)y = 33 \\
(a-1)x + (2b+1)y = 9
\end{array}
\right.
\end{eqnarray}
の解が$x = 3,y = 1$であるとき、$a,b$の値を求めよ。
この動画を見る
$a,b$を定数とする。$x,y$の連立方程式、
\begin{eqnarray}
\left\{
\begin{array}{l}
(a+2)x - (b-1)y = 33 \\
(a-1)x + (2b+1)y = 9
\end{array}
\right.
\end{eqnarray}
の解が$x = 3,y = 1$であるとき、$a,b$の値を求めよ。
【少しでも上手く…!】連立方程式:慶応義塾高等学校~全国入試問題解法

単元:
#数学(中学生)#連立方程式#高校入試過去問(数学)#慶應義塾高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$
\left\{
\begin{array}{l}
(a+2)x + (b-1)y = 33 \\
(a-1)x + (2b+1)y = 9
\end{array}
\right.
$
$の解が x = 3,y = 1であるとき、a = \boxed{ } , b = \boxed{ }である$
この動画を見る
$
\left\{
\begin{array}{l}
(a+2)x + (b-1)y = 33 \\
(a-1)x + (2b+1)y = 9
\end{array}
\right.
$
$の解が x = 3,y = 1であるとき、a = \boxed{ } , b = \boxed{ }である$
代入法どっちにいれてええん?

連立方程式は基礎が大切!~全国入試問題解法 #数学 #数検 #高校入試 #名言 #連立方程式
単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
連立方程式は基礎が大切!~全国入試問題解法
連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x + 3y = 1 \\
8x + 9y = 7
\end{array}
\right.
\end{eqnarray}$
この動画を見る
連立方程式は基礎が大切!~全国入試問題解法
連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x + 3y = 1 \\
8x + 9y = 7
\end{array}
\right.
\end{eqnarray}$
【ぜひ、ここでマスターしたい!】連立方程式:活水高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の方程式を解きなさい.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x + y +1= 0 \\
3x + y +9= 0
\end{array}
\right.
\end{eqnarray}$
活水高等学校過去問
この動画を見る
次の方程式を解きなさい.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x + y +1= 0 \\
3x + y +9= 0
\end{array}
\right.
\end{eqnarray}$
活水高等学校過去問
数学を軽い気持ちで臨む!~全国入試問題解法 #数学 #高校入試 #勉強 #点数 #ライブ

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
数学を軽い気持ちで臨む!
$\begin{eqnarray}
\left\{
\begin{array}{l}
xy + x + 2y= 6 \\
2xy + x-y = 5
\end{array}
\right.
\end{eqnarray}$
を解け。
この動画を見る
数学を軽い気持ちで臨む!
$\begin{eqnarray}
\left\{
\begin{array}{l}
xy + x + 2y= 6 \\
2xy + x-y = 5
\end{array}
\right.
\end{eqnarray}$
を解け。
【短時間でマスター!!】連立方程式 加減法[現役講師解説、中学2年、数学〕

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
3rd School
問題文全文(内容文):
①
$\begin{eqnarray}
\left\{
\begin{array}{l}
x-5y=-2 \\
-x+2y=-1
\end{array}
\right.
\end{eqnarray}$
②
$\begin{eqnarray}
\left\{
\begin{array}{l}
x-2y=5 \\
2x+3y=-4
\end{array}
\right.
\end{eqnarray}$
この動画を見る
①
$\begin{eqnarray}
\left\{
\begin{array}{l}
x-5y=-2 \\
-x+2y=-1
\end{array}
\right.
\end{eqnarray}$
②
$\begin{eqnarray}
\left\{
\begin{array}{l}
x-2y=5 \\
2x+3y=-4
\end{array}
\right.
\end{eqnarray}$
連立方程式だけど2次式 清風南海

単元:
#数学(中学生)#中2数学#中3数学#連立方程式#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
以下の連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
(2x^2+4x)-(y^2-4y)=2 \\
(x^2+2x)+(y^2-4y)=-5
\end{array}
\right.
\end{eqnarray}$
出典:清風南海高等学校
この動画を見る
以下の連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
(2x^2+4x)-(y^2-4y)=2 \\
(x^2+2x)+(y^2-4y)=-5
\end{array}
\right.
\end{eqnarray}$
出典:清風南海高等学校
複雑!?な連立方程式の計算 昭和学院秀英

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{2}{x} + \displaystyle \frac{3}{y} = 10 \\
x-y=xy
\end{array}
\right.
\end{eqnarray}$
出典:昭和学院秀英中学校・高等学校
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{2}{x} + \displaystyle \frac{3}{y} = 10 \\
x-y=xy
\end{array}
\right.
\end{eqnarray}$
出典:昭和学院秀英中学校・高等学校
【短時間でマスター!!】連立方程式 代入法[現役講師解説、中学2年、数学〕

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
3rd School
問題文全文(内容文):
①
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x-2y=7 \\
x=y+4
\end{array}
\right.
\end{eqnarray}$
②
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x+3y=13 \\
y=2x-1
\end{array}
\right.
\end{eqnarray}$
この動画を見る
①
$\begin{eqnarray}
\left\{
\begin{array}{l}
3x-2y=7 \\
x=y+4
\end{array}
\right.
\end{eqnarray}$
②
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x+3y=13 \\
y=2x-1
\end{array}
\right.
\end{eqnarray}$
連立方程式の工夫
単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
数学を数楽に
問題文全文(内容文):
以下の連立方程式、どう解きますか?
$\begin{eqnarray}
\left\{
\begin{array}{l}
140x+70y=2100 \\
x+y=22
\end{array}
\right.
\end{eqnarray}$
この動画を見る
以下の連立方程式、どう解きますか?
$\begin{eqnarray}
\left\{
\begin{array}{l}
140x+70y=2100 \\
x+y=22
\end{array}
\right.
\end{eqnarray}$
分母に文字がある連立方程式 洛南

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#洛南高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
2a+\displaystyle \frac{1}{b}=7 \\
7a-\displaystyle \frac{3}{b}=5
\end{array}
\right.
\end{eqnarray}$
出典:洛南高等学校
この動画を見る
連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
2a+\displaystyle \frac{1}{b}=7 \\
7a-\displaystyle \frac{3}{b}=5
\end{array}
\right.
\end{eqnarray}$
出典:洛南高等学校
こんな解き方知ってる?

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
5x+2y=-9 \\
-2x+9y=-16
\end{array}
\right.
\end{eqnarray}$
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
5x+2y=-9 \\
-2x+9y=-16
\end{array}
\right.
\end{eqnarray}$
平方根と式の値 2024駒込
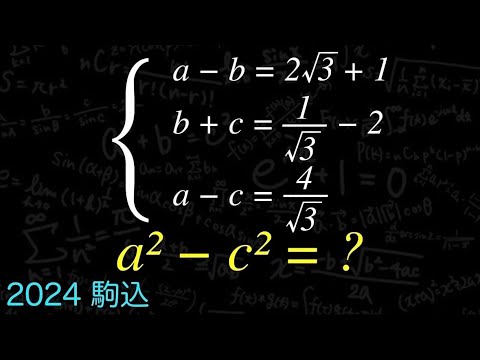
単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
数学を数楽に
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
a-b=2\sqrt{ 3 }+1 \\
b+c=\displaystyle \frac{1}{\sqrt{ 3 }}-2 \\
a-c=\displaystyle \frac{4}{\sqrt{ 3 }}
\end{array}
\right.
\end{eqnarray}$
$a^2-c^2=?$
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
a-b=2\sqrt{ 3 }+1 \\
b+c=\displaystyle \frac{1}{\sqrt{ 3 }}-2 \\
a-c=\displaystyle \frac{4}{\sqrt{ 3 }}
\end{array}
\right.
\end{eqnarray}$
$a^2-c^2=?$
連立方程式の基本的な考え方

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
連立方程式の基本的な考え方について説明動画です
$\begin{cases}
x+2y=5 \\
5x+4y=13
\end{cases}$
この動画を見る
連立方程式の基本的な考え方について説明動画です
$\begin{cases}
x+2y=5 \\
5x+4y=13
\end{cases}$
複雑な連立方程式 久留米大附設

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
\frac{1}{x-1} + y = -1 \\
\frac{2}{x-1} + \frac{y}{2} = 4
\end{array}
\right.
\end{eqnarray}
久留米大学附設高等学校
この動画を見る
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
\frac{1}{x-1} + y = -1 \\
\frac{2}{x-1} + \frac{y}{2} = 4
\end{array}
\right.
\end{eqnarray}
久留米大学附設高等学校
#63 #数検1級1次過去問 #連立方程式

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
ますただ
問題文全文(内容文):
$xy \neq 0$のとき、次の連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x+y)(x^2+y^2)=\displaystyle \frac{40}{3}xy \\
(x^2+y^2)(x^4-y^4)=\displaystyle \frac{800}{9}x^2y^2
\end{array}
\right.
\end{eqnarray}$
出典:数検1級1次
この動画を見る
$xy \neq 0$のとき、次の連立方程式を解け。
$\begin{eqnarray}
\left\{
\begin{array}{l}
(x+y)(x^2+y^2)=\displaystyle \frac{40}{3}xy \\
(x^2+y^2)(x^4-y^4)=\displaystyle \frac{800}{9}x^2y^2
\end{array}
\right.
\end{eqnarray}$
出典:数検1級1次
連立方程式 法政一

単元:
#連立方程式
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
1042x + 347y = 2 \\
1652x + 551y = -2
\end{array}
\right.
\end{eqnarray}
法政大学第一高等学校
この動画を見る
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
1042x + 347y = 2 \\
1652x + 551y = -2
\end{array}
\right.
\end{eqnarray}
法政大学第一高等学校
大学入試の連立方程式 東北学院大

単元:
#連立方程式#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
x(y+z)=5 \\
y(z+x)=8 \\
z(x+y)=9
\end{array}
\right.
\end{eqnarray}
東北学院大学
この動画を見る
連立方程式を解け
\begin{eqnarray}
\left\{
\begin{array}{l}
x(y+z)=5 \\
y(z+x)=8 \\
z(x+y)=9
\end{array}
\right.
\end{eqnarray}
東北学院大学
連立方程式は知ってるカタチに直せ…!~全国入試問題解法 #shorts, #数学, #高校入試, #頭の体操, #連立方程式,
単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x\div(2y+13)=3:1 \\
5x+6y=3
\end{array}
\right.
\end{eqnarray}$
次の連立方程式を解きなさい.
広大付属高校過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
2x\div(2y+13)=3:1 \\
5x+6y=3
\end{array}
\right.
\end{eqnarray}$
次の連立方程式を解きなさい.
広大付属高校過去問
【学んだことを活かせ…!】連立方程式:明治大学付属中野高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#明治大学付属中野高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x,y $についての連立方程式 $ \begin{eqnarray}
\left\{
\begin{array}{l}
4x+3y=11 \\
x-ky=-\dfrac{1}{2}k
\end{array}
\right.
\end{eqnarray}$ の解が $\begin{eqnarray}
\left\{
\begin{array}{l}
x=p \\
y=q
\end{array}
\right.
\end{eqnarray}$ であり,
$ p+q=3 $が成り立つ.$ k $の値を求めなさい.
明治大学付属中野高等学校過去問
この動画を見る
$ x,y $についての連立方程式 $ \begin{eqnarray}
\left\{
\begin{array}{l}
4x+3y=11 \\
x-ky=-\dfrac{1}{2}k
\end{array}
\right.
\end{eqnarray}$ の解が $\begin{eqnarray}
\left\{
\begin{array}{l}
x=p \\
y=q
\end{array}
\right.
\end{eqnarray}$ であり,
$ p+q=3 $が成り立つ.$ k $の値を求めなさい.
明治大学付属中野高等学校過去問
【アナタならどうする…!?】連立方程式:明治大学付属明治高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#明治大学付属明治高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x^2-4y^2-10x+25=0 ・・・① \\
x^2+x-6-2xy+4y=0・・・②
\end{array}
\right.
\end{eqnarray}$
上式が成り立つ$ x,y $の組をすべて求めよ.
明治大学付属明治高等学校過去問
この動画を見る
$ \begin{eqnarray}
\left\{
\begin{array}{l}
x^2-4y^2-10x+25=0 ・・・① \\
x^2+x-6-2xy+4y=0・・・②
\end{array}
\right.
\end{eqnarray}$
上式が成り立つ$ x,y $の組をすべて求めよ.
明治大学付属明治高等学校過去問
【得点源にするために…!】連立方程式:西大和学園高等学校~全国入試問題解法

単元:
#中2数学#連立方程式#高校入試過去問(数学)#西大和学園高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ a $を定数とする.
$ x,y $についての連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
4y-3x=a \\
2x-3y=4
\end{array}
\right.
\end{eqnarray}$の解が$ x+y=a $を満たすとき,
定数$ a $の値を求めよ.
西大和学園高校過去問
この動画を見る
$ a $を定数とする.
$ x,y $についての連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
4y-3x=a \\
2x-3y=4
\end{array}
\right.
\end{eqnarray}$の解が$ x+y=a $を満たすとき,
定数$ a $の値を求めよ.
西大和学園高校過去問
福田のおもしろ数学015〜ジュニア数学オリンピック本戦問題〜2つの式を満たす4つの自然数を求める

単元:
#数学(中学生)#中2数学#連立方程式#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#数学オリンピック
指導講師:
福田次郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
a+b=cd \\
c+d=ab
\end{array}
\right.
\end{eqnarray}$
を満たす正の整数 $a,b,c,d$は?
ジュニア数学オリンピック過去問
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
a+b=cd \\
c+d=ab
\end{array}
\right.
\end{eqnarray}$
を満たす正の整数 $a,b,c,d$は?
ジュニア数学オリンピック過去問
福田のおもしろ数学014〜恒例10秒チャレンジ〜3変数の連立方程式

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
福田次郎
問題文全文(内容文):
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=4 \\
y+z=3 \\
z+x=5
\end{array}
\right.
\end{eqnarray}$
を解け.
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y=4 \\
y+z=3 \\
z+x=5
\end{array}
\right.
\end{eqnarray}$
を解け.
【ミスをなくすひと工夫…!】連立方程式:東京都立立川高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
連立方程式$ \begin{eqnarray}
\left\{
\begin{array}{l}
14x+3y=17.5 \\
3x+2y=\dfrac{69}{7}
\end{array}
\right.
\end{eqnarray}$ を解け.
都立立川高校過去問
この動画を見る
連立方程式$ \begin{eqnarray}
\left\{
\begin{array}{l}
14x+3y=17.5 \\
3x+2y=\dfrac{69}{7}
\end{array}
\right.
\end{eqnarray}$ を解け.
都立立川高校過去問
数学の入試で知る解法~全国入試問題解法 #shorts #直線 #高校受験 #mathematics #sound

単元:
#数学(中学生)#中2数学#連立方程式#1次関数
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2点$ (-1,1),(2,7)$を通る直線の式を答えなさい.
新潟県入試問題過去問
この動画を見る
2点$ (-1,1),(2,7)$を通る直線の式を答えなさい.
新潟県入試問題過去問
【式は2つ、文字は3つ…!】整数:慶応義塾女子高等学校~全国入試問題解法

単元:
#中1数学#中2数学#連立方程式#文字と式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \color{red}{整数x}$に$ \color{red}{6}$を加えると$ \color{red}{整数m}$の平方になり,
$ \color{red}{x}$から$ \color{red}{17}$を引くと$\color{red}{整数n}$の平方になる.
m,nはともに正として$ \color{orange}{m,n,x}$の値を求めなさい.
慶應女子高校過去問
この動画を見る
$ \color{red}{整数x}$に$ \color{red}{6}$を加えると$ \color{red}{整数m}$の平方になり,
$ \color{red}{x}$から$ \color{red}{17}$を引くと$\color{red}{整数n}$の平方になる.
m,nはともに正として$ \color{orange}{m,n,x}$の値を求めなさい.
慶應女子高校過去問
