 中2数学
中2数学
 中2数学
中2数学
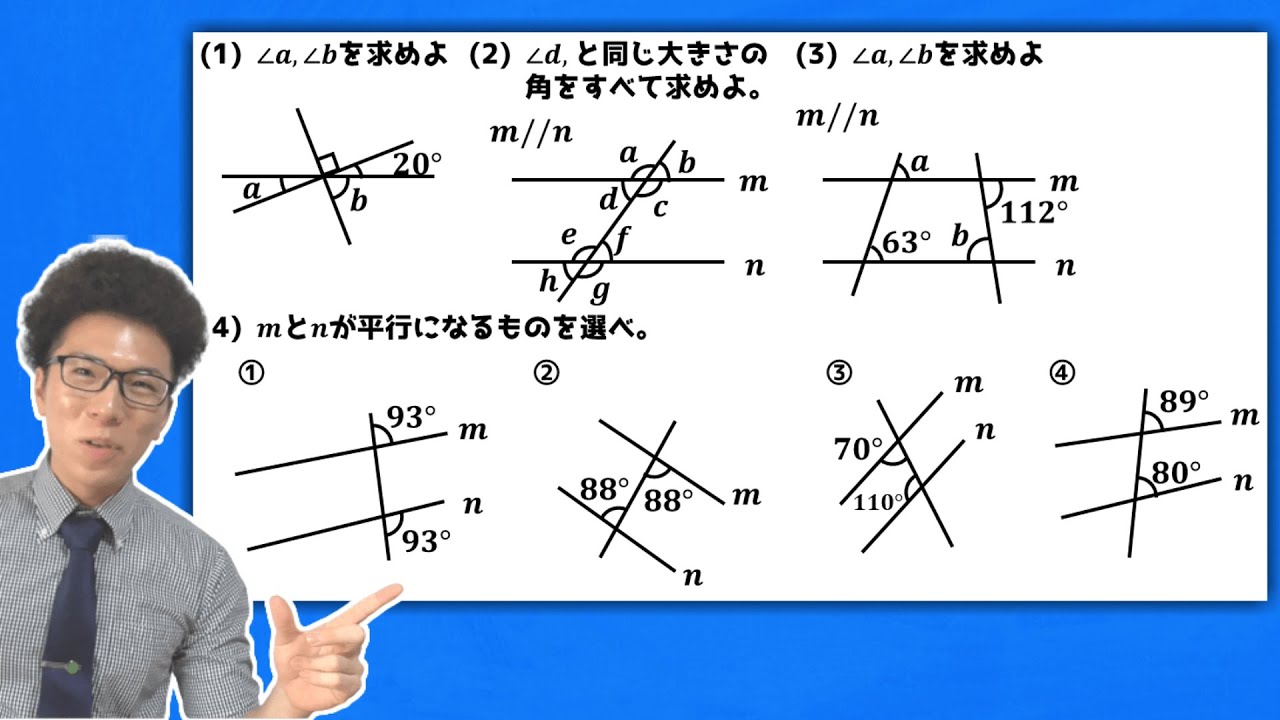
【中学数学】平行線と角の問題演習・基礎 4-1.5【中2数学】
お茶の水女子大 連立二元三次方程式
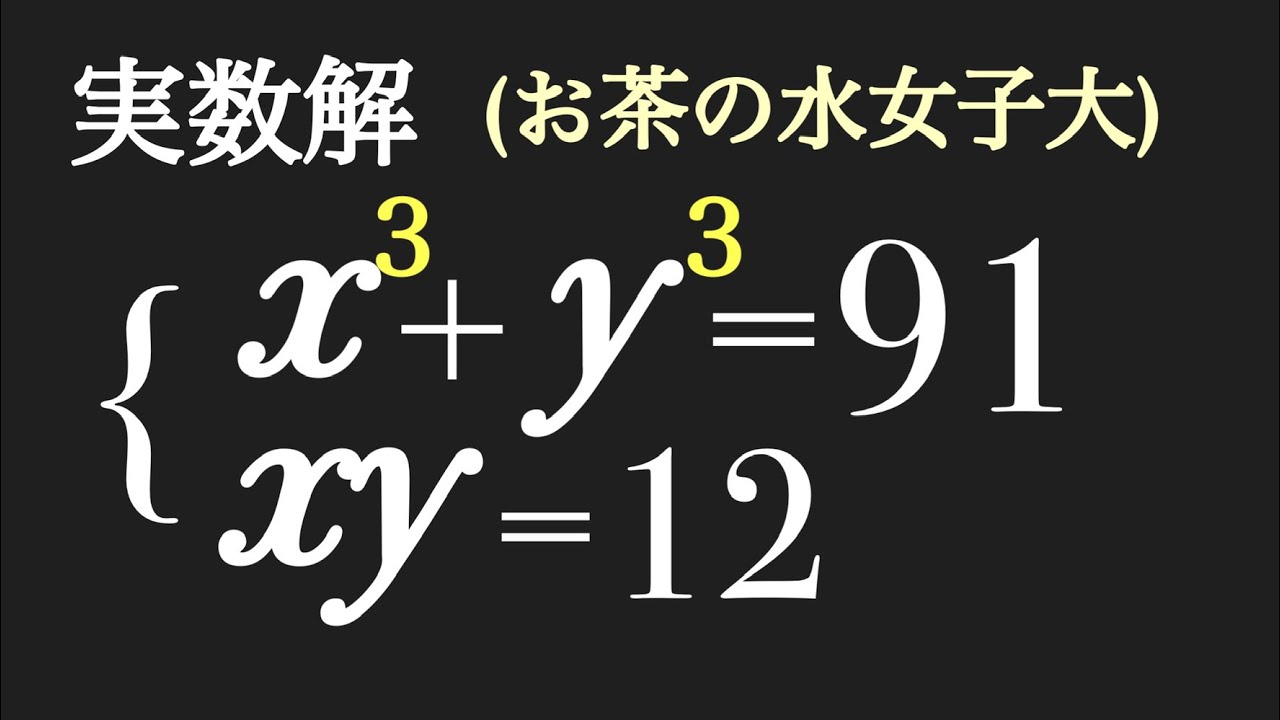
単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
鈴木貫太郎
問題文全文(内容文):
実数解を求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^3+y^3=91 \\
xy=12
\end{array}
\right.
\end{eqnarray}$
お茶の水女子大過去問
この動画を見る
実数解を求めよ.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^3+y^3=91 \\
xy=12
\end{array}
\right.
\end{eqnarray}$
お茶の水女子大過去問
【高校受験対策/数学】死守-78

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#平方根#2次方程式#比例・反比例#1次関数#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守78
①下の図のように、長方形$ABCD$の中に 1辺の長さが$\sqrt{5}cm$と$\sqrt{10}cm$の正方形がある。
このとき、斜線部分の長方形の間の長さを求めなさい。
②葉一くんは、下の図の平行四辺形$ABCD$の面積を求めるために、辺$BC$を底辺とみて、高さを測ろうと考えた。
点を$P$下の図のようにとるとき、線分$PH$が高さとなるような点$H$を作図によって求めなさい。
③1000円で、1個$a$円のクリームパン5個と1個$b$円のジャムパン3個を買うことができる。
ただし消費税は考えないものとする。
この数量の関係を表した不等式としてもっとも適切なものを、次の ア~エの中から一つ選んで、その記号を書きなさい。
ア $1000-(5a+3b) \lt 0$
イ $5a+3b \lt 1000$
ウ $1000-(5a+3b) \geqq 0$
エ $(5a+3b) \geqq 1000$
④ 右の図で、点$A$は関数$y=\frac{2}{x }$と関数$y=ax^2$のグラフの交点である。
点$B$は点$A$を$y$軸を対称の軸として対称移動させたものであり、$x$座標は$-1$である。
このことから、$a$の値はアであり、関数$y=ax^2$について、 $x$の値が1から3まで増加するときの変化の割合はイであることがわ かる。
このとき上のア・イに当てはまる数をそれぞれ書きなさい。
この動画を見る
高校受験対策・死守78
①下の図のように、長方形$ABCD$の中に 1辺の長さが$\sqrt{5}cm$と$\sqrt{10}cm$の正方形がある。
このとき、斜線部分の長方形の間の長さを求めなさい。
②葉一くんは、下の図の平行四辺形$ABCD$の面積を求めるために、辺$BC$を底辺とみて、高さを測ろうと考えた。
点を$P$下の図のようにとるとき、線分$PH$が高さとなるような点$H$を作図によって求めなさい。
③1000円で、1個$a$円のクリームパン5個と1個$b$円のジャムパン3個を買うことができる。
ただし消費税は考えないものとする。
この数量の関係を表した不等式としてもっとも適切なものを、次の ア~エの中から一つ選んで、その記号を書きなさい。
ア $1000-(5a+3b) \lt 0$
イ $5a+3b \lt 1000$
ウ $1000-(5a+3b) \geqq 0$
エ $(5a+3b) \geqq 1000$
④ 右の図で、点$A$は関数$y=\frac{2}{x }$と関数$y=ax^2$のグラフの交点である。
点$B$は点$A$を$y$軸を対称の軸として対称移動させたものであり、$x$座標は$-1$である。
このことから、$a$の値はアであり、関数$y=ax^2$について、 $x$の値が1から3まで増加するときの変化の割合はイであることがわ かる。
このとき上のア・イに当てはまる数をそれぞれ書きなさい。
【中学数学】方程式の演習問題~早稲田の過去問~【高校受験】

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#早稲田大学高等学院
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
黒、白2種類の石がいくつかずつある。
はじめ、白石の個数が全体の個数にしめる割合は40%であった。
白石の個数を14個減らしたところ、白石の個数が全体の個数にしめる割合は25%になった。
はじめにあった黒石、白石の個数をそれぞれ求めよ。
この動画を見る
黒、白2種類の石がいくつかずつある。
はじめ、白石の個数が全体の個数にしめる割合は40%であった。
白石の個数を14個減らしたところ、白石の個数が全体の個数にしめる割合は25%になった。
はじめにあった黒石、白石の個数をそれぞれ求めよ。
【高校受験対策/数学】???

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
【高校受験対策/数学】???
ある中学校の全校の生徒数は、男女合わせて155人です。
この中学校の男子生徒の80%と女子生徒の60%が運動部に所属しており、
運動部に所属している男子の人数は、 運動部に所属している女子の人数より19人多い。
このとき運動部に所属している男子の人数と運動部に所属している女子の人数を、それぞれ求めなさい。
この動画を見る
【高校受験対策/数学】???
ある中学校の全校の生徒数は、男女合わせて155人です。
この中学校の男子生徒の80%と女子生徒の60%が運動部に所属しており、
運動部に所属している男子の人数は、 運動部に所属している女子の人数より19人多い。
このとき運動部に所属している男子の人数と運動部に所属している女子の人数を、それぞれ求めなさい。
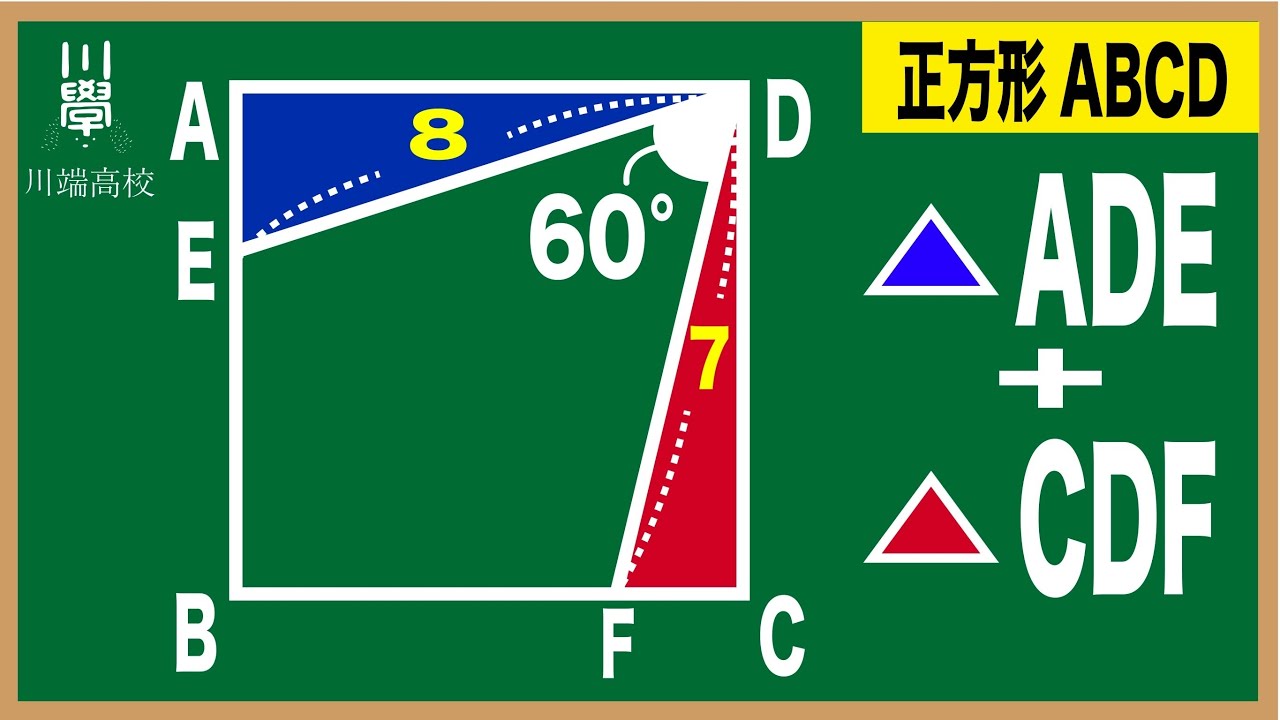
面積の和
67.5° ラ・サール
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
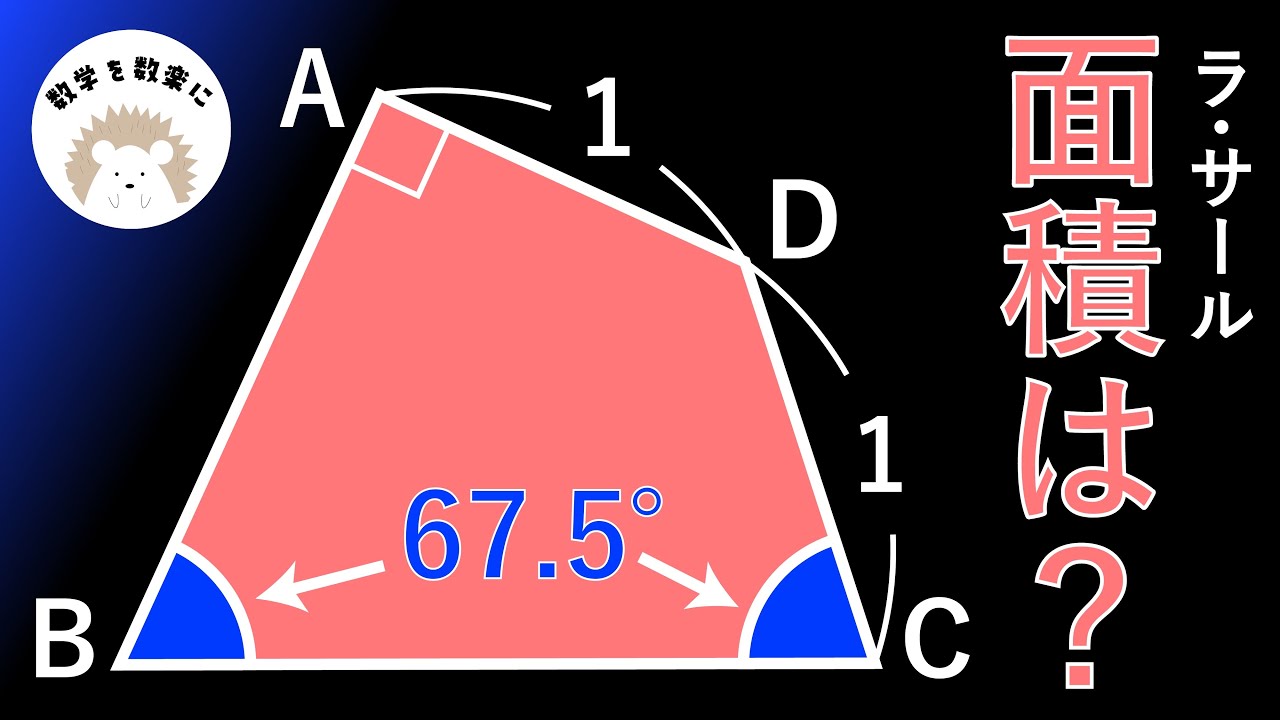
四角形ABCDの面積=?
*図は動画内参照
ラ・サール高等学校
この動画を見る
四角形ABCDの面積=?
*図は動画内参照
ラ・サール高等学校
【高校受験対策/数学】死守77

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#2次方程式#1次関数#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守77
①$-3+(-2)$を計算しなさい。
➁$8-4÷(-2)^2$を計算しなさい。
③$5×(-5a)$を計算しなさい。
④$\frac{1}{2}x^2y÷\frac{1}{4}xy$を計算しなさい。
⑤$\sqrt{48}-\sqrt{3}$を計算しなさい。
⑥$(2a-b)^2$を展開しなさい。
⑦$x^2-x-42$を因数分解しなさい。
⑧半径が$6cm$で中心角が$45°$のおうぎ形の面積を求めなさい。
ただし、円周率は$\pi$とする。
⑨解が$-5,1$の2つの数となる、$x$についての2次方程式を1つ作りなさい。
⑩次のア~エのうち、数の集合と四則との関係について述べた文として正しいものをすべて選び、記号で答えなさい。
ア 自然数と自然数の加法の結果は、いつでも自然数となる。
イ 自然数と自然数の減法の結果は、いつでも整数となる。
ウ 自然数と自然数の乗法の結果は、いつでも自然数となる。
エ 自然数と自然数の除法の結果は、いつでも整数となる。
この動画を見る
高校受験対策・死守77
①$-3+(-2)$を計算しなさい。
➁$8-4÷(-2)^2$を計算しなさい。
③$5×(-5a)$を計算しなさい。
④$\frac{1}{2}x^2y÷\frac{1}{4}xy$を計算しなさい。
⑤$\sqrt{48}-\sqrt{3}$を計算しなさい。
⑥$(2a-b)^2$を展開しなさい。
⑦$x^2-x-42$を因数分解しなさい。
⑧半径が$6cm$で中心角が$45°$のおうぎ形の面積を求めなさい。
ただし、円周率は$\pi$とする。
⑨解が$-5,1$の2つの数となる、$x$についての2次方程式を1つ作りなさい。
⑩次のア~エのうち、数の集合と四則との関係について述べた文として正しいものをすべて選び、記号で答えなさい。
ア 自然数と自然数の加法の結果は、いつでも自然数となる。
イ 自然数と自然数の減法の結果は、いつでも整数となる。
ウ 自然数と自然数の乗法の結果は、いつでも自然数となる。
エ 自然数と自然数の除法の結果は、いつでも整数となる。
これぞ入試問題っていう感じ。easy
【中学数学】平行線と角を丁寧に~対頂角・同位角・錯角~ 4-1【中2数学】

連立方程式
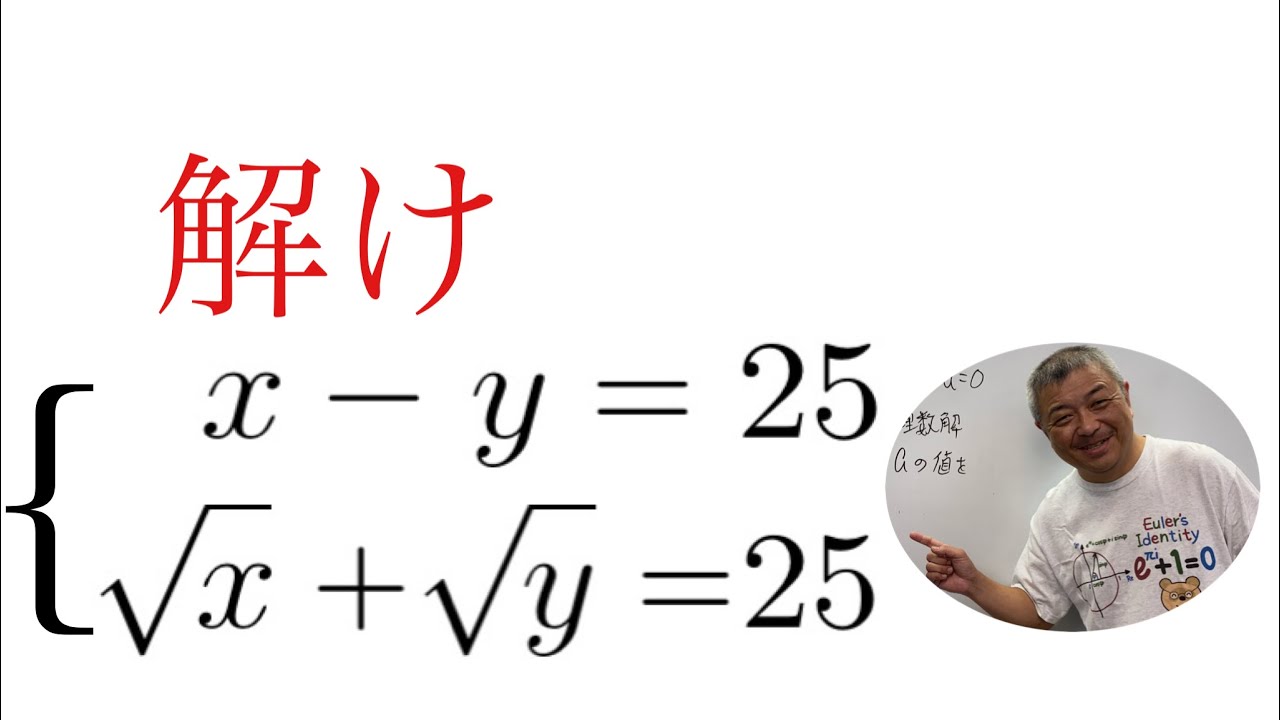
単元:
#連立方程式
指導講師:
鈴木貫太郎
問題文全文(内容文):
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x - y = 25 \\
\sqrt x + \sqrt y = 25
\end{array}
\right.
\end{eqnarray}$
この動画を見る
これを解け.
$\begin{eqnarray}
\left\{
\begin{array}{l}
x - y = 25 \\
\sqrt x + \sqrt y = 25
\end{array}
\right.
\end{eqnarray}$
平行はなんのため?60°はどうする?
単元:
#数学(中学生)#中2数学#平面図形#角度と面積#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
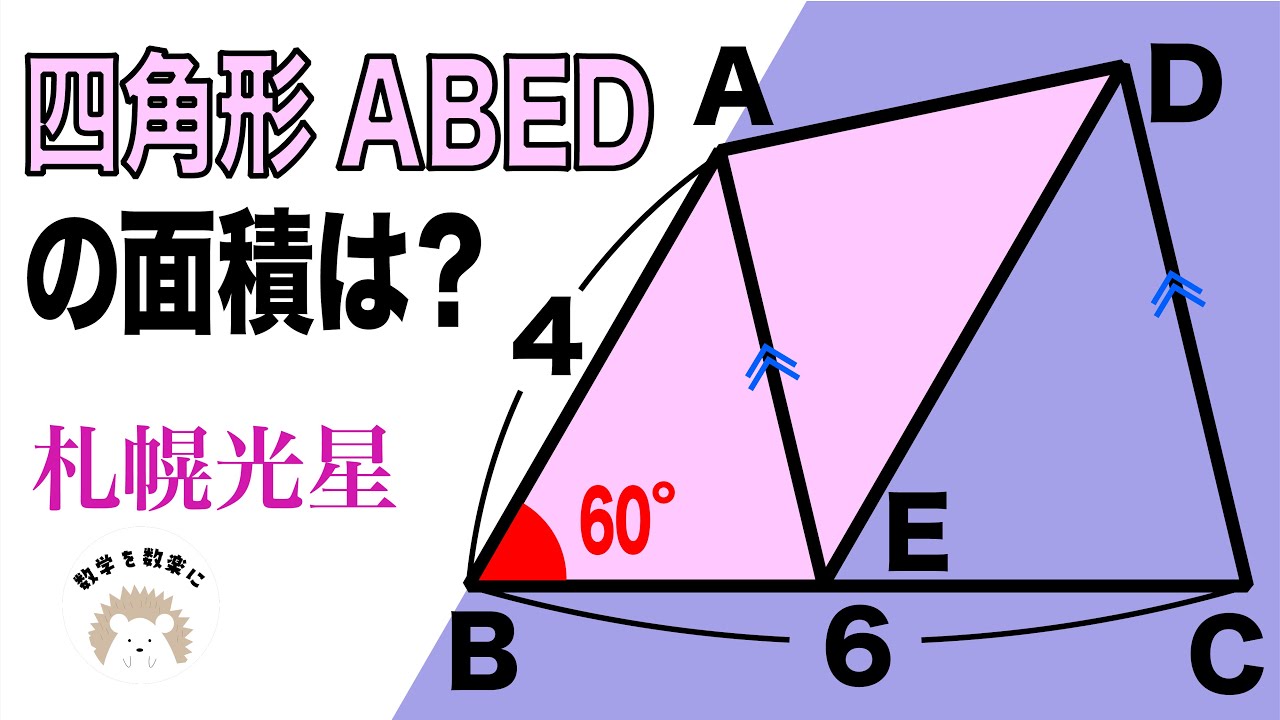
四角形ABEDの面積=?
*図は動画内参照
札幌光星高等学校
この動画を見る
四角形ABEDの面積=?
*図は動画内参照
札幌光星高等学校
気づけばほぼ一瞬
【高校受験対策/数学】死守76

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#比例・反比例#空間図形#確率#文字と式#標本調査
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守76
①$2-(-5)$を計算しなさい。
②$4x-2x×\frac{1}{2}$を計算しなさい。
③$-6a^3b^2÷(-4ab)$を計算しなさい。
④$x=-2$、$y=3$のとき$(2x-y-6)+3(x+y+2)$の値を求めなさい。
③下の図の三角柱$ABC-DEF$において、 辺$AB$とねじれの位置にある辺をすべて答えなさい。
⑥$n$を自然数とする。$\sqrt{24n}$が自然数となるような$n$のうち、最も小さい数を求めなさい。
⑦2つの容器A、Bに牛乳が入っており、容器Bに入っている牛乳の量は、容器Aに入っている牛乳の量の2倍である。
容器Aに$140ml$の牛乳を加えたところ、 容器Aと容器Bの牛乳の量の比が$5:3$となった。
はじめに容器Aに入って いた牛乳の量は何$ml$であったか、求めなさい。
⑧あるクラスの女子生徒20人が体カテストで反復横とびを行い、
その記録を整理したところ、20人の記録の中央値は50回であった。
この20人の記録について、次のア~エのうち、必ず正しいといえるものを1つ選びなさい。
ア 20人の記録の合計は1000回である。
イ 20人のうち、記録が50回であった生徒が最も多い。
ウ 20人のうち、記録が60回以上であった生徒は1人もいない。
エ 20人のうち、記録が50回以上であった生徒が少なくとも10人いる。
この動画を見る
高校受験対策・死守76
①$2-(-5)$を計算しなさい。
②$4x-2x×\frac{1}{2}$を計算しなさい。
③$-6a^3b^2÷(-4ab)$を計算しなさい。
④$x=-2$、$y=3$のとき$(2x-y-6)+3(x+y+2)$の値を求めなさい。
③下の図の三角柱$ABC-DEF$において、 辺$AB$とねじれの位置にある辺をすべて答えなさい。
⑥$n$を自然数とする。$\sqrt{24n}$が自然数となるような$n$のうち、最も小さい数を求めなさい。
⑦2つの容器A、Bに牛乳が入っており、容器Bに入っている牛乳の量は、容器Aに入っている牛乳の量の2倍である。
容器Aに$140ml$の牛乳を加えたところ、 容器Aと容器Bの牛乳の量の比が$5:3$となった。
はじめに容器Aに入って いた牛乳の量は何$ml$であったか、求めなさい。
⑧あるクラスの女子生徒20人が体カテストで反復横とびを行い、
その記録を整理したところ、20人の記録の中央値は50回であった。
この20人の記録について、次のア~エのうち、必ず正しいといえるものを1つ選びなさい。
ア 20人の記録の合計は1000回である。
イ 20人のうち、記録が50回であった生徒が最も多い。
ウ 20人のうち、記録が60回以上であった生徒は1人もいない。
エ 20人のうち、記録が50回以上であった生徒が少なくとも10人いる。
これ説明して

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数学(中学生)#中1数学#中2数学#中3数学#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
2$\div \displaystyle \frac{1}{2}$
この動画を見る
2$\div \displaystyle \frac{1}{2}$
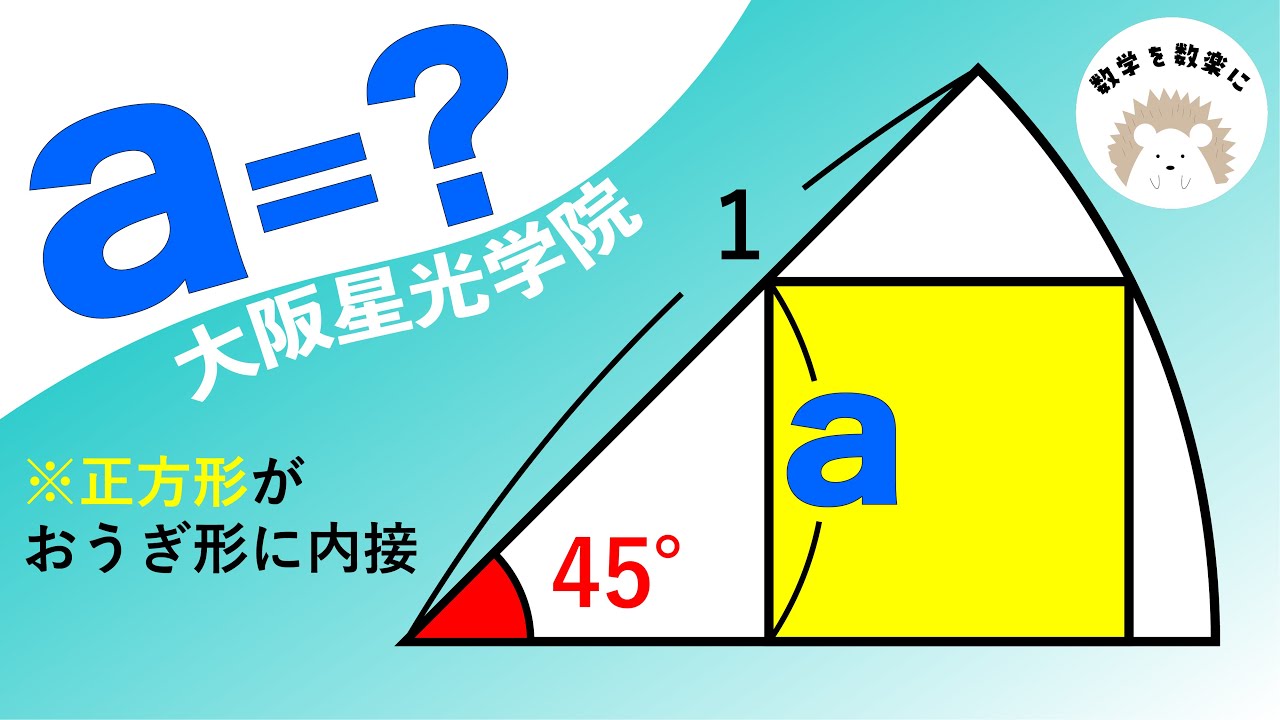
正方形がおうぎ形に内接 大阪星光学院
放物線が回転!!!びびったら負け

単元:
#数学(中学生)#中2数学#中3数学#2次関数#平面図形#角度と面積#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
放物線が原点を中心に30°回転
赤線部の面積=?
*図は動画内参照
早稲田大学 高等学院
この動画を見る
放物線が原点を中心に30°回転
赤線部の面積=?
*図は動画内参照
早稲田大学 高等学院
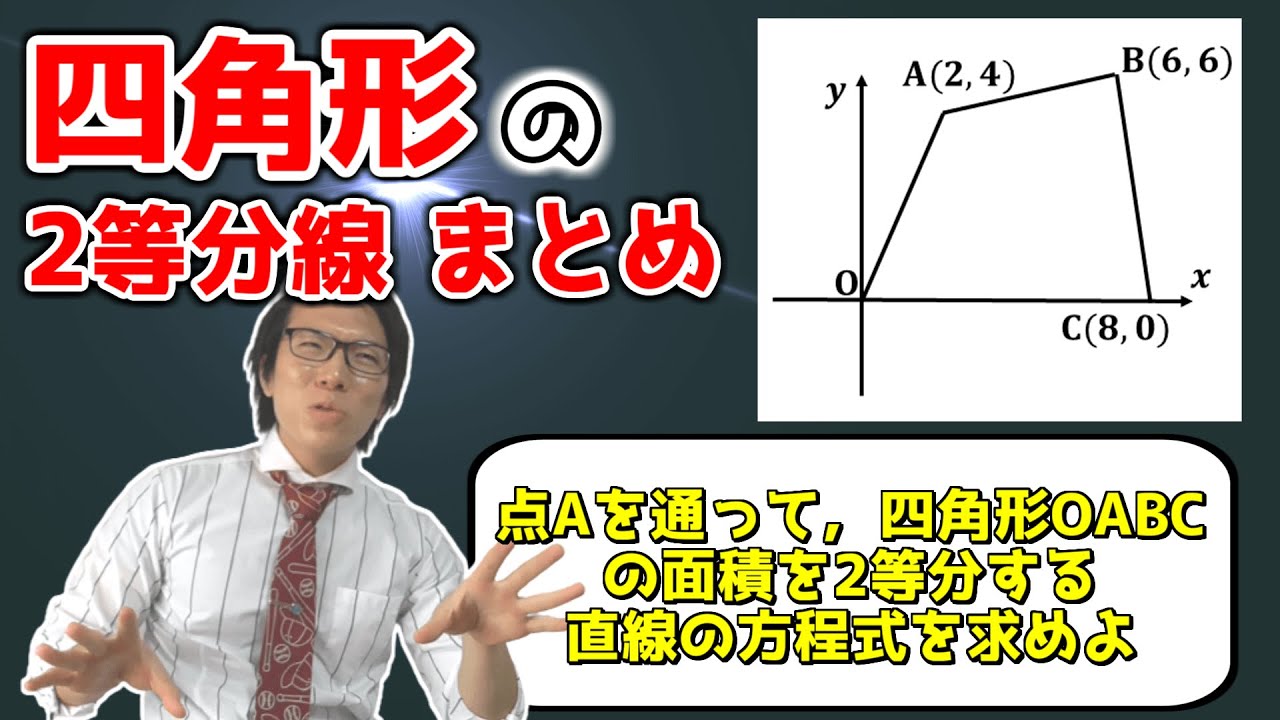
【中学数学】四角形の面積を2等分する直線のまとめ【中2数学】
単元:
#数学(中学生)#中1数学#中2数学#平行と合同#平面図形#三角形と四角形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
動画内の図、点Aを通て、四角形OABCを二等分する直線の式を求めよ。
この動画を見る
動画内の図、点Aを通て、四角形OABCを二等分する直線の式を求めよ。
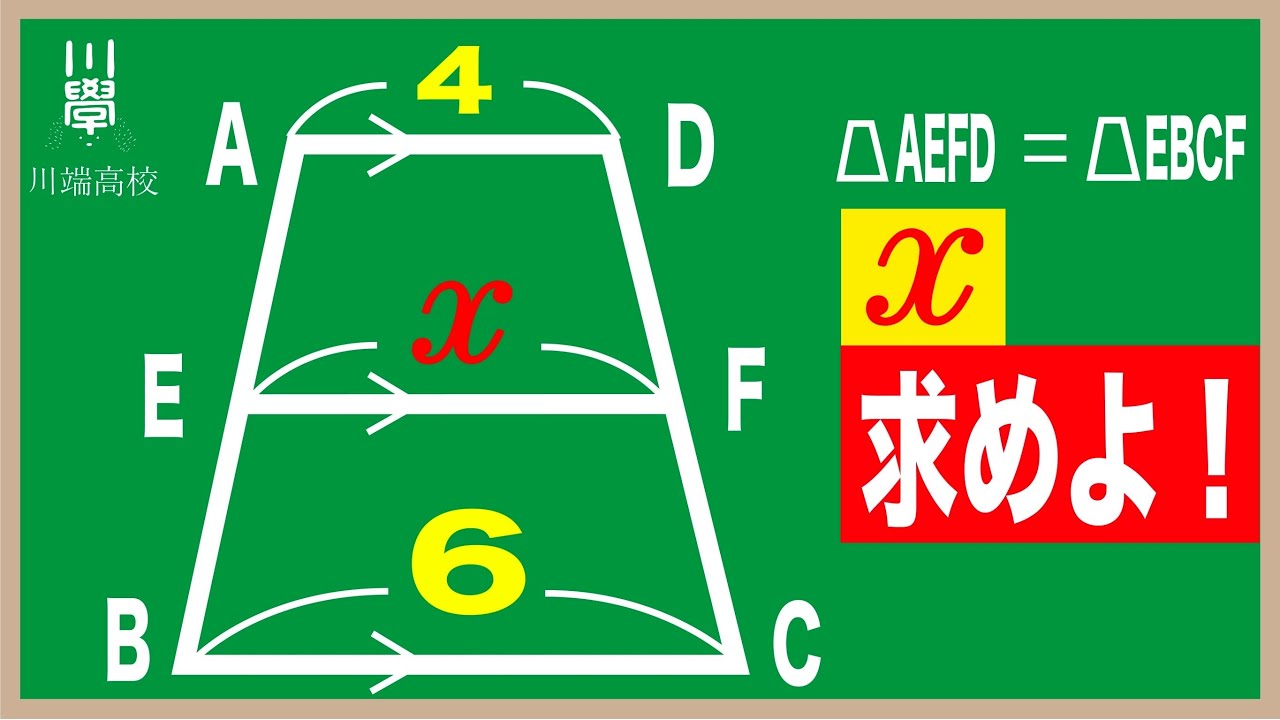
2つの台形の面積が等しいとき。(高校入試 数学)
単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
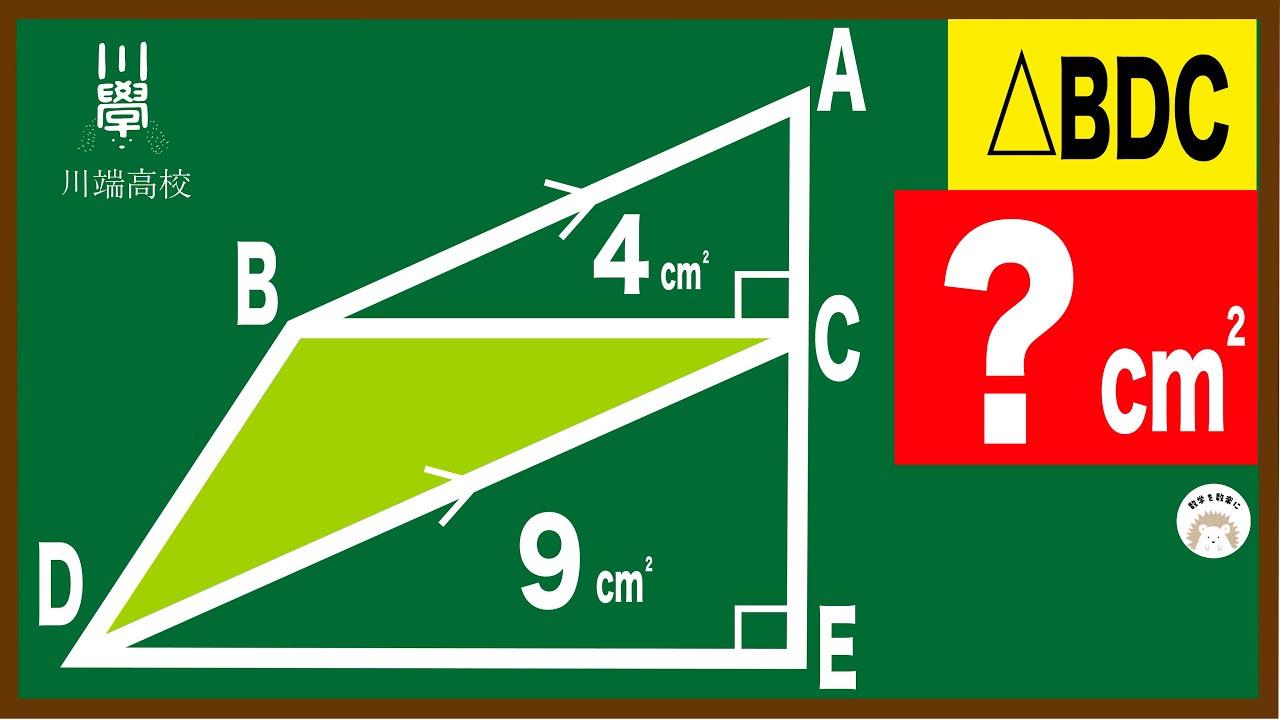
台形AEFD=台形EBCFのとき x=?
*図は動画内参照
川端高校
この動画を見る
台形AEFD=台形EBCFのとき x=?
*図は動画内参照
川端高校
【裏技】〇●の二等分線の図形の問題

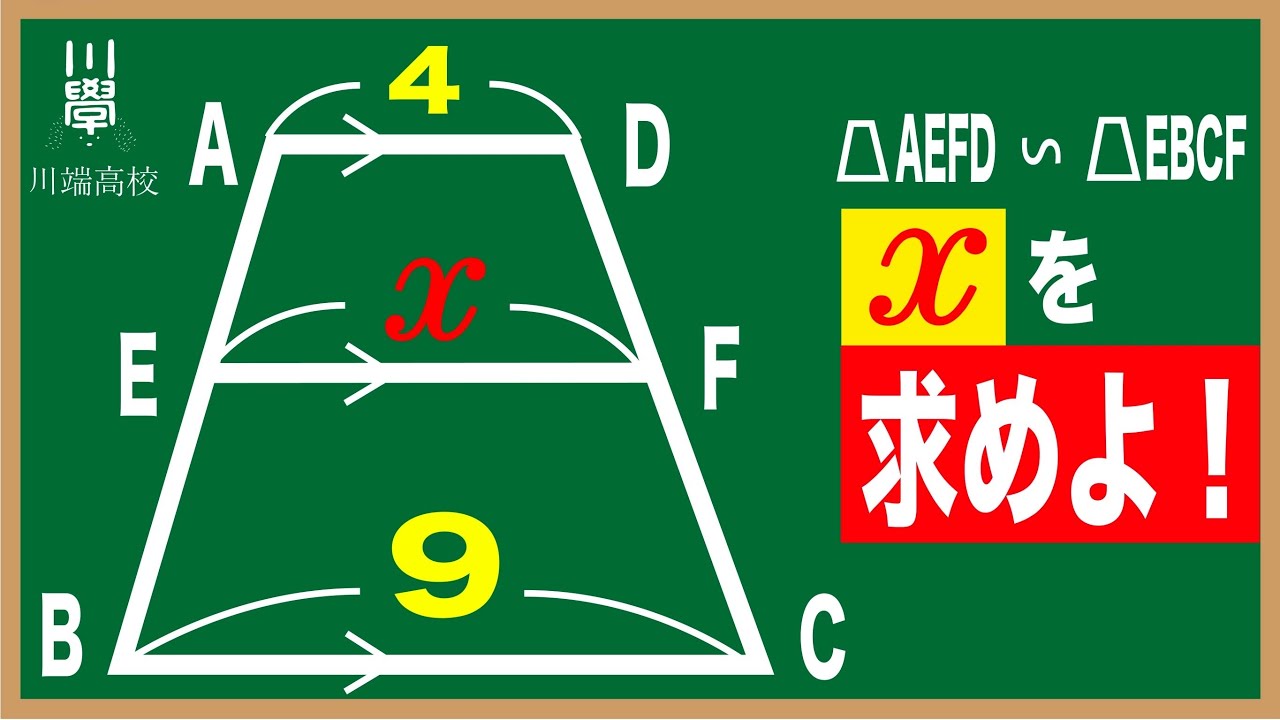
台形の相似 気づけば一瞬!!(高校入試 数学)
単元:
#数学(中学生)#中2数学#中3数学#相似な図形#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
台形AEFD∽台形EBCF
x=?
*図は動画内参照
川端高校
この動画を見る
台形AEFD∽台形EBCF
x=?
*図は動画内参照
川端高校
【高校受験対策/数学】死守75

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#2次方程式#1次関数#平行と合同#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守75
①$-8+5$を計算しなさい。
②$1+3×-(\frac{2}{7})$を計算しなさい。
③$2(a+4b)+3(a-2b)$を計算しなさい。
④$\sqrt{27}-\frac{6}{\sqrt{3}}$を計算しなさい。
⑤$(x+1)^2+(x-4)(x+2)$を計算しなさい。
⑥次の式を因数分解しなさい。
$9x^2-4y^2$
⑦右の図のように、長方形$ABCD$を対角線$AC$を折り目として折り返し、
頂点$B$が移った点を$E$とする。
$\angle ACE=20°$のとき、$\angle x$の大きさを求めなさい。
⑧右の図のように、2点$A(2,6)$、$B(8,2)$がある。
次の文中の(ア)、(イ)にあてはまる数を求めなさい。
直線$y=ax$のグラフが、線分$AB$上の点を通るとき、$a$の値の範囲は、(ア) $ \leqq a\leqq$ (イ)である。
この動画を見る
高校受験対策・死守75
①$-8+5$を計算しなさい。
②$1+3×-(\frac{2}{7})$を計算しなさい。
③$2(a+4b)+3(a-2b)$を計算しなさい。
④$\sqrt{27}-\frac{6}{\sqrt{3}}$を計算しなさい。
⑤$(x+1)^2+(x-4)(x+2)$を計算しなさい。
⑥次の式を因数分解しなさい。
$9x^2-4y^2$
⑦右の図のように、長方形$ABCD$を対角線$AC$を折り目として折り返し、
頂点$B$が移った点を$E$とする。
$\angle ACE=20°$のとき、$\angle x$の大きさを求めなさい。
⑧右の図のように、2点$A(2,6)$、$B(8,2)$がある。
次の文中の(ア)、(イ)にあてはまる数を求めなさい。
直線$y=ax$のグラフが、線分$AB$上の点を通るとき、$a$の値の範囲は、(ア) $ \leqq a\leqq$ (イ)である。
【中学数学】連立方程式の演習~2014年石川県過去問~【高校受験】

ブーメラン型の面積を求める

【裏技】これすげぇ

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#数学(中学生)#中1数学#中2数学#中3数学#約数・倍数を利用する問題#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
約分のテクニック紹介動画です
この動画を見る
約分のテクニック紹介動画です
気づけば一瞬!!2つの正方形
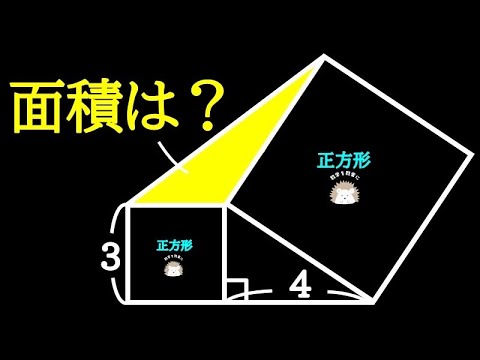
2がたくさん!

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$(2×2)^x=2×2^x+2×2×2$のときx=?
川端高校中間テスト
この動画を見る
$(2×2)^x=2×2^x+2×2×2$のときx=?
川端高校中間テスト
【中学数学】連立方程式:連立3元1次方程式解こう!

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
理数個別チャンネル
問題文全文(内容文):
$x+y+z=0,3x+4y+2z=-1,3x-y+z=10$の連立方程式を解け。
この動画を見る
$x+y+z=0,3x+4y+2z=-1,3x-y+z=10$の連立方程式を解け。
【サイコロが4つ!別解付き♪】確率:明治大学附属明治高等学校~全国入試問題解法
単元:
#数学(中学生)#中2数学#確率#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
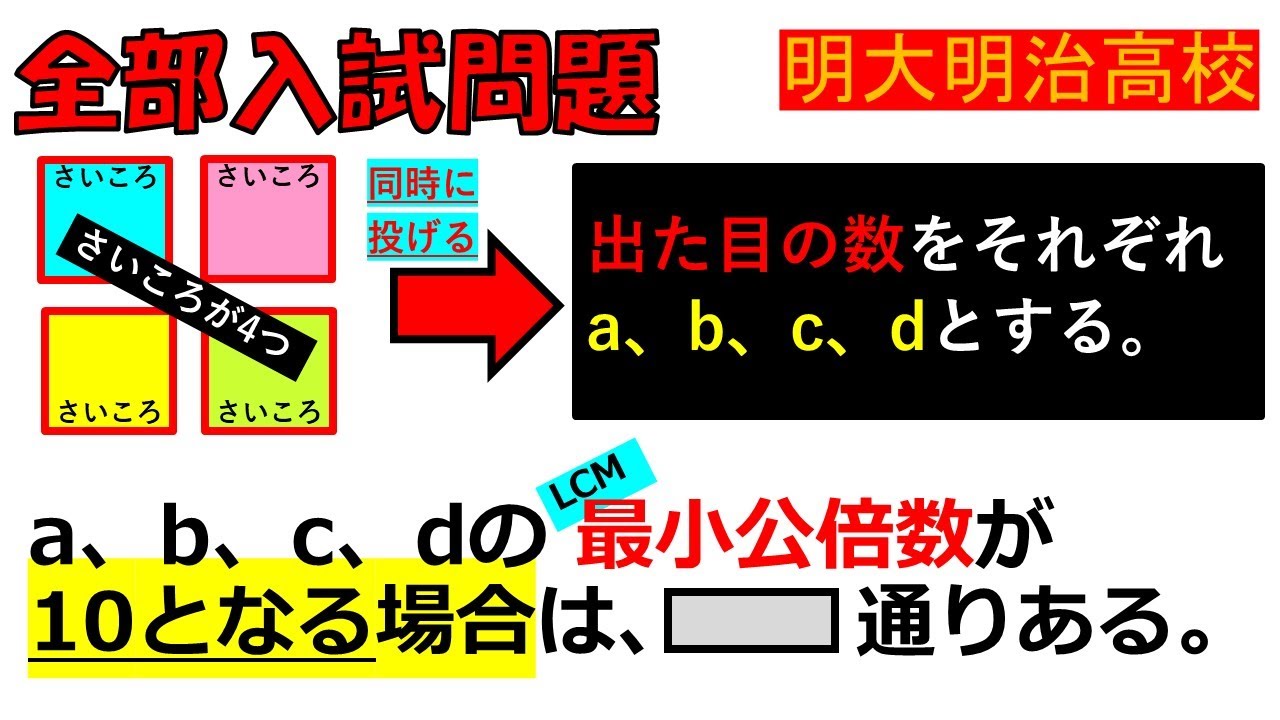
入試問題 明治大学附属明治高等学校
さいころ4つを同時に投げ出た目の数をそれぞれ a、b、c、dとする。
a、b、c、dの最小公倍数が 10となる場合は、▬ 通りある。
▬部分を求めよ。
※図は動画内参照
この動画を見る
入試問題 明治大学附属明治高等学校
さいころ4つを同時に投げ出た目の数をそれぞれ a、b、c、dとする。
a、b、c、dの最小公倍数が 10となる場合は、▬ 通りある。
▬部分を求めよ。
※図は動画内参照
連立方程式の応用。決まってます。解き方は。
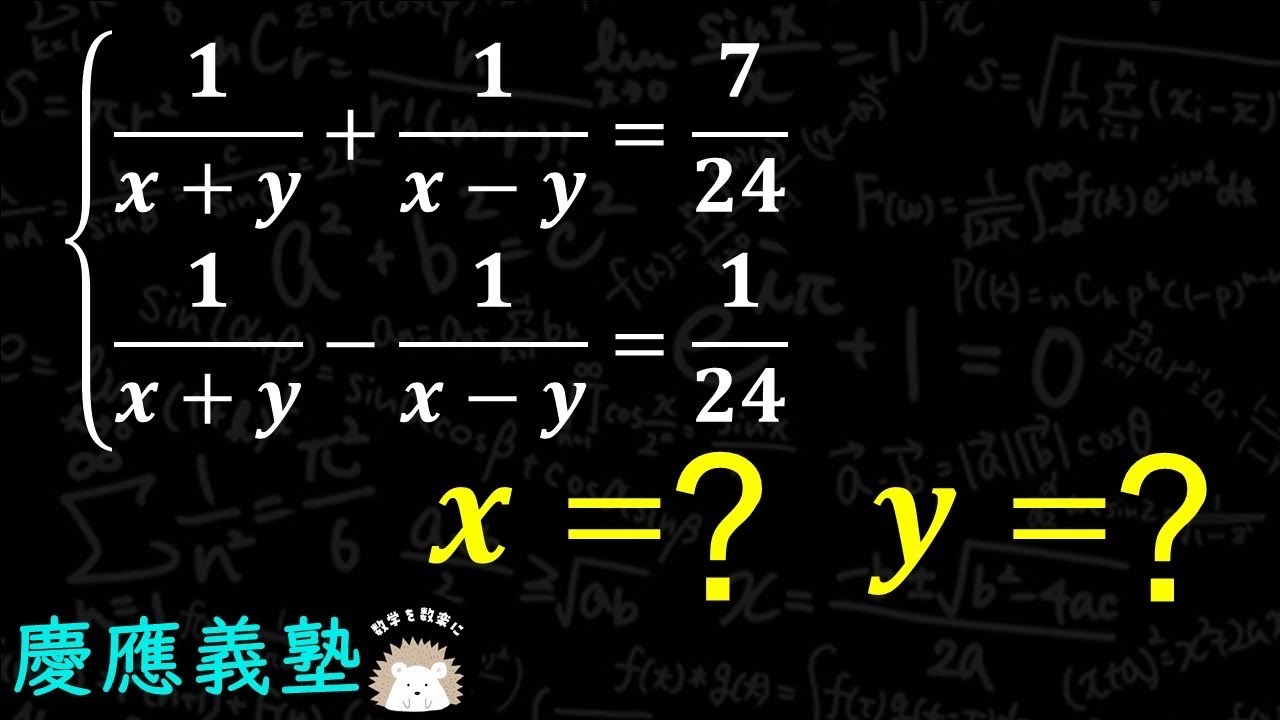
単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$
\begin{eqnarray}
\left\{
\begin{array}{l}
\frac{1}{x+y}+\frac{1}{x-y} = \frac{7}{24} \\
\frac{1}{x+y}-\frac{1}{x-y} = \frac{1}{24}
\end{array}
\right.
\end{eqnarray}
$
慶應義塾高等学校
この動画を見る
$
\begin{eqnarray}
\left\{
\begin{array}{l}
\frac{1}{x+y}+\frac{1}{x-y} = \frac{7}{24} \\
\frac{1}{x+y}-\frac{1}{x-y} = \frac{1}{24}
\end{array}
\right.
\end{eqnarray}
$
慶應義塾高等学校
