 2次方程式
2次方程式
 2次方程式
2次方程式
二次方程式 大阪教育大附属天王寺

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式を解け
$40000x^2-1500x+9 = 0$
大阪教育大学附属高等学校天王寺校舎
この動画を見る
2次方程式を解け
$40000x^2-1500x+9 = 0$
大阪教育大学附属高等学校天王寺校舎
2次方程式 筆算はしたくない。 日大習志野

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式を解け
$\frac{1}{2}x(x+15) = 19 \times 53$
日本大学習志野高等学校
この動画を見る
2次方程式を解け
$\frac{1}{2}x(x+15) = 19 \times 53$
日本大学習志野高等学校
【3分でいろいろ身に付く!】二次方程式:和洋国府台女子高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#和洋国府台女子高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 和洋国府台女子高等学校
次の2次方程式を解け。
$2x^2 + 6 = (x + 2)^2$
この動画を見る
入試問題 和洋国府台女子高等学校
次の2次方程式を解け。
$2x^2 + 6 = (x + 2)^2$
2次方程式の応用

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x^2-10x+\frac{a}{2} = 0$の解が奇数となるような正の整数aをすべて求めよ。
愛光高等学校
この動画を見る
$x^2-10x+\frac{a}{2} = 0$の解が奇数となるような正の整数aをすべて求めよ。
愛光高等学校
解が一個 2次方程式

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
xについての2次方程式
$x^2+5x+m+\frac{1}{4} = 0$の解が1コのときm=?
名古屋高等学校
この動画を見る
xについての2次方程式
$x^2+5x+m+\frac{1}{4} = 0$の解が1コのときm=?
名古屋高等学校
2次方程式 解き方3通り 四天王寺高校

二次方程式の計算 大阪府

二次方程式 どう解く??
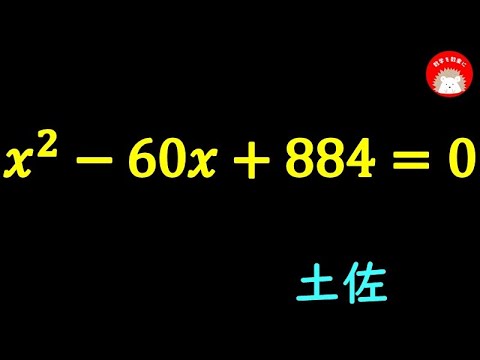
【5分で内容理解!】二次方程式:大阪教育大学附属高等学校池田校舎~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#大阪教育大学附属高等学校池田校舎
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 大阪教育大学附属高等学校池田校舎
次の式を解きなさい。
$7x^2-42x+58=0$
【解の公式は2種類ある!、公式を忘れても解く!】
この動画を見る
入試問題 大阪教育大学附属高等学校池田校舎
次の式を解きなさい。
$7x^2-42x+58=0$
【解の公式は2種類ある!、公式を忘れても解く!】
【トライ!】二次方程式:東京都立八王子東高等学校~全国入試問題解法【個別授業】

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#東京都立八王子東高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立八王子東高等学校
二次方程式を解け。
$(x+4)^2-6(x+4)+7=0$
この動画を見る
入試問題 東京都立八王子東高等学校
二次方程式を解け。
$(x+4)^2-6(x+4)+7=0$
〇〇するな!!

2021 立川 2次方程式の応用 B
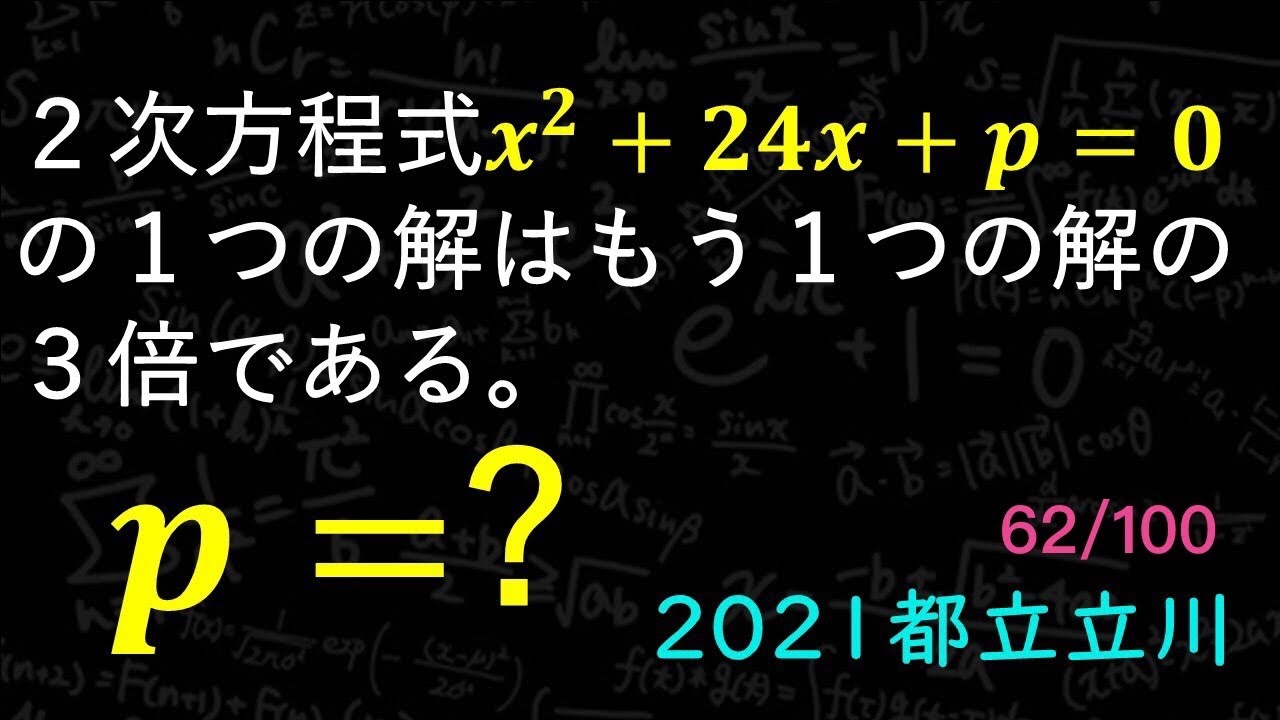
単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式$x^2+24x+p=0$の1つの解はもう1つの解の3倍である。
p=?
2021東京都立立川高等学校
この動画を見る
2次方程式$x^2+24x+p=0$の1つの解はもう1つの解の3倍である。
p=?
2021東京都立立川高等学校
変な解き方でごめんなさい。

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式を解け
$(2021-x)(2022-x) = 2023 - x$
2021慶應義塾高等学校
この動画を見る
2次方程式を解け
$(2021-x)(2022-x) = 2023 - x$
2021慶應義塾高等学校
2021 灘高校 2次方程式の応用D
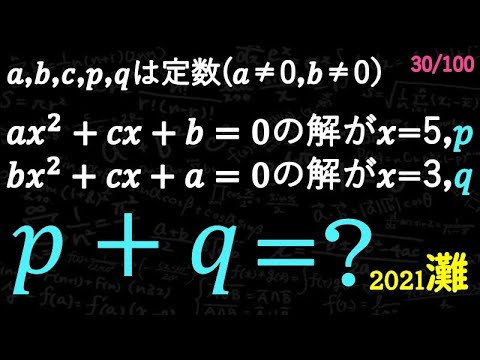
単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
a,b,c,p,qは定数(a≠0,b≠0)
$ax^2+cx+b=0$の解がx=5,p -①
$bx^2+cx+a=0$の解がx=3,q -②
のときp+q=?
2021灘高等学校
この動画を見る
a,b,c,p,qは定数(a≠0,b≠0)
$ax^2+cx+b=0$の解がx=5,p -①
$bx^2+cx+a=0$の解がx=3,q -②
のときp+q=?
2021灘高等学校
二次方程式:お茶の水女子大附属高校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#お茶の水女子大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
二次方程式:お茶の水女子大附属高校~全国入試問題解法
点$A$:①上にあるy=aである点($ a \gt 0$)。
点$B$:$A$を通り$X$軸に平行な直線と②の交点。
点$C$:$A$を通り$X$軸に垂直な直線と②の交点。
$AB=AC$のとき、$a$の値を求めよ。
① :$y=x^2(x \geqq 0)$
② : $y=\displaystyle \frac{1}{4}x^2(x \geqq 0)$
この動画を見る
二次方程式:お茶の水女子大附属高校~全国入試問題解法
点$A$:①上にあるy=aである点($ a \gt 0$)。
点$B$:$A$を通り$X$軸に平行な直線と②の交点。
点$C$:$A$を通り$X$軸に垂直な直線と②の交点。
$AB=AC$のとき、$a$の値を求めよ。
① :$y=x^2(x \geqq 0)$
② : $y=\displaystyle \frac{1}{4}x^2(x \geqq 0)$
二次方程式:渋谷教育学園幕張高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#渋谷教育学園幕張高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 渋谷教育学園幕張高等学校
共通解をもつとき、その解を求めなさい。
$2x^2-kx-8=0$
$x^2-x-2k = 0$
この動画を見る
入試問題 渋谷教育学園幕張高等学校
共通解をもつとき、その解を求めなさい。
$2x^2-kx-8=0$
$x^2-x-2k = 0$
【高校受験対策/数学】文章題9

単元:
#数学(中学生)#中3数学#2次方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・文章題9
Q.
右のカレンダーの中にある3つの日付の数で、次の①~③の関係が成り立つものを求める。
※図は動画参照
①最も小さい数と2番目に小さい数の2つの数は、上下に隣接 している。
②2番目に小さい数と最も大きい数の2つの数は、左右に隣接している。
③最も小さい数の2乗と2番目に小さい数の2乗との和が、最も大きい数の2乗に等しい。
問1
2番目に小さい数を$x$とする。
最も小さい数と最も大きい数を$x$を使った式でそれぞれ表しなさい。
問2
3つの数を求めなさい。
この動画を見る
高校受験対策・文章題9
Q.
右のカレンダーの中にある3つの日付の数で、次の①~③の関係が成り立つものを求める。
※図は動画参照
①最も小さい数と2番目に小さい数の2つの数は、上下に隣接 している。
②2番目に小さい数と最も大きい数の2つの数は、左右に隣接している。
③最も小さい数の2乗と2番目に小さい数の2乗との和が、最も大きい数の2乗に等しい。
問1
2番目に小さい数を$x$とする。
最も小さい数と最も大きい数を$x$を使った式でそれぞれ表しなさい。
問2
3つの数を求めなさい。
【高校受験対策/数学】死守70

単元:
#数学(中学生)#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#2次方程式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・数学 死守70
①$x^2-36y^2$
➁$(x+3)(x-4)-8$
③$(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})$
④$x(x-6)=-4(x-2)$
⑤$3x^2-5x+1=0$
⑥$3a+b=10$
⑦$-6+9÷\frac{1}{4}$
⑧$x^2+xy$
⑨$5xy^2×7xy÷(-x)^2$
➉$\frac{5x-3y}{3}-\frac{3x-7y}{4}$
⑪$3x+4y=x+y=2$
⑫$(2\sqrt{10}-5)(\sqrt{10}+4)$
⑬$x^2-6x-18$
⑭$(x-5)^2-7(x-5)+12$
⑮$0.2(x-2)=x+1.2$
⑯$\frac{x-2}{4}+\frac{2-5x}{6}=1$
この動画を見る
高校受験対策・数学 死守70
①$x^2-36y^2$
➁$(x+3)(x-4)-8$
③$(\sqrt{5}+\sqrt{3})(\sqrt{5}-\sqrt{3})$
④$x(x-6)=-4(x-2)$
⑤$3x^2-5x+1=0$
⑥$3a+b=10$
⑦$-6+9÷\frac{1}{4}$
⑧$x^2+xy$
⑨$5xy^2×7xy÷(-x)^2$
➉$\frac{5x-3y}{3}-\frac{3x-7y}{4}$
⑪$3x+4y=x+y=2$
⑫$(2\sqrt{10}-5)(\sqrt{10}+4)$
⑬$x^2-6x-18$
⑭$(x-5)^2-7(x-5)+12$
⑮$0.2(x-2)=x+1.2$
⑯$\frac{x-2}{4}+\frac{2-5x}{6}=1$
【高校受験対策/数学】死守69

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#平方根#2次方程式#標本調査
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守69
①$-3-6$を計算しなさい。
②$7+(-2^3)×4$を計算しなさい。
③$(-3ab)^2÷\frac{6}{5}a^2b$を計算しなさい。
④$\frac{x+3y}{4}-\frac{2x-y}{3}$を計算しなさい。
⑥次の方程式を解きなさい。
$x^2+5x-3=0$
⑦$x=\sqrt{7}+\sqrt{2}$、$y=\sqrt{7}-\sqrt{2}$のとき
$x^2-y^2$の値を求めなさい。
⑧折り紙が$a$枚ある。この折り紙を1人に5枚ずつ$b$人に配ったら 20枚以上余った。
このときの数量の間の関係を、不等式で表しなさい。
⑨太郎さんのクラス生徒全員について、ある期間に図書室から借りた本の冊数を調べ、表にまとめた。
しかし、表の一部が破れてしまい、いくつかの数値がわからなくなった。
このときこのクラスの生徒がある期間に借りた本の冊数の平均値を求めなさい。
➉
$ax+by=11$
$ax-by=-2$
$x$と$y$についての連立方程式の解が$x=3$、$y=-4$であるとき
$a,b$の値を求めなさい。
この動画を見る
高校受験対策・死守69
①$-3-6$を計算しなさい。
②$7+(-2^3)×4$を計算しなさい。
③$(-3ab)^2÷\frac{6}{5}a^2b$を計算しなさい。
④$\frac{x+3y}{4}-\frac{2x-y}{3}$を計算しなさい。
⑥次の方程式を解きなさい。
$x^2+5x-3=0$
⑦$x=\sqrt{7}+\sqrt{2}$、$y=\sqrt{7}-\sqrt{2}$のとき
$x^2-y^2$の値を求めなさい。
⑧折り紙が$a$枚ある。この折り紙を1人に5枚ずつ$b$人に配ったら 20枚以上余った。
このときの数量の間の関係を、不等式で表しなさい。
⑨太郎さんのクラス生徒全員について、ある期間に図書室から借りた本の冊数を調べ、表にまとめた。
しかし、表の一部が破れてしまい、いくつかの数値がわからなくなった。
このときこのクラスの生徒がある期間に借りた本の冊数の平均値を求めなさい。
➉
$ax+by=11$
$ax-by=-2$
$x$と$y$についての連立方程式の解が$x=3$、$y=-4$であるとき
$a,b$の値を求めなさい。
【高校受験対策/数学】死守68

単元:
#算数(中学受験)#数学(中学生)#中3数学#2次方程式#平面図形#平面図形その他#標本調査
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
①$5+(-3)×2$を計算しなさい。
②$3xy^2÷ (-2x^2y)×4y$を計算しなさい。
③$a=\sqrt{6}$のとき$a(a+2)-2(a+2)$の値を求めなさい。
④二次方程式$x^2+6x-16=0$を解きなさい。
⑤$\sqrt{45}+\sqrt{5}-\sqrt{20}$を計算しなさい。
⑥定価1500円のTシャツを$a$割引で買ったときの代金を、$a$を使った式で表しなさい。
ただし消費税は考えないものとする。
⑦右の図は、ある中学校3年生男子50人の50m走の記録をヒストグラムに表したも のである。
図において、例えば6.0から 6.5の区間は、6.0秒以上6.5秒未満の階級を表したものである。
このとき最頻値を求めなさい。
⑧右の図のように、$\angle B=90°$である直角三角形$ABC$がある。
$DA=DB=BC$となるような点$D$が辺$AC$上にあるとき、$\angle x$の大きさを求めなさい。
③右の図のような$\triangle ABC$がある。
線分$AC$上にあり、$\angle PAB=\angle PBA$となる点$P$を作図によって求め、$P$の記号をつけなさい。
ただし作図に用いた線は残しておくこと。
この動画を見る
①$5+(-3)×2$を計算しなさい。
②$3xy^2÷ (-2x^2y)×4y$を計算しなさい。
③$a=\sqrt{6}$のとき$a(a+2)-2(a+2)$の値を求めなさい。
④二次方程式$x^2+6x-16=0$を解きなさい。
⑤$\sqrt{45}+\sqrt{5}-\sqrt{20}$を計算しなさい。
⑥定価1500円のTシャツを$a$割引で買ったときの代金を、$a$を使った式で表しなさい。
ただし消費税は考えないものとする。
⑦右の図は、ある中学校3年生男子50人の50m走の記録をヒストグラムに表したも のである。
図において、例えば6.0から 6.5の区間は、6.0秒以上6.5秒未満の階級を表したものである。
このとき最頻値を求めなさい。
⑧右の図のように、$\angle B=90°$である直角三角形$ABC$がある。
$DA=DB=BC$となるような点$D$が辺$AC$上にあるとき、$\angle x$の大きさを求めなさい。
③右の図のような$\triangle ABC$がある。
線分$AC$上にあり、$\angle PAB=\angle PBA$となる点$P$を作図によって求め、$P$の記号をつけなさい。
ただし作図に用いた線は残しておくこと。
【高校受験対策/数学】死守67

単元:
#数学(中学生)#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#平方根#2次方程式#比例・反比例#平行と合同#確率#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守67
① 2次方程式を$x^3+3x-1=0$を解きなさい。
②$\sqrt{24}\div\sqrt{3}-\sqrt{2}$を計算しなさい。
③関数$y=\frac{3}{x}$について、$x$の変域が$1 \leqq x \leqq 6$のとき、$y$の変域を答えなさい。
④
$x$枚の空の封筒と$y$本の鉛筆がある。
封筒の中に鉛筆を4本ずつ入れると8本足りず、3本ずつ入れると12本余る。
このとき$x$と$y$の値を求めなさい。
⑤
右の図のような、$AD=2cm$、$BC=5cm$、$AD/\!/BC$である台形$ABCD$があり、対角線$AC$、$BD$の交点を$E$とする。
点$E$から辺$DC$上に辺$BC$と線分$EF$が平行となる点$F$をとるとき、線分$EF$の長さを答えなさい。
⑥
1から6までの目のついた大、小2つのさいころを同時に投げたとき、大きいさいころの出た目の数を$a$、小さいさいころの出た目の数を$b$とする。
このとき、出た目の数の積$a×b$の値が25以下となる確率を求めなさい。
⑦
右の図のように直線$l$と2つの点$A$、$B$がある。
直線$l$上にあって、2つの点$A$、$B$を通る円の中心$P$を、定規とコンパスを用いて作図しなさい。
ただし作図に使った線は消さずに残しておくこと。
この動画を見る
高校受験対策・死守67
① 2次方程式を$x^3+3x-1=0$を解きなさい。
②$\sqrt{24}\div\sqrt{3}-\sqrt{2}$を計算しなさい。
③関数$y=\frac{3}{x}$について、$x$の変域が$1 \leqq x \leqq 6$のとき、$y$の変域を答えなさい。
④
$x$枚の空の封筒と$y$本の鉛筆がある。
封筒の中に鉛筆を4本ずつ入れると8本足りず、3本ずつ入れると12本余る。
このとき$x$と$y$の値を求めなさい。
⑤
右の図のような、$AD=2cm$、$BC=5cm$、$AD/\!/BC$である台形$ABCD$があり、対角線$AC$、$BD$の交点を$E$とする。
点$E$から辺$DC$上に辺$BC$と線分$EF$が平行となる点$F$をとるとき、線分$EF$の長さを答えなさい。
⑥
1から6までの目のついた大、小2つのさいころを同時に投げたとき、大きいさいころの出た目の数を$a$、小さいさいころの出た目の数を$b$とする。
このとき、出た目の数の積$a×b$の値が25以下となる確率を求めなさい。
⑦
右の図のように直線$l$と2つの点$A$、$B$がある。
直線$l$上にあって、2つの点$A$、$B$を通る円の中心$P$を、定規とコンパスを用いて作図しなさい。
ただし作図に使った線は消さずに残しておくこと。
2次方程式の応用 (灘)C

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
a>0 , b>0でaは奇数、bは素数
xの2次方程式
$x^2-ax-b^3=0$が
整数解をもつときa=? b=?
灘高等学校
この動画を見る
a>0 , b>0でaは奇数、bは素数
xの2次方程式
$x^2-ax-b^3=0$が
整数解をもつときa=? b=?
灘高等学校
【高校受験対策/数学】死守66

単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#2次方程式#空間図形#文字と式
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守66
①$6x\times2xy\div3y$を計算しなさい。
②$\sqrt{18}-6\sqrt{2}$を計算しなさい。
③$x^2+4x-12$を因数分解しなさい。
④2次方程式$3x^2-5x+1=0$を解きなさい。
⑤方程式$5x+3=2x+6$を解きなさい。
⑥$\frac{1}{2}(3x-y)-\frac{4x-y}{3}$を計算しなさい。
⑦2次方程式$2(x-2)^2-3(x-2)+1=0$を解きなさい。
⑧$x=2+\sqrt{3}$、$y=2-\sqrt{3}$のとき、$(1+\frac{1}{x})(1+\frac{1}{y})$の値を求めなさい。
⑨右の図のような、底面の半径が3cm、高さが4cmの円錐があります。この円錐の表面積を求めなさい。ただし円周率は$\pi$とします。
➉右の図のように、円Oとこの円の外部の点Pがあります。
点Pを通る円の接線をコンパスと定規を使って1つ作図しなさい。
ただし、作するためにかいた線は消さないでおきなさい。
この動画を見る
高校受験対策・死守66
①$6x\times2xy\div3y$を計算しなさい。
②$\sqrt{18}-6\sqrt{2}$を計算しなさい。
③$x^2+4x-12$を因数分解しなさい。
④2次方程式$3x^2-5x+1=0$を解きなさい。
⑤方程式$5x+3=2x+6$を解きなさい。
⑥$\frac{1}{2}(3x-y)-\frac{4x-y}{3}$を計算しなさい。
⑦2次方程式$2(x-2)^2-3(x-2)+1=0$を解きなさい。
⑧$x=2+\sqrt{3}$、$y=2-\sqrt{3}$のとき、$(1+\frac{1}{x})(1+\frac{1}{y})$の値を求めなさい。
⑨右の図のような、底面の半径が3cm、高さが4cmの円錐があります。この円錐の表面積を求めなさい。ただし円周率は$\pi$とします。
➉右の図のように、円Oとこの円の外部の点Pがあります。
点Pを通る円の接線をコンパスと定規を使って1つ作図しなさい。
ただし、作するためにかいた線は消さないでおきなさい。
【中学数学】2次方程式:x=-5+√19のとき、x²+10x+11の値を求めよ。
【高校受験対策/数学】死守65

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(展開、因数分解)#2次方程式#比例・反比例#平行と合同#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守65
①右の図のように、直線$l$、直線$m$と2つの直線が交わっている。
$\angle a,\angle b,\angle c,\angle d,\angle e$のうち、どの角とどの角が等しければ、直線$l$と直線$m$が平行であるといえるか、その2つの角を答えなさい。
②$x^2-10x+25$を因数分解しなさい。
③2次方程式$(2x-5)^2=18$を解きなさい。
④右のア~オのうち、絶対値が最も大きい数を選び、記号で答えなさい。
ア $3.2$
イ $-\frac{7}{2}$
ウ $2\sqrt{2}$
エ $\frac{10}{3}$
オ $-3$
⑤右のア~オのうち、$y$が$x$に比例するものをすべて選び、記号で答えなさい。
ア 自然数$x$の約数の個数は$y$ 個である。
イ $x$ 円の商品を1000円支払って買うとき、おつりは$y$ 円である。
ウ 1200mの道のりを分速$x$ mの速さで進むとき、かかる時間は$y$ 分である。
エ 15%の食塩水が$x$ gあるとき、この食塩水に含まれる食塩の量は$y$ gである。
オ 何も入っていない容器に水を毎分2Lずつ$x$ 分間入れるとき、たまる水の量は$y$ Lである。
⑥右のア~オのうち、関数$y=2x^2$ついて述べた文として正しいものをすべて選び、記号で答えなさい。
ア この関数のグラフは、原点を通る。
イ $x \gt 0$のとき、$x$が増加すると$y$は減少する。
ウ この関数のグラフは$x$ 軸について対称である。
エ $x$の変域が$-1 \leqq x \leqq 2$のとき、$y$の変域は$0 \leqq y \leqq 8$である。
オ $x$の値がどの値からどの値まで増加するかに関わらず、変化の割合は常に2である。
この動画を見る
高校受験対策・死守65
①右の図のように、直線$l$、直線$m$と2つの直線が交わっている。
$\angle a,\angle b,\angle c,\angle d,\angle e$のうち、どの角とどの角が等しければ、直線$l$と直線$m$が平行であるといえるか、その2つの角を答えなさい。
②$x^2-10x+25$を因数分解しなさい。
③2次方程式$(2x-5)^2=18$を解きなさい。
④右のア~オのうち、絶対値が最も大きい数を選び、記号で答えなさい。
ア $3.2$
イ $-\frac{7}{2}$
ウ $2\sqrt{2}$
エ $\frac{10}{3}$
オ $-3$
⑤右のア~オのうち、$y$が$x$に比例するものをすべて選び、記号で答えなさい。
ア 自然数$x$の約数の個数は$y$ 個である。
イ $x$ 円の商品を1000円支払って買うとき、おつりは$y$ 円である。
ウ 1200mの道のりを分速$x$ mの速さで進むとき、かかる時間は$y$ 分である。
エ 15%の食塩水が$x$ gあるとき、この食塩水に含まれる食塩の量は$y$ gである。
オ 何も入っていない容器に水を毎分2Lずつ$x$ 分間入れるとき、たまる水の量は$y$ Lである。
⑥右のア~オのうち、関数$y=2x^2$ついて述べた文として正しいものをすべて選び、記号で答えなさい。
ア この関数のグラフは、原点を通る。
イ $x \gt 0$のとき、$x$が増加すると$y$は減少する。
ウ この関数のグラフは$x$ 軸について対称である。
エ $x$の変域が$-1 \leqq x \leqq 2$のとき、$y$の変域は$0 \leqq y \leqq 8$である。
オ $x$の値がどの値からどの値まで増加するかに関わらず、変化の割合は常に2である。
二次方程式:法政大学高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#法政大学高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 法政大学高等学校
$a(x + 3)(x + 5)-b(x + 4)(x + 6) = 0$
(1)$a:b$をもっとも簡単な整数の比で表しなさ い。
(2)この方程式の残りの 解を求めなさい。
解の1つが$x = 0$
この動画を見る
入試問題 法政大学高等学校
$a(x + 3)(x + 5)-b(x + 4)(x + 6) = 0$
(1)$a:b$をもっとも簡単な整数の比で表しなさ い。
(2)この方程式の残りの 解を求めなさい。
解の1つが$x = 0$
【高校受験対策/数学】死守62

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#2次方程式#空間図形#文字と式#平面図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守62
①$1+(-0.2)\times 2$を計算しなさい。
②方程式$\frac{2x+4}{3}=4$を解きなさい。
③$a=\frac{1}{2},b=3$のとき、 $3(a-2b)-5(3a-b)$の値を 求めなさい。
④$x$についての方程式
$x^2-2ax+3=0$の解の1つが$-1$であるとき、もう1つの解を求めなさい。
⑤1個$a$ kgの品物3個と1個$b$ kgの品物2個の合計の重さは20kg以上である。
この数量の関係を不等式で表しなさい。
⑥右の図のように、側面がすべて長方形の正六角柱がある。
このとき、辺ABとねじれの位置にある辺の数を求めなさい。
⑦家から$a$ m離れた博物館まで、行きは毎分60m、帰りは毎分90mの速さで往復した。
往復の平均の速さは分速( )mである。( )にあてはまる数を求めなさい。
⑧次のア~エのことがらについて、逆が正しいものを1つ選んで記号を書きなさい。
ア 正三角形はすべての内角が等しい三角形である。
イ 長方形は対角線がそれぞれの中点で交わる四角形である。
ウ $x \geqq 5$ならば$x \gt 4$である。
エ $x=1$ならば$x^2=1$である。
⑨右図のように直線$l$上に2点O,Pがある。
点Oを回転の中心として点Pを時計回りに45°回転移動させた点Qを、定規とコンパスを用いて作図しなさい。
ただし作図に用いた線は消さないこと。
この動画を見る
高校受験対策・死守62
①$1+(-0.2)\times 2$を計算しなさい。
②方程式$\frac{2x+4}{3}=4$を解きなさい。
③$a=\frac{1}{2},b=3$のとき、 $3(a-2b)-5(3a-b)$の値を 求めなさい。
④$x$についての方程式
$x^2-2ax+3=0$の解の1つが$-1$であるとき、もう1つの解を求めなさい。
⑤1個$a$ kgの品物3個と1個$b$ kgの品物2個の合計の重さは20kg以上である。
この数量の関係を不等式で表しなさい。
⑥右の図のように、側面がすべて長方形の正六角柱がある。
このとき、辺ABとねじれの位置にある辺の数を求めなさい。
⑦家から$a$ m離れた博物館まで、行きは毎分60m、帰りは毎分90mの速さで往復した。
往復の平均の速さは分速( )mである。( )にあてはまる数を求めなさい。
⑧次のア~エのことがらについて、逆が正しいものを1つ選んで記号を書きなさい。
ア 正三角形はすべての内角が等しい三角形である。
イ 長方形は対角線がそれぞれの中点で交わる四角形である。
ウ $x \geqq 5$ならば$x \gt 4$である。
エ $x=1$ならば$x^2=1$である。
⑨右図のように直線$l$上に2点O,Pがある。
点Oを回転の中心として点Pを時計回りに45°回転移動させた点Qを、定規とコンパスを用いて作図しなさい。
ただし作図に用いた線は消さないこと。
反比例と2次方程式 B
単元:
#数学(中学生)#中1数学#中3数学#2次方程式#比例・反比例#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
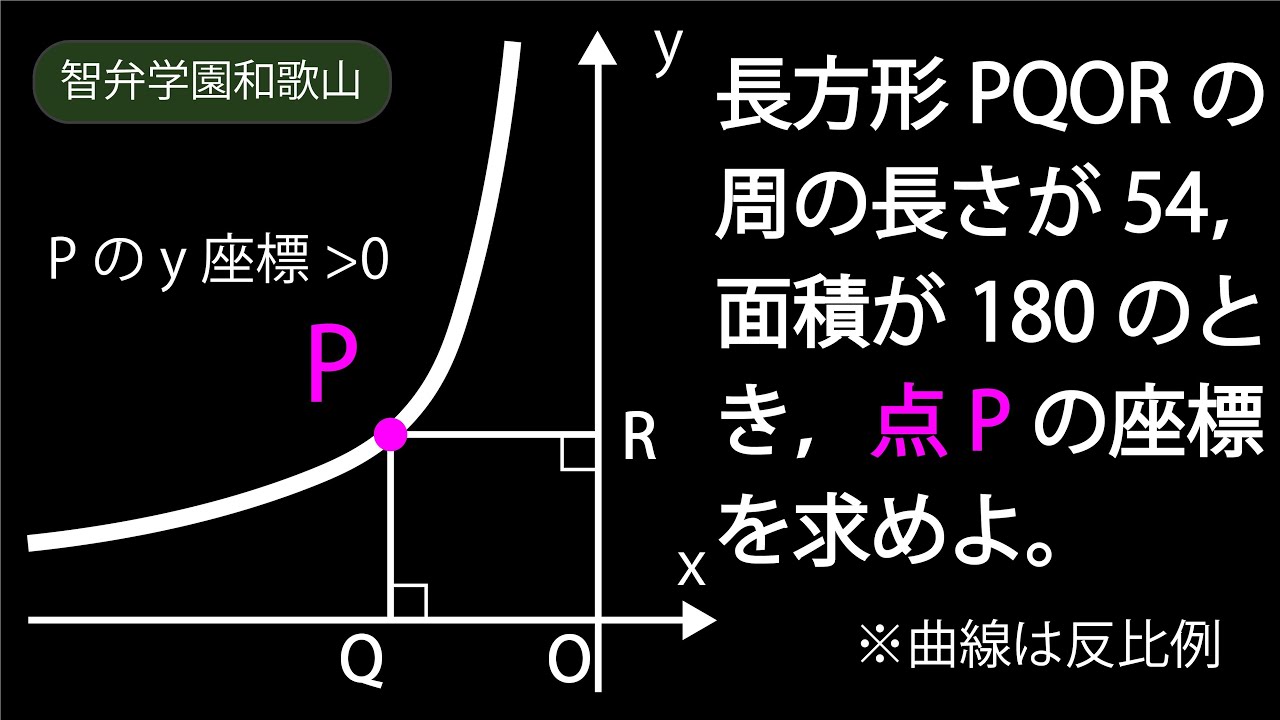
長方形PQORの周の=54、面積=180
点Pの座標は?
(点Pのy座標>0)
*図は動画内参照
智辯学園和歌山高等学校
この動画を見る
長方形PQORの周の=54、面積=180
点Pの座標は?
(点Pのy座標>0)
*図は動画内参照
智辯学園和歌山高等学校
二次方程式:東京都立八王子東高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#東京都立八王子東高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立八王子東高等学校
次の問いに答えよ。
2次方程式
$(x + 4)^2−6(x + 4) + 7 = 0 $
を解け。
この動画を見る
入試問題 東京都立八王子東高等学校
次の問いに答えよ。
2次方程式
$(x + 4)^2−6(x + 4) + 7 = 0 $
を解け。
【中学数学】2次方程式:図形に関する問題⑪ 右図で、点Pは関数y=1/2x+3上の点で、そのx座標はaである。また、点QはPからx軸に下した垂線とx軸との交点である。a>0のとき、次の問いに答えよ。

単元:
#数学(中学生)#中3数学#2次方程式
教材:
#新中学問題集#新中学問題集(数学)3標準編#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
右図で、点Pは関数$y=\dfrac{1}{2}x+3$上の点で、そのx座標はaである。また、点QはPからx軸に下した垂線とx軸との交点である。a>0のとき、次の問いに答えよ。
(1)点Pのy座標をaの式で表せ。
(2)△POQの面積が10のとき、点Pの座標を求めよ。
(3)関数$y=\dfrac{1}{2}x+3$とy軸との交点をRとする。△POQの面積が△PORの面積より16大きくなるときの点Pの座標を求めよ。
この動画を見る
右図で、点Pは関数$y=\dfrac{1}{2}x+3$上の点で、そのx座標はaである。また、点QはPからx軸に下した垂線とx軸との交点である。a>0のとき、次の問いに答えよ。
(1)点Pのy座標をaの式で表せ。
(2)△POQの面積が10のとき、点Pの座標を求めよ。
(3)関数$y=\dfrac{1}{2}x+3$とy軸との交点をRとする。△POQの面積が△PORの面積より16大きくなるときの点Pの座標を求めよ。
