 2次関数
2次関数
 2次関数
2次関数
【覚えるのは数式じゃない。方法だ!】公式:二次関数の変化の割合~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
全国入試問題
覚えたら3秒で正解!?
$y=ax^2$に対して、変化の割合は
$a(x_1+x_2)$
$A:(x_1,y_1)$
$B:(x_2,y_2)$
この動画を見る
全国入試問題
覚えたら3秒で正解!?
$y=ax^2$に対して、変化の割合は
$a(x_1+x_2)$
$A:(x_1,y_1)$
$B:(x_2,y_2)$
見えない変域 xの遺言

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
数学を数楽に
問題文全文(内容文):
x,yを実数とし、$2x^2+y^2=4$とする。
$P=x^2+y$をyの式で表すとP=$\boxed{ア}$であり、Pの最小値は$\boxed{イ}$である。
この動画を見る
x,yを実数とし、$2x^2+y^2=4$とする。
$P=x^2+y$をyの式で表すとP=$\boxed{ア}$であり、Pの最小値は$\boxed{イ}$である。
【白板、爆破⁉】二次関数:同志社高等学校~全国入試問題解法【数楽】

単元:
#中3数学#2次関数#高校入試過去問(数学)#同志社高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x$軸を回転の軸として $\triangle OAC$を1回転させて できる立体の体積を求めよ。
放物線:$ y = x^2$ 直線: $y = ax + b$ が2点$A$と$B$で交わる。
2点$A$、$B$を通る直線が、 $X$軸と交わる点をCとする。
この動画を見る
$x$軸を回転の軸として $\triangle OAC$を1回転させて できる立体の体積を求めよ。
放物線:$ y = x^2$ 直線: $y = ax + b$ が2点$A$と$B$で交わる。
2点$A$、$B$を通る直線が、 $X$軸と交わる点をCとする。
【高校受験対策/数学】関数54

単元:
#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数54
Q.
右の図1、2において、①は関数$y=ax^2$のグラフである。
2点$A$、$B$は①上の点であり、点$A$の座標は$(-2,2)$、点$B$の座標は$(3,2)$である。
また①上において、点$C$は$x$座標が点$A$の$x$座標より1だけ大きい点であり、点$D$は$x$座標が点$B$の$x$座標より1だけ小さい点である。
問1
$a$の値を求めなさい。
問2
4点$A$、$C$、$D$、$B$を頂点とする四角形$ACDB$の面積を求めなさい。
問3
図2のように、①上において$x$座標が点$A$の$x$座標より1だけ小さい点を$E$とし、$x$座標が点$B$の$x$座標より1だけ大きい点を$F$とする。
このとき、3点$F$、$E$、$C$を頂点とする$\triangle FEC$の面積と、3点$F$、$C$、$D$を頂点とする$\triangle FCD$の面積の比を最も簡単な整数の比で表しなさい。
この動画を見る
高校受験対策・関数54
Q.
右の図1、2において、①は関数$y=ax^2$のグラフである。
2点$A$、$B$は①上の点であり、点$A$の座標は$(-2,2)$、点$B$の座標は$(3,2)$である。
また①上において、点$C$は$x$座標が点$A$の$x$座標より1だけ大きい点であり、点$D$は$x$座標が点$B$の$x$座標より1だけ小さい点である。
問1
$a$の値を求めなさい。
問2
4点$A$、$C$、$D$、$B$を頂点とする四角形$ACDB$の面積を求めなさい。
問3
図2のように、①上において$x$座標が点$A$の$x$座標より1だけ小さい点を$E$とし、$x$座標が点$B$の$x$座標より1だけ大きい点を$F$とする。
このとき、3点$F$、$E$、$C$を頂点とする$\triangle FEC$の面積と、3点$F$、$C$、$D$を頂点とする$\triangle FCD$の面積の比を最も簡単な整数の比で表しなさい。
【裏ワザ】二次関数と2点で交わる直線の求め方~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
【裏ワザ】二次関数と2点で交わる直線の求め方~全国入試問題解法
2点で交わる直線を導いてみた
$y=ax^2$に対して
$y=mx+n$
【$y=a(p+g)x-apg$】
a:二次関数の係数
P:点$A$の$X$座標
g:点$B$の$X$座標
ポイント:覚えるならば完璧に!!
※図は動画内参照
この動画を見る
【裏ワザ】二次関数と2点で交わる直線の求め方~全国入試問題解法
2点で交わる直線を導いてみた
$y=ax^2$に対して
$y=mx+n$
【$y=a(p+g)x-apg$】
a:二次関数の係数
P:点$A$の$X$座標
g:点$B$の$X$座標
ポイント:覚えるならば完璧に!!
※図は動画内参照
二次関数と台形 桃山学院(改) 2021 B

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
台形ABCD=5のときa=?(a>0)
*図は動画内参照
2021桃山学院高等学校
この動画を見る
台形ABCD=5のときa=?(a>0)
*図は動画内参照
2021桃山学院高等学校
二次関数:早稲田大学系属早稲田実業学校高等部~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#早稲田大学系属早稲田実業学校高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 早稲田大学系属早稲田実業学校高等部
異なる$2$つの整数解をもつとき、
$p,q$の値をそれぞれ求めよ。
$x^2 - px + q^2 = 0$
$p,q$を異なる$2$つの素数とする。
この動画を見る
入試問題 早稲田大学系属早稲田実業学校高等部
異なる$2$つの整数解をもつとき、
$p,q$の値をそれぞれ求めよ。
$x^2 - px + q^2 = 0$
$p,q$を異なる$2$つの素数とする。
【高校受験対策/数学】関数53

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数53
Q.
図1のように、関数$y=x^2$のグラフがある。
$A$はグラフ上の点で、$x$座標は$-1$である。また、2点$P,Q$はグラフ上を動くものとする。
このとき次の各問に答えなさい。ただし円周率は$\pi$とする。
①
関数$y=x^2$について、$x$の変域が$-3 \leqq x\leqq 2$のときの$y$の変域を求めなさい。
②
2点$P,Q$の$x$座標をそれぞれ$1$と$3$とする。
図2のように、$\triangle APQ$を原点$O$を中心として矢印の方向に$360°$回転移動させ、$\triangle APQ$が回転移動しながら通った部分に色をつけた。
このとき色がついている図形の面積を求めなさい。
③
2点$P,Q$の$x$座標をそれぞれ$3$と$4$とする。
直線$OA$上に四角形$OPQA$と$\triangle OPR$の面積が等しくなるように点$R$を取るとき、$R$の座標を求めなさい。
ただし$R$の$x$座標は負とする。
この動画を見る
高校受験対策・関数53
Q.
図1のように、関数$y=x^2$のグラフがある。
$A$はグラフ上の点で、$x$座標は$-1$である。また、2点$P,Q$はグラフ上を動くものとする。
このとき次の各問に答えなさい。ただし円周率は$\pi$とする。
①
関数$y=x^2$について、$x$の変域が$-3 \leqq x\leqq 2$のときの$y$の変域を求めなさい。
②
2点$P,Q$の$x$座標をそれぞれ$1$と$3$とする。
図2のように、$\triangle APQ$を原点$O$を中心として矢印の方向に$360°$回転移動させ、$\triangle APQ$が回転移動しながら通った部分に色をつけた。
このとき色がついている図形の面積を求めなさい。
③
2点$P,Q$の$x$座標をそれぞれ$3$と$4$とする。
直線$OA$上に四角形$OPQA$と$\triangle OPR$の面積が等しくなるように点$R$を取るとき、$R$の座標を求めなさい。
ただし$R$の$x$座標は負とする。
二次関数:駿台甲府高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#駿台甲府高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
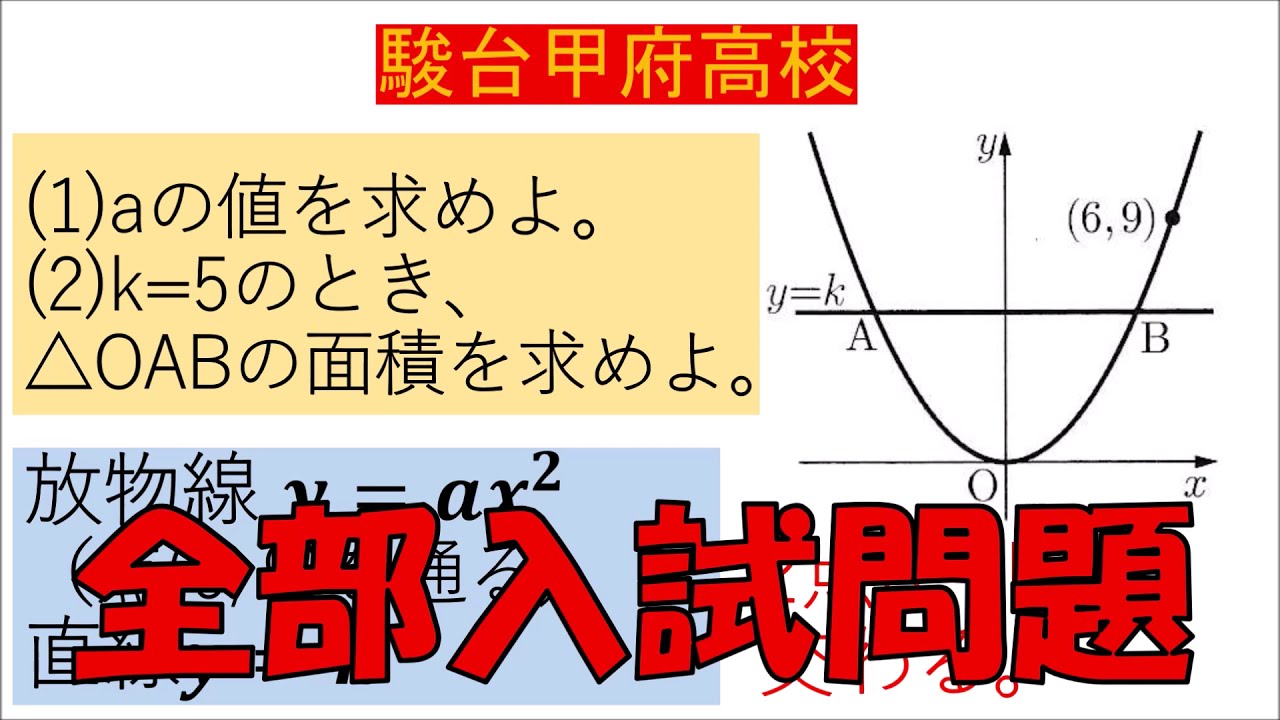
入試問題 駿台甲府高等学校
(1)$a$の値を求めよ。
(2)$k=5$のとき、$\triangle OAB$の面積を求めよ。
放物線 $y = ax^2$
(点(6,9)を通る)
直線$y=k$
※図は動画内参照
この動画を見る
入試問題 駿台甲府高等学校
(1)$a$の値を求めよ。
(2)$k=5$のとき、$\triangle OAB$の面積を求めよ。
放物線 $y = ax^2$
(点(6,9)を通る)
直線$y=k$
※図は動画内参照
二次関数:國學院大學久我山高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#國學院大學久我山高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
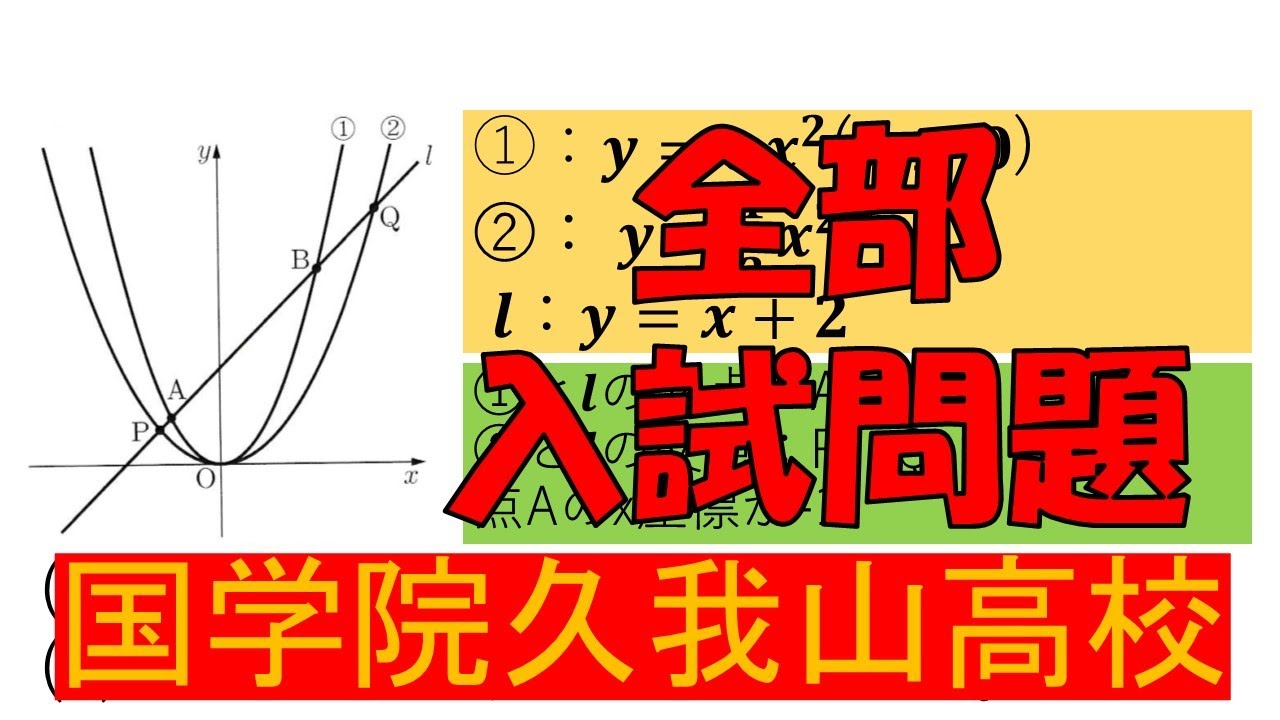
入試問題 國學院大學久我山高等学校
①$:y=ax^2(a \gt 0)$
②$:y=\displaystyle \frac{1}{2}x^2$
$l:y=x+2$
①と$l$の交点:$A、B$
②と$l$の交点:$P、Q$
点$A$の$x$座標が$-1$
(1)$a$の値を求めなさい。
(2)$\triangle POB$の面積を求めなさい。
※図は動画内参照
この動画を見る
入試問題 國學院大學久我山高等学校
①$:y=ax^2(a \gt 0)$
②$:y=\displaystyle \frac{1}{2}x^2$
$l:y=x+2$
①と$l$の交点:$A、B$
②と$l$の交点:$P、Q$
点$A$の$x$座標が$-1$
(1)$a$の値を求めなさい。
(2)$\triangle POB$の面積を求めなさい。
※図は動画内参照
二次関数:関西学院高等部~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#関西学院高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 関西学院高等部
放物線$y=x^2$
直線$y = ax + a(a \gt 0)$
$2$点$A$と$B$で交わる。
点$P:y=a$のとき、$x=a$
$\triangle OAB$の面積を求めよ。
※図は動画内参照
この動画を見る
入試問題 関西学院高等部
放物線$y=x^2$
直線$y = ax + a(a \gt 0)$
$2$点$A$と$B$で交わる。
点$P:y=a$のとき、$x=a$
$\triangle OAB$の面積を求めよ。
※図は動画内参照
二次関数:東京都立産業技術高等専門学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#東京都立産業技術高等専門学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立産業技術高等専門学校
次の等式が成り立つように
$x^2 - 6x − 7 = (x − \boxed{ ① } )^2 -\boxed{ ② }$
$\boxed{ ① },\boxed{ ② }$
に当てはまる 正の数を求めよ。
この動画を見る
入試問題 東京都立産業技術高等専門学校
次の等式が成り立つように
$x^2 - 6x − 7 = (x − \boxed{ ① } )^2 -\boxed{ ② }$
$\boxed{ ① },\boxed{ ② }$
に当てはまる 正の数を求めよ。
二次関数:法政大学第二高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#法政大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 法政大学第二高等学校
定義域がともに$-1 \leqq x \leqq 3$である$2$つの関数
$y =\displaystyle \frac{4}{3}x^2, y = ax + b (a \lt 0)$
値域が一致するような $a, b$の値を求めなさい。
この動画を見る
入試問題 法政大学第二高等学校
定義域がともに$-1 \leqq x \leqq 3$である$2$つの関数
$y =\displaystyle \frac{4}{3}x^2, y = ax + b (a \lt 0)$
値域が一致するような $a, b$の値を求めなさい。
【高校受験対策/数学】死守65

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(展開、因数分解)#2次方程式#比例・反比例#平行と合同#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守65
①右の図のように、直線$l$、直線$m$と2つの直線が交わっている。
$\angle a,\angle b,\angle c,\angle d,\angle e$のうち、どの角とどの角が等しければ、直線$l$と直線$m$が平行であるといえるか、その2つの角を答えなさい。
②$x^2-10x+25$を因数分解しなさい。
③2次方程式$(2x-5)^2=18$を解きなさい。
④右のア~オのうち、絶対値が最も大きい数を選び、記号で答えなさい。
ア $3.2$
イ $-\frac{7}{2}$
ウ $2\sqrt{2}$
エ $\frac{10}{3}$
オ $-3$
⑤右のア~オのうち、$y$が$x$に比例するものをすべて選び、記号で答えなさい。
ア 自然数$x$の約数の個数は$y$ 個である。
イ $x$ 円の商品を1000円支払って買うとき、おつりは$y$ 円である。
ウ 1200mの道のりを分速$x$ mの速さで進むとき、かかる時間は$y$ 分である。
エ 15%の食塩水が$x$ gあるとき、この食塩水に含まれる食塩の量は$y$ gである。
オ 何も入っていない容器に水を毎分2Lずつ$x$ 分間入れるとき、たまる水の量は$y$ Lである。
⑥右のア~オのうち、関数$y=2x^2$ついて述べた文として正しいものをすべて選び、記号で答えなさい。
ア この関数のグラフは、原点を通る。
イ $x \gt 0$のとき、$x$が増加すると$y$は減少する。
ウ この関数のグラフは$x$ 軸について対称である。
エ $x$の変域が$-1 \leqq x \leqq 2$のとき、$y$の変域は$0 \leqq y \leqq 8$である。
オ $x$の値がどの値からどの値まで増加するかに関わらず、変化の割合は常に2である。
この動画を見る
高校受験対策・死守65
①右の図のように、直線$l$、直線$m$と2つの直線が交わっている。
$\angle a,\angle b,\angle c,\angle d,\angle e$のうち、どの角とどの角が等しければ、直線$l$と直線$m$が平行であるといえるか、その2つの角を答えなさい。
②$x^2-10x+25$を因数分解しなさい。
③2次方程式$(2x-5)^2=18$を解きなさい。
④右のア~オのうち、絶対値が最も大きい数を選び、記号で答えなさい。
ア $3.2$
イ $-\frac{7}{2}$
ウ $2\sqrt{2}$
エ $\frac{10}{3}$
オ $-3$
⑤右のア~オのうち、$y$が$x$に比例するものをすべて選び、記号で答えなさい。
ア 自然数$x$の約数の個数は$y$ 個である。
イ $x$ 円の商品を1000円支払って買うとき、おつりは$y$ 円である。
ウ 1200mの道のりを分速$x$ mの速さで進むとき、かかる時間は$y$ 分である。
エ 15%の食塩水が$x$ gあるとき、この食塩水に含まれる食塩の量は$y$ gである。
オ 何も入っていない容器に水を毎分2Lずつ$x$ 分間入れるとき、たまる水の量は$y$ Lである。
⑥右のア~オのうち、関数$y=2x^2$ついて述べた文として正しいものをすべて選び、記号で答えなさい。
ア この関数のグラフは、原点を通る。
イ $x \gt 0$のとき、$x$が増加すると$y$は減少する。
ウ この関数のグラフは$x$ 軸について対称である。
エ $x$の変域が$-1 \leqq x \leqq 2$のとき、$y$の変域は$0 \leqq y \leqq 8$である。
オ $x$の値がどの値からどの値まで増加するかに関わらず、変化の割合は常に2である。
塾技!学校では教えてくれない!?二次関数の変化の割合を3秒で求める最強公式はコレだ!!【生徒からの質問19】

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
こばちゃん塾
問題文全文(内容文):
$y=ax^2$について、$- \frac{1}{3} \leqq x \leqq \frac{4}{3}$のときの変化の割合が、$y= - \frac{2}{5} x + 300$と同じであるとき、aの値を求めよう
この動画を見る
$y=ax^2$について、$- \frac{1}{3} \leqq x \leqq \frac{4}{3}$のときの変化の割合が、$y= - \frac{2}{5} x + 300$と同じであるとき、aの値を求めよう
【高校受験対策/数学】関数52

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数52
Q
太郎さんが所属するサッカー部で、オリジナルタオルを作ることになり、かかる費用を調べたところ、A店とB店の料金はそれぞれ表1、表2のようになっていた。
また、右の図はA店で タオルを作る枚数を$x$ 枚としたときのかかる費用を$y$ 円として、$x$と$y$の関係をグラフに 表したものである。
ただし、このグラフで端の点をふくむ場合は●、ふくまない場合は○で表している。
ただし、消費税は考えないものとする。
【表1】 A店の料金
枚数によって、金額は次の通りです。
・20枚までは何枚でも、3500円
・21枚から50枚までは何枚でも6500円
・51枚から80枚までは何枚でも9000円
【表2】 B店の料金
注文の時に初期費用として3000円かかり、それに加えてタオル1枚につき100円かかります。
①B店でタオルを作る枚数を$x$ 枚としたときのかかる費用を$y$ 円として、$y$を$x$の式で表しなさい。
②A店、B店でそれぞれタオルを30枚作るとき、かかる費用はどちらの店がいくら安いか求めなさい。
③タオルを作る枚数を40枚から80枚までとしたとき、B店で作るときにかかる費用がA店で作るときにかかる費用よりも安くなるのは、何枚以上何枚以下のときか求めなさい。
この動画を見る
高校受験対策・関数52
Q
太郎さんが所属するサッカー部で、オリジナルタオルを作ることになり、かかる費用を調べたところ、A店とB店の料金はそれぞれ表1、表2のようになっていた。
また、右の図はA店で タオルを作る枚数を$x$ 枚としたときのかかる費用を$y$ 円として、$x$と$y$の関係をグラフに 表したものである。
ただし、このグラフで端の点をふくむ場合は●、ふくまない場合は○で表している。
ただし、消費税は考えないものとする。
【表1】 A店の料金
枚数によって、金額は次の通りです。
・20枚までは何枚でも、3500円
・21枚から50枚までは何枚でも6500円
・51枚から80枚までは何枚でも9000円
【表2】 B店の料金
注文の時に初期費用として3000円かかり、それに加えてタオル1枚につき100円かかります。
①B店でタオルを作る枚数を$x$ 枚としたときのかかる費用を$y$ 円として、$y$を$x$の式で表しなさい。
②A店、B店でそれぞれタオルを30枚作るとき、かかる費用はどちらの店がいくら安いか求めなさい。
③タオルを作る枚数を40枚から80枚までとしたとき、B店で作るときにかかる費用がA店で作るときにかかる費用よりも安くなるのは、何枚以上何枚以下のときか求めなさい。
【中学数学】関数y=ax²:y=1/2x²とy=ax+bが2点A,Bで交わっている。点A,Bのx座標がそれぞれ-2,3のとき (1)点Aの座標 (2)直線ABの式 (3)△OABの面積 を求めよ。
単元:
#数学(中学生)#中3数学#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
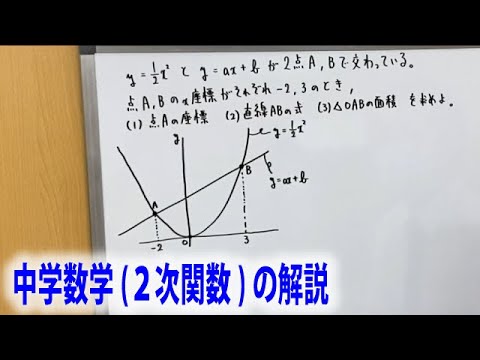
関数$y=ax^2:y=\dfrac{1}{2}x^2$と$y=ax+b$が2点A,Bで交わっている。点A,Bのx座標がそれぞれ-2,3のとき
(1)点Aの座標
(2)直線ABの式
(3)△OABの面積
を求めよ。
この動画を見る
関数$y=ax^2:y=\dfrac{1}{2}x^2$と$y=ax+b$が2点A,Bで交わっている。点A,Bのx座標がそれぞれ-2,3のとき
(1)点Aの座標
(2)直線ABの式
(3)△OABの面積
を求めよ。
【高校受験対策/数学】死守61

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#式の計算(単項式・多項式・式の四則計算)#連立方程式#平方根#1次関数#2次関数#文字と式#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守6
①$-5+2$を計算しなさい。
➁$6 \times \frac{2a+1}{3}$を計算しなさい。
③$(\sqrt{7}-1)(\sqrt{7}+1)$を計算しなさい。
④連立方程式を解きなさい。
$y=x+6$
$y=-2x+3$
⑤2次方程式$x^2-3x-2=0$を解きなさい。
⑥1辺の長さが$x$ cmの正方形が あります。
この正方形の周の長さを$y$ cmとするとき、$y$を$x$の式で表しなさい。
⑦34人の団体Xと40人の団体Yが博物館に行きます。
この博物館の1人分の入館料は$a$円で、40人以上の団体の入館料は20%引きになります。
このとき、団体Xと団体Yでは入館料の合計はどちらが多くかかりますか。
その理由をことばや式を用いて書きなさい。ただし消費税は考えないものとする。
⑧右の図で、3点、A、B、Cは円$o$の周上にあります。 このとき$\angle x$の大きさを求めなさい。
⑨右下の図のような長方形ABCDの紙を、 頂点Aが頂点Cに重なるように折ったときの折り目の線分を作図によって求めなさい。
ただし、作図には定規とコンパスを用い作図に使った線は消さないでおくこと。
この動画を見る
高校受験対策・死守6
①$-5+2$を計算しなさい。
➁$6 \times \frac{2a+1}{3}$を計算しなさい。
③$(\sqrt{7}-1)(\sqrt{7}+1)$を計算しなさい。
④連立方程式を解きなさい。
$y=x+6$
$y=-2x+3$
⑤2次方程式$x^2-3x-2=0$を解きなさい。
⑥1辺の長さが$x$ cmの正方形が あります。
この正方形の周の長さを$y$ cmとするとき、$y$を$x$の式で表しなさい。
⑦34人の団体Xと40人の団体Yが博物館に行きます。
この博物館の1人分の入館料は$a$円で、40人以上の団体の入館料は20%引きになります。
このとき、団体Xと団体Yでは入館料の合計はどちらが多くかかりますか。
その理由をことばや式を用いて書きなさい。ただし消費税は考えないものとする。
⑧右の図で、3点、A、B、Cは円$o$の周上にあります。 このとき$\angle x$の大きさを求めなさい。
⑨右下の図のような長方形ABCDの紙を、 頂点Aが頂点Cに重なるように折ったときの折り目の線分を作図によって求めなさい。
ただし、作図には定規とコンパスを用い作図に使った線は消さないでおくこと。
【一度は解きたい入試の良問】二次方程式:お茶の水女子大学付属高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#お茶の水女子大学附属高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 お茶の水女子大学付属高等学校
$x$についての$2$次方程式
$x^2 + (a + 2)x + a^2+2a − 1 = 0$
解の$1$つが$a$である。
$a$の値を求めよ。
この動画を見る
入試問題 お茶の水女子大学付属高等学校
$x$についての$2$次方程式
$x^2 + (a + 2)x + a^2+2a − 1 = 0$
解の$1$つが$a$である。
$a$の値を求めよ。
【高校数学へのパスポート】二次関数:滋賀県高校入試~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#滋賀県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 滋賀県の高校
次の問いに答えなさい。
関数$y = ax^2$ について、
$ -3\leqq x \leqq 1$のとき、
$ 0\leqq y \leqq 1$である。
このとき、$a$の値を求めなさい。
この動画を見る
入試問題 滋賀県の高校
次の問いに答えなさい。
関数$y = ax^2$ について、
$ -3\leqq x \leqq 1$のとき、
$ 0\leqq y \leqq 1$である。
このとき、$a$の値を求めなさい。
【中学数学】2次関数の演習~北海道公立高校入試標準2019~【高校受験】
単元:
#数学(中学生)#中3数学#2次関数#北海道公立高校入試
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
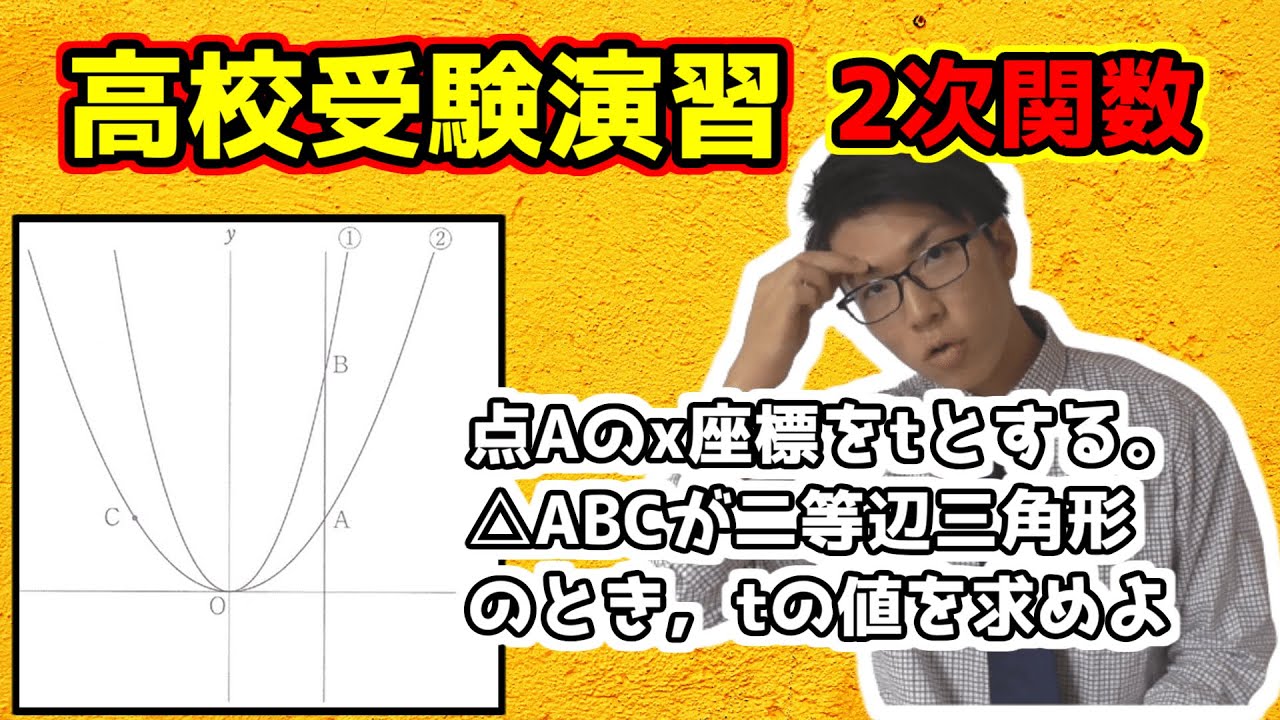
動画内図のように2つの関数$y= x^2$...①、$y= \displaystyle \frac{1}{3} x^2$・・・②のグラフがあります。
②のグラフ上に点Aがあり、点Aの$x$座標が正の数とします。
点Aを通り、$y$軸に平行な直線と①のグラフの交点をBとし、点Aと$y$軸について対称な点をCとします。
点0は原点とします。
【問】
1⃣
点Aの$x$座標が2のとき、点Cの座標を求めなさい。
2⃣
点Bの$x$座標が6のとき、2点B,Cを通る直線の傾きを求めなさい。
3⃣
点Aの$x$座標をtとします。
△ABCが直角二等辺三角形となるとき、tの値を求めよ。
この動画を見る
動画内図のように2つの関数$y= x^2$...①、$y= \displaystyle \frac{1}{3} x^2$・・・②のグラフがあります。
②のグラフ上に点Aがあり、点Aの$x$座標が正の数とします。
点Aを通り、$y$軸に平行な直線と①のグラフの交点をBとし、点Aと$y$軸について対称な点をCとします。
点0は原点とします。
【問】
1⃣
点Aの$x$座標が2のとき、点Cの座標を求めなさい。
2⃣
点Bの$x$座標が6のとき、2点B,Cを通る直線の傾きを求めなさい。
3⃣
点Aの$x$座標をtとします。
△ABCが直角二等辺三角形となるとき、tの値を求めよ。
【高校受験対策/数学】関数50

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・関数50
右の図のように、2つの関数$y=\frac{1}{2}x^2$・・・①、$y=x^2$・・・②のグラフがあります。
①のグラフ上に、点Aがあり、点Aの$x$座標を$t$とします。
点Aと軸について対称な点をBとし、点Aと$x$座標が等しい②のグラフ上の点をCとします。
また、②のグラフ上に点Dがあり、点Dの$x$座標を負の数とします。
$t \gt 0$として、次の問いに答えなさい。
問1 四角形ABCDが長方形となるとき、点Dの座標を$t$を使って表しなさい。
問2 $t=4$とします。点Cを通り傾きが$ー3$の直線の式を求めなさい。
問3 2点B,Cを通る直線の傾きが$-2と$なるとき、点Aの座標を求めなさい。
この動画を見る
高校受験対策・関数50
右の図のように、2つの関数$y=\frac{1}{2}x^2$・・・①、$y=x^2$・・・②のグラフがあります。
①のグラフ上に、点Aがあり、点Aの$x$座標を$t$とします。
点Aと軸について対称な点をBとし、点Aと$x$座標が等しい②のグラフ上の点をCとします。
また、②のグラフ上に点Dがあり、点Dの$x$座標を負の数とします。
$t \gt 0$として、次の問いに答えなさい。
問1 四角形ABCDが長方形となるとき、点Dの座標を$t$を使って表しなさい。
問2 $t=4$とします。点Cを通り傾きが$ー3$の直線の式を求めなさい。
問3 2点B,Cを通る直線の傾きが$-2と$なるとき、点Aの座標を求めなさい。
【必出!グラフを意識できるか】二次関数:高知県高校入試~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#高知県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 高知県の高校
次の問いに答えなさい。
関数$y=-x^2 $について、
$-2 \leqq x \leqq 3$とき、
$a \leqq y \leqq b$である。
このとき、$a、b$の値を 求めよ。
この動画を見る
入試問題 高知県の高校
次の問いに答えなさい。
関数$y=-x^2 $について、
$-2 \leqq x \leqq 3$とき、
$a \leqq y \leqq b$である。
このとき、$a、b$の値を 求めよ。
【中学数学】2次関数の演習~京都府公立高校入試前期選抜2019~【高校受験】

単元:
#中3数学#2次関数
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
動画内図のように、関数$y=ax^2$のグラフ上に2点A,Bがあり、2点A,Bの$x$座標はそれぞれ-3,6である。
また、2点0,Bを通る直線の傾きは$\displaystyle \frac{3}{2}$である。
2点A、Bを通る直線と$y$軸との交点をCとする。
(1) aの値を求めよ。
(2) 直線ABの式を求めよ。
(3) $x$軸上に$x$座標が正である点Dをとる。
点Dを通り、傾きが$\displaystyle \frac{6}{25}$である直線を$y$軸との交点をEとする。
△OCA=△OEDであるとき、2点D,Eの座標をそれぞれ求めよ。
この動画を見る
動画内図のように、関数$y=ax^2$のグラフ上に2点A,Bがあり、2点A,Bの$x$座標はそれぞれ-3,6である。
また、2点0,Bを通る直線の傾きは$\displaystyle \frac{3}{2}$である。
2点A、Bを通る直線と$y$軸との交点をCとする。
(1) aの値を求めよ。
(2) 直線ABの式を求めよ。
(3) $x$軸上に$x$座標が正である点Dをとる。
点Dを通り、傾きが$\displaystyle \frac{6}{25}$である直線を$y$軸との交点をEとする。
△OCA=△OEDであるとき、2点D,Eの座標をそれぞれ求めよ。
【中学数学】テストによく出るグラフのイメージ 4-0【中3数学】

関数:豊島岡女子学園高校~全国入試問題解法

単元:
#数学(中学生)#中1数学#中2数学#中3数学#比例・反比例#1次関数#2次関数#高校入試過去問(数学)#豊島岡女子高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 豊島岡女子学園高等学校
$y=\displaystyle \frac{1}{2}x^2$と$y=\displaystyle \frac{a}{x}$について、
$x=\displaystyle \frac{1}{2}$から$x = 3$までの変化の割合が 等しいとき、
定数の$a$値を求めなさい。
この動画を見る
入試問題 豊島岡女子学園高等学校
$y=\displaystyle \frac{1}{2}x^2$と$y=\displaystyle \frac{a}{x}$について、
$x=\displaystyle \frac{1}{2}$から$x = 3$までの変化の割合が 等しいとき、
定数の$a$値を求めなさい。
グラフ:山口県高校入試~全国入試問題解法
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#山口県公立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
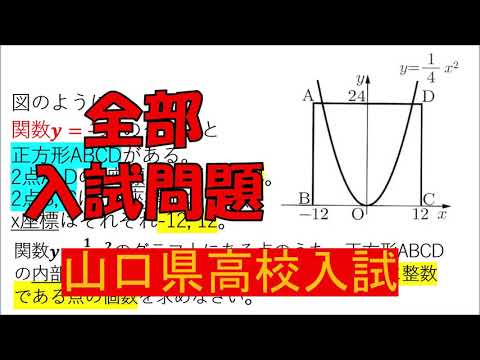
入試問題 山口県の高校
図のように
関数$y= x^2$のグラフと$4$正方形$ABCD$がある。
$2$点$A, D$の$y$座標はいずれも$24$。
$2$点$B,C$は、$x$座標上の点で、
$x$座標はそれぞれ$-12,12$。
関数$y=\displaystyle \frac{1}{4}x^2$のグラフ上にある点のうち、正方形$ABCD$の内部および辺上にあり、
$x$座標、$y$座標がともに整数である点の個数を求めなさい。
※図は動画内参照
この動画を見る
入試問題 山口県の高校
図のように
関数$y= x^2$のグラフと$4$正方形$ABCD$がある。
$2$点$A, D$の$y$座標はいずれも$24$。
$2$点$B,C$は、$x$座標上の点で、
$x$座標はそれぞれ$-12,12$。
関数$y=\displaystyle \frac{1}{4}x^2$のグラフ上にある点のうち、正方形$ABCD$の内部および辺上にあり、
$x$座標、$y$座標がともに整数である点の個数を求めなさい。
※図は動画内参照
【中学数学】関数y=ax²:点A,Bは放物線y=x²上の点であり、そのx座標はそれぞれ 3,2である。△AOBの面積を求めよう。

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
点A,Bは放物線$y=x^2$上の点であり、そのx座標はそれぞれ 3,2である。△AOBの面積を求めよう。
この動画を見る
点A,Bは放物線$y=x^2$上の点であり、そのx座標はそれぞれ 3,2である。△AOBの面積を求めよう。
【中学数学】関数y=ax²:変域③ 関数y=2/3x²とy=-1/3x²について、xの変域が次のときyの変域をそれぞれ求めなさい。(1)-6≦x≦0 (2)3≦x≦9 (3)-6≦x≦9

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
関数$y=\dfrac{2}{3}x^2$と$y=-\dfrac{1}{3}x^2$について、xの変域が次のときyの変域をそれぞれ求めなさい。
(1)$-6\leqq x\leqq 0$ (2)$3\leqq x\leqq 9$ (3)$-6\leqq x\leqq 9$
この動画を見る
関数$y=\dfrac{2}{3}x^2$と$y=-\dfrac{1}{3}x^2$について、xの変域が次のときyの変域をそれぞれ求めなさい。
(1)$-6\leqq x\leqq 0$ (2)$3\leqq x\leqq 9$ (3)$-6\leqq x\leqq 9$
【中学数学】関数y=ax²:変域② 次のそれぞれについて、yの変域を求めよ。(1)関数y=x²で、xの変域が-4≦x≦2。(2)関数y=-x²で、xの変域が-4≦x≦2

単元:
#数学(中学生)#中3数学#2次関数
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のそれぞれについて、yの変域を求めよ。
(1)関数$y=x^2$で、xの変域が$-4\leqq x\leqq 2$。
(2)関数$y=-x^2$で、xの変域が$-4\leqq x\leqq 2$
この動画を見る
次のそれぞれについて、yの変域を求めよ。
(1)関数$y=x^2$で、xの変域が$-4\leqq x\leqq 2$。
(2)関数$y=-x^2$で、xの変域が$-4\leqq x\leqq 2$
