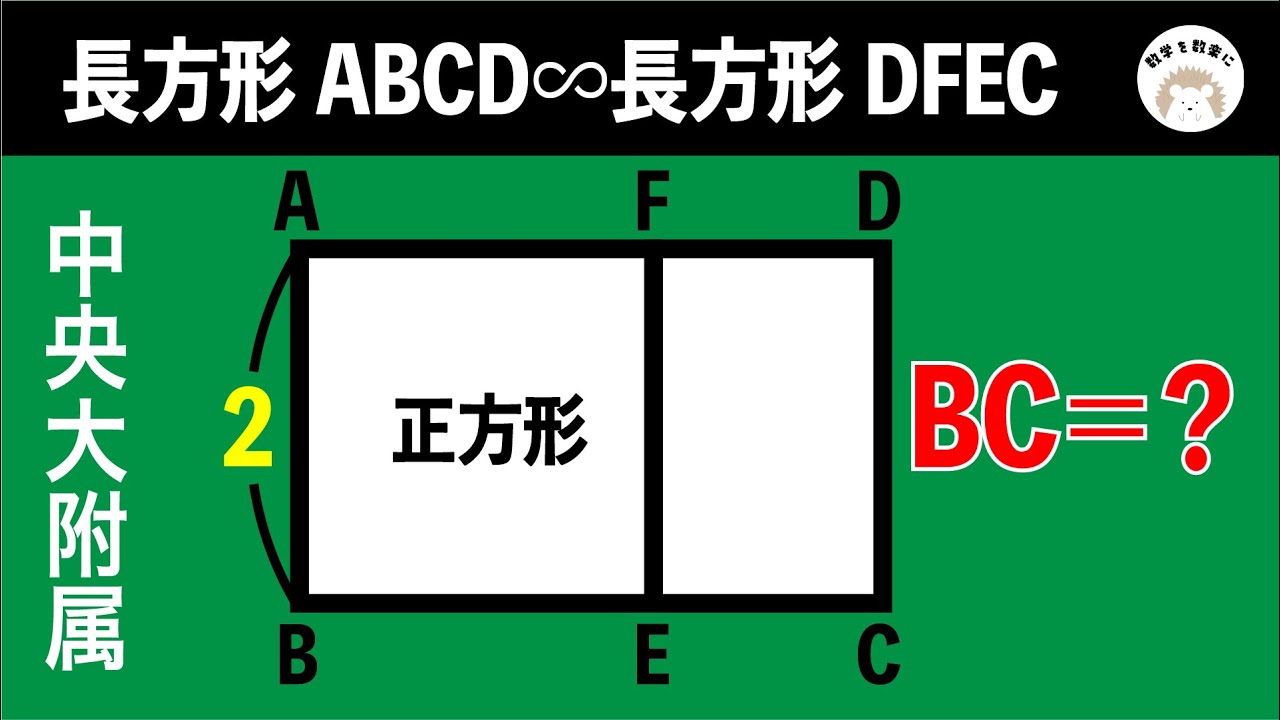
相似な図形
相似な図形
 相似な図形
相似な図形
斜めの正方形

図形の問題に見えて〇〇の問題 2通りで解説 正方形
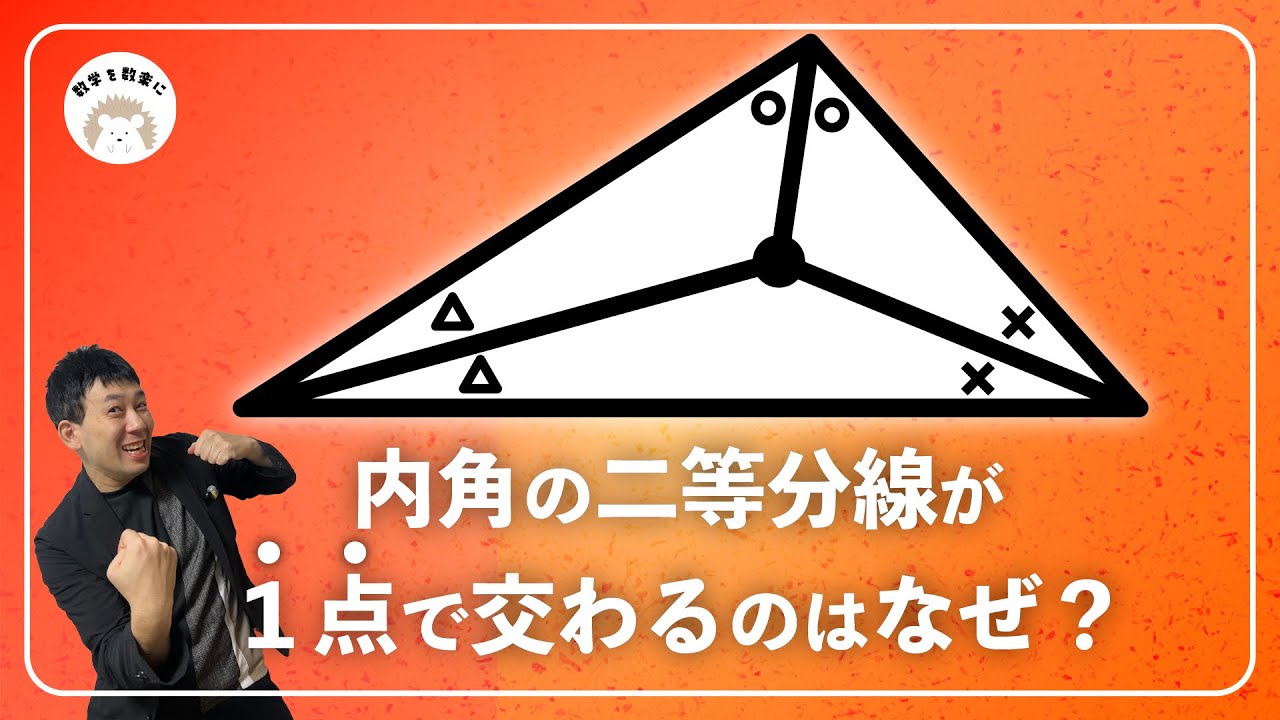
三角形の重心 一点で交わるのはなぜ?

内心 内角の二等分線が一点で交わるのはなぜ?
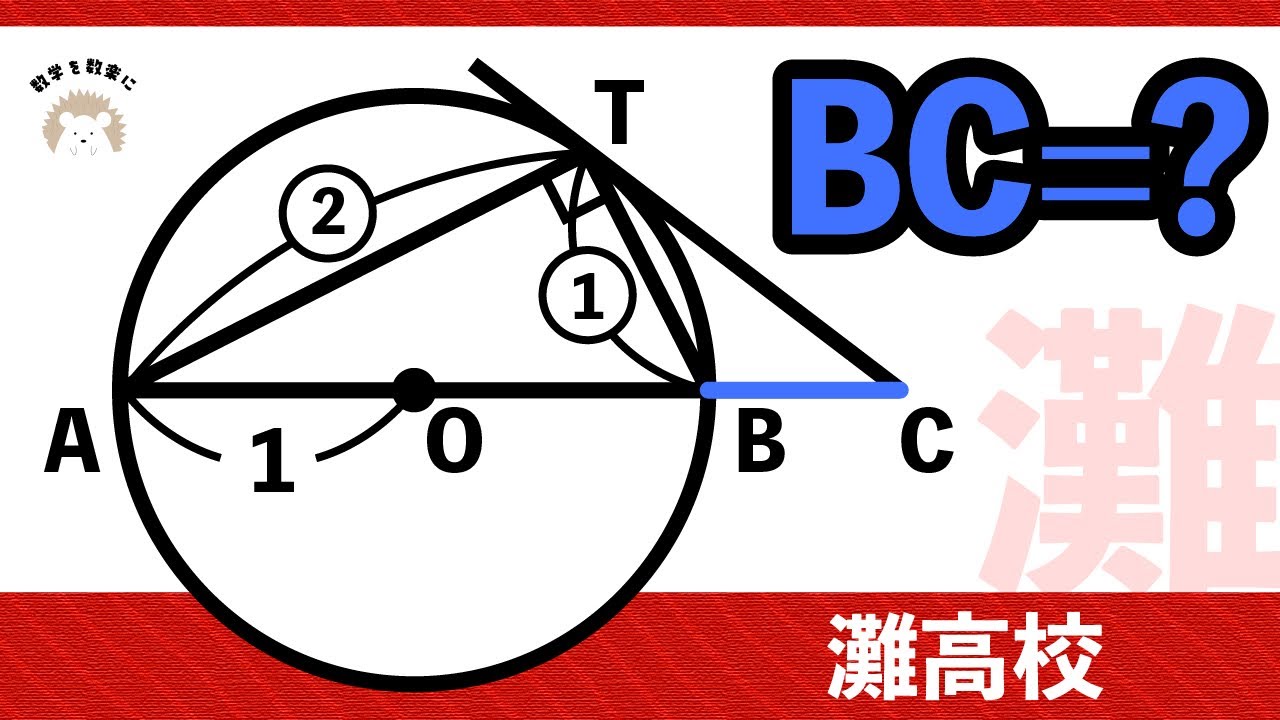
よくある円のパターン 〇〇をみつけろ! 灘高校
4つの正方形
正方形の折り返し 大分東明
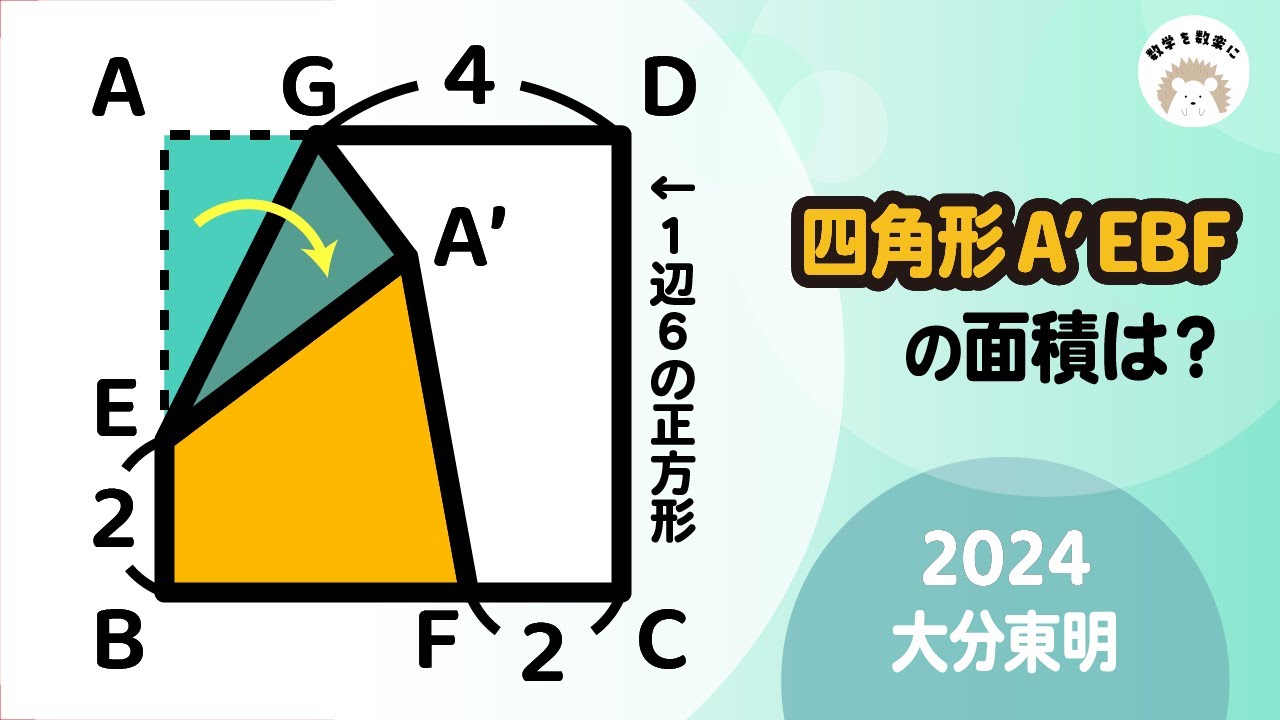
正方形の折り返し 大分東明

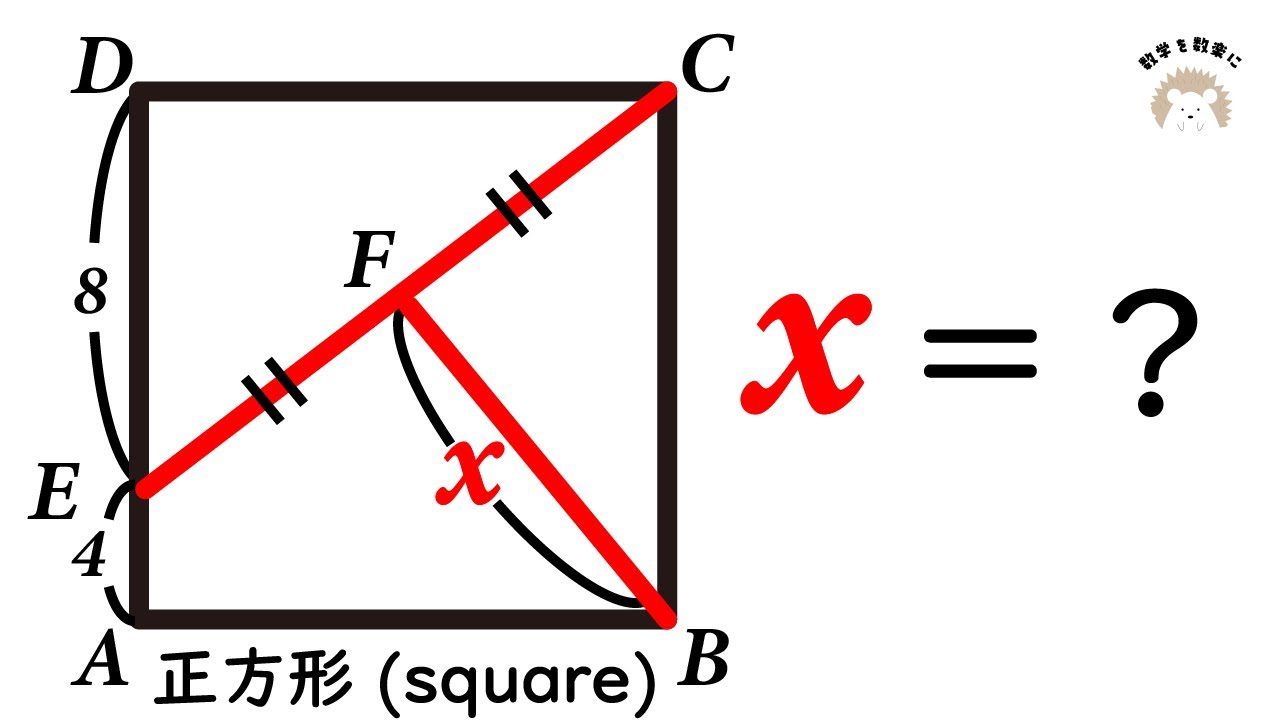
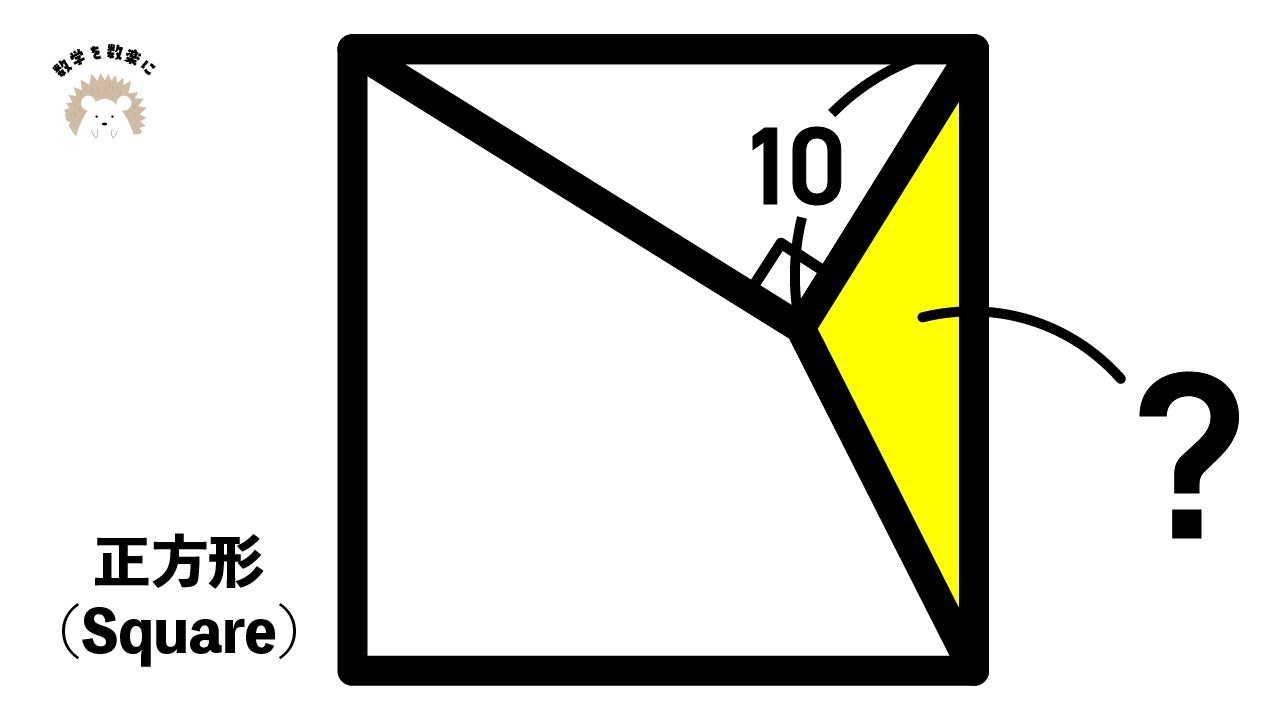
気付けば爽快!!正方形(square)
単元:
#数学(中学生)#中2数学#平行と合同#相似な図形#三角形と四角形
指導講師:
数学を数楽に
問題文全文(内容文):
動画の四角形において、その中にある$\triangle \rm{CDE}$を求めよ。
この動画を見る
動画の四角形において、その中にある$\triangle \rm{CDE}$を求めよ。
サウンドを聞きながら数学が好きになる!~全国入試問題解法 #数学 #数検 #高校入試 #勉強 #ライブ

単元:
#数学(中学生)#中3数学#相似な図形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
サウンドを聞きながら数学が好きになる!
直角三角形$ABC$において
$a^2 + b^2 = c^2$
が成り立つ。
【$BC = a$】
【$CA=b$】
【$ AB=c$】
図を用いて 証明せよ。
※図は動画内参照
この動画を見る
サウンドを聞きながら数学が好きになる!
直角三角形$ABC$において
$a^2 + b^2 = c^2$
が成り立つ。
【$BC = a$】
【$CA=b$】
【$ AB=c$】
図を用いて 証明せよ。
※図は動画内参照
台形の中の面積比

正方形の面積🟰❓

長方形の面積🟰❓
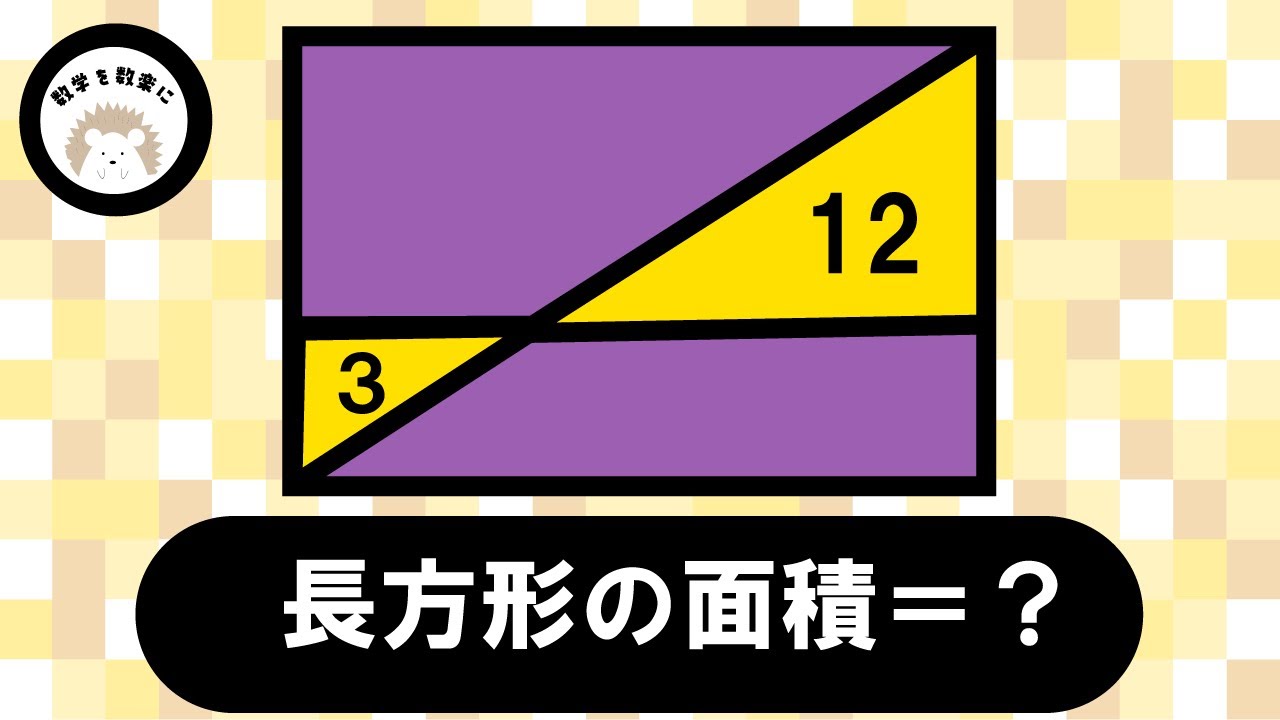
気付けば一瞬!!2通りで解説
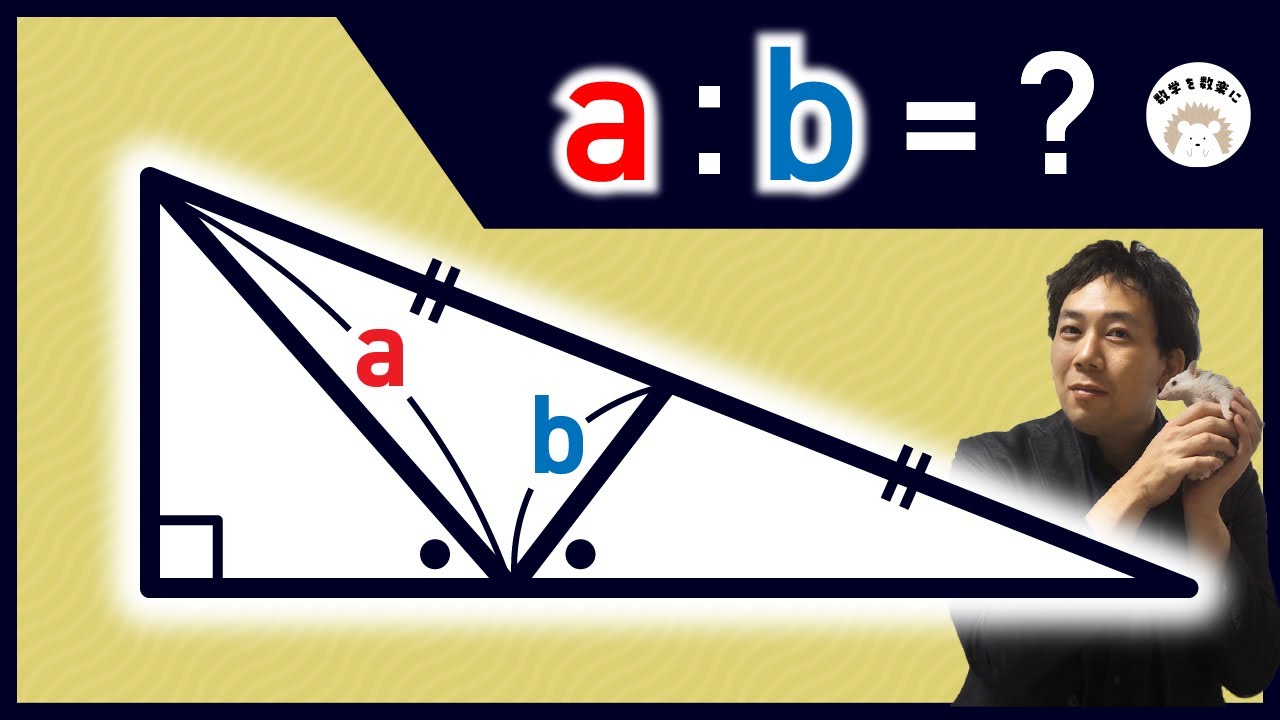
二等辺三角形と正方形

気付けば一瞬!!正方形の面積

三角形の内角の二等分線と言われたら?
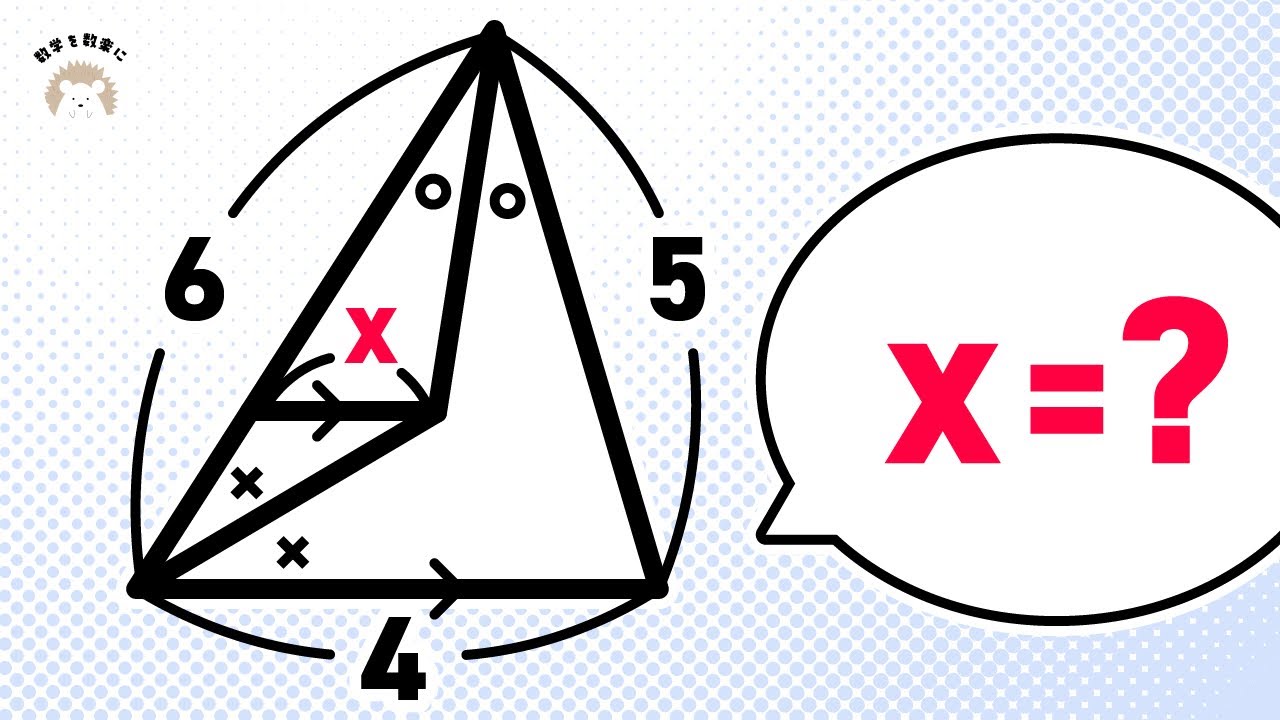
補助線引けるかな?
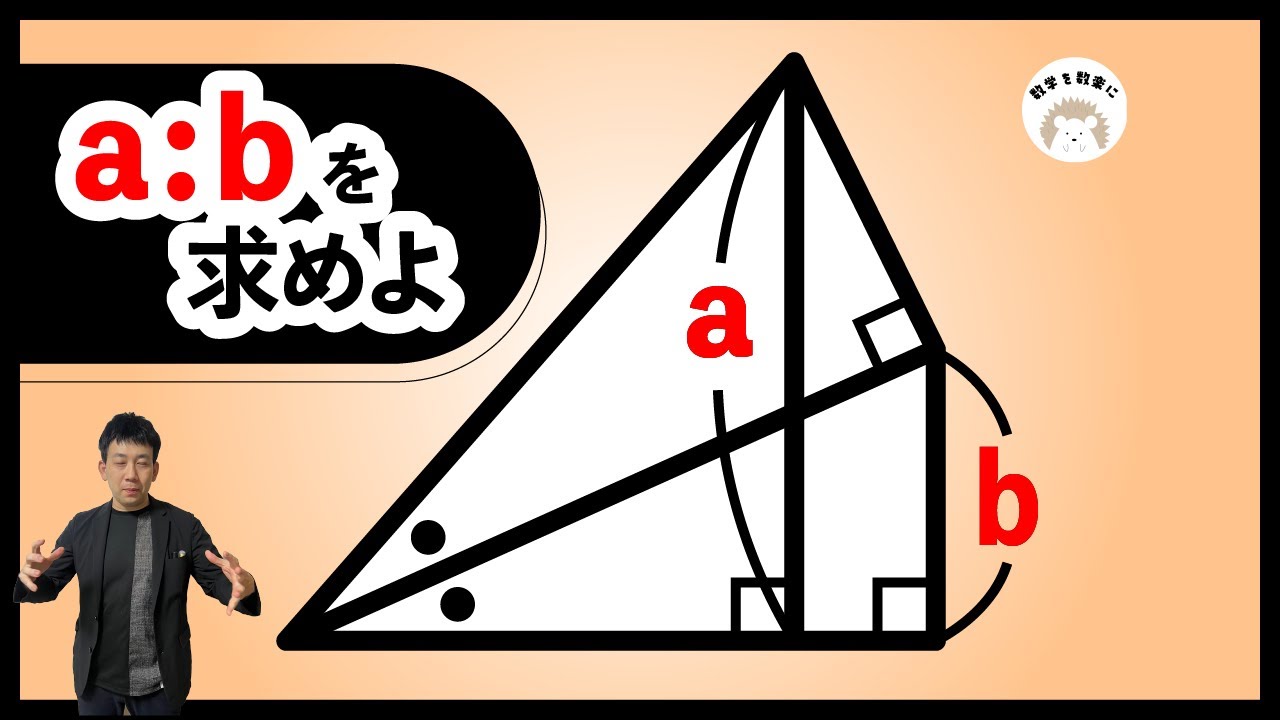
疑うところからすべては始まる 聖徳学園
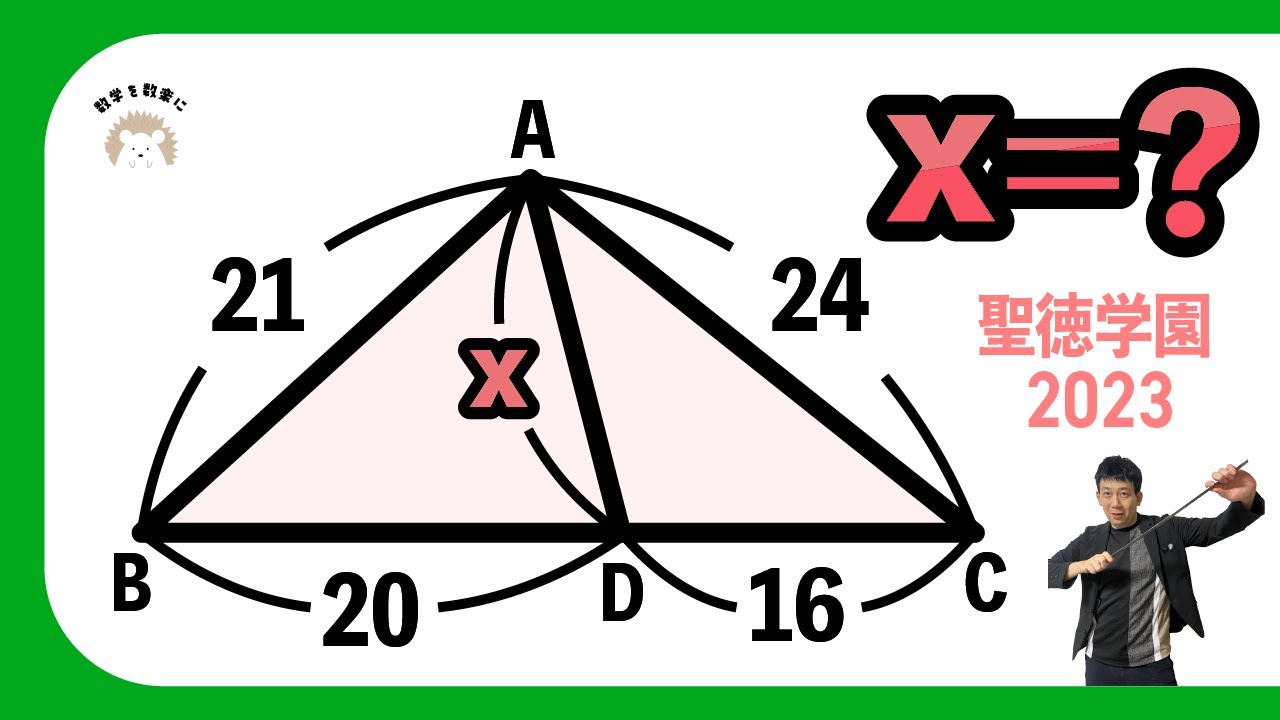
単元:
#大学入試過去問(数学)#相似な図形#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
x=?
*図は動画内参照
聖徳学園高等学校2023
この動画を見る
x=?
*図は動画内参照
聖徳学園高等学校2023
福田のおもしろ数学082〜正方形の面積は
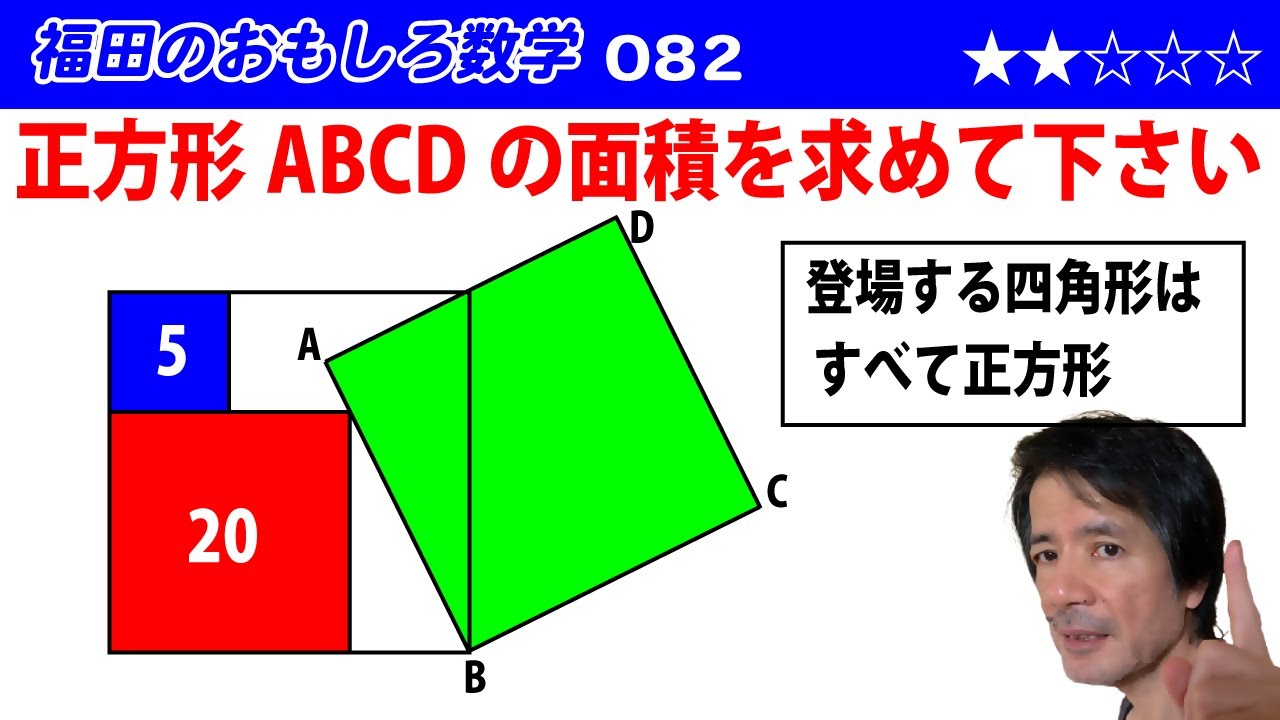
福田のおもしろ数学076〜三角形の外接円の半径は
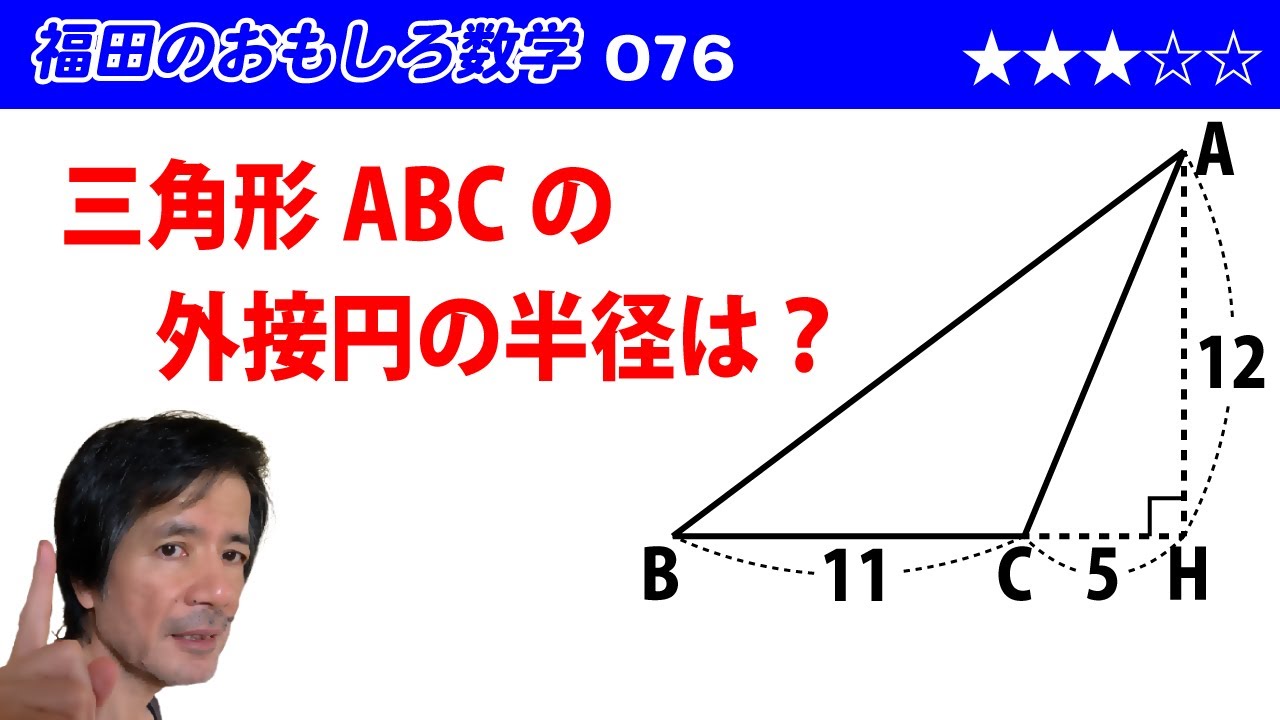
円と回転体 2024愛知県のラスボス
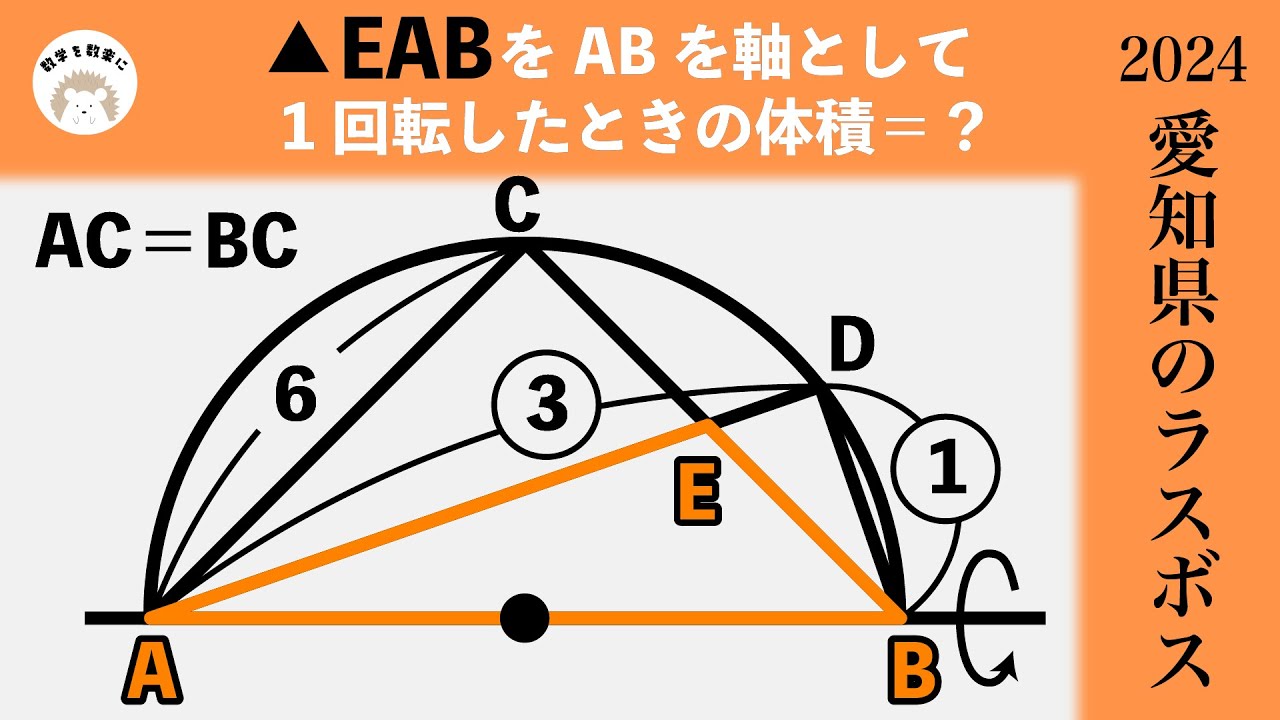
福田のおもしろ数学024〜10秒でできたら天才〜三角形の中の線分の長さ

単元:
#数学(中学生)#中3数学#数A#図形の性質#相似な図形#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
小学生でも解ける!?
xを求めよ
図は動画内参照
この動画を見る
小学生でも解ける!?
xを求めよ
図は動画内参照
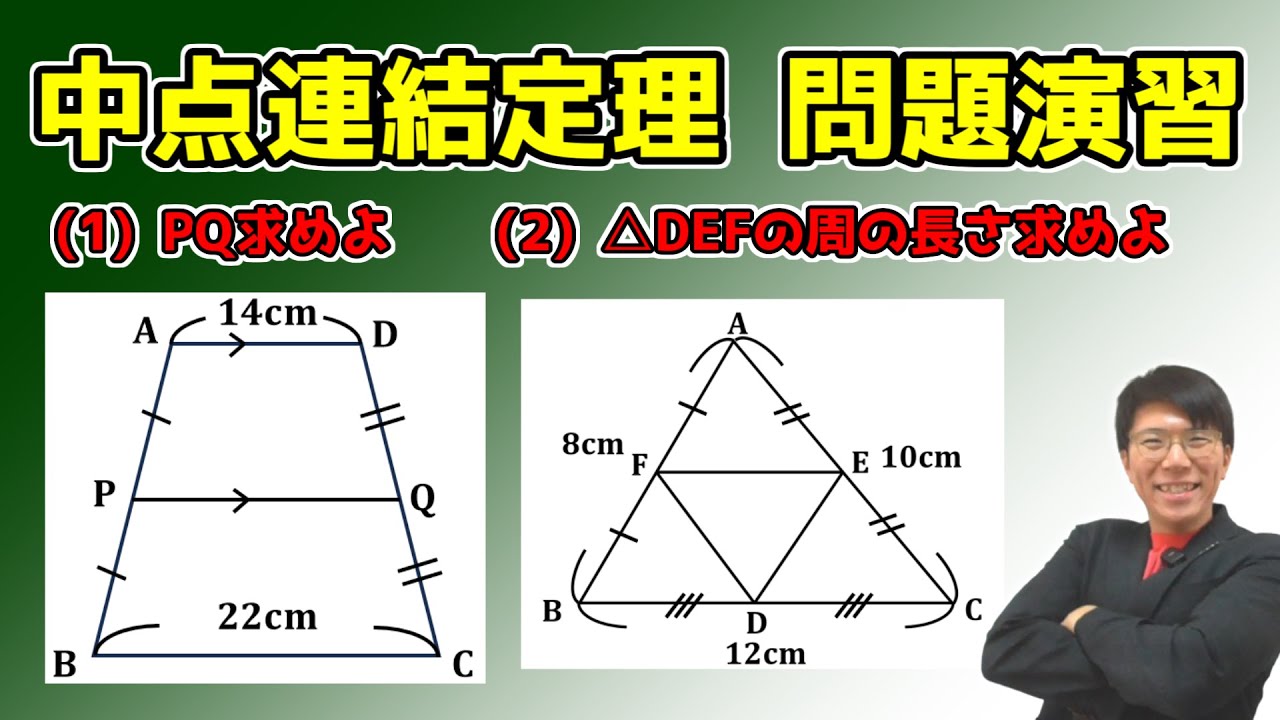
【中学数学】中点連結定理の問題演習~有名例題2問~ 5-4.5【中3理科】
単元:
#数学(中学生)#中3数学#相似な図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1)四角形ABCDはAD//BDの台形で2点PQはそれぞれ辺AB,DCの中点である。
AD=14cm,BC=22cmのときPQの長さを求めよ。
問題の図形は動画参照
(2)△ABCの辺AB,BC,CAの中点をそれぞれF,D,Eとする。
△DEFの周りの長さを求めよ。
問題の図形は動画参照
この動画を見る
(1)四角形ABCDはAD//BDの台形で2点PQはそれぞれ辺AB,DCの中点である。
AD=14cm,BC=22cmのときPQの長さを求めよ。
問題の図形は動画参照
(2)△ABCの辺AB,BC,CAの中点をそれぞれF,D,Eとする。
△DEFの周りの長さを求めよ。
問題の図形は動画参照
【中学数学】中点連結定理の問題演習~有名例題2問~

単元:
#数学(中学生)#中3数学#相似な図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
(1) 四角形ABCDはAD //BCの台形で, 2点P,Qはそれぞれ辺AB, DCの中点である。
AD = 14cm, BC = 22cm, のとき, PQの長さを求めよ
(2) △ABCの辺AB, BC, CAの中点をそれぞれF,D,Eとする。
△DEFの周りの長さを求めよ。
この動画を見る
(1) 四角形ABCDはAD //BCの台形で, 2点P,Qはそれぞれ辺AB, DCの中点である。
AD = 14cm, BC = 22cm, のとき, PQの長さを求めよ
(2) △ABCの辺AB, BC, CAの中点をそれぞれF,D,Eとする。
△DEFの周りの長さを求めよ。
【中学数学】中点連結定理を分かりやすく~証明~ 5-4【中3数学】

数学の先生こうじゃない?

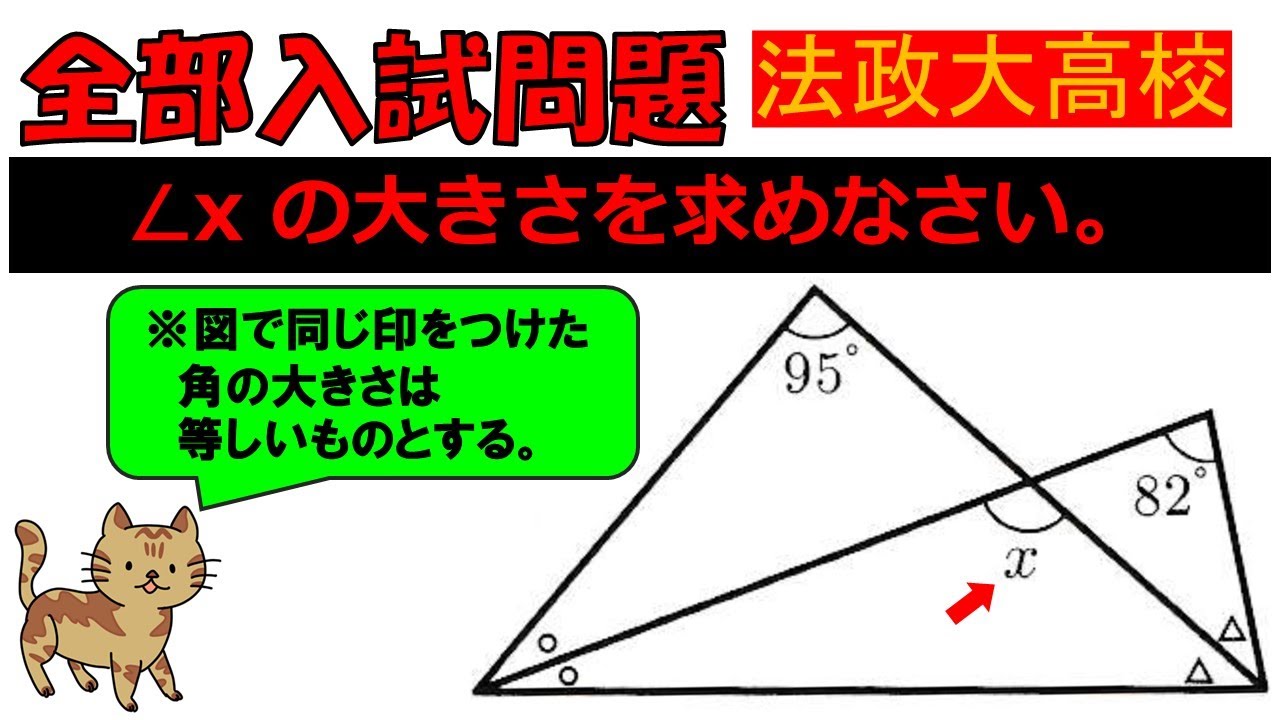
【三角形を活かす!】図形:法政大学高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)#法政大学高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \angle x $の大きさを求めなさい.
法政大高校過去問
この動画を見る
$ \angle x $の大きさを求めなさい.
法政大高校過去問
静かな気持ちで図形問題を解く動画~全国入試問題解法 #shorts #数学 #高校入試 #動体視力

長方形の相似 中央大学附属