相似な図形
相似な図形
 相似な図形
相似な図形
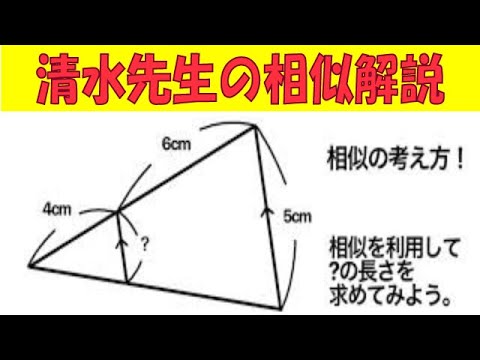
何個見つけられるかな?相似をすべて見つけろ!! 浜松開誠館(静岡)改題
速さを相似で 筑波大附属

単元:
#数学(中学生)#中3数学#相似な図形#速さ#速さその他#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
36km離れている2地点A,Bがある。
PさんはAを出発し、時速5kmでBへ向かった。QさんはPと同時にBを出発し、一定の速さでAへ向かったところ、途中でPとすれ違い、その5時間後にAに到着した。
2人がすれ違ったのは同時に出発してから何時間後か。
筑波大学付属高等学校
この動画を見る
36km離れている2地点A,Bがある。
PさんはAを出発し、時速5kmでBへ向かった。QさんはPと同時にBを出発し、一定の速さでAへ向かったところ、途中でPとすれ違い、その5時間後にAに到着した。
2人がすれ違ったのは同時に出発してから何時間後か。
筑波大学付属高等学校
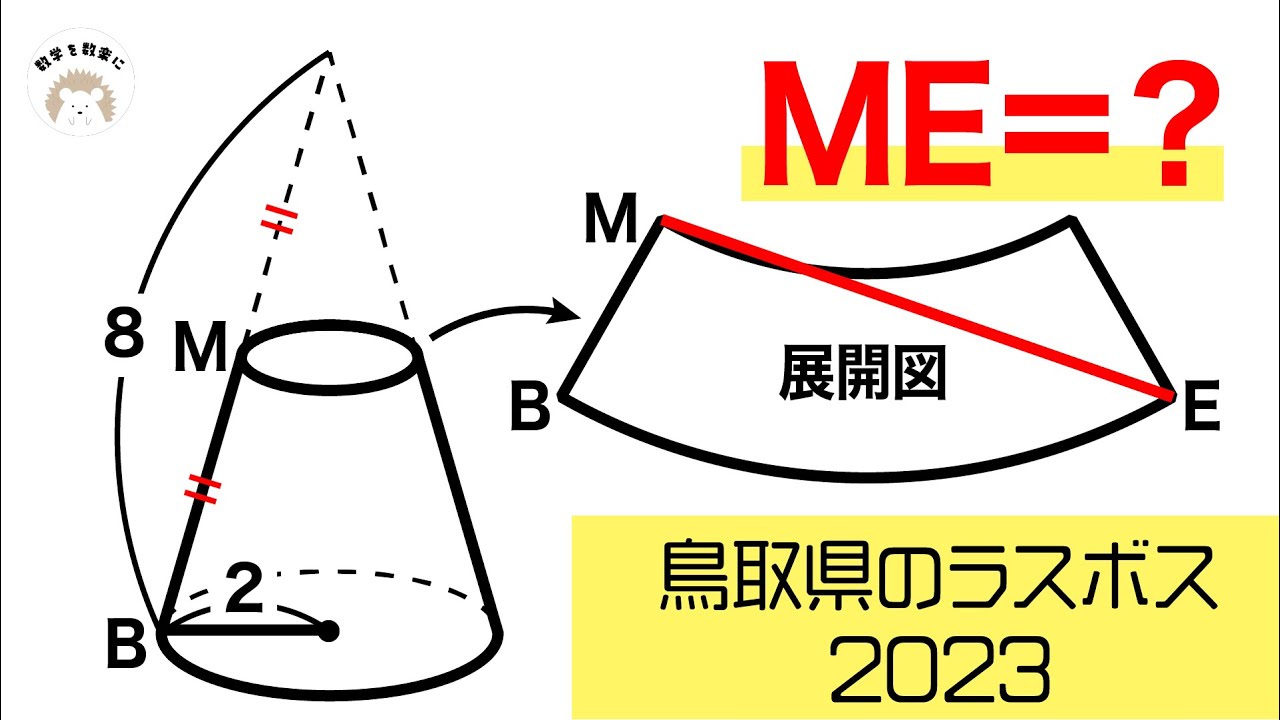
2023高校入試数学解説99問目 円錐の展開図 鳥取県(改)
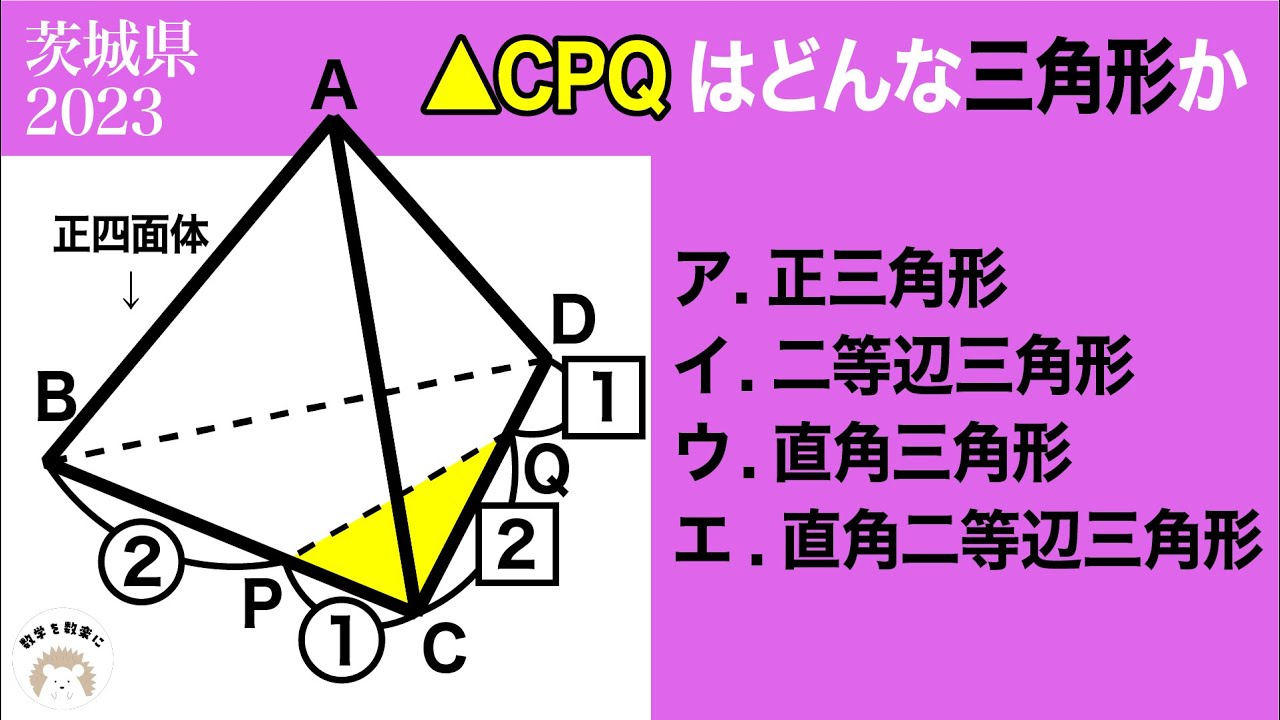
2023高校入試数学解説94問目 正四面体の中の三角形 茨城県
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
△CPQはどんな三角形か
ア.正三角形
イ.二等辺三角形
ウ.直角三角形
エ.直角二等辺三角形
*図は動画内参照
2023茨城県
この動画を見る
△CPQはどんな三角形か
ア.正三角形
イ.二等辺三角形
ウ.直角三角形
エ.直角二等辺三角形
*図は動画内参照
2023茨城県
佐賀県立高校入試2021年5⃣(4)「相似」
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
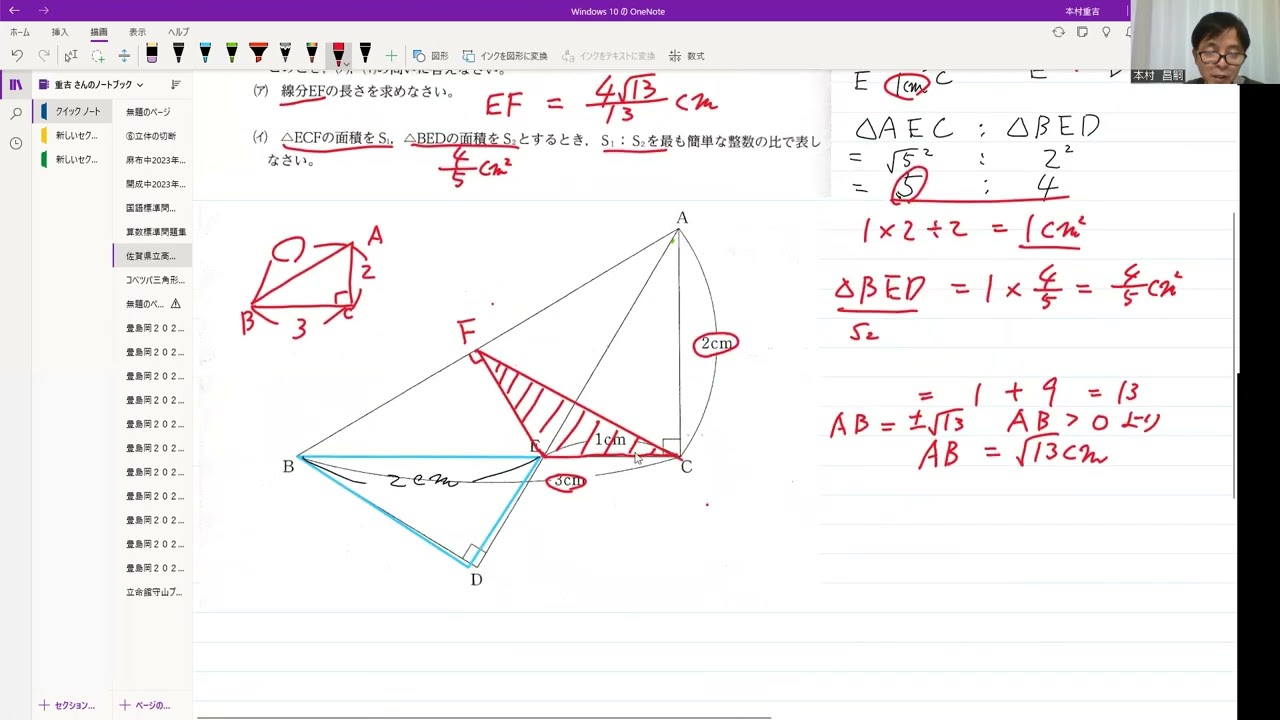
佐賀県立高校入試2021年5⃣(4)「相似」
-----------------
動画内の図のように、ABを斜辺とする2つの直角三角形ABCとABDがあり、辺BCとADの交点をEとする。
また、AC=2cm、BC=3cm、CE=1cmとする。
点Eから辺ABに重線をひき、その交点をFとする。 このとき、(ア)、(イ)の問いに答えなさい。
(ア)線分EFの長さを求めなさい。
(イ)△BCFの面積をS$_{1}$、△BEDの面積をS$_{2}$とするとき、S$_{1}$:S$_{2}$を
最も簡単な整数の比で表しなさい。
この動画を見る
佐賀県立高校入試2021年5⃣(4)「相似」
-----------------
動画内の図のように、ABを斜辺とする2つの直角三角形ABCとABDがあり、辺BCとADの交点をEとする。
また、AC=2cm、BC=3cm、CE=1cmとする。
点Eから辺ABに重線をひき、その交点をFとする。 このとき、(ア)、(イ)の問いに答えなさい。
(ア)線分EFの長さを求めなさい。
(イ)△BCFの面積をS$_{1}$、△BEDの面積をS$_{2}$とするとき、S$_{1}$:S$_{2}$を
最も簡単な整数の比で表しなさい。
高等学校入学試験予想問題:秋田県公立高等学校~全部入試問題
単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#2次方程式#空間図形#相似な図形#文章題#文章題その他#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$\dfrac{15}{2}\times \left(-\dfrac{4}{5}\right)$
(2)$ 10a-(6a+8)$
(3)$ 27ab^2\div 9ab $
(4)二次方程式$ x^2-3x+1=0$を解け.
$ \boxed{2}$
(1)底面が1辺6cmの正方形,体積$ 96cm^3$の四角錐の高さは?
(2)$ 4 \lt \sqrt a \lt \dfrac{13}{3}$に当てはまるaの値をすべて求めよ.
(3)$ \ell \parallel m $のとき,$ \angle x $は?
$ \boxed{3}$
n番目の白タイルの枚数をnの式で表せ.
この動画を見る
$ \boxed{1}$
(1)$\dfrac{15}{2}\times \left(-\dfrac{4}{5}\right)$
(2)$ 10a-(6a+8)$
(3)$ 27ab^2\div 9ab $
(4)二次方程式$ x^2-3x+1=0$を解け.
$ \boxed{2}$
(1)底面が1辺6cmの正方形,体積$ 96cm^3$の四角錐の高さは?
(2)$ 4 \lt \sqrt a \lt \dfrac{13}{3}$に当てはまるaの値をすべて求めよ.
(3)$ \ell \parallel m $のとき,$ \angle x $は?
$ \boxed{3}$
n番目の白タイルの枚数をnの式で表せ.
佐賀県立高校入試2021年5⃣(1)~(3)「相似」
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
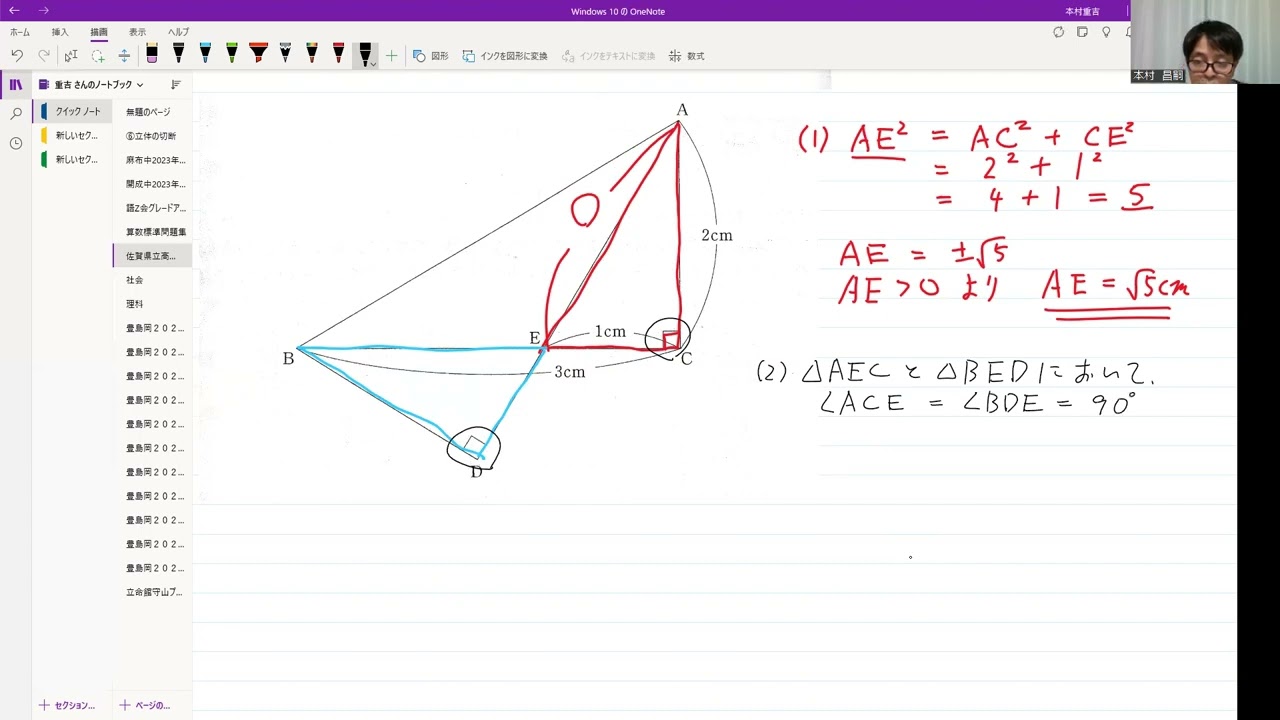
佐賀県立高校入試2021年5⃣(1)~(3)「相似」
-----------------
動画内の図のように、ABを斜辺とする2つの直角三角形ABCとABDがあり、辺BCとADの交点をEとする。
また、AC=2cm、BC=3cm、CE=1cmとする。
(1)線分AEの長さを求めなさい。
(2)△ABC$\sim$△BEDであることを証明しなさい。
(3)△ABEの面積を求めなさい。
この動画を見る
佐賀県立高校入試2021年5⃣(1)~(3)「相似」
-----------------
動画内の図のように、ABを斜辺とする2つの直角三角形ABCとABDがあり、辺BCとADの交点をEとする。
また、AC=2cm、BC=3cm、CE=1cmとする。
(1)線分AEの長さを求めなさい。
(2)△ABC$\sim$△BEDであることを証明しなさい。
(3)△ABEの面積を求めなさい。
中学生向け図形問題
佐賀県立高校入試2022年5⃣相似(4)~(6)
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
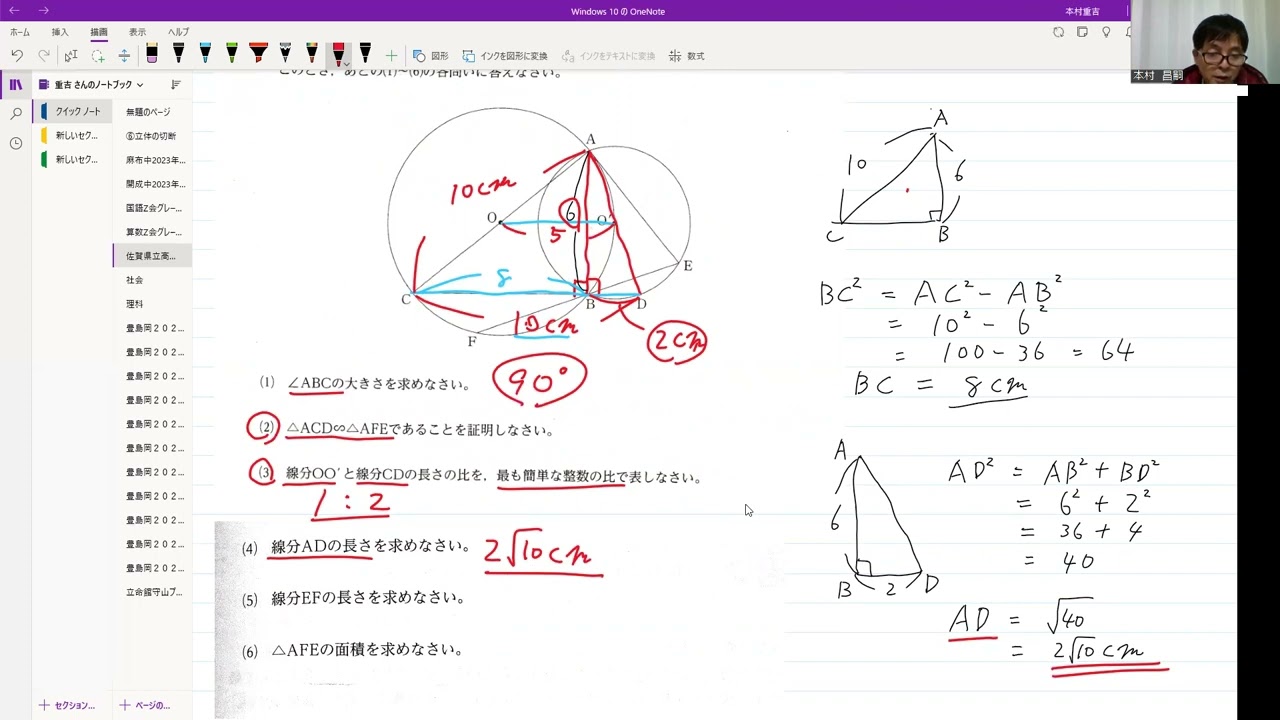
佐賀県立高校入試2022年5⃣相似(4)~(6)
-----------------
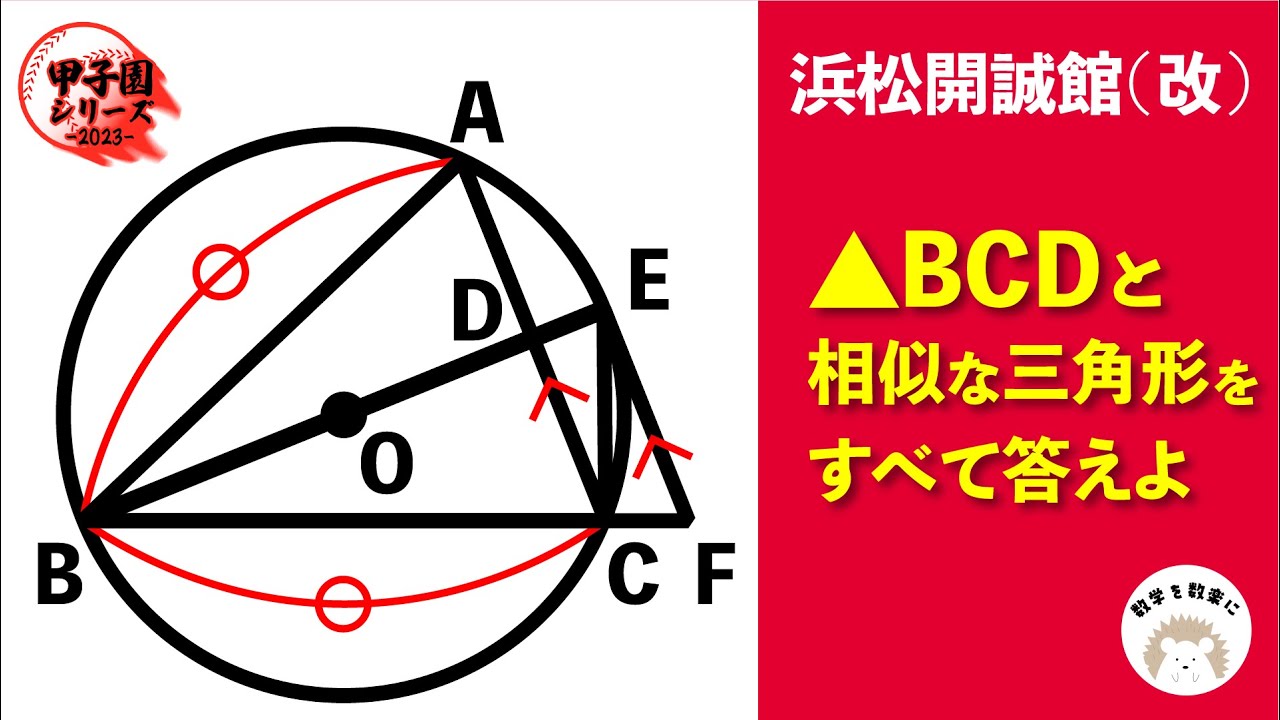
動画内の図のように、半径が5cmの円Oと、半径が円Oの半径よりも短い円O'があり、円O'の中心は円Oの周上にある。
2つの円の交点をA、Bとし、AB=6cmとする。
円Oの周上に線分ACが円Oの直径となるように点Cをとり、直線CBと円O'との交点のうち点Bと異なる点をDとする。
また、円O'の周上にAE=6cmとなるように点Eをとり、直線EBと円Oとの交点のうち点Bと異なる点をFとする。ただし、点Eは点Bと異なる点とする。
(4) 線分ADの長さを求めなさい。
(5) 線分EFの長さを求めなさい。
(6) △AFEの面積を求めなさい。
この動画を見る
佐賀県立高校入試2022年5⃣相似(4)~(6)
-----------------
動画内の図のように、半径が5cmの円Oと、半径が円Oの半径よりも短い円O'があり、円O'の中心は円Oの周上にある。
2つの円の交点をA、Bとし、AB=6cmとする。
円Oの周上に線分ACが円Oの直径となるように点Cをとり、直線CBと円O'との交点のうち点Bと異なる点をDとする。
また、円O'の周上にAE=6cmとなるように点Eをとり、直線EBと円Oとの交点のうち点Bと異なる点をFとする。ただし、点Eは点Bと異なる点とする。
(4) 線分ADの長さを求めなさい。
(5) 線分EFの長さを求めなさい。
(6) △AFEの面積を求めなさい。
佐賀県立高校入試2022年5⃣相似(1)~(3)
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
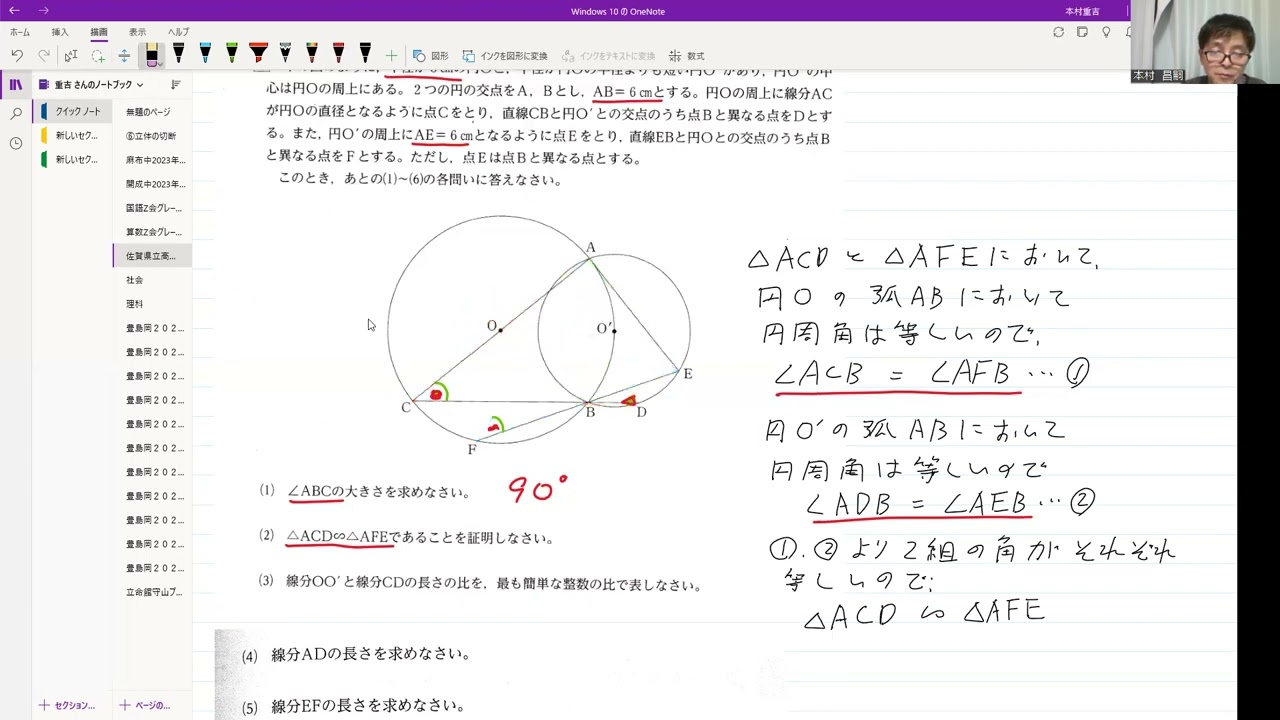
佐賀県立高校入試2022年5⃣相似(1)~(3)
-----------------
動画内の図のように、半径が5cmの円Oと、半径が円Oの半径よりも短い円O'があり、円O'の中心は円Oの周上にある。
2つの円の交点をA、Bとし、AB=6cmとする。
円Oの周上に線分ACが円Oの直径となるように点Cをとり、直線CBと円O'との交点のうち点Bと異なる点をDとする。
また、円O'の周上にAE=6cmとなるように点Eをとり、直線EBと円Oとの交点のうち点Bと異なる点をFとする。ただし、点Eは点Bと異なる点とする。
(1) ∠ABCの大きさを求めなさい。
(2) △ACD$\backsim$△AFEであることを証明しなさい。
(3) 線分OO'と線分CDの長さの比を、最も簡単な整数の比で表しなさい。
この動画を見る
佐賀県立高校入試2022年5⃣相似(1)~(3)
-----------------
動画内の図のように、半径が5cmの円Oと、半径が円Oの半径よりも短い円O'があり、円O'の中心は円Oの周上にある。
2つの円の交点をA、Bとし、AB=6cmとする。
円Oの周上に線分ACが円Oの直径となるように点Cをとり、直線CBと円O'との交点のうち点Bと異なる点をDとする。
また、円O'の周上にAE=6cmとなるように点Eをとり、直線EBと円Oとの交点のうち点Bと異なる点をFとする。ただし、点Eは点Bと異なる点とする。
(1) ∠ABCの大きさを求めなさい。
(2) △ACD$\backsim$△AFEであることを証明しなさい。
(3) 線分OO'と線分CDの長さの比を、最も簡単な整数の比で表しなさい。
難関高校受験者必見!!公式まとめます。図形

単元:
#数学(中学生)#中1数学#中2数学#中3数学#空間図形#平行と合同#相似な図形#円#三平方の定理#平面図形#三角形と四角形
指導講師:
数学を数楽に
問題文全文(内容文):
難関高校受験者必見!!公式まとめます。図形
この動画を見る
難関高校受験者必見!!公式まとめます。図形
難関高校受験する生徒へ 塾で習う公式まとめてみた。図形編はまた、いつかやります!!

単元:
#数学(中学生)#中1数学#中2数学#中3数学#空間図形#平行と合同#相似な図形#円#三平方の定理#平面図形#三角形と四角形
指導講師:
数学を数楽に
問題文全文(内容文):
難関高校受験する生徒へ 塾で習う公式まとめてみた。図形編はまた、いつかやります!!
この動画を見る
難関高校受験する生徒へ 塾で習う公式まとめてみた。図形編はまた、いつかやります!!
半円と正方形
【中学数学】三角形の相似をどこよりも丁寧に~相似条件~ 5-1【中3数学】

福田の数学〜上智大学2022年理工学部第3問〜複素数平面上の点列と三角形の相似

単元:
#大学入試過去問(数学)#複素数平面#相似な図形#数列#漸化式#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#上智大学#数学(高校生)#数B#数C
指導講師:
福田次郎
問題文全文(内容文):
複素数からなる数列${z_n}$を、次の条件で定める。
$z_1=0,\ \ \ z_{n+1}=(1+i)z_n-i \ \ \ (i=1,2,3, \ \ ...)$
正の整数nに対し、z_nに対応する負素数平面上の点をA_nとおく。
(1)$z_2=\boxed{ツ }+\boxed{ツ }\ i, \ \ \ z_3=\boxed{ト}+$
$\boxed{ナ}\ i,\ \ \ z_4=\boxed{二}+\boxed{ヌ}\ i $である。
(2)$r \gt 0,\ 0 \leqq θ \lt 2\pi$ を用いて、$1+i=r(\cos θ+i\sin θ)$のように$1+i$を極形式で
表すとき、$r=\sqrt{\boxed{ネ}},\ θ=\frac{\boxed{ノ }}{\boxed{ハ}}\pi$である。
(3)すべての正の整数nに対する$\triangle PA_nA_{n+1}$が互いに相似になる点Pに対応する
複素数は、$\boxed{ヒ}+\boxed{フ }\ i$である。
(4)$|z_n| \gt 1000$となる最小のnは$n=\boxed{へ}$である。
(5)$A_{2022+k}$が実軸上にある最小の正の整数kは$k=\boxed{ホ}$である。
2022上智大学理工学部過去問
この動画を見る
複素数からなる数列${z_n}$を、次の条件で定める。
$z_1=0,\ \ \ z_{n+1}=(1+i)z_n-i \ \ \ (i=1,2,3, \ \ ...)$
正の整数nに対し、z_nに対応する負素数平面上の点をA_nとおく。
(1)$z_2=\boxed{ツ }+\boxed{ツ }\ i, \ \ \ z_3=\boxed{ト}+$
$\boxed{ナ}\ i,\ \ \ z_4=\boxed{二}+\boxed{ヌ}\ i $である。
(2)$r \gt 0,\ 0 \leqq θ \lt 2\pi$ を用いて、$1+i=r(\cos θ+i\sin θ)$のように$1+i$を極形式で
表すとき、$r=\sqrt{\boxed{ネ}},\ θ=\frac{\boxed{ノ }}{\boxed{ハ}}\pi$である。
(3)すべての正の整数nに対する$\triangle PA_nA_{n+1}$が互いに相似になる点Pに対応する
複素数は、$\boxed{ヒ}+\boxed{フ }\ i$である。
(4)$|z_n| \gt 1000$となる最小のnは$n=\boxed{へ}$である。
(5)$A_{2022+k}$が実軸上にある最小の正の整数kは$k=\boxed{ホ}$である。
2022上智大学理工学部過去問
【数検3級】数学検定3級2次 問題8

単元:
#数学(中学生)#中3数学#数学検定・数学甲子園・数学オリンピック等#相似な図形#数学検定#数学検定3級
指導講師:
理数個別チャンネル
問題文全文(内容文):
問題8.右の図のような、∠A=90°の直角三角形ABCについて、次の問いに答えなさい。
(18) 辺BC上にあり、△ABC∽△PBAとなる点Pを、下の<注>にしたがって作図しなさい。作図をする代わりに、作図の方法を言葉で説明してもかまいません。
<注> a コンパスとものさしを使って作図してください。ただし、ものさしは直線を引くことだけに用いてください。
b コンパスの線は、はっきりと見えるようにかいてください。コンパスの針をさした位置に、・の印をつけてください。
c 作図に用いた線は消さないで残しておき、線を引いた順に①、②、③、・・・の番号を書いてください。
この動画を見る
問題8.右の図のような、∠A=90°の直角三角形ABCについて、次の問いに答えなさい。
(18) 辺BC上にあり、△ABC∽△PBAとなる点Pを、下の<注>にしたがって作図しなさい。作図をする代わりに、作図の方法を言葉で説明してもかまいません。
<注> a コンパスとものさしを使って作図してください。ただし、ものさしは直線を引くことだけに用いてください。
b コンパスの線は、はっきりと見えるようにかいてください。コンパスの針をさした位置に、・の印をつけてください。
c 作図に用いた線は消さないで残しておき、線を引いた順に①、②、③、・・・の番号を書いてください。
台形の中にできる三角形の相似 西南学院高校
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
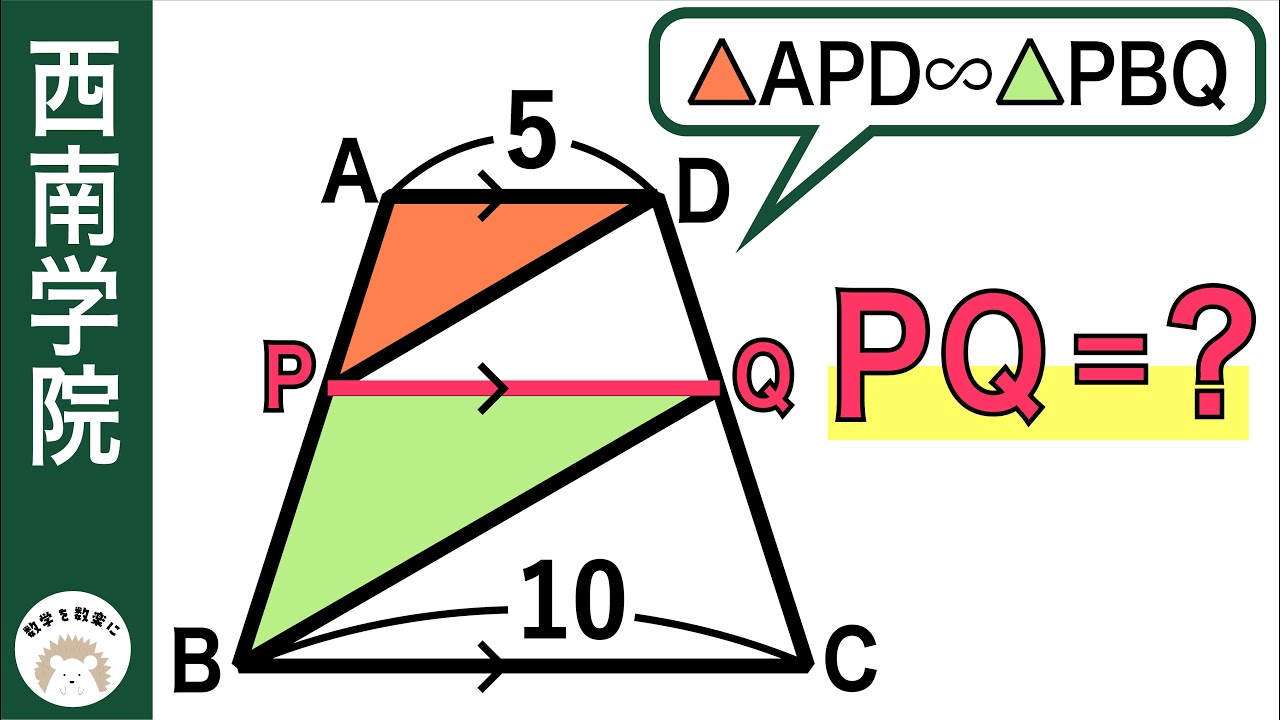
△APD∽△PBQ
PQ=?
*図は動画内参照
西南学院高等学校
この動画を見る
△APD∽△PBQ
PQ=?
*図は動画内参照
西南学院高等学校
サクッと解こう!高校入試レベル
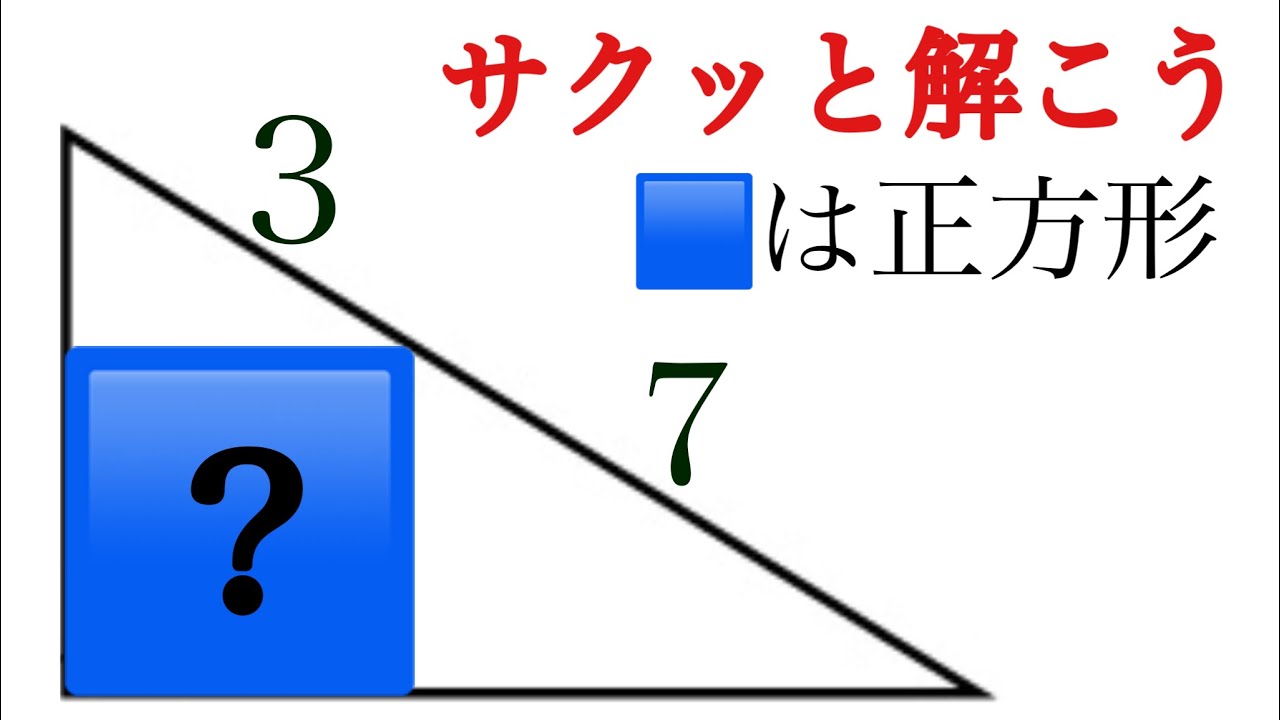
【裏技】これ知ってる?

【中学数学】相似な図形:線分比と面積比の巧みな利用
単元:
#数学(中学生)#中3数学#相似な図形
指導講師:
理数個別チャンネル
問題文全文(内容文):
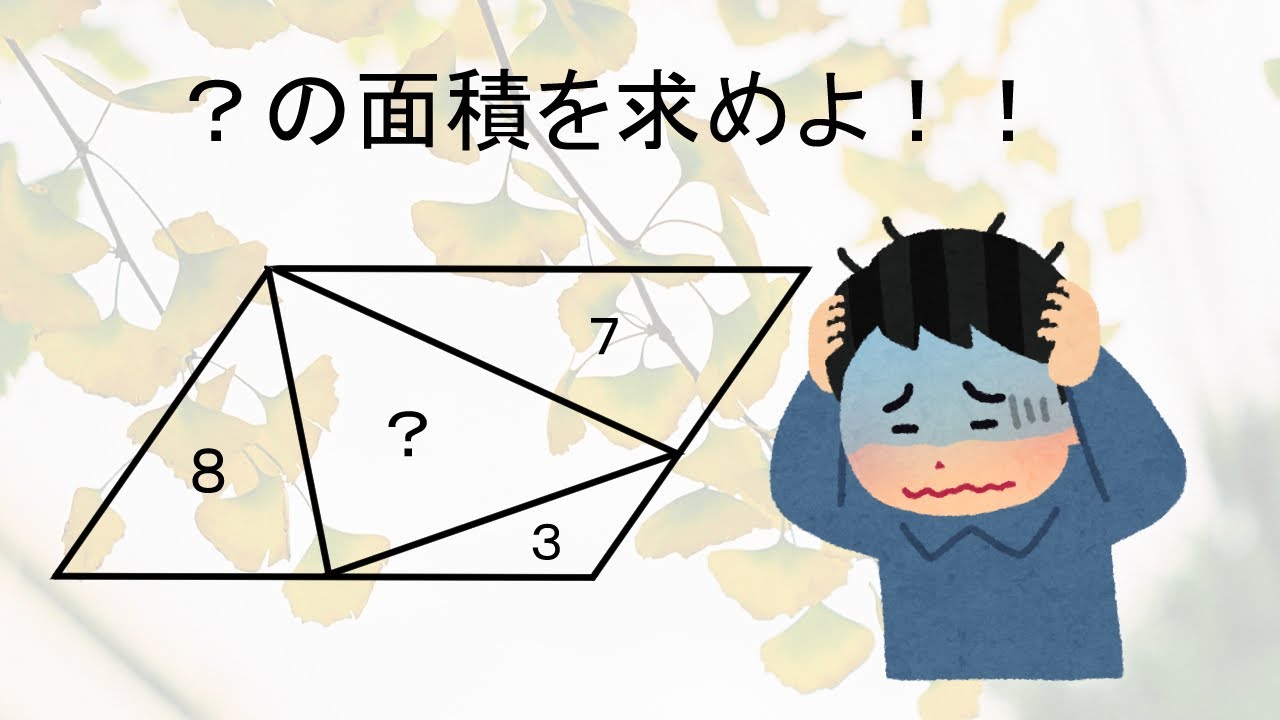
【中学数学 相似な図形】
平行四辺形ABCDにおいて、△ABE=8、△ADF=7、△CEF=3のとき、△AEFの面積を求めよ。
この動画を見る
【中学数学 相似な図形】
平行四辺形ABCDにおいて、△ABE=8、△ADF=7、△CEF=3のとき、△AEFの面積を求めよ。
【中学数学】苦手かどうか分かる問題~相似の問題演習~【中3数学】
単元:
#数学(中学生)#中3数学#相似な図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
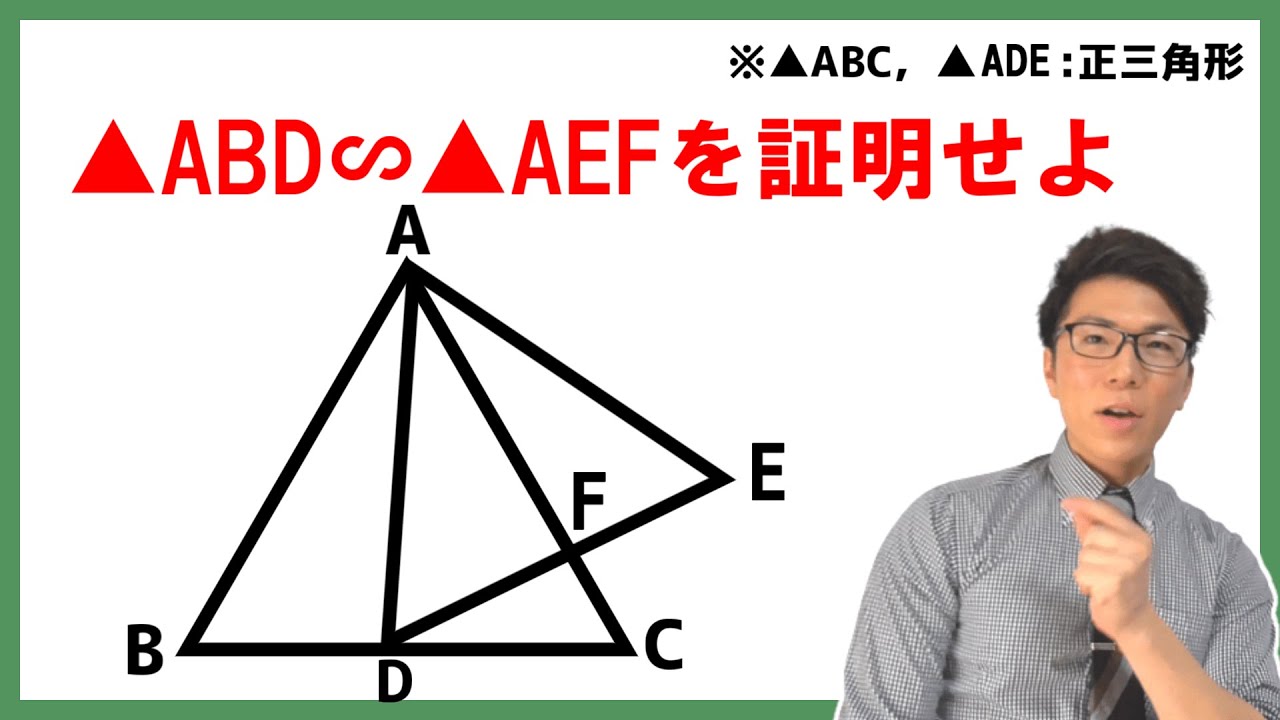
$\triangle ABC$と$\triangle ADE$はともに正三角形である。この時$\triangle ABC$ ∽ $\triangle AEF$を証明せよ。
(図は動画参照)
この動画を見る
$\triangle ABC$と$\triangle ADE$はともに正三角形である。この時$\triangle ABC$ ∽ $\triangle AEF$を証明せよ。
(図は動画参照)
中3の問題
【高校受験対策/数学】死守-97

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#平方根#2次方程式#空間図形#相似な図形#円#文字と式#平面図形#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守97
①$5-(-7)$を計算しなさい。
➁$\sqrt{ 27 }+\sqrt{ 12 }$を計算しなさい。
③$(\sqrt{ 2 }-1)^2$を計算しなさい。
④連立方程式を解きなさい。
$2x-3y=-4$
$x+2y=5$
⑤二次方程式$3x^2+7x+1=0$を解きなさい。
⑥相似な2つの立体$F,G$がある。
$F$と$G$の相似比が$3:5$であり、$F$の体積が$81\pi$$cm^3$のとき、$G$の体積を求めなさい。
⑦右の図のように、4点$A,B,C,D$が線分$BC$を直径とする 同じ円周上にあるとき、
$\angle ADB$の大きさを求めなさい。
⑧右下の図のような線分$OA$がある。
$\angle AOB=30°,OA=OB$となる二等辺三角形$OAB$を作図しなさい。
また点$B$の位置を示す文字$B$も図の中に書き入れなさい。
ただし、作図には定規とコンパスを用い、作図に用いた線は消えずに残しておくこと。
この動画を見る
高校受験対策・死守97
①$5-(-7)$を計算しなさい。
➁$\sqrt{ 27 }+\sqrt{ 12 }$を計算しなさい。
③$(\sqrt{ 2 }-1)^2$を計算しなさい。
④連立方程式を解きなさい。
$2x-3y=-4$
$x+2y=5$
⑤二次方程式$3x^2+7x+1=0$を解きなさい。
⑥相似な2つの立体$F,G$がある。
$F$と$G$の相似比が$3:5$であり、$F$の体積が$81\pi$$cm^3$のとき、$G$の体積を求めなさい。
⑦右の図のように、4点$A,B,C,D$が線分$BC$を直径とする 同じ円周上にあるとき、
$\angle ADB$の大きさを求めなさい。
⑧右下の図のような線分$OA$がある。
$\angle AOB=30°,OA=OB$となる二等辺三角形$OAB$を作図しなさい。
また点$B$の位置を示す文字$B$も図の中に書き入れなさい。
ただし、作図には定規とコンパスを用い、作図に用いた線は消えずに残しておくこと。
【高校受験対策/数学】死守-96

単元:
#数学(中学生)#中1数学#中2数学#中3数学#正の数・負の数#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#2次方程式#比例・反比例#確率#2次関数#相似な図形#円#文字と式#平面図形#三角形と四角形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・死守96
①$7+2×(-6)$を計算せよ。
②$3(2a+b)-2(4a-5b)$を計算せよ。
③$\frac{14}{\sqrt2}-\sqrt32$を計算せよ。
④2次方程式$(x+6)(x-5)=9x-10$を解け。
⑤関数$y=\frac{1}{2}x^2$について、$x$の変域が$-4 \leqq x\leqq2$のとき、$y$の変域を求めよ。
⑥関数$y=\frac{ 6 }{ x }$のグラフをかけ。
⑦$△ABC$において、$\angle A=90°,AB=6cm,BC=10cm$のとき、辺$AC$の長さを求めよ。
⑧4枚の硬質A、B、C、Dを同時に投げるとき、少なくとも1枚は表が出る確率を求めよ。
ただし、表と裏が出ることは同様に確からしいとする。
⑨右図のように、円$0$の円周上に3点、$A,B,C$を$AB=AC$となるようにとり、$△ABC$をつくる。
線分$BO$を延長した直線と線分$AC$と交点を$D$とする。
$\angle BAC=48°$のとき$\angle ADB$の大きさを求めよ。
この動画を見る
高校受験対策・死守96
①$7+2×(-6)$を計算せよ。
②$3(2a+b)-2(4a-5b)$を計算せよ。
③$\frac{14}{\sqrt2}-\sqrt32$を計算せよ。
④2次方程式$(x+6)(x-5)=9x-10$を解け。
⑤関数$y=\frac{1}{2}x^2$について、$x$の変域が$-4 \leqq x\leqq2$のとき、$y$の変域を求めよ。
⑥関数$y=\frac{ 6 }{ x }$のグラフをかけ。
⑦$△ABC$において、$\angle A=90°,AB=6cm,BC=10cm$のとき、辺$AC$の長さを求めよ。
⑧4枚の硬質A、B、C、Dを同時に投げるとき、少なくとも1枚は表が出る確率を求めよ。
ただし、表と裏が出ることは同様に確からしいとする。
⑨右図のように、円$0$の円周上に3点、$A,B,C$を$AB=AC$となるようにとり、$△ABC$をつくる。
線分$BO$を延長した直線と線分$AC$と交点を$D$とする。
$\angle BAC=48°$のとき$\angle ADB$の大きさを求めよ。
【高校受験対策/数学】図形-43

単元:
#数学(中学生)#中3数学#相似な図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形43
Q.
$AB=10cm$、$AB<AD$の長方形$ABCD$を、
右の図1のように、折り目が点$C$を通り、点$B$が辺$AD$上にくるように折り返す。
点$B$が移った点を$E$とし、折り目を線分$CF$とすると、$AF=4cm$であった。
このとき、次の問いに答えなさい。
①$\triangle AEF \backsim \triangle DCE$であることを証明せよ。
②線分$AE$の長さを求めよ。
③右の図2のように、折り返した部分をもとにもどし、線分$CE$と線分$BD$との交点を$G$とする。
このとき、四角形$BGEF$の面積を求めよ。
この動画を見る
高校受験対策・図形43
Q.
$AB=10cm$、$AB<AD$の長方形$ABCD$を、
右の図1のように、折り目が点$C$を通り、点$B$が辺$AD$上にくるように折り返す。
点$B$が移った点を$E$とし、折り目を線分$CF$とすると、$AF=4cm$であった。
このとき、次の問いに答えなさい。
①$\triangle AEF \backsim \triangle DCE$であることを証明せよ。
②線分$AE$の長さを求めよ。
③右の図2のように、折り返した部分をもとにもどし、線分$CE$と線分$BD$との交点を$G$とする。
このとき、四角形$BGEF$の面積を求めよ。
【高校受験対策/数学】図形-41

単元:
#数学(中学生)#中3数学#相似な図形
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
高校受験対策・図形41
Q.
右の図において、点$A,B,C,D$は円$O$の周上にあり、点$E$は直線$AB$上の点で、$AD /\!/ EC$である。
このとき次の各問に答えなさい。
①三角形$AEC$と三角形$DCB$が相似であることを証明しなさい。
②$AE=4cm$、$BC=5cm$、$EC=6cm$、$\angle ACD=\angle CBD$とする。
直線$AB$と直線$CD$の交点を$F$としたとき、$FD$の長さを求めなさい。
この動画を見る
高校受験対策・図形41
Q.
右の図において、点$A,B,C,D$は円$O$の周上にあり、点$E$は直線$AB$上の点で、$AD /\!/ EC$である。
このとき次の各問に答えなさい。
①三角形$AEC$と三角形$DCB$が相似であることを証明しなさい。
②$AE=4cm$、$BC=5cm$、$EC=6cm$、$\angle ACD=\angle CBD$とする。
直線$AB$と直線$CD$の交点を$F$としたとき、$FD$の長さを求めなさい。
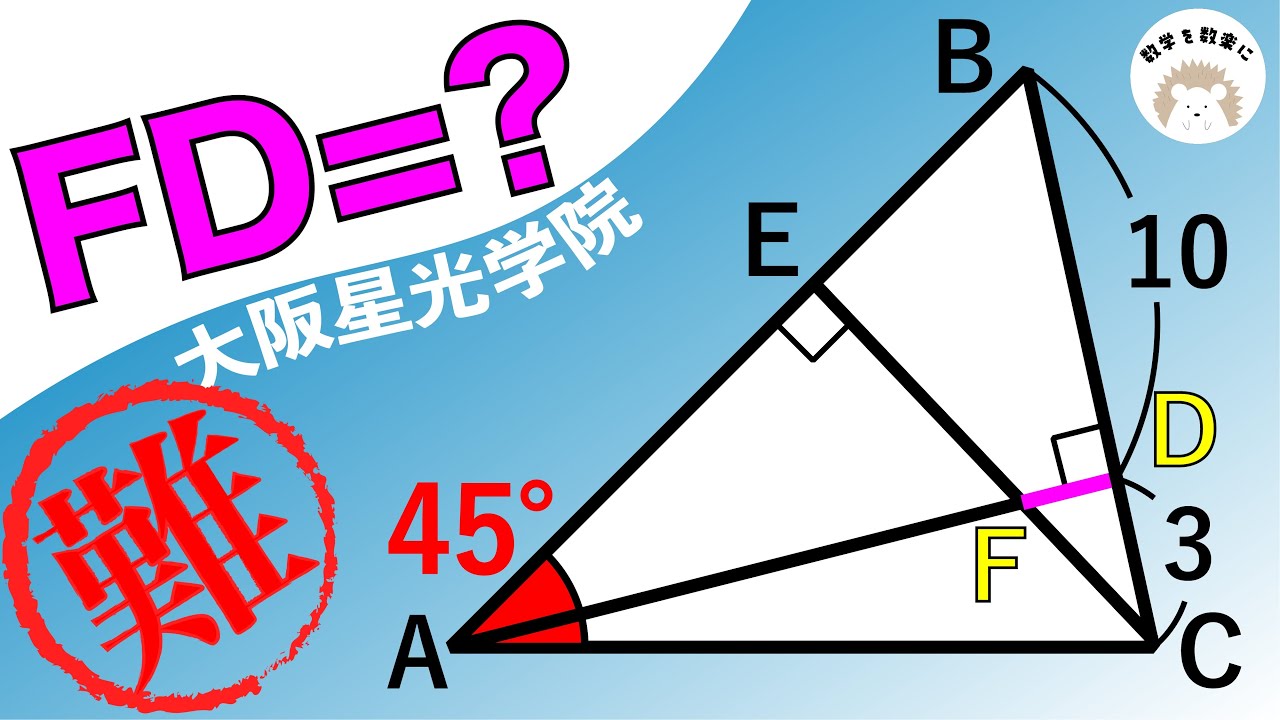
相似より〇〇を見つける方が難しい 大阪星光学院(改)
単元:
#数学(中学生)#中2数学#中3数学#相似な図形#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
FD=?
*図は動画内参照
大阪星光学院高等学校
この動画を見る
FD=?
*図は動画内参照
大阪星光学院高等学校
【中学数学】相似の問題演習~一緒に解いて考え方を身に付けよう~【中3数学】
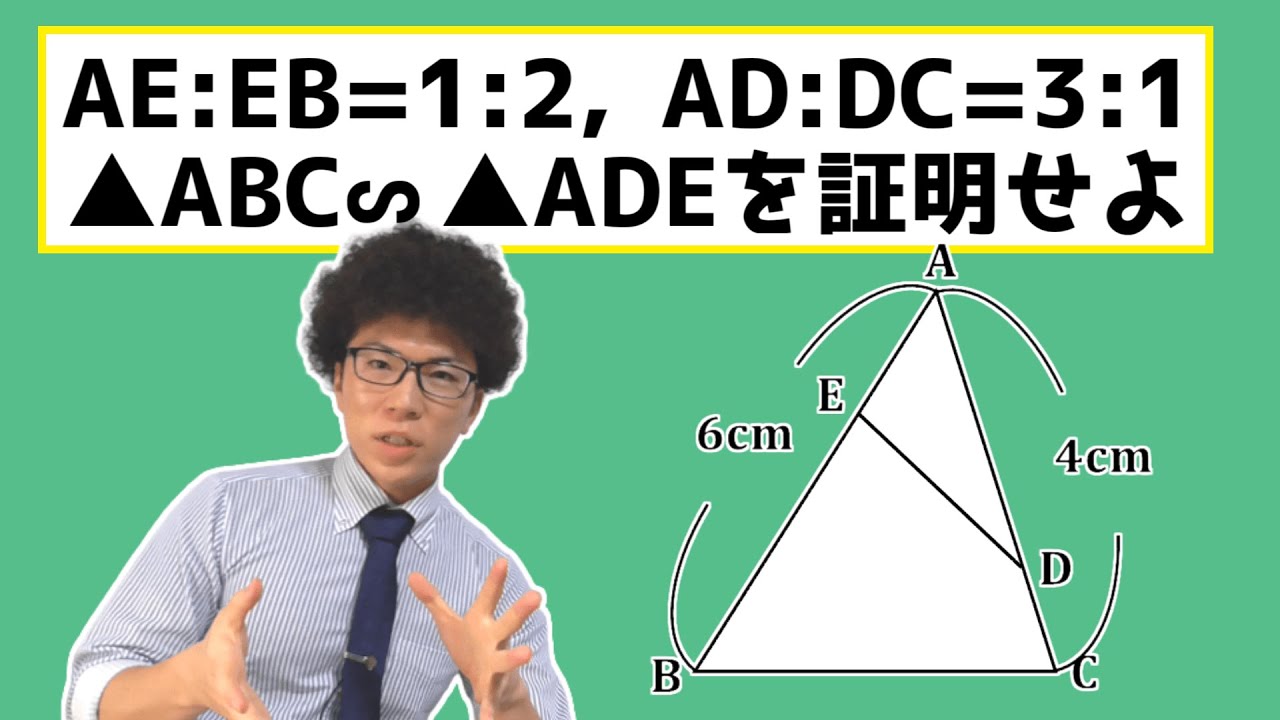
【中学数学】相似の証明が誰でもできるようになる動画 5-2【中3数学】

【数学】相似な図形:相似の考え方!