相似な図形
相似な図形
相似より〇〇を見つける方が難しい 大阪星光学院（改）
単元：
#数学(中学生)#中２数学#中３数学#相似な図形#三角形と四角形#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
FD=?
＊図は動画内参照
大阪星光学院高等学校
この動画を見る
FD=?
＊図は動画内参照
大阪星光学院高等学校
【中学数学】相似の問題演習～一緒に解いて考え方を身に付けよう～【中３数学】
【中学数学】相似の証明が誰でもできるようになる動画 5-2【中３数学】
【数学】相似な図形：相似の考え方！
【高校受験対策/数学】図形40
単元：
#数学(中学生)#中３数学#相似な図形
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・図形40
図1のように、点$O$を中心とし線分$AB$を直径とする 半径$3cm$の半円がある。
$\stackrel{\huge\frown}{AB}$上に2点$P,Q$があり、$A$に近い方を$P$、$B$に近い方を$Q$とする。
また、線分$BP$と線分$OQ$の交点を$R$とし、線分$AQ$と線分$BP$の交点を$S$とする。
このとき、次の問いに答えなさい。
①$\triangle RQC \backsim \triangle RPQ$を証明しなさい。
②図2のように、$\angle QOC=90°$、$OS /\!/ BQ$となるとき、線分$BR$の長さを求めなさい。
この動画を見る
高校受験対策・図形40
図1のように、点$O$を中心とし線分$AB$を直径とする 半径$3cm$の半円がある。
$\stackrel{\huge\frown}{AB}$上に2点$P,Q$があり、$A$に近い方を$P$、$B$に近い方を$Q$とする。
また、線分$BP$と線分$OQ$の交点を$R$とし、線分$AQ$と線分$BP$の交点を$S$とする。
このとき、次の問いに答えなさい。
①$\triangle RQC \backsim \triangle RPQ$を証明しなさい。
②図2のように、$\angle QOC=90°$、$OS /\!/ BQ$となるとき、線分$BR$の長さを求めなさい。
台形の相似 気づけば一瞬！！（高校入試 数学）
単元：
#数学(中学生)#中２数学#中３数学#相似な図形#三角形と四角形#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
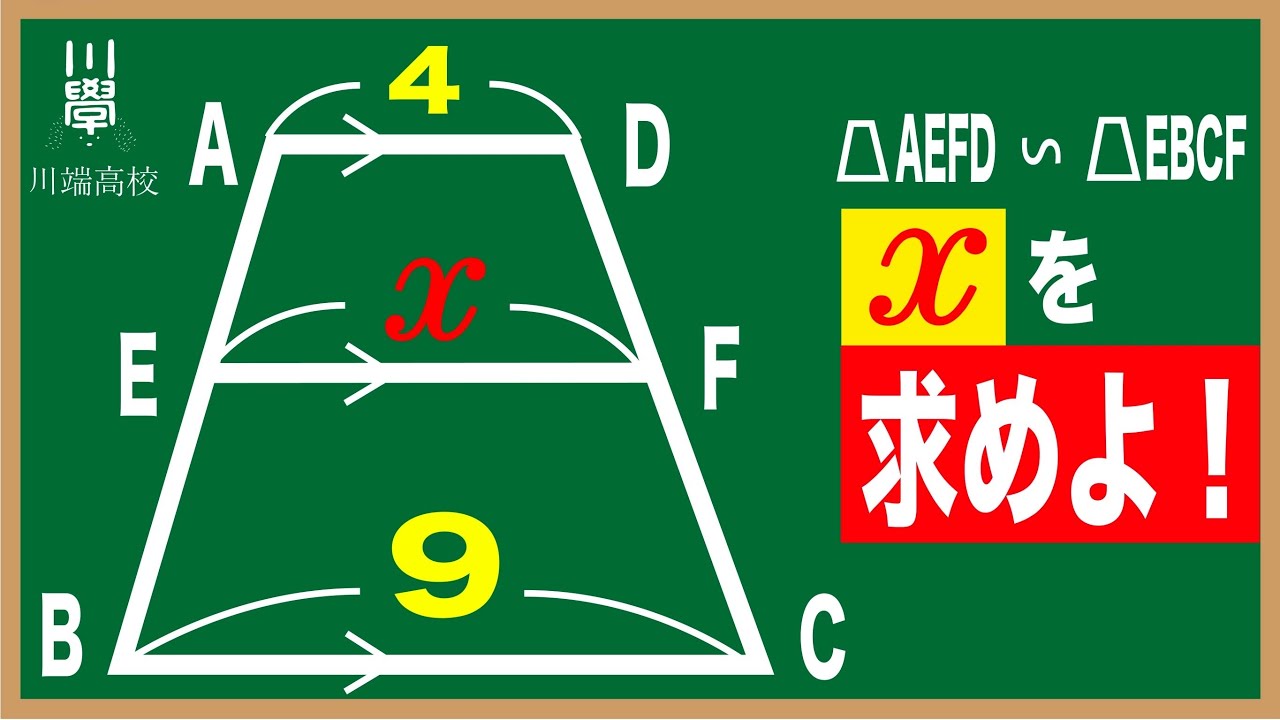
台形AEFD∽台形EBCF
x=?
＊図は動画内参照
川端高校
この動画を見る
台形AEFD∽台形EBCF
x=?
＊図は動画内参照
川端高校
【思考力を高める5分間！一度は解きたい！】図形：日本大学習志野高等学校～全国入試問題解法
単元：
#数学(中学生)#中１数学#中２数学#相似な図形#平面図形#高校入試過去問(数学)#日本大学習志野高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
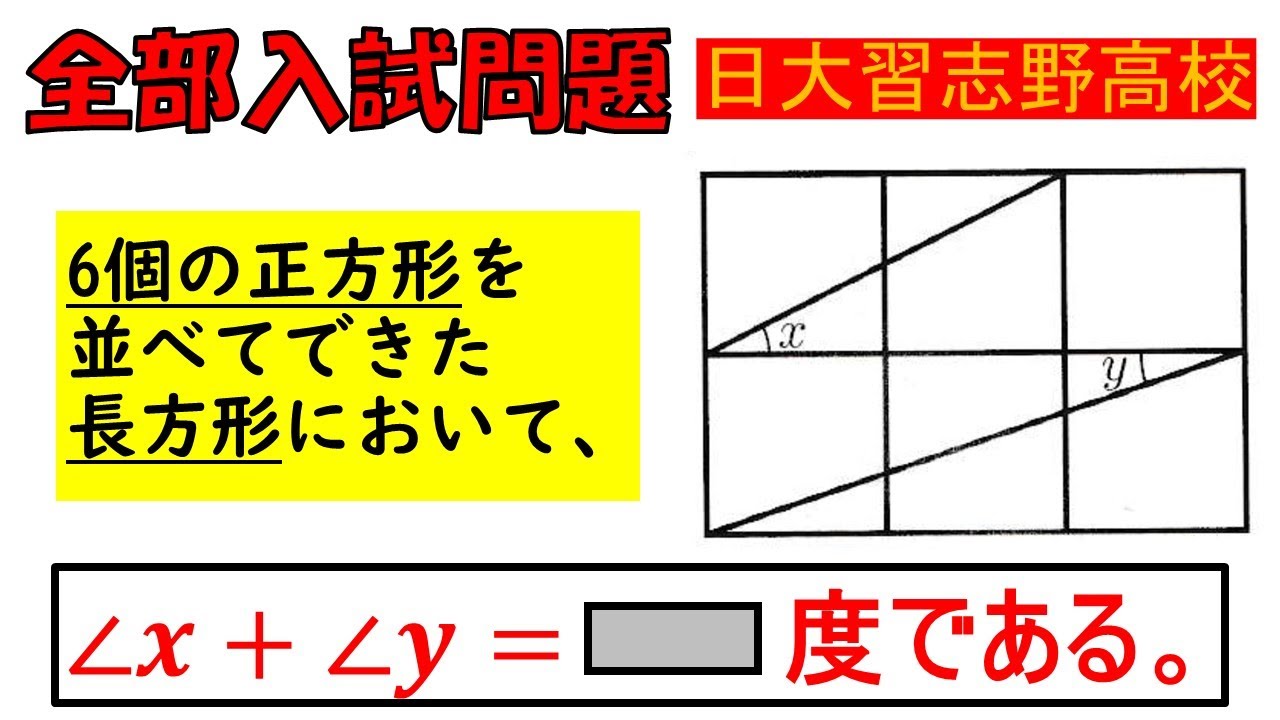
入試問題 日本大学習志野高等学校
6個の正方形を 並べてできた 長方形において、
$\angle x+ \angle y=$▬度である。
四角部分の角度を求めよ。
※図は動画内参照
この動画を見る
入試問題 日本大学習志野高等学校
6個の正方形を 並べてできた 長方形において、
$\angle x+ \angle y=$▬度である。
四角部分の角度を求めよ。
※図は動画内参照
【3分で証明問題の理解を深める！】図形：熊本県～全国入試問題解法
単元：
#数学(中学生)#中３数学#相似な図形#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
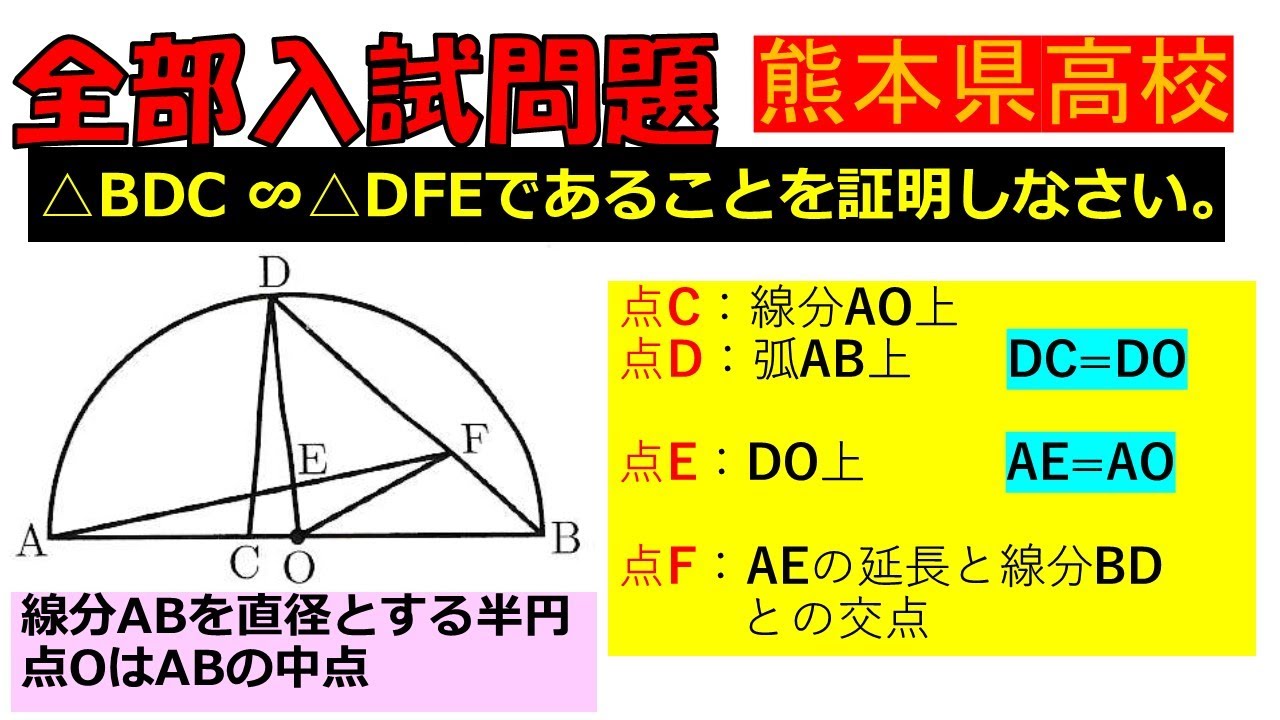
入試問題 熊本県の公立高校
$\triangle BDC ∞ \triangle DFE$であることを証明しなさい。
点C:線分AO上
点D:弧AB上
DC=DO
点E:DO上
ΑΕ=ΑΟ
点F: AEの延長と線分BD との交点
【線分ABを直径とする半円点○はABの中点】
※図は動画内参照
この動画を見る
入試問題 熊本県の公立高校
$\triangle BDC ∞ \triangle DFE$であることを証明しなさい。
点C:線分AO上
点D:弧AB上
DC=DO
点E:DO上
ΑΕ=ΑΟ
点F: AEの延長と線分BD との交点
【線分ABを直径とする半円点○はABの中点】
※図は動画内参照
相似の典型問題！！
本日の一問「図形の性質の証明」【中3数学テスト対策】
単元：
#数学(中学生)#中１数学#中３数学#数A#図形の性質#空間図形#相似な図形#整数の性質#平面図形
指導講師：
いつもの先生
問題文全文(内容文)：
右の図のように、
1辺がPの長さの正方形の池のまわりに、
幅aの道がついている。
この道の面積をS.、道の真ん中を
通る線の長さを$\ell$とすると、
$S=a\ell$となることを証明せよ。
＊図は動画内参照
この動画を見る
右の図のように、
1辺がPの長さの正方形の池のまわりに、
幅aの道がついている。
この道の面積をS.、道の真ん中を
通る線の長さを$\ell$とすると、
$S=a\ell$となることを証明せよ。
＊図は動画内参照
99%の人が間違える三角形の面積を求めよ
「図形のセンス」を身につけよう！
三平方の定理❓相似❓B
パックマン
相似の証明 面積比 B 2021 埼玉県
単元：
#数学(中学生)#中３数学#相似な図形#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
△ADH∽△ACFを示せ
△ABC=18のとき△GFC=?
＊図は動画内参照
2021埼玉県
この動画を見る
△ADH∽△ACFを示せ
△ABC=18のとき△GFC=?
＊図は動画内参照
2021埼玉県
証明：沖縄県高校入試～全国入試問題解法
単元：
#数学(中学生)#平行と合同#相似な図形#平面図形#高校入試過去問(数学)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
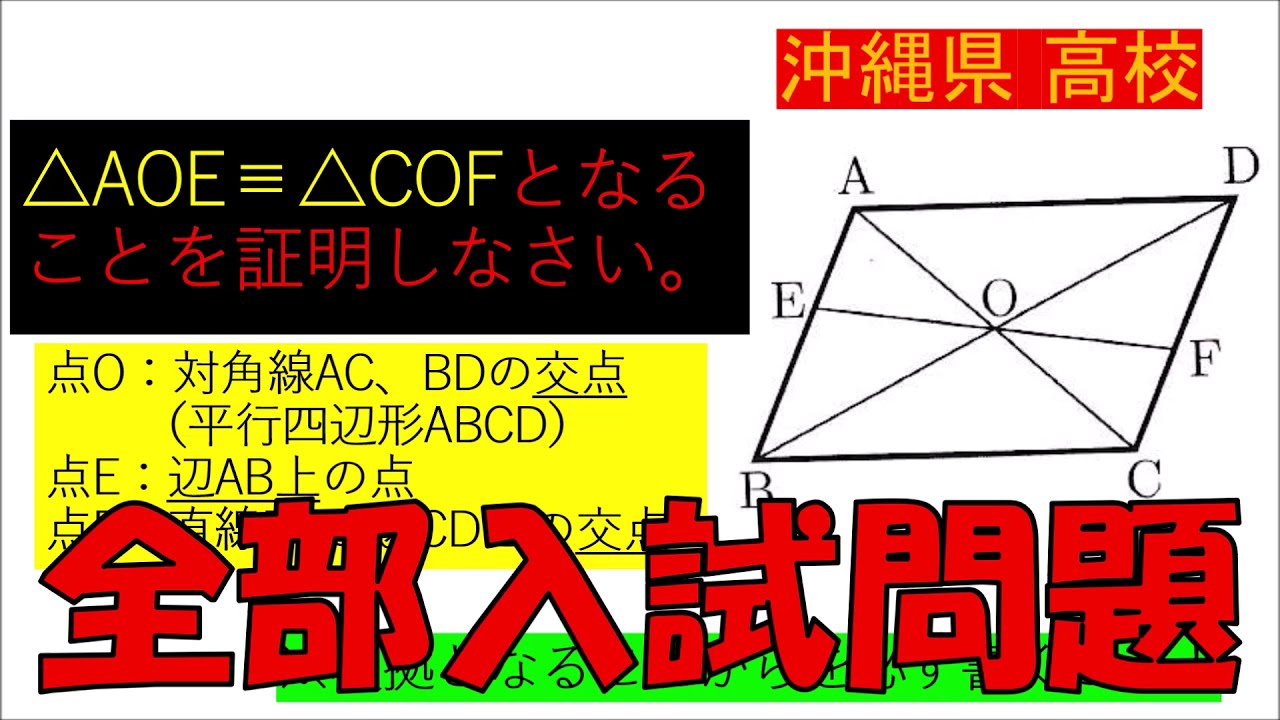
入試問題 沖縄県の高校
$\triangle AOE \equiv \triangle COF$となる
ことを証明しなさい。
点O:対角線$AC$、$BD$の交点 (平行四辺形$ABCD$)
点E:辺$AB$上の点
点F:直線$EO$と辺$CD$との交点
※根拠となることがらを必ず書くこと！
※図は動画内参照
この動画を見る
入試問題 沖縄県の高校
$\triangle AOE \equiv \triangle COF$となる
ことを証明しなさい。
点O:対角線$AC$、$BD$の交点 (平行四辺形$ABCD$)
点E:辺$AB$上の点
点F:直線$EO$と辺$CD$との交点
※根拠となることがらを必ず書くこと！
※図は動画内参照
相似な図形の面積比 A 専大松戸
単元：
#数学(中学生)#中２数学#中３数学#相似な図形#三角形と四角形#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
四角形EBCGの面積=?
＊図は動画内参照
2021専修大学松戸高等学校
この動画を見る
四角形EBCGの面積=?
＊図は動画内参照
2021専修大学松戸高等学校
秋田県 2021 相似and三平方 A
単元：
#数学(中学生)#中３数学#相似な図形#三平方の定理#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
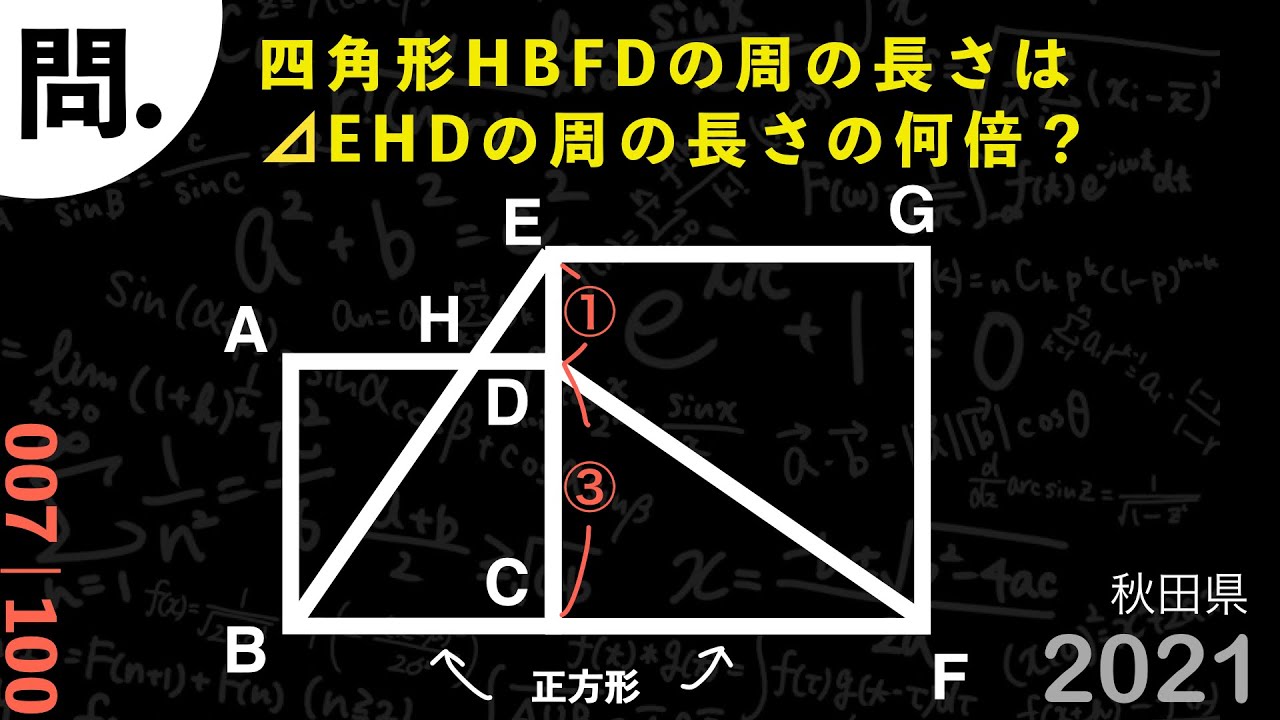
四角形HBFDの周の長さは△EHDの周の長さの何倍？
＊図は動画内参照
2021秋田県
この動画を見る
四角形HBFDの周の長さは△EHDの周の長さの何倍？
＊図は動画内参照
2021秋田県
【中学数学】三角形の合同・相似の部分点の取り方～最後の悪あがき～
単元：
#数学(中学生)#中２数学#中３数学#平行と合同#相似な図形#高校入試過去問(数学)#大阪府公立高等学校#北海道公立高等学校
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
三角形の合同・相似の部分点の取り方についての説明動画です
この動画を見る
三角形の合同・相似の部分点の取り方についての説明動画です
受験生必見！！円と相似
単元：
#数学(中学生)#中３数学#数A#図形の性質#相似な図形#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#方べきの定理と２つの円の関係#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
円と相似まとめ
＊図は動画内参照
この動画を見る
円と相似まとめ
＊図は動画内参照
【中学数学】平面図形の演習・証明～山口県公立高校入試2019年度～【高校数学】
単元：
#数学(中学生)#中３数学#相似な図形#円
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
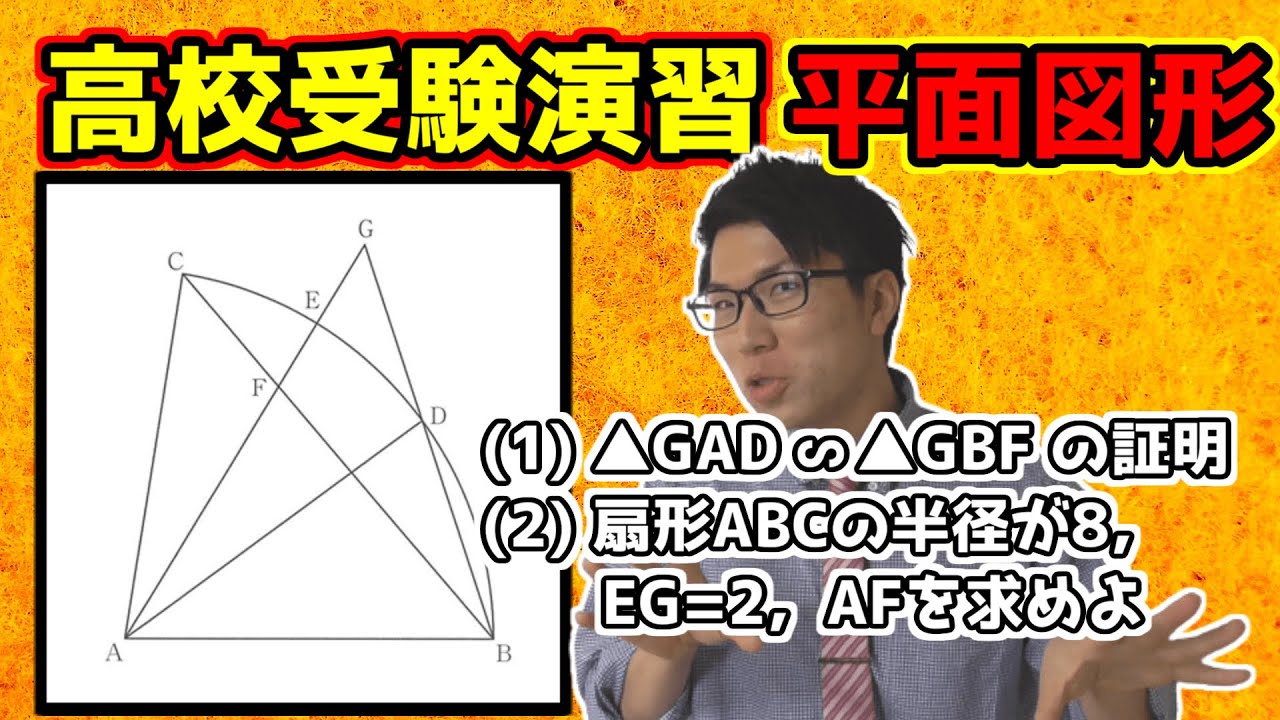
動画内図のような、扇形のABCがあり、$\stackrel{\huge\frown}{BC}$上に点Dをとり、$\stackrel{\huge\frown}{DC}$上に点Eを、$\stackrel{\huge\frown}{DE} = \stackrel{\huge\frown}{EC}$なるようにとる。
また、線分AEと線分BCの交点をF、線分AEの延長と線分BDの延長の交点をGとする。
(1) $\triangle GAD \sim \triangle GBF$を証明せよ。
(2) 扇形ABCの半径が8cm、線分EGの長さが2cmであるとき、線分AFの長さを求めよ。
この動画を見る
動画内図のような、扇形のABCがあり、$\stackrel{\huge\frown}{BC}$上に点Dをとり、$\stackrel{\huge\frown}{DC}$上に点Eを、$\stackrel{\huge\frown}{DE} = \stackrel{\huge\frown}{EC}$なるようにとる。
また、線分AEと線分BCの交点をF、線分AEの延長と線分BDの延長の交点をGとする。
(1) $\triangle GAD \sim \triangle GBF$を証明せよ。
(2) 扇形ABCの半径が8cm、線分EGの長さが2cmであるとき、線分AFの長さを求めよ。
相似 三平方の定理 芝浦工大柏
単元：
#数学(中学生)#中３数学#相似な図形#三平方の定理#高校入試過去問(数学)
指導講師：
数学を数楽に
問題文全文(内容文)：
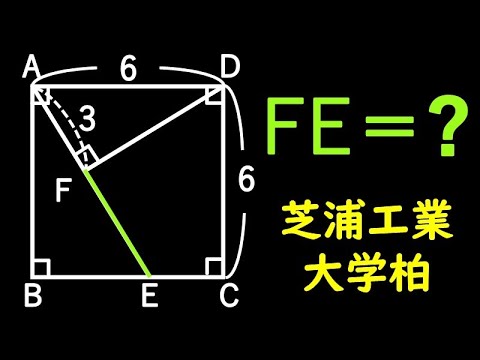
四角形ABCDは正方形
EF=?
＊図は動画内参照
芝浦工業大学柏高等学校
この動画を見る
四角形ABCDは正方形
EF=?
＊図は動画内参照
芝浦工業大学柏高等学校
【高校受験対策/数学/図形33】円と相似
単元：
#数学(中学生)#中３数学#相似な図形#円
指導講師：
とある男が授業をしてみた
問題文全文(内容文)：
高校受験対策・図形33
Q
右の図のように、線分ABを直径とする円$O$がある。
円$O$の周上に点$C$をとり、$BC \lt AC$である三角形$ABC$をつくる。
三角形$ACD$が$AC=AD$の直角二等辺三角形となるような点$D$をとり、辺$CD$と直径$AB$の交点を$E$とする。
また、点$D$から直径$AB$に垂線をひき、直径$AB$との交点を$F$とする。
このとき次の各問いに答えなさい。
①$\triangle ABC \backsim \triangle DAF$を証明せよ。
②$AB=10cm$、$BC=6cm$、$CA=8cm$とするとき、線分$FE$の長さを求めよ。
この動画を見る
高校受験対策・図形33
Q
右の図のように、線分ABを直径とする円$O$がある。
円$O$の周上に点$C$をとり、$BC \lt AC$である三角形$ABC$をつくる。
三角形$ACD$が$AC=AD$の直角二等辺三角形となるような点$D$をとり、辺$CD$と直径$AB$の交点を$E$とする。
また、点$D$から直径$AB$に垂線をひき、直径$AB$との交点を$F$とする。
このとき次の各問いに答えなさい。
①$\triangle ABC \backsim \triangle DAF$を証明せよ。
②$AB=10cm$、$BC=6cm$、$CA=8cm$とするとき、線分$FE$の長さを求めよ。
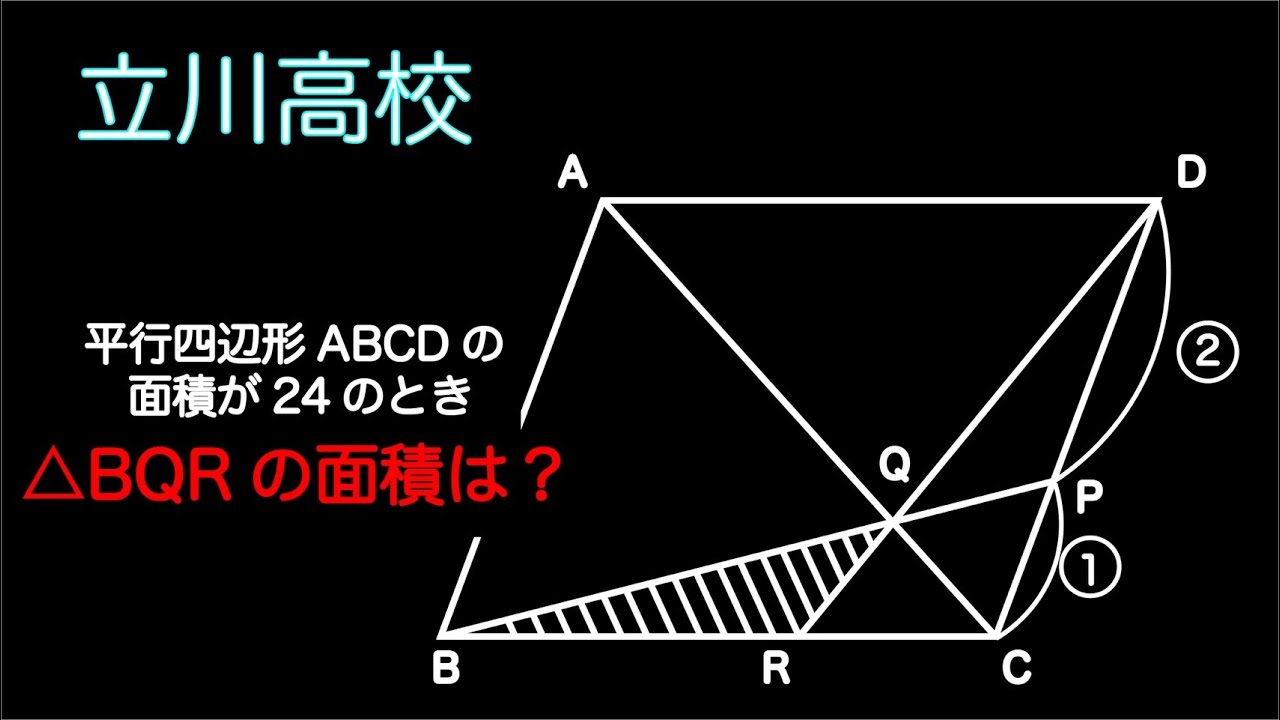
面積比！！
単元：
#数学(中学生)#中３数学#相似な図形#高校入試過去問(数学)#東京都立立川高等学校
指導講師：
数学を数楽に
問題文全文(内容文)：
動画内の図の斜線部分の面積を求めよ
出典：2004年都立立川高校
この動画を見る
動画内の図の斜線部分の面積を求めよ
出典：2004年都立立川高校
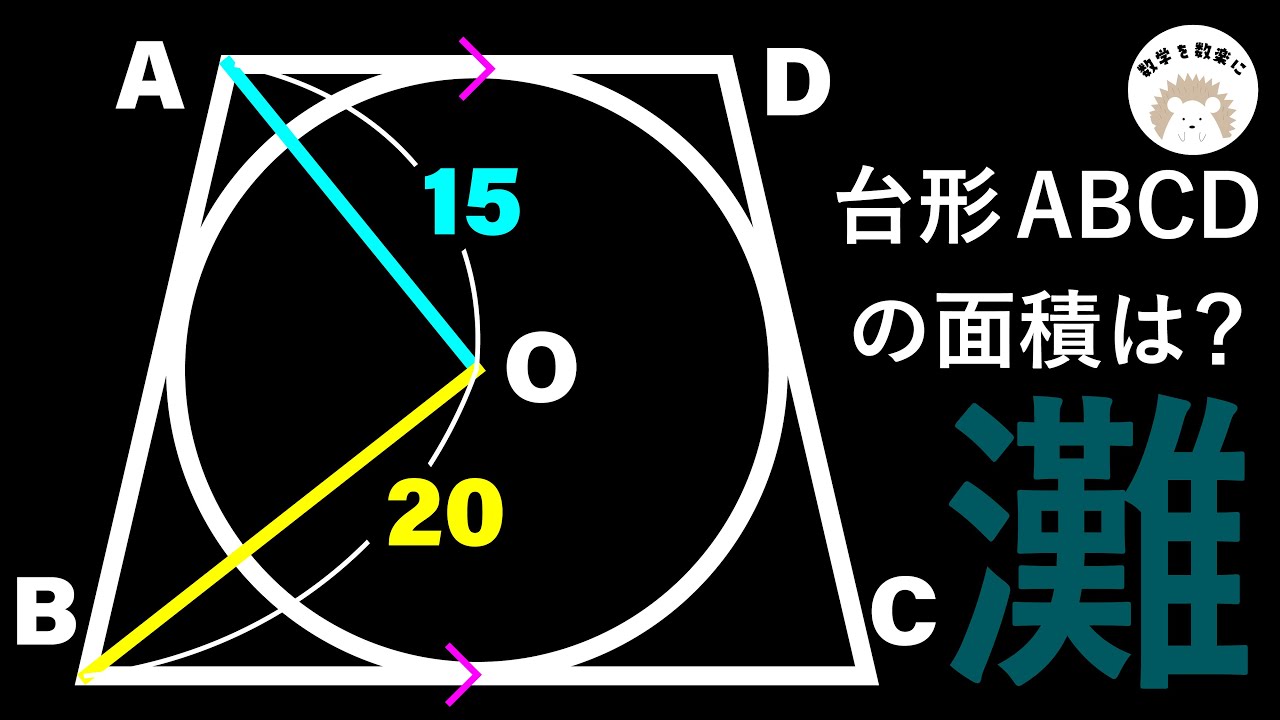
円と台形 灘高校の小問
単元：
#数学(中学生)#中３数学#相似な図形#高校入試過去問(数学)#灘高等学校
指導講師：
数学を数楽に
問題文全文(内容文)：
円と台形からできる相似
台形$\textrm{ABCD}$の面積を求めよ。
出典：2012年灘高等学校
この動画を見る
円と台形からできる相似
台形$\textrm{ABCD}$の面積を求めよ。
出典：2012年灘高等学校
蝶ネクタイの左と右が等しいとき
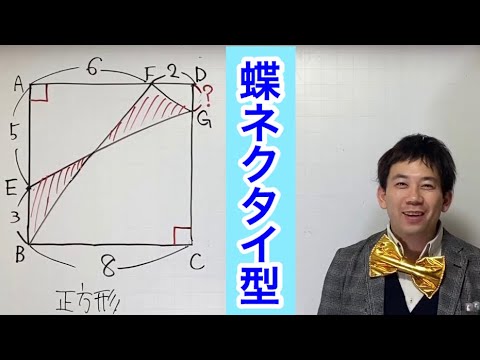
角度を求める！（都立西2005 2006）
正五角形の対角線の長さ（高校入試数学、大学入試数学）
直角三角形の垂線の長さ（高校受験数学）
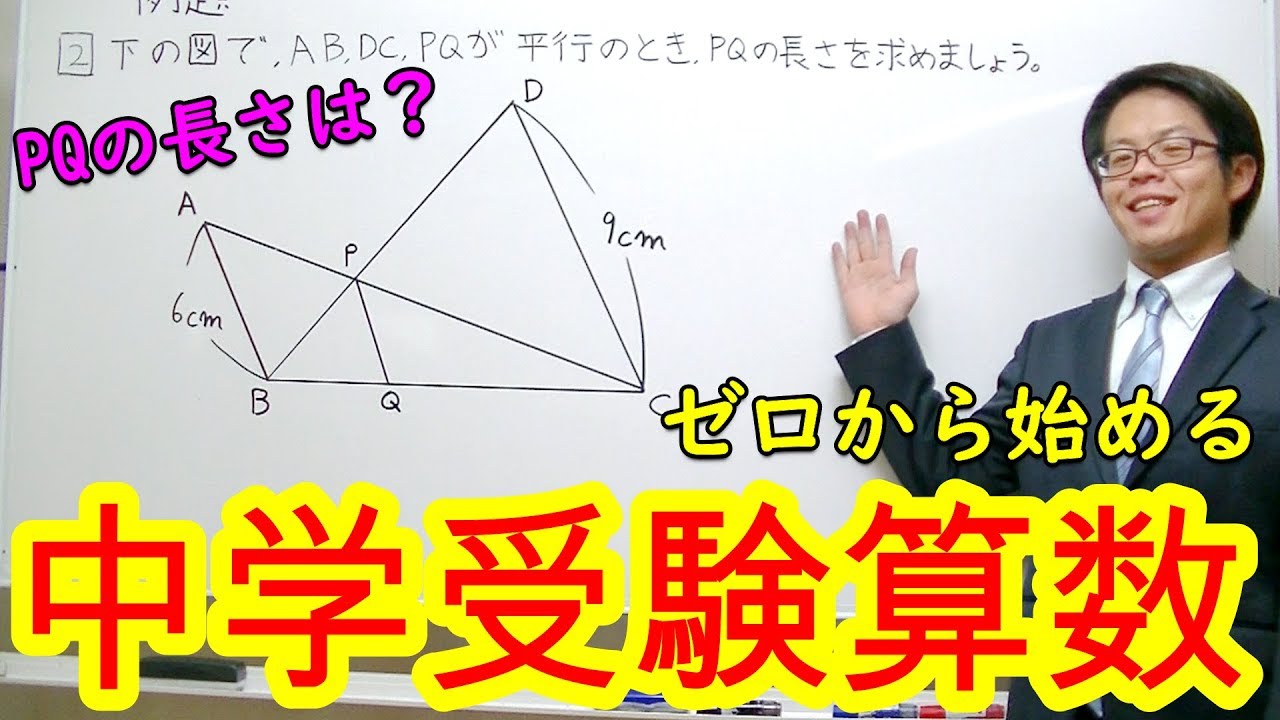
【中学受験算数】ピラミッド相似、リボン相似、色々な相似問題はこう解け！ ゼロから始める中学受験算数４１
単元：
#算数(中学受験)#数学(中学生)#中３数学#相似な図形#平面図形#相似と相似を利用した問題
指導講師：
こばちゃん塾
問題文全文(内容文)：
1⃣下の図で、BCとDEが平行のとき、XYの値を求めましょう。
2⃣下の図で、AB、DC、PQが平行のとき、PQの長さを求めましょう。
＊図は動画内参照
この動画を見る
1⃣下の図で、BCとDEが平行のとき、XYの値を求めましょう。
2⃣下の図で、AB、DC、PQが平行のとき、PQの長さを求めましょう。
＊図は動画内参照