 中3数学
中3数学
 中3数学
中3数学
2023高校入試数学解説84問目 一次関数と二次関数 埼玉県学校選択問題
単元:
#数学(中学生)#中2数学#中3数学#1次関数#2次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$y=ax^2$
$y=bx+c$
a,b,c大小関係を不等号で表せ
*図は動画内参照
2023埼玉県
この動画を見る
$y=ax^2$
$y=bx+c$
a,b,c大小関係を不等号で表せ
*図は動画内参照
2023埼玉県
2023高校入試数学解説83問目 球の切り口の面積は? 埼玉県
高等学校入学試験予想問題:秋田県公立高等学校~全部入試問題
単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#2次方程式#空間図形#相似な図形#文章題#文章題その他#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$\dfrac{15}{2}\times \left(-\dfrac{4}{5}\right)$
(2)$ 10a-(6a+8)$
(3)$ 27ab^2\div 9ab $
(4)二次方程式$ x^2-3x+1=0$を解け.
$ \boxed{2}$
(1)底面が1辺6cmの正方形,体積$ 96cm^3$の四角錐の高さは?
(2)$ 4 \lt \sqrt a \lt \dfrac{13}{3}$に当てはまるaの値をすべて求めよ.
(3)$ \ell \parallel m $のとき,$ \angle x $は?
$ \boxed{3}$
n番目の白タイルの枚数をnの式で表せ.
この動画を見る
$ \boxed{1}$
(1)$\dfrac{15}{2}\times \left(-\dfrac{4}{5}\right)$
(2)$ 10a-(6a+8)$
(3)$ 27ab^2\div 9ab $
(4)二次方程式$ x^2-3x+1=0$を解け.
$ \boxed{2}$
(1)底面が1辺6cmの正方形,体積$ 96cm^3$の四角錐の高さは?
(2)$ 4 \lt \sqrt a \lt \dfrac{13}{3}$に当てはまるaの値をすべて求めよ.
(3)$ \ell \parallel m $のとき,$ \angle x $は?
$ \boxed{3}$
n番目の白タイルの枚数をnの式で表せ.
2023高校入試数学解説81問目 二次関数の変域 埼玉県

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$y=2x^2$において
xの変域は$a \leqq x \leqq 1$
yの変域は$0 \leqq y \leqq 18$
aの値を求めよ
2023埼玉県
この動画を見る
$y=2x^2$において
xの変域は$a \leqq x \leqq 1$
yの変域は$0 \leqq y \leqq 18$
aの値を求めよ
2023埼玉県
2023高校入試数学解説80問目 標本調査と全数調査 埼玉県

単元:
#数学(中学生)#中3数学#標本調査#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
標本調査で行われるものを2つ選べ
ア.ある河川の水質調査
イ.ある学校でおこなう健康診断
ウ.テレビ番組の視聴率調査
エ.日本の人口を調べる国勢調査
2023埼玉県
この動画を見る
標本調査で行われるものを2つ選べ
ア.ある河川の水質調査
イ.ある学校でおこなう健康診断
ウ.テレビ番組の視聴率調査
エ.日本の人口を調べる国勢調査
2023埼玉県
佐賀県立高校入試2021年5⃣(1)~(3)「相似」
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
佐賀県立高校入試2021年5⃣(1)~(3)「相似」
-----------------
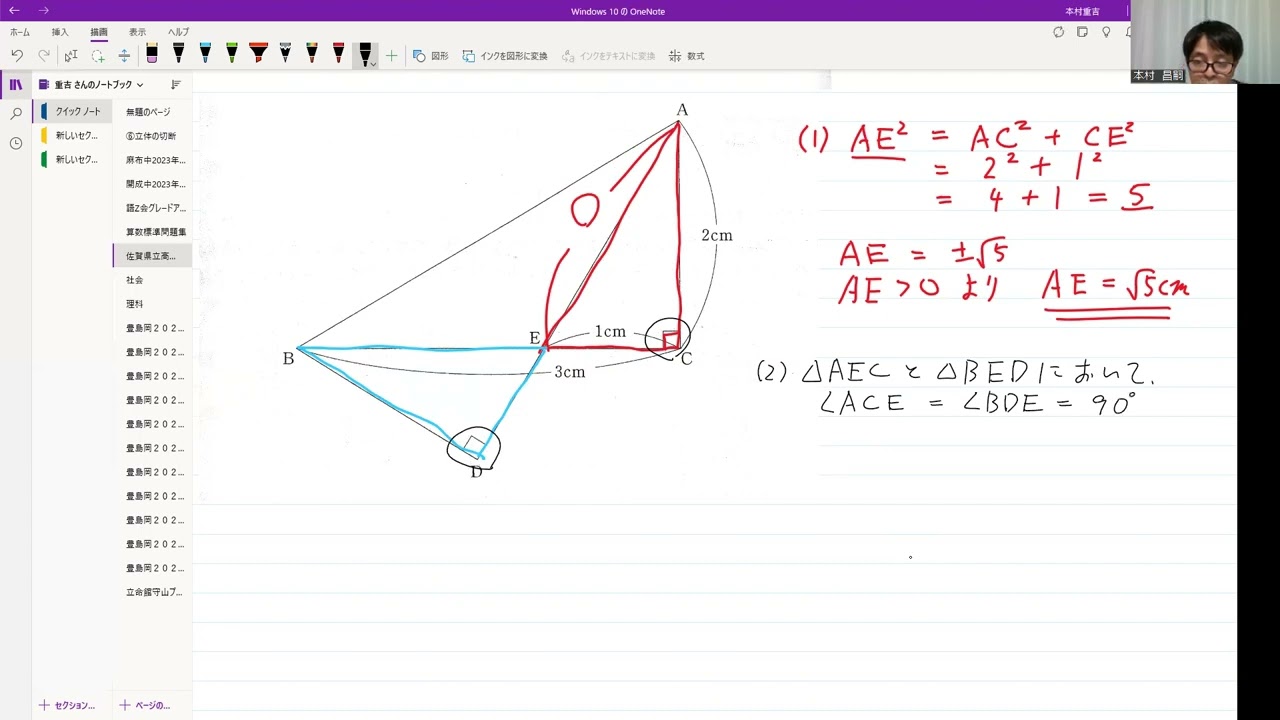
動画内の図のように、ABを斜辺とする2つの直角三角形ABCとABDがあり、辺BCとADの交点をEとする。
また、AC=2cm、BC=3cm、CE=1cmとする。
(1)線分AEの長さを求めなさい。
(2)△ABC$\sim$△BEDであることを証明しなさい。
(3)△ABEの面積を求めなさい。
この動画を見る
佐賀県立高校入試2021年5⃣(1)~(3)「相似」
-----------------
動画内の図のように、ABを斜辺とする2つの直角三角形ABCとABDがあり、辺BCとADの交点をEとする。
また、AC=2cm、BC=3cm、CE=1cmとする。
(1)線分AEの長さを求めなさい。
(2)△ABC$\sim$△BEDであることを証明しなさい。
(3)△ABEの面積を求めなさい。
2023高校入試数学解説77問目 円周角 愛知県
【たったこれだけの条件で…!】図形:広島大学附属高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#円#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
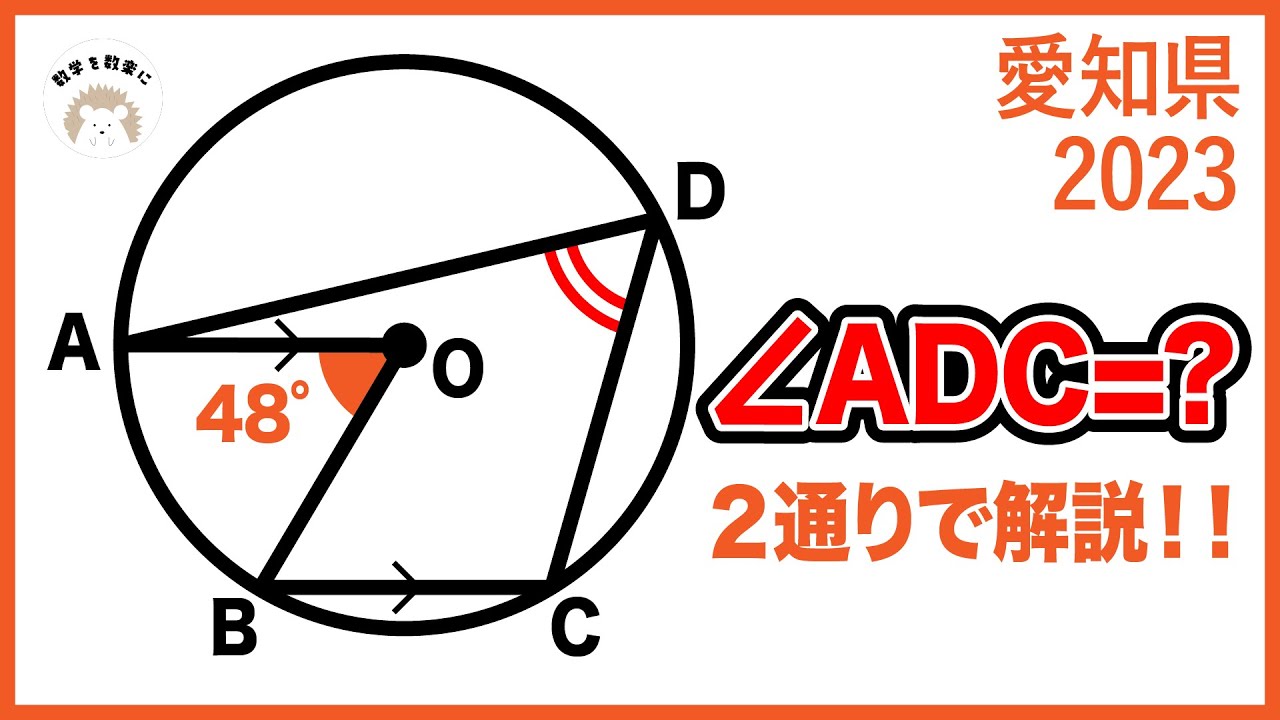
点A,C,Dは円O上の点である.
円の中心Oおよび点Dは線分BC上の点である.
$ \angle AOC=68°$のとき,$ \angle ABC $の大きさを求めよ.
広大付属高校過去問
この動画を見る
点A,C,Dは円O上の点である.
円の中心Oおよび点Dは線分BC上の点である.
$ \angle AOC=68°$のとき,$ \angle ABC $の大きさを求めよ.
広大付属高校過去問
佐賀県立高校入試2021年4⃣(5)「二次関数、一次関数」
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
佐賀県立高校入試2021年4⃣(5)「二次関数、一次関数」
-----------------
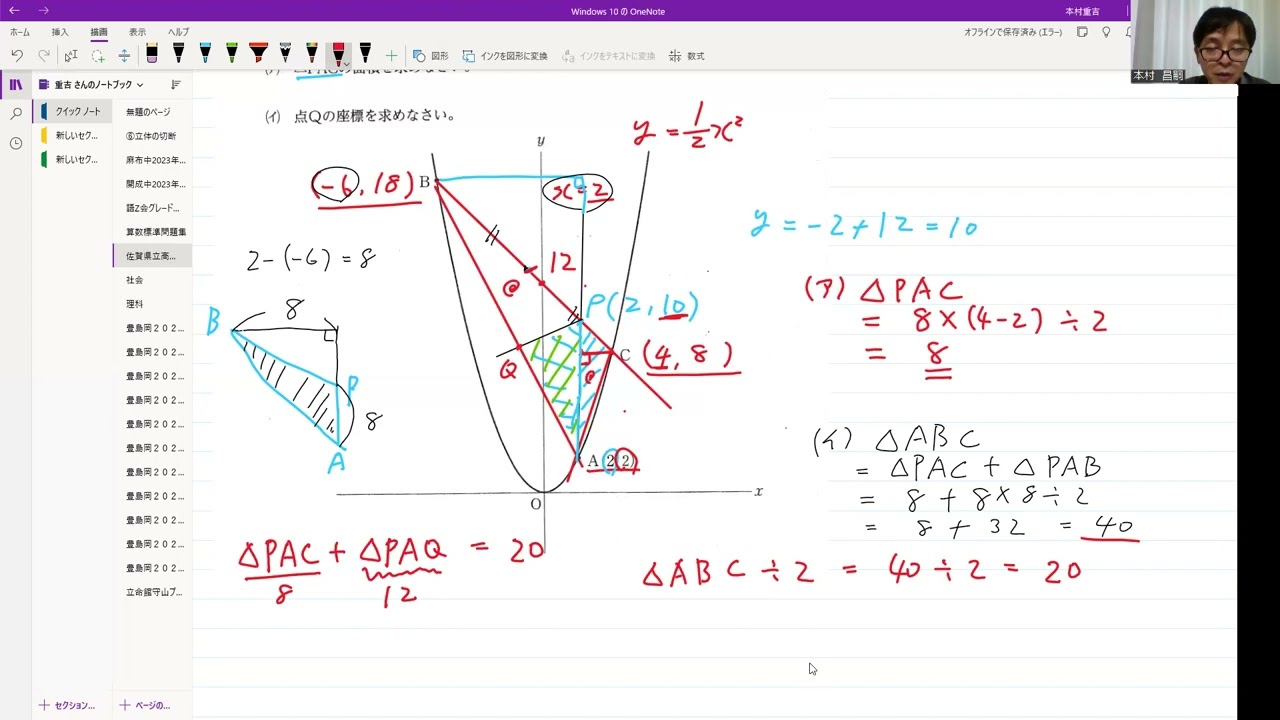
動画内の図のように、関数 $y = ax^2$のグラフ上に3点A、B、Cがある。
点の座標は A(2, 2) 、点Bのx座標は-6、点Cのx座標は4である。
点Aを通りy軸に平行な直線と、2点B、Cを通る直線との交点をPとする。
また、点Pを通り△ABCの面積を2等分する直線と、2点A、Bを通る直線との交点をQとする。
このとき(ア)、(イ)の問いに答えなさい。
(ア) △PACの面積を求めなさい。
(イ) 点Qの座標を求めなさい。
この動画を見る
佐賀県立高校入試2021年4⃣(5)「二次関数、一次関数」
-----------------
動画内の図のように、関数 $y = ax^2$のグラフ上に3点A、B、Cがある。
点の座標は A(2, 2) 、点Bのx座標は-6、点Cのx座標は4である。
点Aを通りy軸に平行な直線と、2点B、Cを通る直線との交点をPとする。
また、点Pを通り△ABCの面積を2等分する直線と、2点A、Bを通る直線との交点をQとする。
このとき(ア)、(イ)の問いに答えなさい。
(ア) △PACの面積を求めなさい。
(イ) 点Qの座標を求めなさい。
2023高校入試数学解説71問目 2次関数の変域 千葉県

単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$y= \frac{1}{3}x^2$において
xの変域は$-3 \leqq x \leqq a$
yの変域は$0 \leqq y \leqq 3$
整数aの値をすべて求めよ
2023千葉県
この動画を見る
$y= \frac{1}{3}x^2$において
xの変域は$-3 \leqq x \leqq a$
yの変域は$0 \leqq y \leqq 3$
整数aの値をすべて求めよ
2023千葉県
2023高校入試数学解説65問目 気付けば一瞬!!座標平面上の円 城北高校 (再)
単元:
#数学(中学生)#中3数学#円#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
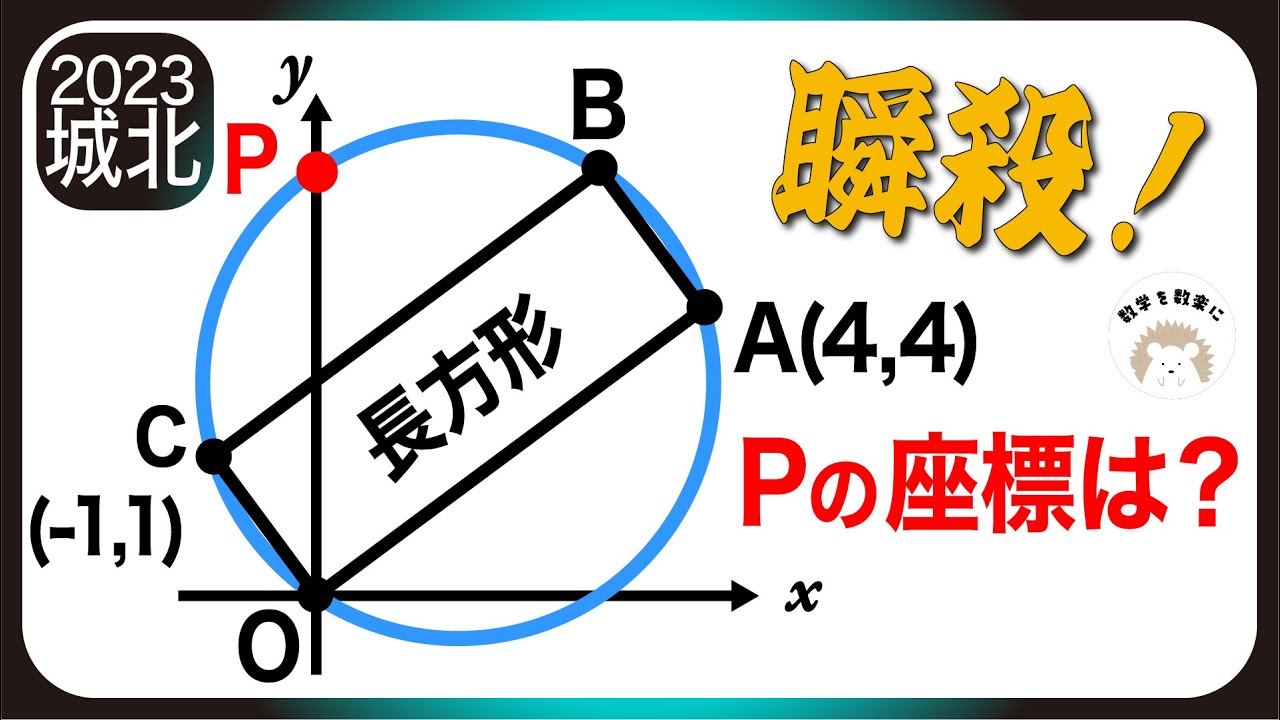
四角形OCBAは長方形
Pの座標は?
*図は動画内参照
2023城北学園高等学校
この動画を見る
四角形OCBAは長方形
Pの座標は?
*図は動画内参照
2023城北学園高等学校
2023高校入試数学解説66問目 式の値 千葉県

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x= \sqrt 3 + 2 , y= \sqrt 3 -2$
$5x^2 -5y^2 = ?$
2023千葉県
この動画を見る
$x= \sqrt 3 + 2 , y= \sqrt 3 -2$
$5x^2 -5y^2 = ?$
2023千葉県
高等学校入学試験予想問題:鳥取県公立高等学校~全部入試問題
単元:
#数学(中学生)#中1数学#中2数学#中3数学#方程式#式の計算(単項式・多項式・式の四則計算)#連立方程式#式の計算(展開、因数分解)#2次方程式#数Ⅰ#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#平面図形#三角形と四角形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$ 10xy^2\div(-5y)\times 3x$
(2)$ 2x-y-\dfrac{5x+y}{3}$
(3)$ \begin{eqnarray}
\left\{
\begin{array}{l}
2x-3y=2 \\
x+2y=8
\end{array}
\right.
\end{eqnarray}$
$ x=?,y=? $
(4)$ 2x^2+3x-1=0 $
$ x=? $
$ \boxed{2}$
$\dfrac{3a-5}{2}=b ・・・・①$
$ 3a-5=2b・・・・②$
$ 3a=2b+5・・・・③$
$ a=\dfrac{2b+5}{3}・・・・④$
「等式の両辺に同じ数を足しても等式が成り立つ」に導く式変形か?
$\boxed{3}$
$ AD\parallel BC,BC=2AD,AD \lt CD,\angle ADC=90°$
$ 台形ABCD,\angle CAE=90°$である.
①$ \triangle ACD \backsim \triangle ECA $の証明をせよ.
②(1)$ DE=? $
(2)$ \triangle EHD=?$
(3)$ FH:GH=?$
この動画を見る
$ \boxed{1}$
(1)$ 10xy^2\div(-5y)\times 3x$
(2)$ 2x-y-\dfrac{5x+y}{3}$
(3)$ \begin{eqnarray}
\left\{
\begin{array}{l}
2x-3y=2 \\
x+2y=8
\end{array}
\right.
\end{eqnarray}$
$ x=?,y=? $
(4)$ 2x^2+3x-1=0 $
$ x=? $
$ \boxed{2}$
$\dfrac{3a-5}{2}=b ・・・・①$
$ 3a-5=2b・・・・②$
$ 3a=2b+5・・・・③$
$ a=\dfrac{2b+5}{3}・・・・④$
「等式の両辺に同じ数を足しても等式が成り立つ」に導く式変形か?
$\boxed{3}$
$ AD\parallel BC,BC=2AD,AD \lt CD,\angle ADC=90°$
$ 台形ABCD,\angle CAE=90°$である.
①$ \triangle ACD \backsim \triangle ECA $の証明をせよ.
②(1)$ DE=? $
(2)$ \triangle EHD=?$
(3)$ FH:GH=?$
賀県立高校入試2021年4⃣(1)~(4)「二次関数、一次関数」
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
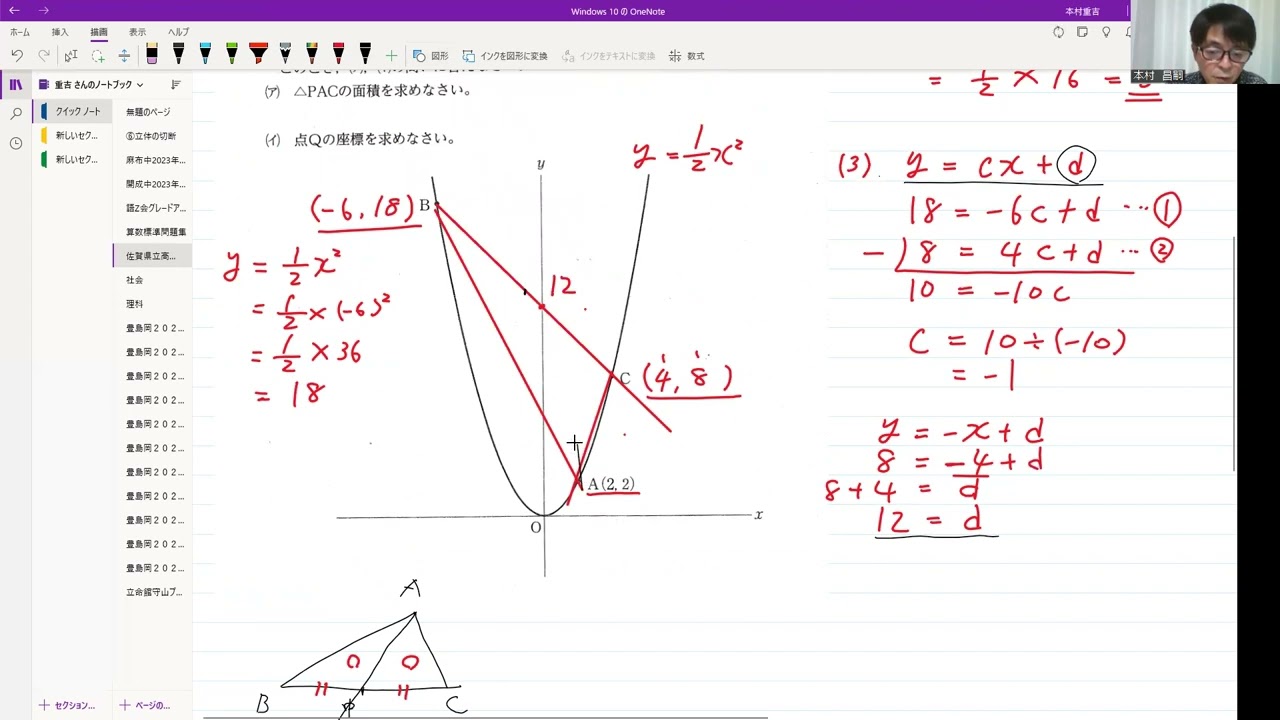
賀県立高校入試2021年4⃣(1)~(4)「二次関数、一次関数」
-----------------
動画内の図のように、関数$y=ax^2$のグラフ上に3点A、B、Cがある。
点Aの座標はA(2.2)、点Bの$x$座標は-6、点Cの$x$座標は4である。
(1)aの値を求めなさい。
(2)点Cの$y$座標を求めなさい。
(3)2点B、Cを通る直線の切片を求めなさい。
(4)点Aを通り△ABCの面積を2等分する直線と、2点B、Cを通る直線との交点の座標を求めなさい。
この動画を見る
賀県立高校入試2021年4⃣(1)~(4)「二次関数、一次関数」
-----------------
動画内の図のように、関数$y=ax^2$のグラフ上に3点A、B、Cがある。
点Aの座標はA(2.2)、点Bの$x$座標は-6、点Cの$x$座標は4である。
(1)aの値を求めなさい。
(2)点Cの$y$座標を求めなさい。
(3)2点B、Cを通る直線の切片を求めなさい。
(4)点Aを通り△ABCの面積を2等分する直線と、2点B、Cを通る直線との交点の座標を求めなさい。
【今後増える傾向 !?】整数:大阪教育大学附属高等学校池田校舎~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
18の正の約数の平方根のうち,すべての正の数の和は
$ (1+\sqrt2)x $
という式で表される.
$ x $の値を求めなさい.
大教大高校池田過去問
この動画を見る
18の正の約数の平方根のうち,すべての正の数の和は
$ (1+\sqrt2)x $
という式で表される.
$ x $の値を求めなさい.
大教大高校池田過去問
2023高校入試数学解説58問目 式の値 明大中野
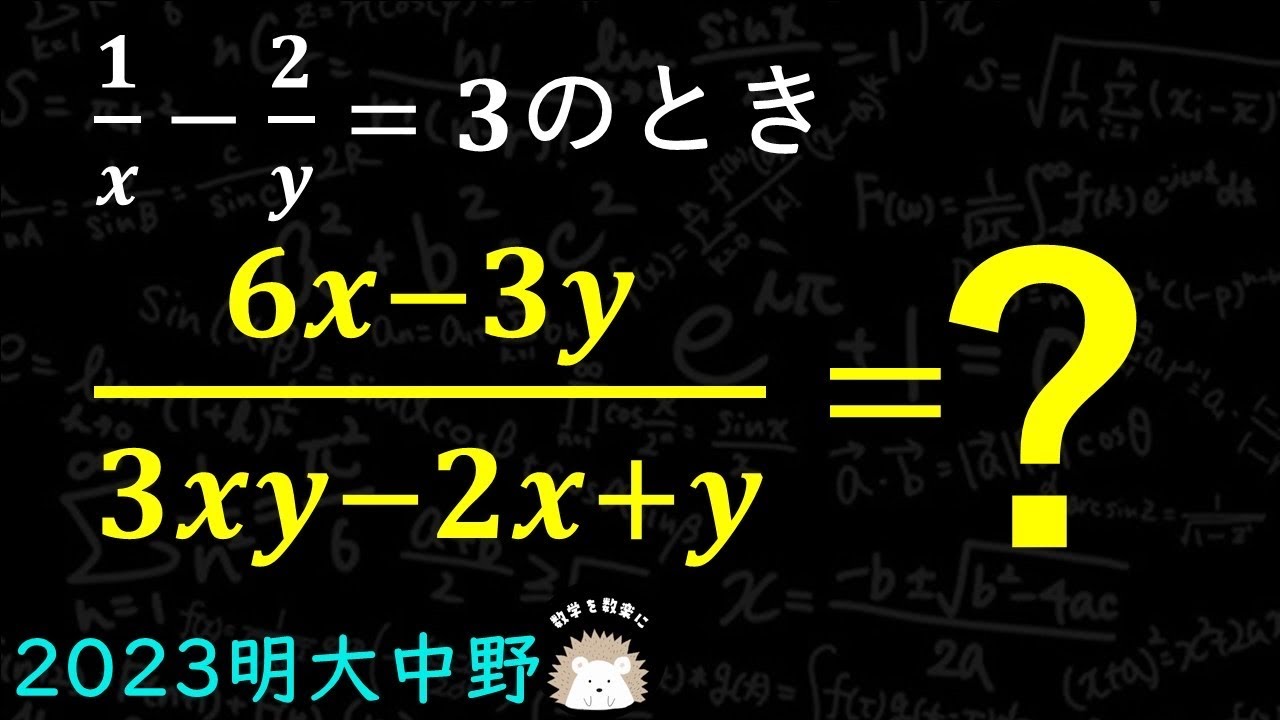
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{x} - \frac{2}{y} = 3$のとき
$\frac{6x-3y}{3xy -2x+y} = ?$
2023明治大学付属中野高等学校
この動画を見る
$\frac{1}{x} - \frac{2}{y} = 3$のとき
$\frac{6x-3y}{3xy -2x+y} = ?$
2023明治大学付属中野高等学校
中学生向け図形問題
🍫【流れが分れば必ず解ける!】二次方程式:明治大学付属明治高等学校高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#中3数学#方程式#2次方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ q $の値を求めよ.
①$ x^2+(a+1)(a+2)x-2a-8=0 $
②$ x^2-(a+4)x+2a^2+6a+4=0 $
①②は,$ x-q $を共通な解としてもつ.
①の解が$ x=p,q $
②の解が$ x=p,r $
($ p,q,r$はすべて異なる数とする.)
明大明治学校過去問
この動画を見る
$ q $の値を求めよ.
①$ x^2+(a+1)(a+2)x-2a-8=0 $
②$ x^2-(a+4)x+2a^2+6a+4=0 $
①②は,$ x-q $を共通な解としてもつ.
①の解が$ x=p,q $
②の解が$ x=p,r $
($ p,q,r$はすべて異なる数とする.)
明大明治学校過去問
【中学数学】有名な三平方の定理の比~有名角の覚え方など~【中3数学】

単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
三平方の定理から導ける直角三角形の有名な比です。
これは受験生全員が知っているといってもいいくらい有名なので、みなさんは必ず使えるようになりましょう。
この動画を見る
三平方の定理から導ける直角三角形の有名な比です。
これは受験生全員が知っているといってもいいくらい有名なので、みなさんは必ず使えるようになりましょう。
2023高校入試解説37問目 早稲田実業最初の一問 因数分解

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
因数分解せよ
$(x+1)a^2 -2xa +x -1$
2023早稲田実業学校
この動画を見る
因数分解せよ
$(x+1)a^2 -2xa +x -1$
2023早稲田実業学校
佐賀県立高校入試2021年「二次方程式」
単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
佐賀県立高校入試2021年「二次方程式」
-----------------
三角形と長方形がある。
三角形は高さが底辺の長さの3倍であり、長方形は横の長さが縦の長さよりも2cm長い。
このとき、(ア)~(ウ)の各問いに答えなさい。
(ア)
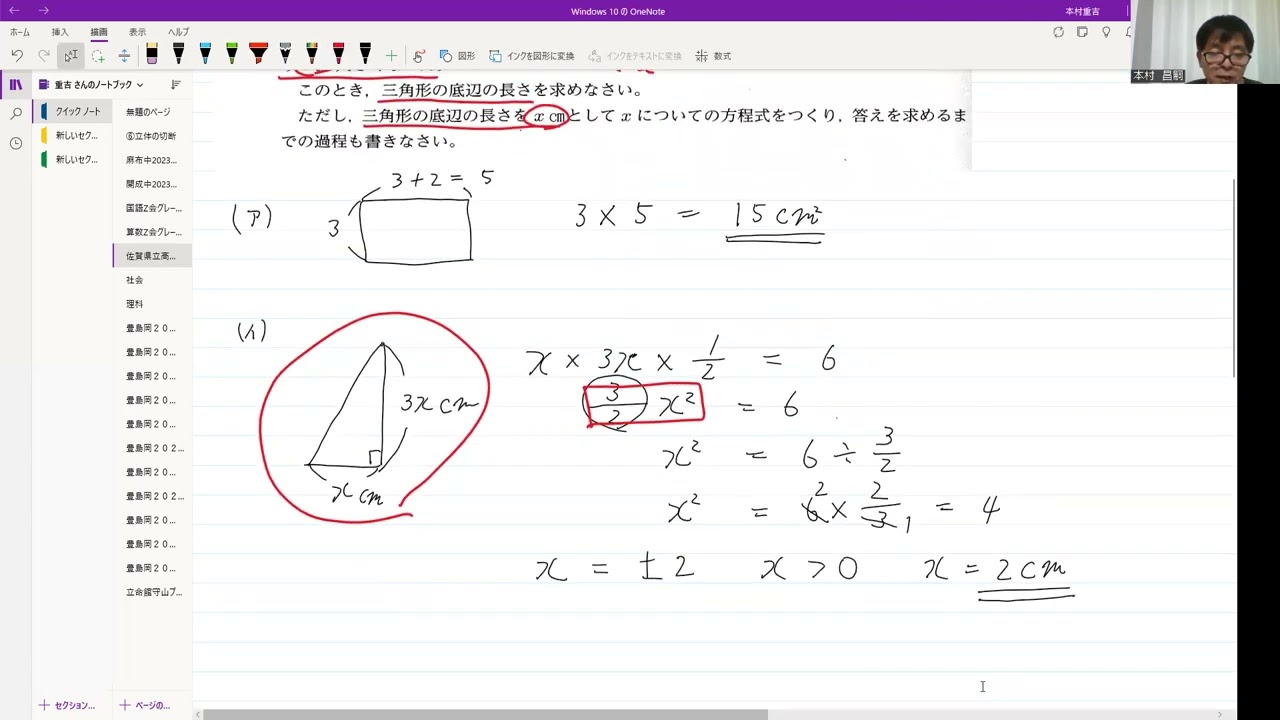
長方形の縦の長さが$3cm$のとき、長方形の面積を求めなさい。
(イ)
三角形の面積が$6cm^2$とき、三角形の底辺の長さを求めなさい。
(ウ)
三角形の底辺の長さと、長方形の縦の長さが等しいとき、三角形の面積が長方形の面積より$6cm^2$回大きくなった。
このとき、三角形の底辺の長さを求めなさい。
ただし、三角形の底辺の長さを$xcm$として$x$についての方程式をつくり、答えを求めるまでの過程も書きなさい。
この動画を見る
佐賀県立高校入試2021年「二次方程式」
-----------------
三角形と長方形がある。
三角形は高さが底辺の長さの3倍であり、長方形は横の長さが縦の長さよりも2cm長い。
このとき、(ア)~(ウ)の各問いに答えなさい。
(ア)
長方形の縦の長さが$3cm$のとき、長方形の面積を求めなさい。
(イ)
三角形の面積が$6cm^2$とき、三角形の底辺の長さを求めなさい。
(ウ)
三角形の底辺の長さと、長方形の縦の長さが等しいとき、三角形の面積が長方形の面積より$6cm^2$回大きくなった。
このとき、三角形の底辺の長さを求めなさい。
ただし、三角形の底辺の長さを$xcm$として$x$についての方程式をつくり、答えを求めるまでの過程も書きなさい。
三平方の定理の逆を分かりやすく

放物線と二等辺三角形 国立高専
単元:
#数学(中学生)#中3数学#数A#図形の性質#三平方の定理#三角形の辺の比(内分・外分・二等分線)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
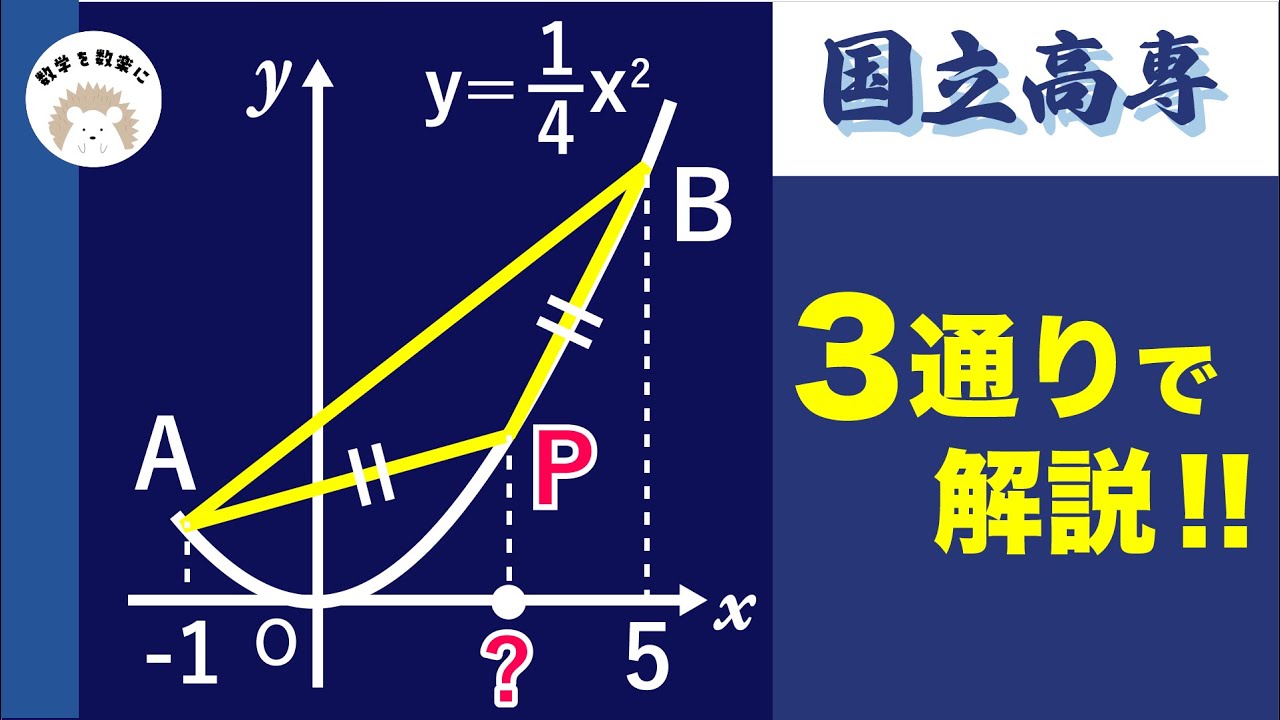
$y=\frac{1}{4}x^2$
P=?
*図は動画内参照
国立高専
この動画を見る
$y=\frac{1}{4}x^2$
P=?
*図は動画内参照
国立高専
佐賀県立高校入試2022年5⃣相似(4)~(6)
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
佐賀県立高校入試2022年5⃣相似(4)~(6)
-----------------
動画内の図のように、半径が5cmの円Oと、半径が円Oの半径よりも短い円O'があり、円O'の中心は円Oの周上にある。
2つの円の交点をA、Bとし、AB=6cmとする。
円Oの周上に線分ACが円Oの直径となるように点Cをとり、直線CBと円O'との交点のうち点Bと異なる点をDとする。
また、円O'の周上にAE=6cmとなるように点Eをとり、直線EBと円Oとの交点のうち点Bと異なる点をFとする。ただし、点Eは点Bと異なる点とする。
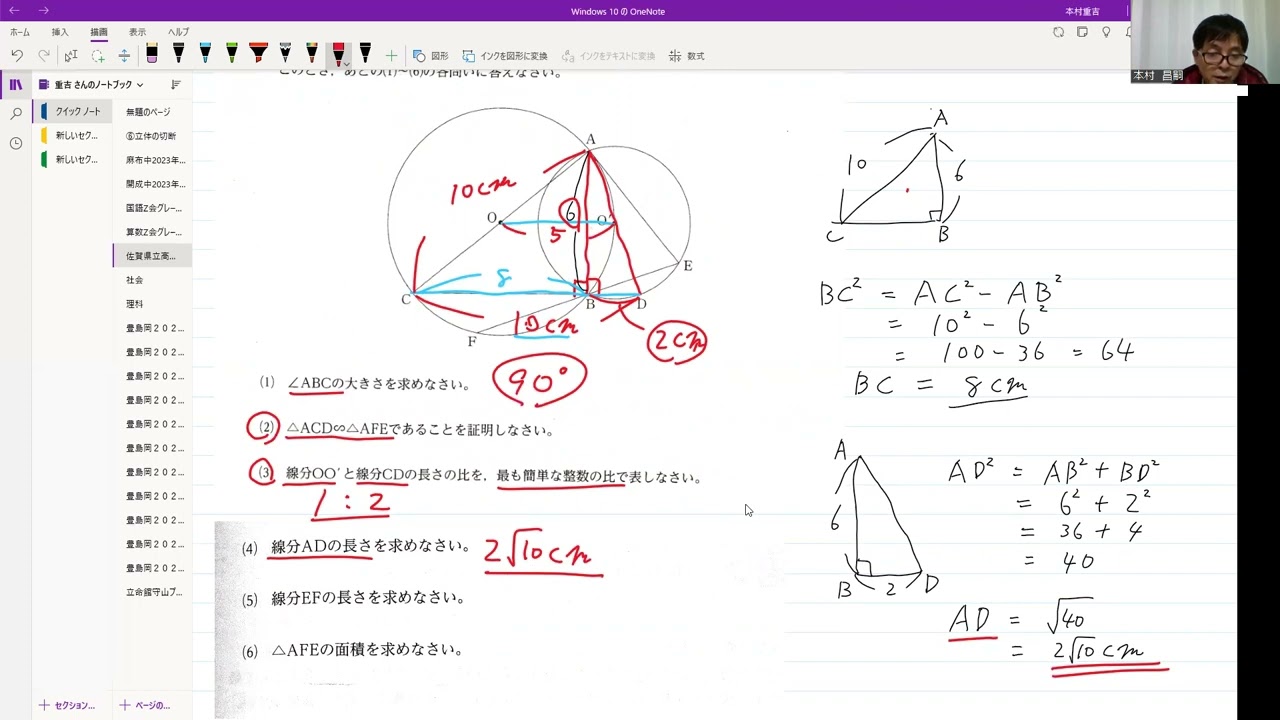
(4) 線分ADの長さを求めなさい。
(5) 線分EFの長さを求めなさい。
(6) △AFEの面積を求めなさい。
この動画を見る
佐賀県立高校入試2022年5⃣相似(4)~(6)
-----------------
動画内の図のように、半径が5cmの円Oと、半径が円Oの半径よりも短い円O'があり、円O'の中心は円Oの周上にある。
2つの円の交点をA、Bとし、AB=6cmとする。
円Oの周上に線分ACが円Oの直径となるように点Cをとり、直線CBと円O'との交点のうち点Bと異なる点をDとする。
また、円O'の周上にAE=6cmとなるように点Eをとり、直線EBと円Oとの交点のうち点Bと異なる点をFとする。ただし、点Eは点Bと異なる点とする。
(4) 線分ADの長さを求めなさい。
(5) 線分EFの長さを求めなさい。
(6) △AFEの面積を求めなさい。
佐賀県立高校入試2022年5⃣相似(1)~(3)
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
佐賀県立高校入試2022年5⃣相似(1)~(3)
-----------------
動画内の図のように、半径が5cmの円Oと、半径が円Oの半径よりも短い円O'があり、円O'の中心は円Oの周上にある。
2つの円の交点をA、Bとし、AB=6cmとする。
円Oの周上に線分ACが円Oの直径となるように点Cをとり、直線CBと円O'との交点のうち点Bと異なる点をDとする。
また、円O'の周上にAE=6cmとなるように点Eをとり、直線EBと円Oとの交点のうち点Bと異なる点をFとする。ただし、点Eは点Bと異なる点とする。
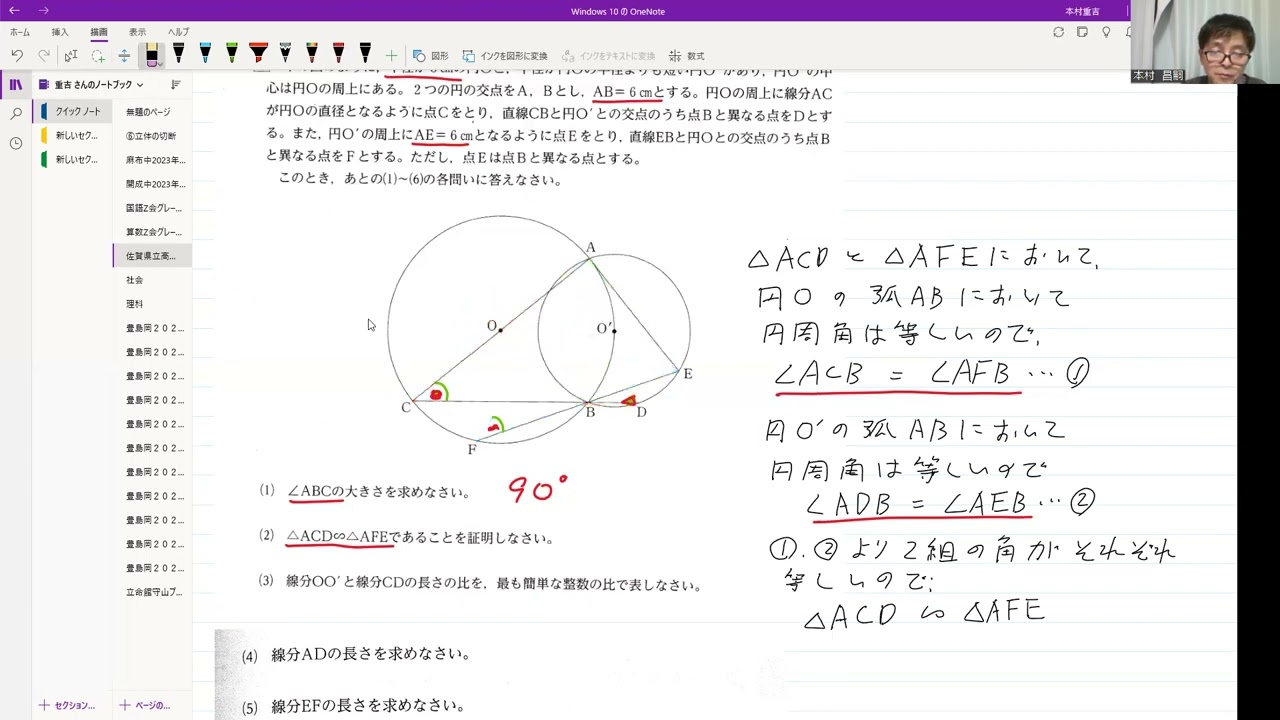
(1) ∠ABCの大きさを求めなさい。
(2) △ACD$\backsim$△AFEであることを証明しなさい。
(3) 線分OO'と線分CDの長さの比を、最も簡単な整数の比で表しなさい。
この動画を見る
佐賀県立高校入試2022年5⃣相似(1)~(3)
-----------------
動画内の図のように、半径が5cmの円Oと、半径が円Oの半径よりも短い円O'があり、円O'の中心は円Oの周上にある。
2つの円の交点をA、Bとし、AB=6cmとする。
円Oの周上に線分ACが円Oの直径となるように点Cをとり、直線CBと円O'との交点のうち点Bと異なる点をDとする。
また、円O'の周上にAE=6cmとなるように点Eをとり、直線EBと円Oとの交点のうち点Bと異なる点をFとする。ただし、点Eは点Bと異なる点とする。
(1) ∠ABCの大きさを求めなさい。
(2) △ACD$\backsim$△AFEであることを証明しなさい。
(3) 線分OO'と線分CDの長さの比を、最も簡単な整数の比で表しなさい。
福田の1.5倍速演習〜合格する重要問題100〜慶應義塾大学2020年度総合政策学部第3問〜半円に接する5つの円

単元:
#数A#大学入試過去問(数学)#図形の性質#三平方の定理#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 図のように(※動画参照)半円の中に、半径1の4つの円A, B, C, Dと、別の半径の円Eがあり、次のように接している。円Aは半円の円弧と直径と円Bに接し、円Bは半円の円弧と円A, C, Eに接し、円Cは半円の円弧と円B, D, Eに接し、円Dは半円の円弧と直径と円Cに接している。また、円Eじゃ半円の直径と円B, Cに接している。
このとき、半円の半径は
$\boxed{\ \ アイ\ \ }+\sqrt{\boxed{\ \ ウエ\ \ }+\boxed{\ \ オカ\ \ }\sqrt{\boxed{\ \ キク\ \ }}}$
であり、円Eの半径は
$\frac{\boxed{\ \ ケコ\ \ }+\sqrt{\boxed{\ \ サシ\ \ }}}{\boxed{\ \ スセ\ \ }}$
である。
2020慶應義塾大学総合政策学部過去問
この動画を見る
$\Large\boxed{3}$ 図のように(※動画参照)半円の中に、半径1の4つの円A, B, C, Dと、別の半径の円Eがあり、次のように接している。円Aは半円の円弧と直径と円Bに接し、円Bは半円の円弧と円A, C, Eに接し、円Cは半円の円弧と円B, D, Eに接し、円Dは半円の円弧と直径と円Cに接している。また、円Eじゃ半円の直径と円B, Cに接している。
このとき、半円の半径は
$\boxed{\ \ アイ\ \ }+\sqrt{\boxed{\ \ ウエ\ \ }+\boxed{\ \ オカ\ \ }\sqrt{\boxed{\ \ キク\ \ }}}$
であり、円Eの半径は
$\frac{\boxed{\ \ ケコ\ \ }+\sqrt{\boxed{\ \ サシ\ \ }}}{\boxed{\ \ スセ\ \ }}$
である。
2020慶應義塾大学総合政策学部過去問
大阪大 無理数の無理数乗=有理数

単元:
#数学(中学生)#中3数学#平方根
指導講師:
鈴木貫太郎
問題文全文(内容文):
(1)$\log_3 4$は無理数であることを証明せよ.
(2)a,bは無理数で$a^b$が有理数であるような数の組a,bを求めよ.
大阪大過去問
この動画を見る
(1)$\log_3 4$は無理数であることを証明せよ.
(2)a,bは無理数で$a^b$が有理数であるような数の組a,bを求めよ.
大阪大過去問
【中学数学】三平方の定理の証明~一緒にしよう~【中3数学】

佐賀県立高校入試2022年4⃣関数(5)
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)#佐賀県立高校
指導講師:
重吉
問題文全文(内容文):
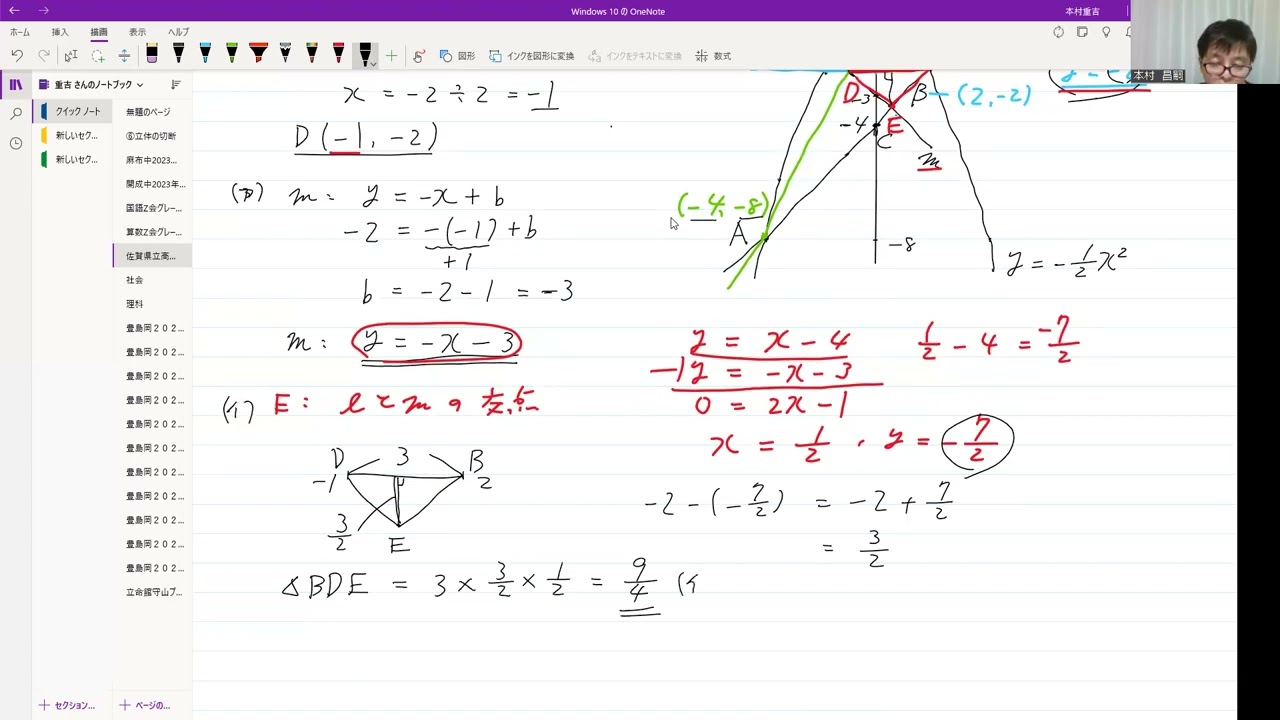
佐賀県立高校入試2022年4⃣関数(5)
-----------------
点Bを通り$x$軸に平行な直線と、原点と点Aを通る直線との交点をDとする。
また、点Dを通り、傾き-1の直線を$m$とし、直線$l$と直線$m$との交点をEとする。
このとき、(ア)~(ウ)の各問いに答えなさい。
(ア)直線$m$の式を求めなさい。
(イ)△BDEの面積を求めなさい。
(ウ)△ACDの面積を$S$.△BDEの面積を$T$とするとき、$S:T$を最も簡単な整数の比で表しなさい。
この動画を見る
佐賀県立高校入試2022年4⃣関数(5)
-----------------
点Bを通り$x$軸に平行な直線と、原点と点Aを通る直線との交点をDとする。
また、点Dを通り、傾き-1の直線を$m$とし、直線$l$と直線$m$との交点をEとする。
このとき、(ア)~(ウ)の各問いに答えなさい。
(ア)直線$m$の式を求めなさい。
(イ)△BDEの面積を求めなさい。
(ウ)△ACDの面積を$S$.△BDEの面積を$T$とするとき、$S:T$を最も簡単な整数の比で表しなさい。
高等学校入学試験予想問題:洛南高等学校~全部入試問題
単元:
#数学(中学生)#中1数学#中2数学#中3数学#式の計算(単項式・多項式・式の四則計算)#式の計算(展開、因数分解)#平方根#空間図形#1次関数#2次関数#平面図形
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \boxed{1}$
(1)$ \left(4-\dfrac{7}{3}\right)\times \left(-\dfrac{3}{5}+\dfrac{1}{2}\right)$を計算せよ.
(2)$ \ell:y=(a+2)x+b-1$
$ m:y=bx-a^2 $について,
$ a=\sqrt2,b=1$のとき,$ \ell,m$の交点は?
(3)$ a=\sqrt5-\sqrt3,b=\sqrt5+\sqrt3 $のとき,$ a^2-ab-b^2$の値は?
$ \boxed{2}$
図のように,2点$ A,B $が$ y-ax^2 $のグラフ上にあり,$ A $の座標は$ (3,27)$,$B$のx座標は-2である.
3点$ C,D,E $は直線$ OA $上,$ \triangle OBC,\triangle BCF,\triangle CFD,\triangle FDG,
\triangle DGE,\triangle GEA $の面積はすべて等しい.
このとき,次の問いに答えよ.
(1)点$ B$のy座標を求めよ.
(2)点$ C $の座標を求めよ.
(3)直線$ EG $の傾きを求めよ.
$ \boxed{3}$
図のように,底面の半径が3cm,母線の長さが5cmの円錐の中に半径の等しい2つの球$ P,Q $があります.
2つの球$ P,Q $は互いに接し,円錐の底面と側面に接しているとき,次の問いに答えなさい.
ただし,2つの球の中心と,円錐の頂点と,円錐の底面の中心は同じ平面上にあるものとする.
(1)球$ P$の半径を求めよ.
(2)円錐の体積は,$ P $の体積の何倍か.
(3)球$ P $と円錐の側面が接する点を$ A $とする.
点$ A $を通り,円錐の底面に平行な平面で球$ P $を切断するとき,球$ P $の切断面の面積を求めよ.
この動画を見る
$ \boxed{1}$
(1)$ \left(4-\dfrac{7}{3}\right)\times \left(-\dfrac{3}{5}+\dfrac{1}{2}\right)$を計算せよ.
(2)$ \ell:y=(a+2)x+b-1$
$ m:y=bx-a^2 $について,
$ a=\sqrt2,b=1$のとき,$ \ell,m$の交点は?
(3)$ a=\sqrt5-\sqrt3,b=\sqrt5+\sqrt3 $のとき,$ a^2-ab-b^2$の値は?
$ \boxed{2}$
図のように,2点$ A,B $が$ y-ax^2 $のグラフ上にあり,$ A $の座標は$ (3,27)$,$B$のx座標は-2である.
3点$ C,D,E $は直線$ OA $上,$ \triangle OBC,\triangle BCF,\triangle CFD,\triangle FDG,
\triangle DGE,\triangle GEA $の面積はすべて等しい.
このとき,次の問いに答えよ.
(1)点$ B$のy座標を求めよ.
(2)点$ C $の座標を求めよ.
(3)直線$ EG $の傾きを求めよ.
$ \boxed{3}$
図のように,底面の半径が3cm,母線の長さが5cmの円錐の中に半径の等しい2つの球$ P,Q $があります.
2つの球$ P,Q $は互いに接し,円錐の底面と側面に接しているとき,次の問いに答えなさい.
ただし,2つの球の中心と,円錐の頂点と,円錐の底面の中心は同じ平面上にあるものとする.
(1)球$ P$の半径を求めよ.
(2)円錐の体積は,$ P $の体積の何倍か.
(3)球$ P $と円錐の側面が接する点を$ A $とする.
点$ A $を通り,円錐の底面に平行な平面で球$ P $を切断するとき,球$ P $の切断面の面積を求めよ.
