 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
【5分でスッキリ!】整数:慶応義塾女子高等学校~全国入試問題解法【神授業】

単元:
#数学(中学生)#高校入試過去問(数学)#慶應義塾女子高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 慶応義塾女子高等学校
自然数$N$の約数は3個で、
その和は183である。
$N$の値を求めなさい。
この動画を見る
入試問題 慶応義塾女子高等学校
自然数$N$の約数は3個で、
その和は183である。
$N$の値を求めなさい。
【数学】中2-88 箱ひげ図②(読み取り編)

単元:
#数学(中学生)#中1数学#資料の活用
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数学(箱ひげ図②・読み取り編)
Q.
右の2つの箱ひげ図は、Aグループ15人とBグループ15人のテストの得点を表したものです。
この箱ひげ図から読み取れることとして、次の①~④は正しいといえますか。
「正しい」「正しくない」「このデータからはわからない」のどれかで答えなさい。
①Bグループの平均値は6点である。
②どちらのグループも、半分以上の生徒が5点以上である。
③Aグループは7点以上の人が4人いる。
④範囲も四分位範囲もBグループの方が大きい。
この動画を見る
数学(箱ひげ図②・読み取り編)
Q.
右の2つの箱ひげ図は、Aグループ15人とBグループ15人のテストの得点を表したものです。
この箱ひげ図から読み取れることとして、次の①~④は正しいといえますか。
「正しい」「正しくない」「このデータからはわからない」のどれかで答えなさい。
①Bグループの平均値は6点である。
②どちらのグループも、半分以上の生徒が5点以上である。
③Aグループは7点以上の人が4人いる。
④範囲も四分位範囲もBグループの方が大きい。
ピタゴラスも絶賛!!解き方5通り!
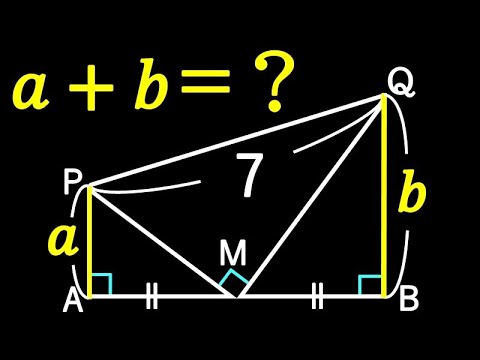
【この動画で数学が好きになる!?】平方根:渋谷教育学園幕張高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#渋谷教育学園幕張高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 渋谷教育学園幕張高等学校
$x+\displaystyle \frac{1}{x}=5-\sqrt{ 5 }$のとき
$\displaystyle \frac{\sqrt{ x^4-10x^3+25x^2-10x+1 }}{x}$
の値を求めなさい。
この動画を見る
入試問題 渋谷教育学園幕張高等学校
$x+\displaystyle \frac{1}{x}=5-\sqrt{ 5 }$のとき
$\displaystyle \frac{\sqrt{ x^4-10x^3+25x^2-10x+1 }}{x}$
の値を求めなさい。
【朝勉!】朝の因数分解DoJo No.2【因数分解】

【数学】中2-87 箱ひげ図①(基本編)

単元:
#数学(中学生)#中1数学#資料の活用
指導講師:
とある男が授業をしてみた
問題文全文(内容文):
数学(箱ひげ図①・基本編)
Q.
下の資料は、とある生徒9人が行った小テストの得点である。
7 5 4 9 6 7 10 3 6
①最小値は?
➁最大値は?
③第1四分位数は?
④第2四分位数は?
⑤第3四分位数は?
⑥範囲は?
⑦四分位範囲は?
⑧箱ひげ図に表しなさい。
この動画を見る
数学(箱ひげ図①・基本編)
Q.
下の資料は、とある生徒9人が行った小テストの得点である。
7 5 4 9 6 7 10 3 6
①最小値は?
➁最大値は?
③第1四分位数は?
④第2四分位数は?
⑤第3四分位数は?
⑥範囲は?
⑦四分位範囲は?
⑧箱ひげ図に表しなさい。
数字がない。。。
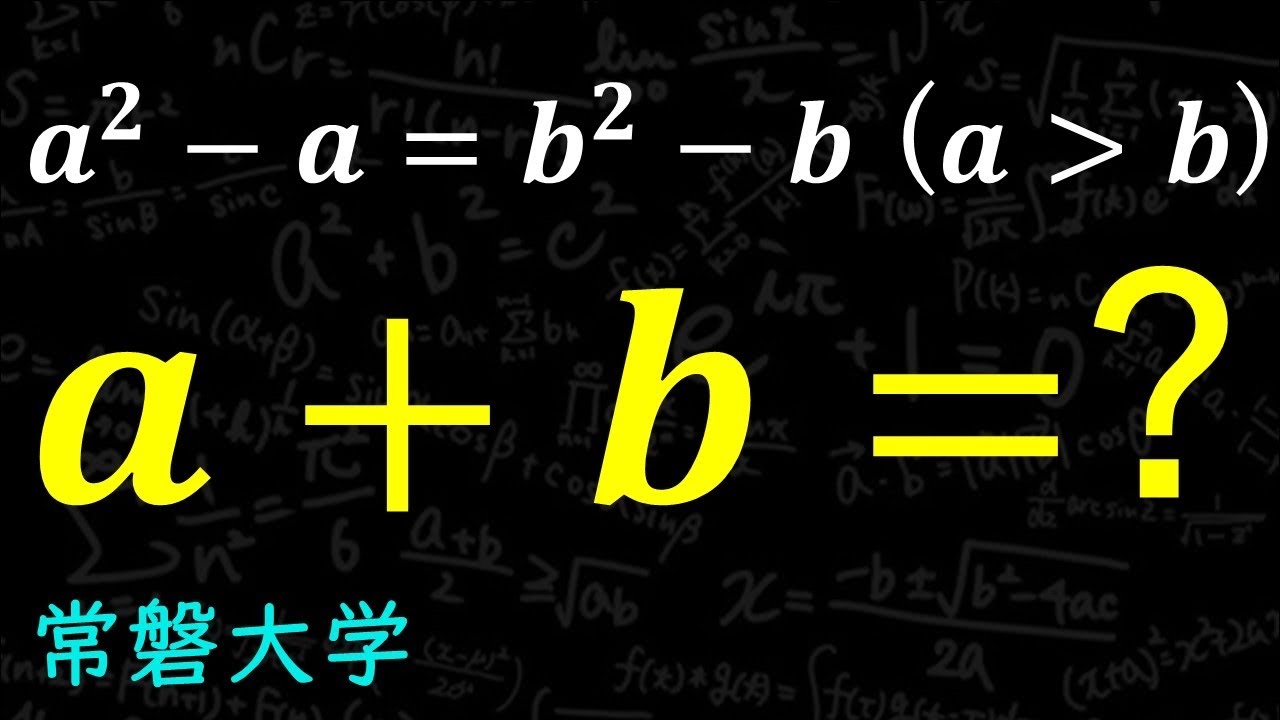
連立方程式:東京都立国立高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)#東京都立国立高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立国立高等学校
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{4x+y-5}{2}=x+0.25y-2 \\
4x + 3y = -6
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け。
この動画を見る
入試問題 東京都立国立高等学校
$\begin{eqnarray}
\left\{
\begin{array}{l}
\displaystyle \frac{4x+y-5}{2}=x+0.25y-2 \\
4x + 3y = -6
\end{array}
\right.
\end{eqnarray}$
連立方程式を解け。
気づけば一瞬!!長方形の面積=❓
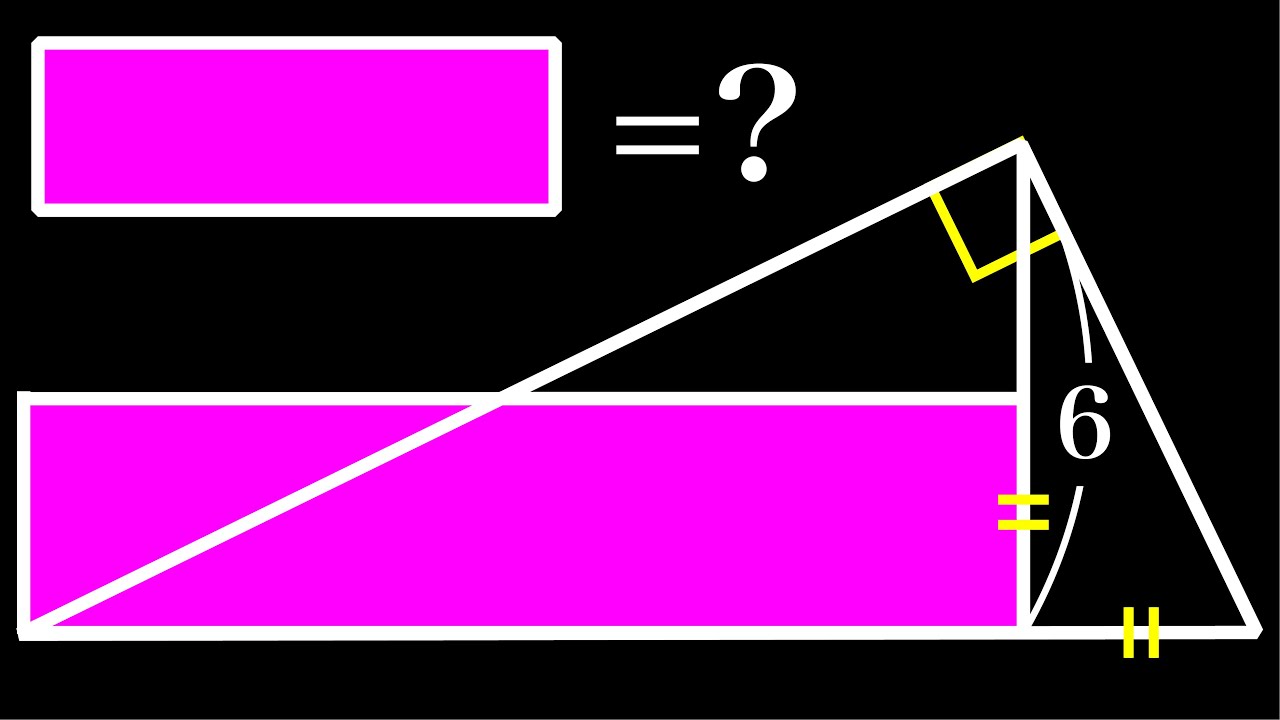
単元:
#数学(中学生)#中2数学#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#角度と面積#三角形と四角形#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
長方形の面積=?
*図は動画内参照
この動画を見る
長方形の面積=?
*図は動画内参照
【中学数学】三平方の定理:正四面体の頂点から底面に引いた垂線は、底面の正三角形の重心を通る。一辺の長さがaの正四面体OABCについて、Oから底面ABCに引いた垂線をOHとするとき(続きは概要欄)

単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
理数個別チャンネル
問題文全文(内容文):
正四面体の頂点から底面に引いた垂線は、底面の正三角形の重心を通る。一辺の長さがaの正四面体OABCについて、Oから底面ABCに引いた垂線をOHとするとき、次の問いに答えよう。
(1)線分AHの長さを求めよう。
(2)正四面体OABCの高さOHを求めよう。
(3)正四面体OABCの体積Vを求めよう。
この動画を見る
正四面体の頂点から底面に引いた垂線は、底面の正三角形の重心を通る。一辺の長さがaの正四面体OABCについて、Oから底面ABCに引いた垂線をOHとするとき、次の問いに答えよう。
(1)線分AHの長さを求めよう。
(2)正四面体OABCの高さOHを求めよう。
(3)正四面体OABCの体積Vを求めよう。
√ひとりぼっち大作戦!! 愛知高校

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt 3 +\sqrt 5 = x$のとき
$\sqrt 5$をxで表せ。(ただし根号は使用禁止)
この動画を見る
$\sqrt 3 +\sqrt 5 = x$のとき
$\sqrt 5$をxで表せ。(ただし根号は使用禁止)
【中学数学】三平方の定理:半径6cmの円と半径4cmの円が外接している。これら2つの円に外接して、かつ1つの共通外接線に接する円のうち小さい方の円の半径を求めよう。

単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
理数個別チャンネル
問題文全文(内容文):
半径6cmの円と半径4cmの円が外接している。これら2つの円に外接して、かつ1つの共通外接線に接する円のうち小さい方の円の半径を求めよう。
この動画を見る
半径6cmの円と半径4cmの円が外接している。これら2つの円に外接して、かつ1つの共通外接線に接する円のうち小さい方の円の半径を求めよう。
【トライ!】二次方程式:東京都立八王子東高等学校~全国入試問題解法【個別授業】

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#東京都立八王子東高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 東京都立八王子東高等学校
二次方程式を解け。
$(x+4)^2-6(x+4)+7=0$
この動画を見る
入試問題 東京都立八王子東高等学校
二次方程式を解け。
$(x+4)^2-6(x+4)+7=0$
【中学数学】三平方の定理:半径aの半円に内接する半径a_2の円Oがある。円Oに外接して、半円の直径と弧に接する円の半径を求めよう。
単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
理数個別チャンネル
問題文全文(内容文):
半径aの半円に内接する半径$\dfrac{a}{2}$の円Oがある。円Oに外接して、半円の直径と弧に接する円の半径を求めよう。
この動画を見る
半径aの半円に内接する半径$\dfrac{a}{2}$の円Oがある。円Oに外接して、半円の直径と弧に接する円の半径を求めよう。
分数が入ってる因数分解

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
数学を数楽に
問題文全文(内容文):
$\frac{1}{6}(x+1)(2x+1) - \frac{3}{2}(x+1)$を因数分解せよ。
この動画を見る
$\frac{1}{6}(x+1)(2x+1) - \frac{3}{2}(x+1)$を因数分解せよ。
100以下の素数全部~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
100以下の素数全部~全国入試問題解法
【100までの素数】
2,3,5,7,11
13, 17, 19, 23, 29
31.37,41,43,47
53, 59, 61, 67, 71
73,79,83,89.97
全部で25個
【合成数(総数と勘違いしやすい)】
51,57,87,91
素数・・・1とその数以外に約数外 ない正の数。
この動画を見る
100以下の素数全部~全国入試問題解法
【100までの素数】
2,3,5,7,11
13, 17, 19, 23, 29
31.37,41,43,47
53, 59, 61, 67, 71
73,79,83,89.97
全部で25個
【合成数(総数と勘違いしやすい)】
51,57,87,91
素数・・・1とその数以外に約数外 ない正の数。
反比例の変域 桃山学院
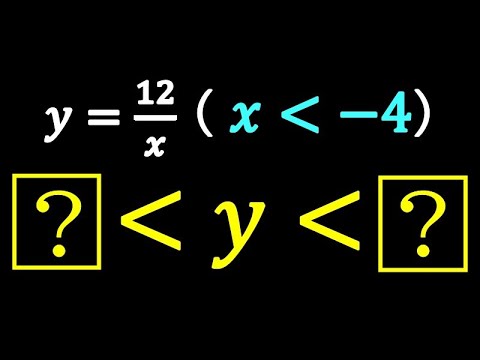
単元:
#数学(中学生)#中1数学#比例・反比例#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$y=\frac{12}{x} $ (x < -4)
$\boxed{?} <y< \boxed{?}$
桃山学院高等学校
この動画を見る
$y=\frac{12}{x} $ (x < -4)
$\boxed{?} <y< \boxed{?}$
桃山学院高等学校
【中学数学】 正負の数:指数計算の注意点

ペアを作ろう!!A 大阪教育大学附属池田 洛南
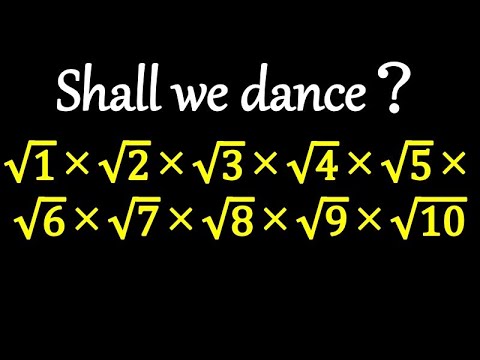
単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{1} \times \sqrt{2} \times \sqrt{3} \times \sqrt{4} \times \sqrt{5} \times \sqrt{6} \times \sqrt{7} \times \sqrt{8} \times \sqrt{9} \times \sqrt{10} =$
大阪教育大学附属高等学校池田校舎
この動画を見る
$\sqrt{1} \times \sqrt{2} \times \sqrt{3} \times \sqrt{4} \times \sqrt{5} \times \sqrt{6} \times \sqrt{7} \times \sqrt{8} \times \sqrt{9} \times \sqrt{10} =$
大阪教育大学附属高等学校池田校舎
【中学数学】連立方程式:基礎の基礎から解説!その2 元と次って何?

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
理数個別チャンネル
問題文全文(内容文):
x-y=6は何元何次方程式でしょうか?意外ときちんと習わない”元”について解説します!
この動画を見る
x-y=6は何元何次方程式でしょうか?意外ときちんと習わない”元”について解説します!
【朝勉!】朝の因数分解DoJo No.1【因数分解】

正しいものを選べ!!大阪星光学院

単元:
#数学(中学生)#中2数学#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
正しいものをすべて選べ
①4辺の長さが等しい四角形をひし形という
②4つの角の大きさが等しい四角形を長方形という
③6辺の長さが等しい六角形を正六角形という
④6つの角の大きさが等しい六角形を正六角形という
大阪星光学院高等学校
この動画を見る
正しいものをすべて選べ
①4辺の長さが等しい四角形をひし形という
②4つの角の大きさが等しい四角形を長方形という
③6辺の長さが等しい六角形を正六角形という
④6つの角の大きさが等しい六角形を正六角形という
大阪星光学院高等学校
整数問題 筑紫女学園(改)

単元:
#数学(中学生)#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$n^3-4n=105$をみたす自然数n=?
筑紫女学園高等学校(改)
この動画を見る
$n^3-4n=105$をみたす自然数n=?
筑紫女学園高等学校(改)
単純そうで少し難しい B
【中学数学】連立方程式:基礎の基礎から解説!その1 連立方程式って?

単元:
#数学(中学生)#中2数学#連立方程式
指導講師:
理数個別チャンネル
問題文全文(内容文):
$x+y=10,x-y=6$を同時に満たす整数解を考えながら連立方程式を学んでいこう。
この動画を見る
$x+y=10,x-y=6$を同時に満たす整数解を考えながら連立方程式を学んでいこう。
連立方程式:豊島岡女子学園高等学校~全国入試問題解法【神授業】
単元:
#数学(中学生)#中1数学#中2数学#方程式#連立方程式#高校入試過去問(数学)#豊島岡女子高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 豊島岡女子学園高等学校
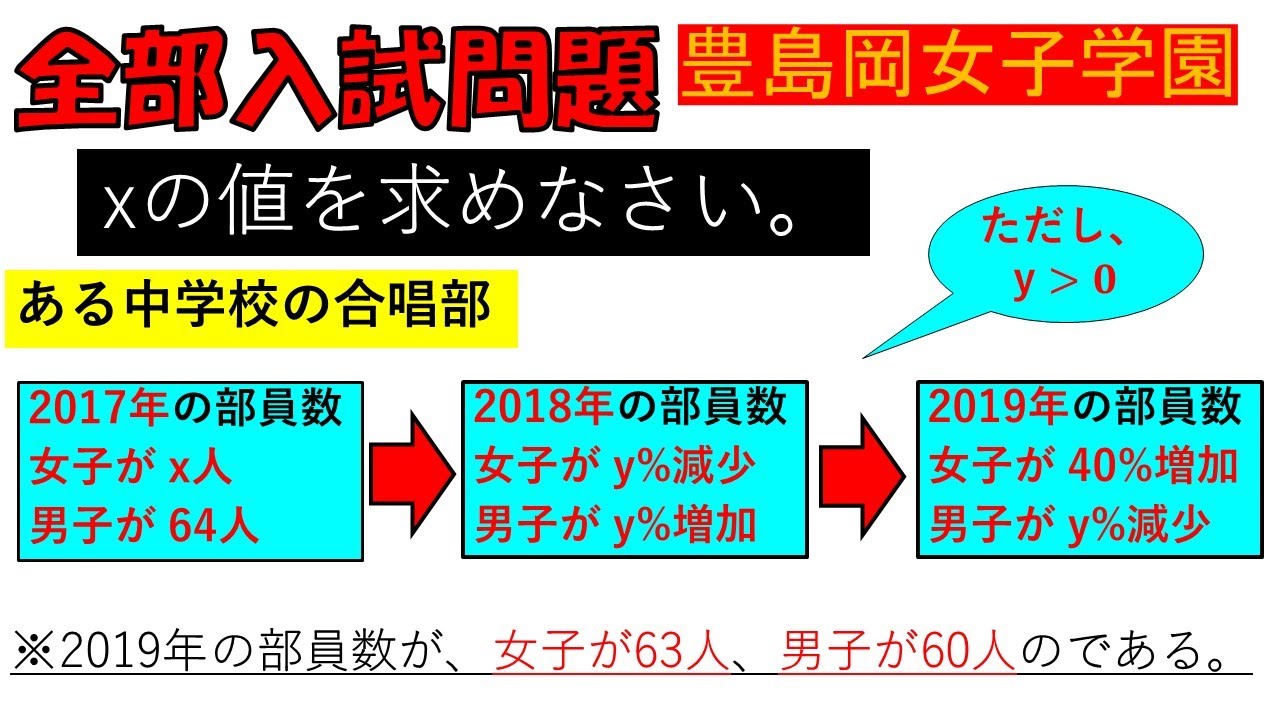
ある中学校の合唱部の2017年の部員数は、女子が$x$ 人、男子が64人でした。2018年の部員数は、2017 年と比べて女子が$y$%減り、男子が$y$%増えました。 2019年の部員数は、2018年と比べて女子が40%増 え、男子が$y$%減りました。
2019年の部員数が、女子が63人、男子が60人のとき
$x$の値を求めなさい。
(ただし、$ y\gt 0$)
この動画を見る
入試問題 豊島岡女子学園高等学校
ある中学校の合唱部の2017年の部員数は、女子が$x$ 人、男子が64人でした。2018年の部員数は、2017 年と比べて女子が$y$%減り、男子が$y$%増えました。 2019年の部員数は、2018年と比べて女子が40%増 え、男子が$y$%減りました。
2019年の部員数が、女子が63人、男子が60人のとき
$x$の値を求めなさい。
(ただし、$ y\gt 0$)
【5分で完答 !?】空間図形:函館ラ・サール高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#空間図形#高校入試過去問(数学)#函館ラ・サール高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 函館ラ・サール高等学校
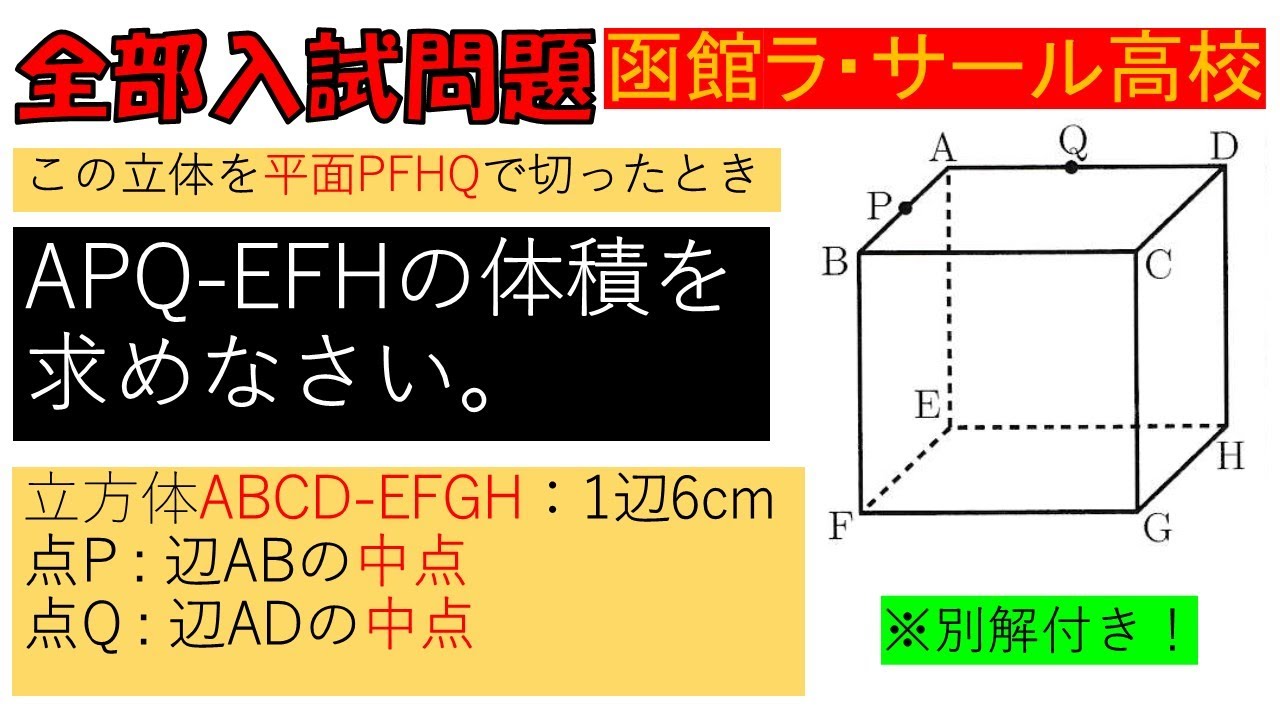
この立体を平面$PFHQ$で切ったとき
$APQ-EFH$の体積を 求めなさい。
立方体$ABCD-EFGH$:1辺6cm
点$P$:辺$AB$の中点
点$Q$:辺$AD$の中点
※図は動画内参照
この動画を見る
入試問題 函館ラ・サール高等学校
この立体を平面$PFHQ$で切ったとき
$APQ-EFH$の体積を 求めなさい。
立方体$ABCD-EFGH$:1辺6cm
点$P$:辺$AB$の中点
点$Q$:辺$AD$の中点
※図は動画内参照
【中学数学】比例と反比例:変域(何で大小が変わるの?)

計算:土浦日本大学高等学校~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#土浦日本大学高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題 土浦日本大学高等学校
次の▭を埋めなさい。
$624^2-623\times 625=▭$
この動画を見る
入試問題 土浦日本大学高等学校
次の▭を埋めなさい。
$624^2-623\times 625=▭$
リーグ戦の試合数 B (長野県)
単元:
#計算と数の性質#数学(中学生)#規則性(周期算・方陣算・数列・日暦算・N進法)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
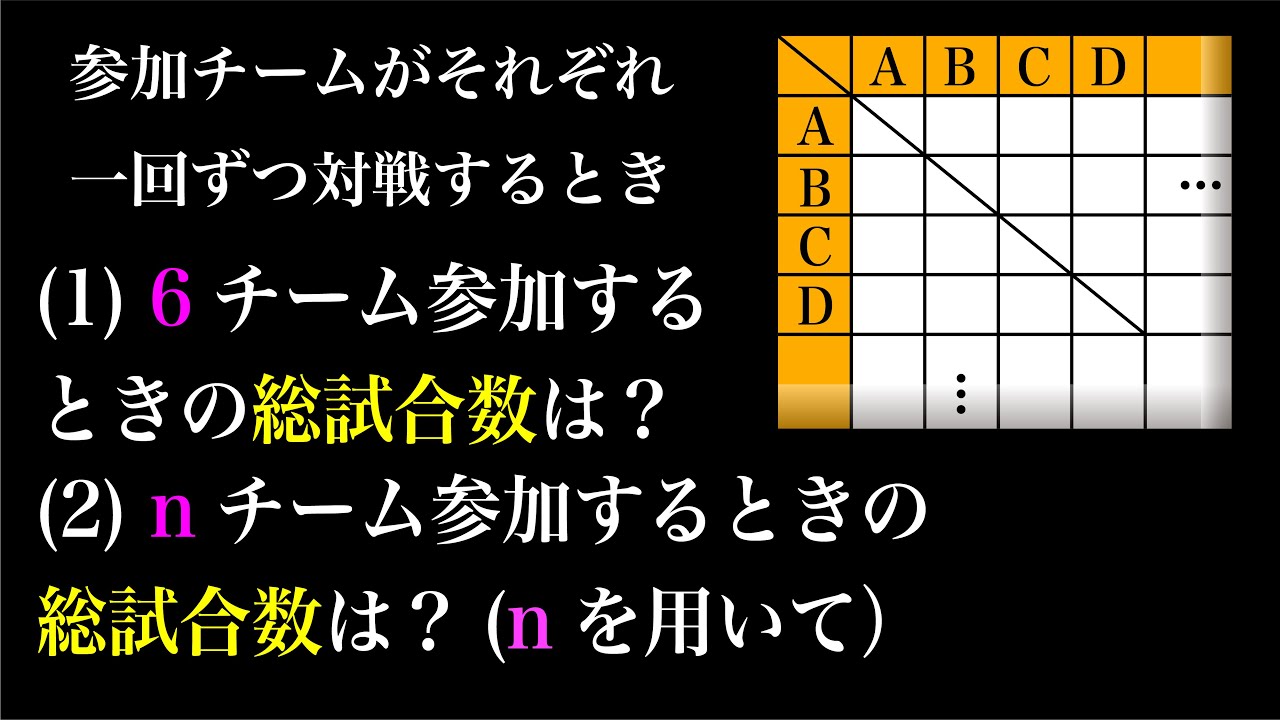
リーグ戦(総当たり戦)
1回ずつ対戦するとき
(1)6チーム参加するときの総試合数は?
(2)nチーム参加するときの総試合数は?
*図は動画内参照
この動画を見る
リーグ戦(総当たり戦)
1回ずつ対戦するとき
(1)6チーム参加するときの総試合数は?
(2)nチーム参加するときの総試合数は?
*図は動画内参照
