 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
【入試らしい一問…!】図形:ノートルダム女学院高校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#ノートルダム女学院高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
印のついた角の大きさの和を求めよ。
この動画を見る
印のついた角の大きさの和を求めよ。
整数問題 中学生にはキツいか。。

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
数学を数楽に
問題文全文(内容文):
$n^4-3n^2+1は素数 \ \ n= \ ? \ (n: 自然数)$
この動画を見る
$n^4-3n^2+1は素数 \ \ n= \ ? \ (n: 自然数)$
【良問だよね…!】整数:秋田県~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#秋田県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$n^2-20n+91$の値が素数になる自然数$n$をすべて求めよ。
この動画を見る
$n^2-20n+91$の値が素数になる自然数$n$をすべて求めよ。
【道筋は人それぞれ…!】図形:国立高等専門学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#国立高等専門学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2直線$l,m$は平行であり、同じ印のつけられている角が等しいとき、$\angle x$を求めよ。
この動画を見る
2直線$l,m$は平行であり、同じ印のつけられている角が等しいとき、$\angle x$を求めよ。
【順番に当たるか…!】平方根:宮城県~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#宮城県公立高校入試
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\sqrt{10},\frac{7}{\sqrt{7}},3$の大小を、不等号を使って表しなさい。
この動画を見る
$\sqrt{10},\frac{7}{\sqrt{7}},3$の大小を、不等号を使って表しなさい。
a√bの形に直せ!!

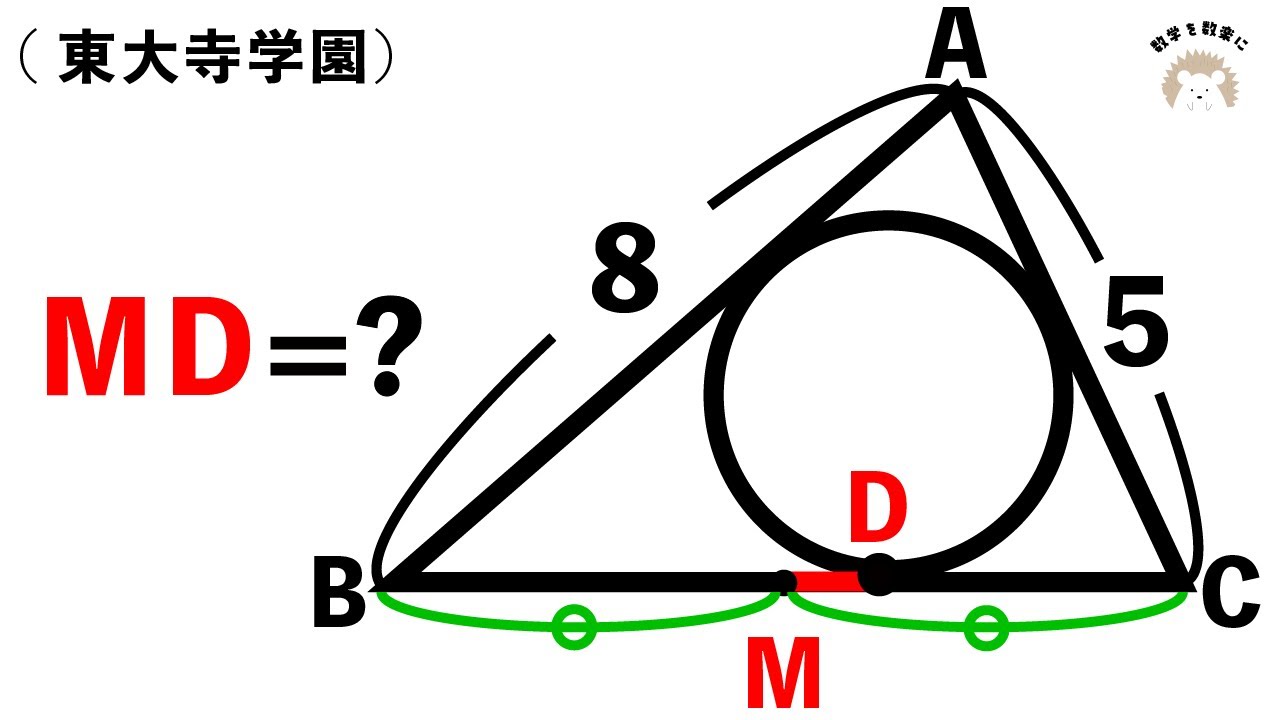
三角形と内接円 東大寺学園
【解法のテクニック…!】平方根:渋谷教育学園幕張高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#渋谷教育学園幕張高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$\sqrt{7}+\sqrt{19}$の整数部分の値を求めなさい。
この動画を見る
$\sqrt{7}+\sqrt{19}$の整数部分の値を求めなさい。
【早解きしなくても…!】整数:大阪教育大学附属高等学校平野校舎~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#大阪教育大学附属高等学校平野校舎
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
連続する4つの自然数があり、小さい2数の和と大きい2数の和の積が2021になるとき、この4つの自然数を求めなさい。
この動画を見る
連続する4つの自然数があり、小さい2数の和と大きい2数の和の積が2021になるとき、この4つの自然数を求めなさい。
【大切な考え方の全て…!】確率:平安女学院高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#平安女学院高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
1~5の数字が書かれた5枚のカードが入っている箱から、カードを順に2枚取り出す。ただし、1枚目にひいたカードは元に戻さない。1枚目を十の位、2枚目を一の位として2桁の整数を作るとき、3の倍数になる確率を求めよ。
この動画を見る
1~5の数字が書かれた5枚のカードが入っている箱から、カードを順に2枚取り出す。ただし、1枚目にひいたカードは元に戻さない。1枚目を十の位、2枚目を一の位として2桁の整数を作るとき、3の倍数になる確率を求めよ。
二次方程式 法政ニ

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#法政大学第二高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
次の方程式を解け
$7(x^2-10x+25)-3=0$
この動画を見る
次の方程式を解け
$7(x^2-10x+25)-3=0$
直角三角形の中に直角

直角三角形の中に直角

単元:
#数学(中学生)#中1数学#数A#図形の性質#三角形の辺の比(内分・外分・二等分線)#平面図形#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
次の図のxを求めよ。
(図は動画参照)
この動画を見る
次の図のxを求めよ。
(図は動画参照)
中学受験解き方は高校受験の解き方より難しい
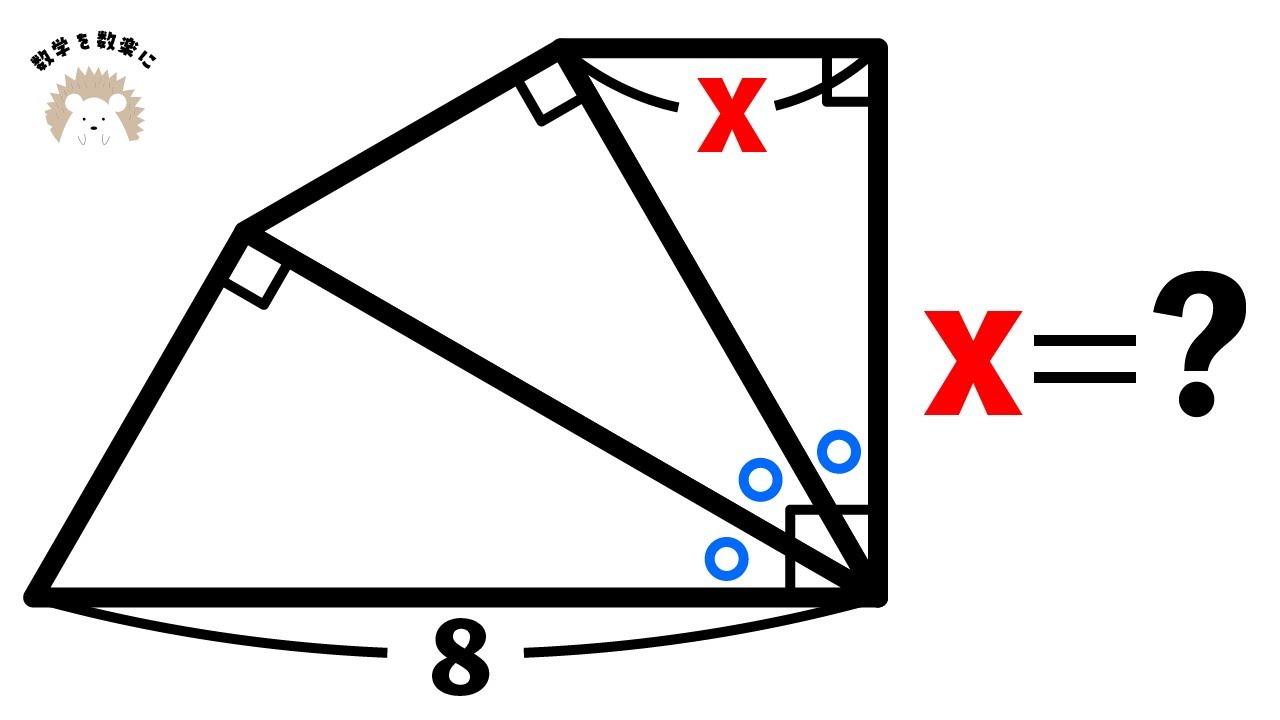
中学受験解き方は高校受験の解き方より難しい

単元:
#算数(中学受験)#数学(中学生)#中3数学#三平方の定理#平面図形#角度と面積#相似と相似を利用した問題
指導講師:
数学を数楽に
問題文全文(内容文):
$x=?$
図は動画内を参照
この動画を見る
$x=?$
図は動画内を参照
中学受験解き方は高校受験の解き方より難しい

分数式の計算
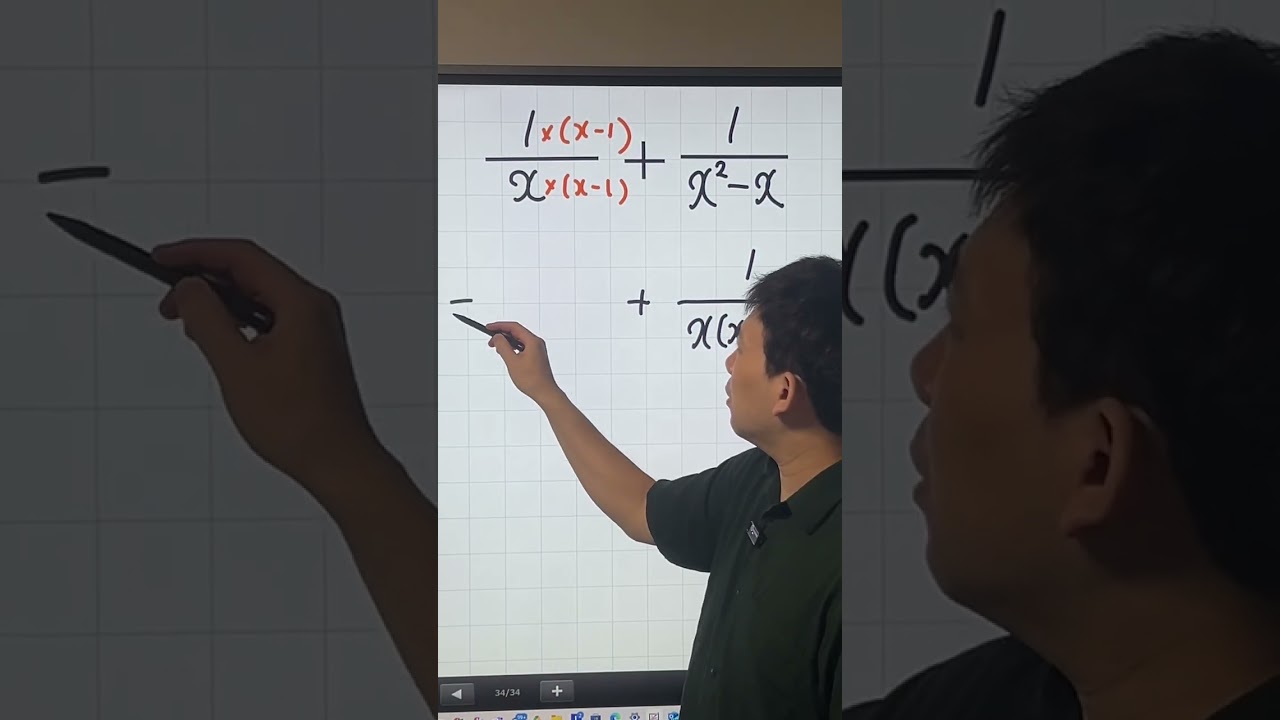
【二匹目のドジョウはいるのか…!?】計算:東海高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#東海高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$2024^2-1976^2$を計算せよ。
この動画を見る
$2024^2-1976^2$を計算せよ。
平行線と比
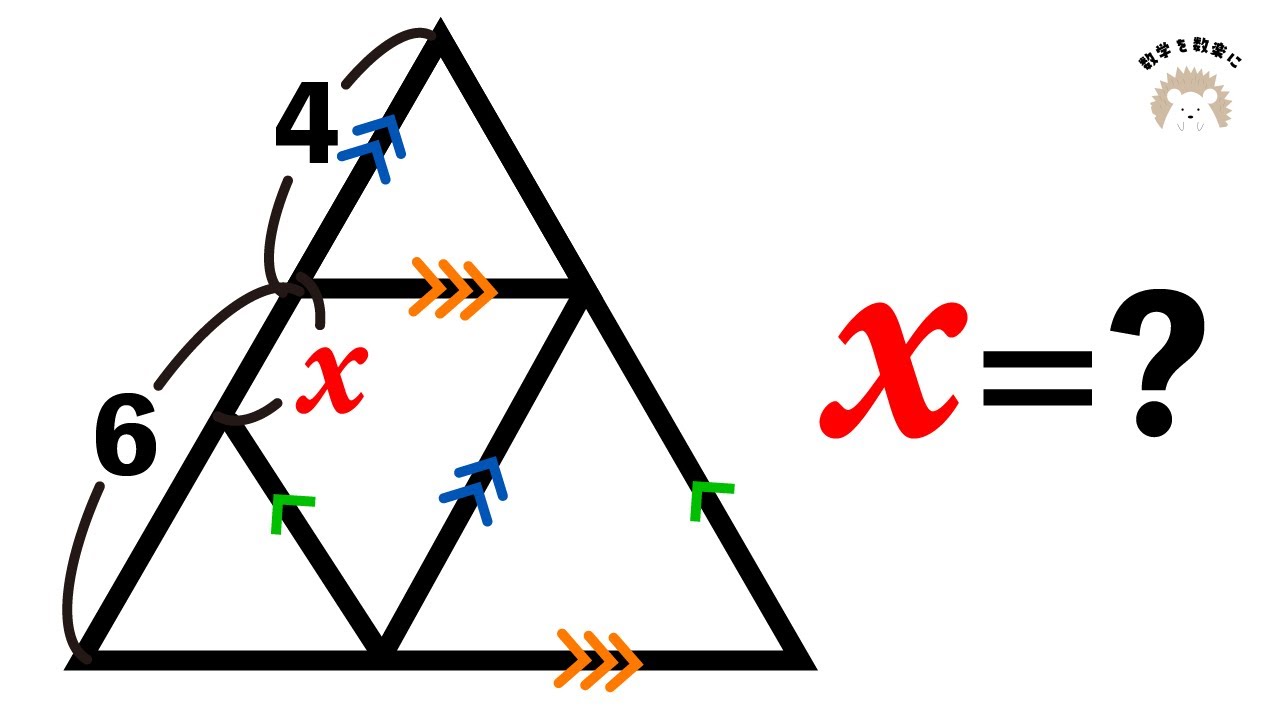
どう計算する?

【スマートに軽やかに…!】因数分解:明治大学付属中野高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#明治大学付属中野高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$x^2+3xy+3x-18y-54$を因数分解しなさい。
この動画を見る
$x^2+3xy+3x-18y-54$を因数分解しなさい。
これなんなん?

単元:
#算数(中学受験)#数学(中学生)#中3数学#三平方の定理#平面図形#角度と面積#図形の移動
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
これなんなん?
※問題文は動画内参照
この動画を見る
これなんなん?
※問題文は動画内参照
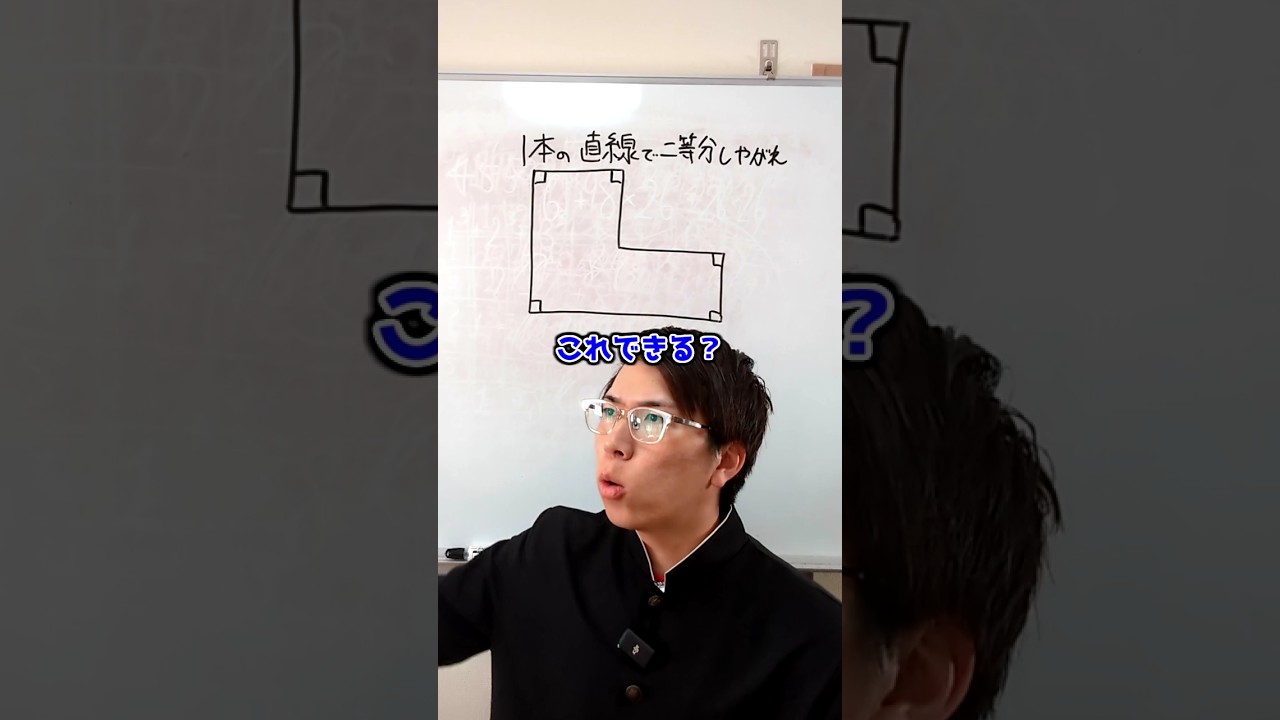
これできる?
単元:
#算数(中学受験)#数学(中学生)#中1数学#平面図形#平面図形その他#平面図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
これできる?
【問題文】1本の直線で二等分しなさい。
※図は動画内参照
この動画を見る
これできる?
【問題文】1本の直線で二等分しなさい。
※図は動画内参照
a√bの形に直せ!!

【そのままでも…!】平方根:法政大学第二高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#法政大学第二高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$(5+\sqrt3+\sqrt5)(5+\sqrt3-\sqrt5)$を展開しなさい。
この動画を見る
$(5+\sqrt3+\sqrt5)(5+\sqrt3-\sqrt5)$を展開しなさい。
これできる?

二次方程式 あなたはどう解く? 東邦大附属東邦

【保存版】円を三等分する方法

単元:
#数学(中学生)#中3数学#三平方の定理#平面図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
【保存版】円を三等分する方法について解説しています。
※図は動画内参照
この動画を見る
【保存版】円を三等分する方法について解説しています。
※図は動画内参照
【分かりやすく順を追って…!】整数:福岡大学附属大濠高等学校~全国入試問題解法
単元:
#整数の性質#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
二つの正の整数を $m,n$とする。
$1 < \sqrt m < 2$, $5 < \sqrt n < 6 $ のとき、$ m + n $ で作られる素数は $\Box$ 通りある。
この動画を見る
二つの正の整数を $m,n$とする。
$1 < \sqrt m < 2$, $5 < \sqrt n < 6 $ のとき、$ m + n $ で作られる素数は $\Box$ 通りある。
【分かりやすく順を追って…!】整数:福岡大学附属大濠高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#福岡大学附属大濠高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
正の整数$m,n$:$1 \lt \sqrt{m} \lt 2, 5 \lt \sqrt{n} \lt 6$のとき、$m+n$で作られる素数は何通りか求めよ。
この動画を見る
正の整数$m,n$:$1 \lt \sqrt{m} \lt 2, 5 \lt \sqrt{n} \lt 6$のとき、$m+n$で作られる素数は何通りか求めよ。
