 数学(中学生)
数学(中学生)
 数学(中学生)
数学(中学生)
2つの接線に囲まれた円の面積 西武文理 2022入試問題解説 20問目
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
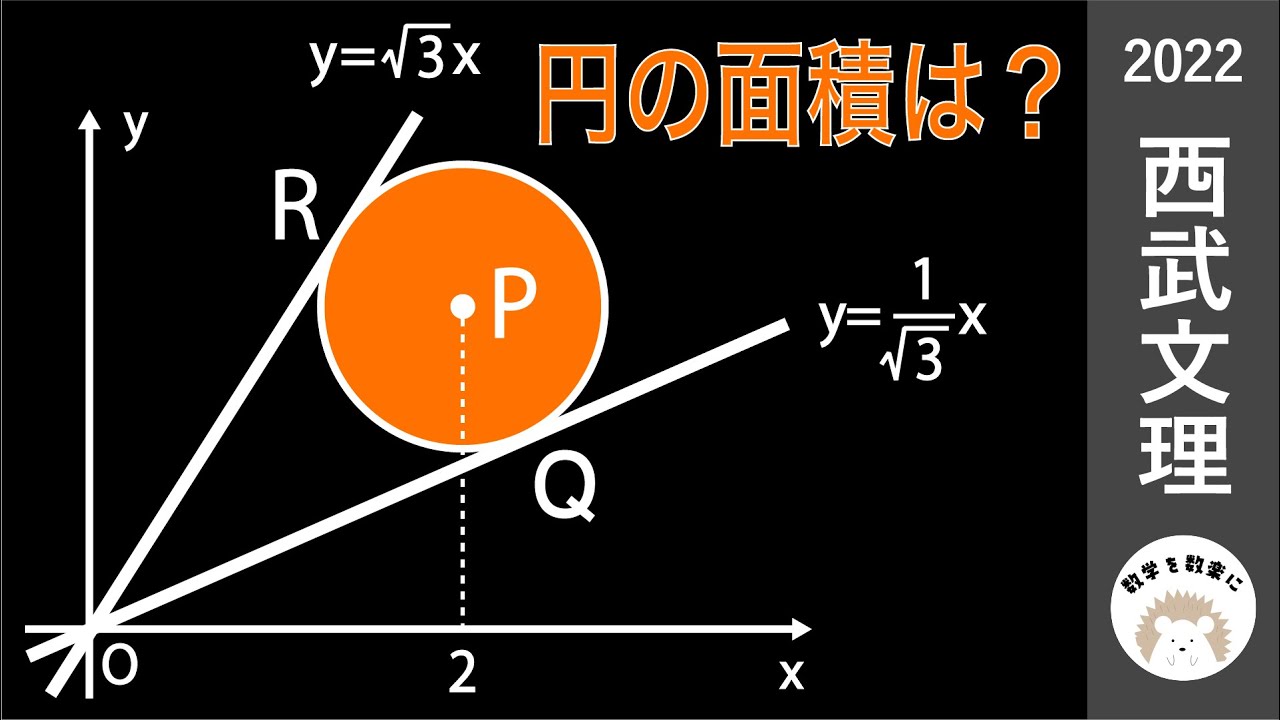
円の面積は?
*図は動画内参照
2022西武学園文理高等学校
この動画を見る
円の面積は?
*図は動画内参照
2022西武学園文理高等学校
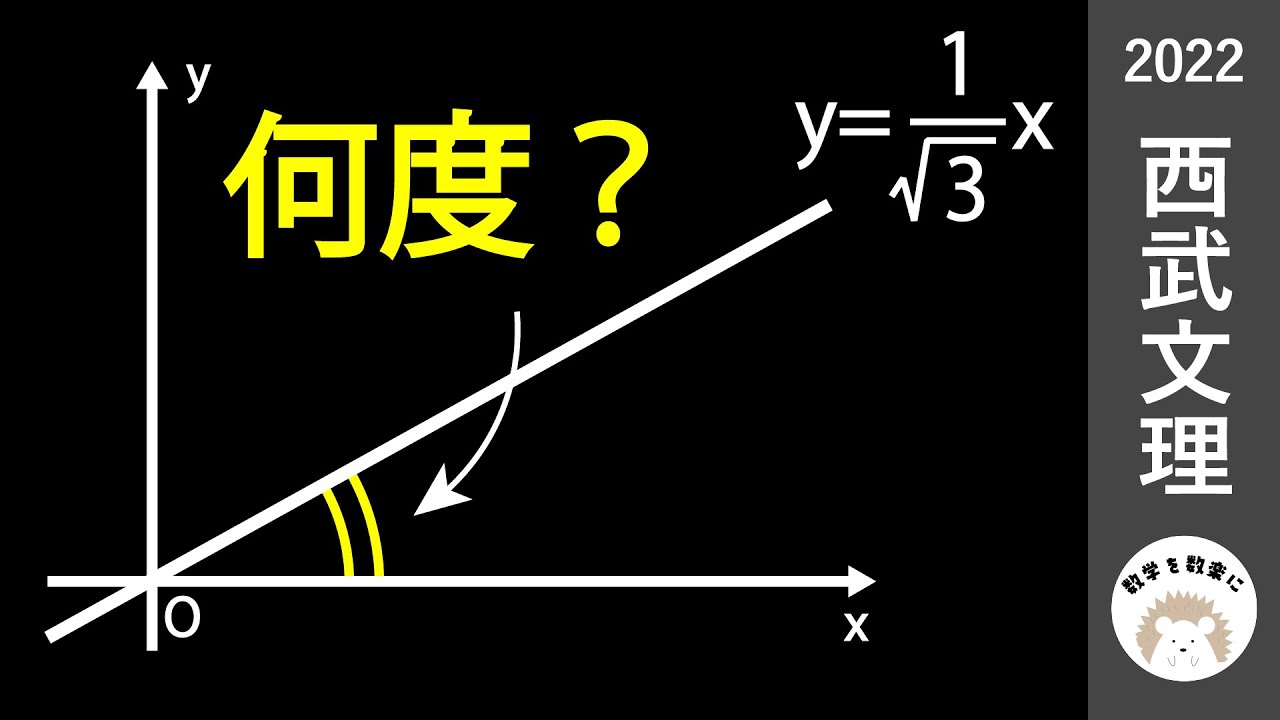
【裏技】三平方の定理の規則

ルートの傾き 西武文理 2022入試問題解説19問目
2022東北医科薬科大(医)微分・積分の基本問題

単元:
#数学(中学生)#数Ⅱ#微分法と積分法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$f(x)=x^4-4x^3$上の$(P,f(P))$における接線を$\ell $とする.
(1)$f(x)$と$\ell$の共有点が接線のみである$P$の範囲を求めよ.
(2)$P$が最小値のとき,$f(x)$と$\ell$で囲まれる面積を求めよ.
東北医科薬科大(医)過去問
この動画を見る
$f(x)=x^4-4x^3$上の$(P,f(P))$における接線を$\ell $とする.
(1)$f(x)$と$\ell$の共有点が接線のみである$P$の範囲を求めよ.
(2)$P$が最小値のとき,$f(x)$と$\ell$で囲まれる面積を求めよ.
東北医科薬科大(医)過去問
球 中央大学附属(推薦)2022入試問題解説18問目

単元:
#数学(中学生)#数A#図形の性質#方べきの定理と2つの円の関係#立体図形#体積・表面積・回転体・水量・変化のグラフ#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
半径の差が1
表面積の和が34π
2つの球の体積の和は?
2022中央大学附属高等学校(推薦)
この動画を見る
半径の差が1
表面積の和が34π
2つの球の体積の和は?
2022中央大学附属高等学校(推薦)
連立方程式 ラ・サール 2022入試問題解説17問目

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=y(z+2) = (x+y)z$ (x,y,z:正の数)
$z=?$ $\frac{y}{x} =?$
2022ラ・サール高等学校
この動画を見る
$x=y(z+2) = (x+y)z$ (x,y,z:正の数)
$z=?$ $\frac{y}{x} =?$
2022ラ・サール高等学校
三平方の定理のこれ知ってる?

色々解き方あると思いますが僕はこう解きました 2次方程式と比 専修大学松戸 2022入試問題解説16問目

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式
$ax^2-2ax-b=0$
1つの解が$x=1+ \sqrt {10}$
a:b=?
2022専修大学松戸高等学校
この動画を見る
2次方程式
$ax^2-2ax-b=0$
1つの解が$x=1+ \sqrt {10}$
a:b=?
2022専修大学松戸高等学校
【まず、オーソドックスに正解を出そう!】文字式:久留米大学附設高等学校~全国入試問題解法
単元:
#数学(中学生)#高校入試過去問(数学)#久留米大学附設高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
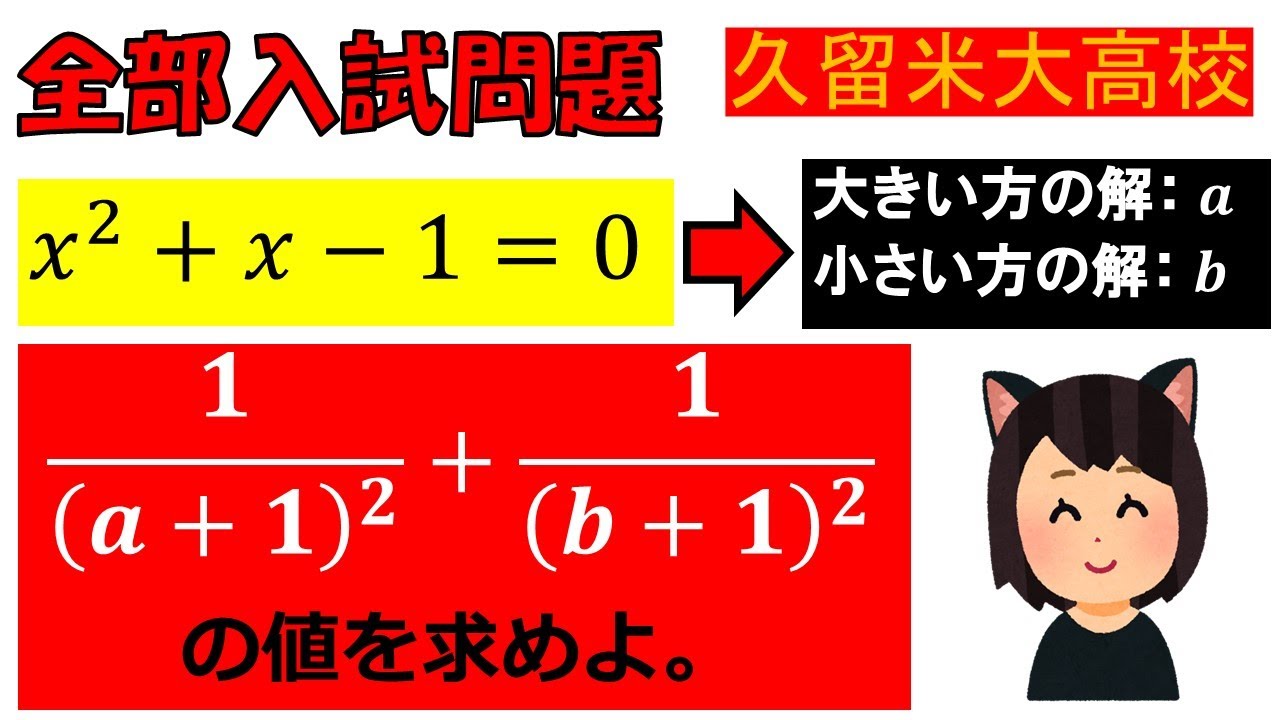
$x^2+x-1=0$
↓
大きいほうの解:a
小さいほうの解:b
$\displaystyle \frac{1}{(a+1)^2}+\displaystyle \frac{1}{(b+1)^2}$
の値を求めよ。
この動画を見る
$x^2+x-1=0$
↓
大きいほうの解:a
小さいほうの解:b
$\displaystyle \frac{1}{(a+1)^2}+\displaystyle \frac{1}{(b+1)^2}$
の値を求めよ。
【中学数学】苦手かどうか分かる問題~相似の問題演習~【中3数学】
単元:
#数学(中学生)#中3数学#相似な図形
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
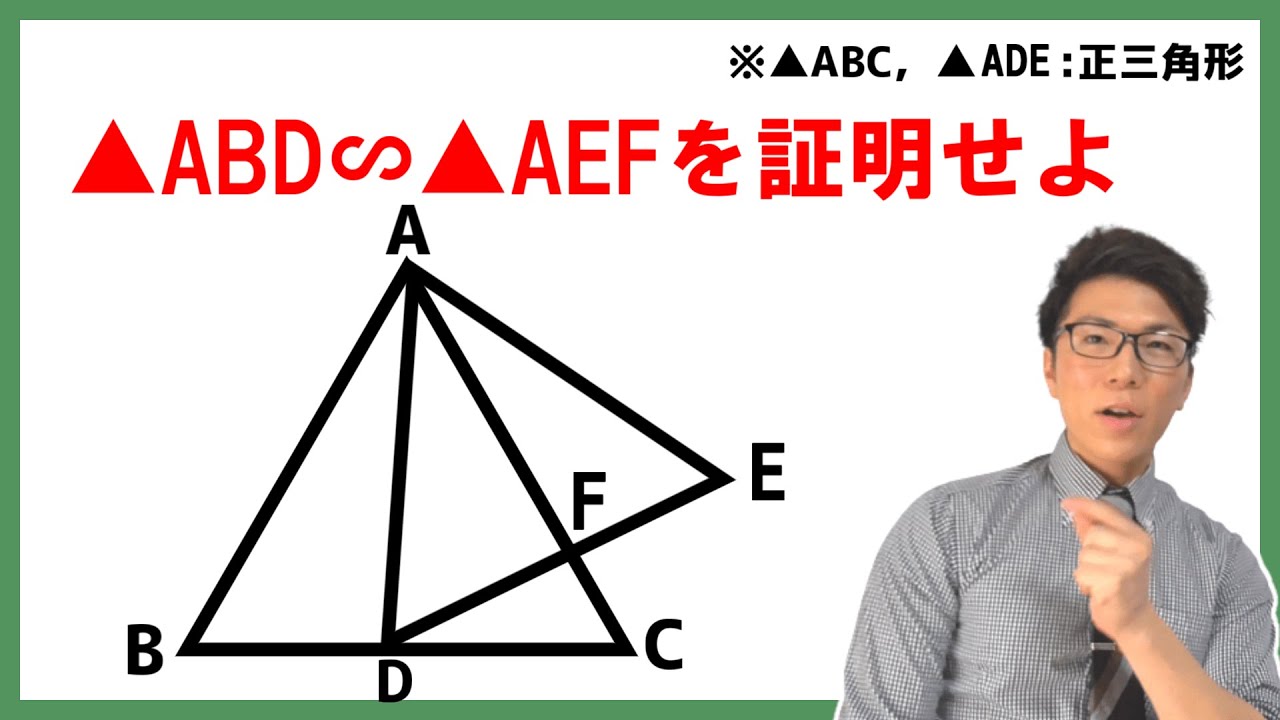
$\triangle ABC$と$\triangle ADE$はともに正三角形である。この時$\triangle ABC$ ∽ $\triangle AEF$を証明せよ。
(図は動画参照)
この動画を見る
$\triangle ABC$と$\triangle ADE$はともに正三角形である。この時$\triangle ABC$ ∽ $\triangle AEF$を証明せよ。
(図は動画参照)
2022年市川高校 ヒントがなければ超難問

単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$a,b$を正の数とする.
$a^2+4b^2=4$のとき,$ab$の最大値を求めよ.
図を参考にしても良い.
市川高校過去問
この動画を見る
$a,b$を正の数とする.
$a^2+4b^2=4$のとき,$ab$の最大値を求めよ.
図を参考にしても良い.
市川高校過去問
四乗の和 渋谷教育学園幕張の最初の一題 動画内に続きの問題あり 2022入試問題解説15問目

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
A=x+y
B=xy
$x^4+y^4=?$
A,Bを用いて表せ
2022渋谷教育学園幕張
この動画を見る
A=x+y
B=xy
$x^4+y^4=?$
A,Bを用いて表せ
2022渋谷教育学園幕張
【3分で理解!流れをつかめ!】確率:東京都立西高等学校~全国入試問題解法
単元:
#数学(中学生)#確率#高校入試過去問(数学)#東京都立西高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
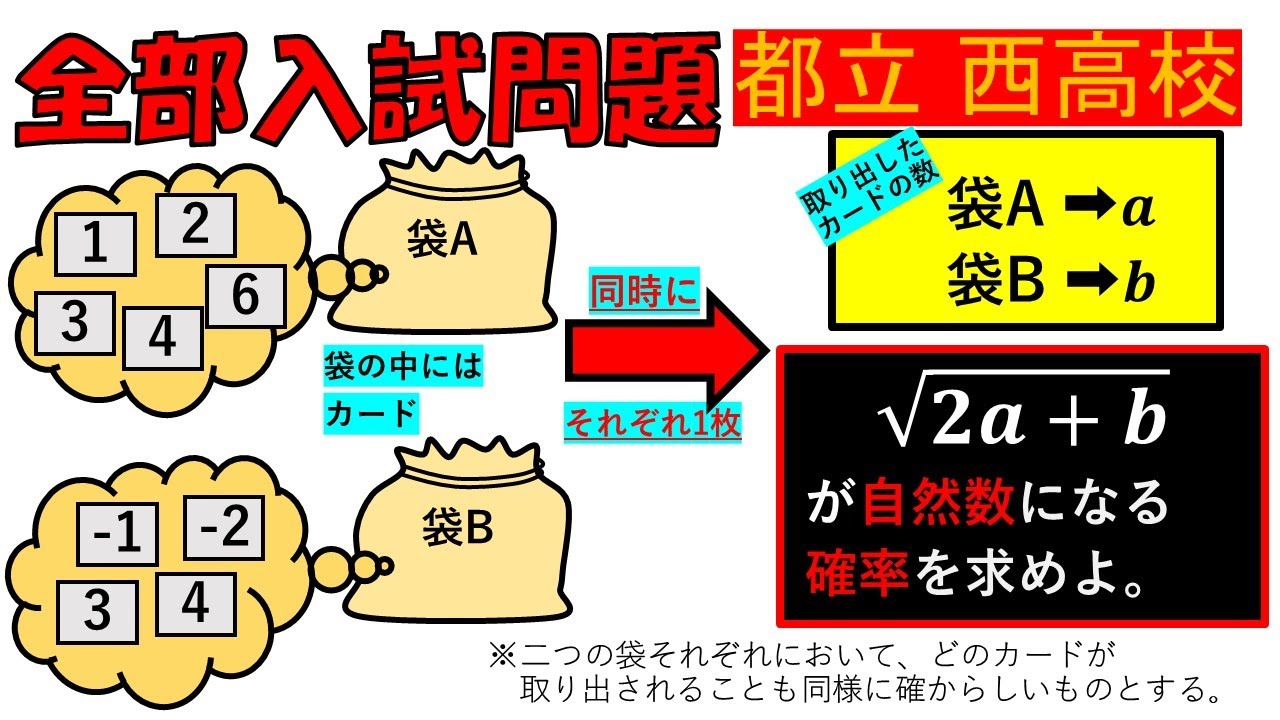
東京都立西高等学校 入試問題
袋A→a
袋B→b
(取り出した カードの数)
$\sqrt{ 2a+b}$が自然数になる 確率を求めよ。
※二つの袋それぞれにおいて、どのカードが取り出されことも
同様に確からしいものとする。
この動画を見る
東京都立西高等学校 入試問題
袋A→a
袋B→b
(取り出した カードの数)
$\sqrt{ 2a+b}$が自然数になる 確率を求めよ。
※二つの袋それぞれにおいて、どのカードが取り出されことも
同様に確からしいものとする。
🟨にあてはまる数は? 連分数 渋谷教育学園幕張 2022入試問題解説14問目
単元:
#数学(中学生)#数Ⅱ#式と証明#整式の除法・分数式・二項定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
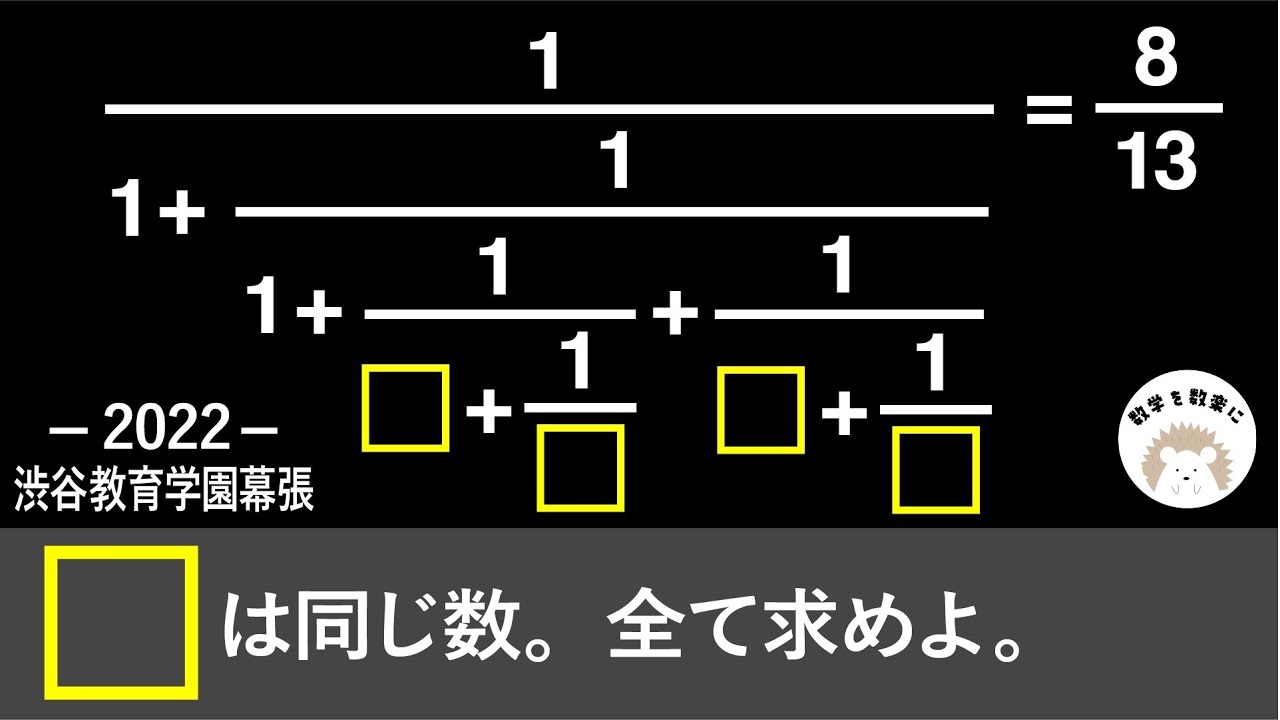
$\frac{1}{1+\frac{1}{1+\frac{1}{▢+\frac{1}{▢}}+\frac{1}{▢+\frac{1}{▢}}}}$=$\frac{8}{13}$
▢は同じ数。全て求めよ。
2022渋谷教育学園幕張
この動画を見る
$\frac{1}{1+\frac{1}{1+\frac{1}{▢+\frac{1}{▢}}+\frac{1}{▢+\frac{1}{▢}}}}$=$\frac{8}{13}$
▢は同じ数。全て求めよ。
2022渋谷教育学園幕張
平均値=中央値 昭和学院秀英 2022入試問題解説13問目

単元:
#数学(中学生)#数Ⅰ#データの分析#データの分析#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
x点 2点 4点 8点 3点 3点 7点 7点
この得点の平均値と中央値が一致したとき
x=?(*$x \geqq 0$)
2022昭和学院秀英高等学校
この動画を見る
x点 2点 4点 8点 3点 3点 7点 7点
この得点の平均値と中央値が一致したとき
x=?(*$x \geqq 0$)
2022昭和学院秀英高等学校
2022乗 昭和学院秀英2022入試問題解説12問目

単元:
#数学(中学生)#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$(\sqrt 5 + 2)^{2022}(\sqrt 5 -2)^{2020}+(\sqrt 5 +2)^{2020}(\sqrt 5 -2)^{2022}$
2022昭和学院秀英高等学校
この動画を見る
$(\sqrt 5 + 2)^{2022}(\sqrt 5 -2)^{2020}+(\sqrt 5 +2)^{2020}(\sqrt 5 -2)^{2022}$
2022昭和学院秀英高等学校
因数分解 中学生の解き方 高校生の解き方 昭和学院秀英 2022入試問題解説11問目

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$ax^2-(a^2+a-2)x-2(a+1)$を因数分解せよ
2022昭和学院秀英高等学校
この動画を見る
$ax^2-(a^2+a-2)x-2(a+1)$を因数分解せよ
2022昭和学院秀英高等学校
正五角形の対角線の長さと面積比 日大習志野2022 入試問題解説 9問目
単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
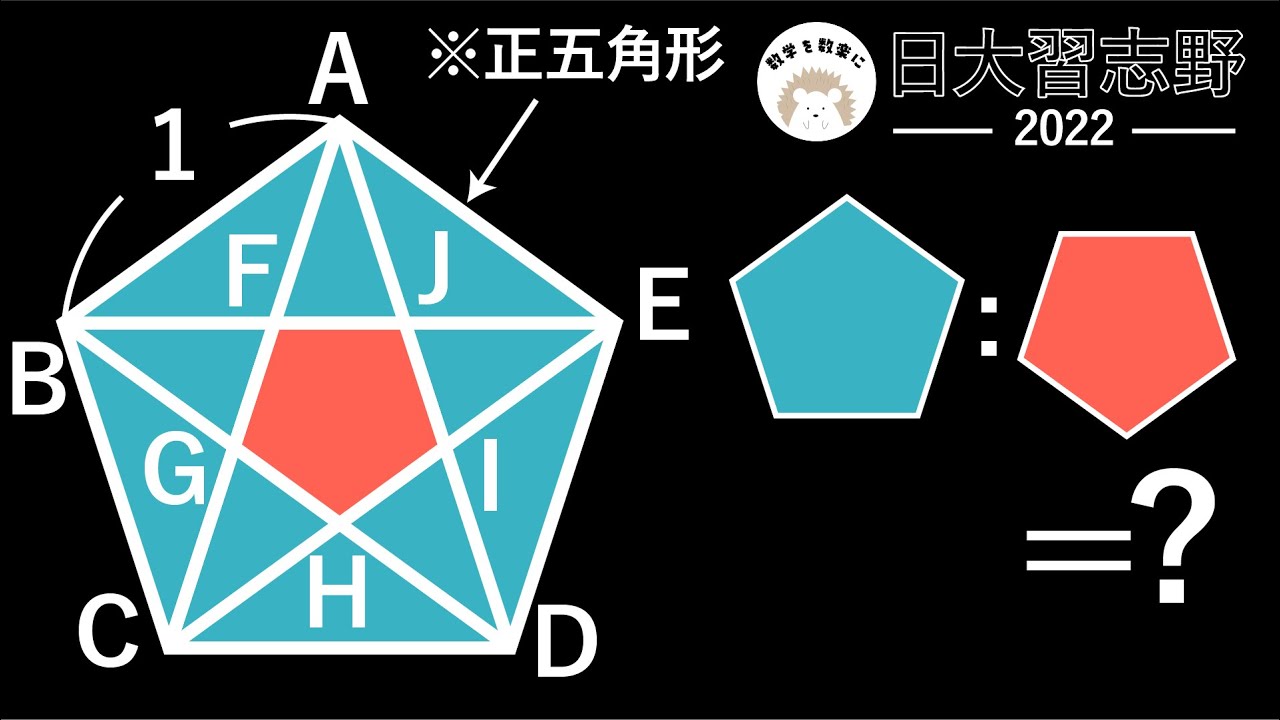
(1)AC=?
(2)五角形ABCDE:五角形FGHIJ
*図は動画内参照
2022日本大学習志野高等学校
この動画を見る
(1)AC=?
(2)五角形ABCDE:五角形FGHIJ
*図は動画内参照
2022日本大学習志野高等学校
時が止まった。。。日大習志野 2022入試問題解説8問目

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=2-3 \sqrt 2 $
$x^2 -4x-15 = ?$
2022日本大学習志野高等学校
この動画を見る
$x=2-3 \sqrt 2 $
$x^2 -4x-15 = ?$
2022日本大学習志野高等学校
最小公倍数 意外に難しい!?青雲 2022入試問題解説 7問目

単元:
#計算と数の性質#数学(中学生)#約数・倍数を利用する問題#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
nと12の最小公倍数は180
nの値をすべて求めよ
2022青雲高等学校
この動画を見る
nと12の最小公倍数は180
nの値をすべて求めよ
2022青雲高等学校
見える? 青雲 2022入試問題解説6問目
単元:
#数学(中学生)#中1数学#中2数学#平面図形#角度と面積#平面図形#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
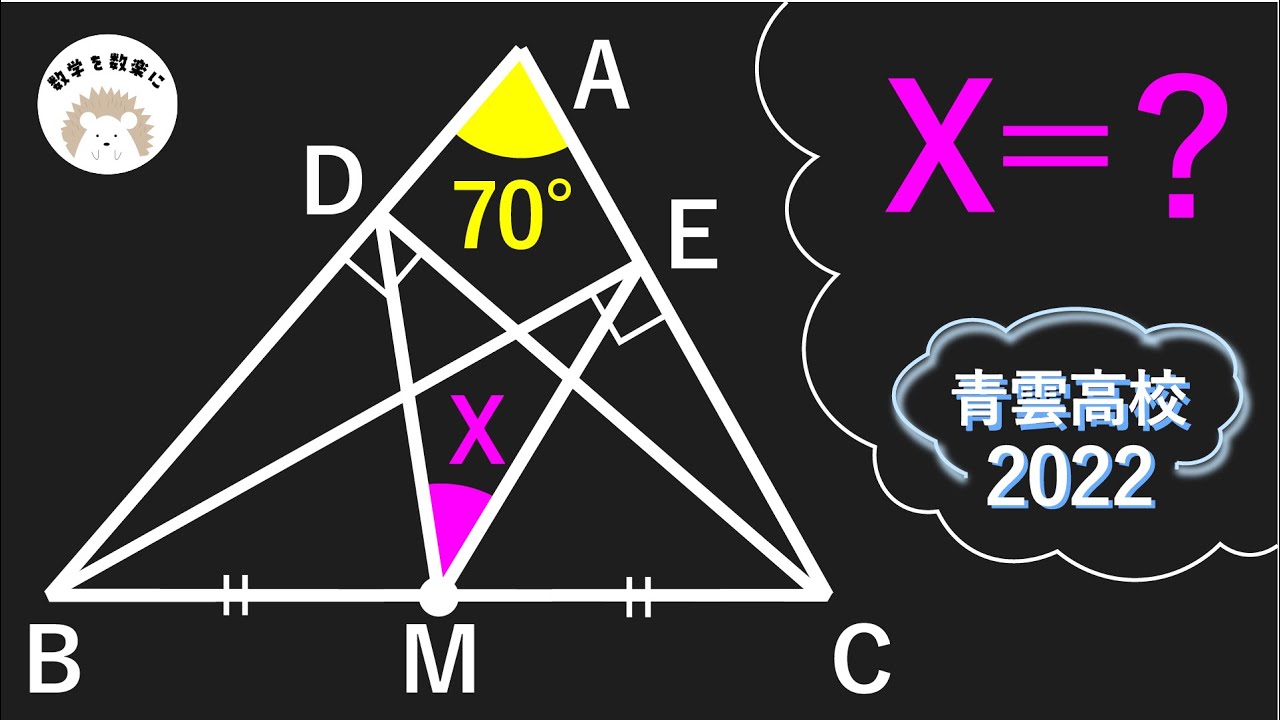
$\angle DME =?$
*図は動画内参照
2022青雲高等学校
この動画を見る
$\angle DME =?$
*図は動画内参照
2022青雲高等学校
2次方程式 〇〇するな! 青雲 2022入試問題解説5問目

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
2次方程式を解け
$\frac{1}{2}(\sqrt 2x-1)^2 -1 = 0$
2022青雲高等学校
この動画を見る
2次方程式を解け
$\frac{1}{2}(\sqrt 2x-1)^2 -1 = 0$
2022青雲高等学校
【文章題から図形をイメージする!!】図形:青山学院高等部~全国入試問題解法
単元:
#数学(中学生)#平面図形#高校入試過去問(数学)#青山学院高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
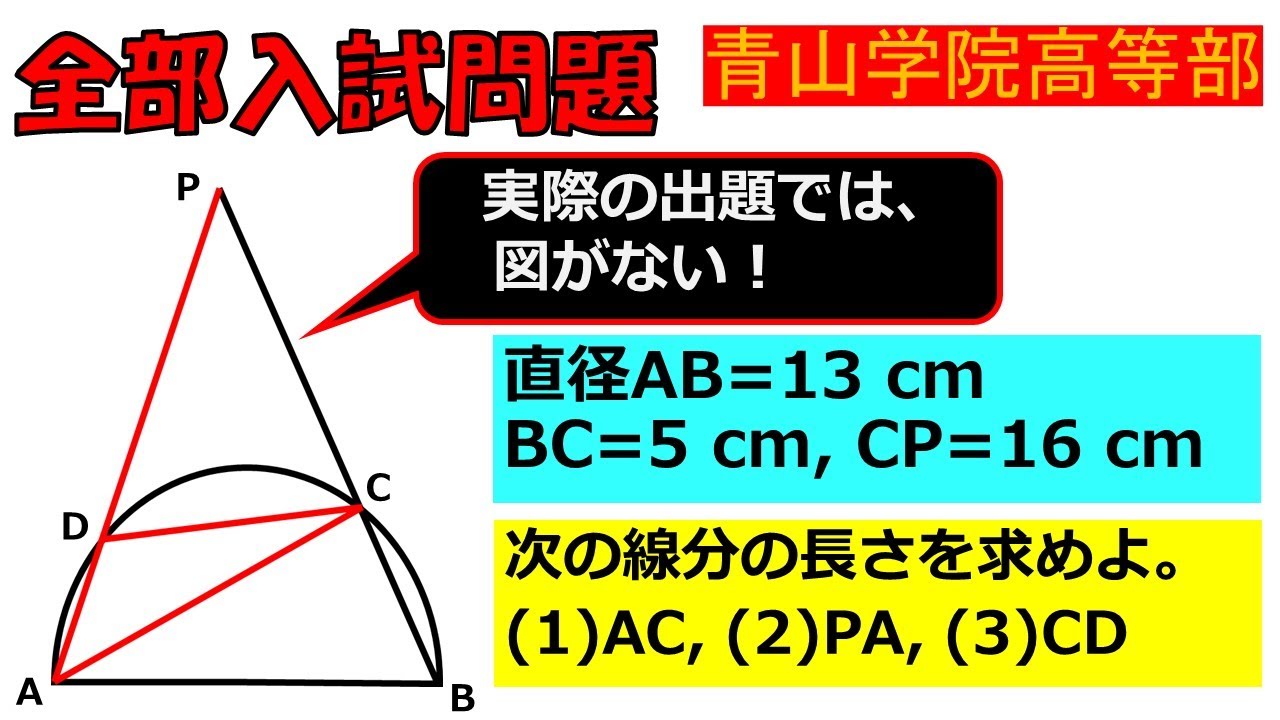
入試問題~青山学院高等部
直径AB=13 cm
BC=5 cm, CP=16 cm
次の線分の長さを求めよ。
録 (1)AC, (2)PA, (3)CD
※図は動画内参照
この動画を見る
入試問題~青山学院高等部
直径AB=13 cm
BC=5 cm, CP=16 cm
次の線分の長さを求めよ。
録 (1)AC, (2)PA, (3)CD
※図は動画内参照
【中学数学】平行線の使い方知ってる?~合同の証明の問題演習~【中2数学】
気づけば一瞬!! 平均値 早稲田佐賀 2022入試問題解説4問目

単元:
#数学(中学生)#数Ⅰ#データの分析#データの分析#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
箱の中に1⃣、2⃣、3⃣、4⃣、5⃣のカードがある。
中から3枚を取り出し、出た順に一の位、十の位、百の位として3ケタの整数を作った。
作られる3ケタの整数全ての平均値を求めよ。
2022早稲田佐賀高等学校
この動画を見る
箱の中に1⃣、2⃣、3⃣、4⃣、5⃣のカードがある。
中から3枚を取り出し、出た順に一の位、十の位、百の位として3ケタの整数を作った。
作られる3ケタの整数全ての平均値を求めよ。
2022早稲田佐賀高等学校
【実践!計算しながら思考する!】整数:青山学院高等部~全国入試問題解法

単元:
#数学(中学生)#高校入試過去問(数学)#青山学院高等部
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
入試問題~青山学院高等部
自然数を5で割ったときの 余りを$\lt n \gt $で表すものとする。
例)
$ \lt 17 \gt =2$
$ \lt 43 \gt =4$
$ \lt 1 \gt =1$
次の値を求めよ。
$ \lt 1^9 \gt + \lt 2^9 \gt +\lt 3^9 \gt +・・・・+\lt 9^9 \gt +\lt 10^9 \gt $
この動画を見る
入試問題~青山学院高等部
自然数を5で割ったときの 余りを$\lt n \gt $で表すものとする。
例)
$ \lt 17 \gt =2$
$ \lt 43 \gt =4$
$ \lt 1 \gt =1$
次の値を求めよ。
$ \lt 1^9 \gt + \lt 2^9 \gt +\lt 3^9 \gt +・・・・+\lt 9^9 \gt +\lt 10^9 \gt $
【中学数学】コラッツ予想が高校入試に~愛知県公立高校入試2020~【高校受験】

単元:
#数学(中学生)#高校入試過去問(数学)#愛知県公立高校入試
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
次の文章は、自然数の計算について述べたものである。
文章中のa、bにあてはまる数を書け。
与えられた自然数を次の規則にしたがって計算する。
奇数ならば、3倍して1を加え、偶数ならば、2で割る。
結果が1となれば計算を終わり、結果が1とならなければ、上の計算を続ける。
例えば、与えられた自然数が3のときは、下のように7回の計算で1となる。
3→10→5→16→8→4→2→1
このとき、7回の計算で1となる自然数は、3を含めて4個あり、小さい順に並べると、3、a、b、128である。
この動画を見る
次の文章は、自然数の計算について述べたものである。
文章中のa、bにあてはまる数を書け。
与えられた自然数を次の規則にしたがって計算する。
奇数ならば、3倍して1を加え、偶数ならば、2で割る。
結果が1となれば計算を終わり、結果が1とならなければ、上の計算を続ける。
例えば、与えられた自然数が3のときは、下のように7回の計算で1となる。
3→10→5→16→8→4→2→1
このとき、7回の計算で1となる自然数は、3を含めて4個あり、小さい順に並べると、3、a、b、128である。
面積比 早稲田佐賀 動画内誘導あり 2022入試問題解説3問目

単元:
#数学(中学生)#中2数学#平面図形#角度と面積#三角形と四角形#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
△ABC=Sとする
(1)△GDPをSで表せ
(2)AD,BE,CFを3辺にもつ三角形の面積をSで表せ。
*図は動画内参照
2022早稲田佐賀高等学校(改)
この動画を見る
△ABC=Sとする
(1)△GDPをSで表せ
(2)AD,BE,CFを3辺にもつ三角形の面積をSで表せ。
*図は動画内参照
2022早稲田佐賀高等学校(改)
慶應義塾高校の小問です

【裏技】三平方の定理

