数学検定1級
数学検定1級
#68数学検定1級1次「答えはめっちゃスッキリ」 #定積分
単元：
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-1}^{ 1 } \displaystyle \frac{x^4+2x^3+4x^2+6x+2}{x^3+2x^2+2x+4}$ $dx$
出典：数検1級1次
この動画を見る
$\displaystyle \int_{-1}^{ 1 } \displaystyle \frac{x^4+2x^3+4x^2+6x+2}{x^3+2x^2+2x+4}$ $dx$
出典：数検1級1次
#67数学検定1級1次「こんな問題で時間使いたくない」 #因数分解
単元：
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
$xy(x^2-y^2)+yz(y^2-z^2)+zx(z^2-x^2)$を因数分解せよ
出典：数検1級1次
この動画を見る
$xy(x^2-y^2)+yz(y^2-z^2)+zx(z^2-x^2)$を因数分解せよ
出典：数検1級1次
#66数学検定1級1次過去問「怖いのは計算ミスのみ」 #式変形
単元：
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
$(1-\sqrt[ 3 ]{ 2 }+\sqrt[ 3 ]{ 4 })^3$を簡単にせよ
出典：数検1級1次
この動画を見る
$(1-\sqrt[ 3 ]{ 2 }+\sqrt[ 3 ]{ 4 })^3$を簡単にせよ
出典：数検1級1次
#64 #数検1級1次過去問 #高次方程式
単元：
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
$4$次方程式
$x^4-4x-1=0$について、次の問いに答えよ。
１．上の方程式の実数解を求めよ。
２．上の方程式の虚数解を求めよ
出典：数検1級1次過去問
この動画を見る
$4$次方程式
$x^4-4x-1=0$について、次の問いに答えよ。
１．上の方程式の実数解を求めよ。
２．上の方程式の虚数解を求めよ
出典：数検1級1次過去問
#64 #数検1級1次過去問「久しぶりに重積分やってみよー」 #重積分 #高専
単元：
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
領域$D$が次のように与えられている。
$D=\{(x,y)|0 \leq x \leq 1,0 \leq y \leq 1\}$
このとき、次の2重積分を計算せよ。
$\displaystyle \int\displaystyle \int_{D}|x-y|^{-\frac{2}{3}}dxdy$
出典：数検1級1次
この動画を見る
領域$D$が次のように与えられている。
$D=\{(x,y)|0 \leq x \leq 1,0 \leq y \leq 1\}$
このとき、次の2重積分を計算せよ。
$\displaystyle \int\displaystyle \int_{D}|x-y|^{-\frac{2}{3}}dxdy$
出典：数検1級1次
#60数検1級1次「ええ問題！落とし穴に注意」 数検1級1次
単元：
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
全ての実数$x$について
$\displaystyle \frac{\pi}{2} \lt \tan^{-1}x \lt \displaystyle \frac{\pi}{2}$とするとき、次の値を求めよ。
$\tan^{-1}1+\tan^{-1}2+\tan^{-1}3$
出典：数検1級1次
この動画を見る
全ての実数$x$について
$\displaystyle \frac{\pi}{2} \lt \tan^{-1}x \lt \displaystyle \frac{\pi}{2}$とするとき、次の値を求めよ。
$\tan^{-1}1+\tan^{-1}2+\tan^{-1}3$
出典：数検1級1次
#58数検1級1次「ぱっと見はちょろそうだけど・・・」 #方程式
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
方程式
$x^6-14x^4+17x^2-4=0$を解け。
出典：数検1級1次
この動画を見る
方程式
$x^6-14x^4+17x^2-4=0$を解け。
出典：数検1級1次
#56数検１級１次 過去問 #4次方程式
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
方程式
$x^4-4x-1=0$の実数解を求めよ
出典：数検1級1次
この動画を見る
方程式
$x^4-4x-1=0$の実数解を求めよ
出典：数検1級1次
数検1級1次過去問 #微分方程式
単元：
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
$y(0)=1,\ y'(0)=5$
$y''-6y'+9y=6e^{3x}$を満たす微分方程式の解を求めよ。
出典：数字検定1級1次
この動画を見る
$y(0)=1,\ y'(0)=5$
$y''-6y'+9y=6e^{3x}$を満たす微分方程式の解を求めよ。
出典：数字検定1級1次
#51 数検1級1次 過去問 逆三角関数
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#三角関数とグラフ#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
$\sin(\sin^{-1}(-\displaystyle \frac{5}{13})+\cos^{-1}(\displaystyle \frac{4}{5}))$の値を求めよ。
出典：数検1級1次 過去問
この動画を見る
$\sin(\sin^{-1}(-\displaystyle \frac{5}{13})+\cos^{-1}(\displaystyle \frac{4}{5}))$の値を求めよ。
出典：数検1級1次 過去問
#50数検1級１次 過去問 重積分の積分順序の変更
単元：
#数学検定・数学甲子園・数学オリンピック等#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{2}dy\displaystyle \int_{y}^{2}x\sqrt{ x^3+1 }\ dx$を計算せよ。
この動画を見る
$\displaystyle \int_{0}^{2}dy\displaystyle \int_{y}^{2}x\sqrt{ x^3+1 }\ dx$を計算せよ。
#49 数検1級1次 過去問 根号を外す
単元：
#数Ⅰ#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#数と式#２次関数#複素数と方程式#式の計算（整式・展開・因数分解）#2次方程式と2次不等式#2次関数とグラフ#解と判別式・解と係数の関係#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\sqrt[ 3 ]{ -5+2\sqrt{ 13 } }\ $の二重根号をはずせ
この動画を見る
$\sqrt[ 3 ]{ -5+2\sqrt{ 13 } }\ $の二重根号をはずせ
#48 数検1級2次 過去問 整数問題
単元：
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$m,n$：正の整数
$3^m=n^2-117^2$を満たす$m,n$の値を求めよ。
この動画を見る
$m,n$：正の整数
$3^m=n^2-117^2$を満たす$m,n$の値を求めよ。
#47 数検1級1次 過去問 二項定理
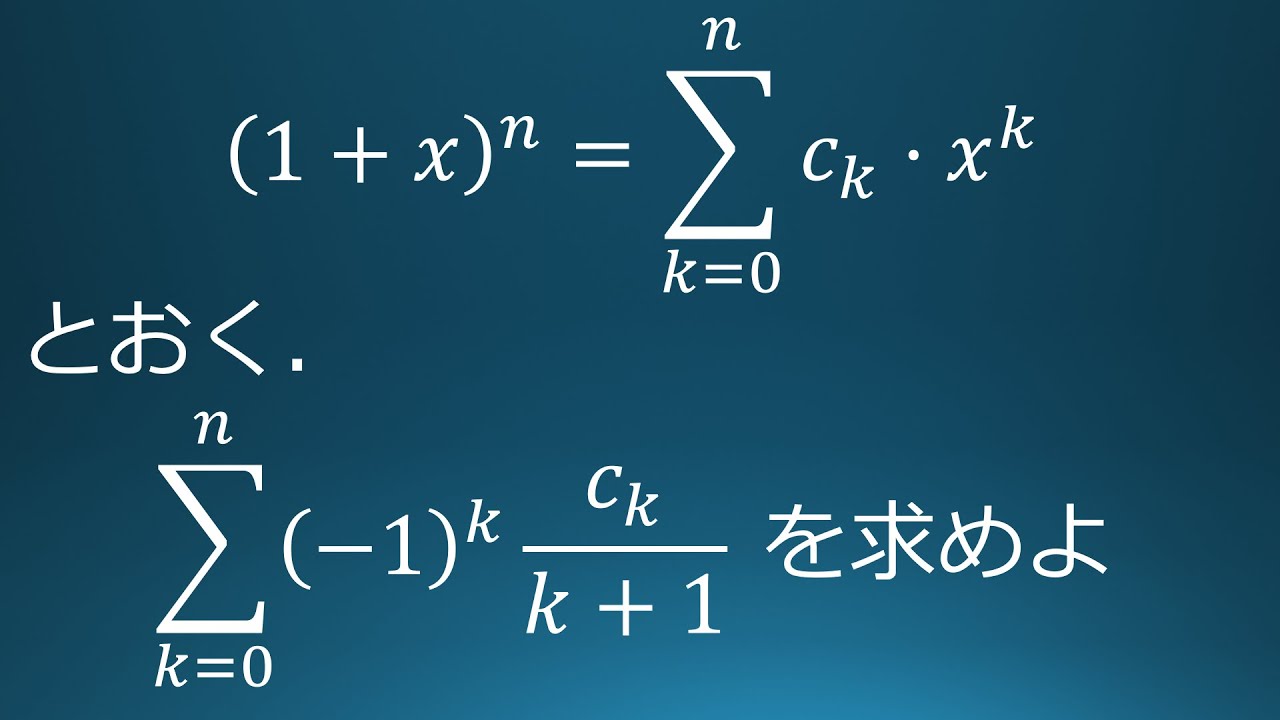
単元：
#数Ⅰ#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#式と証明#微分法と積分法#整式の除法・分数式・二項定理#不定積分・定積分#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$(1+x)^n$を$c_0+c_1x+・・・+c_nx^n$とおく。
$\displaystyle \sum_{k=1}^n(-1)^k\displaystyle \frac{c_k}{k+1}$の値を求めよ。
この動画を見る
$(1+x)^n$を$c_0+c_1x+・・・+c_nx^n$とおく。
$\displaystyle \sum_{k=1}^n(-1)^k\displaystyle \frac{c_k}{k+1}$の値を求めよ。
#39 数検1級1次 過去問 解と係数の関係 整数問題
単元：
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$m,n:$正の整数
$x^3-mx^2+nx-n=0$のすべての解が正の整数であるような組$(m,n)$を求めよ。
この動画を見る
$m,n:$正の整数
$x^3-mx^2+nx-n=0$のすべての解が正の整数であるような組$(m,n)$を求めよ。
#38 数検1級1次 過去問 解と係数の関係
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#解と判別式・解と係数の関係#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$z^3+2z^2+2z+1=0$の3つの解を$\alpha,\beta,\gamma$とする
$\alpha^{2019}+\beta^{2019}+\gamma^{2019}$の値を求めよ。
この動画を見る
$z^3+2z^2+2z+1=0$の3つの解を$\alpha,\beta,\gamma$とする
$\alpha^{2019}+\beta^{2019}+\gamma^{2019}$の値を求めよ。
#37 数検1級1次 過去問 重積分
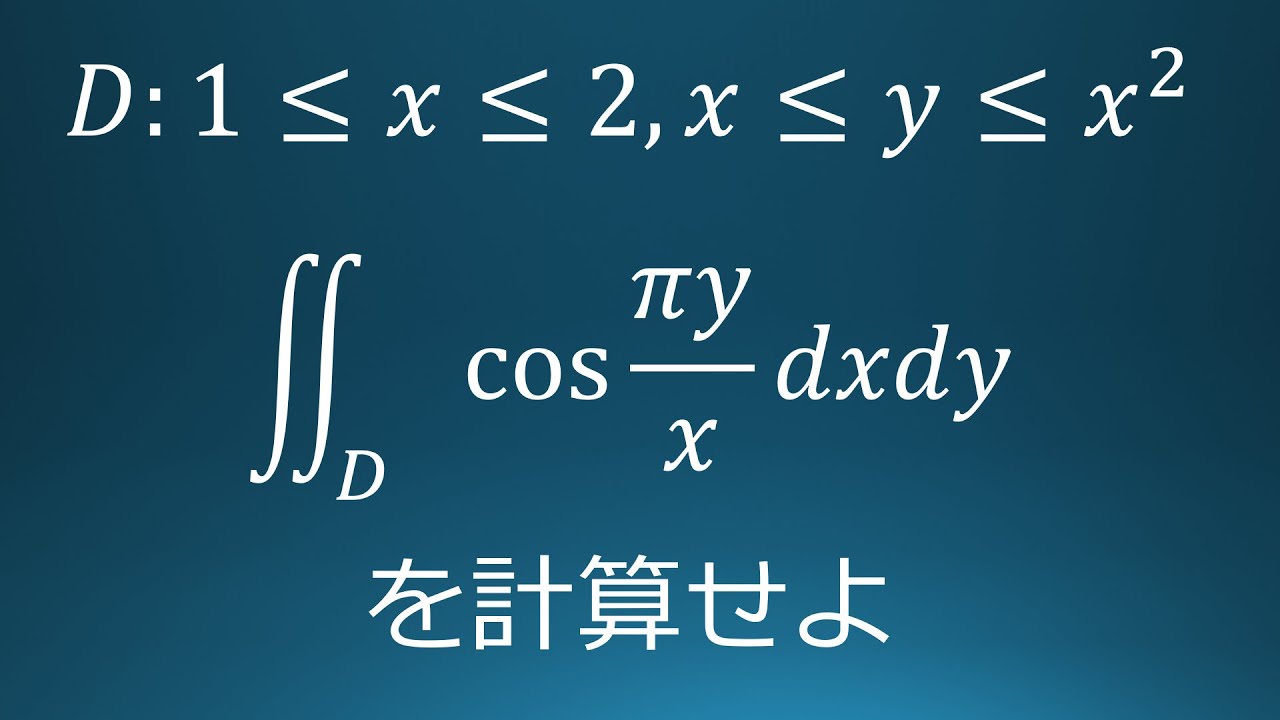
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$D:1 \leqq x \leqq 2,x \leqq y \leqq x^2$
$\displaystyle \int \displaystyle \int \cos\displaystyle \frac{\pi y}{x}\ dxdy$を計算せよ。
この動画を見る
$D:1 \leqq x \leqq 2,x \leqq y \leqq x^2$
$\displaystyle \int \displaystyle \int \cos\displaystyle \frac{\pi y}{x}\ dxdy$を計算せよ。
#36 数検1級1次 過去問 積分
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-1}^{1}\sqrt{ \displaystyle \frac{1+x}{1-x} }\ dx$を計算せよ。
この動画を見る
$\displaystyle \int_{-1}^{1}\sqrt{ \displaystyle \frac{1+x}{1-x} }\ dx$を計算せよ。
#35 数検１級１次 過去問 複素数
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数平面#複素数#複素数平面#数学検定#数学検定1級#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$\sqrt{ 1+\sqrt{ 3 }i }+\sqrt{ 1-\sqrt{ 3 }i }$を簡単にせよ
ただし、外側の平方根の実数部の値は正とする。
この動画を見る
$\sqrt{ 1+\sqrt{ 3 }i }+\sqrt{ 1-\sqrt{ 3 }i }$を簡単にせよ
ただし、外側の平方根の実数部の値は正とする。
#34 数検1級1次 過去問 積分
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{\infty}\displaystyle \frac{1}{(x^2+1)^4}\ dx$を計算せよ。
この動画を見る
$\displaystyle \int_{0}^{\infty}\displaystyle \frac{1}{(x^2+1)^4}\ dx$を計算せよ。
#33 数検1級1次 過去問 区分求積法
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#微分法と積分法#積分とその応用#定積分#不定積分・定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n\displaystyle \frac{1}{\sqrt{ 2nk-k^2 }}$の極限値を求めよ。
この動画を見る
$\displaystyle \lim_{ n \to \infty }\displaystyle \sum_{k=1}^n\displaystyle \frac{1}{\sqrt{ 2nk-k^2 }}$の極限値を求めよ。
#32 数検1級1次 過去問 複素数の方程式
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#複素数平面#複素数#複素数平面#数学検定#数学検定1級#数学(高校生)#数C
指導講師：
ますただ
問題文全文(内容文)：
$z:$複素数
方程式$z^2-z+i\bar{ z }=i$を解け。
この動画を見る
$z:$複素数
方程式$z^2-z+i\bar{ z }=i$を解け。
#31 数検1級1次 過去問 整数問題
単元：
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x^3-y^3=331$を満たす正の整数$x,y$を求めよ。
この動画を見る
$x^3-y^3=331$を満たす正の整数$x,y$を求めよ。
#30 数検1級1次 過去問 複雑な定積分
単元：
#数学検定・数学甲子園・数学オリンピック等#積分とその応用#不定積分#定積分#数学検定#数学検定1級#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
定積分
$\displaystyle \int_{-1}^{1}\displaystyle \frac{x^4+2x^3+4x^2+6x+2}{x^3+2x^2+2x+4}\ dx$を計算せよ。
この動画を見る
定積分
$\displaystyle \int_{-1}^{1}\displaystyle \frac{x^4+2x^3+4x^2+6x+2}{x^3+2x^2+2x+4}\ dx$を計算せよ。
#29 数検1級1次 過去問 解と係数の関係
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#複素数と方程式#解と判別式・解と係数の関係#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x^3+2x^2+4x+7=0$の3つの解を$\alpha,\beta,\gamma$とする
$\alpha^4,\beta^4,\gamma^4$の値を求めよ。
この動画を見る
$x^3+2x^2+4x+7=0$の3つの解を$\alpha,\beta,\gamma$とする
$\alpha^4,\beta^4,\gamma^4$の値を求めよ。
#28 数検1級1次 過去問 Arctanの加法定理
単元：
#数Ⅱ#数学検定・数学甲子園・数学オリンピック等#三角関数#三角関数とグラフ#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
$\tan^{-1}1+\tan^{-1}2+\tan^{-1}3$の値を求めよ。
この動画を見る
$\tan^{-1}1+\tan^{-1}2+\tan^{-1}3$の値を求めよ。
#27 数検1級1次 過去問 整数問題
単元：
#数A#数学検定・数学甲子園・数学オリンピック等#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x,y:$正の整数
$x+y=316$
$x:13$の倍数
$y:11$の倍数
をみたす組$(x,y)$をすべて求めよ。
この動画を見る
$x,y:$正の整数
$x+y=316$
$x:13$の倍数
$y:11$の倍数
をみたす組$(x,y)$をすべて求めよ。
#26 数検1級1次 過去問 複雑な方程式
単元：
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#数と式#数学検定#数学検定1級
指導講師：
ますただ
問題文全文(内容文)：
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y+z=6 \\
x^3+y^3+z^3=36 \\
xyz=6
\end{array}
\right.
\end{eqnarray}$
において、$x \gt y \gt z$を満たす解を求めよ。
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+y+z=6 \\
x^3+y^3+z^3=36 \\
xyz=6
\end{array}
\right.
\end{eqnarray}$
において、$x \gt y \gt z$を満たす解を求めよ。
#25 数検1級1次 過去問 複雑な方程式
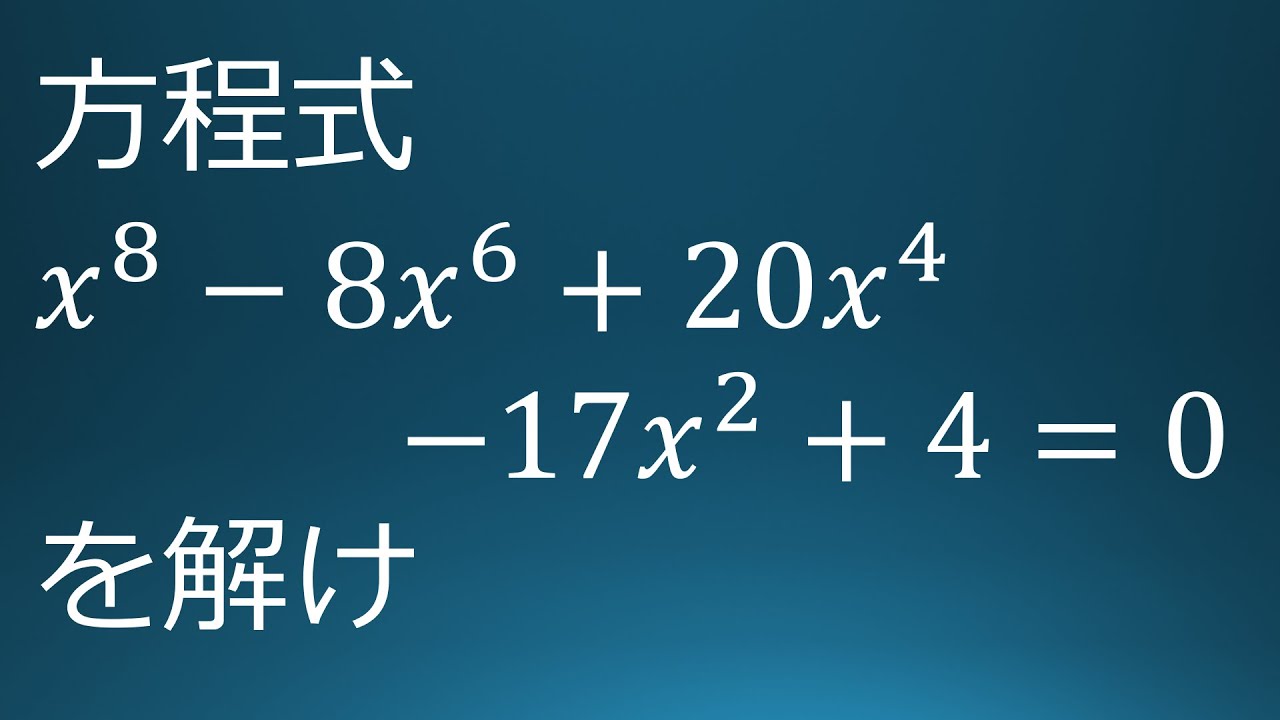
単元：
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#数と式#数学検定#数学検定1級#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
方程式
$x^8-8x^6+20x^4-17x^2+4=0$を解け。
この動画を見る
方程式
$x^8-8x^6+20x^4-17x^2+4=0$を解け。
練習問題44 東京工業大学 極限値 数検1級 教員採用試験（数学）
単元：
#数学検定・数学甲子園・数学オリンピック等#関数と極限#数列の極限#その他#数学検定#数学検定1級#数学(高校生)#数Ⅲ#教員採用試験
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \lim_{ n \to \infty }(\displaystyle \frac{{}_{ 3n } C_n}{{}_{ 2n } C_n})^\frac{1}{n}$の極限値を求めよ。
$\displaystyle \int_{0}^{1}f(x)dx=\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\displaystyle \sum_{k=1}^n f(\displaystyle \frac{k}{n})$
出典：東京工業大学 練習問題
この動画を見る
$\displaystyle \lim_{ n \to \infty }(\displaystyle \frac{{}_{ 3n } C_n}{{}_{ 2n } C_n})^\frac{1}{n}$の極限値を求めよ。
$\displaystyle \int_{0}^{1}f(x)dx=\displaystyle \lim_{ n \to \infty }\displaystyle \frac{1}{n}\displaystyle \sum_{k=1}^n f(\displaystyle \frac{k}{n})$
出典：東京工業大学 練習問題