 中高教材
中高教材
 中高教材
中高教材
【数Ⅰ】【図形と計量】空間の応用2 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
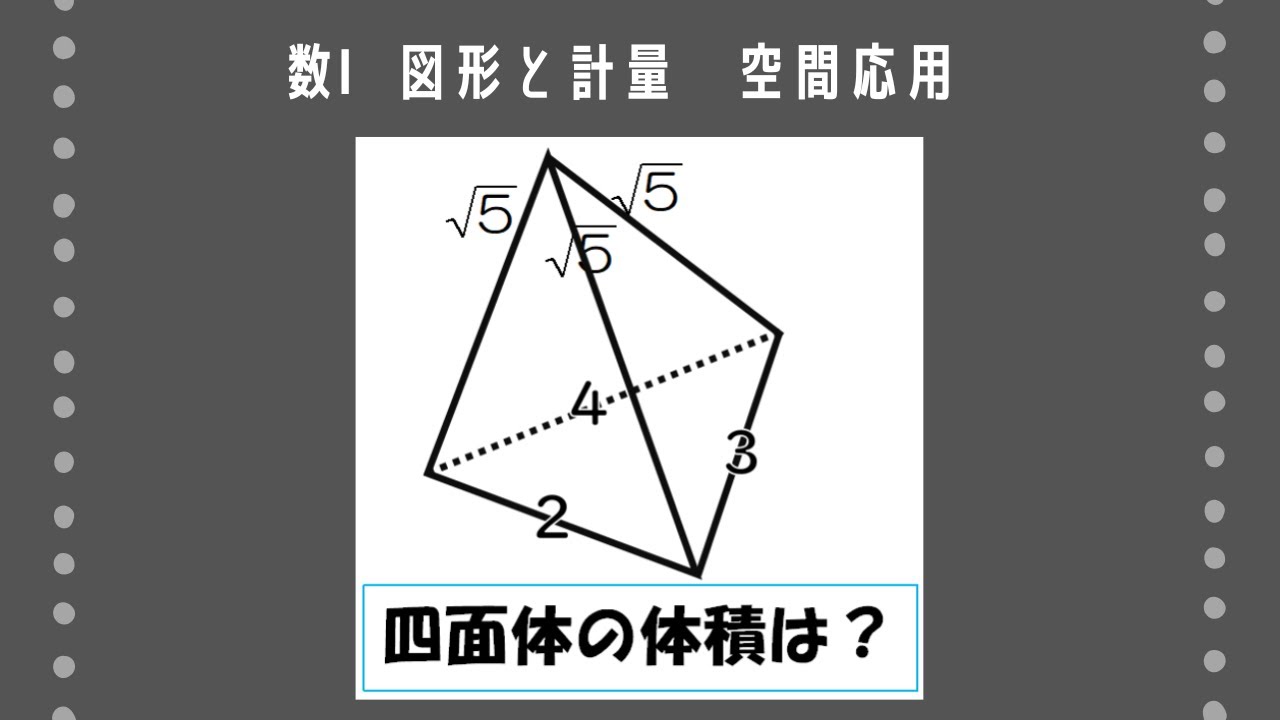
$\rm PA=PB=PC=\sqrt5,AB=3,BC=3,CA=4$である三角錐PABCの体積を求めよ。
この動画を見る
$\rm PA=PB=PC=\sqrt5,AB=3,BC=3,CA=4$である三角錐PABCの体積を求めよ。
【数Ⅰ】【図形と計量】空間の応用1 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
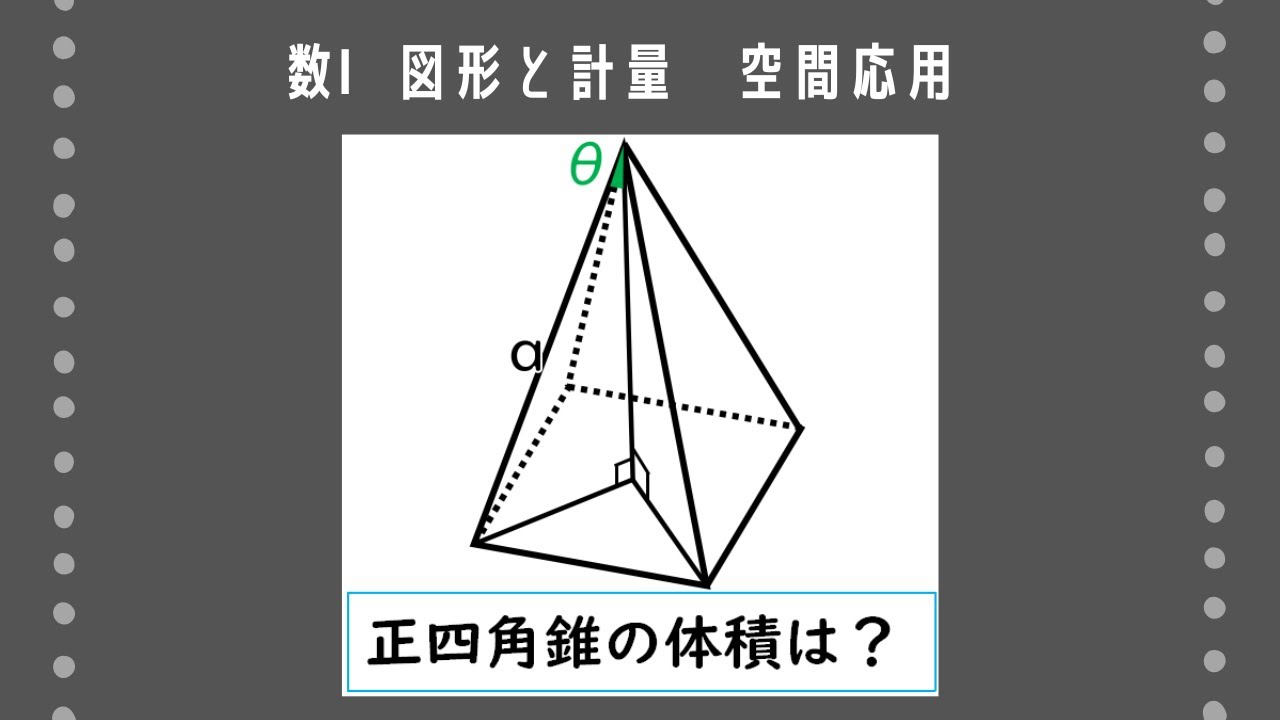
図のような正四角錐$\rm PABCD$において、頂点$\rm P$から正方形$\rm ABCD$に下ろした垂線を$\rm PH$とする。$\rm PA=a,\angle APH=\theta$であるとき、正四角錐の体積を求めよ。
この動画を見る
図のような正四角錐$\rm PABCD$において、頂点$\rm P$から正方形$\rm ABCD$に下ろした垂線を$\rm PH$とする。$\rm PA=a,\angle APH=\theta$であるとき、正四角錐の体積を求めよ。
【数Ⅰ】【図形と計量】空間の基本2 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
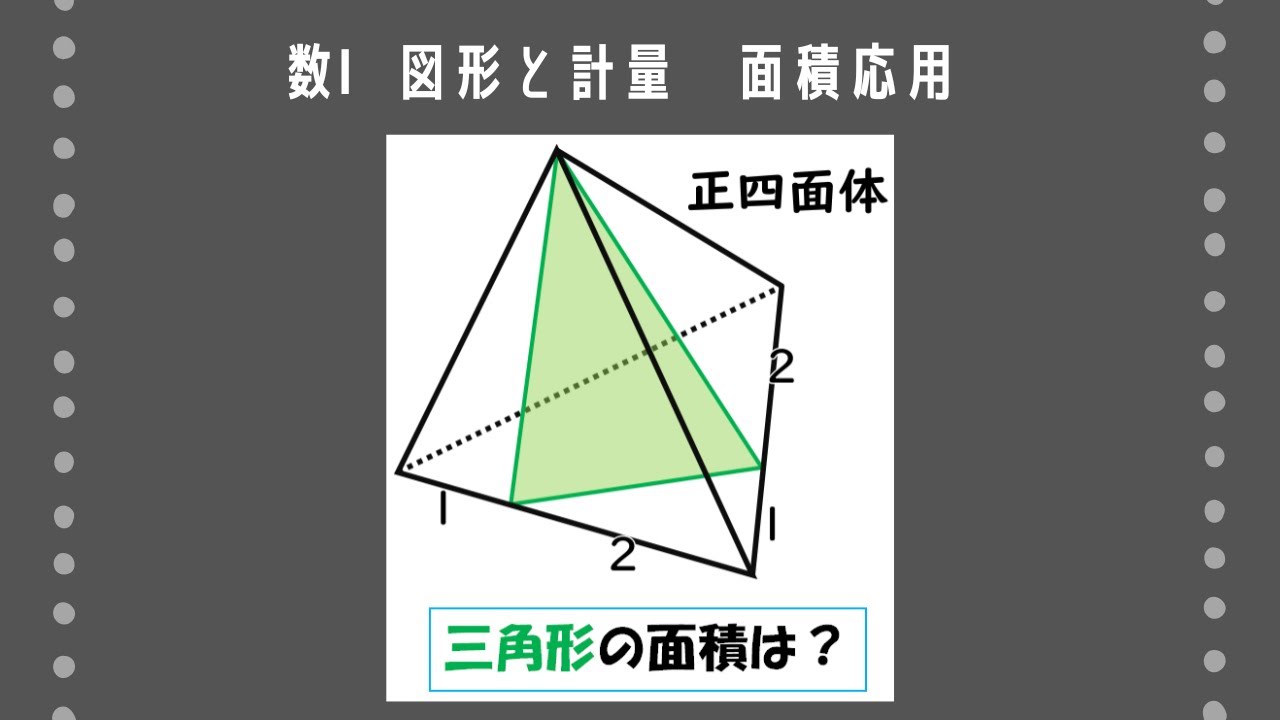
1辺の長さが3の正四面体$\rm ABCD$において、辺$\rm BC,CD$を$1:2$に分ける点を、それぞれ$\rm P,Q$とする。このとき、次のものを求めよ。
(1)$\rm AP,AQ,PQ$の長さ (2)$\cos \angle \rm PAQ$の値 (3)$\rm \triangle APQ$の面積
この動画を見る
1辺の長さが3の正四面体$\rm ABCD$において、辺$\rm BC,CD$を$1:2$に分ける点を、それぞれ$\rm P,Q$とする。このとき、次のものを求めよ。
(1)$\rm AP,AQ,PQ$の長さ (2)$\cos \angle \rm PAQ$の値 (3)$\rm \triangle APQ$の面積
【数Ⅰ】【図形と計量】空間の基本3 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
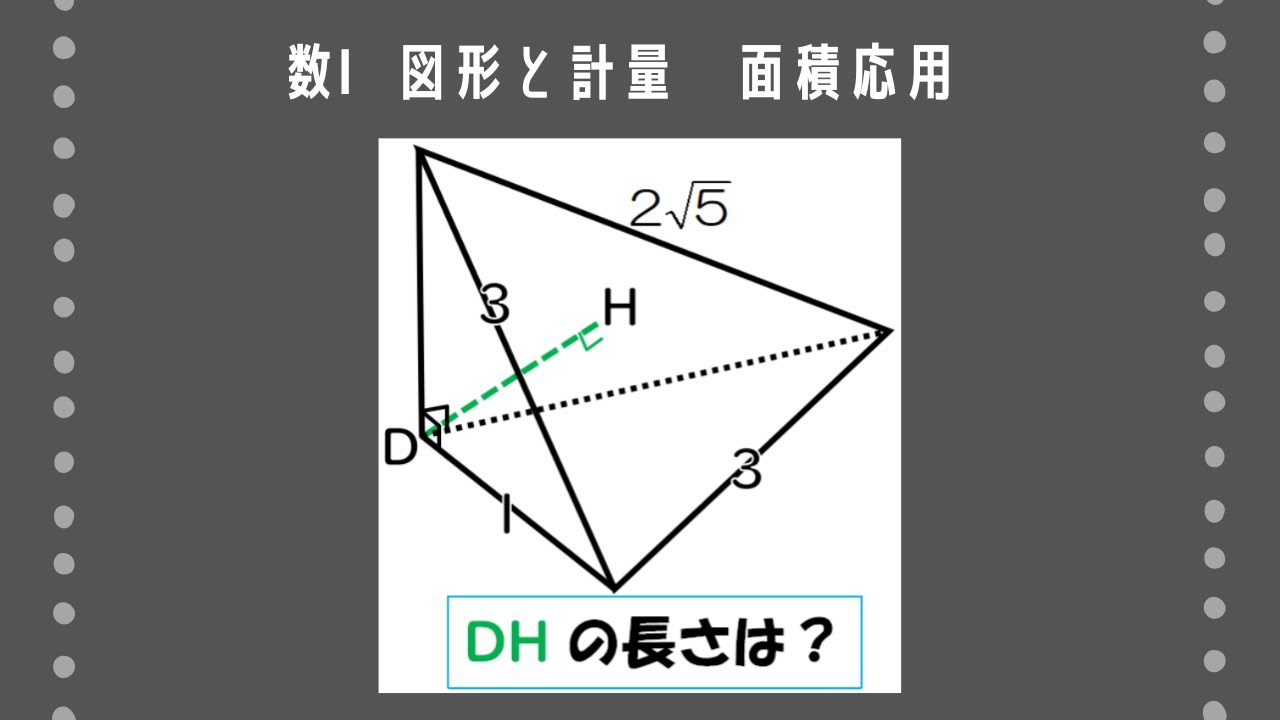
四面体$\rm ABCD$において、$\rm AB=BC=3,CA=2\sqrt5,BD=1,\angle ADB=\angle ADC=90^{\circ}$であるとき、次のものを求めよ。
(1)$\rm CD$の長さ (2)四面体$\rm ABCD$の体積 (3)$\triangle \rm ABC$の面積 (4)頂点$\rm D$から平面
この動画を見る
四面体$\rm ABCD$において、$\rm AB=BC=3,CA=2\sqrt5,BD=1,\angle ADB=\angle ADC=90^{\circ}$であるとき、次のものを求めよ。
(1)$\rm CD$の長さ (2)四面体$\rm ABCD$の体積 (3)$\triangle \rm ABC$の面積 (4)頂点$\rm D$から平面
【数Ⅰ】【図形と計量】空間の基本1 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
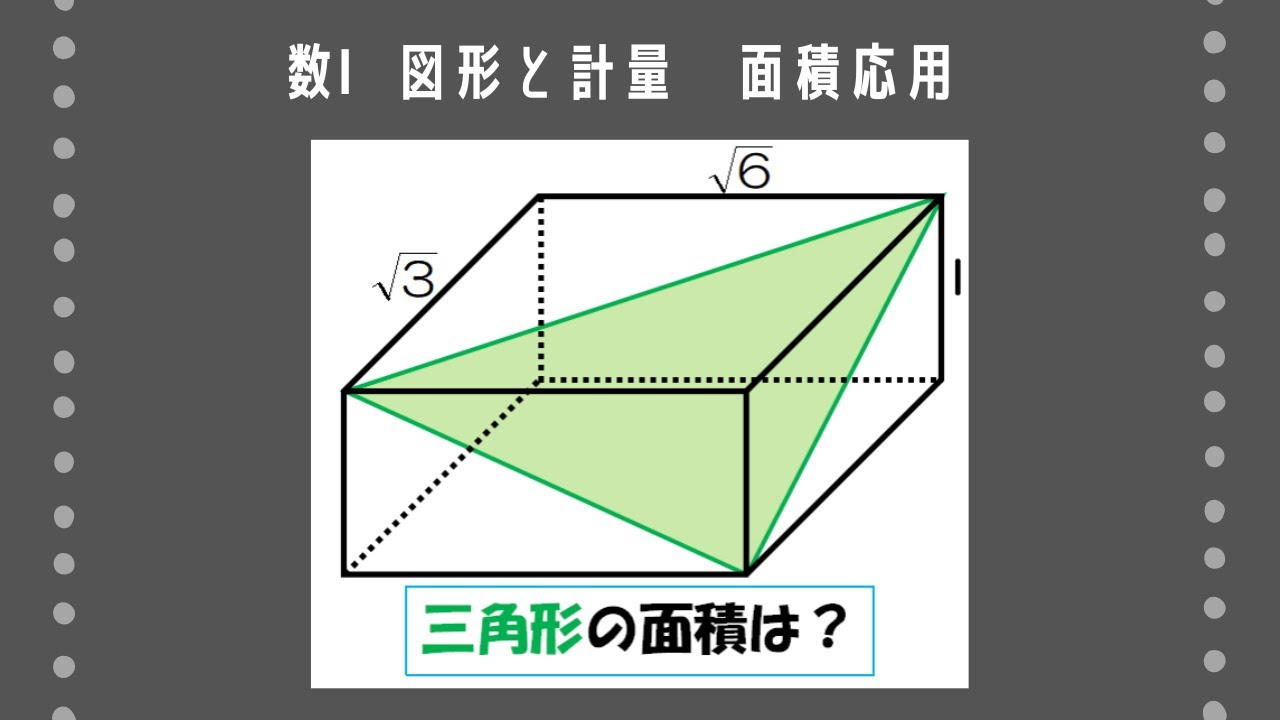
問題文全文(内容文):
右の図のような$\rm AB=\sqrt6,AD=\sqrt3,AE=1$である直方体$\rm ABCD-EFGH$がある。このとき、次のものを求めよ。
(1)$\rm\angle ACF$の大きさ
(2)$\rm \triangle ACF$の面積
この動画を見る
右の図のような$\rm AB=\sqrt6,AD=\sqrt3,AE=1$である直方体$\rm ABCD-EFGH$がある。このとき、次のものを求めよ。
(1)$\rm\angle ACF$の大きさ
(2)$\rm \triangle ACF$の面積
【数Ⅰ】【図形と計量】面積応用10 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
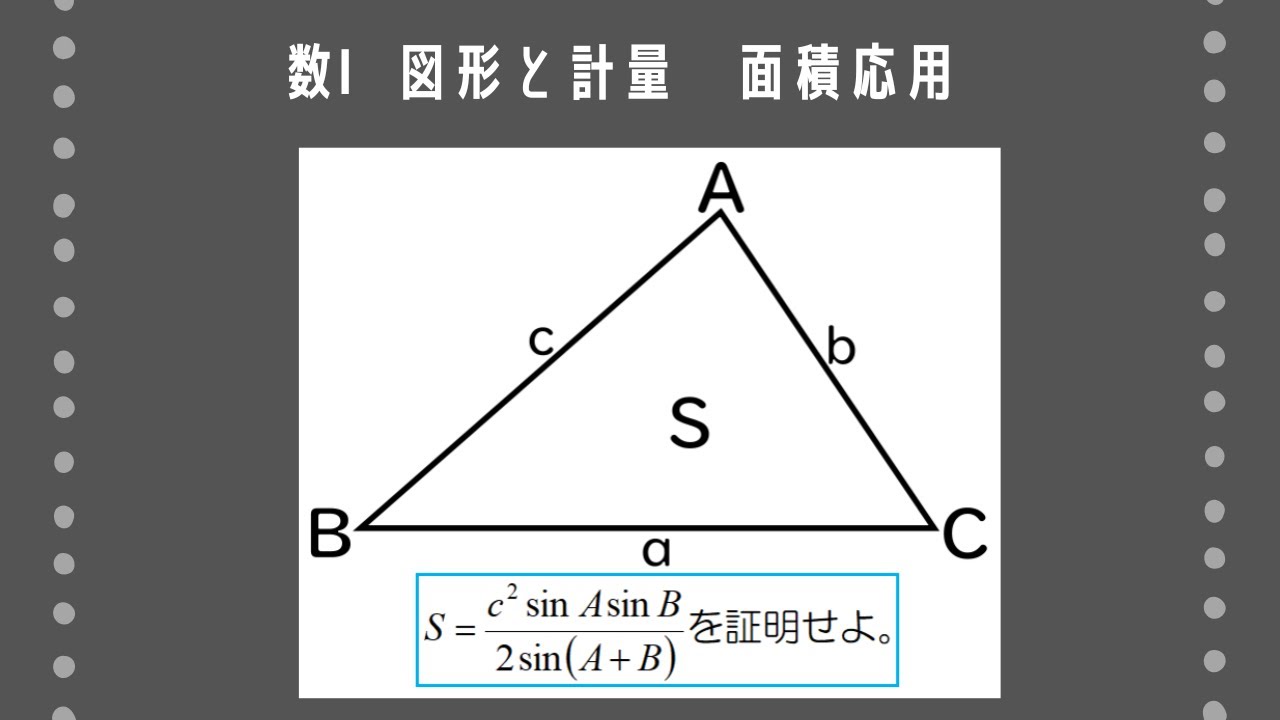
問題文全文(内容文):
1辺$c$と2つの角$\rm A,B$が与えられた$rm\triangle ABC$の面積を$S$とするとき、次の問いに答えよ。
(1)$a$を$c,\rm A,B$で表せ。 (2)$S=\dfrac{c^2\rm\sin A\sin B}{2\sin\rm(A+B)}$を証明せよ。
この動画を見る
1辺$c$と2つの角$\rm A,B$が与えられた$rm\triangle ABC$の面積を$S$とするとき、次の問いに答えよ。
(1)$a$を$c,\rm A,B$で表せ。 (2)$S=\dfrac{c^2\rm\sin A\sin B}{2\sin\rm(A+B)}$を証明せよ。
【数Ⅰ】【図形と計量】面積応用9 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
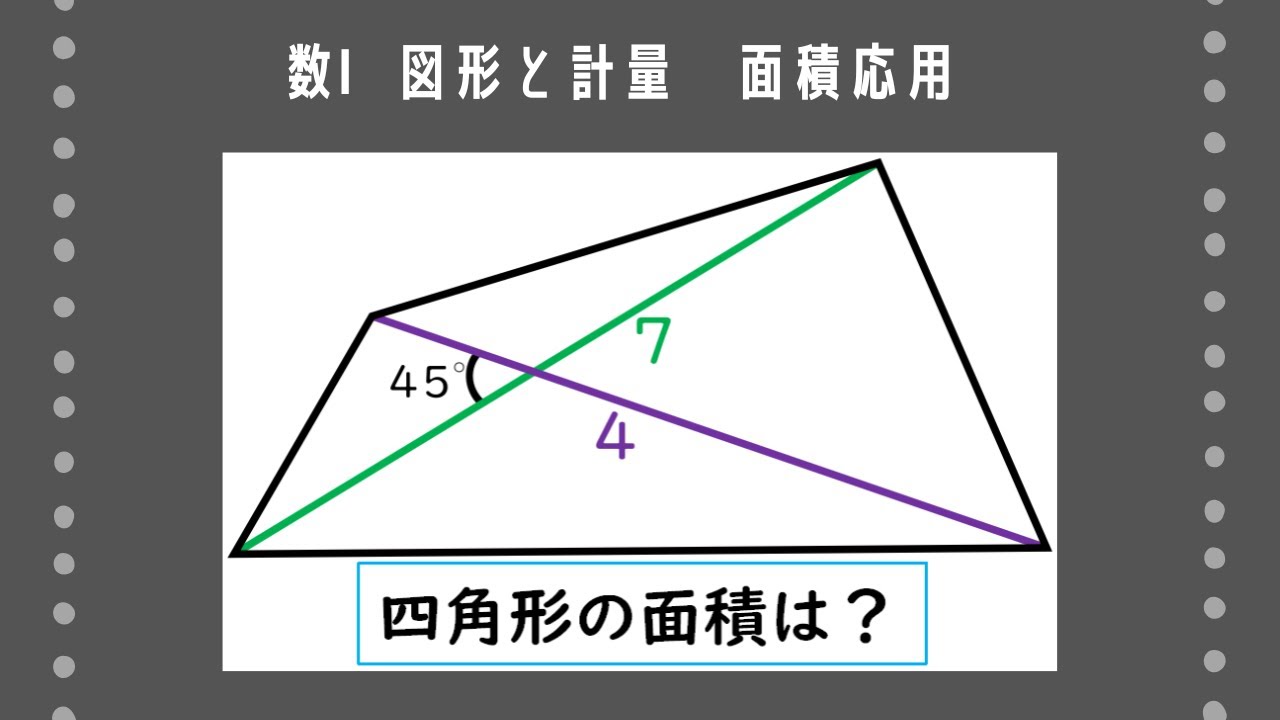
問題文全文(内容文):
四角形$\rm ABCD$の2つの対角線$\rm AC,BD$の交点を$\rm O$とする。$\rm AC=4,BD=7,\angle AOB=45^{\circ}$であるとき、四角形$\rm ABCD$の面積$S$を求めよ。
この動画を見る
四角形$\rm ABCD$の2つの対角線$\rm AC,BD$の交点を$\rm O$とする。$\rm AC=4,BD=7,\angle AOB=45^{\circ}$であるとき、四角形$\rm ABCD$の面積$S$を求めよ。
【数Ⅰ】【図形と計量】面積応用8 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
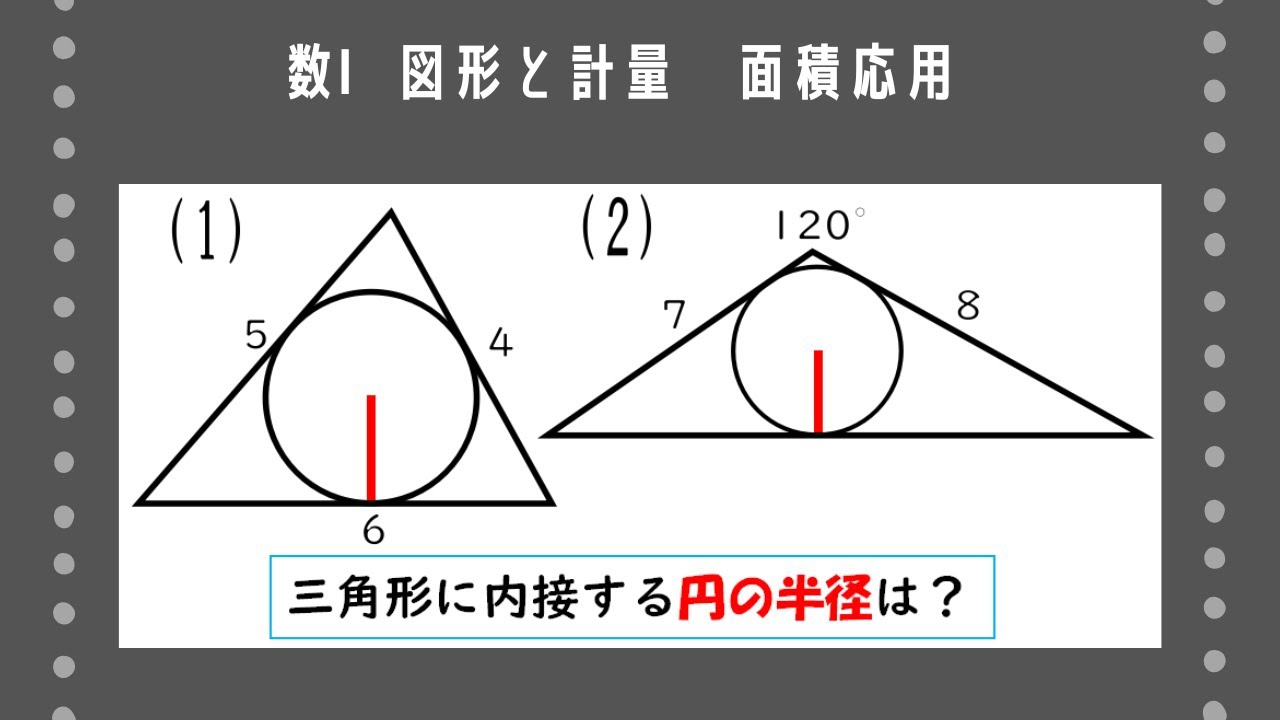
問題文全文(内容文):
次のような$\rm \triangle ABC$に内接する円の半径$r$を求めよ。
(1)$a=4,b=5,c=6$ (2)${\rm A=120^{\circ}},b=7,c=8$
この動画を見る
次のような$\rm \triangle ABC$に内接する円の半径$r$を求めよ。
(1)$a=4,b=5,c=6$ (2)${\rm A=120^{\circ}},b=7,c=8$
【数Ⅰ】【図形と計量】面積応用3 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
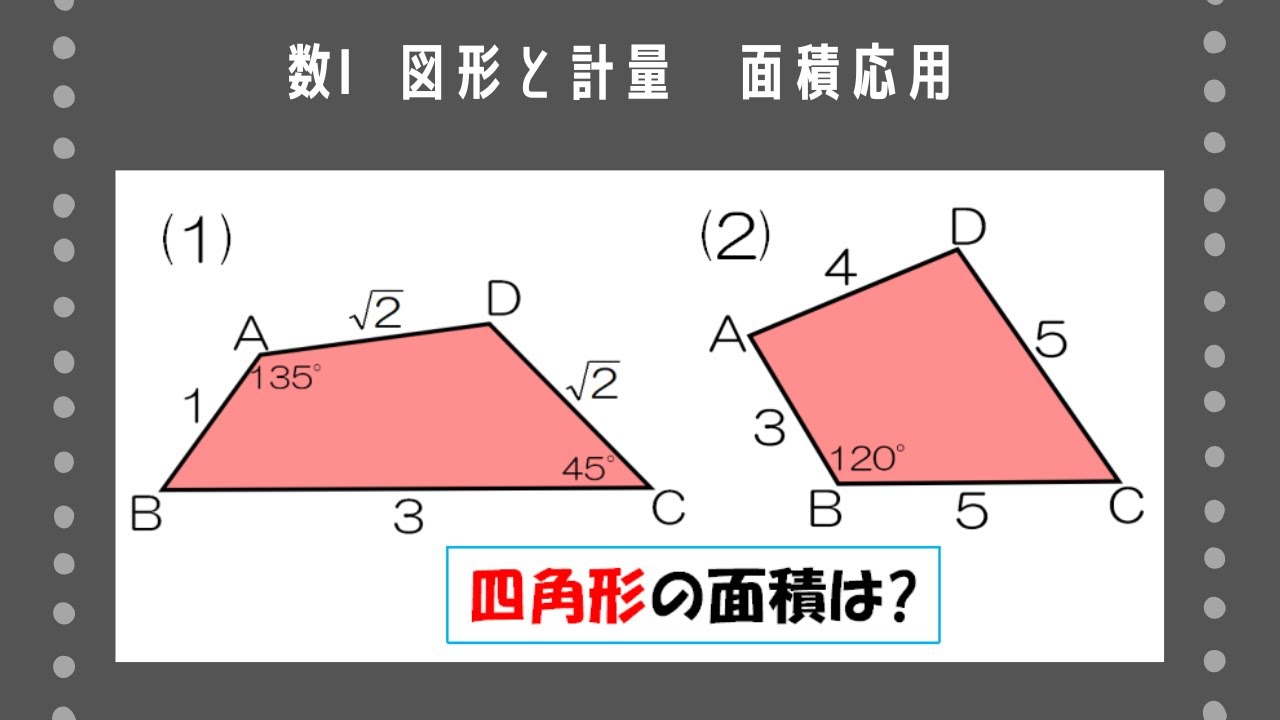
次のような四角形ABCDの面積を求めよ。
(1)∠A=135°、∠C=45°、AB=1、BC=3、CD=$\sqrt{2}$、DA=$\sqrt{2}$
(2)∠B=120°、AB=3、BC=5、CD=5、DA=4
この動画を見る
次のような四角形ABCDの面積を求めよ。
(1)∠A=135°、∠C=45°、AB=1、BC=3、CD=$\sqrt{2}$、DA=$\sqrt{2}$
(2)∠B=120°、AB=3、BC=5、CD=5、DA=4
【数Ⅰ】【図形と計量】面積応用7 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
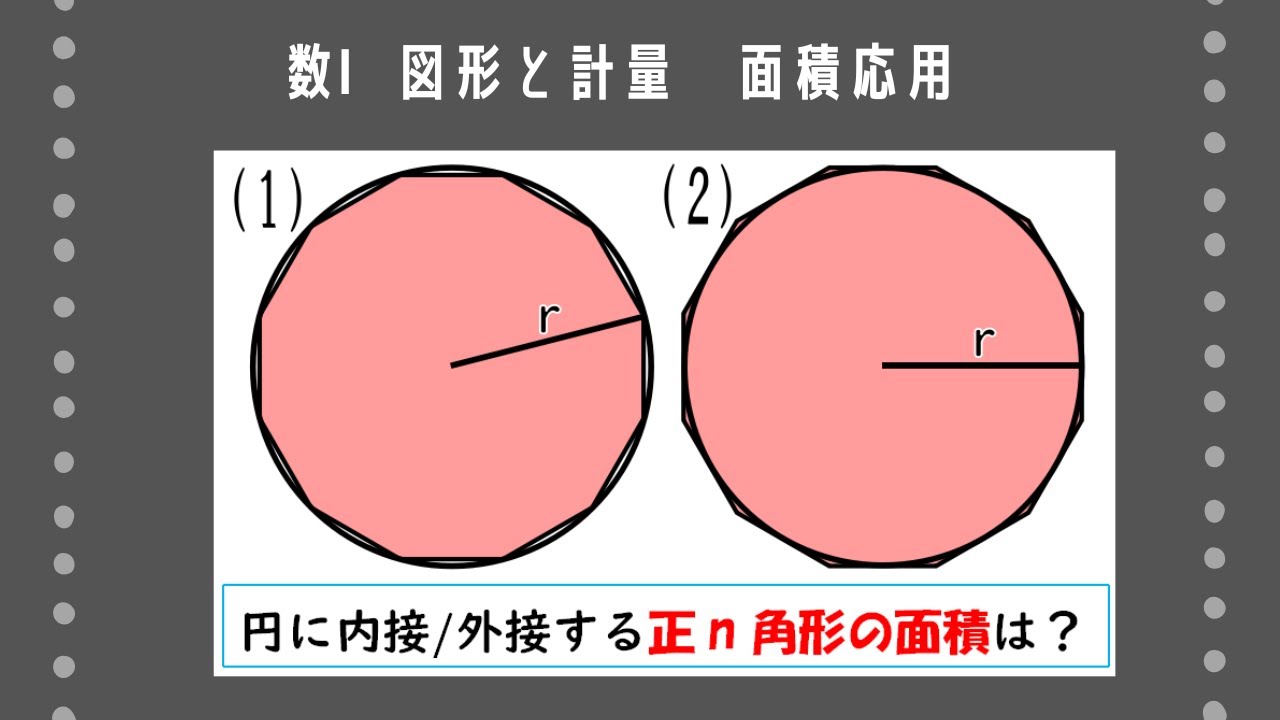
半径$r$の円に内接する正$n$角形の面積、および外接する正$n$角形の面積を、それぞれ$r$と$n$を用いて求めよ。
この動画を見る
半径$r$の円に内接する正$n$角形の面積、および外接する正$n$角形の面積を、それぞれ$r$と$n$を用いて求めよ。
【数Ⅰ】【図形と計量】面積応用2 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
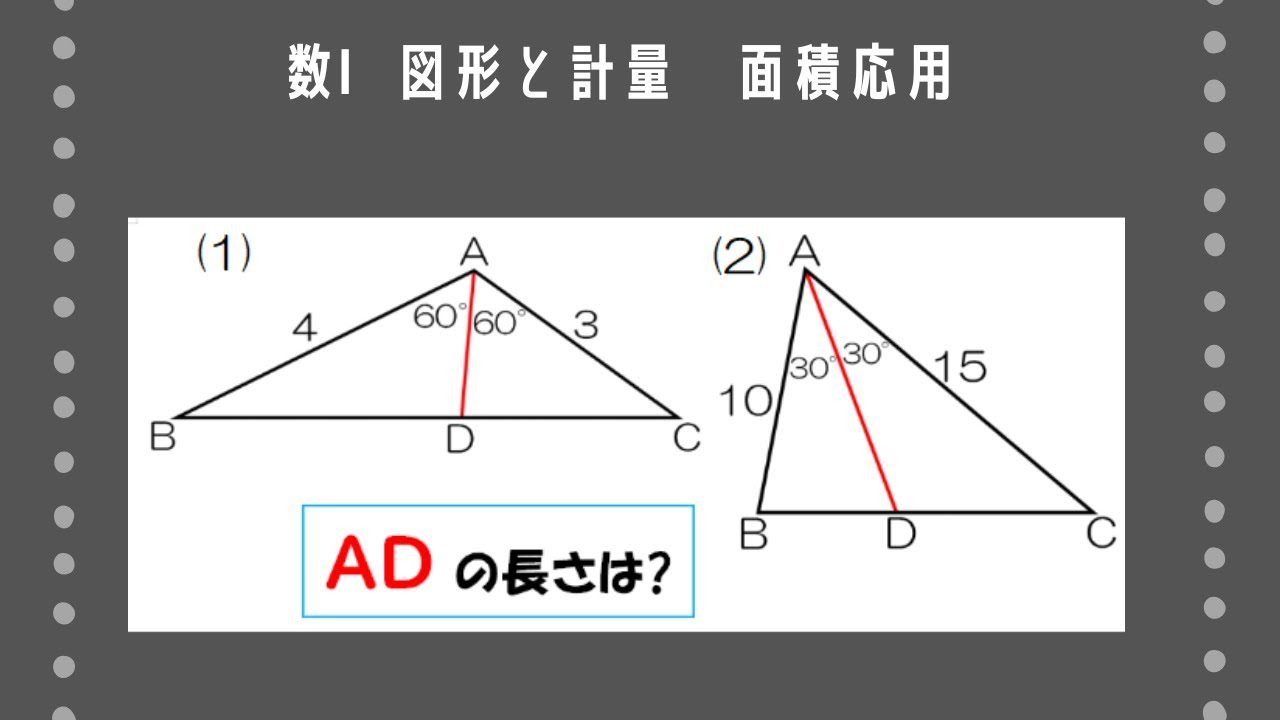
次のような△ABCについて、∠Aの二等分線と辺BCの交点をDとするとき、線分ADの長さを求めよ。
(1)AB=4、AC=3、A=120°
(2)AB=10、AC=15、A=60°
この動画を見る
次のような△ABCについて、∠Aの二等分線と辺BCの交点をDとするとき、線分ADの長さを求めよ。
(1)AB=4、AC=3、A=120°
(2)AB=10、AC=15、A=60°
【数Ⅰ】【図形と計量】面積応用6 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
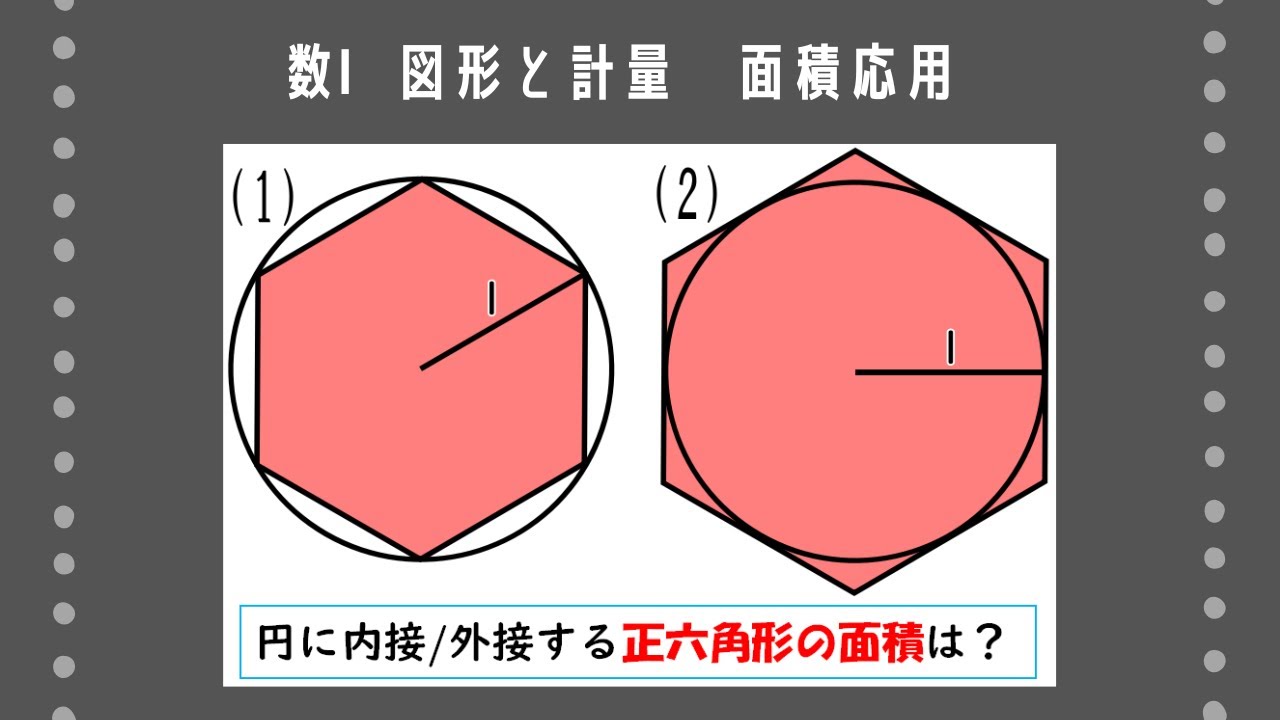
(1)半径1の円に内接する正六角形の面積を求めよ。
(2)半径1の円に外接する正六角形の面積を求めよ。
この動画を見る
(1)半径1の円に内接する正六角形の面積を求めよ。
(2)半径1の円に外接する正六角形の面積を求めよ。
【数Ⅰ】【図形と計量】面積応用5 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
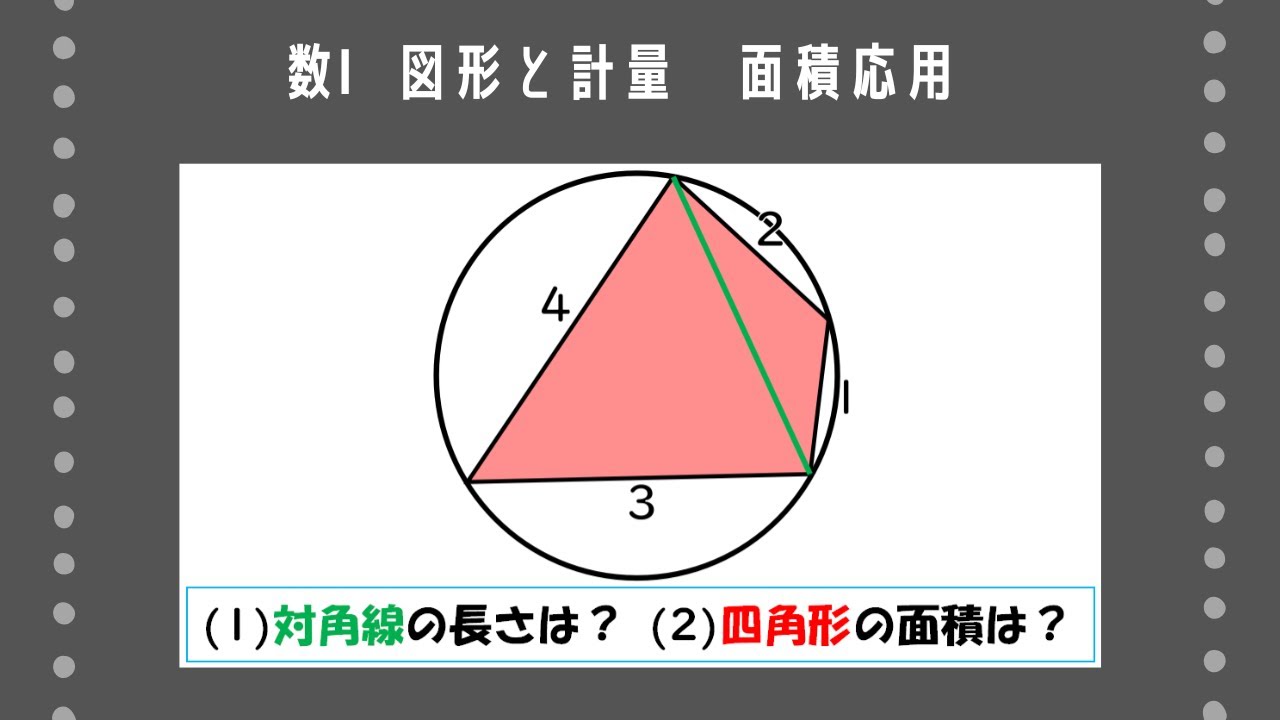
問題文全文(内容文):
円に内接する四角形$\rm ABCD$において、$\rm AB=4,BC=3,CD=1,DA=2$とするとき、次のものを求めよ。
(1)対角線$\rm AC$の長さ
(2)四角形$\rm ABCD$の面積
この動画を見る
円に内接する四角形$\rm ABCD$において、$\rm AB=4,BC=3,CD=1,DA=2$とするとき、次のものを求めよ。
(1)対角線$\rm AC$の長さ
(2)四角形$\rm ABCD$の面積
【数Ⅰ】【図形と計量】面積応用4 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
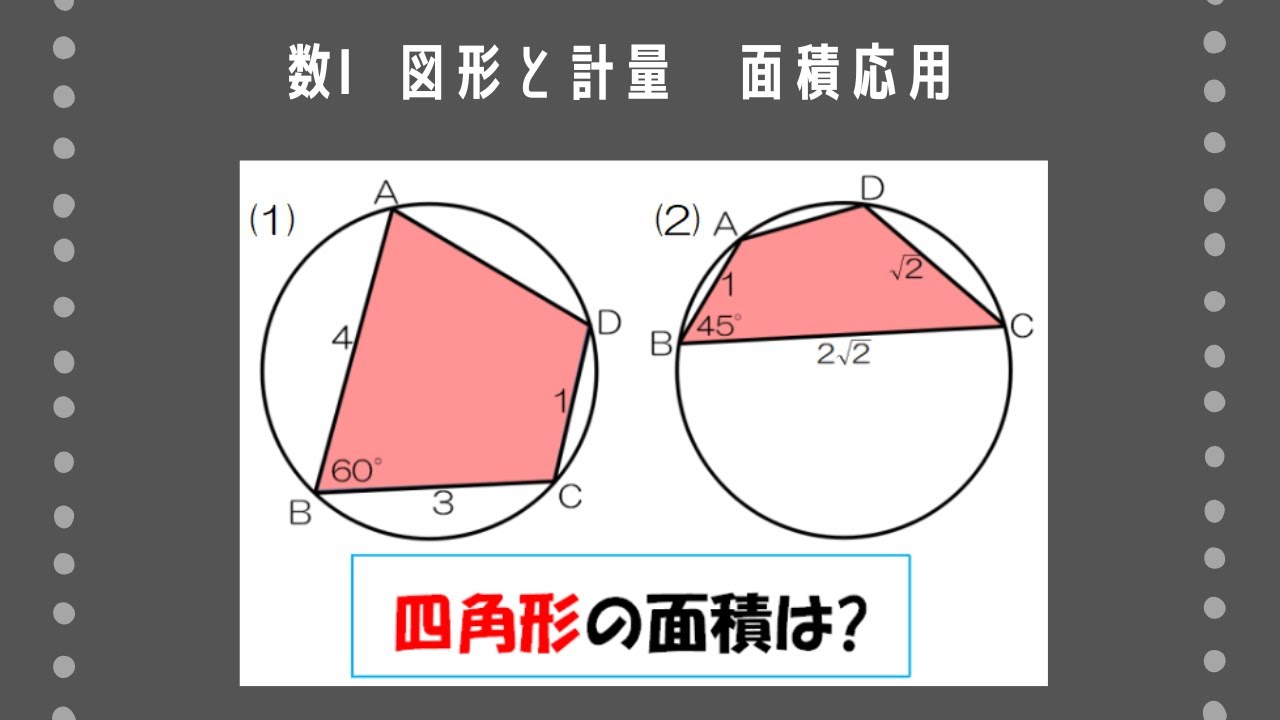
問題文全文(内容文):
次のような四角形$\rm ABCD$の面積を求めよ。
(1)円に内接し、$\rm AB=4,BC=3,CD=1,\angle B=60^{\circ}$
(2)円に内接し、$\rm AB=1,BC=2\sqrt2,CD=\sqrt2,\angle B=45^{\circ}$
この動画を見る
次のような四角形$\rm ABCD$の面積を求めよ。
(1)円に内接し、$\rm AB=4,BC=3,CD=1,\angle B=60^{\circ}$
(2)円に内接し、$\rm AB=1,BC=2\sqrt2,CD=\sqrt2,\angle B=45^{\circ}$
【数Ⅰ】【図形と計量】面積応用1 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
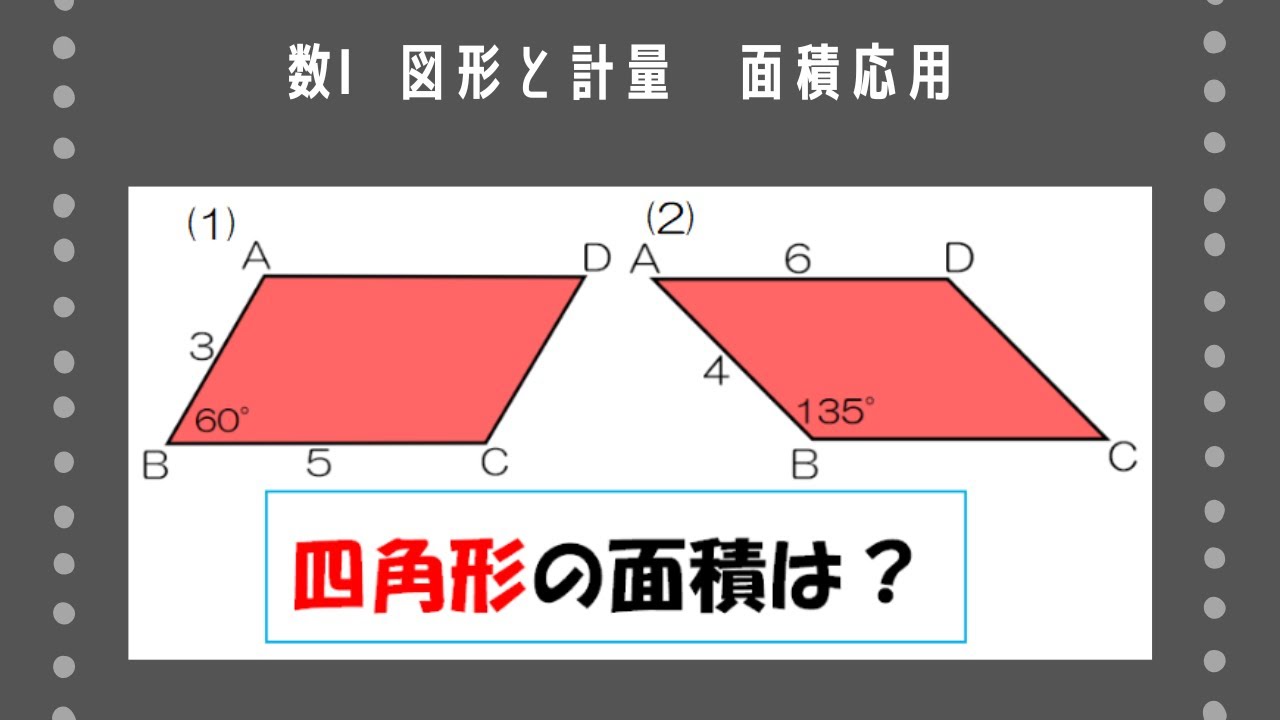
問題文全文(内容文):
次のような平行四辺形ABCDの面積を求めよ。
(1)AB=3、BC=5、∠ABC=60°
(2)AB=4、AD=6、∠ABC=135°
この動画を見る
次のような平行四辺形ABCDの面積を求めよ。
(1)AB=3、BC=5、∠ABC=60°
(2)AB=4、AD=6、∠ABC=135°
【高校物理】鉛直投げ上げ【毎週土曜日16時更新!】

単元:
#物理#力学#理科(高校生)
教材:
#中高教材#セミナー物理基礎・物理
指導講師:
理数個別チャンネル
問題文全文(内容文):
地面から、速さ19.6m/sで鉛直上向きに小球を投げ上げた。重力加速度の大きさを9.8m/s²とする。
(1)地上14.7mの点を小球が通り過ぎるのは何s後か。
(2)小球が最高点に達するまでの時間は何sか。
(3)最高点の高さは何mか。
(4)小球が再び地面に落ちてくるまでの時間と、そのときの速度をそれぞれ求めよ。
この動画を見る
地面から、速さ19.6m/sで鉛直上向きに小球を投げ上げた。重力加速度の大きさを9.8m/s²とする。
(1)地上14.7mの点を小球が通り過ぎるのは何s後か。
(2)小球が最高点に達するまでの時間は何sか。
(3)最高点の高さは何mか。
(4)小球が再び地面に落ちてくるまでの時間と、そのときの速度をそれぞれ求めよ。
【高校化学】芳香族化合物の識別【毎週土曜日16時更新!】

単元:
#化学#有機#芳香族化合物#理科(高校生)
教材:
#中高教材#セミナー化学基礎・化学
指導講師:
理数個別チャンネル
問題文全文(内容文):
芳香族化合物の識別次の(1)~(4)の各組み合わせの化合物を識別できる試薬を下の(ア)~(オ)から1つずつ選べ。
(1) アニリンとニトロベンゼン (2) ベンゼンとベンズアルデヒド (3) フェノールとサリチル酸 (4)サリチル酸とアセチルサリチル酸
(ア) 水酸化ナトリウム水溶液 (イ) 炭酸水素ナトリウム水溶液 (ウ) 塩化鉄(Ⅲ) 水溶液 (エ) アンモニア性硝酸銀水溶液 (オ) さらし粉水溶液
この動画を見る
芳香族化合物の識別次の(1)~(4)の各組み合わせの化合物を識別できる試薬を下の(ア)~(オ)から1つずつ選べ。
(1) アニリンとニトロベンゼン (2) ベンゼンとベンズアルデヒド (3) フェノールとサリチル酸 (4)サリチル酸とアセチルサリチル酸
(ア) 水酸化ナトリウム水溶液 (イ) 炭酸水素ナトリウム水溶液 (ウ) 塩化鉄(Ⅲ) 水溶液 (エ) アンモニア性硝酸銀水溶液 (オ) さらし粉水溶液
【数Ⅰ】【図形と計量】正弦定理と余弦定理の応用3 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
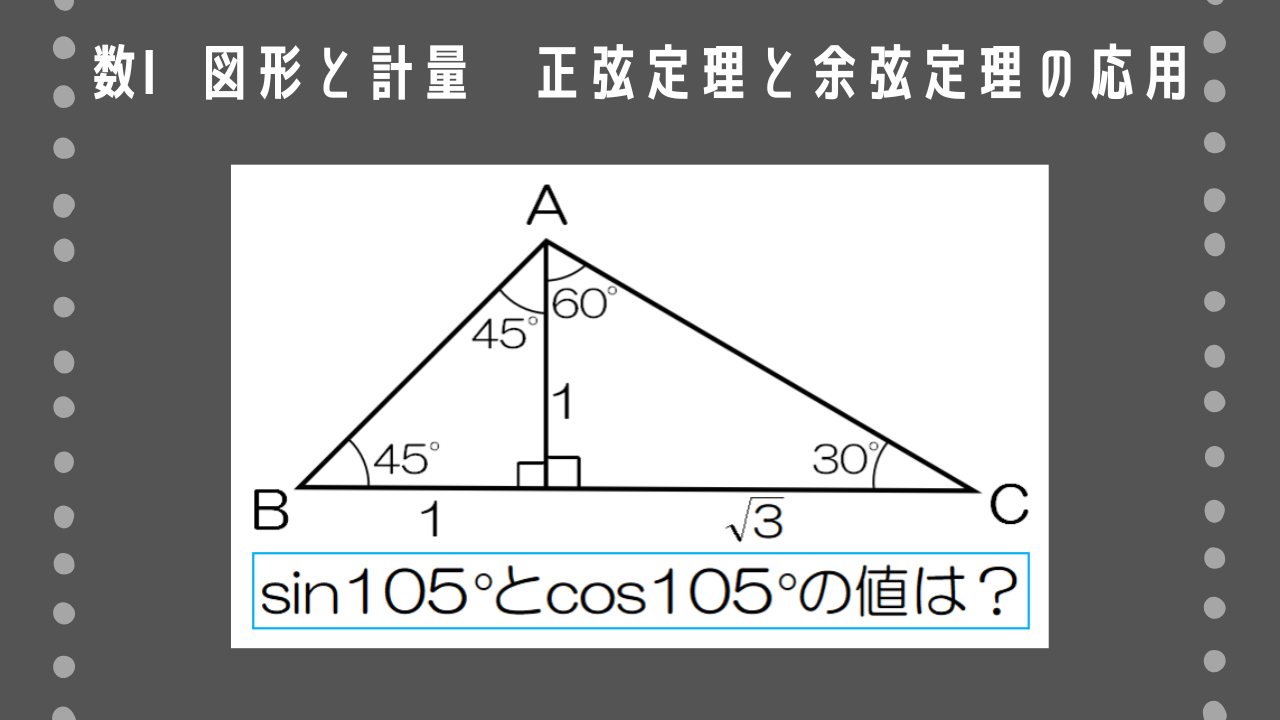
問題文全文(内容文):
図を利用して、sin105°とcos105°の値を求めよ。
この動画を見る
図を利用して、sin105°とcos105°の値を求めよ。
【数Ⅰ】【図形と計量】正弦定理と余弦定理の応用2 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
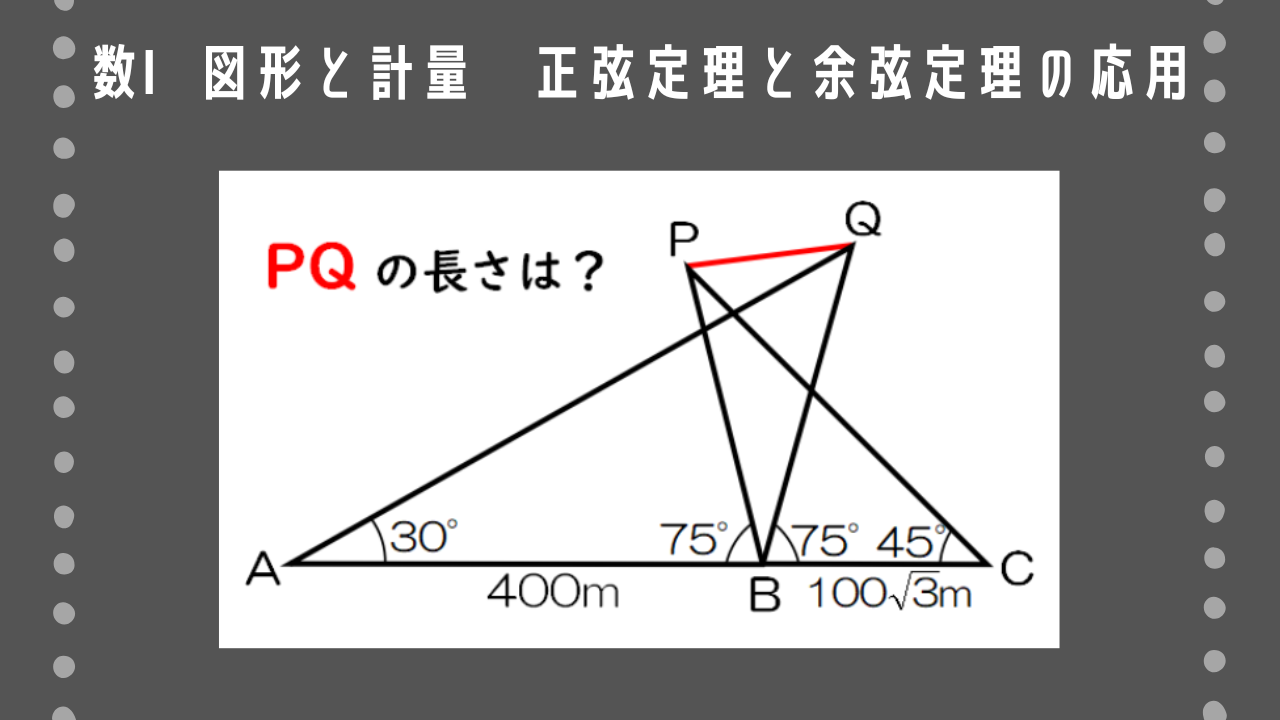
2地点P、Q間の距離を求めるために、1つの直線上にある3地点A、B、Cをとったら、AB=400m、BC=$100\sqrt{3}$m、∠QAB=30°、∠PBA=∠QBC=75°、∠PCB=45°であった。P、Q間の距離を求めよ。
この動画を見る
2地点P、Q間の距離を求めるために、1つの直線上にある3地点A、B、Cをとったら、AB=400m、BC=$100\sqrt{3}$m、∠QAB=30°、∠PBA=∠QBC=75°、∠PCB=45°であった。P、Q間の距離を求めよ。
【数Ⅰ】【図形と計量】正弦定理と余弦定理の応用1 ※問題文は概要欄
単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
教材:
#4S数学#4S数学Ⅰ+AのB問題解説(新課程2022年以降)#図形と計量#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
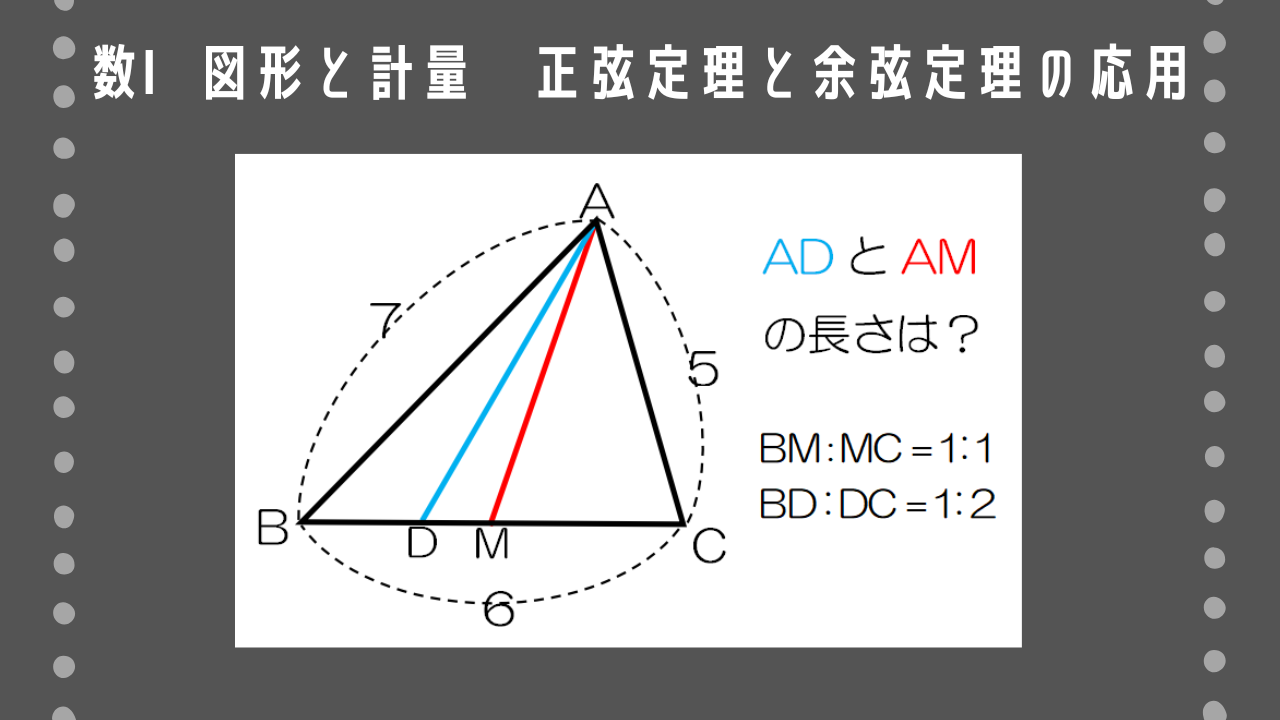
△ABCにおいて、辺BCの中点をM、辺BCを1:2に分ける点をDとする。a=6、b=5、c=7のとき、AM、ADの長さを求めよ。
この動画を見る
△ABCにおいて、辺BCの中点をM、辺BCを1:2に分ける点をDとする。a=6、b=5、c=7のとき、AM、ADの長さを求めよ。
【数C】【平面上のベクトル】ベクトルの成分5 ※問題文は概要欄

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\vec{ a }=(3 ,1)$ ,$\vec{ b }=(1 ,2)$ のとし、$\vec{ c }=\vec{ a }+t\vec{ b }$ (tは実数)とする。
(1) $| \vec{ c } |=\sqrt{15}$ のとき、tの値を求めよ。
(2) $| \vec{ c } |$の最小値と、そのときのtの値を求めよ。
この動画を見る
$\vec{ a }=(3 ,1)$ ,$\vec{ b }=(1 ,2)$ のとし、$\vec{ c }=\vec{ a }+t\vec{ b }$ (tは実数)とする。
(1) $| \vec{ c } |=\sqrt{15}$ のとき、tの値を求めよ。
(2) $| \vec{ c } |$の最小値と、そのときのtの値を求めよ。
【数C】【平面上のベクトル】ベクトルの成分4 ※問題文は概要欄

単元:
#平面上のベクトル#平面上のベクトルと内積#数学(高校生)#数C
教材:
#4S数学#中高教材#4S数学CのB問題解説#平面上のベクトル
指導講師:
理数個別チャンネル
問題文全文(内容文):
$\vec{ a }=(2 ,2)$ ,$\vec{ b }=(3 ,1)$ のとき、$\vec{ x }-\vec{ b }$ が $\vec{ a }$に平行で、
かつ $| \vec{ x }+\vec{ b } |=4$ となるような$\vec{ x }$ を成分表示せよ。
この動画を見る
$\vec{ a }=(2 ,2)$ ,$\vec{ b }=(3 ,1)$ のとき、$\vec{ x }-\vec{ b }$ が $\vec{ a }$に平行で、
かつ $| \vec{ x }+\vec{ b } |=4$ となるような$\vec{ x }$ を成分表示せよ。
【数B】【確率分布と統計的な推測】正規分布8 ※問題文は概要欄

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある植物の種子の発芽率は80%であるという。この植物の種子を900個まいたとき、次の問いに答えよ。
(1) 750個以上の種子が発芽する確率を求めよ。
(2) 900個のうちn個以上の種子が発芽する確率が80%以上となるようなnの最大値を求めよ。
この動画を見る
ある植物の種子の発芽率は80%であるという。この植物の種子を900個まいたとき、次の問いに答えよ。
(1) 750個以上の種子が発芽する確率を求めよ。
(2) 900個のうちn個以上の種子が発芽する確率が80%以上となるようなnの最大値を求めよ。
【数B】【確率分布と統計的な推測】正規分布7 ※問題文は概要欄

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある2つの試験の平均は、それぞれ57.6点、81.8点、標準偏差は、それぞれ 10.3点、5.7点であった。Aは前者の試験を受けて75点、Bは後者の試験を受けて88点であった。どちらの試験を受けても、受験者全体としては優劣がないものとすると、AとBはどちらが優れていると考えられるか。ただし、得点は正規分布に従うものとする。
この動画を見る
ある2つの試験の平均は、それぞれ57.6点、81.8点、標準偏差は、それぞれ 10.3点、5.7点であった。Aは前者の試験を受けて75点、Bは後者の試験を受けて88点であった。どちらの試験を受けても、受験者全体としては優劣がないものとすると、AとBはどちらが優れていると考えられるか。ただし、得点は正規分布に従うものとする。
【数B】【確率分布と統計的な推測】正規分布6 ※問題文は概要欄

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある試験での成績の結果は、平均71点、標準偏差8点であった。得点の分布は正規分布に従うものとするとき、次の問いに答えよ。
(1) 63点から87点のものが450人いた。受験者の総数は約何人か。
(2) (1)のとき、合格点を55点とすると、約何人が合格することになるか。
この動画を見る
ある試験での成績の結果は、平均71点、標準偏差8点であった。得点の分布は正規分布に従うものとするとき、次の問いに答えよ。
(1) 63点から87点のものが450人いた。受験者の総数は約何人か。
(2) (1)のとき、合格点を55点とすると、約何人が合格することになるか。
【数B】【確率分布と統計的な推測】正規分布5 ※問題文は概要欄

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
1000人の生徒に数学のテストを行ったところ、その成績は、平均48点,標準偏差15点であった。成績が正規分布に従うものとするとき、次の問いに答えよ。
(1) ある生徒の点数が78点以上である確率を求めよ。
(2) 78点以上の生徒は約何人いると考えられるか。
(3) 30点以下の生徒は約何人いると考えられるか。
この動画を見る
1000人の生徒に数学のテストを行ったところ、その成績は、平均48点,標準偏差15点であった。成績が正規分布に従うものとするとき、次の問いに答えよ。
(1) ある生徒の点数が78点以上である確率を求めよ。
(2) 78点以上の生徒は約何人いると考えられるか。
(3) 30点以下の生徒は約何人いると考えられるか。
【数B】【確率分布と統計的な推測】正規分布4 ※問題文は概要欄

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
ある県における高校2年生の男子の身長が、平均170.0cm,標準偏差5.2 cm の正規分布に従うものとする。
(1) 身長が165cm以上の生徒は、約何%いるか。整数値で答えよ。
(2) 身長の高い方から10%の中に入るのは、何cm以上の生徒か。最も小さい整数値で答えよ。
この動画を見る
ある県における高校2年生の男子の身長が、平均170.0cm,標準偏差5.2 cm の正規分布に従うものとする。
(1) 身長が165cm以上の生徒は、約何%いるか。整数値で答えよ。
(2) 身長の高い方から10%の中に入るのは、何cm以上の生徒か。最も小さい整数値で答えよ。
【数B】【確率分布と統計的な推測】正規分布3 ※問題文は概要欄

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
正規分布N(m,δ²)に従う確率変数Xについて、Xのとる値を
m-1.5δ, m-0.5δ, m+0.5δ, m+1.5δ
によって、5つの階級に分けると、各階級に何%ずつ含まれるか。
この動画を見る
正規分布N(m,δ²)に従う確率変数Xについて、Xのとる値を
m-1.5δ, m-0.5δ, m+0.5δ, m+1.5δ
によって、5つの階級に分けると、各階級に何%ずつ含まれるか。
【数B】【確率分布と統計的な推測】正規分布2 ※問題文は概要欄

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
正規分布N (10,5²)に従う確率変数について、次の等式が成り立つように、 定数の値を定めよ。
(1) P(10 ≦ X ≦ a) = 0.4772
(2) P(X ≧ a) = 0.0082
(3) P(|X - 10| ≦ a) = 0.8664
(4) P(|X - 10| ≦ a) = 0.0278
正規分布N(m、δ²)において、変数Xが|X - m|≦kδ の範囲に入る確率が、
次の値になるように、正の定数の値を定めよ。
(1) 0.006
(2) 0.016
(3) 0.242
この動画を見る
正規分布N (10,5²)に従う確率変数について、次の等式が成り立つように、 定数の値を定めよ。
(1) P(10 ≦ X ≦ a) = 0.4772
(2) P(X ≧ a) = 0.0082
(3) P(|X - 10| ≦ a) = 0.8664
(4) P(|X - 10| ≦ a) = 0.0278
正規分布N(m、δ²)において、変数Xが|X - m|≦kδ の範囲に入る確率が、
次の値になるように、正の定数の値を定めよ。
(1) 0.006
(2) 0.016
(3) 0.242
【数B】【確率分布と統計的な推測】正規分布1 ※問題文は概要欄

単元:
#確率分布と統計的な推測#統計的な推測#数学(高校生)#数B
教材:
#4S数学#4S数学Ⅱ+BのB問題解説(新課程2022年以降)#確率分布と統計的推測#中高教材
指導講師:
理数個別チャンネル
問題文全文(内容文):
確率変数Xのとる値の範囲が-1≦x≦1で、その確率密度関数f(x)が f(x)-1-x(-1≦x≦1) で与えられるとき、次の確率を求めよ。
(1) P(0 ≦ X ≦ 0.25)
(2) P(X≦0.25)
(3) P(- 0.5 ≦ X ≦ 0.3)
確率変数Xのとる値の範囲が0≤x≤10で、その確率密度関数がkを定数として f(x) = kx(10 - x) (0≦x≦10) で与えられるとする。
このとき、kの値は□であり、確率 P(3 ≦ X ≦ 7) は□となる。
この動画を見る
確率変数Xのとる値の範囲が-1≦x≦1で、その確率密度関数f(x)が f(x)-1-x(-1≦x≦1) で与えられるとき、次の確率を求めよ。
(1) P(0 ≦ X ≦ 0.25)
(2) P(X≦0.25)
(3) P(- 0.5 ≦ X ≦ 0.3)
確率変数Xのとる値の範囲が0≤x≤10で、その確率密度関数がkを定数として f(x) = kx(10 - x) (0≦x≦10) で与えられるとする。
このとき、kの値は□であり、確率 P(3 ≦ X ≦ 7) は□となる。
