 福田次郎
福田次郎
 福田次郎
福田次郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
福田のおもしろ数学122〜どれがどれですか?該当する関数を見つけてください

単元:
#数Ⅱ#三角関数#指数関数と対数関数#三角関数とグラフ
指導講師:
福田次郎
問題文全文(内容文):
$\begin{array}{|c|c|c|c|}
\hline
x & a & b & c\\ \hline
f_1(x) & 0.980 & 0.921 & 0.825 \\ \hline
f_2(x) & 0.063 & 0.251 & 0.565 \\ \hline
f_3(x) & 0.803 & 0.644 & 0.517 \\ \hline
f_4(x) & 0.199 & 0.389 & 0.565 \\ \hline
\end{array}$
上の数表において、$f_1(x)$, $f_2(x)$, $f_3(x)$, $f_4(x)$は関数
$\sin x$, $\cos x$, $\frac{\pi}{2}x^2$, $3^{-x}$
のうちのどれかである。どれがどれか?
ただし、$a$, $b$, $c$は0<$a$<$b$<$c$<$\frac{\pi}{2}$, $b$=$\frac{a+c}{2}$ を満たし、数値はどれも小数第4位を四捨五入してある。
この動画を見る
$\begin{array}{|c|c|c|c|}
\hline
x & a & b & c\\ \hline
f_1(x) & 0.980 & 0.921 & 0.825 \\ \hline
f_2(x) & 0.063 & 0.251 & 0.565 \\ \hline
f_3(x) & 0.803 & 0.644 & 0.517 \\ \hline
f_4(x) & 0.199 & 0.389 & 0.565 \\ \hline
\end{array}$
上の数表において、$f_1(x)$, $f_2(x)$, $f_3(x)$, $f_4(x)$は関数
$\sin x$, $\cos x$, $\frac{\pi}{2}x^2$, $3^{-x}$
のうちのどれかである。どれがどれか?
ただし、$a$, $b$, $c$は0<$a$<$b$<$c$<$\frac{\pi}{2}$, $b$=$\frac{a+c}{2}$ を満たし、数値はどれも小数第4位を四捨五入してある。
福田の数学〜一橋大学2024年文系第1問〜シグマが2024になるような2変数の値

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ $\displaystyle\sum_{k=1}^mk(n-2k)$=2024 を満たす正の整数の組($m$, $n$)を求めよ。
この動画を見る
$\Large\boxed{1}$ $\displaystyle\sum_{k=1}^mk(n-2k)$=2024 を満たす正の整数の組($m$, $n$)を求めよ。
福田のおもしろ数学121〜この賭けは有理か不利か

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
2つのサイコロを25回投げるとき少なくとも1回は両方のサイコロの目が共に6となる確率$p$を求めよ。
この動画を見る
2つのサイコロを25回投げるとき少なくとも1回は両方のサイコロの目が共に6となる確率$p$を求めよ。
福田の数学〜東北大学2024年文系第4問〜連立漸化式と不定方程式の整数解

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ $n$を正の整数とする。2つの整数$a_n$, $b_n$を条件
$(1+\sqrt 2)^n$=$a_n$+$b_n\sqrt 2$
により定める。ここで$\sqrt 2$は無理数なので、このような整数の組($a_n$, $b_n$)はただ1つに定まる。
(1)$a_{n+1}$, $b_{n+1}$を$a_n$, $b_n$を用いてそれぞれ表せ。さらに$b_4$, $b_5$, $b_6$の値をそれぞれ求めよ。
(2)等式$(1-\sqrt 2)^n$=$a_n$-$b_n\sqrt 2$ が成り立つことを数学的帰納法を用いて示せ。
(3)$n$≧2 のとき、$b_{n+1}b_{n-1}$-$b_n^2$ を求めよ。
(4)$pb_6$-$qb_5$=1, 0≦$p$≦100, 0≦$q$≦100 をすべて満たす整数$p$, $q$の組($p$, $q$)を1組求めよ。
この動画を見る
$\Large\boxed{4}$ $n$を正の整数とする。2つの整数$a_n$, $b_n$を条件
$(1+\sqrt 2)^n$=$a_n$+$b_n\sqrt 2$
により定める。ここで$\sqrt 2$は無理数なので、このような整数の組($a_n$, $b_n$)はただ1つに定まる。
(1)$a_{n+1}$, $b_{n+1}$を$a_n$, $b_n$を用いてそれぞれ表せ。さらに$b_4$, $b_5$, $b_6$の値をそれぞれ求めよ。
(2)等式$(1-\sqrt 2)^n$=$a_n$-$b_n\sqrt 2$ が成り立つことを数学的帰納法を用いて示せ。
(3)$n$≧2 のとき、$b_{n+1}b_{n-1}$-$b_n^2$ を求めよ。
(4)$pb_6$-$qb_5$=1, 0≦$p$≦100, 0≦$q$≦100 をすべて満たす整数$p$, $q$の組($p$, $q$)を1組求めよ。
福田のおもしろ数学120〜n変数の条件付き最大最小問題

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
実数$x_1$,$x_2$,...,$x_n$が$x_1^2$+$x_2^2$+...+$x_n^2$=1 を満たすとき、$x_1^2$+$2x_2^2$+...+$nx_n^2$ の最大値と最小値を求めよ。
この動画を見る
実数$x_1$,$x_2$,...,$x_n$が$x_1^2$+$x_2^2$+...+$x_n^2$=1 を満たすとき、$x_1^2$+$2x_2^2$+...+$nx_n^2$ の最大値と最小値を求めよ。
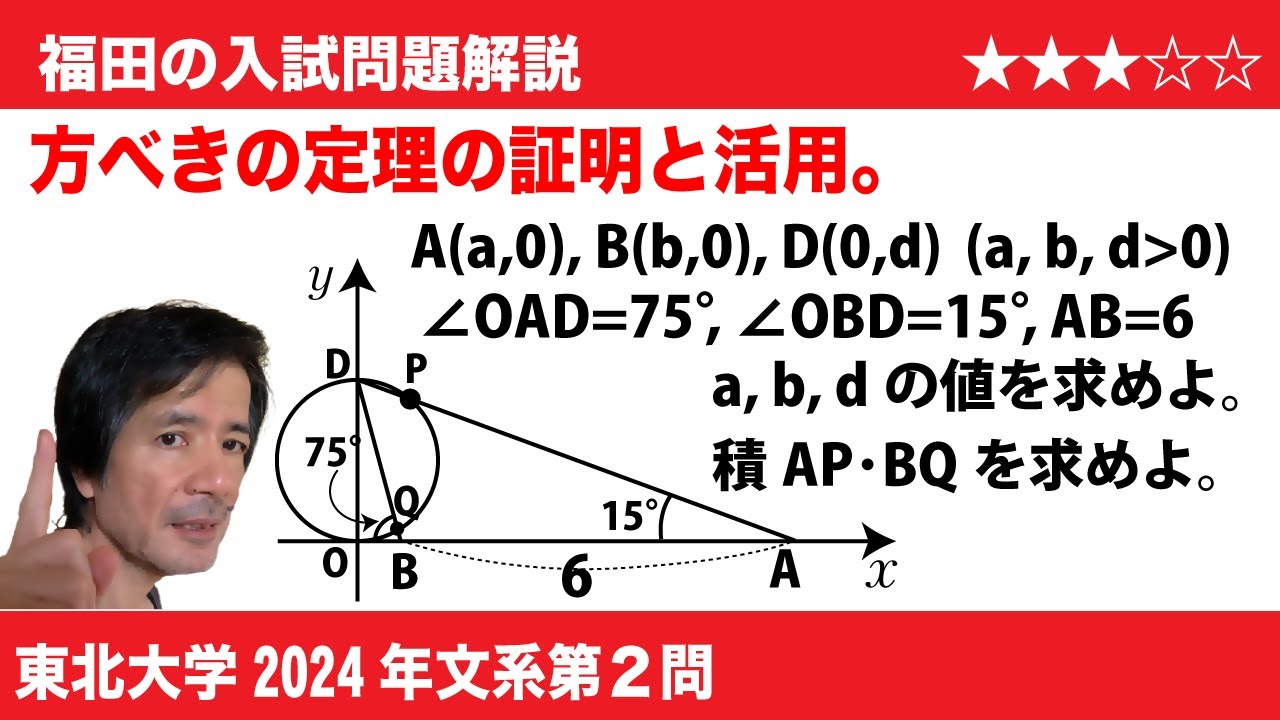
福田の数学〜東北大学2024年文系第2問〜75°の三角比と図形の計量
単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#方べきの定理と2つの円の関係#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ $a$, $b$, $d$を正の実数とし、$xy$平面上の点O(0,0), A($a$,0), B($b$,0), D(0,$d$)が次の条件をすべて満たすとする。
$\angle OAD$=15°, $\angle OBD$=75°, AB=6
以下の問いに答えよ。
(1)$\tan 75°$の値を求めよ。
(2)$a$, $b$, $d$の値をそれぞれ求めよ。
(3)2点O, Dを直径の両端とする円をCとする。線分ADとCの交点のうちDと異なるものをPとする。また、線分BDとCの交点のうちDと異なるものをQとする。このとき、方べきの定理AP・AD=$\textrm{AO}^2$, BP・BD=$\textrm{BO}^2$ を示せ。
(4)(3)の点P,Qに対し、積AP・BQの値を求めよ。
この動画を見る
$\Large{\boxed{2}}$ $a$, $b$, $d$を正の実数とし、$xy$平面上の点O(0,0), A($a$,0), B($b$,0), D(0,$d$)が次の条件をすべて満たすとする。
$\angle OAD$=15°, $\angle OBD$=75°, AB=6
以下の問いに答えよ。
(1)$\tan 75°$の値を求めよ。
(2)$a$, $b$, $d$の値をそれぞれ求めよ。
(3)2点O, Dを直径の両端とする円をCとする。線分ADとCの交点のうちDと異なるものをPとする。また、線分BDとCの交点のうちDと異なるものをQとする。このとき、方べきの定理AP・AD=$\textrm{AO}^2$, BP・BD=$\textrm{BO}^2$ を示せ。
(4)(3)の点P,Qに対し、積AP・BQの値を求めよ。
福田のおもしろ数学119〜アイデア募集〜対数の大小比較

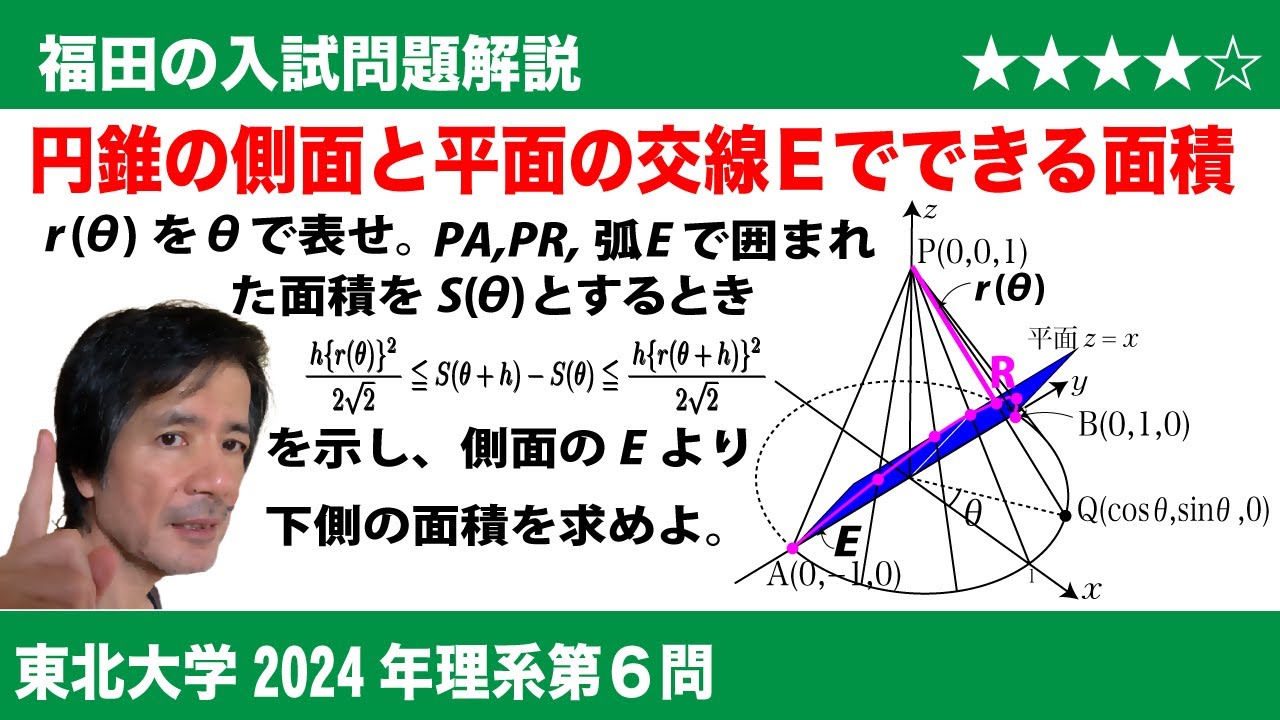
福田の数学〜東北大学2024年理系第6問〜円錐の側面と平面の交わりの曲線
単元:
#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{6}}$ $xyz$空間内の$xy$平面上にある円C:$x^2$+$y^2$=1および円盤D:$x^2$+$y^2$≦1を考える。Dを底面とし点P(0,0,1)を頂点とする円錐をKとする。A(0,-1,0), B(0,1,0)とする。$xyz$空間内の平面H:$z$=$x$を考える。すなわち、Hは$xz$平面上の直線$z$=$x$と線分ABをともに含む平面である。Kの側面とHの交わりとしてできる曲線をEとする。$-\frac{\pi}{2}$≦$\theta$≦$\frac{\pi}{2}$を満たす実数$\theta$に対し、円C上の点Q($\cos\theta$,$\sin\theta$,0)をとり、線分PQとEの共有点をRとする。
(1)線分PRの長さを$r(\theta)$とおく。$r(\theta)$を$\theta$を用いて表せ。
(2)円錐Kの側面のうち、曲線Eの点Aから点Rまでを結ぶ部分、線分PA、および線分PRにより囲まれた部分の面積を$S(\theta)$とおく。$\theta$と実数$h$が条件0≦$\theta$<$\theta$+$h$≦$\frac{\pi}{2}$ を満たすとき、次の不等式が成り立つことを示せ。
$\frac{h\left\{r(\theta)\right\}^2}{2\sqrt 2}$≦$S(\theta+h)-S(\theta)$≦$\frac{h\left\{r(\theta+h)\right\}^2}{2\sqrt 2}$
(3)円錐Kの側面のうち、円Cの$x$≧0の部分と曲線Eにより囲まれた部分の面積をTとおく。Tを求めよ。必要であれば$\tan\frac{\theta}{2}$=$uとおく置換積分を用いてもよい。
この動画を見る
$\Large{\boxed{6}}$ $xyz$空間内の$xy$平面上にある円C:$x^2$+$y^2$=1および円盤D:$x^2$+$y^2$≦1を考える。Dを底面とし点P(0,0,1)を頂点とする円錐をKとする。A(0,-1,0), B(0,1,0)とする。$xyz$空間内の平面H:$z$=$x$を考える。すなわち、Hは$xz$平面上の直線$z$=$x$と線分ABをともに含む平面である。Kの側面とHの交わりとしてできる曲線をEとする。$-\frac{\pi}{2}$≦$\theta$≦$\frac{\pi}{2}$を満たす実数$\theta$に対し、円C上の点Q($\cos\theta$,$\sin\theta$,0)をとり、線分PQとEの共有点をRとする。
(1)線分PRの長さを$r(\theta)$とおく。$r(\theta)$を$\theta$を用いて表せ。
(2)円錐Kの側面のうち、曲線Eの点Aから点Rまでを結ぶ部分、線分PA、および線分PRにより囲まれた部分の面積を$S(\theta)$とおく。$\theta$と実数$h$が条件0≦$\theta$<$\theta$+$h$≦$\frac{\pi}{2}$ を満たすとき、次の不等式が成り立つことを示せ。
$\frac{h\left\{r(\theta)\right\}^2}{2\sqrt 2}$≦$S(\theta+h)-S(\theta)$≦$\frac{h\left\{r(\theta+h)\right\}^2}{2\sqrt 2}$
(3)円錐Kの側面のうち、円Cの$x$≧0の部分と曲線Eにより囲まれた部分の面積をTとおく。Tを求めよ。必要であれば$\tan\frac{\theta}{2}$=$uとおく置換積分を用いてもよい。
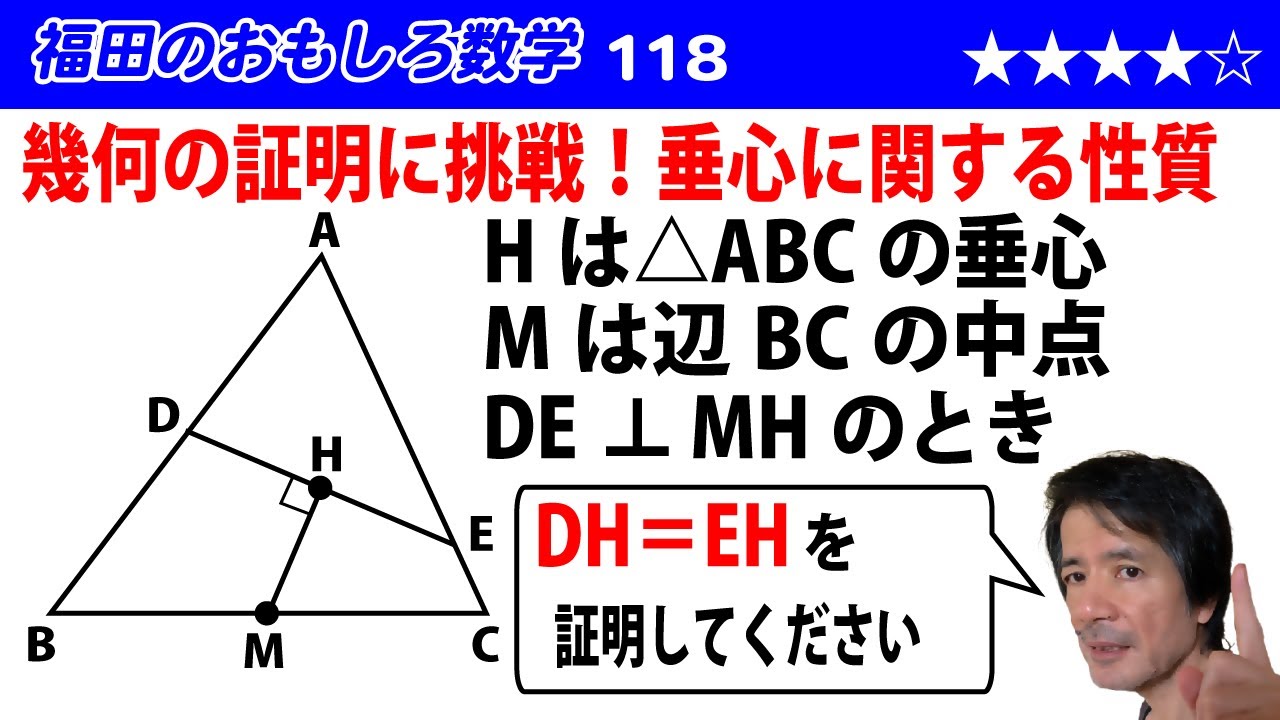
福田のおもしろ数学118〜幾何の証明〜垂心に関する命題の証明
単元:
#数A#図形の性質#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
動画の三角形ABCにおいて、点Hは三角形ABCの垂心、Mは辺BCの中点である。
DE$\bot$MHのとき、DH=EHを証明せよ。
この動画を見る
動画の三角形ABCにおいて、点Hは三角形ABCの垂心、Mは辺BCの中点である。
DE$\bot$MHのとき、DH=EHを証明せよ。
福田の数学〜東北大学2024年理系第5問〜関数の増減と方程式の整数解

単元:
#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{5}}$ $x$≧2 を満たす実数$x$に対し、
$f(x)$=$\displaystyle\frac{\log(2x-3)}{x}$
とおく。必要ならば、$\displaystyle\lim_{t \to \infty}\frac{\log t}{t}$=0 であること、および自然対数の底$e$が2<$e$<3 を満たすことを証明なしで用いてもよい。
(1)$f'(x)$=$\displaystyle\frac{g(x)}{x^2(2x-3)}$ とおくとき、関数$g(x)$ ($x$≧2)を求めよ。
(2)(1)で求めた関数$g(x)$に対し、$g(\alpha)$=0 を満たす2以上の実数$\alpha$がただ一つ存在することを示せ。
(3)関数$f(x)$ ($x$≧2)の増減と極限$\displaystyle\lim_{t \to \infty}f(x)$ を調べ、$y$=$f(x)$ ($x$≧2)のグラフの概形を$xy$平面上に描け。ただし(2)の$\alpha$を用いてよい。グラフの凹凸は調べなくてよい。
(4)2≦$m$<$n$ を満たす整数$m$,$n$の組($m$,$n$)に対して、等式
(*)$(2m-3)^n$=$(2n-3)^m$
が成り立つとする。このような組($m$,$n$)をすべて求めよ。
この動画を見る
$\Large{\boxed{5}}$ $x$≧2 を満たす実数$x$に対し、
$f(x)$=$\displaystyle\frac{\log(2x-3)}{x}$
とおく。必要ならば、$\displaystyle\lim_{t \to \infty}\frac{\log t}{t}$=0 であること、および自然対数の底$e$が2<$e$<3 を満たすことを証明なしで用いてもよい。
(1)$f'(x)$=$\displaystyle\frac{g(x)}{x^2(2x-3)}$ とおくとき、関数$g(x)$ ($x$≧2)を求めよ。
(2)(1)で求めた関数$g(x)$に対し、$g(\alpha)$=0 を満たす2以上の実数$\alpha$がただ一つ存在することを示せ。
(3)関数$f(x)$ ($x$≧2)の増減と極限$\displaystyle\lim_{t \to \infty}f(x)$ を調べ、$y$=$f(x)$ ($x$≧2)のグラフの概形を$xy$平面上に描け。ただし(2)の$\alpha$を用いてよい。グラフの凹凸は調べなくてよい。
(4)2≦$m$<$n$ を満たす整数$m$,$n$の組($m$,$n$)に対して、等式
(*)$(2m-3)^n$=$(2n-3)^m$
が成り立つとする。このような組($m$,$n$)をすべて求めよ。
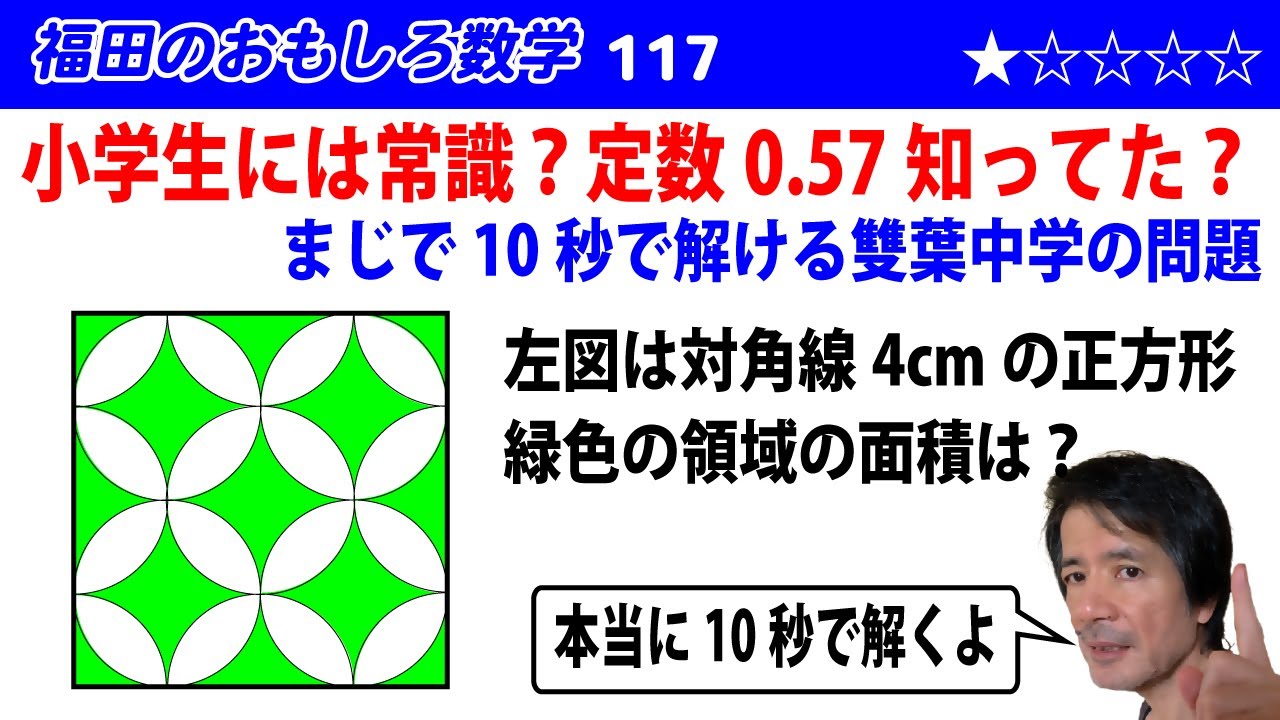
福田のおもしろ数学117〜小学生の常識なのか?0.57という定数は大切〜雙葉中学の問題
福田の数学〜東北大学2024年理系第4問〜2つの球面の交わりの円

単元:
#空間ベクトル#空間ベクトル#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{4}}$ $xyz$空間において、点$P_1$(3,-1,1)を中心とした半径$\sqrt 5$の球面$S_1$と、点$P_2$(5,0,-1)を中心とし半径が$\sqrt 2$の球面$S_2$を考える。
(1)線分$P_1P_2$の長さを求めよ。
(2)$S_1$と$S_2$が交わりをもつことを示せ。この交わりは円となる。この円をCとし、その中心を$P_3$とする。Cの半径および中心$P_3$の座標を求めよ。
(3)(2)の円Cに対し、Cを含む平面をHとする。$xy$平面とHの両方に平行で、大きさが1のベクトルを全て求めよ。
(4)点Qが(2)の円C上を動くとき、Qと$xy$平面の距離dの最大値を求めよ。
また、dの最大値を与える点Qの座標を求めよ。
この動画を見る
$\Large{\boxed{4}}$ $xyz$空間において、点$P_1$(3,-1,1)を中心とした半径$\sqrt 5$の球面$S_1$と、点$P_2$(5,0,-1)を中心とし半径が$\sqrt 2$の球面$S_2$を考える。
(1)線分$P_1P_2$の長さを求めよ。
(2)$S_1$と$S_2$が交わりをもつことを示せ。この交わりは円となる。この円をCとし、その中心を$P_3$とする。Cの半径および中心$P_3$の座標を求めよ。
(3)(2)の円Cに対し、Cを含む平面をHとする。$xy$平面とHの両方に平行で、大きさが1のベクトルを全て求めよ。
(4)点Qが(2)の円C上を動くとき、Qと$xy$平面の距離dの最大値を求めよ。
また、dの最大値を与える点Qの座標を求めよ。
福田のおもしろ数学116〜円の内部の点(a,b)に対してax+by=r^2はどんな直線を表しているか
単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
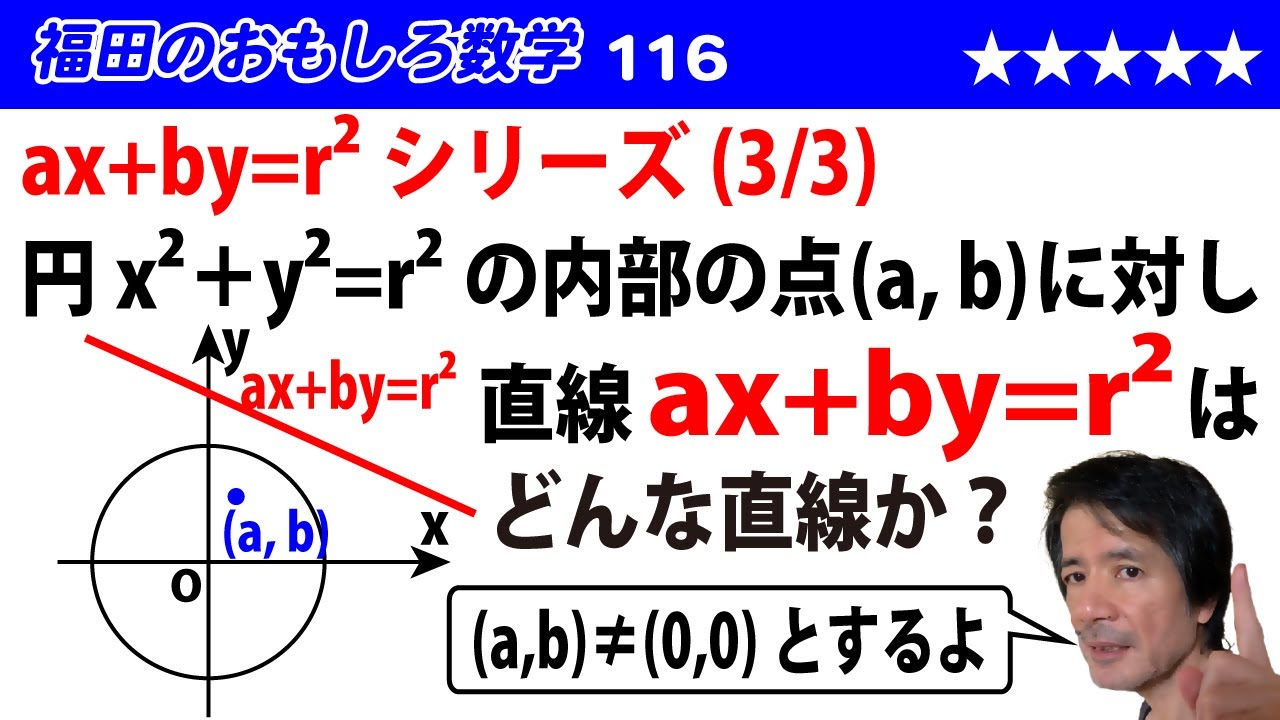
円$x^2$+$y^2$=$r^2$ の内部の点($a$,$b$)に対して直線$ax$+$by$=$r^2$ はどんな直線か。ただし、($a$,$b$)$\ne$(0,0)とする。
この動画を見る
円$x^2$+$y^2$=$r^2$ の内部の点($a$,$b$)に対して直線$ax$+$by$=$r^2$ はどんな直線か。ただし、($a$,$b$)$\ne$(0,0)とする。
福田の数学〜東北大学2024年理系第3問〜確率漸化式と複素数平面の融合

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ $n$ を2以上の整数とする。それぞれ $A$, $A$, $B$ と書かれた $3$ 枚のカードから無作為に $1$ 枚抜き出し、カードをもとに戻す試行を考える。この試行を $n$ 回繰り返し、抜き出したカードの文字を順に左から右に並べ、$n$ 文字の文字列を作る。作った文字列内に $AAA$ の並びがある場合は 不可 とする。また、作った文字列内に $BB$ の並びがある場合も 不可 とする。これらの場合以外は 可 とする。
例えば $n = 6$ のとき、文字列 $AAAABA$ や $ABBBAA$ や $ABBABB$ や $BBBAAA$ などは 不可 で、文字列 $BABAAB$ や $BABABA$ などは 可 である。
作った文字列が 可 でかつ右端の $2$ 文字が $AA$ である確率を $p_n$、作った文字列が 可 でかつ右端の $2$ 文字が $BA$ である確率を $q_n$、作った文字列が 可 でかつ右端の文字が $B$ である確率を $r_n$ とそれぞれおく。
(1) $p_2$, $q_2$, $r_2$ をそれぞれ求めよ。また、$p_{n+1}$, $q_{n+1}$, $r_{n+1}$ を $p_n$, $q_n$, $r_n$ を用いてそれぞれ表せ。
(2)$p_n$+$2q_n$+$2r_n$を$n$を用いて表せ。
(3)$p_n$+$iq_n$-$(1+i)r_n$を$n$を用いて表せ。ただし、$i$は虚数単位である。
(4)$p_n$=$r_n$ を満たすための、$n$の必要十分条件を求めよ。
この動画を見る
$\Large{\boxed{3}}$ $n$ を2以上の整数とする。それぞれ $A$, $A$, $B$ と書かれた $3$ 枚のカードから無作為に $1$ 枚抜き出し、カードをもとに戻す試行を考える。この試行を $n$ 回繰り返し、抜き出したカードの文字を順に左から右に並べ、$n$ 文字の文字列を作る。作った文字列内に $AAA$ の並びがある場合は 不可 とする。また、作った文字列内に $BB$ の並びがある場合も 不可 とする。これらの場合以外は 可 とする。
例えば $n = 6$ のとき、文字列 $AAAABA$ や $ABBBAA$ や $ABBABB$ や $BBBAAA$ などは 不可 で、文字列 $BABAAB$ や $BABABA$ などは 可 である。
作った文字列が 可 でかつ右端の $2$ 文字が $AA$ である確率を $p_n$、作った文字列が 可 でかつ右端の $2$ 文字が $BA$ である確率を $q_n$、作った文字列が 可 でかつ右端の文字が $B$ である確率を $r_n$ とそれぞれおく。
(1) $p_2$, $q_2$, $r_2$ をそれぞれ求めよ。また、$p_{n+1}$, $q_{n+1}$, $r_{n+1}$ を $p_n$, $q_n$, $r_n$ を用いてそれぞれ表せ。
(2)$p_n$+$2q_n$+$2r_n$を$n$を用いて表せ。
(3)$p_n$+$iq_n$-$(1+i)r_n$を$n$を用いて表せ。ただし、$i$は虚数単位である。
(4)$p_n$=$r_n$ を満たすための、$n$の必要十分条件を求めよ。
福田のおもしろ数学115〜円外の点から引いた2本の接線の接点を結んでできる直線の方程式
単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
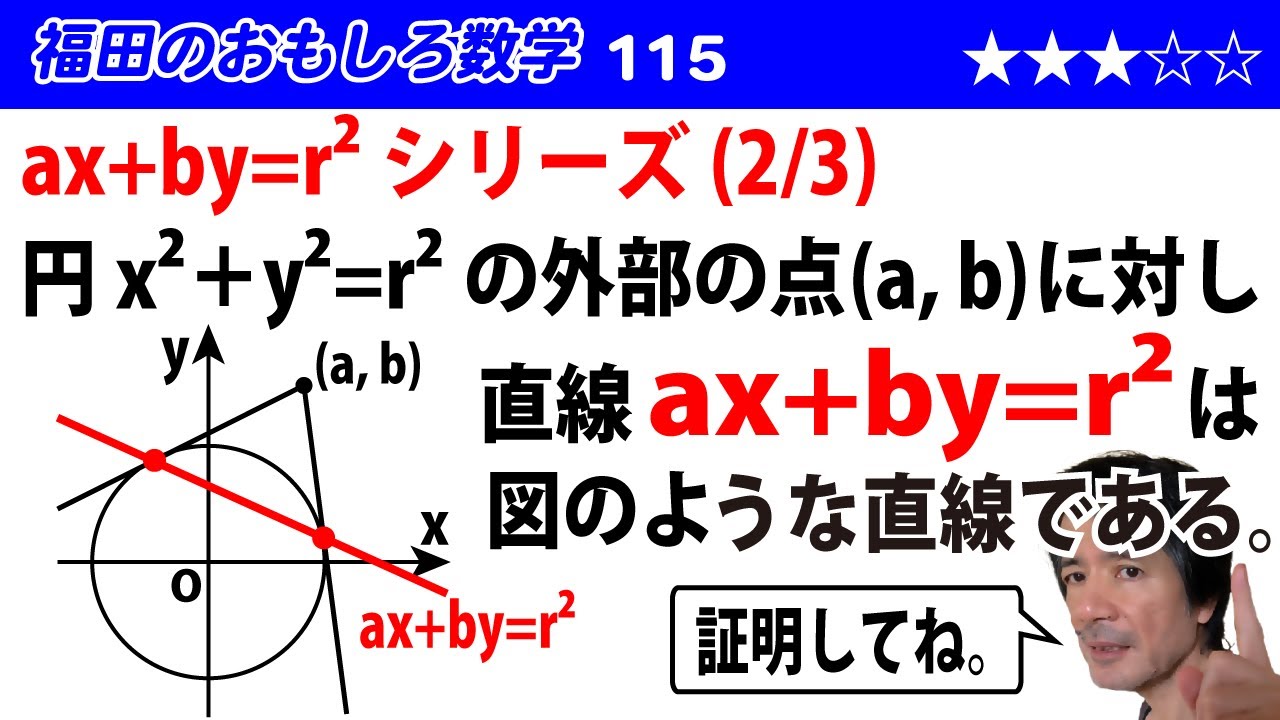
円$x^2$+$y^2$=$r^2$ 上に円外の点($a$,$b$)から2本の接線を引く。このとき2接点P,Qを結ぶ直線の方程式は$ax$+$by$=$r^2$ であることを証明せよ。
この動画を見る
円$x^2$+$y^2$=$r^2$ 上に円外の点($a$,$b$)から2本の接線を引く。このとき2接点P,Qを結ぶ直線の方程式は$ax$+$by$=$r^2$ であることを証明せよ。
福田の数学〜東北大学2024年理系第2問〜対数不等式の証明と自然数解

単元:
#数Ⅱ#指数関数と対数関数#対数関数#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ 以下の問いに答えよ。
(1)$t$を$t$>1 を満たす実数とする。正の実数$x$が2つの条件
(a)$x$>$\displaystyle\frac{1}{\sqrt t-1}$
(b)$x$≧$2\log_tx$
をともに満たすとする。このとき、不等式
$x$+1>$2\log_t(x+1)$
を示せ。
(2)$n$≦$2\log_2n$ を満たす正の整数$n$をすべて求めよ。
この動画を見る
$\Large{\boxed{2}}$ 以下の問いに答えよ。
(1)$t$を$t$>1 を満たす実数とする。正の実数$x$が2つの条件
(a)$x$>$\displaystyle\frac{1}{\sqrt t-1}$
(b)$x$≧$2\log_tx$
をともに満たすとする。このとき、不等式
$x$+1>$2\log_t(x+1)$
を示せ。
(2)$n$≦$2\log_2n$ を満たす正の整数$n$をすべて求めよ。
福田のおもしろ数学114〜円の接線の公式の証明

単元:
#数Ⅱ#図形と方程式#円と方程式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
円$x^2$+$y^2$=$r^2$ 上の点($a$,$b$)における接線の方程式は
$ax$+$by$=$r^2$ であることを証明せよ。
この動画を見る
円$x^2$+$y^2$=$r^2$ 上の点($a$,$b$)における接線の方程式は
$ax$+$by$=$r^2$ であることを証明せよ。
福田の数学〜東北大学2024年理系第1問〜放物線と接線と面積

単元:
#数Ⅱ#微分法と積分法#面積、体積#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ $a$を正の実数とし、$f(x)$=$x^2$-$2ax$+$4a^2$ とする。Oを原点とする$xy$平面上の放物線C:$y$=$f(x)$の頂点をAとする。直線OAとCの交点のうちAと異なるものをP($p$,$f(p)$)とし、OからCへ引いた接線の接点をQ($q$,$f(q)$)とする。ただし、$q$>0 とする。
(1)$p$,$q$の値を$a$を用いて表せ。また、$p$>$q$であることを示せ。
(2)放物線Cの$q$≦$x$≦$p$の部分、線分OP、および線分OQで囲まれた図形の面積をSとおく。Sを$a$を用いて表せ。
(3)(2)のSに対し、S=$\frac{2}{3}$ となるときの$a$の値を求めよ。
この動画を見る
$\Large{\boxed{1}}$ $a$を正の実数とし、$f(x)$=$x^2$-$2ax$+$4a^2$ とする。Oを原点とする$xy$平面上の放物線C:$y$=$f(x)$の頂点をAとする。直線OAとCの交点のうちAと異なるものをP($p$,$f(p)$)とし、OからCへ引いた接線の接点をQ($q$,$f(q)$)とする。ただし、$q$>0 とする。
(1)$p$,$q$の値を$a$を用いて表せ。また、$p$>$q$であることを示せ。
(2)放物線Cの$q$≦$x$≦$p$の部分、線分OP、および線分OQで囲まれた図形の面積をSとおく。Sを$a$を用いて表せ。
(3)(2)のSに対し、S=$\frac{2}{3}$ となるときの$a$の値を求めよ。
福田のおもしろ数学113〜1分チャレンジ〜連立方程式を解こう

単元:
#数Ⅱ#複素数と方程式#解と判別式・解と係数の関係#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
次の連立方程式を解け。ただし、$a$,$b$,$c$は0ではない異なる実数とする。
$\begin{array}{1}
a^3x+a^2y+az=1 ...①\\
b^3x+b^2y+bz=1 ...②\\
c^3x+c^2y+cz=1 ...③\\
\end{array}$
この動画を見る
次の連立方程式を解け。ただし、$a$,$b$,$c$は0ではない異なる実数とする。
$\begin{array}{1}
a^3x+a^2y+az=1 ...①\\
b^3x+b^2y+bz=1 ...②\\
c^3x+c^2y+cz=1 ...③\\
\end{array}$
福田の数学〜北海道大学2024年文系第4問〜正八面体のサイコロと反復試行の確率

単元:
#数A#場合の数と確率#確率#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{4}}$ 各面に1つずつ数が書かれた正八面体のさいころがある。「1」、「2」、「3」が書かれた面がそれぞれ1つずつあり、残りの5つの面には「0」が書かれている。このさいころを水平な面に投げて、出た面に書かれた数を持ち点に加えるという試行を考える。最初の持ち点は0とし、この試行を繰り返す。例えば、3回の試行を行ったとき、出た面に書かれた数が「0」、「2」、「3」であれば、持ち点は5となる。なお、さいころが水平な床面にあるとき、さいころの上部の水平な面を出た面とよぶ。また、さいころを投げるとき、各面が出ることは同様に確からしいとする。
(1)この試行を2回行ったとき、持ち点が1である確率を求めよ。
(2)この試行を4回行ったとき、持ち点が10以下である確率を求めよ。
この動画を見る
$\Large{\boxed{4}}$ 各面に1つずつ数が書かれた正八面体のさいころがある。「1」、「2」、「3」が書かれた面がそれぞれ1つずつあり、残りの5つの面には「0」が書かれている。このさいころを水平な面に投げて、出た面に書かれた数を持ち点に加えるという試行を考える。最初の持ち点は0とし、この試行を繰り返す。例えば、3回の試行を行ったとき、出た面に書かれた数が「0」、「2」、「3」であれば、持ち点は5となる。なお、さいころが水平な床面にあるとき、さいころの上部の水平な面を出た面とよぶ。また、さいころを投げるとき、各面が出ることは同様に確からしいとする。
(1)この試行を2回行ったとき、持ち点が1である確率を求めよ。
(2)この試行を4回行ったとき、持ち点が10以下である確率を求めよ。
福田のおもしろ数学112〜多変数の式の最大最小

単元:
#数Ⅱ#図形と方程式#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
実数$x$,$y$,$z$が0≦$x$≦1, 0≦$y$≦1, 2≦$z$≦3 を満たして変わるとき、$\displaystyle\frac{z-y}{z-x}$ の最大値、最小値を求めよ。
この動画を見る
実数$x$,$y$,$z$が0≦$x$≦1, 0≦$y$≦1, 2≦$z$≦3 を満たして変わるとき、$\displaystyle\frac{z-y}{z-x}$ の最大値、最小値を求めよ。
福田の数学〜北海道大学2024年文系第3問〜3次関数のグラフと面積

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ $a$を0でない実数とする。$C$を$y$=$-x^3$+$x^2$ で表される曲線、$l$を$y$=$a$ で表される直線とし、$C$と$l$は共有点をちょうど2つもつとする。
(1)$a$の値を求めよ。
(2)$C$と$l$の共有点の$x$座標をすべて求めよ。
(3)$C$と$l$で囲まれた図形の面積を求めよ。
この動画を見る
$\Large{\boxed{3}}$ $a$を0でない実数とする。$C$を$y$=$-x^3$+$x^2$ で表される曲線、$l$を$y$=$a$ で表される直線とし、$C$と$l$は共有点をちょうど2つもつとする。
(1)$a$の値を求めよ。
(2)$C$と$l$の共有点の$x$座標をすべて求めよ。
(3)$C$と$l$で囲まれた図形の面積を求めよ。
福田のおもしろ数学111〜論証力をチェックしよう〜3変数の基本対称式の性質

単元:
#数Ⅱ#式と証明#恒等式・等式・不等式の証明
指導講師:
福田次郎
問題文全文(内容文):
実数$a$,$b$,$c$が$a$+$b$+$c$>0, $ab$+$bc$+$ca$>0, $abc$>0 を満たすとき、$a$>0, $b$>0, $c$>0 であることを証明せよ。
この動画を見る
実数$a$,$b$,$c$が$a$+$b$+$c$>0, $ab$+$bc$+$ca$>0, $abc$>0 を満たすとき、$a$>0, $b$>0, $c$>0 であることを証明せよ。
福田の数学〜北海道大学2024年文系第2問〜漸化式を解く

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ 次の条件によって定められる数列$\left\{a_n\right\}$について考える。
$a_1$=3, $a_{n+1}$=$3a_n$-$\displaystyle\frac{3^{n+1}}{n(n+1)}$
(1)$b_n$=$\frac{a_n}{3^n}$ とおくとき、$b_{n+1}$を$b_n$と$n$の式で表せ。
(2)数列$\left\{a_n\right\}$ の一般項を求めよ。
この動画を見る
$\Large{\boxed{2}}$ 次の条件によって定められる数列$\left\{a_n\right\}$について考える。
$a_1$=3, $a_{n+1}$=$3a_n$-$\displaystyle\frac{3^{n+1}}{n(n+1)}$
(1)$b_n$=$\frac{a_n}{3^n}$ とおくとき、$b_{n+1}$を$b_n$と$n$の式で表せ。
(2)数列$\left\{a_n\right\}$ の一般項を求めよ。
福田のおもしろ数学110〜豊島岡女子中学の問題〜面積を求める難問
単元:
#算数(中学受験)#平面図形#角度と面積
指導講師:
福田次郎
問題文全文(内容文):
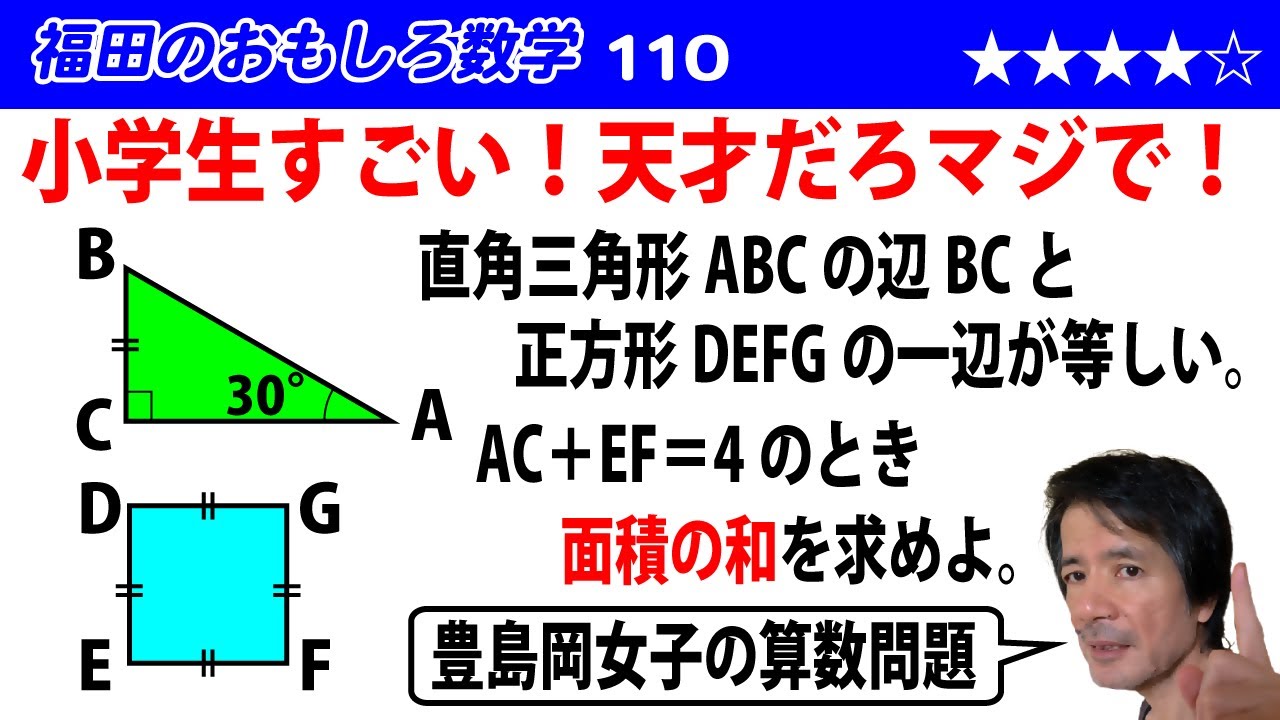
図のような(※動画参照)直角三角形ABCと正方形DEFGがあります。辺BCの長さと正方形の一辺の長さが等しく、辺ACの長さと正方形の一辺の長さの和が4 cmであるとき、2つの図形の面積の和は何$\textrm{cm}^2$か。
この動画を見る
図のような(※動画参照)直角三角形ABCと正方形DEFGがあります。辺BCの長さと正方形の一辺の長さが等しく、辺ACの長さと正方形の一辺の長さの和が4 cmであるとき、2つの図形の面積の和は何$\textrm{cm}^2$か。
福田の数学〜北海道大学2024年文系第1問〜約数の個数と総和

単元:
#数A#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ 次の問いに答えよ。
(1)自然数$m$, $n$について、$2^m・3^n$の正の約数の個数を求めよ。
(2)6912の正の約数のうち、12で割り切れないものの総和を求めよ。
この動画を見る
$\Large{\boxed{1}}$ 次の問いに答えよ。
(1)自然数$m$, $n$について、$2^m・3^n$の正の約数の個数を求めよ。
(2)6912の正の約数のうち、12で割り切れないものの総和を求めよ。
福田のおもしろ数学109〜桜蔭中学の問題〜正三角形の回転移動で通過する範囲の面積
単元:
#算数(中学受験)#平面図形#図形の移動
指導講師:
福田次郎
問題文全文(内容文):
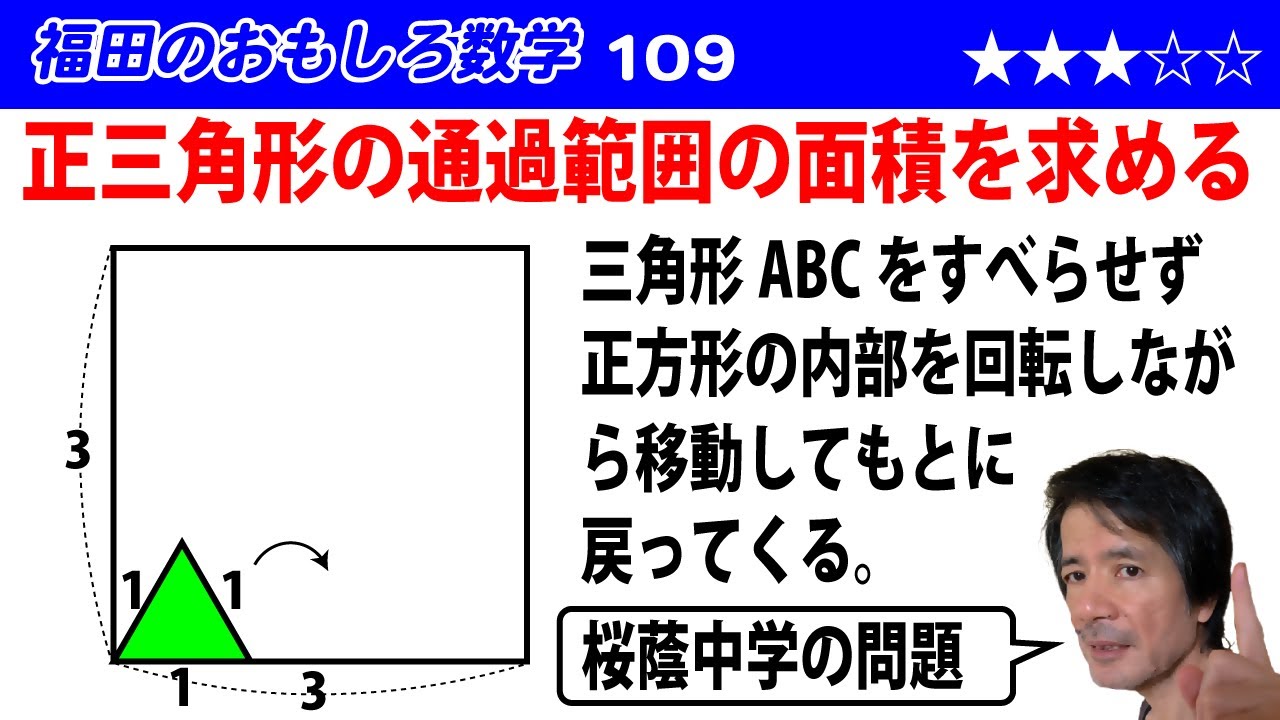
一辺が1の正三角形ABCが図のように(※動画参照)一辺が3の正方形PQRTの内部にあります。
この正三角形を元の位置に戻るまで、矢印の向きにすべらないように回転させながら移動させます。
正三角形ABCの面積をSとするとき、通過範囲の面積をSを用いて表しなさい。
この動画を見る
一辺が1の正三角形ABCが図のように(※動画参照)一辺が3の正方形PQRTの内部にあります。
この正三角形を元の位置に戻るまで、矢印の向きにすべらないように回転させながら移動させます。
正三角形ABCの面積をSとするとき、通過範囲の面積をSを用いて表しなさい。
福田の数学〜北海道大学2024年理系第5問〜対数関数の増減凹凸と面積

単元:
#積分とその応用#面積・体積・長さ・速度#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{5}}$ 関数$f(x)$=$x\log(x+2)$+1 ($x$>-2)
を考える。$y$=$f(x)$で表される曲線を$C$とする。$C$の接線のうち傾きが正で原点を通るものを$l$とする。ただし$\log t$は$t$の自然対数である。
(1)直線$l$の方程式を求めよ。
(2)曲線$C$は下に凸であることを証明せよ。
(3)$C$と$l$および$y$軸で囲まれた部分の面積を求めよ。
この動画を見る
$\Large{\boxed{5}}$ 関数$f(x)$=$x\log(x+2)$+1 ($x$>-2)
を考える。$y$=$f(x)$で表される曲線を$C$とする。$C$の接線のうち傾きが正で原点を通るものを$l$とする。ただし$\log t$は$t$の自然対数である。
(1)直線$l$の方程式を求めよ。
(2)曲線$C$は下に凸であることを証明せよ。
(3)$C$と$l$および$y$軸で囲まれた部分の面積を求めよ。
福田のおもしろ数学108〜虚数単位iは数直線上に存在するか
福田の数学〜北海道大学2024年理系第4問〜三角形の内心の位置ベクトル

単元:
#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{4}}$ 三角形OABが、|$\overrightarrow{OA}$|=3, |$\overrightarrow{AB}$|=5, $\overrightarrow{OA}・\overrightarrow{OB}$=10 を満たしているとする。
三角形OABの内接円の中心をIとし、この内接円と辺OAの接点をHとする。
(1)辺OBの長さを求めよ。
(2)$\overrightarrow{OI}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
(3)$\overrightarrow{HI}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
この動画を見る
$\Large{\boxed{4}}$ 三角形OABが、|$\overrightarrow{OA}$|=3, |$\overrightarrow{AB}$|=5, $\overrightarrow{OA}・\overrightarrow{OB}$=10 を満たしているとする。
三角形OABの内接円の中心をIとし、この内接円と辺OAの接点をHとする。
(1)辺OBの長さを求めよ。
(2)$\overrightarrow{OI}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。
(3)$\overrightarrow{HI}$を$\overrightarrow{OA}$と$\overrightarrow{OB}$を用いて表せ。



