 高校入試から見た数学の世界「全部入試問題」by しろたん
高校入試から見た数学の世界「全部入試問題」by しろたん
 高校入試から見た数学の世界「全部入試問題」by しろたん
高校入試から見た数学の世界「全部入試問題」by しろたん
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
【ここは無理せず安全に!】因数分解:江戸川学園取手高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ a^2-4b^2+12bc-9c^2$を因数分解しなさい.
江戸川取手高校過去問
この動画を見る
$ a^2-4b^2+12bc-9c^2$を因数分解しなさい.
江戸川取手高校過去問
【作問者の掌(てのひら)で踊る…!】平方根:城北高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \sqrt{2023\times2021-4044+2}$の値を求めよ.
城北高校過去問
この動画を見る
$ \sqrt{2023\times2021-4044+2}$の値を求めよ.
城北高校過去問
【考え方が大切!一度は挑戦したい。】一次関数:駿台甲府高等学校~全部入試問題
単元:
#数学(中学生)#高校入試過去問(数学)#駿台甲府高等学校
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
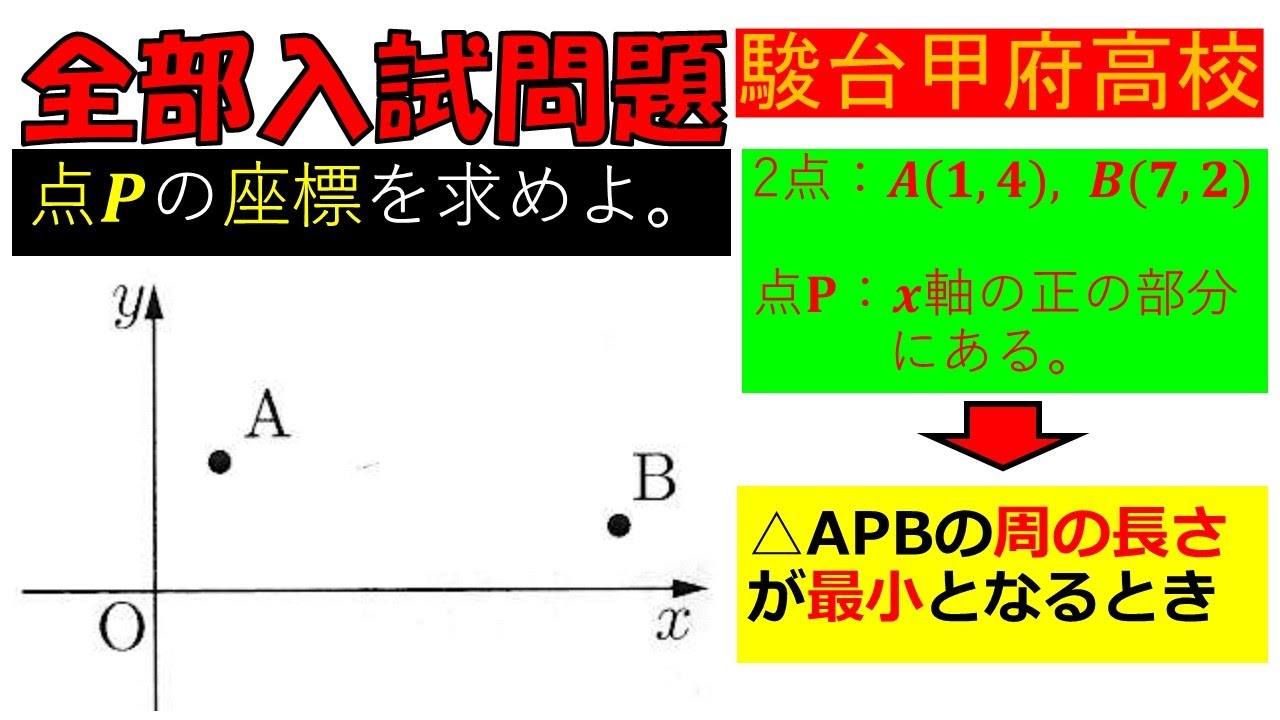
入試問題 駿台甲府高等学校
2点:A(1,4), B(7,2)
点P:x軸の正の部分にある。
↓
$\triangle APB$の周の長さ -が最小となるとき
点Pの座標を求めよ。
※図は動画内参照
この動画を見る
入試問題 駿台甲府高等学校
2点:A(1,4), B(7,2)
点P:x軸の正の部分にある。
↓
$\triangle APB$の周の長さ -が最小となるとき
点Pの座標を求めよ。
※図は動画内参照
冬の澄み切った空気の中で数学を解くショート~全国入試問題解法 #Shorts #数学 #高校入試 #shorts

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \dfrac{1}{6}x^2-ax-18$を因数分解すると,$\dfrac{1}{6}(x-12)(x+b)$となる.
定数$a,b$の値を求めよ.
明治学院高校過去問
この動画を見る
$ \dfrac{1}{6}x^2-ax-18$を因数分解すると,$\dfrac{1}{6}(x-12)(x+b)$となる.
定数$a,b$の値を求めよ.
明治学院高校過去問
【解法はいろいろあるから!】図形:新潟県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#円#角度と面積#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
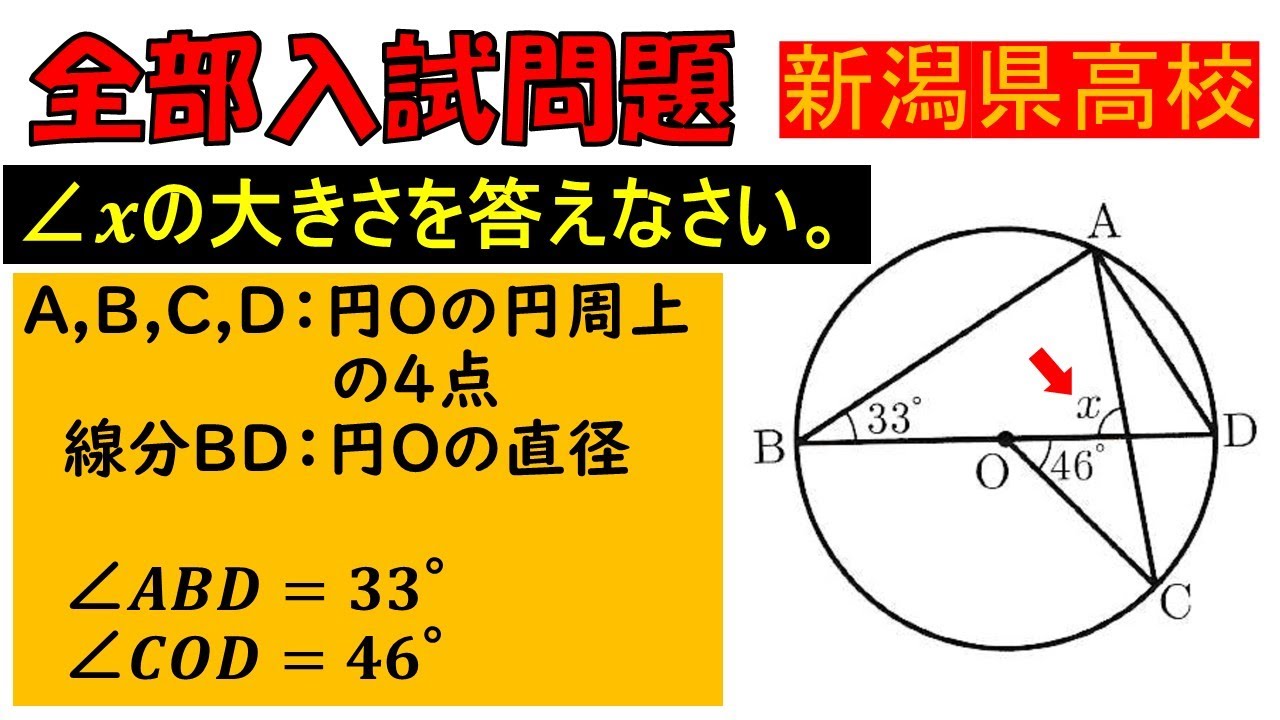
$A,B,C,D$は円$O$の円周上の4点であり,線分$BD$は円$O$の直径である.
$ \angle ABD=33°,\angle COD=46°$である.
$ \angle x$の大きさを答えなさい.
新潟県高校過去問
この動画を見る
$A,B,C,D$は円$O$の円周上の4点であり,線分$BD$は円$O$の直径である.
$ \angle ABD=33°,\angle COD=46°$である.
$ \angle x$の大きさを答えなさい.
新潟県高校過去問
西暦"2023"を含む入試予想問題(その5)~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式$(2023-x)(2024-x)=2025-x$の解は,$x=\Box $である.
$x$を求めよ.
この動画を見る
2次方程式$(2023-x)(2024-x)=2025-x$の解は,$x=\Box $である.
$x$を求めよ.
西暦"2023"を含む入試予想問題(その4)~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#数と式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$N$の整数部分が$ N=\sqrt{2023+x}$とする.
整数$x$はいくつあるか.
この動画を見る
$N$の整数部分が$ N=\sqrt{2023+x}$とする.
整数$x$はいくつあるか.
西暦"2023"を含む入試予想問題(その3)~全国入試問題解法

単元:
#計算と数の性質#数の性質その他#数学(中学生)#中1数学
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$20^{23}$は何桁の数ですか.
なお,$2^{10}=1024$です.
この動画を見る
$20^{23}$は何桁の数ですか.
なお,$2^{10}=1024$です.
西暦"2023"を含む入試予想問題(その2)~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \sqrt{2023}x+\sqrt{2021}y=2,\sqrt{2021}x+\sqrt{2023}y=1$
$ x^2-y^2=\Box $である.
この動画を見る
$ \sqrt{2023}x+\sqrt{2021}y=2,\sqrt{2021}x+\sqrt{2023}y=1$
$ x^2-y^2=\Box $である.
🎍西暦"2023"を含む入試予想問題(その1)~全国入試問題解法

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ 2023\times2021-2020^2-2022\times2025+2021^2+2022$を計算せよ.
この動画を見る
$ 2023\times2021-2020^2-2022\times2025+2021^2+2022$を計算せよ.
♪その場で考える数学の問題を音楽と共に楽しむ数秒間~全国入試問題解法 #shorts #math #sound #数学 #高校入試

単元:
#数学(中学生)#中1数学#方程式
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$【a】=a^2-4,[b]=\dfrac{b}{2}+3$と定める.
$【[x]】=4$を解け.
明治学院高校過去問
この動画を見る
$【a】=a^2-4,[b]=\dfrac{b}{2}+3$と定める.
$【[x]】=4$を解け.
明治学院高校過去問
🎍西暦"2023"を含む入試予想問題(考察編)~全国入試問題解法
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
次の入試問題を導け.
$ 2023=?$
この動画を見る
次の入試問題を導け.
$ 2023=?$
【「式の形」が見えればOK!】平方根:東京都立国立高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ \left(\dfrac{\sqrt5+\sqrt3}{\sqrt2}\right)^2+ \left(\dfrac{\sqrt5+\sqrt3}{\sqrt2}\right) \left(\dfrac{\sqrt5-\sqrt3}{\sqrt2}\right)-\left(\dfrac{\sqrt5-\sqrt3}{\sqrt2}\right)^2$を計算せよ.
都立国立高校過去問
この動画を見る
$ \left(\dfrac{\sqrt5+\sqrt3}{\sqrt2}\right)^2+ \left(\dfrac{\sqrt5+\sqrt3}{\sqrt2}\right) \left(\dfrac{\sqrt5-\sqrt3}{\sqrt2}\right)-\left(\dfrac{\sqrt5-\sqrt3}{\sqrt2}\right)^2$を計算せよ.
都立国立高校過去問
【最初の2分間が全て!今年の的中問題】図形:高知県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#中2数学#平面図形#三角形と四角形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
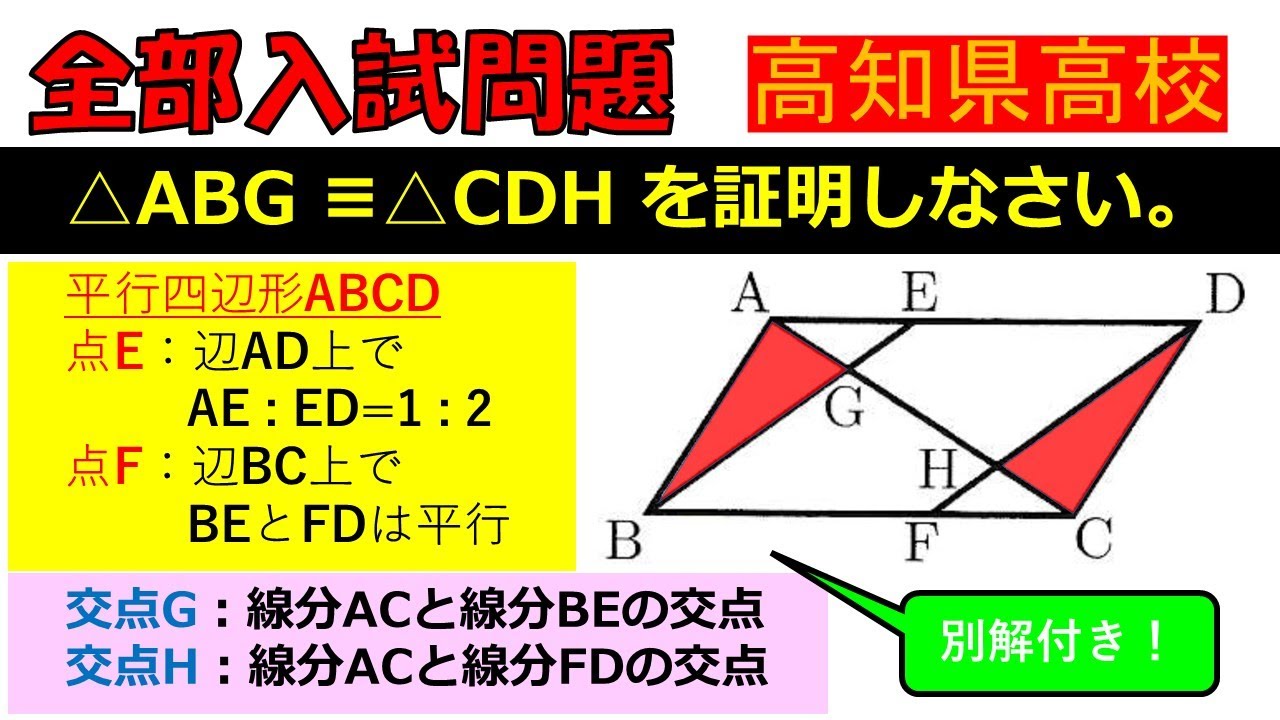
平行四辺形$ABCD$の点$E$は辺$AD$上で$AE:ED=1:2$である.
点$F$は辺$BC$上で$BE$と$FD$は平行である.
交点$G$は線分$AC$と線分$BE$の交点であり,交点$H$は線分$AC$と線分$FD$の交点である.
$ \triangle ABG \equiv CDH$を証明しなさい.
高知県高校過去問
この動画を見る
平行四辺形$ABCD$の点$E$は辺$AD$上で$AE:ED=1:2$である.
点$F$は辺$BC$上で$BE$と$FD$は平行である.
交点$G$は線分$AC$と線分$BE$の交点であり,交点$H$は線分$AC$と線分$FD$の交点である.
$ \triangle ABG \equiv CDH$を証明しなさい.
高知県高校過去問
🎄【メイン・テーマは番外編で…】二次方程式:開成高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式$ 7x^2-4\sqrt2x+1=0$を考える.
2つの解を求めよ.
開成高校過去問
この動画を見る
2次方程式$ 7x^2-4\sqrt2x+1=0$を考える.
2つの解を求めよ.
開成高校過去問
【これぞ、数学の「応用」…!】文章題:埼玉県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#比例・反比例#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
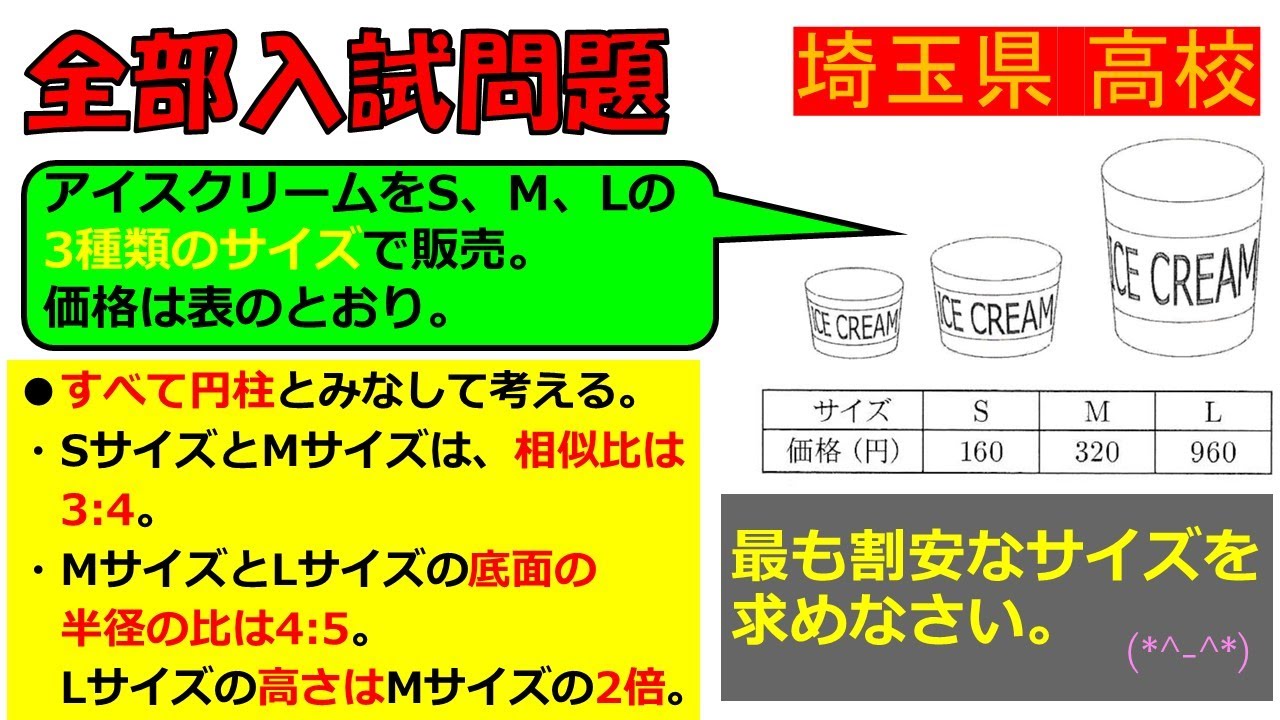
アイスクリームをS,M,Lの3種類のサイズで販売している.
最も割安なサイズを求めなさい.
埼玉県高校過去問
この動画を見る
アイスクリームをS,M,Lの3種類のサイズで販売している.
最も割安なサイズを求めなさい.
埼玉県高校過去問
【2つの解法!2分で?4分30秒で?】二次関数:宮城県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#2次関数#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
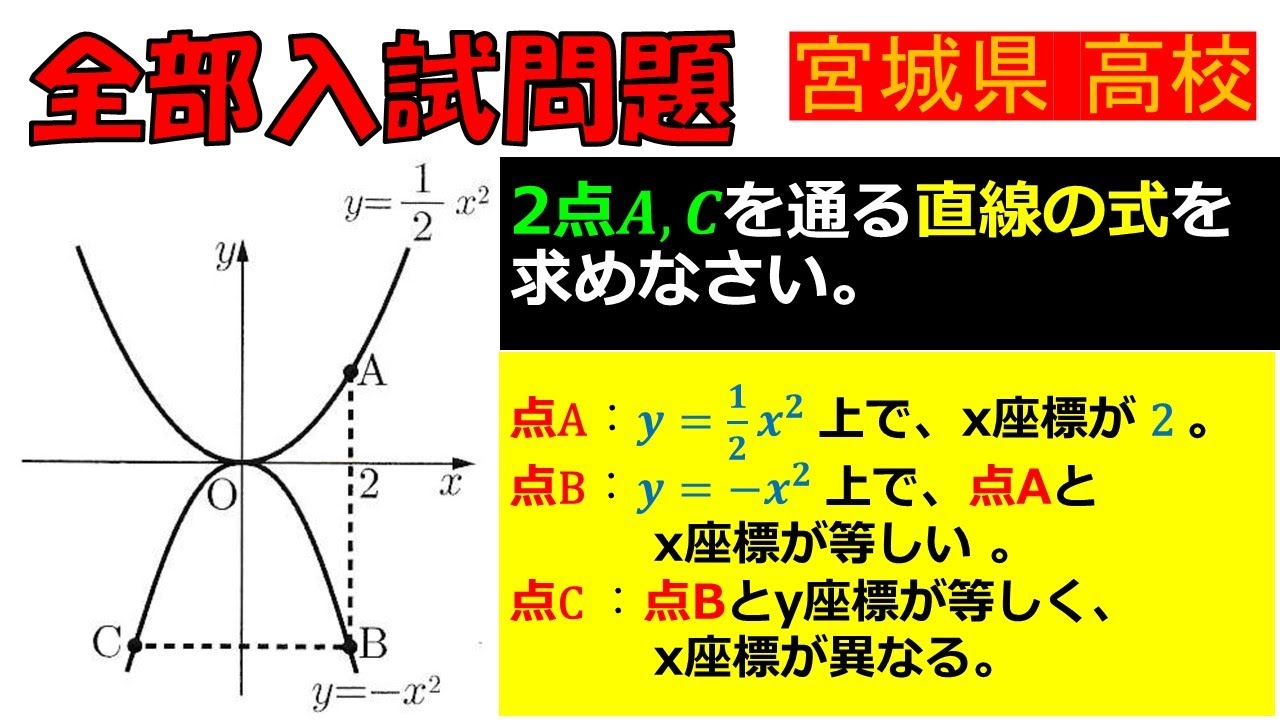
2点$A,C$を通る直線の式を求めなさい.
宮城県高校過去問
この動画を見る
2点$A,C$を通る直線の式を求めなさい.
宮城県高校過去問
【初めが肝心!】整数:秋田県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#正の数・負の数
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2つの整数$148,245$を自然数$n$で割ったとき,余りがそれぞれ$4,5$となる.
自然数$n$は全部で何個あるか.
秋田県高校過去問
この動画を見る
2つの整数$148,245$を自然数$n$で割ったとき,余りがそれぞれ$4,5$となる.
自然数$n$は全部で何個あるか.
秋田県高校過去問
【さらに学べば見方も変わる!】二次方程式:成蹊高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
方程式$ 3\left(x-\dfrac{1}{2}\right)^2=3x+\dfrac{7}{4}$を解け.
成蹊高校過去問
この動画を見る
方程式$ 3\left(x-\dfrac{1}{2}\right)^2=3x+\dfrac{7}{4}$を解け.
成蹊高校過去問
【そして経験したことを思い出して】図形:国立高等専門学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#角度と面積#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
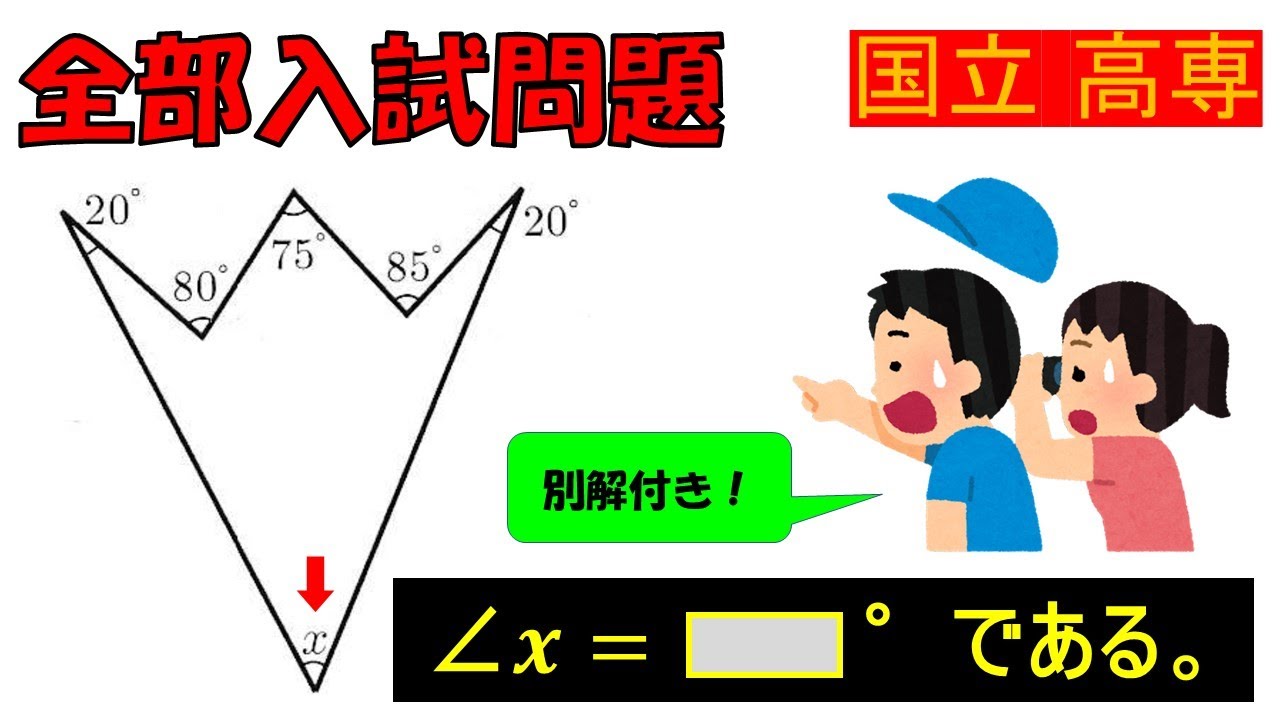
$ \angle x$は$\Box$である.
この動画を見る
$ \angle x$は$\Box$である.
眠れない夜に学ぶ数学~全国入試問題解法 #shorts #数学 #sound

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ x-\dfrac{\sqrt2-2}{2}$のとき,$x^2+2x+\dfrac{1}{x+1}+1$の値を求めなさい.
立命館高校過去問
この動画を見る
$ x-\dfrac{\sqrt2-2}{2}$のとき,$x^2+2x+\dfrac{1}{x+1}+1$の値を求めなさい.
立命館高校過去問
【よく出題される形式!4問分の解説】平方根:群馬県公立高等学校~全国入試問題解法

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
数について述べた次のア~エのうち,正しいものをすべて選びなさい.
ア すべての自然数は,その逆数も自然数となる.
イ 異なる2つの整数について,大きい方から小さい方をひいた差は,いつでも自然数となる.
ウ すべての2次方程式の解は,無理数となる.
エ すべての有理数や無理数は,数直線上に対応する点がある.
群馬県高校過去問
この動画を見る
数について述べた次のア~エのうち,正しいものをすべて選びなさい.
ア すべての自然数は,その逆数も自然数となる.
イ 異なる2つの整数について,大きい方から小さい方をひいた差は,いつでも自然数となる.
ウ すべての2次方程式の解は,無理数となる.
エ すべての有理数や無理数は,数直線上に対応する点がある.
群馬県高校過去問
【一本道が見えますか】連立方程式:巣鴨高等学校~全国入試問題解法

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2つの連立方程式
$ \begin{eqnarray}
\left\{
\begin{array}{l}
3x + 2y = 14 \\
ax + by = 3
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
bx -ay = -5 \\
4x-5y = 11
\end{array}
\right.
\end{eqnarray}$
の解が一致するとき$a,b$の値をそれぞれ求めなさい.
巣鴨高校過去問
この動画を見る
2つの連立方程式
$ \begin{eqnarray}
\left\{
\begin{array}{l}
3x + 2y = 14 \\
ax + by = 3
\end{array}
\right.
\end{eqnarray}$
$\begin{eqnarray}
\left\{
\begin{array}{l}
bx -ay = -5 \\
4x-5y = 11
\end{array}
\right.
\end{eqnarray}$
の解が一致するとき$a,b$の値をそれぞれ求めなさい.
巣鴨高校過去問
【今年も全国で類題が出るよ】図形:栃木県公立高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#中2数学#平面図形#三角形と四角形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
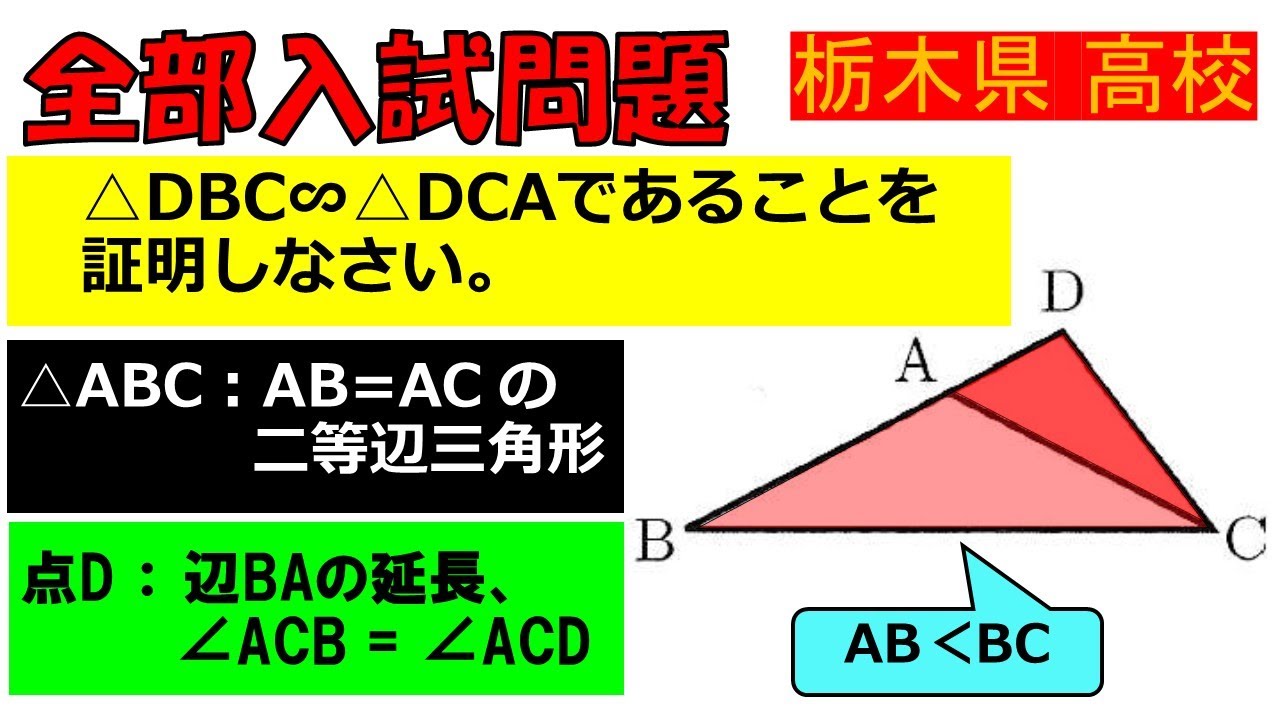
$ \triangle ABC$は$AB=AC$の二等辺三角形である.
点$D$は辺$BA$の延長であり,$ \angle ACB=\angle ACD$である.
$ \triangle DBC \backsim \triangle DCA$であることを証明しなさい.
栃木県高校過去問
この動画を見る
$ \triangle ABC$は$AB=AC$の二等辺三角形である.
点$D$は辺$BA$の延長であり,$ \angle ACB=\angle ACD$である.
$ \triangle DBC \backsim \triangle DCA$であることを証明しなさい.
栃木県高校過去問
連立方程式なんだけど解を直接求めようとすると自滅する問題~全国入試問題解法 #Shorts #数学 #高校入試

単元:
#数学(中学生)#中2数学#連立方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
の比$ x:y$を最も簡単な整数の比で答えなさい.
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
37x-53y=2 \\
17x-19y=1
\end{array}
\right.
\end{eqnarray}$
法政第二高校過去問
この動画を見る
の比$ x:y$を最も簡単な整数の比で答えなさい.
連立方程式$\begin{eqnarray}
\left\{
\begin{array}{l}
37x-53y=2 \\
17x-19y=1
\end{array}
\right.
\end{eqnarray}$
法政第二高校過去問
【中学生のひらめき!】因数分解:中央大学杉並高等学校~全国入試問題解法
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
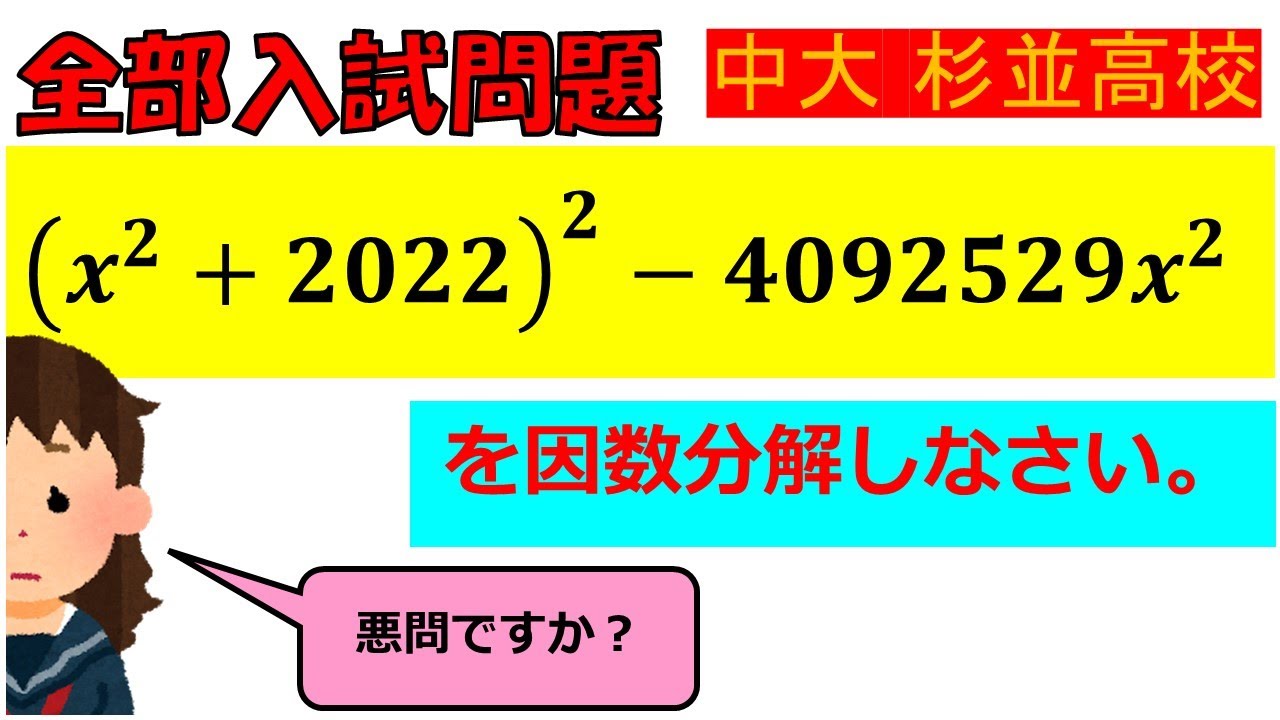
$ (x^2+2022)^2-4092529x^2$を因数分解しなさい.
中大杉並高校過去問
この動画を見る
$ (x^2+2022)^2-4092529x^2$を因数分解しなさい.
中大杉並高校過去問
ポップな気分で視覚的に数学を解く動画~全国入試問題解法 #Shorts #数学 #高校受験
単元:
#数学(中学生)#中1数学#平面図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
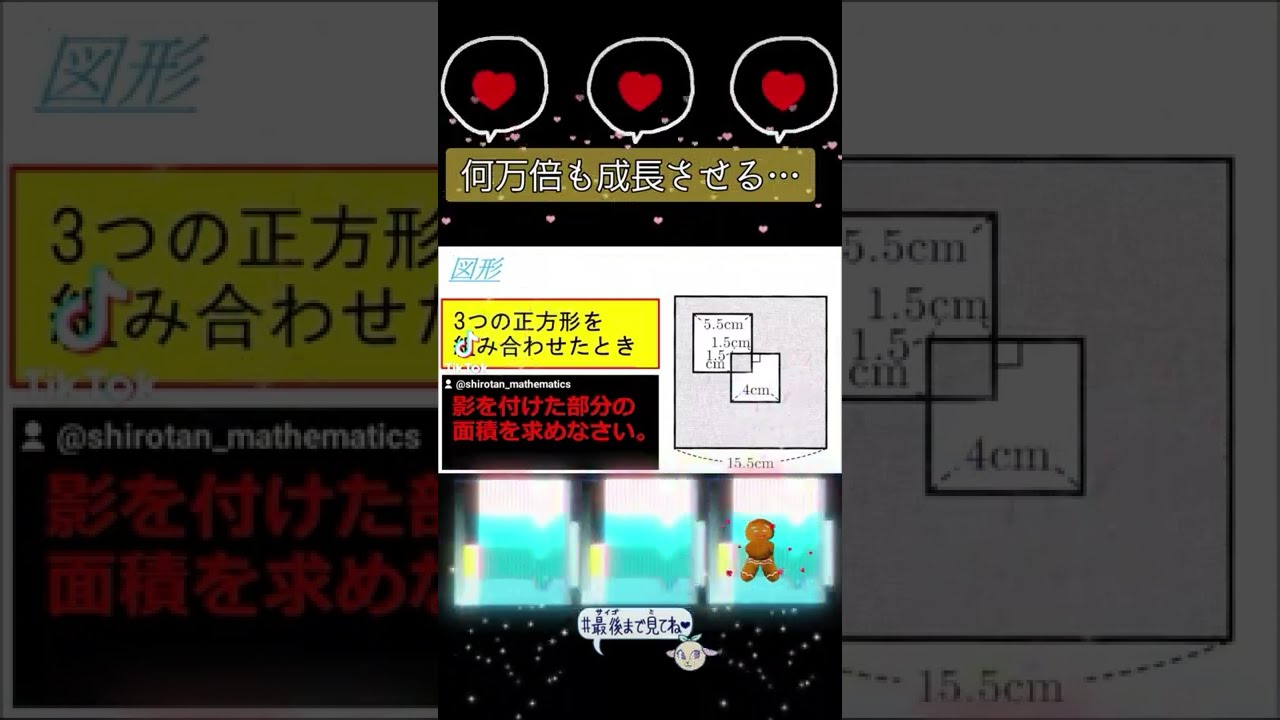
3つの正方形を組み合わせたとき,影を付けた部分の面積を求めなさい.
東工大科技高校過去問
この動画を見る
3つの正方形を組み合わせたとき,影を付けた部分の面積を求めなさい.
東工大科技高校過去問
【考え方は大切、いろんな意味で】文字式:大阪星光学院高等学校~全国入試問題解法

単元:
#数学(中学生)#中1数学#文字と式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
$ a=\dfrac{1}{\sqrt3+1}$
$ b=\dfrac{1}{\sqrt3-1}$のとき,$ a^3+a^2b+ab^2+b^3=\Box $である.
大阪星光高校過去問
この動画を見る
$ a=\dfrac{1}{\sqrt3+1}$
$ b=\dfrac{1}{\sqrt3-1}$のとき,$ a^3+a^2b+ab^2+b^3=\Box $である.
大阪星光高校過去問
音楽と数学が共に生きる二次方程式~全国入試問題解法 #shorts #数学 #高校受験

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
2次方程式$ ax^2+2x+b=0$の解が$x=2$のただ一つである.
定数$a,b$の値をそれぞれ求めなさい.
立命館高校過去問
この動画を見る
2次方程式$ ax^2+2x+b=0$の解が$x=2$のただ一つである.
定数$a,b$の値をそれぞれ求めなさい.
立命館高校過去問
【2分で理解!大切な考え方】空間図形:大阪星光学院高等学校~全国入試問題解法
単元:
#数学(中学生)#中1数学#空間図形#高校入試過去問(数学)
指導講師:
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文):
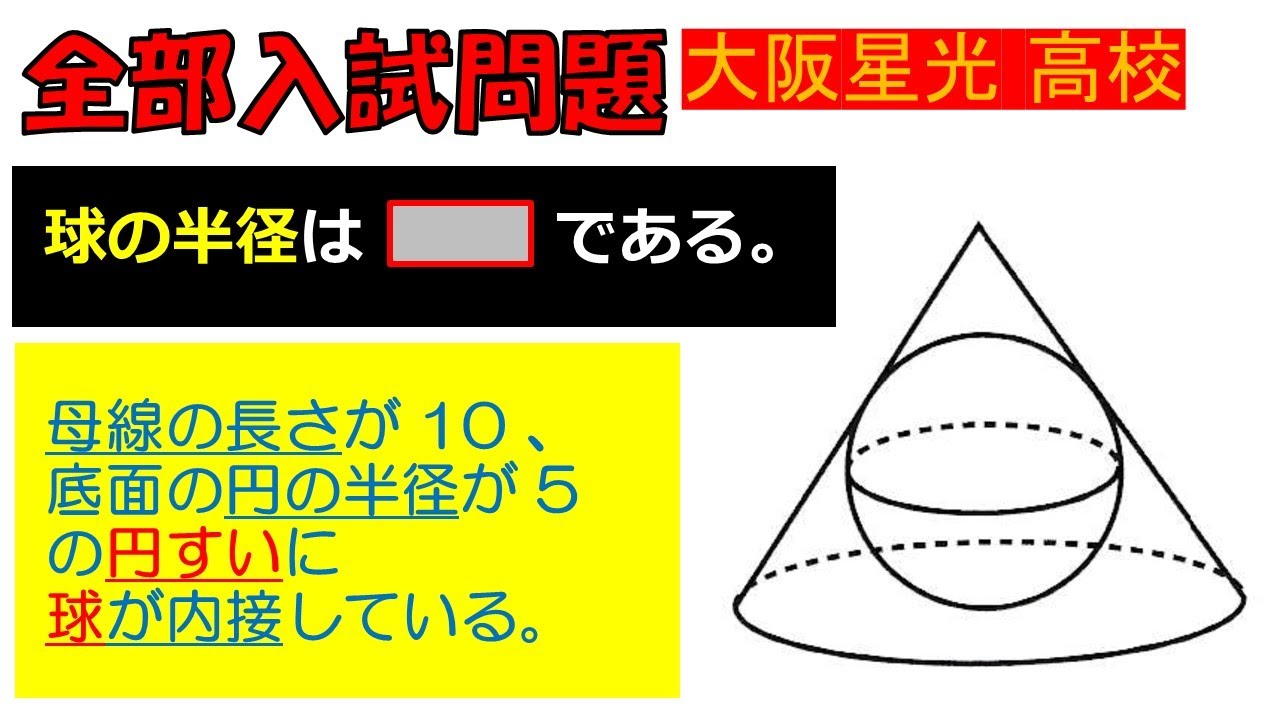
母線の長さが10,底面の円の半径が5の円錐に球が内接している.
球の半径は$\Box$である.
大阪星光高校過去問
この動画を見る
母線の長さが10,底面の円の半径が5の円錐に球が内接している.
球の半径は$\Box$である.
大阪星光高校過去問



