 数学を数楽に
数学を数楽に
 数学を数楽に
数学を数楽に
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
高校入試だけど多項定理 江戸川学園取手

6つの小さい円と大きい円 2024城北高校

3つの円と三角形の面積 ラ・サール
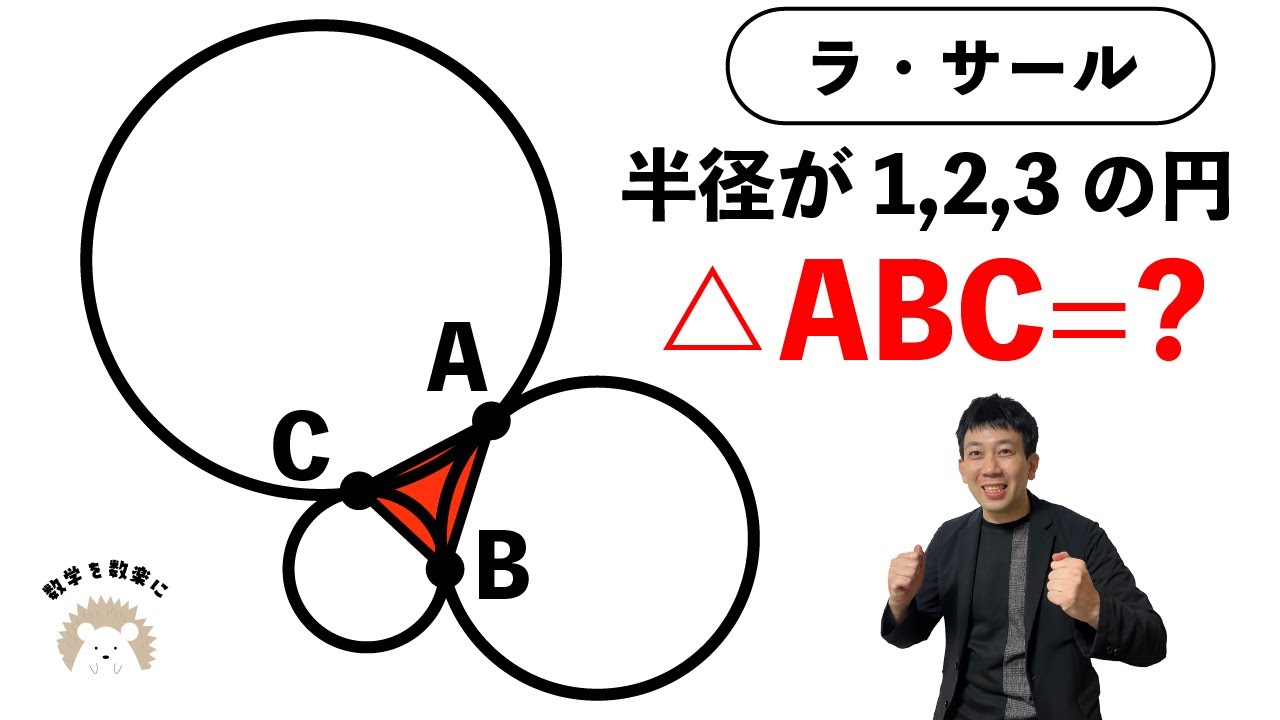
円と接線 2通りで解説
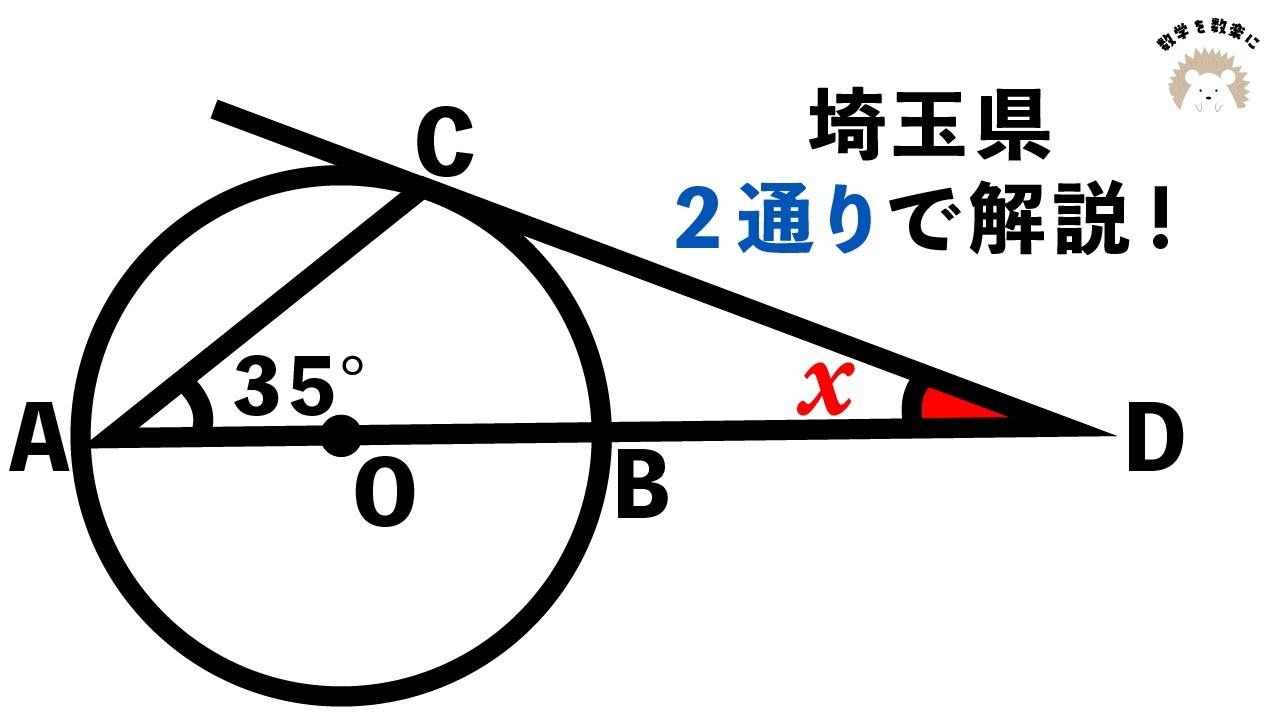
正三角形の折り返し
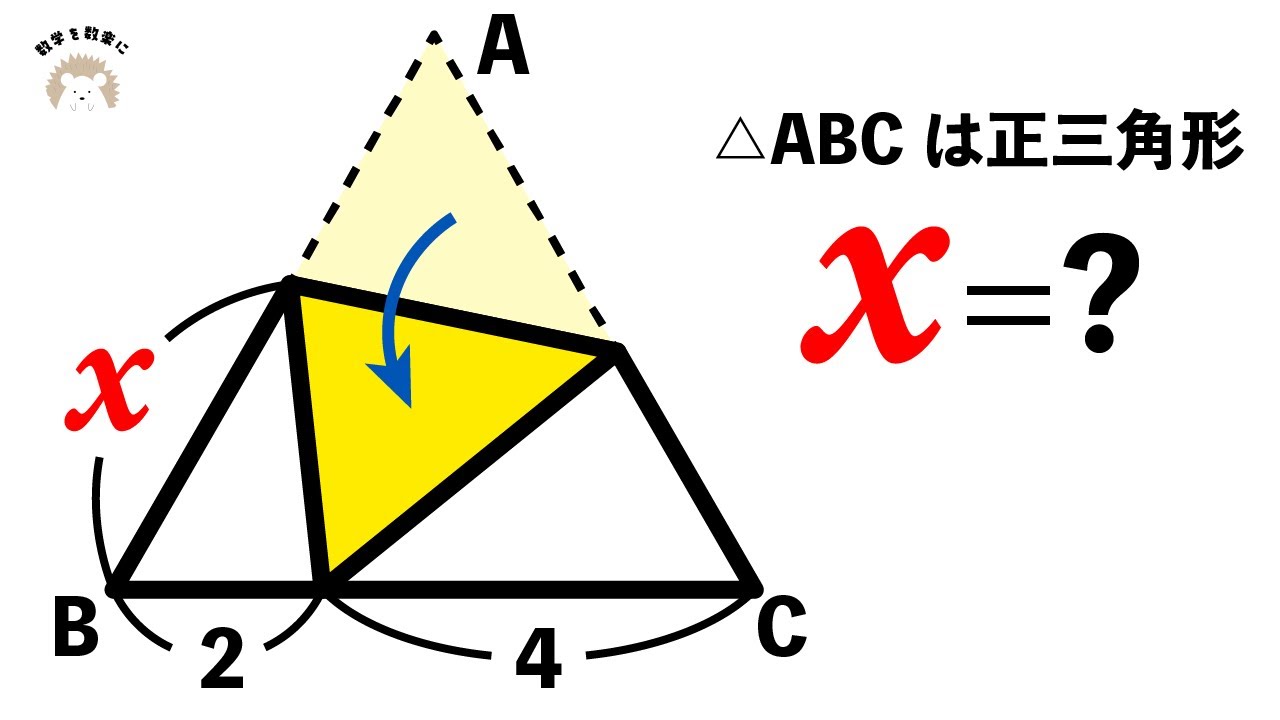
台形の中の線分 岩手県
今年の受験生必見!!

二乗せよ

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a>b>0
a^2=2+√3
a^2=2-√3
ab=?
この動画を見る
a>b>0
a^2=2+√3
a^2=2-√3
ab=?
ごめんなさい

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
b>a>0
a^2=2+√3
a^2=2-√3
(1)abの値を求めよ。
(2)a-b
この動画を見る
b>a>0
a^2=2+√3
a^2=2-√3
(1)abの値を求めよ。
(2)a-b
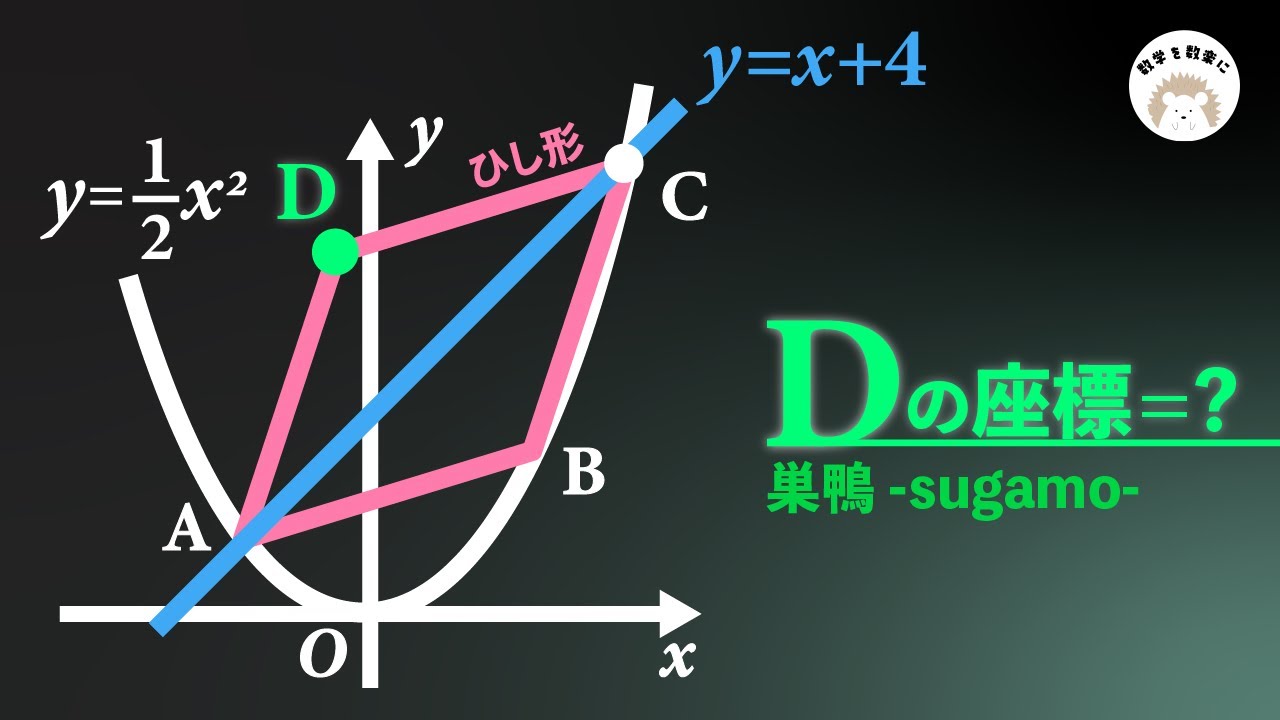
バリバリの高校入試問題 巣鴨高校 座標平面上のひし形
文字を含む二次方程式 嵯峨野2025

高校入試だけど絶対値記号

さぁどうやって計算する?2025堀川高校最初の一問
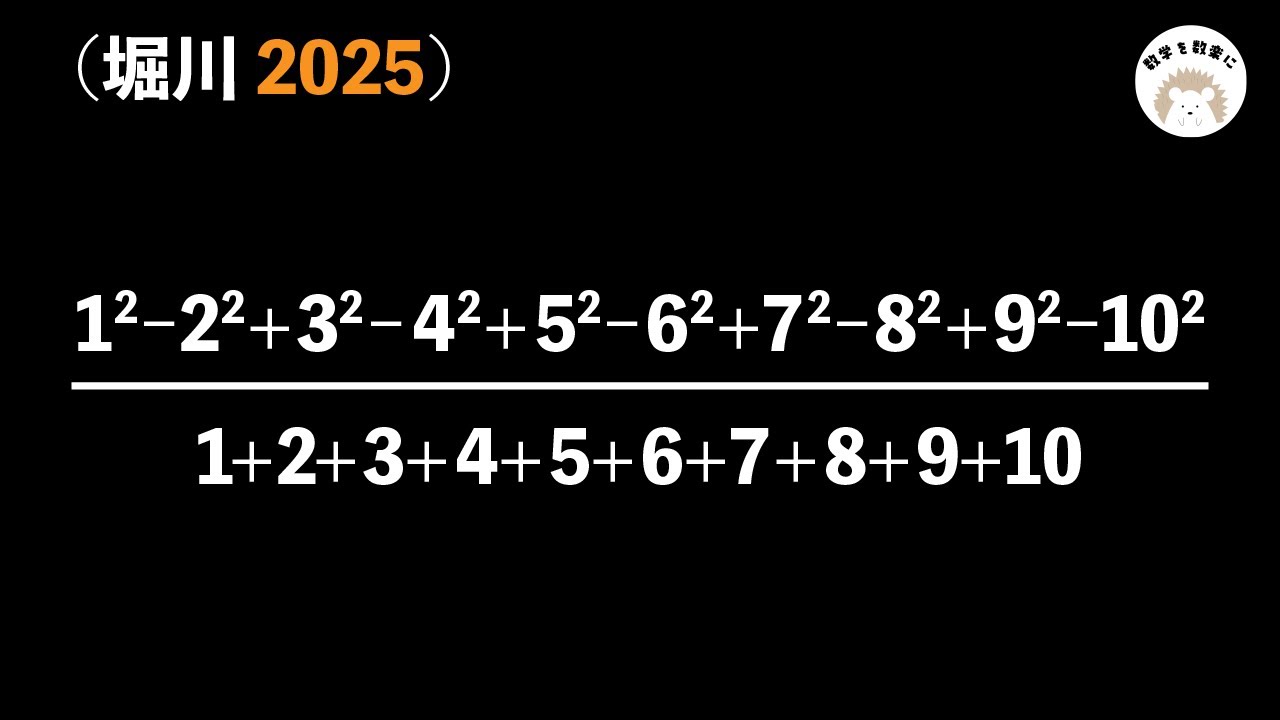
単元:
#数学(中学生)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$\displaystyle \frac{1^2-2^2+3^2-4^2+5^2-6^2+7^2-8^2+9^2-10^2}{1+2+3+4+5+6+7+8+9+10}$
この動画を見る
$\displaystyle \frac{1^2-2^2+3^2-4^2+5^2-6^2+7^2-8^2+9^2-10^2}{1+2+3+4+5+6+7+8+9+10}$
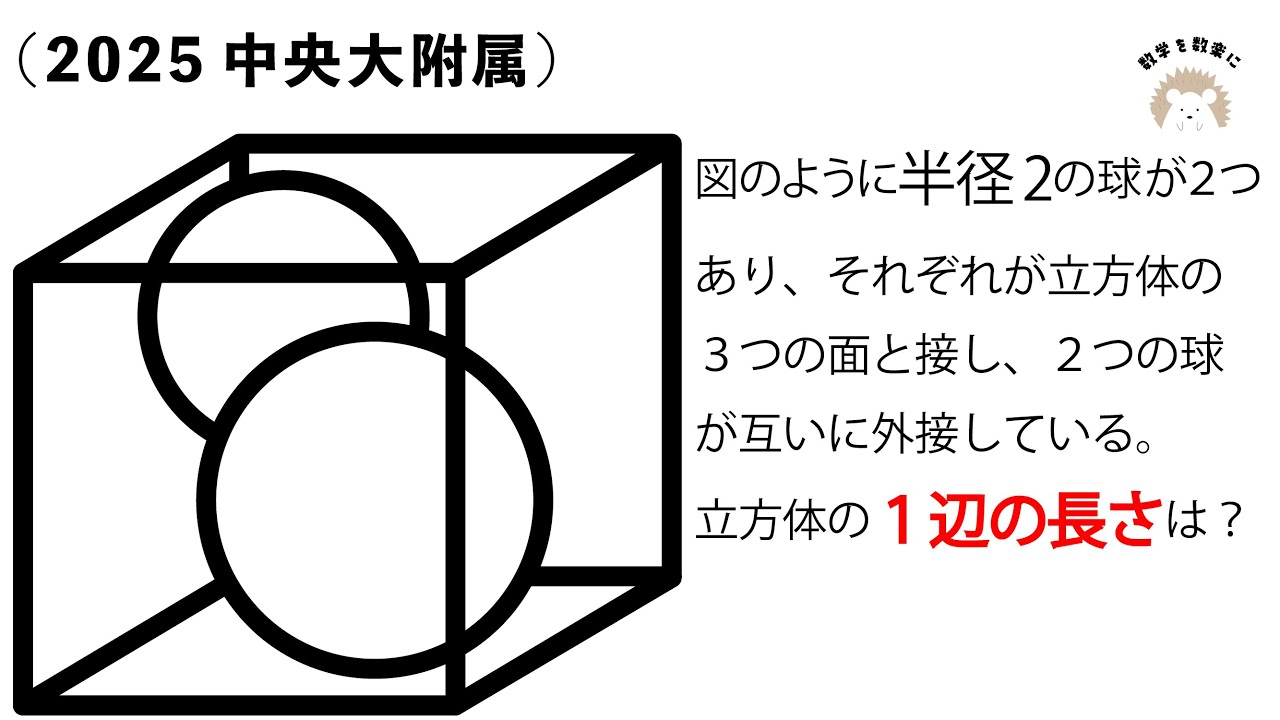
立方体の中に球2つ 2025中央大附属
単元:
#数学(中学生)#中3数学#三平方の定理
指導講師:
数学を数楽に
問題文全文(内容文):
図のように半径2の球が2つあり、それぞれが立方体の3つの面と接し、2つの球が互いに外接している。
*図は動画内を参照
立方体の1辺の長さは?
この動画を見る
図のように半径2の球が2つあり、それぞれが立方体の3つの面と接し、2つの球が互いに外接している。
*図は動画内を参照
立方体の1辺の長さは?
小数を含む二次方程式の計算 2025桐光学園

2025灘高校最初の一問!!因数分解せよ

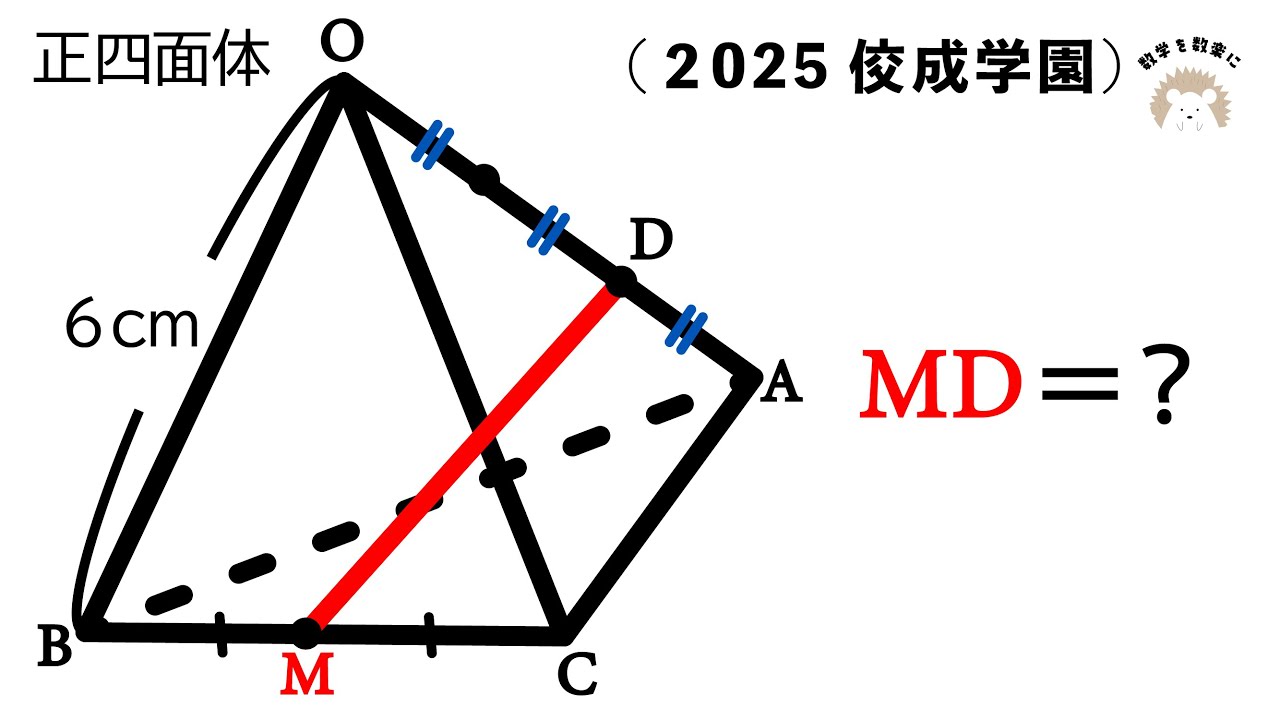
正四面体上の2点間の距離 2025佼成学園
ルートを外せ!!芝浦工業大学附属 2025

単元:
#数学(中学生)#中3数学#平方根
指導講師:
数学を数楽に
問題文全文(内容文):
(芝浦工業大学附属2025)
$n$は自然数とする。
$\sqrt{2025+n} \\$の値が自然数となる
最小の$n$の値を求めよ。
この動画を見る
(芝浦工業大学附属2025)
$n$は自然数とする。
$\sqrt{2025+n} \\$の値が自然数となる
最小の$n$の値を求めよ。
整数問題 2025 早稲田本庄

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
数学を数楽に
問題文全文(内容文):
次の2つの等式を同時に満たす整数の組
$(m,n)$をすべて求めよ。
$(m-2n+20)(m+n)=-12$
$(3n-25)(m+n)=6$
この動画を見る
次の2つの等式を同時に満たす整数の組
$(m,n)$をすべて求めよ。
$(m-2n+20)(m+n)=-12$
$(3n-25)(m+n)=6$
ルートが入っている等式の変形 2025早稲田本庄
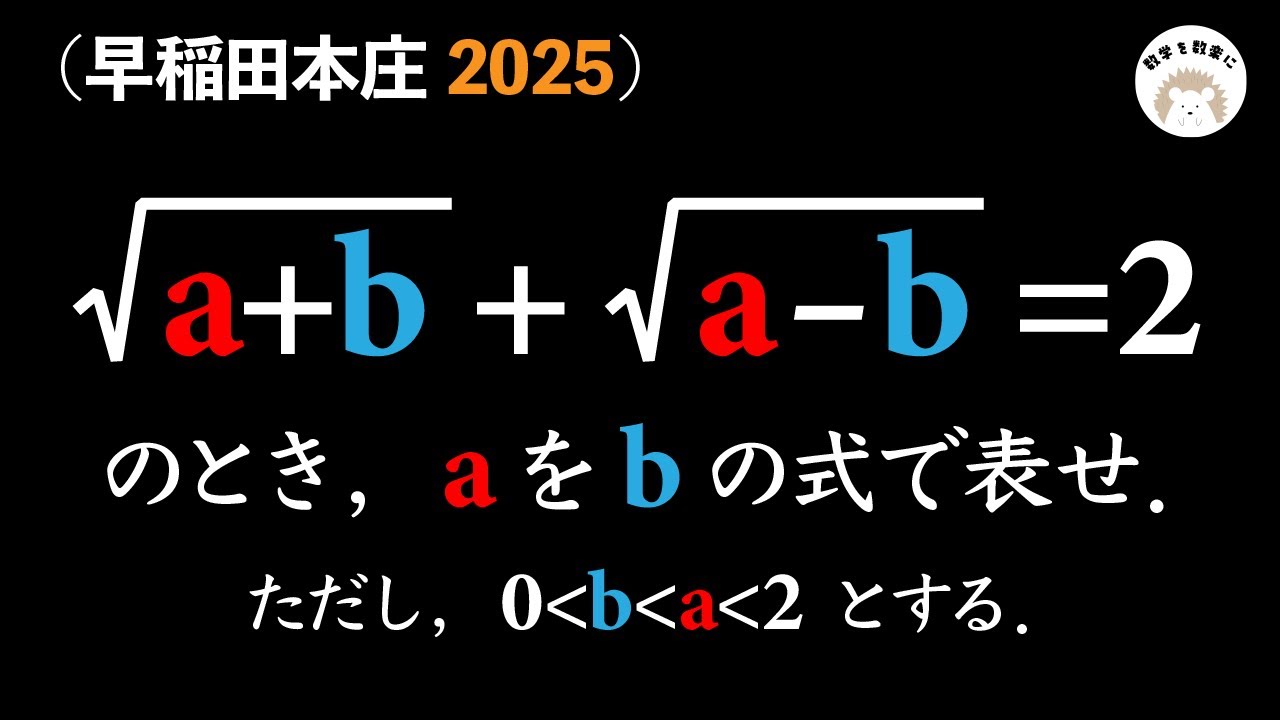
単元:
#数学(中学生)#中3数学#平方根
指導講師:
数学を数楽に
問題文全文(内容文):
(早稲田本庄2025)
$\sqrt{a+b}+\sqrt{a-b}=2$
のとき,$a$を$b$の式で表せ.
ただし,$0<b<a<2$とする.
この動画を見る
(早稲田本庄2025)
$\sqrt{a+b}+\sqrt{a-b}=2$
のとき,$a$を$b$の式で表せ.
ただし,$0<b<a<2$とする.
因数分解せよ 2025早稲田本庄

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
数学を数楽に
問題文全文(内容文):
(早稲田本庄$\color{orange}{2025 }$)
$3x^2+12y^2+12xy+2x+4y-8$
を$\color{yellow}{因数分解 }$せよ
この動画を見る
(早稲田本庄$\color{orange}{2025 }$)
$3x^2+12y^2+12xy+2x+4y-8$
を$\color{yellow}{因数分解 }$せよ
2つの二次方程式 2025立教新座

単元:
#算数(中学受験)#数学(中学生)#中2数学#中3数学#連立方程式#2次方程式#過去問解説(学校別)#立教新座中学
指導講師:
数学を数楽に
問題文全文(内容文):
2つの2次方程式
$x^2-kx-10=0$
$x^2+5x+2k=0$
が共通解を1つだけ持つ。この共有解と定数$k$の値を求めよ。
ただし$k≠5$
この動画を見る
2つの2次方程式
$x^2-kx-10=0$
$x^2+5x+2k=0$
が共通解を1つだけ持つ。この共有解と定数$k$の値を求めよ。
ただし$k≠5$
2つの二次方程式 2025立教新座

単元:
#2次関数#2次方程式と2次不等式
指導講師:
数学を数楽に
問題文全文(内容文):
2つの2次方程式 \begin{eqnarray}
x^2 -kx-10 = 0
\end{eqnarray}
\begin{eqnarray}
x^2+5x+2k=0
\end{eqnarray}
が共通解を1つだけ持つ。この共通解と定数kを求めよ。ただしk≠-5
この動画を見る
2つの2次方程式 \begin{eqnarray}
x^2 -kx-10 = 0
\end{eqnarray}
\begin{eqnarray}
x^2+5x+2k=0
\end{eqnarray}
が共通解を1つだけ持つ。この共通解と定数kを求めよ。ただしk≠-5
2つの二次方程式 2025立教新座

単元:
#数学(中学生)#中3数学#2次方程式#高校入試過去問(数学)#立教新座高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
立教新座高等学校過去問
2つの2次方程式
\begin{eqnarray}
\left\{
\begin{array}{l}
x^2 - kx - 10&=& 0 \\
x^2 + 5x + 2k&=& 0
\end{array}
\right.
\end{eqnarray}
が共通解を1つだけ持つ。
この共通解と定数$k$の値を求めよ。ただし$k\ne5$
この動画を見る
立教新座高等学校過去問
2つの2次方程式
\begin{eqnarray}
\left\{
\begin{array}{l}
x^2 - kx - 10&=& 0 \\
x^2 + 5x + 2k&=& 0
\end{array}
\right.
\end{eqnarray}
が共通解を1つだけ持つ。
この共通解と定数$k$の値を求めよ。ただし$k\ne5$
式の値 昭和学院秀英
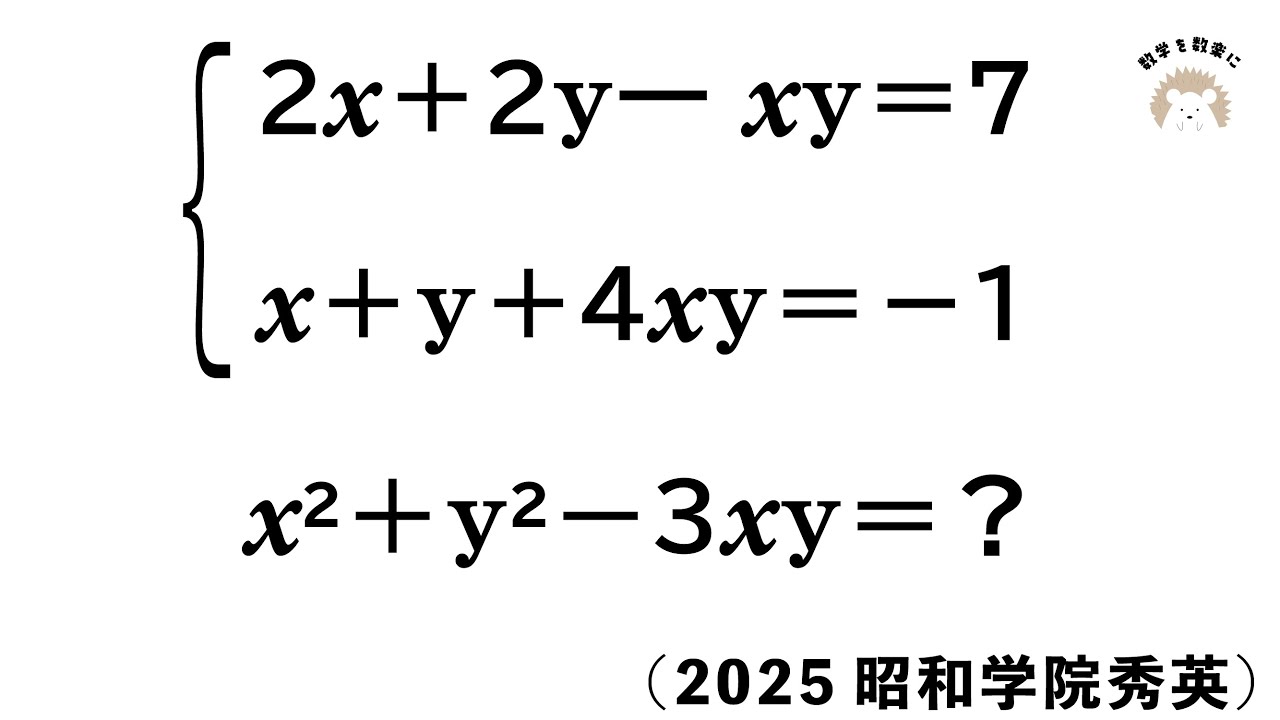
単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)
指導講師:
数学を数楽に
問題文全文(内容文):
昭和学院秀英高等学校過去問
\begin{eqnarray}
\left\{
\begin{array}{l}
2x + 2y - xy&=& 7 \\
x + y + 4xy&=& -1
\end{array}
\right.
\end{eqnarray}
$$x^2 + y^2 - 3xy = ?$$
この動画を見る
昭和学院秀英高等学校過去問
\begin{eqnarray}
\left\{
\begin{array}{l}
2x + 2y - xy&=& 7 \\
x + y + 4xy&=& -1
\end{array}
\right.
\end{eqnarray}
$$x^2 + y^2 - 3xy = ?$$
式の値 昭和学院秀英
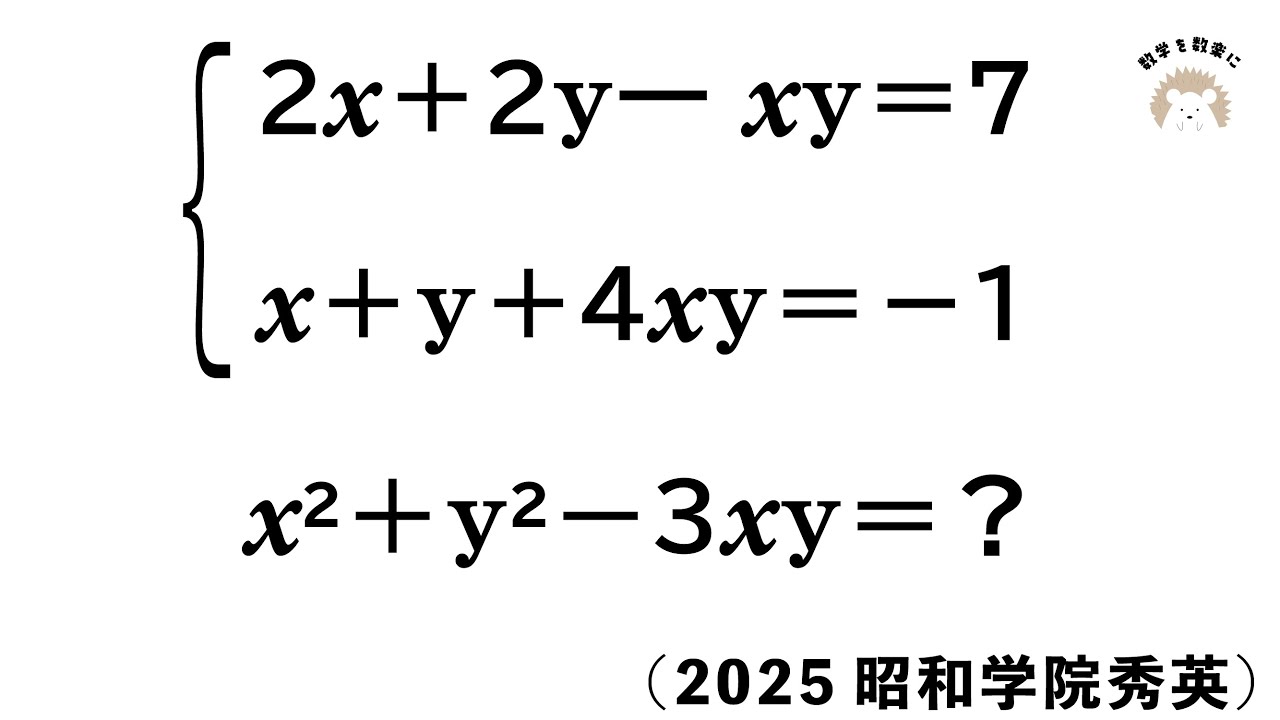
単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#昭和学院秀英中学
指導講師:
数学を数楽に
問題文全文(内容文):
$2x+2y-xy=7$
$x+y+4xy=-1$
$x^2+y^2-3xy=?$
この動画を見る
$2x+2y-xy=7$
$x+y+4xy=-1$
$x^2+y^2-3xy=?$
平方根と式の値 2025昭和学院秀英

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根
指導講師:
数学を数楽に
問題文全文(内容文):
昭和学院秀英高等学校過去問
$a=2025$ $b=118$ のとき
$\sqrt{a^2+b^2+2ab+4a+4b+4}=?$
この動画を見る
昭和学院秀英高等学校過去問
$a=2025$ $b=118$ のとき
$\sqrt{a^2+b^2+2ab+4a+4b+4}=?$
平方根と式の値 2025昭和学院秀英

平方根と式の値 2025昭和学院秀英

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
a = 2025 b = 118のとき √a²+b²+2ab+4a+4b+4 = ?
この動画を見る
a = 2025 b = 118のとき √a²+b²+2ab+4a+4b+4 = ?





