 数学を数楽に
数学を数楽に
 数学を数楽に
数学を数楽に
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
円と台形 灘高校の小問
単元:
#数学(中学生)#中3数学#相似な図形#高校入試過去問(数学)#灘高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
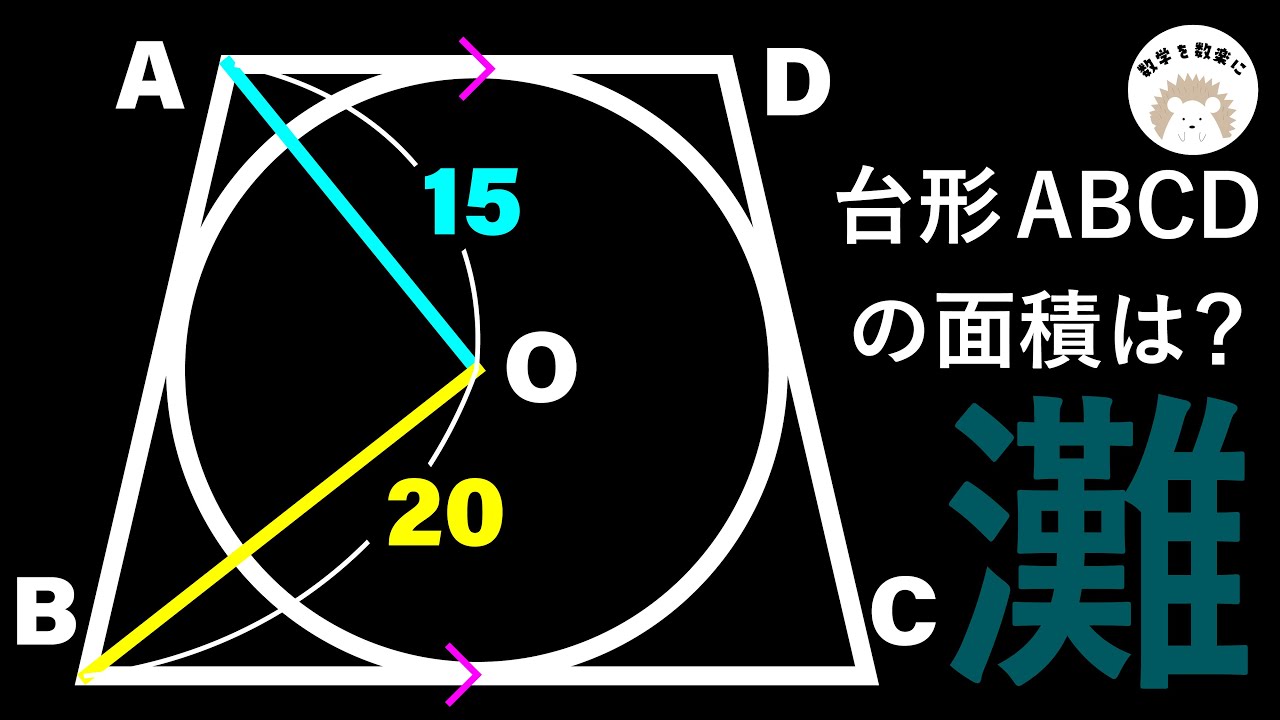
円と台形からできる相似
台形$\textrm{ABCD}$の面積を求めよ。
出典:2012年灘高等学校
この動画を見る
円と台形からできる相似
台形$\textrm{ABCD}$の面積を求めよ。
出典:2012年灘高等学校
直角三角形と内接円の問題
単元:
#数学(中学生)#中3数学#円#三平方の定理#高校入試過去問(数学)#函館ラ・サール高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
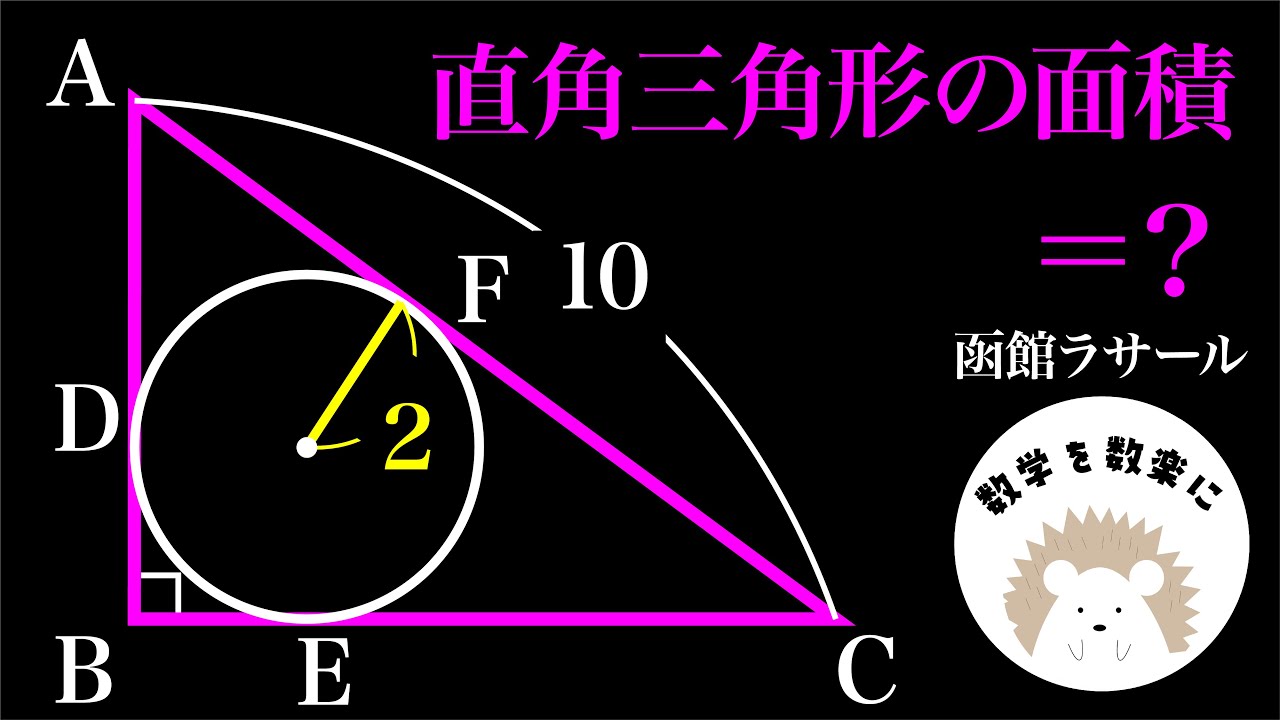
動画内の図を参照し、直角三角形ABCの面積を求めよ。
出典:2017年函館ラサール
この動画を見る
動画内の図を参照し、直角三角形ABCの面積を求めよ。
出典:2017年函館ラサール
角の二等分線+平行、垂直=?
単元:
#数学(中学生)#中2数学#平行と合同#三角形と四角形#高校入試過去問(数学)#江戸川学園取手高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
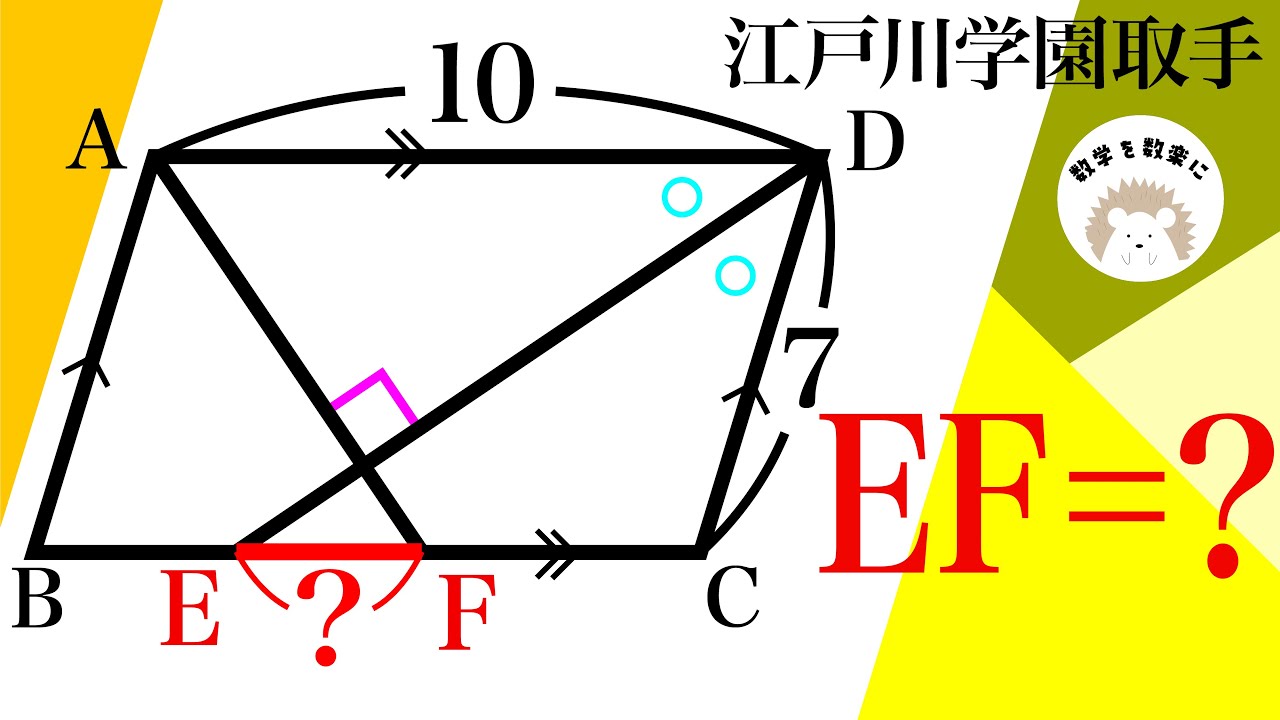
動画内の図を参照し、$\textrm{EF}$の長さを求めよ。
出典:2017年江戸川学園取手
この動画を見る
動画内の図を参照し、$\textrm{EF}$の長さを求めよ。
出典:2017年江戸川学園取手
円周角と中心角の問題(高校受験数学)
約束記号(高校受験数学)

単元:
#数学(中学生)#中2数学#式の計算(単項式・多項式・式の四則計算)#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
$a☆b=2ab-a-b$のとき方程式$x☆(x-2)=0$を解け。
出典:2017年智辯学園和歌山高等学校 受験数学
この動画を見る
$a☆b=2ab-a-b$のとき方程式$x☆(x-2)=0$を解け。
出典:2017年智辯学園和歌山高等学校 受験数学
3直線で三角形ができない時の条件とは?

単元:
#数学(中学生)#中2数学#1次関数
指導講師:
数学を数楽に
問題文全文(内容文):
直線$y=x,y=3x,y=ax+(a+2)$がある。
3つの直線で三角形ができないとき$a=?$
この動画を見る
直線$y=x,y=3x,y=ax+(a+2)$がある。
3つの直線で三角形ができないとき$a=?$
日比谷高校の計算問題(2003)

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#東京都立日比谷高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
$(\displaystyle \frac{\sqrt{ 6 }+\sqrt{ 5 }}{\sqrt{ 2 }})^2-(\sqrt{ 6 }+\sqrt{ 5 })(\sqrt{ 6 }-\sqrt{ 5 })+(\displaystyle \frac{\sqrt{ 6 }-\sqrt{ 5 }}{\sqrt{ 2 }})^2$
出典:2003年東京都立日比谷高等学校
この動画を見る
$(\displaystyle \frac{\sqrt{ 6 }+\sqrt{ 5 }}{\sqrt{ 2 }})^2-(\sqrt{ 6 }+\sqrt{ 5 })(\sqrt{ 6 }-\sqrt{ 5 })+(\displaystyle \frac{\sqrt{ 6 }-\sqrt{ 5 }}{\sqrt{ 2 }})^2$
出典:2003年東京都立日比谷高等学校
傾きの範囲(応用)

順列と組合せを組み合わせてみました

単元:
#数A#場合の数と確率#場合の数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
5人の中から3人を選ぶ。
(1)全部で何通り?
(2)横1列に並べるとき何通り?
この動画を見る
5人の中から3人を選ぶ。
(1)全部で何通り?
(2)横1列に並べるとき何通り?
蝶ネクタイの左と右が等しいとき
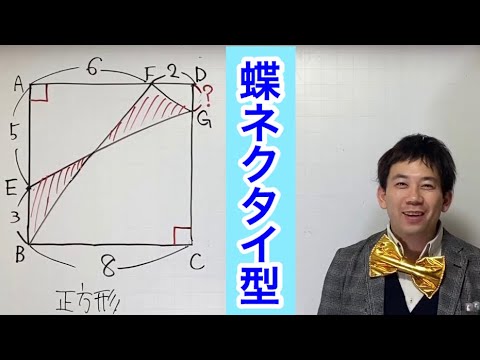
2019 都立共通問題の最後の一問

単元:
#数A#大学入試過去問(数学)#図形の性質#学校別大学入試過去問解説(数学)#空間における垂直と平行と多面体(オイラーの法則)#数学(高校生)#東京都立大学
指導講師:
数学を数楽に
問題文全文(内容文):
動画内の図を参照し、$\textrm{R-APQ}$の体積は?
出典:東京都立大学
この動画を見る
動画内の図を参照し、$\textrm{R-APQ}$の体積は?
出典:東京都立大学
1の虚数3乗根ω(数II)

単元:
#数Ⅱ#複素数と方程式#複素数#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
1の虚数3乗根$\omega$についての解説動画です
以下を求めよ
(1)$\omega^{99}=?$
(2)$\omega^6+\omega^5+\omega^4=?$
この動画を見る
1の虚数3乗根$\omega$についての解説動画です
以下を求めよ
(1)$\omega^{99}=?$
(2)$\omega^6+\omega^5+\omega^4=?$
立教新座2016(高校入試)
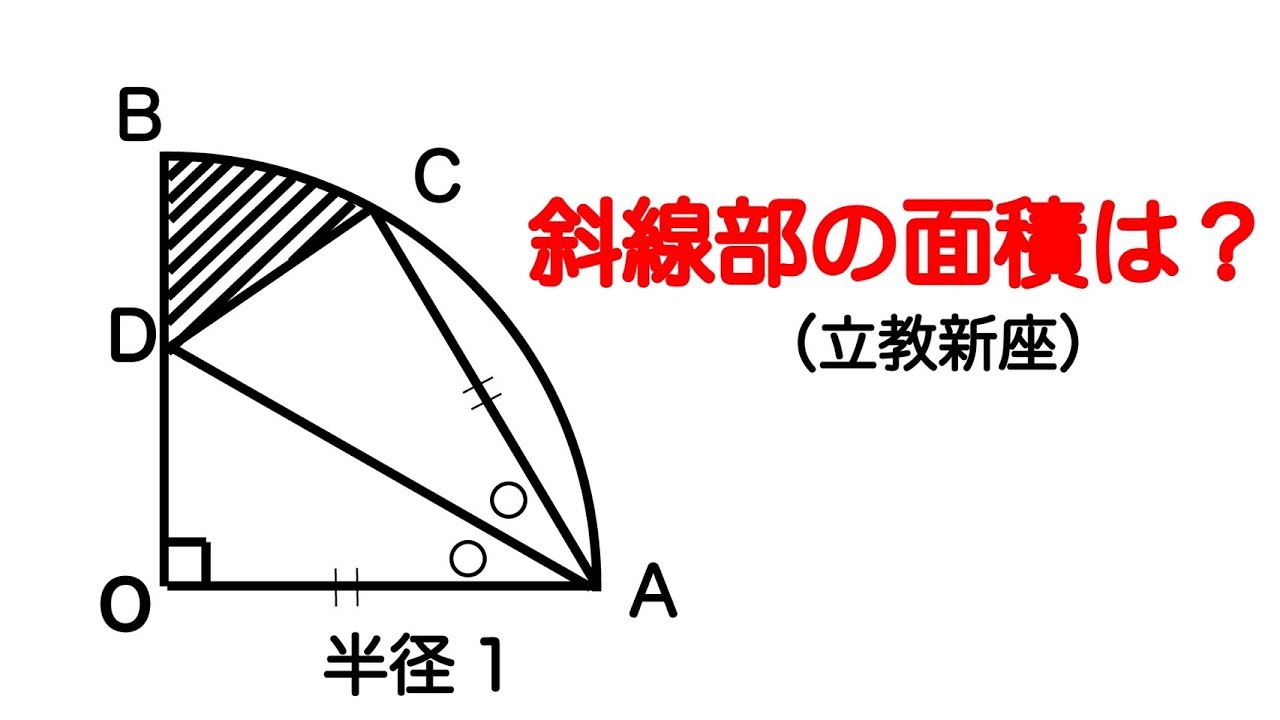
単元:
#数学(中学生)#中3数学#円#高校入試過去問(数学)#立教新座高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
動画内の図を参照し、斜線部の面積を求めよ。
出典:2016年立教新座高等学校 高校入試問題
この動画を見る
動画内の図を参照し、斜線部の面積を求めよ。
出典:2016年立教新座高等学校 高校入試問題
斜めの正方形(豊島岡女子2016)
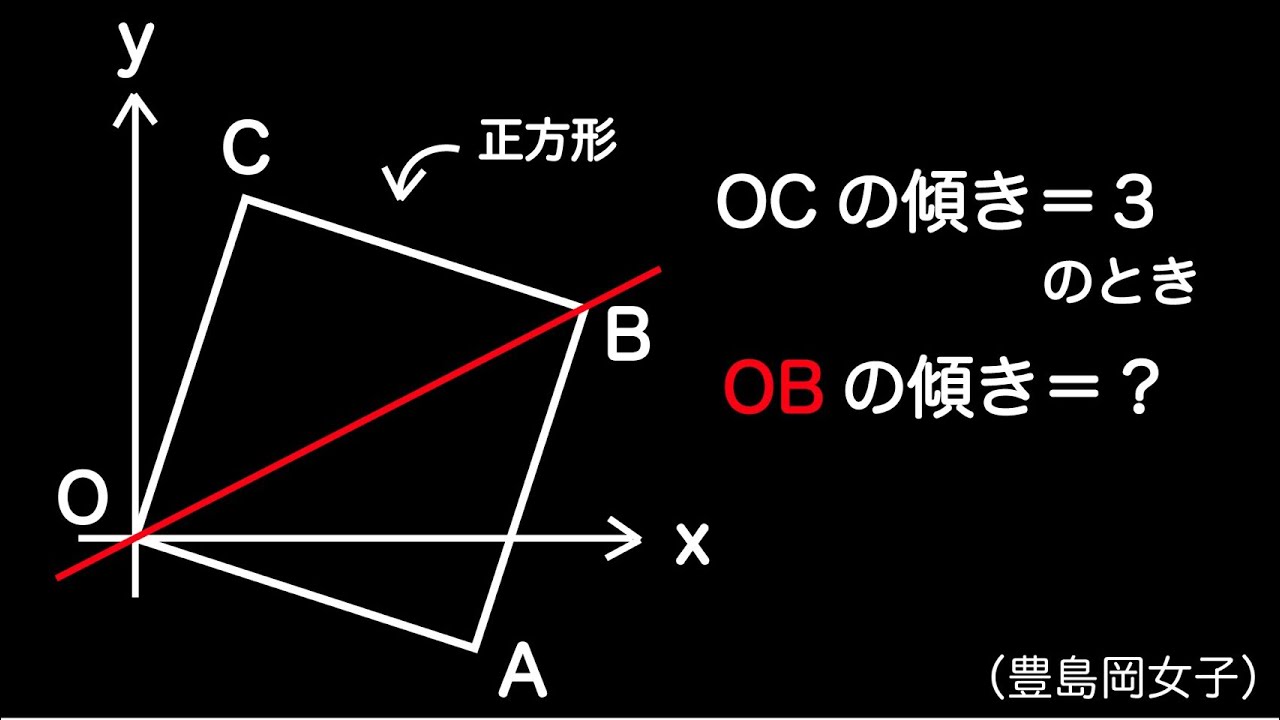
単元:
#数学(中学生)#中2数学#1次関数#高校入試過去問(数学)#豊島岡女子高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
動画内の図を参照してください。
座標平面上に傾いた正方形があります。
点$\textrm{OB}$の傾きを求めよ。
出典:2016年豊島岡女子学園 中学校・高等学校
この動画を見る
動画内の図を参照してください。
座標平面上に傾いた正方形があります。
点$\textrm{OB}$の傾きを求めよ。
出典:2016年豊島岡女子学園 中学校・高等学校
素因数分解せよ!(2000慶應女子)

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#高校入試過去問(数学)#慶應義塾女子高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
$110\times90+13\times7$を素因数分解せよ。
出典:2000年慶應義塾女子高等学校
この動画を見る
$110\times90+13\times7$を素因数分解せよ。
出典:2000年慶應義塾女子高等学校
角度を求める(2006国立高校)
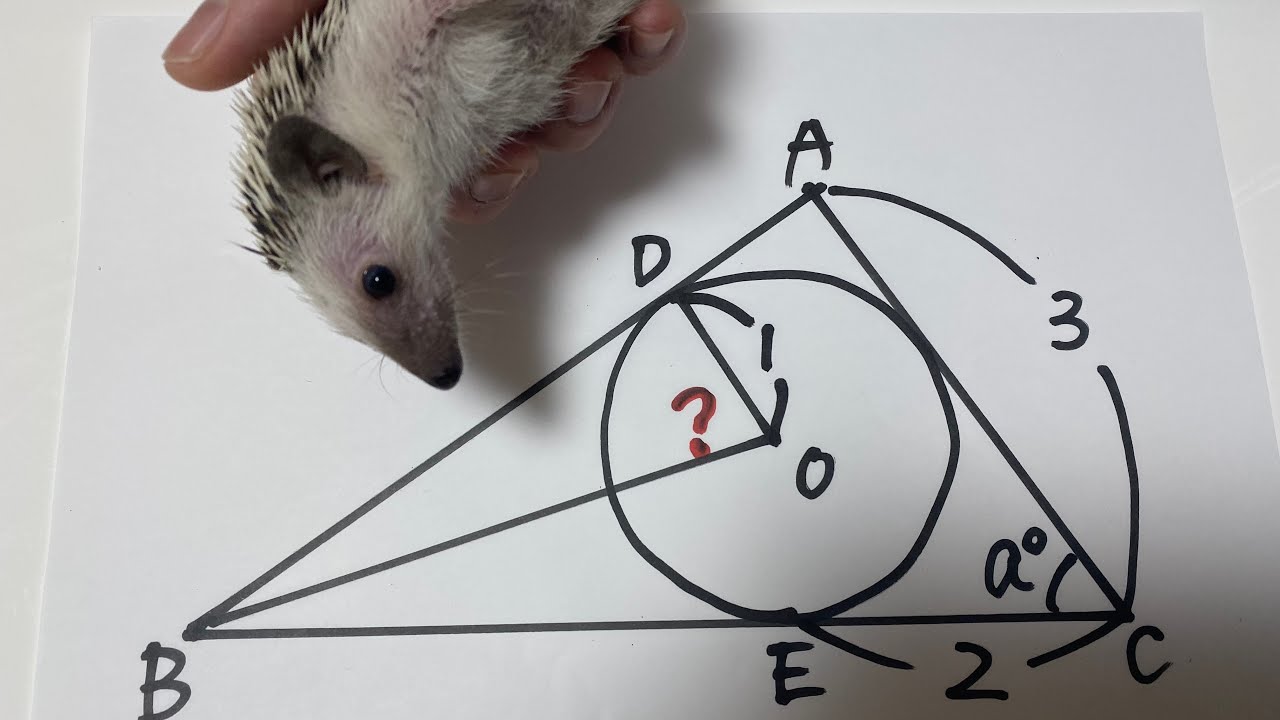
単元:
#数学(中学生)#中2数学#中3数学#円#三角形と四角形#高校入試過去問(数学)#東京都立国立高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
動画内の図を参照し、?の角度を求めよ。
出典:2006年国立高校
この動画を見る
動画内の図を参照し、?の角度を求めよ。
出典:2006年国立高校
平方根の計算!!(2019立命館)
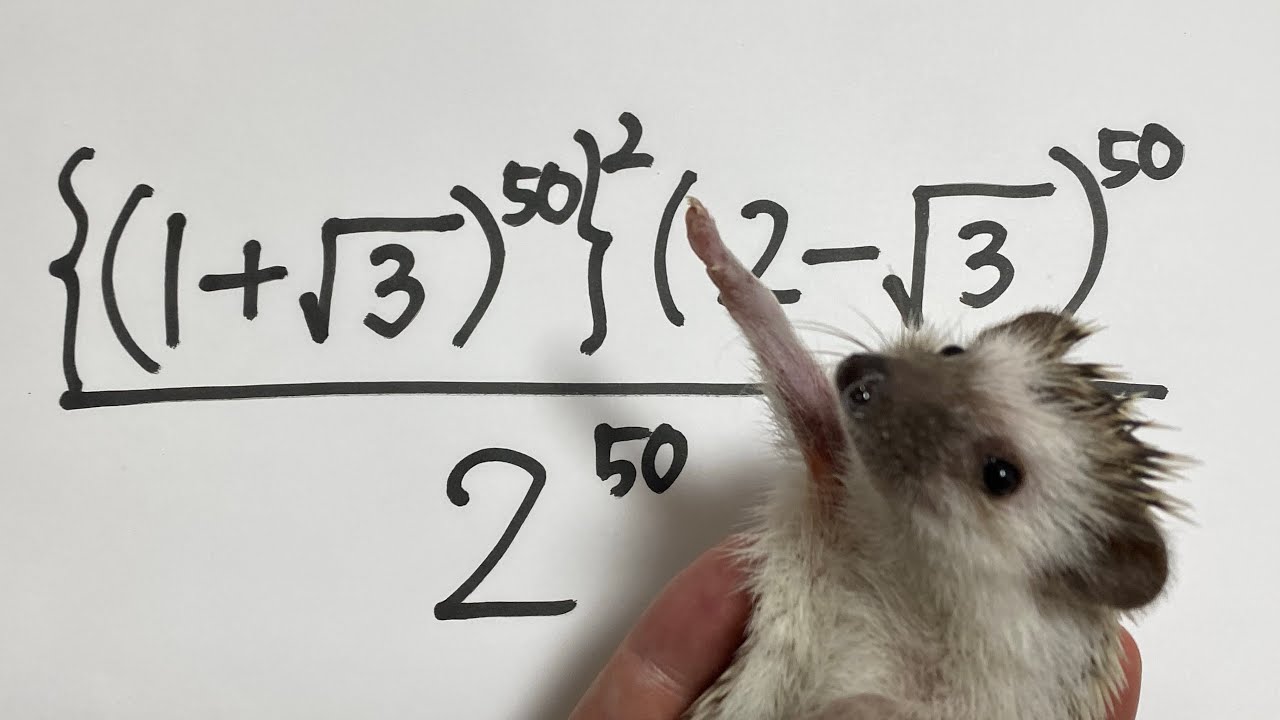
単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#立命館高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
以下を計算せよ
$\displaystyle \frac{\{(1+\sqrt{ 3 })^{50}\}^2(2-\sqrt{ 3 })^{50}}{2^{50}}$
出典:2019年立命館大学
この動画を見る
以下を計算せよ
$\displaystyle \frac{\{(1+\sqrt{ 3 })^{50}\}^2(2-\sqrt{ 3 })^{50}}{2^{50}}$
出典:2019年立命館大学
都立西2010の最初の1問

単元:
#数学(中学生)#中3数学#平方根#高校入試過去問(数学)#東京都立西高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
$\sqrt{ (\displaystyle \frac{13}{23}-\displaystyle \frac{16}{31})^2 }+\sqrt{ (\displaystyle \frac{11}{23}-\displaystyle \frac{16}{31})^2 }$
出典:2010年東京都立西高等学校
この動画を見る
$\sqrt{ (\displaystyle \frac{13}{23}-\displaystyle \frac{16}{31})^2 }+\sqrt{ (\displaystyle \frac{11}{23}-\displaystyle \frac{16}{31})^2 }$
出典:2010年東京都立西高等学校
角度を求める!(都立西2005 2006)

高次方程式を解く!その1(3次方程式4次方程式)

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
高次方程式を解け。
(1)$x^3=1$
(2)$x^4=4$
(3)$x^4-3x^2-10=0$
この動画を見る
高次方程式を解け。
(1)$x^3=1$
(2)$x^4=4$
(3)$x^4-3x^2-10=0$
2019日比谷高校数学の最初の2問!!(高校入試数学)

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#平方根#高校入試過去問(数学)#東京都立日比谷高等学校
指導講師:
数学を数楽に
問題文全文(内容文):
問1
$(3-\displaystyle \frac{1}{\sqrt{ 3 }})^2+\displaystyle \frac{(\sqrt{ 6 }-\sqrt{ 2 })(3+-\sqrt{ 3 })}{\sqrt{ 2 }}$
問2
$(6-x)^2+9(x-6)-90$を因数分解せよ
出典:2019年東京都立日比谷高等学校 高校入試
この動画を見る
問1
$(3-\displaystyle \frac{1}{\sqrt{ 3 }})^2+\displaystyle \frac{(\sqrt{ 6 }-\sqrt{ 2 })(3+-\sqrt{ 3 })}{\sqrt{ 2 }}$
問2
$(6-x)^2+9(x-6)-90$を因数分解せよ
出典:2019年東京都立日比谷高等学校 高校入試
部分分数分解を利用した数列の和(数B)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
以下を求めよ。
$\displaystyle \frac{1}{1・2}+\displaystyle \frac{1}{2・3}+\displaystyle \frac{1}{3・4}+…+\displaystyle \frac{1}{n(n+1)}=??$
$\displaystyle \frac{1}{1・3}+\displaystyle \frac{1}{3・5}+\displaystyle \frac{1}{5・7}+…+\displaystyle \frac{1}{(2n-1)(2n+1)}=??$
この動画を見る
以下を求めよ。
$\displaystyle \frac{1}{1・2}+\displaystyle \frac{1}{2・3}+\displaystyle \frac{1}{3・4}+…+\displaystyle \frac{1}{n(n+1)}=??$
$\displaystyle \frac{1}{1・3}+\displaystyle \frac{1}{3・5}+\displaystyle \frac{1}{5・7}+…+\displaystyle \frac{1}{(2n-1)(2n+1)}=??$
階差数列(数B)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
次の数列{$a_n$}の一般項を求めよ。
$\begin{array}{c|c|c|c|c|c|c|c}
① & ② & ③ & ④ & ⑤ & ⑥ & … & n \\
\hline
3 & 5 & 9 & 15 & 23 & & … & ?
\end{array}$
この動画を見る
次の数列{$a_n$}の一般項を求めよ。
$\begin{array}{c|c|c|c|c|c|c|c}
① & ② & ③ & ④ & ⑤ & ⑥ & … & n \\
\hline
3 & 5 & 9 & 15 & 23 & & … & ?
\end{array}$
放物線と平行な2直線(高校受験数学)

放物線上の2点を通る直線

円周角を一発で!!(中3数学)

なぜ?がわかる組立除法(数II)

組立除法(数II)

単元:
#数Ⅱ#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
次の整式$A$を$B$で割った商と余りは?
(1)$A=x^3+3x^2+4x-2,B=x+1$
(2)$A=x^3-4x^2-5,B=x-3$
(3)$A=2x^3-5x^2+5x-3,B=2x-3$
この動画を見る
次の整式$A$を$B$で割った商と余りは?
(1)$A=x^3+3x^2+4x-2,B=x+1$
(2)$A=x^3-4x^2-5,B=x-3$
(3)$A=2x^3-5x^2+5x-3,B=2x-3$
平方の和の公式を導く!!(数B)

単元:
#数列#数列とその和(等差・等比・階差・Σ)#数学(高校生)#数B
指導講師:
数学を数楽に
問題文全文(内容文):
$\displaystyle \sum_{k=1}^n k^2=\displaystyle \frac{1}{6}n(n+1)(2n+1)$を解け
この動画を見る
$\displaystyle \sum_{k=1}^n k^2=\displaystyle \frac{1}{6}n(n+1)(2n+1)$を解け
30°、30°、120°の二等辺三角形(高校入試数学)






