 鈴木貫太郎
鈴木貫太郎
 鈴木貫太郎
鈴木貫太郎
※下の画像部分をクリックすると、先生の紹介ページにリンクします。
灘中 中学入試 整数問題

単元:
#算数(中学受験)#約数・倍数を利用する問題#過去問解説(学校別)#灘中学校
指導講師:
鈴木貫太郎
問題文全文(内容文):
灘中学校過去問題
①4つの異なる数字
1,3,▢,9から異なる数字を取り出して並べる3桁の整数は24個でその平均は555
②5桁の36の倍数で2,3,5のどれもがいずれかの桁に現れる整数のうち最小のもの。
この動画を見る
灘中学校過去問題
①4つの異なる数字
1,3,▢,9から異なる数字を取り出して並べる3桁の整数は24個でその平均は555
②5桁の36の倍数で2,3,5のどれもがいずれかの桁に現れる整数のうち最小のもの。
弘前大(医)3次方程式 極限 Japanese university entrance exam questions

単元:
#大学入試過去問(数学)#関数と極限#微分とその応用#関数の極限#微分法#数学(高校生)#弘前大学#数Ⅲ
指導講師:
鈴木貫太郎
問題文全文(内容文):
弘前大学過去問題
n自然数
$x^3+3nx^2-(3n+2)=0$
(1)全ての自然数nについて正の解をただ1つしかもたないことを示せ。
(2)各自然数nに対して正の解を$a_n$とする。
$\displaystyle\lim_{n \to \infty}a_n$を求めよ。
この動画を見る
弘前大学過去問題
n自然数
$x^3+3nx^2-(3n+2)=0$
(1)全ての自然数nについて正の解をただ1つしかもたないことを示せ。
(2)各自然数nに対して正の解を$a_n$とする。
$\displaystyle\lim_{n \to \infty}a_n$を求めよ。
静岡大 数学的帰納法 高校数学 Japanese university entrance exam questions

単元:
#数Ⅱ#大学入試過去問(数学)#指数関数と対数関数#数列#数学的帰納法#静岡大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
静岡大学過去問題
n自然数
(1)$4^{n+1}+5^{2n-1}$は21で割り切れることを証明
(2)次の条件を満たす定数でない多項式f(x)を推定し、その推定が正しいことを証明せよ。
(a)f(4)=21
(b)すべての自然数nに対し$x^{n+1}+(x+1)^{2n-1}$はf(x)で割り切れる。
この動画を見る
静岡大学過去問題
n自然数
(1)$4^{n+1}+5^{2n-1}$は21で割り切れることを証明
(2)次の条件を満たす定数でない多項式f(x)を推定し、その推定が正しいことを証明せよ。
(a)f(4)=21
(b)すべての自然数nに対し$x^{n+1}+(x+1)^{2n-1}$はf(x)で割り切れる。
香川大 3次方程式実数解 高校数学 Japanese university entrance exam questions

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#複素数と方程式#微分法と積分法#解と判別式・解と係数の関係#数学(高校生)#香川大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
香川大学過去問題
$f(x)=x^3-3a^2x+a^2-a$について
(1)$f(x)=0$が相異3実根をもつようなaの範囲
(2)(1)のとき3つの解は-2aと2aの間にあることを示せ
この動画を見る
香川大学過去問題
$f(x)=x^3-3a^2x+a^2-a$について
(1)$f(x)=0$が相異3実根をもつようなaの範囲
(2)(1)のとき3つの解は-2aと2aの間にあることを示せ
島根大 整数問題 高校数学 Japanese university entrance exam questions

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学(高校生)#島根大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
島根大学過去問題
$2^m!$が$2^n$で割り切れるnの最大値をN(m)とする。(m,n自然数)
(1)N(m)をmの式で表せ。
(2)N(m)が素数ならばmも素数であることを証明せよ。
この動画を見る
島根大学過去問題
$2^m!$が$2^n$で割り切れるnの最大値をN(m)とする。(m,n自然数)
(1)N(m)をmの式で表せ。
(2)N(m)が素数ならばmも素数であることを証明せよ。
灘中 (別件)11の倍数の見分け方

単元:
#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
灘中学校
207,2007,20007のように先頭が2で末尾が7、間はすべて0である整数で、27では割れるが81では割れない最小の数を求めよ。
この動画を見る
灘中学校
207,2007,20007のように先頭が2で末尾が7、間はすべて0である整数で、27では割れるが81では割れない最小の数を求めよ。
東大 整数 高校数学 Japanese university entrance exam questions Tokyo University

単元:
#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2006東京大学過去問題
n自然数
$x^n+y^n+z^n=xyz \cdots$①
(1)n=1のとき、$x \leqq y \leqq z$で①を満たす自然数(x,y,z)を求めよ。
(2)n=3のとき、①を満たす自然数(x,y,z)は存在しないことを示せ。
この動画を見る
2006東京大学過去問題
n自然数
$x^n+y^n+z^n=xyz \cdots$①
(1)n=1のとき、$x \leqq y \leqq z$で①を満たす自然数(x,y,z)を求めよ。
(2)n=3のとき、①を満たす自然数(x,y,z)は存在しないことを示せ。
一橋大学 3次方程式 整数解 高校数学 Japanese university entrance exam questions

単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#数と式#一次不等式(不等式・絶対値のある方程式・不等式)#整数の性質#微分法と積分法#一橋大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
一橋大学過去問題
kは整数$ \ $3次方程式
$x^3-13x+k=0$は3つの異なる整数解をもつ。
kと整数解を求めよ。
この動画を見る
一橋大学過去問題
kは整数$ \ $3次方程式
$x^3-13x+k=0$は3つの異なる整数解をもつ。
kと整数解を求めよ。
東工大 整数問題 高校数学 Japanese university entrance exam questions

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#東京工業大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
神戸薬科大学過去問題
$\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1$
$x<y<z$(自然数)
東京工業大学過去問題
$(ab-1)(bc-1)(ca-1)$がabcで割り切れる1<a<b<c(自然数)
a,b,cをすべて求めよ。
この動画を見る
神戸薬科大学過去問題
$\frac{1}{x}+\frac{1}{y}+\frac{1}{z}=1$
$x<y<z$(自然数)
東京工業大学過去問題
$(ab-1)(bc-1)(ca-1)$がabcで割り切れる1<a<b<c(自然数)
a,b,cをすべて求めよ。
麻布中 中学入試問題に挑戦

単元:
#算数(中学受験)#過去問解説(学校別)
指導講師:
鈴木貫太郎
問題文全文(内容文):
麻布中学校過去問題
あるホテルには500室の部屋があります。4と9の数字を使わずに、
1,2,3,5$\cdots$と順に部屋に番号をつけていくと500番目の部屋は何号室ですか。
この動画を見る
麻布中学校過去問題
あるホテルには500室の部屋があります。4と9の数字を使わずに、
1,2,3,5$\cdots$と順に部屋に番号をつけていくと500番目の部屋は何号室ですか。
京大 信州大 整数 2次方程式 高校数学 Japanese university entrance exam questions Kyoto University

単元:
#数Ⅰ#数A#大学入試過去問(数学)#2次関数#2次関数とグラフ#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#信州大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
京都大学過去問題
①$n$と$n^2+2$がともに素数となるような自然数$n$を求めよ。
信州大学過去問題
②$x^2+(2a-1)x+a^2-3a-4=0$が少なくとも1つの正の解をもつ条件。
この動画を見る
京都大学過去問題
①$n$と$n^2+2$がともに素数となるような自然数$n$を求めよ。
信州大学過去問題
②$x^2+(2a-1)x+a^2-3a-4=0$が少なくとも1つの正の解をもつ条件。
浜松医大 確率 漸化式 高校数学 Japanese university entrance exam questions
単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#浜松医科大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
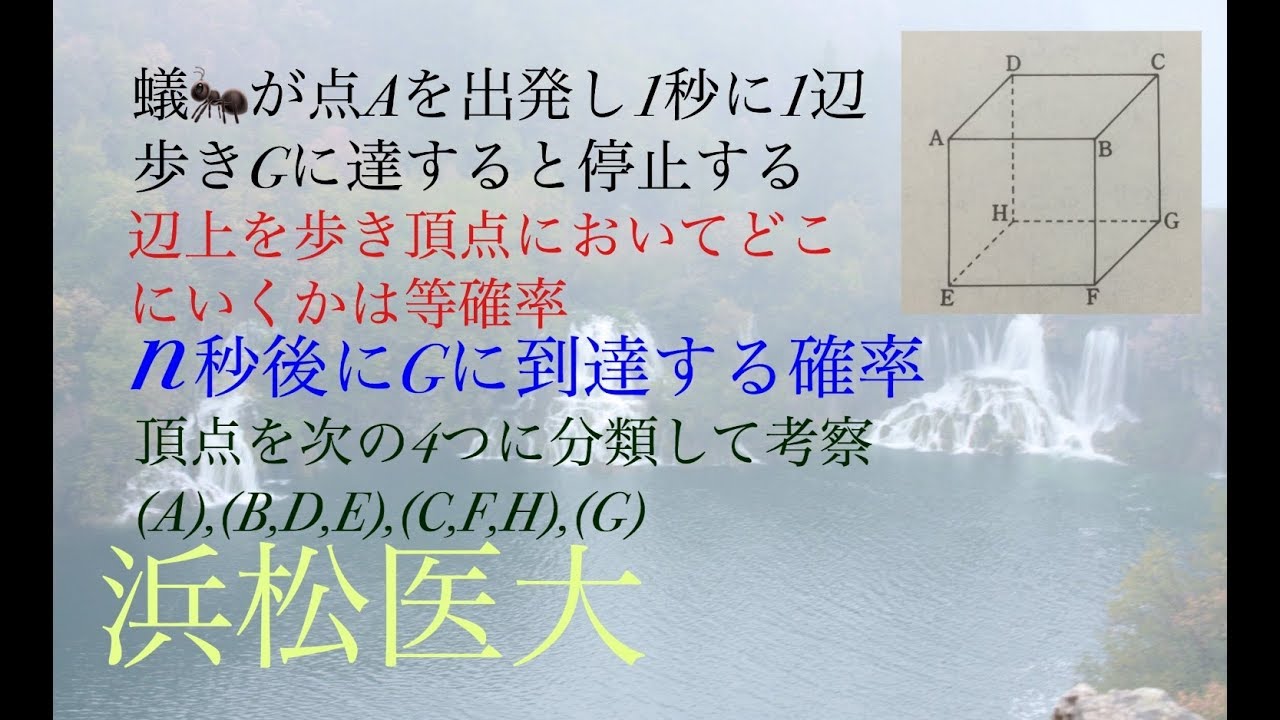
浜松医科大学過去問題
アリがAを出発し、1秒に一辺歩きGに達すると停止する。
辺上を歩き頂点においてどこにいくかは等確率。
n秒後にGに到達する確率。
*図は動画内参照
この動画を見る
浜松医科大学過去問題
アリがAを出発し、1秒に一辺歩きGに達すると停止する。
辺上を歩き頂点においてどこにいくかは等確率。
n秒後にGに到達する確率。
*図は動画内参照
早稲田 整数問題 高校数学 Japanese university entrance exam questions

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
早稲田大学過去問題
m,nは自然数。p,qは素数(p<q)
1~nまでの自然数の中でnと互いに素である自然数の個数をf(n)とする。
(1)$f(pq)=24$となるp,qを求めよ。
(2)$f(2^m3^n)$をm,nで表せ。
この動画を見る
早稲田大学過去問題
m,nは自然数。p,qは素数(p<q)
1~nまでの自然数の中でnと互いに素である自然数の個数をf(n)とする。
(1)$f(pq)=24$となるp,qを求めよ。
(2)$f(2^m3^n)$をm,nで表せ。
久留米(医) 5倍角 Japanese university entrance exam questions

単元:
#数Ⅱ#三角関数#微分法と積分法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
久留米大学過去問題
$0 \leqq x<\frac{\pi}{2}$
$f(x)=cos5x+9cos3x-10cosx$
f(x)の最小値を求めよ。
この動画を見る
久留米大学過去問題
$0 \leqq x<\frac{\pi}{2}$
$f(x)=cos5x+9cos3x-10cosx$
f(x)の最小値を求めよ。
灘中 中学入試問題に挑戦

単元:
#算数(中学受験)#中3数学#式の計算(展開、因数分解)#灘中学校
指導講師:
鈴木貫太郎
問題文全文(内容文):
灘中学校過去問題
数xに対してxを超えない整数のうち最大のものを[x]で表す。
[3.5]=3 , [4] = 4
$[\frac{1×1}{68}],[\frac{2×2}{68}],[\frac{3×3}{68}],\cdots,[\frac{2010×2010}{68}]$
この2010個の整数の中に、全部で何種類の整数があるか。
この動画を見る
灘中学校過去問題
数xに対してxを超えない整数のうち最大のものを[x]で表す。
[3.5]=3 , [4] = 4
$[\frac{1×1}{68}],[\frac{2×2}{68}],[\frac{3×3}{68}],\cdots,[\frac{2010×2010}{68}]$
この2010個の整数の中に、全部で何種類の整数があるか。
一橋大 整数問題 高校数学 Japanese university entrance exam questions

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数学的帰納法#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
'98一橋大学過去問題
すべての自然数nに対して$5^n+an+b$が16の倍数となるような
16以下の自然数a,bを求めよ。
この動画を見る
'98一橋大学過去問題
すべての自然数nに対して$5^n+an+b$が16の倍数となるような
16以下の自然数a,bを求めよ。
大阪市立大 漸化式 Japanese university entrance exam questions
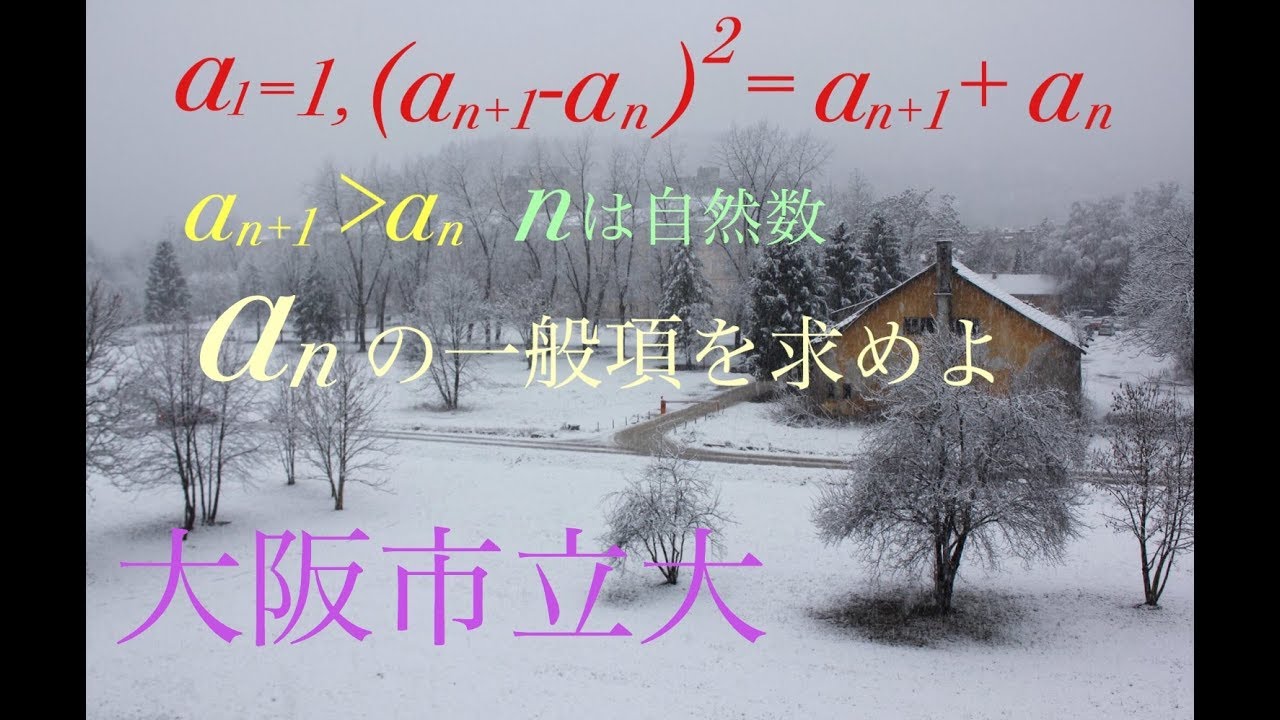
単元:
#数列#漸化式#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
大阪市立大学過去問題
n自然数
$a_1 = 1 \quad a_{n+1}>a_n$
$(a_{n+1}-a_n)^2= a_{n+1}+a_n$
この動画を見る
大阪市立大学過去問題
n自然数
$a_1 = 1 \quad a_{n+1}>a_n$
$(a_{n+1}-a_n)^2= a_{n+1}+a_n$
大阪大 整数 高校数学 Japanese university entrance exam questions

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#大阪大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
'99大阪大学過去問題
自然数の組(a,b)でa以上b以下の整数の和が500となるものをすべて求めよ。
a<b
この動画を見る
'99大阪大学過去問題
自然数の組(a,b)でa以上b以下の整数の和が500となるものをすべて求めよ。
a<b
東大 微分 代講ヨビノリたくみ Japanese university entrance exam questions Tokyo University

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#東京大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
'98東京大学過去問題
aは0でない実数
関数
$f(x)=(3x^2-4)(x-a+\frac{1}{a})$の極大値と極小値の差が最小となるaを求めよ。
この動画を見る
'98東京大学過去問題
aは0でない実数
関数
$f(x)=(3x^2-4)(x-a+\frac{1}{a})$の極大値と極小値の差が最小となるaを求めよ。
東海大(医)漸化式 高校数学 Japanese university entrance exam questions

単元:
#数列#漸化式#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
東海大学過去問題
$a_1=0,a_{n+1=2a_n+n^2}$
一般項$a_n$を求めよ。
この動画を見る
東海大学過去問題
$a_1=0,a_{n+1=2a_n+n^2}$
一般項$a_n$を求めよ。
東邦(医)正五角形の外接円と内接円の半径の比 高校数学 Japanese university entrance exam questions

単元:
#複素数平面#複素数平面#図形への応用#数学(高校生)#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
東邦大学過去問題
正五角形の外接円、内接円の半径をそれぞれR,rとする。
$\frac{r}{R}$の値を求めよ。
この動画を見る
東邦大学過去問題
正五角形の外接円、内接円の半径をそれぞれR,rとする。
$\frac{r}{R}$の値を求めよ。
東北大 三次関数と放物線の共有点の数 高校数学 Japanese university entrance exam questions

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
東北大学過去問題
$y=x^2+k$と$y=|x(x^2-1)|$との共有点の個数
この動画を見る
東北大学過去問題
$y=x^2+k$と$y=|x(x^2-1)|$との共有点の個数
灘中 中学入試にチャレンジ

単元:
#算数(中学受験)#計算と数の性質#いろいろな計算#過去問解説(学校別)#灘中学校
指導講師:
鈴木貫太郎
問題文全文(内容文):
灘中学校過去問題
$\quad$10桁 $\quad\quad$ 10桁
7777777777 7777777777
は計算すると20桁になる。この20桁の上10桁と下10桁の数の和を求めよ。
上2桁と下2桁の和とは1234なら12+34のこと
この動画を見る
灘中学校過去問題
$\quad$10桁 $\quad\quad$ 10桁
7777777777 7777777777
は計算すると20桁になる。この20桁の上10桁と下10桁の数の和を求めよ。
上2桁と下2桁の和とは1234なら12+34のこと
防衛大 漸化式 Japanese university entrance exam questions

単元:
#大学入試過去問(数学)#数列#漸化式#学校別大学入試過去問解説(数学)#防衛大学校#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
防衛大学過去問題
$a_1=1 \quad a_{n+1}=2^{2n-2}(a_n)^2$
n自然数、一般項を求めよ。
この動画を見る
防衛大学過去問題
$a_1=1 \quad a_{n+1}=2^{2n-2}(a_n)^2$
n自然数、一般項を求めよ。
一橋大 整数問題 Japanese university entrance exam questions

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
一橋大学過去問題
(1)$n^3+1$が3で割り切れるnをすべて求めよ。
(2)$n^n+1$が3で割り切れるnをすべて求めよ。
(1)(2)ともにnは自然数
この動画を見る
一橋大学過去問題
(1)$n^3+1$が3で割り切れるnをすべて求めよ。
(2)$n^n+1$が3で割り切れるnをすべて求めよ。
(1)(2)ともにnは自然数
慶應(医)数列 高校数学 Japanese university entrance exam questions
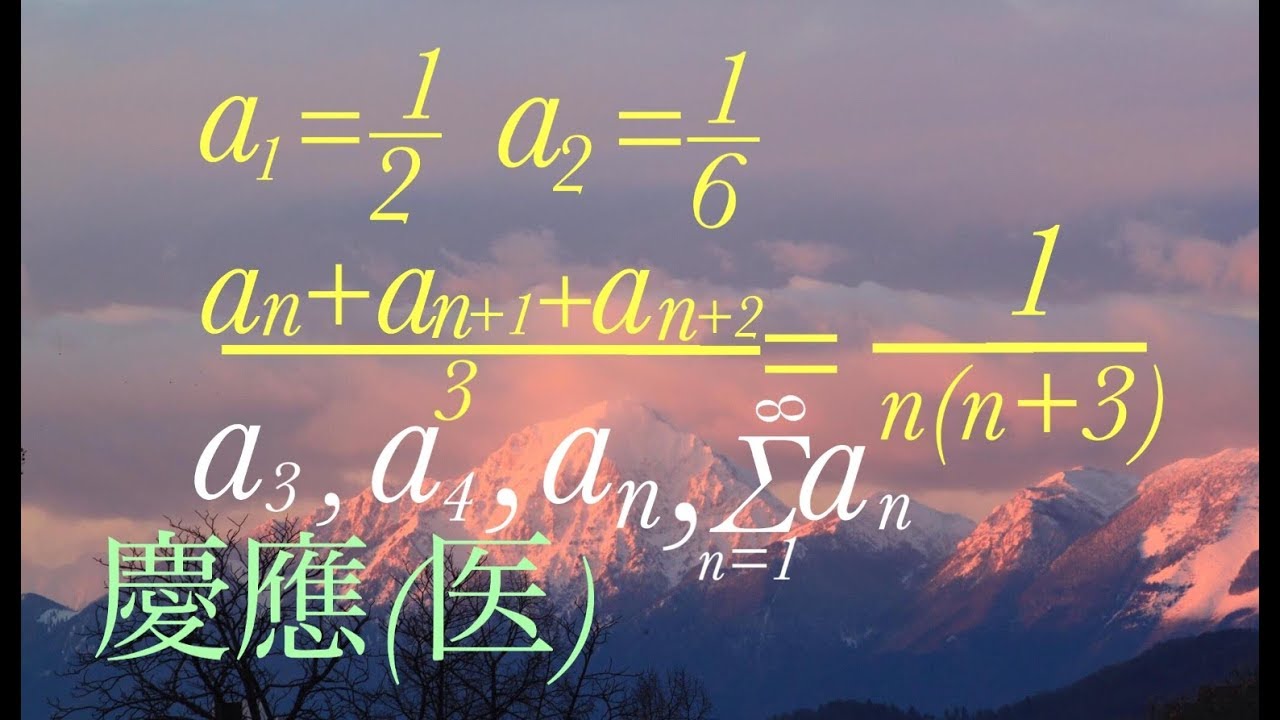
単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数B
指導講師:
鈴木貫太郎
問題文全文(内容文):
慶応義塾大学過去問題
数列$\{ a_n \}$の項の間に次の関係がある。
$a_1=\frac{1}{2},a_2=\frac{1}{6}$
$\frac{a_n+a_{n+1}+a_{n+2}}{3} = \frac{1}{n(n+3)}$
$n=1,2,3\cdots$
$a_3,a_4,a_n,\displaystyle\sum_{k=1}^\infty a_n$を求めよ。
この動画を見る
慶応義塾大学過去問題
数列$\{ a_n \}$の項の間に次の関係がある。
$a_1=\frac{1}{2},a_2=\frac{1}{6}$
$\frac{a_n+a_{n+1}+a_{n+2}}{3} = \frac{1}{n(n+3)}$
$n=1,2,3\cdots$
$a_3,a_4,a_n,\displaystyle\sum_{k=1}^\infty a_n$を求めよ。
名古屋大 微分・積分 高校数学 Japanese university entrance exam questions

単元:
#数Ⅱ#微分法と積分法#接線と増減表・最大値・最小値#面積、体積
指導講師:
鈴木貫太郎
問題文全文(内容文):
名古屋大学過去問題
$y=x^2(x+1)とy=k^2(x+1)$とで囲まれる面積が最小となるkの値を求めよ。
$(0 \leqq k \leqq 1)$
この動画を見る
名古屋大学過去問題
$y=x^2(x+1)とy=k^2(x+1)$とで囲まれる面積が最小となるkの値を求めよ。
$(0 \leqq k \leqq 1)$
広島大 円の方程式 三角比 高校数学 Japanese university entrance exam questions

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#三角関数#円と方程式#加法定理とその応用#学校別大学入試過去問解説(数学)#数学(高校生)#広島大学
指導講師:
鈴木貫太郎
問題文全文(内容文):
広島大学過去問題
2つの円
$x^2+y^2+(2\sqrt2sinθ)x-\frac{\sqrt{17}}{2}y+sin^2θ+$
$\frac{17}{16}=0$
$x^2+y^2=\frac{9}{16} \quad (0^\circ < θ < 180^\circ)$
が共有点をもたないようなθの範囲を求めよ。
この動画を見る
広島大学過去問題
2つの円
$x^2+y^2+(2\sqrt2sinθ)x-\frac{\sqrt{17}}{2}y+sin^2θ+$
$\frac{17}{16}=0$
$x^2+y^2=\frac{9}{16} \quad (0^\circ < θ < 180^\circ)$
が共有点をもたないようなθの範囲を求めよ。
東京女子医大 整数問題 高校数学 Japanese university entrance exam questions

単元:
#数A#整数の性質#ユークリッド互除法と不定方程式・N進法#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
東京女子医科大学過去問題
$2^{40}+1=mn \quad (1<m<n)$を満たす自然数の組m,nがただ1つある。
mの値を求めよ。
この動画を見る
東京女子医科大学過去問題
$2^{40}+1=mn \quad (1<m<n)$を満たす自然数の組m,nがただ1つある。
mの値を求めよ。
和歌山大 ド・モアブルの定理 Japanese university entrance exam questions
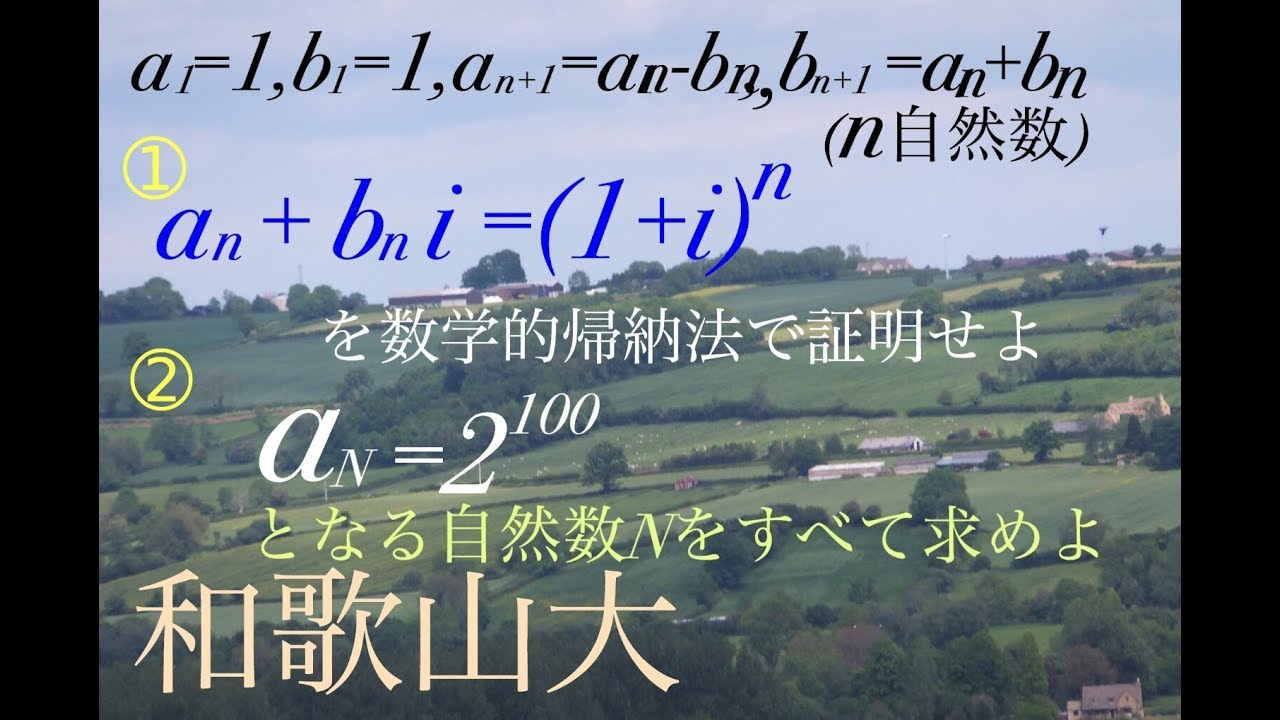
単元:
#大学入試過去問(数学)#複素数平面#数列#数学的帰納法#複素数平面#学校別大学入試過去問解説(数学)#数学(高校生)#和歌山大学#数B#数C
指導講師:
鈴木貫太郎
問題文全文(内容文):
和歌山大学過去問題
$a_1=b_1=1$
$a_{n+1}=a_n-b_n$
$b_{n+1}=a_n+b_n$
(1)$a_n+b_ni= (1+i)^n$を数学的帰納法で証明せよ。
(2)$a_N=2^{100}$となる自然数Nをすべて求めよ。
この動画を見る
和歌山大学過去問題
$a_1=b_1=1$
$a_{n+1}=a_n-b_n$
$b_{n+1}=a_n+b_n$
(1)$a_n+b_ni= (1+i)^n$を数学的帰納法で証明せよ。
(2)$a_N=2^{100}$となる自然数Nをすべて求めよ。



