 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
 学校別大学入試過去問解説(数学)
学校別大学入試過去問解説(数学)
福田の数学〜立教大学2021年理学部第1問(2)〜3直線が1点で交わる条件

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#点と直線#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(2)$t$を実数とする。座標平面上の3つの直線
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+(2t-2)y-4t+2=0 \\
x+(2t+2)y-4t-2=0 \\
2tx+y-4t=0
\end{array}
\right.
(-2 \leqq t \leqq 1)
\end{eqnarray}$
が1つの点で交わるようなtの値を全て求めると$t=\boxed{イ}$である。
2021立教大学理学部過去問
この動画を見る
${\Large\boxed{1}}$(2)$t$を実数とする。座標平面上の3つの直線
$\begin{eqnarray}
\left\{
\begin{array}{l}
x+(2t-2)y-4t+2=0 \\
x+(2t+2)y-4t-2=0 \\
2tx+y-4t=0
\end{array}
\right.
(-2 \leqq t \leqq 1)
\end{eqnarray}$
が1つの点で交わるようなtの値を全て求めると$t=\boxed{イ}$である。
2021立教大学理学部過去問
大学入試問題#24 秋田大学(2020) 定積分
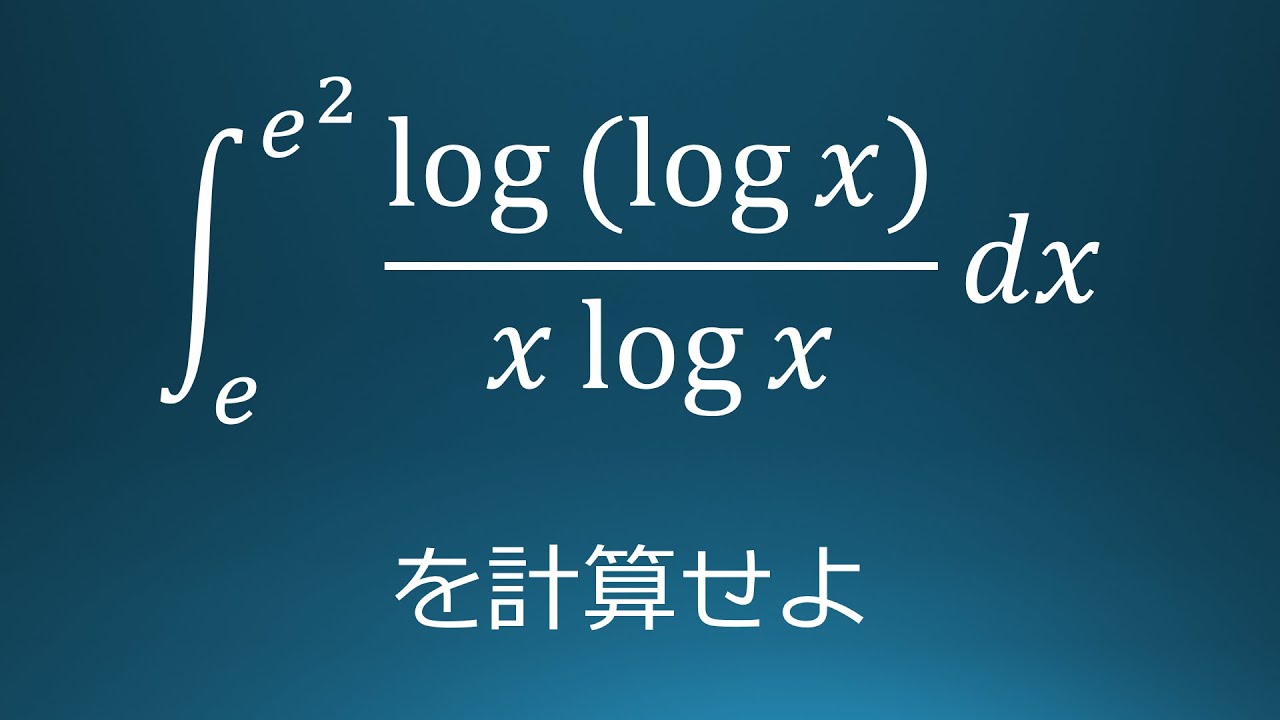
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#秋田大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{e}^{e^2}\displaystyle \frac{log(log\ x)}{x\ log\ x}\ dx$を計算せよ。
出典:2020年秋田大学 入試問題
この動画を見る
$\displaystyle \int_{e}^{e^2}\displaystyle \frac{log(log\ x)}{x\ log\ x}\ dx$を計算せよ。
出典:2020年秋田大学 入試問題
【理数個別の過去問解説】2020年度横浜国立大学 数学 第2問(2)解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
横浜国立大学2020年度大問2(2)
次の問いに答えよ。
(1)実数A,B,C,Dに対して、複素数zを
$z=\dfrac{A+\sqrt5 Bi}{C+\sqrt5 Di}$
で定める。ただし、$C+\sqrt5 Di\neq 0$とする。このとき、$x=x+yi$をみたす実数x,yをA,B,C,Dの式で表せ。
(2)次をみたす整数A,B,C,Dを求めよ。
$\dfrac{16+\sqrt5 i}{29}=\dfrac{A+\sqrt5 Bi}{C+\sqrt5 Di}$
$AD-BC=-1$
$D\gt 0$
この動画を見る
横浜国立大学2020年度大問2(2)
次の問いに答えよ。
(1)実数A,B,C,Dに対して、複素数zを
$z=\dfrac{A+\sqrt5 Bi}{C+\sqrt5 Di}$
で定める。ただし、$C+\sqrt5 Di\neq 0$とする。このとき、$x=x+yi$をみたす実数x,yをA,B,C,Dの式で表せ。
(2)次をみたす整数A,B,C,Dを求めよ。
$\dfrac{16+\sqrt5 i}{29}=\dfrac{A+\sqrt5 Bi}{C+\sqrt5 Di}$
$AD-BC=-1$
$D\gt 0$
【高校数学】明治大学の過去問~確率の問題演習~【大学受験】

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
1から11までの番号をつけた11枚のカードから3枚を取り出すとき、
それらの番号の和が偶数となる確率は、
$\displaystyle \frac{□}{□}$で、それらの番号の積が偶数になる確率は、$\displaystyle \frac{□}{□}$
この動画を見る
1から11までの番号をつけた11枚のカードから3枚を取り出すとき、
それらの番号の和が偶数となる確率は、
$\displaystyle \frac{□}{□}$で、それらの番号の積が偶数になる確率は、$\displaystyle \frac{□}{□}$
福田の数学〜立教大学2021年理学部第1問(1)〜正六角形の対角線ベクトルの内積

単元:
#大学入試過去問(数学)#平面上のベクトル#平面上のベクトルと内積#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(1)1辺の長さが1の正六角形の頂点を反時計回りにA,B,C,D,E,Fとする。
このとき、2つのベクトル$\overrightarrow{ AC },\overrightarrow{ AD }$の内積$\overrightarrow{ AC }・\overrightarrow{ AD }$の値は$\boxed{\ \ ア\ \ }$である。
2021立教大学理学部過去問
この動画を見る
${\Large\boxed{1}}$(1)1辺の長さが1の正六角形の頂点を反時計回りにA,B,C,D,E,Fとする。
このとき、2つのベクトル$\overrightarrow{ AC },\overrightarrow{ AD }$の内積$\overrightarrow{ AC }・\overrightarrow{ AD }$の値は$\boxed{\ \ ア\ \ }$である。
2021立教大学理学部過去問
【誘導あり 概要欄】大学入試問題#24 富山大学(2020) 微積の応用
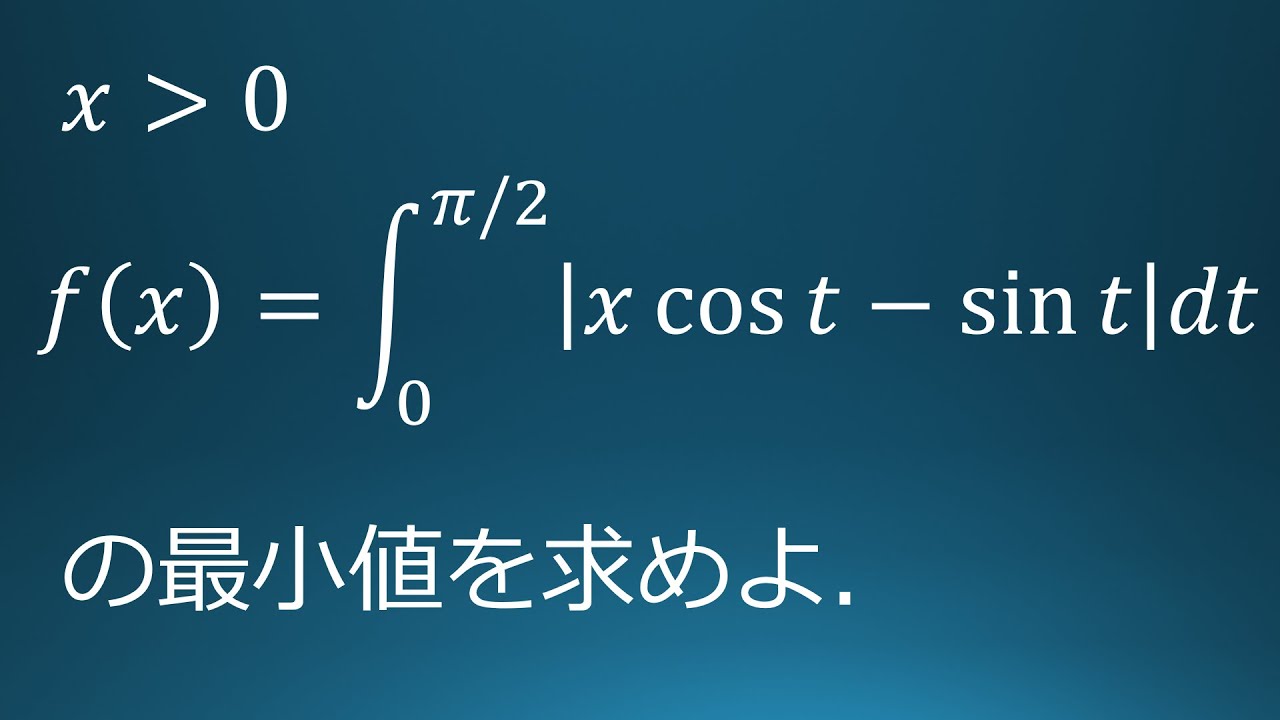
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#富山県立大学
指導講師:
ますただ
問題文全文(内容文):
(1)
$0 \lt \theta \lt \displaystyle \frac{\pi}{2}$
$x\ \cos\theta-\sin\theta=0$のとき
$\sin\theta,\cos\theta$を$x$で表せ。
(2)
$x \gt 0$
$f(x)=\displaystyle \int_{0}^{\frac{\pi}{2}}|x\ \cos\ t-\sin\ t|dt$の最小値を求めよ。
出典:2020年富山大学 入試問題
この動画を見る
(1)
$0 \lt \theta \lt \displaystyle \frac{\pi}{2}$
$x\ \cos\theta-\sin\theta=0$のとき
$\sin\theta,\cos\theta$を$x$で表せ。
(2)
$x \gt 0$
$f(x)=\displaystyle \int_{0}^{\frac{\pi}{2}}|x\ \cos\ t-\sin\ t|dt$の最小値を求めよ。
出典:2020年富山大学 入試問題
【理数個別の過去問解説】2020年度横浜国立大学 数学 第2問(1)解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
横浜国立大学2020年度大問2(1)
次の問いに答えよ。
(1)実数A,B,C,Dに対して、複素数zを
$z=\dfrac{A+\sqrt5 Bi}{C+\sqrt5 Di}$
で定める。ただし、$C+\sqrt5 Di\neq 0$とする。このとき、$x=x+yi$をみたす実数x,yをA,B,C,Dの式で表せ。
(2)次をみたす整数A,B,C,Dを求めよ。
$\dfrac{16+\sqrt5 i}{29}=\dfrac{A+\sqrt5 Bi}{C+\sqrt5 Di}$
$AD-BC=-1$
$D\gt 0$
この動画を見る
横浜国立大学2020年度大問2(1)
次の問いに答えよ。
(1)実数A,B,C,Dに対して、複素数zを
$z=\dfrac{A+\sqrt5 Bi}{C+\sqrt5 Di}$
で定める。ただし、$C+\sqrt5 Di\neq 0$とする。このとき、$x=x+yi$をみたす実数x,yをA,B,C,Dの式で表せ。
(2)次をみたす整数A,B,C,Dを求めよ。
$\dfrac{16+\sqrt5 i}{29}=\dfrac{A+\sqrt5 Bi}{C+\sqrt5 Di}$
$AD-BC=-1$
$D\gt 0$
大学入試問題#23 東北大学(2020) 三角関数

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$y=\sin\ x$の2つの接線が直交するとき
その交点の$y$座標の値をすべて求めよ。
出典:2020年東北大学 入試問題
この動画を見る
$y=\sin\ x$の2つの接線が直交するとき
その交点の$y$座標の値をすべて求めよ。
出典:2020年東北大学 入試問題
数学「大学入試良問集」【14−2 円と直線と平面ベクトルと。】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#数学(高校生)#数C#立命館大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
点$O$を中心とする円に内接する$\triangle ABC$があり、$AB=2,\ AC=3,\ BC=\sqrt{ 7 }$とする。
点$B$を通り直線$AC$の平行な直線と円$O$との交点のうち、点$B$と異なる点を$D$、直線$AO$と直線$CD$の交点を$E$とする。
(1)内積$\overrightarrow{ AB }・\overrightarrow{ AO },\overrightarrow{ AC }・\overrightarrow{ AO }$を求めよ。
(2)$\overrightarrow{ AO }$を$\overrightarrow{ AB }$と$\overrightarrow{ AC }$を用いて表せ。
(3)$\overrightarrow{ AD }$を$\overrightarrow{ AB }$と$\overrightarrow{ AC }$を用いて表せ。
(4)$CE:DE$を求めよ。
この動画を見る
点$O$を中心とする円に内接する$\triangle ABC$があり、$AB=2,\ AC=3,\ BC=\sqrt{ 7 }$とする。
点$B$を通り直線$AC$の平行な直線と円$O$との交点のうち、点$B$と異なる点を$D$、直線$AO$と直線$CD$の交点を$E$とする。
(1)内積$\overrightarrow{ AB }・\overrightarrow{ AO },\overrightarrow{ AC }・\overrightarrow{ AO }$を求めよ。
(2)$\overrightarrow{ AO }$を$\overrightarrow{ AB }$と$\overrightarrow{ AC }$を用いて表せ。
(3)$\overrightarrow{ AD }$を$\overrightarrow{ AB }$と$\overrightarrow{ AC }$を用いて表せ。
(4)$CE:DE$を求めよ。
【理数個別の過去問解説】2020年度横浜国立大学 数学 第1問(2)解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
横浜国立大学2020年度大問1(2)
定積分
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{4}}\dfrac{\log(\sin x)}{\tan x}dx$を求めよ.
この動画を見る
横浜国立大学2020年度大問1(2)
定積分
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{4}}\dfrac{\log(\sin x)}{\tan x}dx$を求めよ.
【問題の詳細は概要欄,誘導あり】大学入試問題#22 千葉大学(2020) 数列

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$a_1=3,a_2=2$
$n \geqq 2$のとき
$a_{n+1}=a_n^2+a_n-1$
(1)
$n \geqq 2$のとき
$a_{n+1}=(a_1・a_2・・・a_n)-1$を示せ
(2)
$\displaystyle \sum_{i=1}^n(a_1)^2=a_1a_2・・・a_n+100$をみたす自然数$n$を求めよ。
出典:2020年千葉大学 入試問題
この動画を見る
$a_1=3,a_2=2$
$n \geqq 2$のとき
$a_{n+1}=a_n^2+a_n-1$
(1)
$n \geqq 2$のとき
$a_{n+1}=(a_1・a_2・・・a_n)-1$を示せ
(2)
$\displaystyle \sum_{i=1}^n(a_1)^2=a_1a_2・・・a_n+100$をみたす自然数$n$を求めよ。
出典:2020年千葉大学 入試問題
【理数個別の過去問解説】2020年度横浜国立大学 数学 第1問(1)解説

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#横浜国立大学#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
横浜国立大学2020年度大問1(1)
関数$f(x)=(e^x-1)\cos x-\sin x\left(-\dfrac{\pi}{2}\leqq x\leqq\dfrac{\pi}{2}\right)$の増減、極値を調べ、そのグラフの概形を描け。ただし、グラフの凹凸、変曲点は調べなくてよい。
この動画を見る
横浜国立大学2020年度大問1(1)
関数$f(x)=(e^x-1)\cos x-\sin x\left(-\dfrac{\pi}{2}\leqq x\leqq\dfrac{\pi}{2}\right)$の増減、極値を調べ、そのグラフの概形を描け。ただし、グラフの凹凸、変曲点は調べなくてよい。
数学「大学入試良問集」【14−1 平面ベクトルと一次独立の様々な解法】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#平面上のベクトル#ベクトルと平面図形、ベクトル方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数C
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$\triangle OAB$を$3:2$に内部する点を$C$、辺$OB$を$3:4$に内分する点を$D$とする。
線分$AD$と線分$BC$との交点を$P$とする。
また、$\triangle OPA,\triangle PDB$の面積をそれぞれ$S_1,S_2$とする。
(1)$\overrightarrow{ OP }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$を用いて表せ。
(2)$S_1:S_2$を求めよ。
この動画を見る
$\triangle OAB$を$3:2$に内部する点を$C$、辺$OB$を$3:4$に内分する点を$D$とする。
線分$AD$と線分$BC$との交点を$P$とする。
また、$\triangle OPA,\triangle PDB$の面積をそれぞれ$S_1,S_2$とする。
(1)$\overrightarrow{ OP }$を$\overrightarrow{ OA }$と$\overrightarrow{ OB }$を用いて表せ。
(2)$S_1:S_2$を求めよ。
大学入試問題#21 千葉大学(2020) tanの定積分
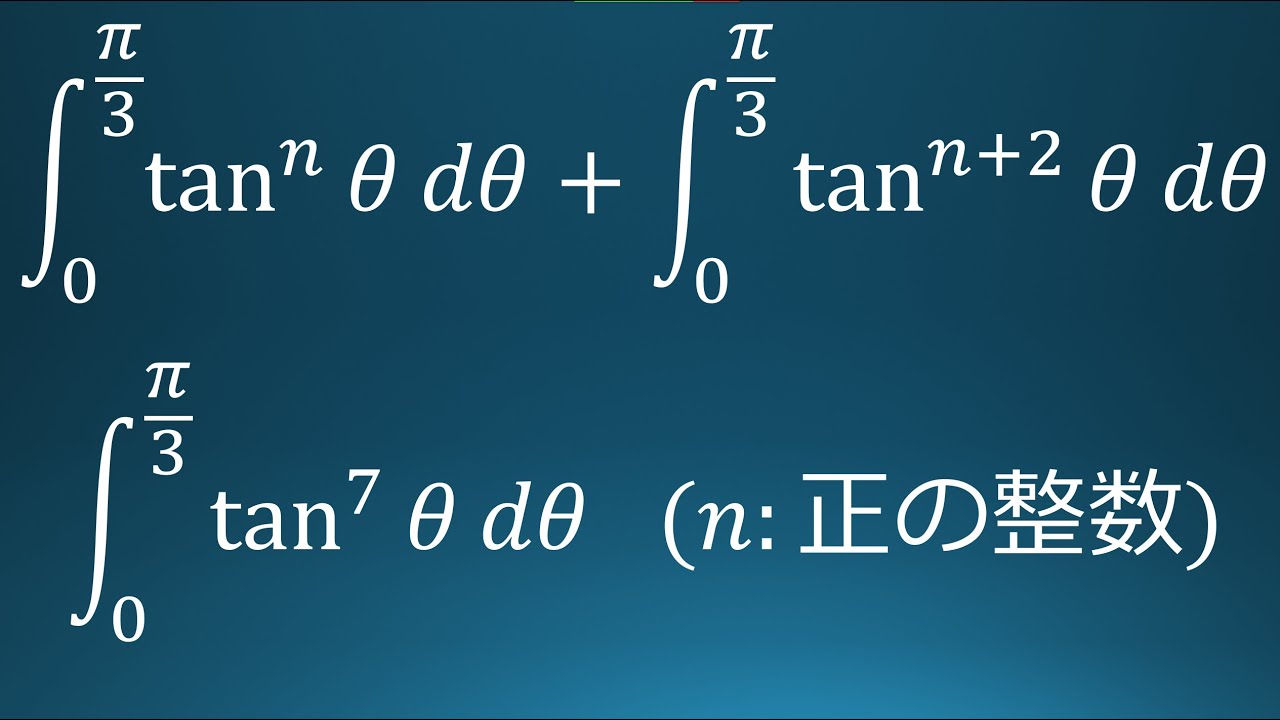
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
(1)
$\displaystyle \int_{0}^{\frac{\pi}{3}}\tan^n\theta\ d\theta+\displaystyle \int_{0}^{\frac{\pi}{3}}\tan^{n+2}\theta\ d\theta$を$n$の式で表せ
(2)
$\displaystyle \int_{0}^{\frac{\pi}{3}}\tan^7\theta\ d\ \theta$を求めよ。
出典:2020年千葉大学 入試問題
この動画を見る
(1)
$\displaystyle \int_{0}^{\frac{\pi}{3}}\tan^n\theta\ d\theta+\displaystyle \int_{0}^{\frac{\pi}{3}}\tan^{n+2}\theta\ d\theta$を$n$の式で表せ
(2)
$\displaystyle \int_{0}^{\frac{\pi}{3}}\tan^7\theta\ d\ \theta$を求めよ。
出典:2020年千葉大学 入試問題
福田のわかった数学〜高校2年生061〜対称式と領域(3)

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#2次関数#2次方程式と2次不等式#図形と方程式#微分法と積分法#軌跡と領域#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 対称式と領域(3)
実数$x,\ y$が$x^2+xy+y^2=6$を
満たしながら動くとき
$x^2y+xy^2-x^2-2xy-y^2+x+y$
の取り得る値の範囲を求めよ。
この動画を見る
数学$\textrm{II}$ 対称式と領域(3)
実数$x,\ y$が$x^2+xy+y^2=6$を
満たしながら動くとき
$x^2y+xy^2-x^2-2xy-y^2+x+y$
の取り得る値の範囲を求めよ。
大学入試問題#20 群馬大医学部(2020) 対数,領域

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#群馬大学
指導講師:
ますただ
問題文全文(内容文):
$0 \lt x \lt 1,0 \lt y \lt 1$
$(log_xy)^2+log_y\displaystyle \frac{x^3}{y^4} \leqq 0$の表す領域を$xy$平面上に図示せよ。
出典:2020年群馬大学医学部 入試問題
この動画を見る
$0 \lt x \lt 1,0 \lt y \lt 1$
$(log_xy)^2+log_y\displaystyle \frac{x^3}{y^4} \leqq 0$の表す領域を$xy$平面上に図示せよ。
出典:2020年群馬大学医学部 入試問題
数学「大学入試良問集」【19−24 空間図形の断面積と体積】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#奈良教育大学#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$xyz$空間の$xy$平面上に曲線$C:y=x^2,z=0$ 直線$l:y=x+a,z=0(a \leqq 1)$がある。
いま$C$と$l$の交点を$P,Q$とし、線分$PQ$を底辺とする正三角形$PQR$を$xy$平面に垂直に作る。
直線$l$を$a=1$から$C$に接するまで動かすとき、この三角形が通過してできる立体の体積$V$を求めよ。
この動画を見る
$xyz$空間の$xy$平面上に曲線$C:y=x^2,z=0$ 直線$l:y=x+a,z=0(a \leqq 1)$がある。
いま$C$と$l$の交点を$P,Q$とし、線分$PQ$を底辺とする正三角形$PQR$を$xy$平面に垂直に作る。
直線$l$を$a=1$から$C$に接するまで動かすとき、この三角形が通過してできる立体の体積$V$を求めよ。
大学入試問題#19 京都大学(2020) 定積分
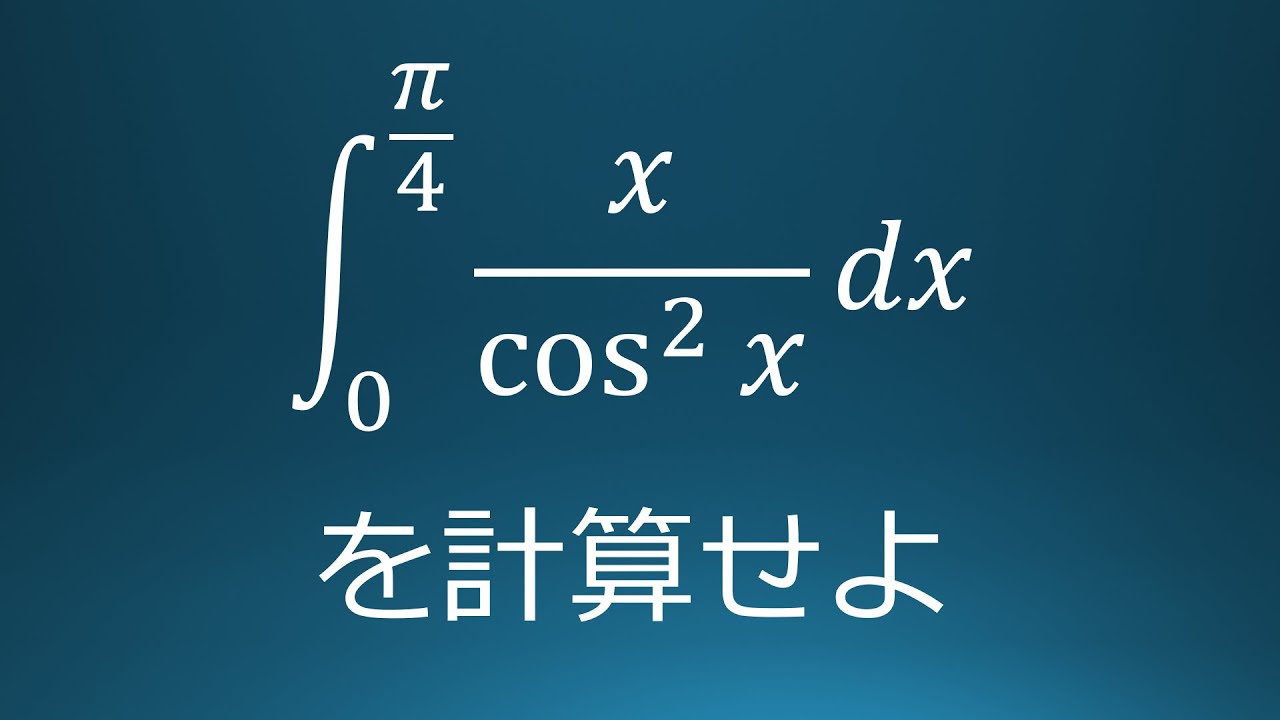
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{x}{\cos^2x}\ dx$を計算せよ。
出典:2020年京都大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{4}}\displaystyle \frac{x}{\cos^2x}\ dx$を計算せよ。
出典:2020年京都大学 入試問題
大学入試問題#18 東北大学(2020) 数列

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$a_1=1,\ a_2=3$
$a_{n+2}a_n=2a_{n+1}^2$のとき
一般項$a_n$を求めよ。
出典:2020年東北大学 入試問題
この動画を見る
$a_1=1,\ a_2=3$
$a_{n+2}a_n=2a_{n+1}^2$のとき
一般項$a_n$を求めよ。
出典:2020年東北大学 入試問題
数学「大学入試良問集」【19−23 空間図形の断面積と体積】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東京学芸大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
図のような1辺の長さ$a$の立方体
$ABCD-EFGH$がある。
線分$AF,BG,CH,DE$上にそれぞれ動点$P,Q,R,S$があり、頂点$A,B,C,D$を同時に出発して同じ速さで頂点$F,G,H,E$まで動く。
このとき、四角形$PQRS$が通過してできる立体の体積を求めよ。
この動画を見る
図のような1辺の長さ$a$の立方体
$ABCD-EFGH$がある。
線分$AF,BG,CH,DE$上にそれぞれ動点$P,Q,R,S$があり、頂点$A,B,C,D$を同時に出発して同じ速さで頂点$F,G,H,E$まで動く。
このとき、四角形$PQRS$が通過してできる立体の体積を求めよ。
大学入試問題#17 埼玉大学(2021) 解と係数の関係
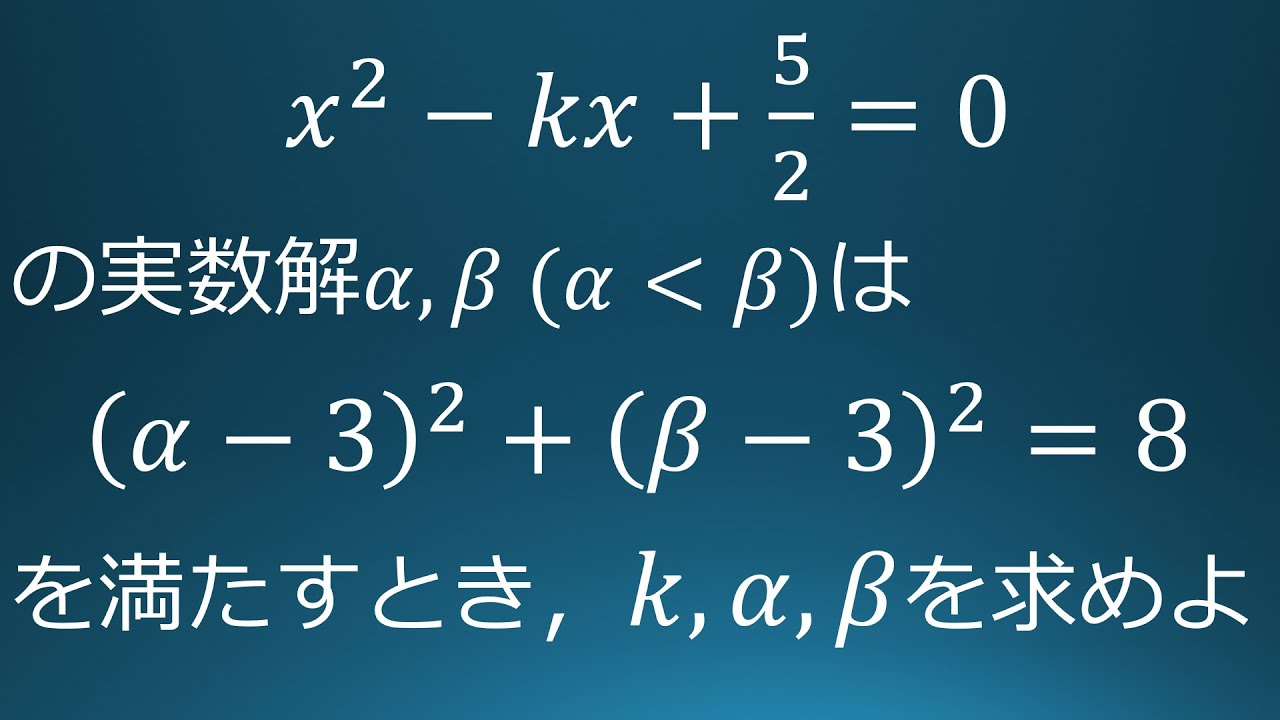
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学
指導講師:
ますただ
問題文全文(内容文):
$x^2-kx+\displaystyle \frac{5}{2}=0$の実数解$\alpha,\beta,(\alpha \lt \beta)$は
$(\alpha-3)^2+(\beta-3)^2=8$をみたす。
$k,\alpha,\beta$の値を求めよ。
出典:2020年埼玉大学 入試問題
この動画を見る
$x^2-kx+\displaystyle \frac{5}{2}=0$の実数解$\alpha,\beta,(\alpha \lt \beta)$は
$(\alpha-3)^2+(\beta-3)^2=8$をみたす。
$k,\alpha,\beta$の値を求めよ。
出典:2020年埼玉大学 入試問題
数学「大学入試良問集」【19−22 積分と不等式・無限級数の良問】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#山形大学#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
自然数$n$に対して$S(x)=\displaystyle \sum_{k=1}^n(-1)^{k-1}x^{2k-2},R(x)=\displaystyle \frac{(-1)^nx^{2n}}{1+x^2}$とする。
さらに$f(x)=\displaystyle \frac{1}{1+x^2}$とする。このとき、次の問いに答えよ。
(1)等式$\displaystyle \frac{0}{1}S(x)dx=\displaystyle \sum_{k=1}^n(-1)^{k-1}\displaystyle \frac{1}{2k-1}$が成り立つことを示せ。
(2)定積分$\displaystyle \int_{0}^{1}f(x)dx$の値を求めよ。
(3)等式$S(x)=f(x)-R(x)$が成り立つことを示せ。
(4)不等式$|\displaystyle \int_{0}^{1}R(x)dx| \leqq \displaystyle \frac{1}{2n+1}$が成り立つことを示せ。
(5)無限階級$1-\displaystyle \frac{1}{3}+\displaystyle \frac{1}{5}-\displaystyle \frac{1}{7}+・・・$の和を求めよ。
この動画を見る
自然数$n$に対して$S(x)=\displaystyle \sum_{k=1}^n(-1)^{k-1}x^{2k-2},R(x)=\displaystyle \frac{(-1)^nx^{2n}}{1+x^2}$とする。
さらに$f(x)=\displaystyle \frac{1}{1+x^2}$とする。このとき、次の問いに答えよ。
(1)等式$\displaystyle \frac{0}{1}S(x)dx=\displaystyle \sum_{k=1}^n(-1)^{k-1}\displaystyle \frac{1}{2k-1}$が成り立つことを示せ。
(2)定積分$\displaystyle \int_{0}^{1}f(x)dx$の値を求めよ。
(3)等式$S(x)=f(x)-R(x)$が成り立つことを示せ。
(4)不等式$|\displaystyle \int_{0}^{1}R(x)dx| \leqq \displaystyle \frac{1}{2n+1}$が成り立つことを示せ。
(5)無限階級$1-\displaystyle \frac{1}{3}+\displaystyle \frac{1}{5}-\displaystyle \frac{1}{7}+・・・$の和を求めよ。
大学入試問題#16 埼玉大学(2020) 式変形

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#埼玉大学
指導講師:
ますただ
問題文全文(内容文):
実数$x,y$が$(x-3)^2+(y-3)^2=8$を満たすとき
$x+y,\ xy$のとりうる値の範囲を求めよ。
出典:2020年埼玉大学 入試問題
この動画を見る
実数$x,y$が$(x-3)^2+(y-3)^2=8$を満たすとき
$x+y,\ xy$のとりうる値の範囲を求めよ。
出典:2020年埼玉大学 入試問題
大学入試問題#15 慶應義塾大学(2021) 整数問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$a,b,c,d:$正の整数
$a^3=b^2$
$c^3=d^2$
$c-a=9$のとき$a,b,c,d$の値を求めよ。
出典:2021年慶應義塾大学 入試問題
この動画を見る
$a,b,c,d:$正の整数
$a^3=b^2$
$c^3=d^2$
$c-a=9$のとき$a,b,c,d$の値を求めよ。
出典:2021年慶應義塾大学 入試問題
数学「大学入試良問集」【19−21 定積分関数の超良問(面積)】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
関数$f(x)$を$f(x)=\displaystyle \int_{0}^{x}\displaystyle \frac{1}{1+t^2}dt$で定める。
(1)$y=f(x)$の$x=1$における法線の方程式を求めよ。
(2)(1)で求めた法線と$x$軸および$y=f(x)$のグラフによって囲まれる図形の面積を求めよ。
この動画を見る
関数$f(x)$を$f(x)=\displaystyle \int_{0}^{x}\displaystyle \frac{1}{1+t^2}dt$で定める。
(1)$y=f(x)$の$x=1$における法線の方程式を求めよ。
(2)(1)で求めた法線と$x$軸および$y=f(x)$のグラフによって囲まれる図形の面積を求めよ。
数学「大学入試良問集」【19−20 媒介変数のグラフと曲線の長さ、面積】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#東邦大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
$r$を正の定数とする。
$xy$平面上を時刻$t=0$から$t=\pi$まで運動する点$P(x,y)$の座標が$x=2r(t-\sin\ t\cos\ t),y=2r\ \sin^2t$であるとき、以下の問いに答えよ。
(1)
点$P$が描く曲線の概形を、$xy$平面上にかけ。
(2)
点$P$が時刻$t=0$から$t=\pi$までに動く道のり$S$は、
$S=\displaystyle \int_{0}^{\pi}\sqrt{ \left[ \dfrac{ dx }{ dt } \right]^2+\left[ \dfrac{ dy }{ dt } \right]^2 }\ dt$で与えられる。
このとき、$S$の値を求めよ。
(3)点$P$が描く曲線と$x$軸で囲まれた部分を、$x$軸の周りに1回転させてできる立体の体積を求めよ。
この動画を見る
$r$を正の定数とする。
$xy$平面上を時刻$t=0$から$t=\pi$まで運動する点$P(x,y)$の座標が$x=2r(t-\sin\ t\cos\ t),y=2r\ \sin^2t$であるとき、以下の問いに答えよ。
(1)
点$P$が描く曲線の概形を、$xy$平面上にかけ。
(2)
点$P$が時刻$t=0$から$t=\pi$までに動く道のり$S$は、
$S=\displaystyle \int_{0}^{\pi}\sqrt{ \left[ \dfrac{ dx }{ dt } \right]^2+\left[ \dfrac{ dy }{ dt } \right]^2 }\ dt$で与えられる。
このとき、$S$の値を求めよ。
(3)点$P$が描く曲線と$x$軸で囲まれた部分を、$x$軸の周りに1回転させてできる立体の体積を求めよ。
数学「大学入試良問集」【19−19 定積分で示された関数の最大最小】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#中京大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
関数$f(x)=\displaystyle \int_{0}^{x}(x\ \cos\ t-\sin\ t)dt(0 \leqq x \leqq 2\pi)$について次の問いに答えよ。
(1)$f(x)$を微分せよ。
(2)$f(x)$の最大値と最小値、およびそのときの$x$の値を求めよ。
この動画を見る
関数$f(x)=\displaystyle \int_{0}^{x}(x\ \cos\ t-\sin\ t)dt(0 \leqq x \leqq 2\pi)$について次の問いに答えよ。
(1)$f(x)$を微分せよ。
(2)$f(x)$の最大値と最小値、およびそのときの$x$の値を求めよ。
数学「大学入試良問集」【19−18 円をy軸回転させた回転体の体積】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#高知大学#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
図形$C:y^2+(x-1)^2 \leqq 4$を$y$軸のまわりに1回転させてできる立体の体積を求めよ。
この動画を見る
図形$C:y^2+(x-1)^2 \leqq 4$を$y$軸のまわりに1回転させてできる立体の体積を求めよ。
数学「大学入試良問集」【19−17 こぼれた水の体積と定積分】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#筑波大学#数Ⅲ
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
水を満たした半径2の半球体の容器がある。
これを静かに$\alpha^{ \circ }$傾けたとき、水面が$h$だけ下がり、こぼれ出た水の量と容器に残った水の量の比が$11:5$になった。
$h$と$\alpha$を求めよ。
この動画を見る
水を満たした半径2の半球体の容器がある。
これを静かに$\alpha^{ \circ }$傾けたとき、水面が$h$だけ下がり、こぼれ出た水の量と容器に残った水の量の比が$11:5$になった。
$h$と$\alpha$を求めよ。
数学「大学入試良問集」【19−16 x軸・y軸回転体の体積の求め方】を宇宙一わかりやすく

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ#富山県立大学
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
双曲線$x^2-\displaystyle \frac{y^2}{3}=1$と$2$直線$y=3,y=-3$で囲まれた部分を、$x$軸、$y$軸のまわりに1回転してできる立体の体積を、それぞれ$V_1,V_2$とする。
$\displaystyle \frac{V_1}{V_2}$を求めよ。
この動画を見る
双曲線$x^2-\displaystyle \frac{y^2}{3}=1$と$2$直線$y=3,y=-3$で囲まれた部分を、$x$軸、$y$軸のまわりに1回転してできる立体の体積を、それぞれ$V_1,V_2$とする。
$\displaystyle \frac{V_1}{V_2}$を求めよ。
