 千葉大学
千葉大学
 千葉大学
千葉大学
福田の数学〜過去の入試問題(期間限定)〜千葉大学理系2020第1問〜確率の基本性質

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
Aさんは1が書かれたカードを1枚、2が書かれたカードを2枚、4が書かれたカードを1枚、計4枚を無作為に横一列に並べて4桁の数Xを作る。Bさんは2が書かれたカードを2枚、3が書かれたカードを2枚、計4枚を無作為に横一列に並べて4桁の数Yを作る。
$$(1)Xが4の倍数となる確率を求めよ。
(2)X \lt Yとなる確率を求めよ。$$
この動画を見る
Aさんは1が書かれたカードを1枚、2が書かれたカードを2枚、4が書かれたカードを1枚、計4枚を無作為に横一列に並べて4桁の数Xを作る。Bさんは2が書かれたカードを2枚、3が書かれたカードを2枚、計4枚を無作為に横一列に並べて4桁の数Yを作る。
$$(1)Xが4の倍数となる確率を求めよ。
(2)X \lt Yとなる確率を求めよ。$$
大学入試問題#923「帰納法で解いても良いのかな」

単元:
#大学入試過去問(数学)#数列#数列とその和(等差・等比・階差・Σ)#数学的帰納法#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数B
指導講師:
ますただ
問題文全文(内容文):
$a_1=1,$ $a_n \neq 0$
$a_n=3(\sqrt{ S_n }-\sqrt{ S_{n-1} }),2 \leq n$
1.$a_2$を求めよ。
2.$\sqrt{ S_n }$を求めよ。
3.$a_n$を求めよ。
出典:1999年 千葉大学
この動画を見る
$a_1=1,$ $a_n \neq 0$
$a_n=3(\sqrt{ S_n }-\sqrt{ S_{n-1} }),2 \leq n$
1.$a_2$を求めよ。
2.$\sqrt{ S_n }$を求めよ。
3.$a_n$を求めよ。
出典:1999年 千葉大学
大学入試問題#921「癖がない綺麗な神問題」

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a \gt 1$
$I(a)=\displaystyle \int_{0}^{ \pi }\displaystyle \frac{a\sin\theta}{(a^2-2a \cos\theta+1)^{\frac{3}{2}}}d\theta$
1.$I(a)$を求めよ。
2.$\displaystyle \sum_{n=2}^{\infty} I(n)$の値を求めよ。
出典:1997年千葉大学
この動画を見る
$a \gt 1$
$I(a)=\displaystyle \int_{0}^{ \pi }\displaystyle \frac{a\sin\theta}{(a^2-2a \cos\theta+1)^{\frac{3}{2}}}d\theta$
1.$I(a)$を求めよ。
2.$\displaystyle \sum_{n=2}^{\infty} I(n)$の値を求めよ。
出典:1997年千葉大学
#千葉大学2016#定積分#元高校教員

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \cos^3x$ $dx$
出典:2016年千葉大学
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{\frac{\pi}{6}}^{\frac{\pi}{3}} \cos^3x$ $dx$
出典:2016年千葉大学
#千葉大学2021#不定積分#元高専教員
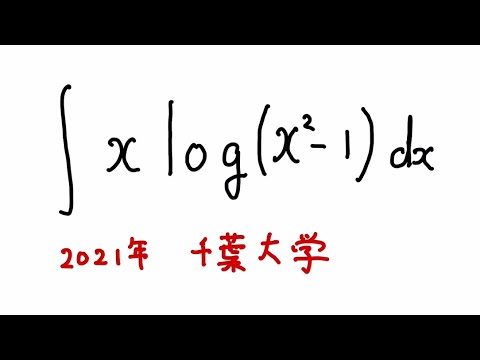
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け。
$\displaystyle \int x log(x^2-1) dx$
出典:2021年千葉大学
この動画を見る
以下の不定積分を解け。
$\displaystyle \int x log(x^2-1) dx$
出典:2021年千葉大学
#千葉大学2018#不定積分#数学者
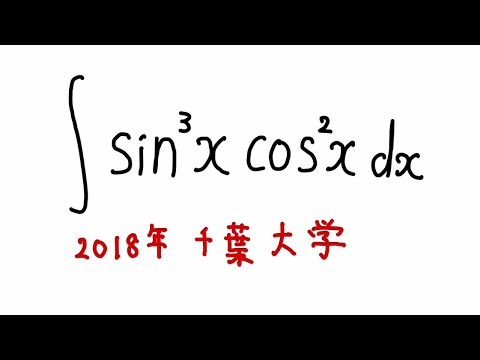
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の不定積分を解け。
$\displaystyle \int \sin^3x \cos^2x$ $dx$
出典:2018年千葉大学
この動画を見る
以下の不定積分を解け。
$\displaystyle \int \sin^3x \cos^2x$ $dx$
出典:2018年千葉大学
#千葉大学2022#極限#ますただ

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } (\sqrt{ n^2+n }-n)$
出典:2022年千葉大学
この動画を見る
$\displaystyle \lim_{ n \to \infty } (\sqrt{ n^2+n }-n)$
出典:2022年千葉大学
大学入試問題#898「教科書例題」 #千葉大学(2024)

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#平均変化率・極限・導関数#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
次の等式を満たす$x \gt 0$で定義された関数$f(x)$と定数$a$の値を求めよ。
ただし、$a \gt 0$とする。
$\displaystyle \int_{a}^{x} f(t) dt=x+\displaystyle \frac{1}{2}log$ $x-1$
出典:2024年千葉大学
この動画を見る
次の等式を満たす$x \gt 0$で定義された関数$f(x)$と定数$a$の値を求めよ。
ただし、$a \gt 0$とする。
$\displaystyle \int_{a}^{x} f(t) dt=x+\displaystyle \frac{1}{2}log$ $x-1$
出典:2024年千葉大学
#千葉大学2020#不定積分#ますただ
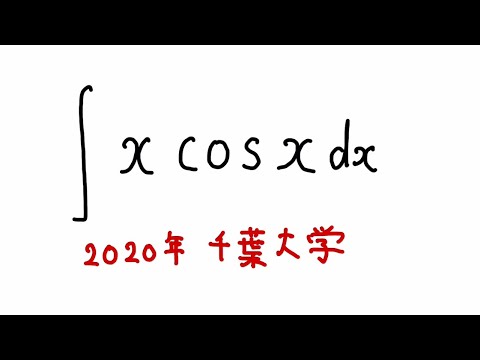
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#不定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int x\cos x$ $dx$
出典:2024年千葉大学
この動画を見る
$\displaystyle \int x\cos x$ $dx$
出典:2024年千葉大学
#千葉大学2024#定積分
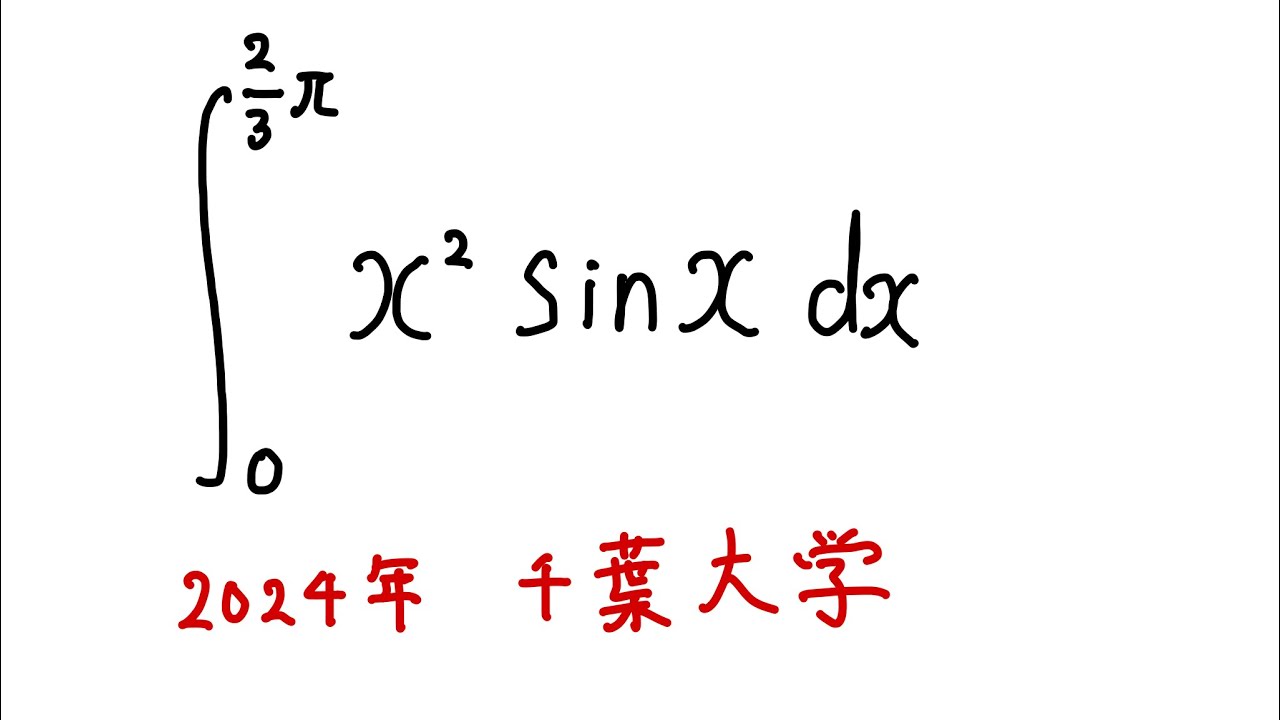
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{2}{3}\pi} x^2\sin x$ $dx$
出典:2024年千葉大学
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{2}{3}\pi} x^2\sin x$ $dx$
出典:2024年千葉大学
#千葉大学2023#定積分#ますただ
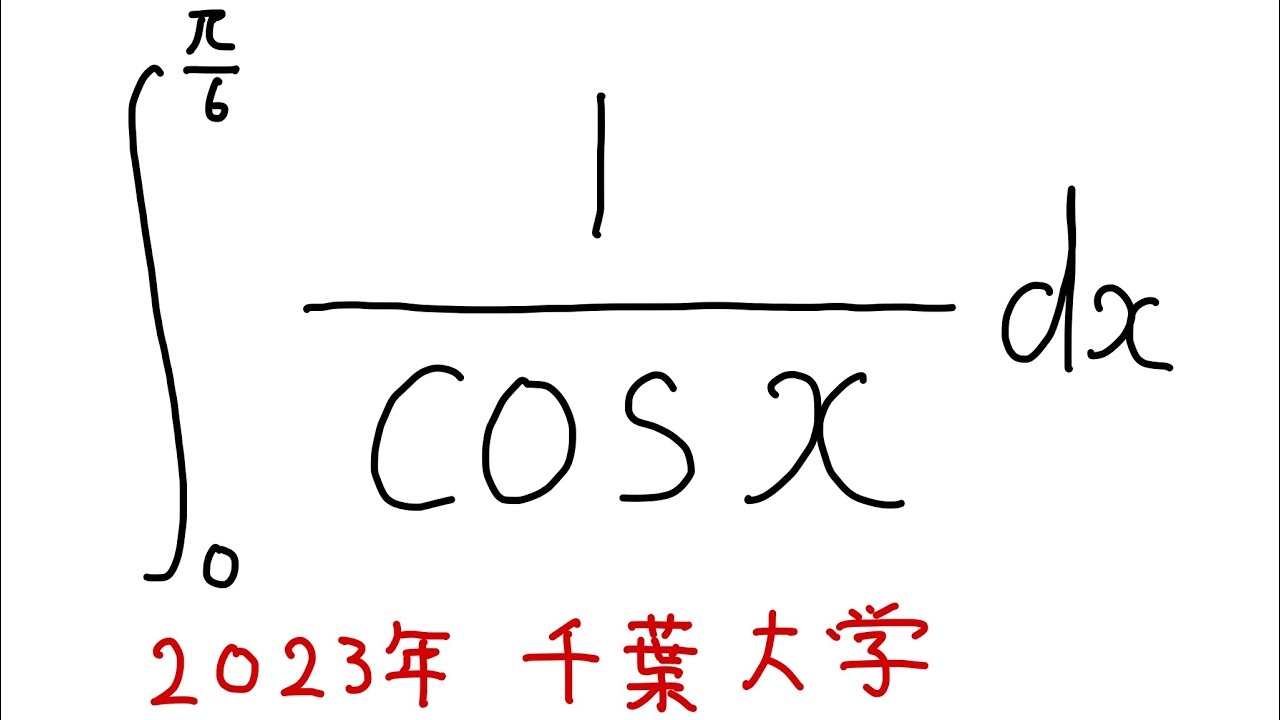
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{1}{\cos x} dx$
出典:2023年千葉大学
この動画を見る
以下の定積分を解け。
$\displaystyle \int_{0}^{\frac{\pi}{6}} \displaystyle \frac{1}{\cos x} dx$
出典:2023年千葉大学
#千葉大学2023#定積分
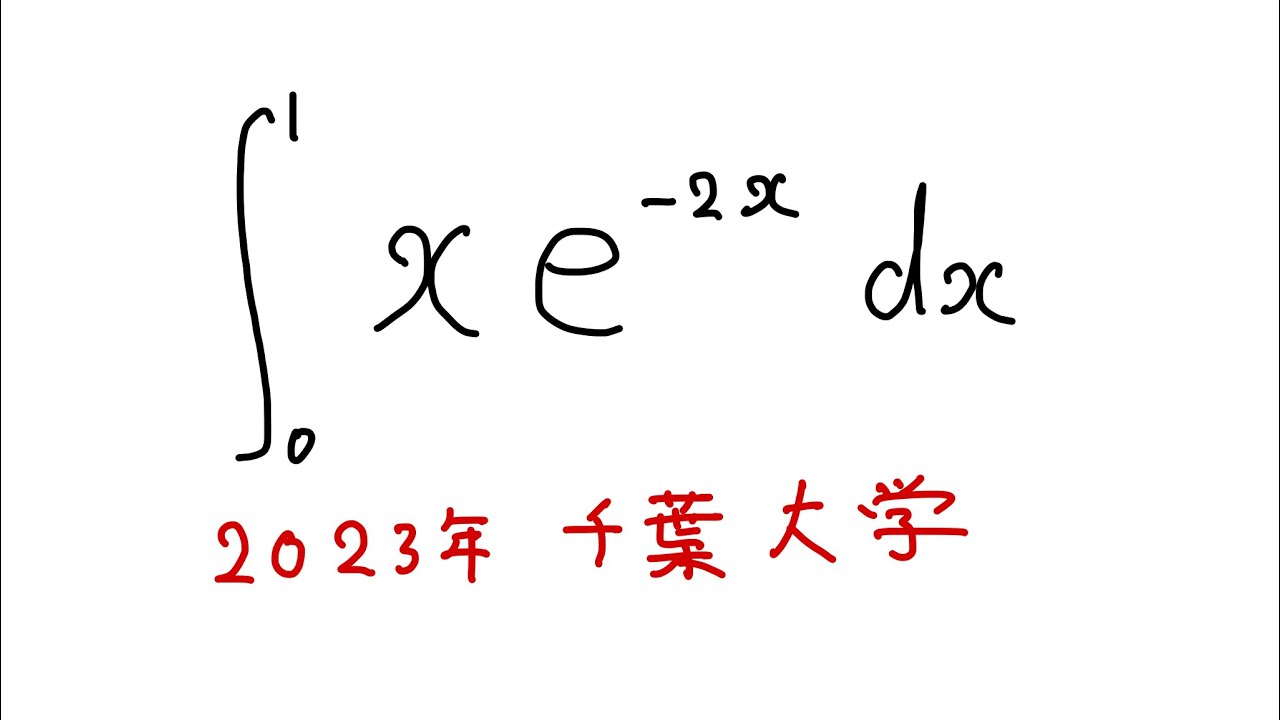
単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
下記の定積分を解け
$\displaystyle \int_{0}^{1} xe^{-2x} dx$
出典:2023年千葉大学
この動画を見る
下記の定積分を解け
$\displaystyle \int_{0}^{1} xe^{-2x} dx$
出典:2023年千葉大学
福田の数学〜千葉大学2024年理系第7問〜3次方程式の解の極限

単元:
#大学入試過去問(数学)#関数と極限#関数の極限#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$n$ を正の整数とする。 $x$ の関数 $f(x) $$= x^3$$-2nx^2$$+(2n-3)x$$+1$ について、以下の問いに答えよ。
$(1)$ $\alpha$ を $f(x)=0$ の$1$ つの解とする。 $\displaystyle f(\frac{1}{1-\alpha})$ の値を求めよ。
$(2)$ 方程式 $f(x) = 0$ は異なる $3$ つの実数解をもつことを示せ。
$(3)$ 方程式 $f(x) = 0$ の解で $2$ 番目に大きいものを $\beta_n$ とする。極限 $\displaystyle \lim_{ n \to \infty } \beta_n$ を求めよ。
この動画を見る
$n$ を正の整数とする。 $x$ の関数 $f(x) $$= x^3$$-2nx^2$$+(2n-3)x$$+1$ について、以下の問いに答えよ。
$(1)$ $\alpha$ を $f(x)=0$ の$1$ つの解とする。 $\displaystyle f(\frac{1}{1-\alpha})$ の値を求めよ。
$(2)$ 方程式 $f(x) = 0$ は異なる $3$ つの実数解をもつことを示せ。
$(3)$ 方程式 $f(x) = 0$ の解で $2$ 番目に大きいものを $\beta_n$ とする。極限 $\displaystyle \lim_{ n \to \infty } \beta_n$ を求めよ。
福田の数学〜千葉大学2024年理系第6問〜最小値と方程式の解と回転体の体積

単元:
#大学入試過去問(数学)#積分とその応用#面積・体積・長さ・速度#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
関数 $f(x)=e^x+e^{-2x}$ について、次の問いに答えよ。
$(1)$ 関数 $f(x)$ の最小値を求めよ。
$(2)$ $f(x)=2$ となる $x$ の値をすべて求めよ。
$(3)$ $(2)$ で求めた $x$ の値のうち最小のものを $a_1$ 、最大のものを $a_2$ とする。 $y=f(x)$ のグラフ、 $x$ 軸、直線 $x=a_1$、直線 $x=a_2$ で囲まれる図形を $x$ 軸の周りに $1$ 回転してできる立体の体積を求めよ。
この動画を見る
関数 $f(x)=e^x+e^{-2x}$ について、次の問いに答えよ。
$(1)$ 関数 $f(x)$ の最小値を求めよ。
$(2)$ $f(x)=2$ となる $x$ の値をすべて求めよ。
$(3)$ $(2)$ で求めた $x$ の値のうち最小のものを $a_1$ 、最大のものを $a_2$ とする。 $y=f(x)$ のグラフ、 $x$ 軸、直線 $x=a_1$、直線 $x=a_2$ で囲まれる図形を $x$ 軸の周りに $1$ 回転してできる立体の体積を求めよ。
福田の数学〜千葉大学2024年理系第5問〜確率と極限

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$n$ を $3$ 以上の整数とする。座標平面上の $2n$ 個の点からなる集合
$\{ (x,y) | x=1,2,3, \cdots , n , y=1,2 \}$
を考える。この集合から異なる $3$ 点を無作為に選び、その $3$ 点を線分で結んで得られる図形の面積を $X$ とする。ただし、 $3$ 点が同一直線上にあるときは $X=0$ とする。
$(1)$ $k$ が $0$ 以上の整数のとき、 $X$ が $\displaystyle \frac{k}{2}$ となる確率 $p_k$ を $n$ と $k$ の式で表せ。
$(2)$ $X$ が $\displaystyle \frac{n}{4}$ 以下となる確率を $q_n$ とおく。 $\displaystyle \lim_{n \to \infty} q_n$ を求めよ。
この動画を見る
$n$ を $3$ 以上の整数とする。座標平面上の $2n$ 個の点からなる集合
$\{ (x,y) | x=1,2,3, \cdots , n , y=1,2 \}$
を考える。この集合から異なる $3$ 点を無作為に選び、その $3$ 点を線分で結んで得られる図形の面積を $X$ とする。ただし、 $3$ 点が同一直線上にあるときは $X=0$ とする。
$(1)$ $k$ が $0$ 以上の整数のとき、 $X$ が $\displaystyle \frac{k}{2}$ となる確率 $p_k$ を $n$ と $k$ の式で表せ。
$(2)$ $X$ が $\displaystyle \frac{n}{4}$ 以下となる確率を $q_n$ とおく。 $\displaystyle \lim_{n \to \infty} q_n$ を求めよ。
福田の数学〜千葉大学2024年理系第4問(3)〜コンビネーションに関する不等式の評価

単元:
#数A#大学入試過去問(数学)#場合の数#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
正の整数$n,p,q$が$p > q$かつ$_p\mathrm{C}_2+_q\mathrm{C}_2=n$を満たすとする。$_m\mathrm{C}_2 \leqq n$となる最大の整数$m$を求めよ。
この動画を見る
正の整数$n,p,q$が$p > q$かつ$_p\mathrm{C}_2+_q\mathrm{C}_2=n$を満たすとする。$_m\mathrm{C}_2 \leqq n$となる最大の整数$m$を求めよ。
福田の数学〜千葉大学2024年理系第4問(2)〜複素数平面乗の正三角形の頂点を求める

単元:
#大学入試過去問(数学)#複素数平面#図形への応用#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数C
指導講師:
福田次郎
問題文全文(内容文):
複素数平面上の3点$\mathrm{P}(z), \mathrm{Q}(-1),\mathrm{R}(\sqrt3-1-i)$が正三角形をなすとき、複素数$z$を求めよ。
この動画を見る
複素数平面上の3点$\mathrm{P}(z), \mathrm{Q}(-1),\mathrm{R}(\sqrt3-1-i)$が正三角形をなすとき、複素数$z$を求めよ。
福田の数学〜千葉大学2024年理系第4問(1)〜部分積分

単元:
#大学入試過去問(数学)#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
定積分$\displaystyle \int_0^{\frac{2\pi}{3}}x^2\sin xdx$を求めよ
この動画を見る
定積分$\displaystyle \int_0^{\frac{2\pi}{3}}x^2\sin xdx$を求めよ
福田の数学〜千葉大学2024年文系第3問〜絶対値の付いた放物線と直線の位置関係

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a$を実数とする。$f(x)=x^2-ax+a^2-2$について、以下の問いに答えよ。
(1) $y=f(x)$のグラフと$x$軸が$x > 0$の範囲に共有点を2個もつような、$a$の値の範囲を求めよ。
(2) $k$を正の定数とし、$g(x)=kx$とする。$a$が(1)の範囲にあるとき、$y=|f(x)|$のグラフと$y=g(x)$のグラフの共有点がちょうど3個となるような$k$を求めよ。
この動画を見る
$a$を実数とする。$f(x)=x^2-ax+a^2-2$について、以下の問いに答えよ。
(1) $y=f(x)$のグラフと$x$軸が$x > 0$の範囲に共有点を2個もつような、$a$の値の範囲を求めよ。
(2) $k$を正の定数とし、$g(x)=kx$とする。$a$が(1)の範囲にあるとき、$y=|f(x)|$のグラフと$y=g(x)$のグラフの共有点がちょうど3個となるような$k$を求めよ。
福田の数学〜千葉大学2024年文系第2問〜袋から元に戻さないで球を取り出し得点を考える確率

単元:
#数A#大学入試過去問(数学)#場合の数と確率#確率#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
白球が3個、黒球が5個、赤球が2個入った袋がある。以下のゲームを続けて$n$回続けて行う。
袋から球を1個取り出す。白球だった場合は1点を獲得する。黒球だった場合はさいころを投げて、出た目が3の倍数だった場合には1点、そうでない場合には0点を獲得する。赤球だった場合はコインを投げて、表が出た場合は2点、裏が出た場合は0点を獲得する。取り出した球は袋に戻さない。
(1) $n=2$のとき、総得点がちょうど3点となる確率を求めよ。
(2) $n=3$のとき、総得点がちょうど5点となる確率を求めよ。
(3) $n=3$のとき、総得点が4点以上となる確率を求めよ。
この動画を見る
白球が3個、黒球が5個、赤球が2個入った袋がある。以下のゲームを続けて$n$回続けて行う。
袋から球を1個取り出す。白球だった場合は1点を獲得する。黒球だった場合はさいころを投げて、出た目が3の倍数だった場合には1点、そうでない場合には0点を獲得する。赤球だった場合はコインを投げて、表が出た場合は2点、裏が出た場合は0点を獲得する。取り出した球は袋に戻さない。
(1) $n=2$のとき、総得点がちょうど3点となる確率を求めよ。
(2) $n=3$のとき、総得点がちょうど5点となる確率を求めよ。
(3) $n=3$のとき、総得点が4点以上となる確率を求めよ。
福田の数学〜千葉大学2024年文系第1問〜三角形の成立条件と対数

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#三角形の辺の比(内分・外分・二等分線)#指数関数と対数関数#対数関数#千葉大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
(1) 3辺の長さが$2,5,a$である三角形が存在するような、$a$の値の範囲を求めよ。
(2) 3辺の長さが$\log_{10}(5x),\log_{10}(x+10),\log_{10}3$である三角形が存在するような、$x$の値の範囲を求めよ。
(3) ある二等辺三角形の3辺の長さが$\log_{10}(5x),\log_{10}(x+10),\log_{10}3$であるとき、$x$の値を求めよ。
この動画を見る
(1) 3辺の長さが$2,5,a$である三角形が存在するような、$a$の値の範囲を求めよ。
(2) 3辺の長さが$\log_{10}(5x),\log_{10}(x+10),\log_{10}3$である三角形が存在するような、$x$の値の範囲を求めよ。
(3) ある二等辺三角形の3辺の長さが$\log_{10}(5x),\log_{10}(x+10),\log_{10}3$であるとき、$x$の値を求めよ。
【高校数学】千葉大学の積分の問題をその場で解説しながら解いてみた!毎日積分94日目~47都道府県制覇への道~【㊲千葉】【毎日17時投稿】

単元:
#大学入試過去問(数学)#積分とその応用#定積分#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)#数Ⅲ
指導講師:
理数個別チャンネル
問題文全文(内容文):
【千葉大学 2023】
等式$\displaystyle f(x)=x^2+\int_{-1}^{2}(xf(t)-t)dt$を満たす関数$f(x)$を求めよ。
この動画を見る
【千葉大学 2023】
等式$\displaystyle f(x)=x^2+\int_{-1}^{2}(xf(t)-t)dt$を満たす関数$f(x)$を求めよ。
大学入試問題#770「減点注意!」 千葉大学(2003) #微積の応用

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#千葉大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$a$は定数とし、$n$は2以上の整数とする。
関数$f(x)=ax^n log\ x-ax(x \gt 0)$の最小値が-1のとき、定積分$\displaystyle \int_{1}^{e} f(x)\ dx$の値を$n$と$e$を用いて表せ。
出典:2003年千葉大学 入試問題
この動画を見る
$a$は定数とし、$n$は2以上の整数とする。
関数$f(x)=ax^n log\ x-ax(x \gt 0)$の最小値が-1のとき、定積分$\displaystyle \int_{1}^{e} f(x)\ dx$の値を$n$と$e$を用いて表せ。
出典:2003年千葉大学 入試問題
大学入試問題#768 「ゴリゴリ音がでそう」 千葉大学(2005) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\pi} |3\ \cos\ 2x+7\cos\ x|\ dx$
出典:2005年千葉大学 入試問題
この動画を見る
$\displaystyle \int_{0}^{\pi} |3\ \cos\ 2x+7\cos\ x|\ dx$
出典:2005年千葉大学 入試問題
大学入試問題#765「まったり解いて大丈夫」 千葉大学(2003) 数列

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
数列$\{a_n\}$を次のように定める。$(n=2,3,・・・)$
$a_1=2$
$a_n=\displaystyle \frac{1}{n}+(1-\displaystyle \frac{1}{n})a_{n-1}$
(1)一般項$a_n$を求めよ
(2)$\displaystyle \sum_{k=1}^n k^2a_k$を求めよ
出典:2003年千葉大学 入試問題
この動画を見る
数列$\{a_n\}$を次のように定める。$(n=2,3,・・・)$
$a_1=2$
$a_n=\displaystyle \frac{1}{n}+(1-\displaystyle \frac{1}{n})a_{n-1}$
(1)一般項$a_n$を求めよ
(2)$\displaystyle \sum_{k=1}^n k^2a_k$を求めよ
出典:2003年千葉大学 入試問題
大学入試問題#724「教科書の例題」 千葉大学(2023) 積分方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$f(x)=x^2+\displaystyle \int_{-1}^{2} (xf(t)-t)dt$を満たす関数$f(x)$を求めよ
出典:2023年千葉大学 入試問題
この動画を見る
$f(x)=x^2+\displaystyle \int_{-1}^{2} (xf(t)-t)dt$を満たす関数$f(x)$を求めよ
出典:2023年千葉大学 入試問題
大学入試問題#722「これはミスれん!」 千葉大学(2023)定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{a}^{b} (x-a)^3(x-b) dx$
ただし、$a,b$は定数とする
出典:2023年千葉大学
この動画を見る
$\displaystyle \int_{a}^{b} (x-a)^3(x-b) dx$
ただし、$a,b$は定数とする
出典:2023年千葉大学
大学入試問題#706 千葉大学(2014) 定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} e^{\sin\ x}(\sin2x-2\cos\ x)dx$
出典:2014年千葉大学 入試問題
この動画を見る
$\displaystyle \int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} e^{\sin\ x}(\sin2x-2\cos\ x)dx$
出典:2014年千葉大学 入試問題
大学入試問題#655「解き方いろいろ」 千葉大学後期(2018) 整数問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#千葉大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \frac{8a+8}{a^2+4a+12}$が整数となるような整数$a$をすべて求めよ
出典:2018年千葉大学 入試問題
この動画を見る
$\displaystyle \frac{8a+8}{a^2+4a+12}$が整数となるような整数$a$をすべて求めよ
出典:2018年千葉大学 入試問題
千葉大 複素数の方程式

単元:
#数Ⅱ#複素数と方程式#複素数#解と判別式・解と係数の関係#千葉大学#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
2023千葉大学過去問題
①$z^3=i$を解け
②$z^{100}=i$の解で 実部$\leqq \frac{1}{2}$
かつ虚部$\geqq 0$は何個あるか?
この動画を見る
2023千葉大学過去問題
①$z^3=i$を解け
②$z^{100}=i$の解で 実部$\leqq \frac{1}{2}$
かつ虚部$\geqq 0$は何個あるか?
