 早稲田大学
早稲田大学
 早稲田大学
早稲田大学
大学入試問題#745「落ち着けばどうにかなる」 早稲田大学理工学部(2002) 微積の応用

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$0 \lt \theta \lt \displaystyle \frac{\pi}{2}$とする。
$I(\theta)=\displaystyle \int_{0}^{\frac{\pi}{2}} |\sin\ x-\tan\theta\cos\ x|\sin2x\ dx$
(1)$I(\theta)$を求めよ。
(2)$I(\theta)$を最小にする$\theta$に対し、$\cos\theta$の値を求めよ。
出典:2002年早稲田大学理工学部 入試問題
この動画を見る
$0 \lt \theta \lt \displaystyle \frac{\pi}{2}$とする。
$I(\theta)=\displaystyle \int_{0}^{\frac{\pi}{2}} |\sin\ x-\tan\theta\cos\ x|\sin2x\ dx$
(1)$I(\theta)$を求めよ。
(2)$I(\theta)$を最小にする$\theta$に対し、$\cos\theta$の値を求めよ。
出典:2002年早稲田大学理工学部 入試問題
大学入試問題#744「ひっかける場所はどこだ?」 早稲田大学政治経済学部(2005) #整数問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \frac{1}{x}+\displaystyle \frac{1}{2y}+\displaystyle \frac{1}{3z}=\displaystyle \frac{4}{3}$を満たす正の整数の組$(x,y,z)$をすべて求めよ。
出典:2005年早稲田大学政治経済学部 入試問題
この動画を見る
$\displaystyle \frac{1}{x}+\displaystyle \frac{1}{2y}+\displaystyle \frac{1}{3z}=\displaystyle \frac{4}{3}$を満たす正の整数の組$(x,y,z)$をすべて求めよ。
出典:2005年早稲田大学政治経済学部 入試問題
大学入試問題#743「単なる場合分け?」 早稲田大学政治経済学部(2003) #対数

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$a \gt 0,a \neq 1$とする。
このとき、$x$の不等式$log_a(x+2) \geq log_{a^2}(3x+16)$を解け
出典:2003年早稲田大学政治経済学部 入試問題
この動画を見る
$a \gt 0,a \neq 1$とする。
このとき、$x$の不等式$log_a(x+2) \geq log_{a^2}(3x+16)$を解け
出典:2003年早稲田大学政治経済学部 入試問題
大学入試問題#742「落としたくないかな~~」 早稲田大学理工学部(2001) #極限

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ M \to \infty } \displaystyle \int_{0}^{M} e^{-2x}\sin^2\ x\ dx$
出典:2001年早稲田大学理工学部 入試問題
この動画を見る
$\displaystyle \lim_{ M \to \infty } \displaystyle \int_{0}^{M} e^{-2x}\sin^2\ x\ dx$
出典:2001年早稲田大学理工学部 入試問題
大学入試問題#739「このタイプ、定期的に難関大学で出題されてる」 早稲田大学国際教養学部(2005)三角関数

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\sin\ x+\sin\ y=\displaystyle \frac{2}{3},\ \cos\ x\ \cos\ y=\displaystyle \frac{1}{2}$のとき、
$\sin\ x\sin\ y,\ \sin\displaystyle \frac{x+y}{2}$の値を求めよ。
出典:2005年早稲田大学国際教養学部 入試問題
この動画を見る
$\sin\ x+\sin\ y=\displaystyle \frac{2}{3},\ \cos\ x\ \cos\ y=\displaystyle \frac{1}{2}$のとき、
$\sin\ x\sin\ y,\ \sin\displaystyle \frac{x+y}{2}$の値を求めよ。
出典:2005年早稲田大学国際教養学部 入試問題
大学入試問題#737「もはや三角関数の問題」 早稲田大学人間科学部(2001)定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{\sin\ 15^{ \circ }}^{\cos\ 15^{ \circ }} (3x^2-1) dx$
出典:2001年早稲田大学人間科学部 入試問題
この動画を見る
$\displaystyle \int_{\sin\ 15^{ \circ }}^{\cos\ 15^{ \circ }} (3x^2-1) dx$
出典:2001年早稲田大学人間科学部 入試問題
大学入試問題#730「総和と間違えそう」 早稲田大学商学部(2011) 個数の処理

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$n$を正の整数とする。
$10^n$の正の約数すべての積の値を求めよ。
出典:2011年早稲田大学商学部 入試問題
この動画を見る
$n$を正の整数とする。
$10^n$の正の約数すべての積の値を求めよ。
出典:2011年早稲田大学商学部 入試問題
大学入試問題#728「たぶん良問」 早稲田大学商学部(2014) 積分方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
任意の実数$x$に対して、
$\displaystyle \int_{0}^{x} f(t) dt-3\displaystyle \int_{-x}^{0} f(t) dt=x^3$を満たす関数$f(x)$を求めよ
出典:2014年早稲田大学商学部 入試問題
この動画を見る
任意の実数$x$に対して、
$\displaystyle \int_{0}^{x} f(t) dt-3\displaystyle \int_{-x}^{0} f(t) dt=x^3$を満たす関数$f(x)$を求めよ
出典:2014年早稲田大学商学部 入試問題
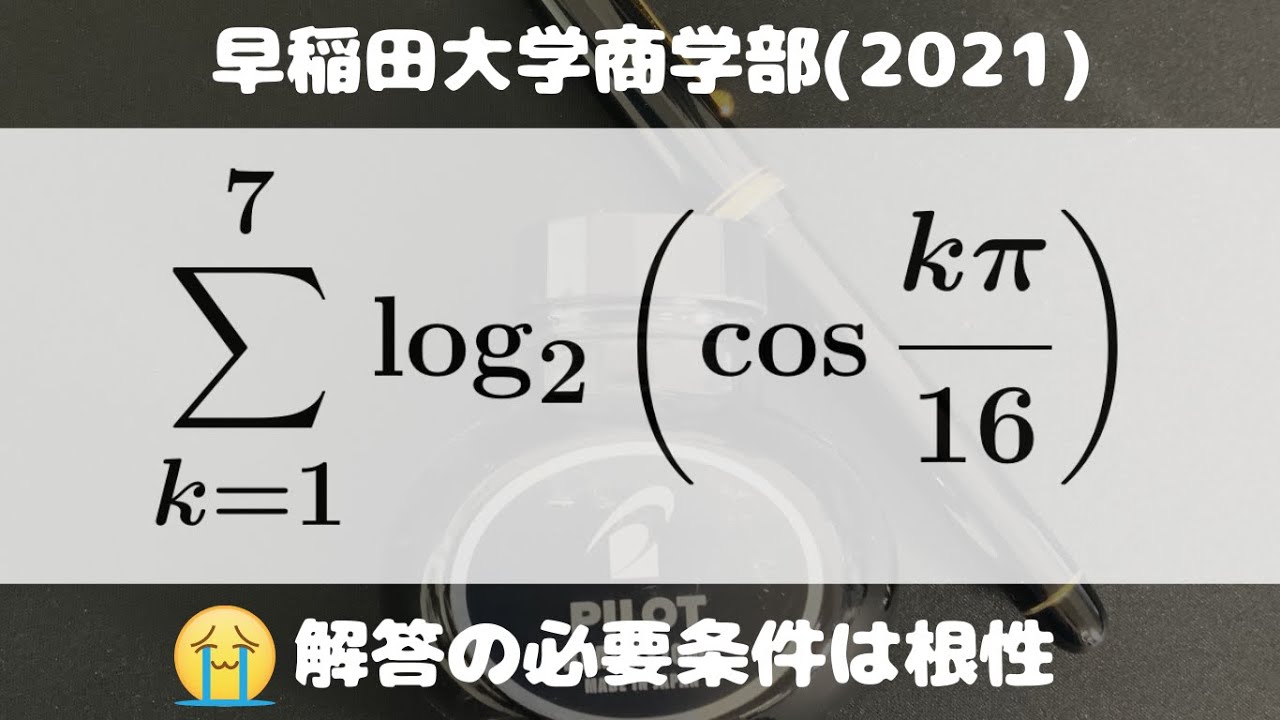
大学入試問題#725「計算ミスだけ注意」 早稲田商学部(2015) 対数と三角関数
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \sum_{k=1}^7 log_2(\cos\displaystyle \frac{k\pi}{16})$
出典:2021年早稲田大学商学部 入試問題
この動画を見る
$\displaystyle \sum_{k=1}^7 log_2(\cos\displaystyle \frac{k\pi}{16})$
出典:2021年早稲田大学商学部 入試問題
大学入試問題#721「落ち着いて計算」 早稲田商学部(2012) 積分方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
定数関数でない関数$f(x)$が
$f(x)=x^2-\displaystyle \int_{0}^{1}(f(t)+x)^2 dt$を満たすとき$f(x)$を求めよ。
出典:2012年早稲田大学商学部 入試問題
この動画を見る
定数関数でない関数$f(x)$が
$f(x)=x^2-\displaystyle \int_{0}^{1}(f(t)+x)^2 dt$を満たすとき$f(x)$を求めよ。
出典:2012年早稲田大学商学部 入試問題
大学入試問題#719「これは落としたくない」 早稲田大学商学部(2005) 3次方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
3次方程式
$x^3-px^2+11x-q=0$が3つの連続する正の整数を解とするとき、$p,q$の値を求めよ。
出典:2005年早稲田大学商学部 入試問題
この動画を見る
3次方程式
$x^3-px^2+11x-q=0$が3つの連続する正の整数を解とするとき、$p,q$の値を求めよ。
出典:2005年早稲田大学商学部 入試問題
大学入試問題#718「理系の偏差値63ではきつい」 早稲田商学部(2011) 微積の応用

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\displaystyle \int_{0}^{1} |t^2-x^2|dt$の最小値を求めよ。
出典:2011年早稲田大学商学部 入試問題
この動画を見る
$f(x)=\displaystyle \int_{0}^{1} |t^2-x^2|dt$の最小値を求めよ。
出典:2011年早稲田大学商学部 入試問題
大学入試問題#717「これはよく考えられた問題だな~~」 早稲田商学部(2012) 対数

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$log_3\ x-\displaystyle \frac{1}{log_9\ x}=(-1)^x$を満たす正の整数$x$の値を求めよ。
出典:2012年早稲田大学商学部 入試問題
この動画を見る
$log_3\ x-\displaystyle \frac{1}{log_9\ x}=(-1)^x$を満たす正の整数$x$の値を求めよ。
出典:2012年早稲田大学商学部 入試問題
大学入試問題#716「文系にはきつくね?」 早稲田商学部(2015) 数列

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
数列$\{a_n\}$は次の条件$(i),(ii)$を満たす
($i$)$a_1=0,\ a_n \leq 0(n=2,3,4・・・)$
($ii$)$n=\displaystyle \int_{a_n}^{a_{n+1}} (x+\displaystyle \frac{1}{2})dx(n=1,2,3,・・・)$
$n=2,3,4,・・・$のとき、$a_n$を求めよ
出典:2015年早稲田大学商学部 入試問題
この動画を見る
数列$\{a_n\}$は次の条件$(i),(ii)$を満たす
($i$)$a_1=0,\ a_n \leq 0(n=2,3,4・・・)$
($ii$)$n=\displaystyle \int_{a_n}^{a_{n+1}} (x+\displaystyle \frac{1}{2})dx(n=1,2,3,・・・)$
$n=2,3,4,・・・$のとき、$a_n$を求めよ
出典:2015年早稲田大学商学部 入試問題
大学入試問題#715「このタイプ苦手」 早稲田理工系学部(2021) 整式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$f(x)=x^4-x^2+1$
1.$x^6$を$f(x)$で割ったときの余りを求めよ
2.$x^{2021}$を$f(x)$で割ったときの余りを求めよ
3.自然数$n$が3の倍数の時、$(x^2-1)^n-1$が$f(x)$で割り切れることを示せ
出典:2021年早稲田大学理工学部 入試問題
この動画を見る
$f(x)=x^4-x^2+1$
1.$x^6$を$f(x)$で割ったときの余りを求めよ
2.$x^{2021}$を$f(x)$で割ったときの余りを求めよ
3.自然数$n$が3の倍数の時、$(x^2-1)^n-1$が$f(x)$で割り切れることを示せ
出典:2021年早稲田大学理工学部 入試問題
大学入試問題#713「さすがに合同式を利用」 早稲田商学部(2016) 合同式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$2^{100}$を$2016$で割ったときの余りを求めよ。
出典:2016年早稲田大学商学部 入試問題
この動画を見る
$2^{100}$を$2016$で割ったときの余りを求めよ。
出典:2016年早稲田大学商学部 入試問題
早稲田人間科学部2012定積分
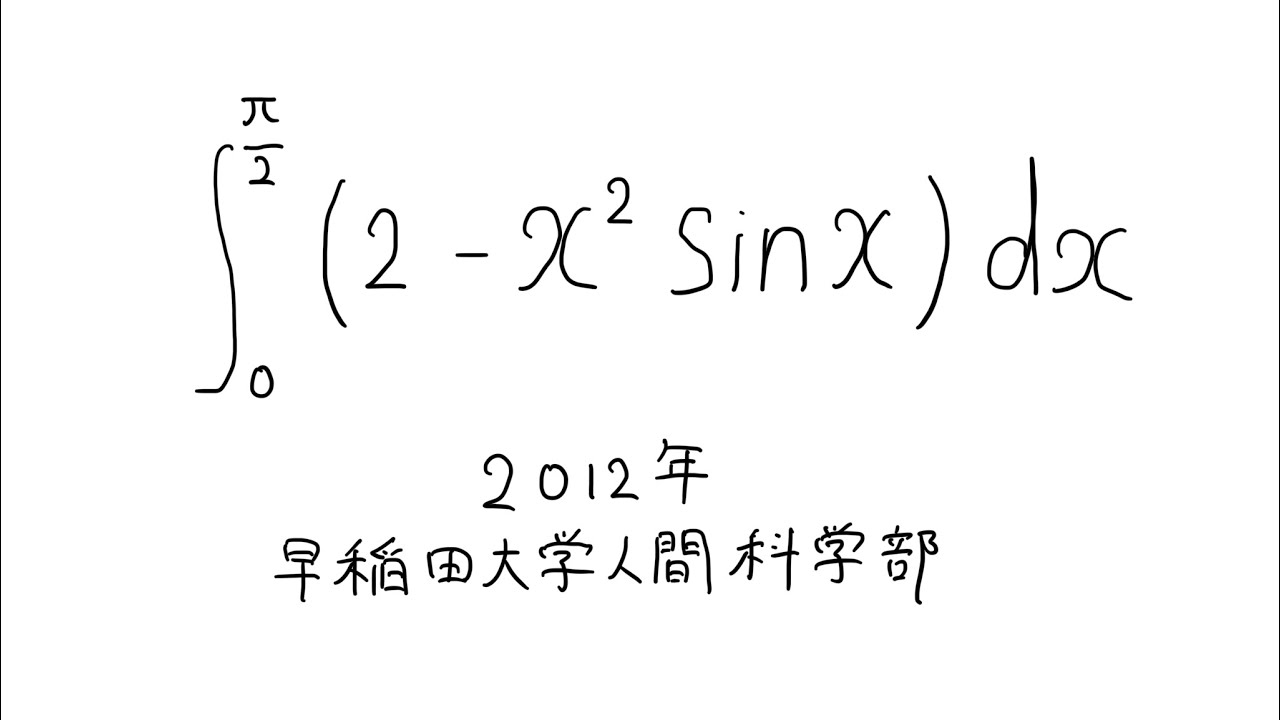
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{\frac{\pi}{2}} (2-x^2\sin\ x) dx$
出典:2012年早稲田大学人間科学部
この動画を見る
$\displaystyle \int_{0}^{\frac{\pi}{2}} (2-x^2\sin\ x) dx$
出典:2012年早稲田大学人間科学部
大学入試問題#700「章末問題」 早稲田大学社会学部(2022)整式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
整式$P(x)$を
$x-1$で割ると1余り、
$(x+1)^2$で割ると$3x+2$余る。
このとき、$P(x)$を$(x-1)(x+1)^2$で割ったときの余りを求めよ
出典:2022年早稲田大学社会学部 入試問題
この動画を見る
整式$P(x)$を
$x-1$で割ると1余り、
$(x+1)^2$で割ると$3x+2$余る。
このとき、$P(x)$を$(x-1)(x+1)^2$で割ったときの余りを求めよ
出典:2022年早稲田大学社会学部 入試問題
大学入試問題#699「まあまあ基本」 早稲田大学社会学部(2023) 整数問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$xyz=x+y+z$を満たす整数$x,y,z$の組をすべて求めよ。
$(0 \lt x \leq y \leq z)$
出典:2023年早稲田大学社会学部 入試問題
この動画を見る
$xyz=x+y+z$を満たす整数$x,y,z$の組をすべて求めよ。
$(0 \lt x \leq y \leq z)$
出典:2023年早稲田大学社会学部 入試問題
大学入試問題#697「正面突破はしないよね」 早稲田人間科学部(2022)方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
方程式
$x(x-1)(x-2)(x-3)+1=0$の解を求めよ
出典:2014年早稲田大学人間科学部 入試問題
この動画を見る
方程式
$x(x-1)(x-2)(x-3)+1=0$の解を求めよ
出典:2014年早稲田大学人間科学部 入試問題
大学入試問題#695「良き整数問題」 早稲田商学部(1999) #整数問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$a,b,c$は整数の定数である。
すべての実数$x$について
$(x-a)(x-99)+2=(x-b)(x-c)$
が成り立つとき、$a,b,c$の値の組をすべて求めよ。
出典:1999年早稲田大学商学部 入試問題
この動画を見る
$a,b,c$は整数の定数である。
すべての実数$x$について
$(x-a)(x-99)+2=(x-b)(x-c)$
が成り立つとき、$a,b,c$の値の組をすべて求めよ。
出典:1999年早稲田大学商学部 入試問題
大学入試問題#685「一言・・・むずい」 早稲田商学部(2018) #整数問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
次の条件を満たす正の整数の組$(a,b,n)$をすべて求めよ。
$n \geq 2$で、$b$は素数
$a^2=b^n+225$
出典:2018年早稲田大学商学部 入試問題
この動画を見る
次の条件を満たす正の整数の組$(a,b,n)$をすべて求めよ。
$n \geq 2$で、$b$は素数
$a^2=b^n+225$
出典:2018年早稲田大学商学部 入試問題
大学入試問題#684「沼にはまると抜けれない」 早稲田商学部(1999) #三角関数

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$\sin\ x+\sin\ y=1$
$\cos\ x+\cos\ y=\displaystyle \frac{1}{3}$
のとき、$\tan\displaystyle \frac{x+y}{2}$の値を求めよ
出典:1999年早稲田大学商学部 入試問題
この動画を見る
$\sin\ x+\sin\ y=1$
$\cos\ x+\cos\ y=\displaystyle \frac{1}{3}$
のとき、$\tan\displaystyle \frac{x+y}{2}$の値を求めよ
出典:1999年早稲田大学商学部 入試問題
大学入試問題#683「早稲田大学人間科学部(2014)と同型」 昭和大学医学部(2023)

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
実数$a,b,c$が
$a+b+c=8$
$a^2+b^2+c^2=32$
を満たすとき、$c$の値が取りうる範囲を求めよ。
出典:2023年昭和大学医学部 入試問題
この動画を見る
実数$a,b,c$が
$a+b+c=8$
$a^2+b^2+c^2=32$
を満たすとき、$c$の値が取りうる範囲を求めよ。
出典:2023年昭和大学医学部 入試問題
大学入試問題#672「最近、このタイプが流行り?」 早稲田大学商学部(2022)

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
実数$x,y$が$x^2+y^2 \leqq 3$を満たしているとき$x-y-xy$の最大値を求めよ
出典:2022年早稲田大学商学部 入試問題
この動画を見る
実数$x,y$が$x^2+y^2 \leqq 3$を満たしているとき$x-y-xy$の最大値を求めよ
出典:2022年早稲田大学商学部 入試問題
ガウス記号!これは取りたい!【早稲田大学】【数学 入試問題】

単元:
#数Ⅰ#大学入試過去問(数学)#2次関数#2次関数とグラフ#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
次の等式を満たす最大の整数aは、a=?である。
[$\displaystyle \frac{a}{2}$]+[$\displaystyle \frac{2a}{3}$]=a
但し、実数xに対して、$\lbrack x \rbrack$は、x以下の最大の整数を表す。
早稲田大過去問
この動画を見る
次の等式を満たす最大の整数aは、a=?である。
[$\displaystyle \frac{a}{2}$]+[$\displaystyle \frac{2a}{3}$]=a
但し、実数xに対して、$\lbrack x \rbrack$は、x以下の最大の整数を表す。
早稲田大過去問
福田の数学〜3乗根のおおよその値を知る方法〜早稲田大学2023年社会科学部第3問〜3乗根と2重根号を簡単にする

単元:
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#指数関数と対数関数#恒等式・等式・不等式の証明#指数関数#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$a=\sqrt[3]{5\sqrt{2}+7}-\sqrt[3]{5\sqrt{2}-7}$とする。
(1)$a^3$を$a$の1次式で表せ。
(2)$a$は整数であることを示せ。
(3)$b=a=\sqrt[3]{5\sqrt{2}+7}+\sqrt[3]{5\sqrt{2}-7}$
を超えない最大の整数を求めよ。
2023早稲田大学社会科学部過去問
この動画を見る
$a=\sqrt[3]{5\sqrt{2}+7}-\sqrt[3]{5\sqrt{2}-7}$とする。
(1)$a^3$を$a$の1次式で表せ。
(2)$a$は整数であることを示せ。
(3)$b=a=\sqrt[3]{5\sqrt{2}+7}+\sqrt[3]{5\sqrt{2}-7}$
を超えない最大の整数を求めよ。
2023早稲田大学社会科学部過去問
福田の数学〜多変数の方程式はこう扱え〜早稲田大学2023年社会科学部第2問〜3変数の不定方程式の整数解

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{2}}$ 定数$m$に対して$x$,$y$,$z$の方程式
$xyz$+$x$+$y$+$z$=$xy$+$yz$+$zx$+$m$ ...①
を考える。次の問いに答えよ。
(1)$m$=1のとき①式を満たす実数$x$,$y$,$z$の組を全て求めよ。
(2)$m$=5のとき①式を満たす整数$x$,$y$,$z$の組を全て求めよ。ただし、
$x$≦$y$≦$z$ とする。
(3)$xyz$=$x$+$y$+$z$ を満たす整数$x$,$y$,$z$の組を全て求めよ。ただし、
0<$x$≦$y$≦$z$ とする。
この動画を見る
$\Large{\boxed{2}}$ 定数$m$に対して$x$,$y$,$z$の方程式
$xyz$+$x$+$y$+$z$=$xy$+$yz$+$zx$+$m$ ...①
を考える。次の問いに答えよ。
(1)$m$=1のとき①式を満たす実数$x$,$y$,$z$の組を全て求めよ。
(2)$m$=5のとき①式を満たす整数$x$,$y$,$z$の組を全て求めよ。ただし、
$x$≦$y$≦$z$ とする。
(3)$xyz$=$x$+$y$+$z$ を満たす整数$x$,$y$,$z$の組を全て求めよ。ただし、
0<$x$≦$y$≦$z$ とする。
福田の数学〜接線と放物線で囲まれた面積3連発だ〜早稲田大学2023年社会科学部第1問〜接線と放物線で囲まれた面積

単元:
#大学入試過去問(数学)#微分とその応用#接線と法線・平均値の定理#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ 曲線$y$=$ax^2$+$b$上に$x$座標が$p$である点Pをとり、点Pにおける接線を$l$とする。ただし、定数$a$,$b$は$a$>0, $b$>0とする。次の問いに答えよ。
(1)接線$l$の方程式を$a$,$b$,$p$を用いて表せ。
(2)接線$l$と曲線$y$=$ax^2$で囲まれた図形の面積Sを$a$,$b$を用いて表せ。
(3)接線$l$と曲線$y$=$ax^2$+$\frac{b}{2}$で囲まれた図形の面積をS'としたとき、S'をSを用いて表せ。
(4)接線$l$と曲線$y$=$ax^2$+$c$で囲まれた図形の面積をS''とする。S"=$\frac{S}{2}$のとき、$c$を$a$,$b$を用いて表せ。ただし、$b$>$c$とする。
この動画を見る
$\Large{\boxed{1}}$ 曲線$y$=$ax^2$+$b$上に$x$座標が$p$である点Pをとり、点Pにおける接線を$l$とする。ただし、定数$a$,$b$は$a$>0, $b$>0とする。次の問いに答えよ。
(1)接線$l$の方程式を$a$,$b$,$p$を用いて表せ。
(2)接線$l$と曲線$y$=$ax^2$で囲まれた図形の面積Sを$a$,$b$を用いて表せ。
(3)接線$l$と曲線$y$=$ax^2$+$\frac{b}{2}$で囲まれた図形の面積をS'としたとき、S'をSを用いて表せ。
(4)接線$l$と曲線$y$=$ax^2$+$c$で囲まれた図形の面積をS''とする。S"=$\frac{S}{2}$のとき、$c$を$a$,$b$を用いて表せ。ただし、$b$>$c$とする。
福田の数学〜剰余類と合同式を練習だ〜早稲田大学2023年商学部第3問〜7で割り切れる条件と91で割り切れる条件

単元:
#数A#数Ⅱ#大学入試過去問(数学)#複素数と方程式#整数の性質#約数・倍数・整数の割り算と余り・合同式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ $n$を正の整数とする。次の設問に答えよ。
(1)$n^2$+$n$+1が7で割り切れるような$n$を小さい順に並べるとき、100番目の整数$n$を求めよ。
(2)$n^2$+$n$+1が91で割り切れるような$n$を小さい順に並べるとき、100番目の整数$n$を求めよ。
この動画を見る
$\Large{\boxed{3}}$ $n$を正の整数とする。次の設問に答えよ。
(1)$n^2$+$n$+1が7で割り切れるような$n$を小さい順に並べるとき、100番目の整数$n$を求めよ。
(2)$n^2$+$n$+1が91で割り切れるような$n$を小さい順に並べるとき、100番目の整数$n$を求めよ。
