 大学入試過去問(数学)
大学入試過去問(数学)
 大学入試過去問(数学)
大学入試過去問(数学)
大学入試問題#804「このタイプは定期的に出題」 #兵庫県立大学中期(2014) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#兵庫県立大学
指導講師:
ますただ
問題文全文(内容文):
$f(x)=2\sin2x-\sin\ x$とする。
定積分$\displaystyle \int_{0}^{\pi} |f(x)| dx$の値を求めよ。
出典:2014年兵庫県立大学中期 入試問題
この動画を見る
$f(x)=2\sin2x-\sin\ x$とする。
定積分$\displaystyle \int_{0}^{\pi} |f(x)| dx$の値を求めよ。
出典:2014年兵庫県立大学中期 入試問題
大学入試問題#803「マジで気合い!」 #大阪市立大学(2000) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#大阪市立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{(1+x^2)^4} dx$
出典:2000年大阪市立大学
この動画を見る
$\displaystyle \int_{0}^{1} \displaystyle \frac{1}{(1+x^2)^4} dx$
出典:2000年大阪市立大学
式の値 名城大附属
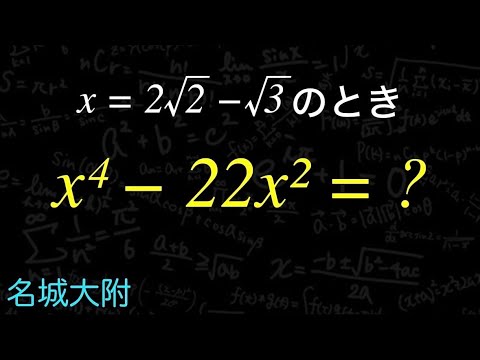
単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$x=2 \sqrt 2 - \sqrt 3$のとき
$x^4-22x^2=?$
名城大学附属高等学校
この動画を見る
$x=2 \sqrt 2 - \sqrt 3$のとき
$x^4-22x^2=?$
名城大学附属高等学校
福田の数学〜一橋大学2024年文系第3問〜多項式の商と余り

単元:
#数Ⅱ#剰余の定理・因数定理・組み立て除法と高次方程式#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ $f(x)$は$x$に関する4次方程式で4次の係数は1である。$f(x)$は$(x+1)^2$で割ると1余り、$(x-1)^2$で割ると2余る。$f(x)$を求めよ。
この動画を見る
$\Large\boxed{3}$ $f(x)$は$x$に関する4次方程式で4次の係数は1である。$f(x)$は$(x+1)^2$で割ると1余り、$(x-1)^2$で割ると2余る。$f(x)$を求めよ。
大学入試問題#802「ほんまに解いてほしい良問」 #岡山大学(2002) #通過領域

単元:
#数Ⅱ#大学入試過去問(数学)#図形と方程式#軌跡と領域#学校別大学入試過去問解説(数学)#数学(高校生)#岡山大学
指導講師:
ますただ
問題文全文(内容文):
座標平面上に点$A(0,2)$と点$B(1,0)$があり線分$AB$上の点$P$から$x$軸、$y$軸におろした垂線の足をそれぞれ$Q,R$とする。
点$P$が$A$から$B$まで動くとき、線分$QR$の通過する部分の面積を求めよ。
出典:2002年岡山大学 入試問題
この動画を見る
座標平面上に点$A(0,2)$と点$B(1,0)$があり線分$AB$上の点$P$から$x$軸、$y$軸におろした垂線の足をそれぞれ$Q,R$とする。
点$P$が$A$から$B$まで動くとき、線分$QR$の通過する部分の面積を求めよ。
出典:2002年岡山大学 入試問題
福田の数学〜一橋大学2024年文系第2問〜2つの放物線が共有点で接線直交する条件

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ $a$, $b$を実数とする。曲線$C$:$y$=$x^2$ と曲線$C'$:$y$=$-x^2$+$ax$+$b$はある点を共有しており、その点におけるそれぞれの接線は直交している。$C$と$C'$で囲まれた部分の面積の最小値を求めよ。
この動画を見る
$\Large\boxed{2}$ $a$, $b$を実数とする。曲線$C$:$y$=$x^2$ と曲線$C'$:$y$=$-x^2$+$ax$+$b$はある点を共有しており、その点におけるそれぞれの接線は直交している。$C$と$C'$で囲まれた部分の面積の最小値を求めよ。
【高校数学】2023年度 第1回 高2K塾記述模試 全問解説

単元:
#大学入試過去問(数学)#全統模試(河合塾)#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
第1問:小問集合
次の□にあてはまる数または式を求めよ.
(1)$(x^2+x)(x^2+x-3)$を展開すると、$\Box$となる.
(2)$2x^2-5xy-3y^2$を因数分解すると、$\Box$となる.
(3)$\alpha=3+\sqrt6、\beta=3-\sqrt6$について、$\alpha\beta$の値は$\Box$であり、$\Box$である.
(4)$\theta$は鋭角とする.$\tan\theta=\sqrt3$のとき、$\cos\theta=\Box$である.
(5)不等式$-x\lt 3x-4\lt x$の解は$\Box$である.
(6)次のデータがある。$6,3,5,2,2,7,1,4,8$ このデータの第3四分位数は$\Box$であり、四分位範囲は$\Box$である.
第2問[1]:図形と計量
三角形$ABC$があり、$AB=4,AC=5,\cos\angle BAC=\dfrac{1}{8}$である。
(1)$\sin\angle BAC$の値を求めよ。また、辺$BC$の長さを求めよ。
(2)辺$AC$(両端を除く)上に点$D$をとり、三角形$BCD$の外接円の半径を$R$とする。
(i)$\angle BDC=\theta$とおくとき、$\sin\theta$を$R$を用いて表せ.
(ii)$R=4$のとき、線分$BD$の長さと線分$AD$の長さを求めよ.
[2]:場合の数
1個のサイコロを4回振り、出た目の数を左から順に並べて4桁の整数Nを作る。例えば、1個のサイコロを4回振り、出た目の数が順に$1,2,3,4$である場合は$N=1234$となる。
(1)$N$は全部で何個できるか.
(2)$2126,3335$のように、同じ数を含む$N$は何個できるか.
(3)$4321$より大きい$N$は何個できるか.
第3問:2次関数
$x$の2次関数$f(x)=x^2-2x+2$があり、放物線$y=f(x)$を$C_1$とする。
(1)(i)$C_1$の座標を求めよ。
(ii)$0\leqq x\leqq 4$における$f(x)$の最大値と最小値を求めよ。
(2)$p$を正の整数とする。$C_1$を$x$軸の方向に$p$、$y$軸方向に$-p$だけ平行移動した放物線を$C_2$とし、$C_2$の方程式を$y=g(x)$とする。
(i)$C_2$の頂点の座標を求めよ。
(ii)$0\leqq x\leqq 4$における$g(x)$の最小値を$m$とする。$m$を$p$を用いて表せ。
(iii)次の2つの条件(A),(B)がともに成り立つような$p$の値の範囲を求めよ。
(A)$0\leqq x\leqq 4$を満たすすべての実数$x$に$g(x)\gt 0$
(B)$0\leqq x\leqq 4$を満たすある実数xに対して$g(x)\gt 8$
第4問:複素数と方程式
$a,b$を実数の定数とし、$c$を0でない実数の定数とする。2つの2次方程式
$x^2-6x+10=0$ …①
$x^2-ax+b=0$ …②
があり、②の2つの解は$1+ci、1-ci$である。ただし、$i$は虚数単位である。
(1)①を解け。
(2)$a$の値を求めよ。また、$b$を$c$を用いて表せ。
(3)$d$を実数の定数とする。多項式$P(x)$があり、$P(x)$を2次式$x^2-ax+b=0$で割ると、商は $x^2-6x+10=0$、余りは$cx+d$である。
(i)$P(1+ci)$を$p+qi$ ($p,q$は実数であり、いずれも$c,d$で表された式)の形で表せ。
(ii)①の2つの解を$\alpha,\beta$と表し、複素数の集合$A,B$を
$A={\alpha,\beta,1+ci,1-ci}、B={P(\alpha),P(\beta),P(1+ci),P(1-ci)}$
と定める。$A=B$となるような$b,c,d$の組($b.c,d$)をすべて求めよ。ただし、$A=B$とは、$A$の要素と$B$の要素がすべて一致することである。
第5問:確率
1が書かれた赤色、白色、青色のカードが1枚ずつ、2が書かれた赤色、白色、青色のカードが1枚ずつ、3が書かれた赤色、白色、青色のカードが1枚ずつ、4が書かれた赤色、白色、青色のカードが1枚ずつ、計12枚のカードが袋の中に入っている。この袋から無作為に3枚のカードを同時に取り出す。
(1)取り出した3枚のカードに書かれた数がすべて同じ数である確率を求めよ。
(2)取り出した3枚のカードに書かれた数がすべて異なる数である確率を求めよ。
(3)取り出した3枚のカードに書かれた数の和が3の倍数である確率を求めよ。
(4)取り出した3枚のカードに書かれた数の和が3の倍数であるとき、その3枚のカードの中に赤色のカードが含まれている条件付き確率を求めよ。
この動画を見る
第1問:小問集合
次の□にあてはまる数または式を求めよ.
(1)$(x^2+x)(x^2+x-3)$を展開すると、$\Box$となる.
(2)$2x^2-5xy-3y^2$を因数分解すると、$\Box$となる.
(3)$\alpha=3+\sqrt6、\beta=3-\sqrt6$について、$\alpha\beta$の値は$\Box$であり、$\Box$である.
(4)$\theta$は鋭角とする.$\tan\theta=\sqrt3$のとき、$\cos\theta=\Box$である.
(5)不等式$-x\lt 3x-4\lt x$の解は$\Box$である.
(6)次のデータがある。$6,3,5,2,2,7,1,4,8$ このデータの第3四分位数は$\Box$であり、四分位範囲は$\Box$である.
第2問[1]:図形と計量
三角形$ABC$があり、$AB=4,AC=5,\cos\angle BAC=\dfrac{1}{8}$である。
(1)$\sin\angle BAC$の値を求めよ。また、辺$BC$の長さを求めよ。
(2)辺$AC$(両端を除く)上に点$D$をとり、三角形$BCD$の外接円の半径を$R$とする。
(i)$\angle BDC=\theta$とおくとき、$\sin\theta$を$R$を用いて表せ.
(ii)$R=4$のとき、線分$BD$の長さと線分$AD$の長さを求めよ.
[2]:場合の数
1個のサイコロを4回振り、出た目の数を左から順に並べて4桁の整数Nを作る。例えば、1個のサイコロを4回振り、出た目の数が順に$1,2,3,4$である場合は$N=1234$となる。
(1)$N$は全部で何個できるか.
(2)$2126,3335$のように、同じ数を含む$N$は何個できるか.
(3)$4321$より大きい$N$は何個できるか.
第3問:2次関数
$x$の2次関数$f(x)=x^2-2x+2$があり、放物線$y=f(x)$を$C_1$とする。
(1)(i)$C_1$の座標を求めよ。
(ii)$0\leqq x\leqq 4$における$f(x)$の最大値と最小値を求めよ。
(2)$p$を正の整数とする。$C_1$を$x$軸の方向に$p$、$y$軸方向に$-p$だけ平行移動した放物線を$C_2$とし、$C_2$の方程式を$y=g(x)$とする。
(i)$C_2$の頂点の座標を求めよ。
(ii)$0\leqq x\leqq 4$における$g(x)$の最小値を$m$とする。$m$を$p$を用いて表せ。
(iii)次の2つの条件(A),(B)がともに成り立つような$p$の値の範囲を求めよ。
(A)$0\leqq x\leqq 4$を満たすすべての実数$x$に$g(x)\gt 0$
(B)$0\leqq x\leqq 4$を満たすある実数xに対して$g(x)\gt 8$
第4問:複素数と方程式
$a,b$を実数の定数とし、$c$を0でない実数の定数とする。2つの2次方程式
$x^2-6x+10=0$ …①
$x^2-ax+b=0$ …②
があり、②の2つの解は$1+ci、1-ci$である。ただし、$i$は虚数単位である。
(1)①を解け。
(2)$a$の値を求めよ。また、$b$を$c$を用いて表せ。
(3)$d$を実数の定数とする。多項式$P(x)$があり、$P(x)$を2次式$x^2-ax+b=0$で割ると、商は $x^2-6x+10=0$、余りは$cx+d$である。
(i)$P(1+ci)$を$p+qi$ ($p,q$は実数であり、いずれも$c,d$で表された式)の形で表せ。
(ii)①の2つの解を$\alpha,\beta$と表し、複素数の集合$A,B$を
$A={\alpha,\beta,1+ci,1-ci}、B={P(\alpha),P(\beta),P(1+ci),P(1-ci)}$
と定める。$A=B$となるような$b,c,d$の組($b.c,d$)をすべて求めよ。ただし、$A=B$とは、$A$の要素と$B$の要素がすべて一致することである。
第5問:確率
1が書かれた赤色、白色、青色のカードが1枚ずつ、2が書かれた赤色、白色、青色のカードが1枚ずつ、3が書かれた赤色、白色、青色のカードが1枚ずつ、4が書かれた赤色、白色、青色のカードが1枚ずつ、計12枚のカードが袋の中に入っている。この袋から無作為に3枚のカードを同時に取り出す。
(1)取り出した3枚のカードに書かれた数がすべて同じ数である確率を求めよ。
(2)取り出した3枚のカードに書かれた数がすべて異なる数である確率を求めよ。
(3)取り出した3枚のカードに書かれた数の和が3の倍数である確率を求めよ。
(4)取り出した3枚のカードに書かれた数の和が3の倍数であるとき、その3枚のカードの中に赤色のカードが含まれている条件付き確率を求めよ。
約束記号 四天王寺
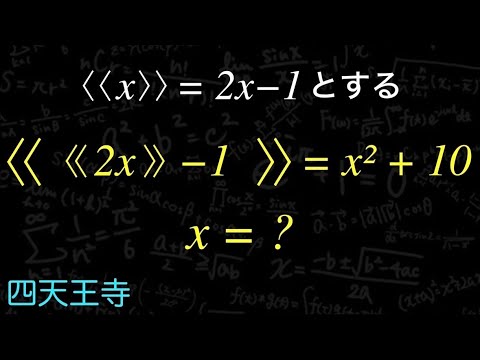
単元:
#大学入試過去問(数学)#関数と極限#関数(分数関数・無理関数・逆関数と合成関数)#学校別大学入試過去問解説(数学)#数学(高校生)#数Ⅲ
指導講師:
数学を数楽に
問題文全文(内容文):
$\langle\langle x \rangle\rangle=2x-1$とする
$\langle\langle \quad \langle\langle 2x \rangle\rangle -1 \rangle\rangle=x^2+10$
$x=?$
四天王寺高等学校
この動画を見る
$\langle\langle x \rangle\rangle=2x-1$とする
$\langle\langle \quad \langle\langle 2x \rangle\rangle -1 \rangle\rangle=x^2+10$
$x=?$
四天王寺高等学校
福田の数学〜一橋大学2024年文系第1問〜シグマが2024になるような2変数の値

単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#数列#数列とその和(等差・等比・階差・Σ)#学校別大学入試過去問解説(数学)#一橋大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ $\displaystyle\sum_{k=1}^mk(n-2k)$=2024 を満たす正の整数の組($m$, $n$)を求めよ。
この動画を見る
$\Large\boxed{1}$ $\displaystyle\sum_{k=1}^mk(n-2k)$=2024 を満たす正の整数の組($m$, $n$)を求めよ。
大学入試問題#800「コメントが難しい」 #兵庫県立大学中期(2012) #極限

単元:
#大学入試過去問(数学)#関数と極限#数列の極限#学校別大学入試過去問解説(数学)#数学(高校生)#兵庫県立大学#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
実数$x$に対して
$f(x)=\displaystyle \lim_{ x \to \infty } n\{\sin(\displaystyle \frac{1+n}{n}x)+\sin(\displaystyle \frac{1-n}{n}x)\}$とおく。
次の問いに答えよ。
1.$f(x)$を求めよ。
2.定積分$\displaystyle \int_{0}^{\pi} f(x) dx$を求めよ。
出典:2012年兵庫県立大学中期 入試問題
この動画を見る
実数$x$に対して
$f(x)=\displaystyle \lim_{ x \to \infty } n\{\sin(\displaystyle \frac{1+n}{n}x)+\sin(\displaystyle \frac{1-n}{n}x)\}$とおく。
次の問いに答えよ。
1.$f(x)$を求めよ。
2.定積分$\displaystyle \int_{0}^{\pi} f(x) dx$を求めよ。
出典:2012年兵庫県立大学中期 入試問題
大学入試問題#799「もう詰んでます!」 #大阪公立大学(2024) #定積分 #King_property

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#大阪公立大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{-\sqrt{ 3 }}^{\sqrt{ 3 }} \displaystyle \frac{log(1+x^2)}{1+e^x} dx$
出典:2024年大阪公立大学
この動画を見る
$\displaystyle \int_{-\sqrt{ 3 }}^{\sqrt{ 3 }} \displaystyle \frac{log(1+x^2)}{1+e^x} dx$
出典:2024年大阪公立大学
福田の数学〜東北大学2024年文系第2問〜75°の三角比と図形の計量
単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#方べきの定理と2つの円の関係#三角関数#加法定理とその応用#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
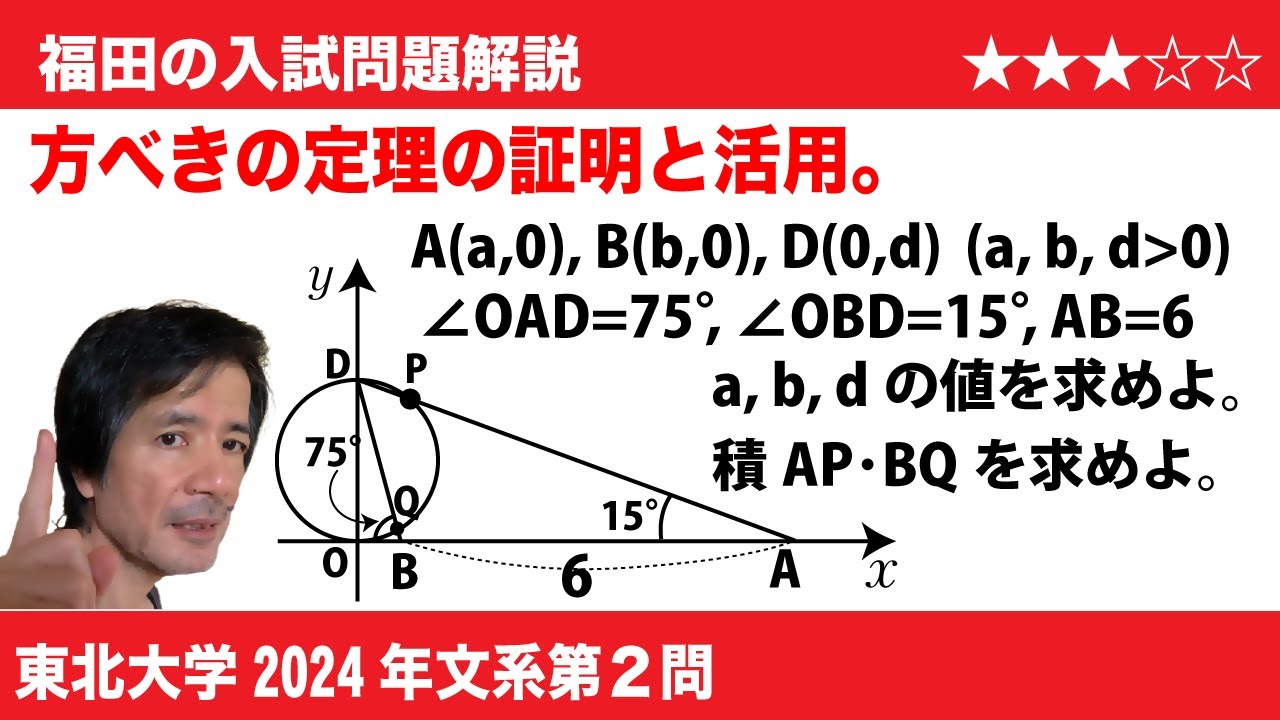
$\Large{\boxed{2}}$ $a$, $b$, $d$を正の実数とし、$xy$平面上の点O(0,0), A($a$,0), B($b$,0), D(0,$d$)が次の条件をすべて満たすとする。
$\angle OAD$=15°, $\angle OBD$=75°, AB=6
以下の問いに答えよ。
(1)$\tan 75°$の値を求めよ。
(2)$a$, $b$, $d$の値をそれぞれ求めよ。
(3)2点O, Dを直径の両端とする円をCとする。線分ADとCの交点のうちDと異なるものをPとする。また、線分BDとCの交点のうちDと異なるものをQとする。このとき、方べきの定理AP・AD=$\textrm{AO}^2$, BP・BD=$\textrm{BO}^2$ を示せ。
(4)(3)の点P,Qに対し、積AP・BQの値を求めよ。
この動画を見る
$\Large{\boxed{2}}$ $a$, $b$, $d$を正の実数とし、$xy$平面上の点O(0,0), A($a$,0), B($b$,0), D(0,$d$)が次の条件をすべて満たすとする。
$\angle OAD$=15°, $\angle OBD$=75°, AB=6
以下の問いに答えよ。
(1)$\tan 75°$の値を求めよ。
(2)$a$, $b$, $d$の値をそれぞれ求めよ。
(3)2点O, Dを直径の両端とする円をCとする。線分ADとCの交点のうちDと異なるものをPとする。また、線分BDとCの交点のうちDと異なるものをQとする。このとき、方べきの定理AP・AD=$\textrm{AO}^2$, BP・BD=$\textrm{BO}^2$ を示せ。
(4)(3)の点P,Qに対し、積AP・BQの値を求めよ。
大学入試問題#798「微分方程式の基礎トレーニング」 横浜国立大学(2024) #微分方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#兵庫県立大学
指導講師:
ますただ
問題文全文(内容文):
実数全体で定義された連続関数$f(x)$が、すべての実数$x$に対して$f(x) \gt 0,$かつ
$f(x)=\displaystyle \int_{0}^{ x } \displaystyle \frac{t}{(t^2+1)f(t)} dt+1$を満たすとき、$f(x)$を求めよ。
出典:2024年横浜国立大学
この動画を見る
実数全体で定義された連続関数$f(x)$が、すべての実数$x$に対して$f(x) \gt 0,$かつ
$f(x)=\displaystyle \int_{0}^{ x } \displaystyle \frac{t}{(t^2+1)f(t)} dt+1$を満たすとき、$f(x)$を求めよ。
出典:2024年横浜国立大学
大学入試問題#797「たぶん部分積分でもいけそう」 #名古屋工業大学(2014) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)#数Ⅲ#名古屋工業大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{log\ 2}^{log\ 3} \displaystyle \frac{xe^x}{(e^x-1)^2} dx$
出典:2014年名古屋工業大学
この動画を見る
$\displaystyle \int_{log\ 2}^{log\ 3} \displaystyle \frac{xe^x}{(e^x-1)^2} dx$
出典:2014年名古屋工業大学
解の公式不要 2024慶應義塾

単元:
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算(整式・展開・因数分解)#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
解け
$2x^2+10\sqrt2x+9=0$
慶応義塾大学2024
この動画を見る
解け
$2x^2+10\sqrt2x+9=0$
慶応義塾大学2024
大学入試問題#796「解法は、ほぼ1択か」 #横浜国立大学(2024) #定積分

単元:
#数Ⅱ#大学入試過去問(数学)#微分法と積分法#積分とその応用#定積分#学校別大学入試過去問解説(数学)#不定積分・定積分#横浜国立大学#数学(高校生)#数Ⅲ
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{log\sqrt{ 3 }} \displaystyle \frac{e^{3x}+4e^{2x}+e^x}{e^{4x}+2e^{2x}+1}dx$
出典:2024年横浜国立大学
この動画を見る
$\displaystyle \int_{0}^{log\sqrt{ 3 }} \displaystyle \frac{e^{3x}+4e^{2x}+e^x}{e^{4x}+2e^{2x}+1}dx$
出典:2024年横浜国立大学
大学入試問題#795「ガウス記号入れて、採点楽にしたいのか!?」 #富山大学(2022) #ガウス記号
単元:
#数A#大学入試過去問(数学)#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#数学(高校生)#富山大学
指導講師:
ますただ
問題文全文(内容文):
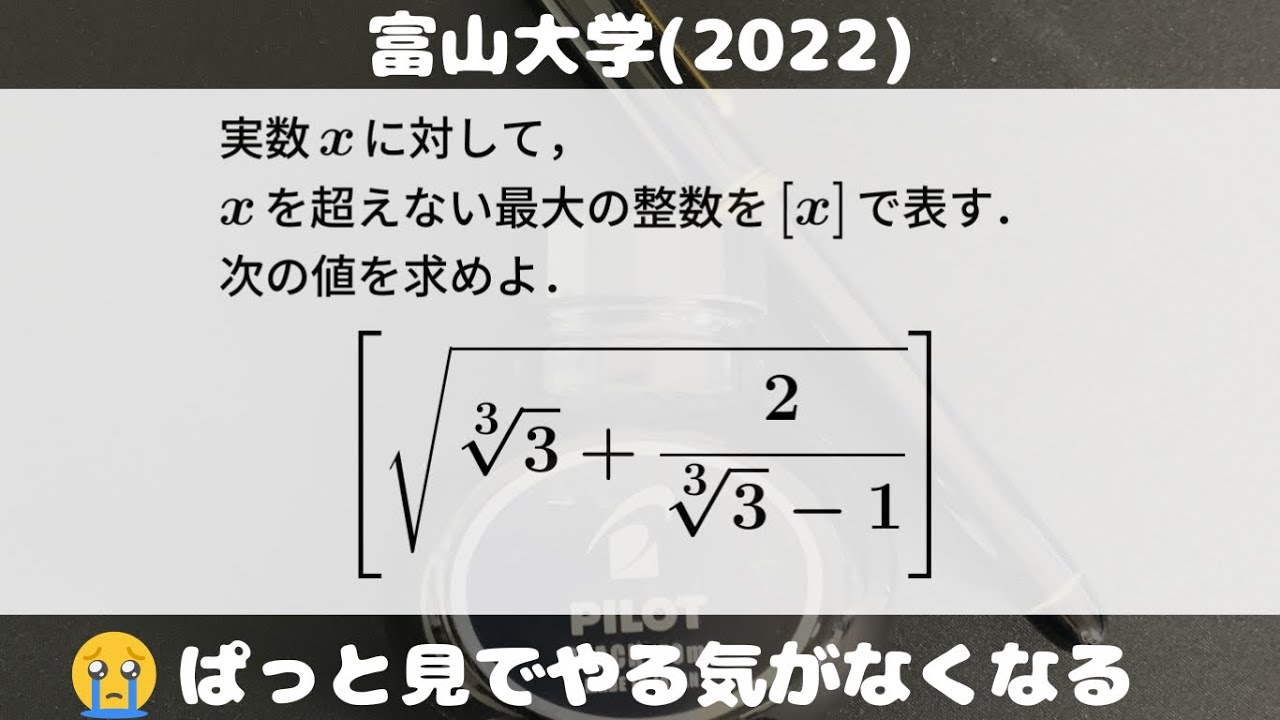
実数$x$に対して、$x$を超えない最大の整数を$[x]$で表す。
次の値を求めよ。
$[\sqrt{ \sqrt[ 3 ]{ 3 }+\displaystyle \frac{2}{\sqrt[ 3 ]{ 3 }-1} }]$
出典:2022年富山大学 入試問題
この動画を見る
実数$x$に対して、$x$を超えない最大の整数を$[x]$で表す。
次の値を求めよ。
$[\sqrt{ \sqrt[ 3 ]{ 3 }+\displaystyle \frac{2}{\sqrt[ 3 ]{ 3 }-1} }]$
出典:2022年富山大学 入試問題
#藤田医科大学(2005) #極限 #Shorts
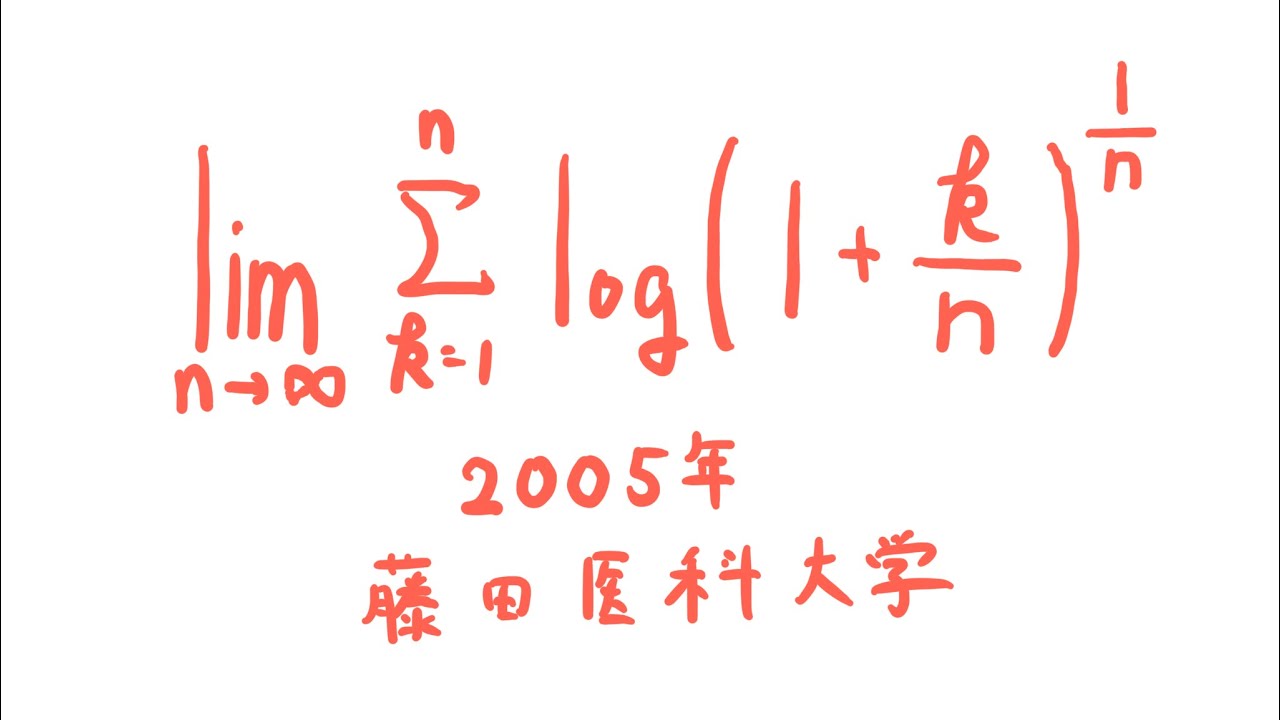
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#藤田医科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n log(1+\displaystyle \frac{k}{n})^\frac{1}{n}$
出典:2005年藤田医科大学
この動画を見る
$\displaystyle \lim_{ n \to \infty } \displaystyle \sum_{k=1}^n log(1+\displaystyle \frac{k}{n})^\frac{1}{n}$
出典:2005年藤田医科大学
大学入試問題#792「なぜサムネに『も』をいれてんだ」 #早稲田大学人間科学部(2024)

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x$が実数であるとき$x(x+1)(x+2)(x+3)$の最小値を求めよ。
出典:2024年早稲田大学人間科学部 入試問題
この動画を見る
$x$が実数であるとき$x(x+1)(x+2)(x+3)$の最小値を求めよ。
出典:2024年早稲田大学人間科学部 入試問題
大学入試問題#793「教科書の章末問題!?」 #室蘭工業大学(2018) #数列

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#室蘭工業大学
指導講師:
ますただ
問題文全文(内容文):
$a_1=\displaystyle \frac{1}{2}, a_{n+1}=\displaystyle \frac{(n+1)a_n}{n+3^na_n}$を満たす数列$\{a_n\}$を求めよ。
出典:2018年室蘭工業大学 入試問題
この動画を見る
$a_1=\displaystyle \frac{1}{2}, a_{n+1}=\displaystyle \frac{(n+1)a_n}{n+3^na_n}$を満たす数列$\{a_n\}$を求めよ。
出典:2018年室蘭工業大学 入試問題
大学入試問題#792「初手が重要!!」 #室蘭工業大学(2020) #定積分

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#室蘭工業大学
指導講師:
ますただ
問題文全文(内容文):
$f(x)=\displaystyle \frac{x^2+x-2}{(2x+1)(x^2+x+1)}$と定める。
定積分$\displaystyle \int_{0}^{\frac{\pi}{2}} f(\cos^2x) \sin(2x)dx$の値を求めよ。
出典:2020年室蘭工業大学 入試問題
この動画を見る
$f(x)=\displaystyle \frac{x^2+x-2}{(2x+1)(x^2+x+1)}$と定める。
定積分$\displaystyle \int_{0}^{\frac{\pi}{2}} f(\cos^2x) \sin(2x)dx$の値を求めよ。
出典:2020年室蘭工業大学 入試問題
大学入試問題#791「第一感で大丈夫」 #慶應義塾大学環境情報学部(2024)

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
$x,y$を正の実数とするとき
$27x+\displaystyle \frac{3x}{y^2}+\displaystyle \frac{2y}{x}$の最小値を求めよ。
また、そのときの$x,y$の値を求めよ。
出典:2024年慶應義塾大学環境情報学部 入試問題
この動画を見る
$x,y$を正の実数とするとき
$27x+\displaystyle \frac{3x}{y^2}+\displaystyle \frac{2y}{x}$の最小値を求めよ。
また、そのときの$x,y$の値を求めよ。
出典:2024年慶應義塾大学環境情報学部 入試問題
大学入試問題#790「解き方はたくさんありそう」 #福島大学(2021) #極限

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \lim_{ x \to a } \displaystyle \frac{\sin\ x-\sin\ a}{\sin(x-a)}$
出典:2021年福島大学 入試問題
この動画を見る
$\displaystyle \lim_{ x \to a } \displaystyle \frac{\sin\ x-\sin\ a}{\sin(x-a)}$
出典:2021年福島大学 入試問題
福田の数学〜北海道大学2024年理系第3問〜関数方程式の解

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#北海道大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{3}}$ 次の問いに答えよ。
(1)$\alpha$ を実数とする。次のように定められた数列$\left\{a_n\right\}$ の一般項を求めよ。
$a_1$=$\alpha$, $a_{n+1}$=$\frac{1}{2}a_n$+1 ($n$=1,2,3,...)
(2)関数$f_1(x)$, $f_2(x)$, $f_3(x)$,... を次の関係式で定める。
$f_1(x)$=$3x$
$f_{n+1}(x)$=$(n+2)x^{n+1}$+$\displaystyle\left(\int_0^1f_n(t)dt\right)x$ ($n$=1,2,3,...)
関数$f_n(x)$を$x$と$n$の式で表せ。
この動画を見る
$\Large{\boxed{3}}$ 次の問いに答えよ。
(1)$\alpha$ を実数とする。次のように定められた数列$\left\{a_n\right\}$ の一般項を求めよ。
$a_1$=$\alpha$, $a_{n+1}$=$\frac{1}{2}a_n$+1 ($n$=1,2,3,...)
(2)関数$f_1(x)$, $f_2(x)$, $f_3(x)$,... を次の関係式で定める。
$f_1(x)$=$3x$
$f_{n+1}(x)$=$(n+2)x^{n+1}$+$\displaystyle\left(\int_0^1f_n(t)dt\right)x$ ($n$=1,2,3,...)
関数$f_n(x)$を$x$と$n$の式で表せ。
2024次方程式の解と係数の関係

単元:
#数Ⅱ#大学入試過去問(数学)#複素数と方程式#剰余の定理・因数定理・組み立て除法と高次方程式#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^{2024}+2x^{2023}+3x^{2022}+$$ ……+2024x+2025=0$の$2024$個の解を
$\alpha,\alpha_{2},\alpha_{3}……\alpha_{2024}$とする
$(1-\displaystyle \frac{1}{\alpha_{1}})(1-\displaystyle \frac{1}{\alpha_{2}})……(1-\displaystyle \frac{1}{\alpha_{2024}})$の値を求めよ
出典:OnLineMath Contest
この動画を見る
$x^{2024}+2x^{2023}+3x^{2022}+$$ ……+2024x+2025=0$の$2024$個の解を
$\alpha,\alpha_{2},\alpha_{3}……\alpha_{2024}$とする
$(1-\displaystyle \frac{1}{\alpha_{1}})(1-\displaystyle \frac{1}{\alpha_{2}})……(1-\displaystyle \frac{1}{\alpha_{2024}})$の値を求めよ
出典:OnLineMath Contest
#高知工科大学(2023) #定積分 #Shorts
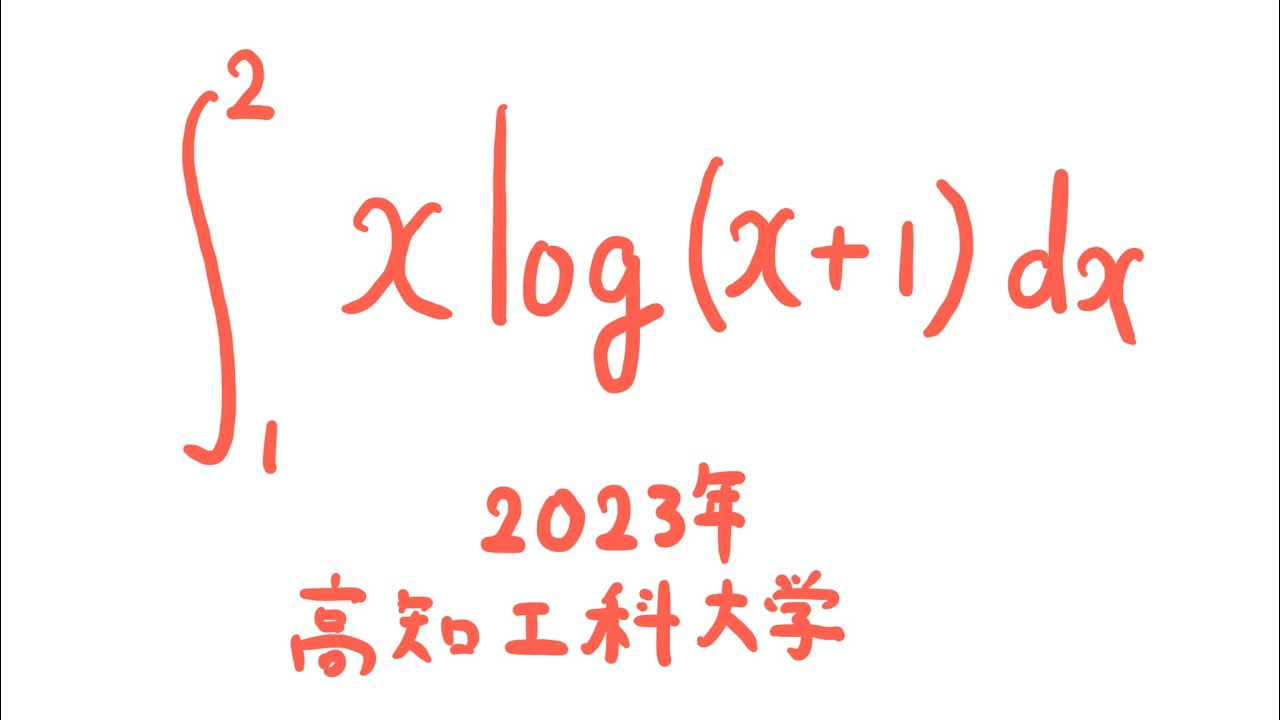
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#高知工科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{1}^{2} x\ log(x+1)dx$
出典:2023年高知工科大学
この動画を見る
$\displaystyle \int_{1}^{2} x\ log(x+1)dx$
出典:2023年高知工科大学
大学入試問題#789「落ち着いて解くだけ」 早稲田大学商学部(2024) #整数問題

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
不等式
$|\displaystyle \frac{2024n}{1-46n}+44| \lt \displaystyle \frac{1}{2025}$を満たす正の整数$n$の最小値を求めよ。
出典:2024年早稲田大学商学部 入試問題
この動画を見る
不等式
$|\displaystyle \frac{2024n}{1-46n}+44| \lt \displaystyle \frac{1}{2025}$を満たす正の整数$n$の最小値を求めよ。
出典:2024年早稲田大学商学部 入試問題
#高知工科大学(2022) #定積分 #Shorts
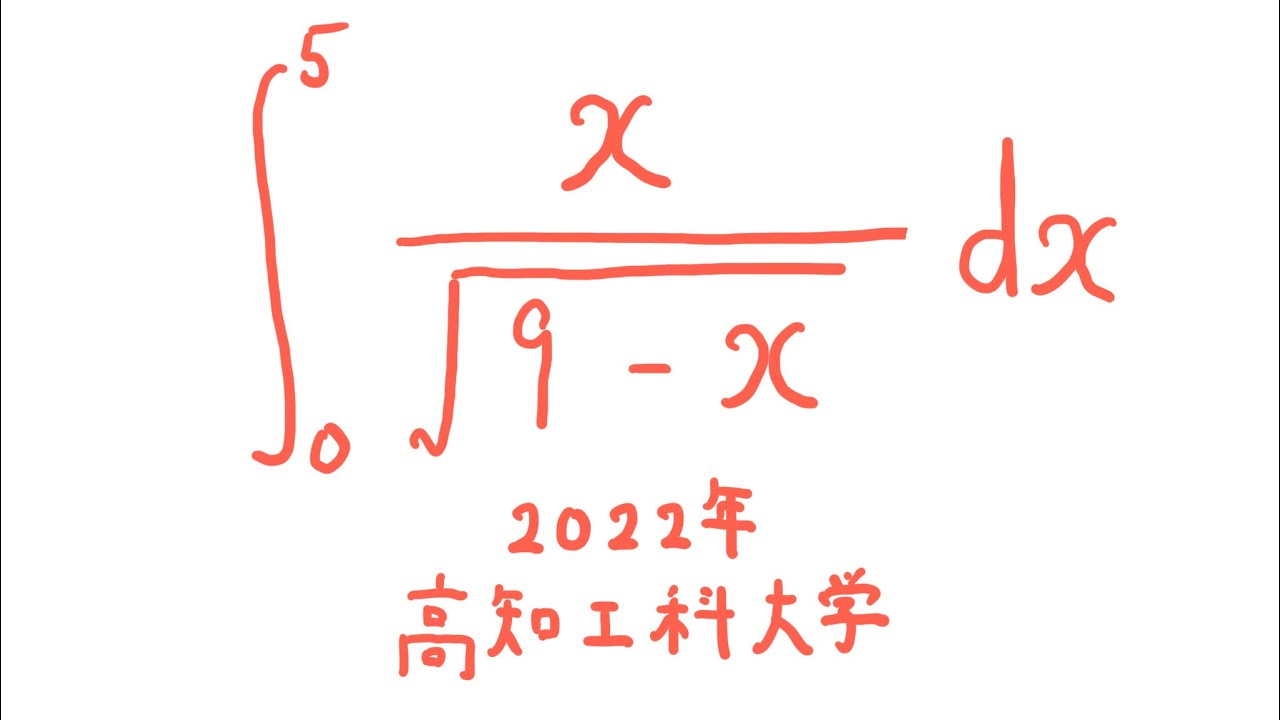
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#高知工科大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{5} \displaystyle \frac{x}{\sqrt{ 9-x }} dx$
出典:2022年高知工科大学
この動画を見る
$\displaystyle \int_{0}^{5} \displaystyle \frac{x}{\sqrt{ 9-x }} dx$
出典:2022年高知工科大学
大学入試問題#788「教科書の例題レベル」 慶應義塾大学商学部(2024) #積分方程式

単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
ますただ
問題文全文(内容文):
等式$f(x)=12x^2+6x\displaystyle \int_{0}^{1} f(t) dt+2\displaystyle \int_{0}^{1} tf(t)dt$を満たす関数$f(x)$を求めよ。
出典:2024年慶應義塾大学商学部 入試問題
この動画を見る
等式$f(x)=12x^2+6x\displaystyle \int_{0}^{1} f(t) dt+2\displaystyle \int_{0}^{1} tf(t)dt$を満たす関数$f(x)$を求めよ。
出典:2024年慶應義塾大学商学部 入試問題
#福島大学(2022) #定積分 #Shorts
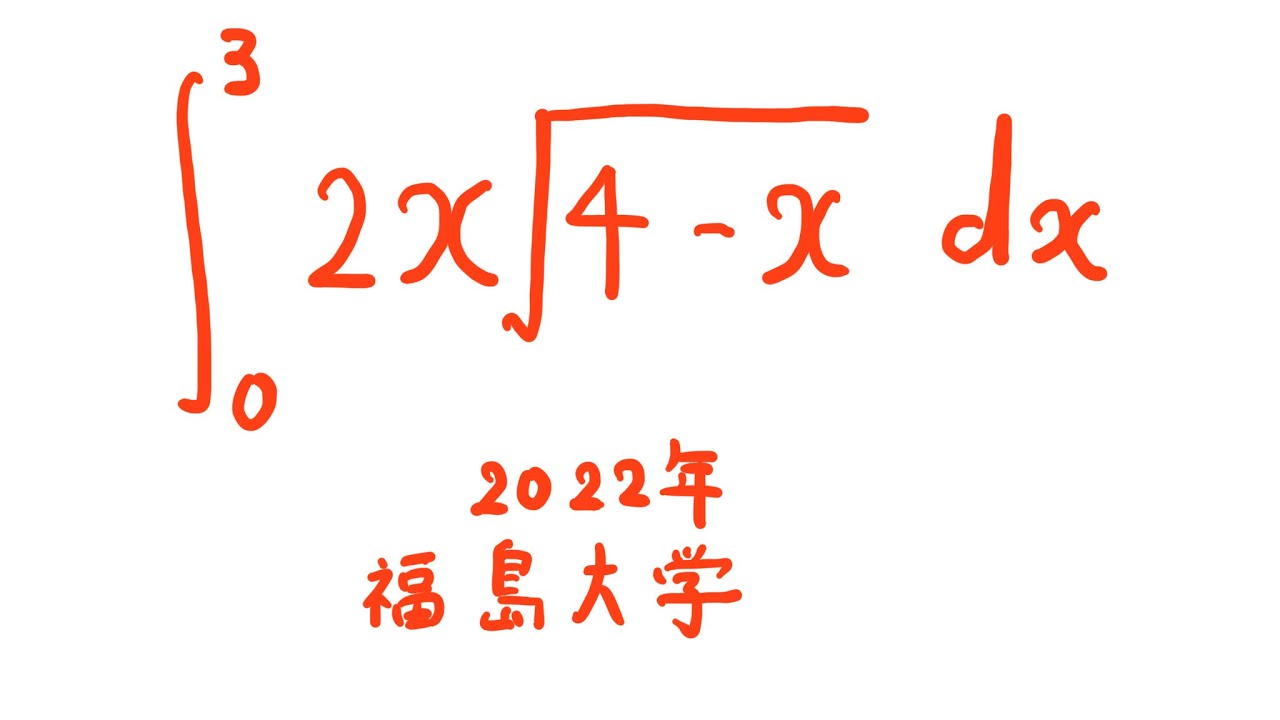
単元:
#大学入試過去問(数学)#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師:
ますただ
問題文全文(内容文):
$\displaystyle \int_{0}^{3} 2x\sqrt{ 4-x }\ dx$
出典:2022年福島大学
この動画を見る
$\displaystyle \int_{0}^{3} 2x\sqrt{ 4-x }\ dx$
出典:2022年福島大学
