実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）
実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）
３乗根が綺麗になっちゃった
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a≧\frac{1}{8}$
$\sqrt[3]{a+\frac{a+1}{3}\sqrt{\frac{8a-1}{3}}}+\sqrt[3]{a-\frac{a+1}{3}\sqrt{\frac{8a-1}{3}}}$
の値を求めよ.
この動画を見る
$a≧\frac{1}{8}$
$\sqrt[3]{a+\frac{a+1}{3}\sqrt{\frac{8a-1}{3}}}+\sqrt[3]{a-\frac{a+1}{3}\sqrt{\frac{8a-1}{3}}}$
の値を求めよ.
3通りで解説！分母の有理化どうする？ 高知中央 （高知）
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$\sqrt 6 + \frac{18}{\sqrt 6}$
高知中央高等学校
この動画を見る
$\sqrt 6 + \frac{18}{\sqrt 6}$
高知中央高等学校
和と差の積不要
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
和と差の積不要
分母を有理化せよ。
$\frac{3+\sqrt 3}{\sqrt 3 + 1}$
この動画を見る
和と差の積不要
分母を有理化せよ。
$\frac{3+\sqrt 3}{\sqrt 3 + 1}$
この球々はなんや？
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
絶対値のグラフの説明動画です
この動画を見る
絶対値のグラフの説明動画です
慣れたら暗算！？平方根の計算 土浦日大（茨城）
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$(\frac{\sqrt 5+ \sqrt 3}{2})^2(\frac{\sqrt 5 - \sqrt 3}{2})^2$
土浦日本大学高等学校
この動画を見る
$(\frac{\sqrt 5+ \sqrt 3}{2})^2(\frac{\sqrt 5 - \sqrt 3}{2})^2$
土浦日本大学高等学校
大学入試問題#608「絶対値・・・・」 横浜市立大学(2009) #定積分
単元：
#数Ⅰ#数Ⅱ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#三角関数#三角関数とグラフ#加法定理とその応用#積分とその応用#定積分#数学(高校生)#数Ⅲ
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{-\frac{\pi}{6}}^{\frac{\pi}{2}} |\sin2\ x| \sin\ x\ dx$
出典：2009年横浜市立大学 入試問題
この動画を見る
$\displaystyle \int_{-\frac{\pi}{6}}^{\frac{\pi}{2}} |\sin2\ x| \sin\ x\ dx$
出典：2009年横浜市立大学 入試問題
大学入試問題#606「見るからに落とせない気がする」 福島大学(2012) #方程式
単元：
#数Ⅰ#２次関数#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#2次方程式と2次不等式#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$x=\sqrt{ 2+\sqrt{ x^2-2 } }$を満たす実数$x$を求めよ
出典：2012年福島大学 入試問題
この動画を見る
$x=\sqrt{ 2+\sqrt{ x^2-2 } }$を満たす実数$x$を求めよ
出典：2012年福島大学 入試問題
解の公式でなくて，解ける？ 平方完成による解き方 市川高校
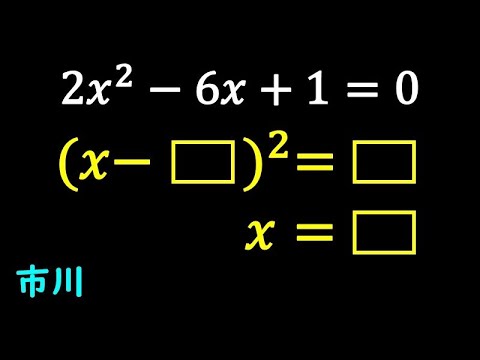
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$2x^2-6x+1=0$
$(x-▢)^2=▢$
$x=▢$
市川高等学校
この動画を見る
$2x^2-6x+1=0$
$(x-▢)^2=▢$
$x=▢$
市川高等学校
ルートがキレイに外れる？
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
式の値を求めよ
$\sqrt{11112^2 - 44444}$
この動画を見る
式の値を求めよ
$\sqrt{11112^2 - 44444}$
ルートの計算だけど図形
単元：
#数Ⅰ#数と式#図形と計量#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$\sqrt {33^2 + 44^2} = $
この動画を見る
$\sqrt {33^2 + 44^2} = $
実は一瞬！！ルートの計算
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
計算せよ
$\sqrt{333^2 + 444^2}$
この動画を見る
計算せよ
$\sqrt{333^2 + 444^2}$
２つの平方の和
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
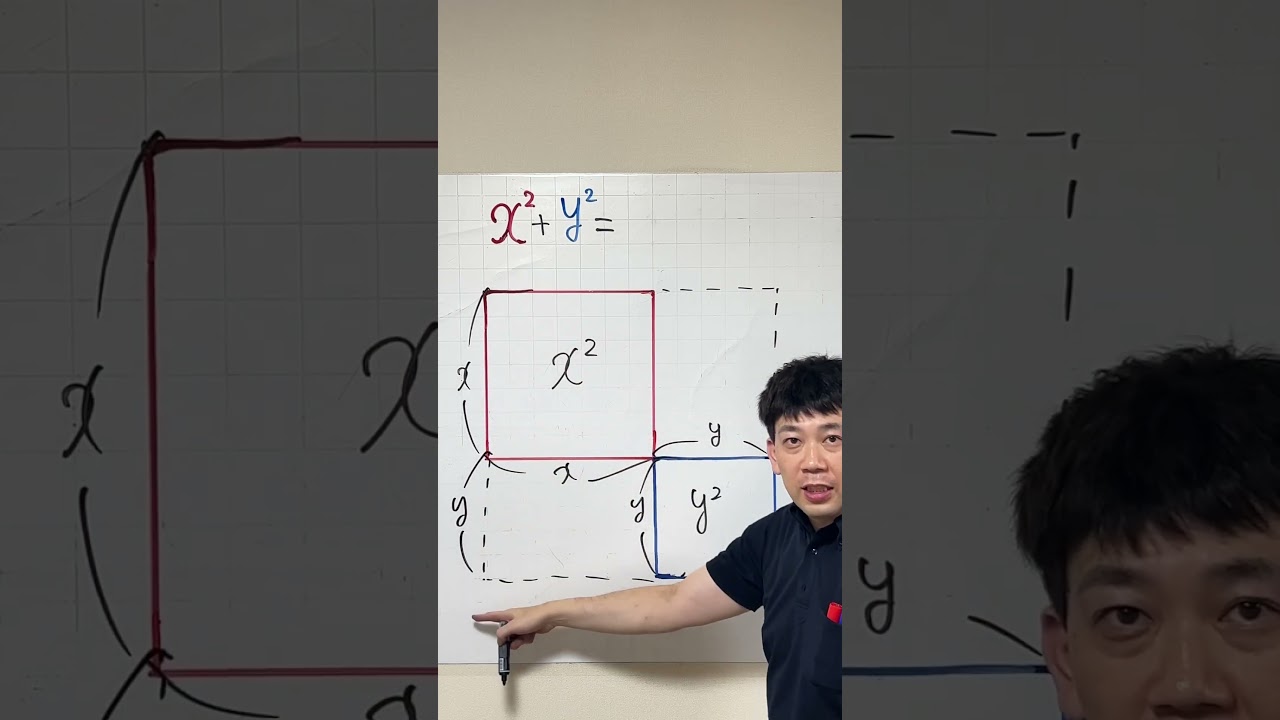
$x^2+y^2$=
＊図は動画内参照
この動画を見る
$x^2+y^2$=
＊図は動画内参照
難問！？奇問！？
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$\frac{\sqrt 6}{2}$の▢数は$\frac{\sqrt 6}{3}$である。
▢=?
この動画を見る
$\frac{\sqrt 6}{2}$の▢数は$\frac{\sqrt 6}{3}$である。
▢=?
□＝❓
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$\sqrt {▢ \frac{2}{3}} = ▢\sqrt {\frac{2}{3}}$
▢=?
＊▢は同じ自然数
この動画を見る
$\sqrt {▢ \frac{2}{3}} = ▢\sqrt {\frac{2}{3}}$
▢=?
＊▢は同じ自然数
東京医科大 楽ちん問題
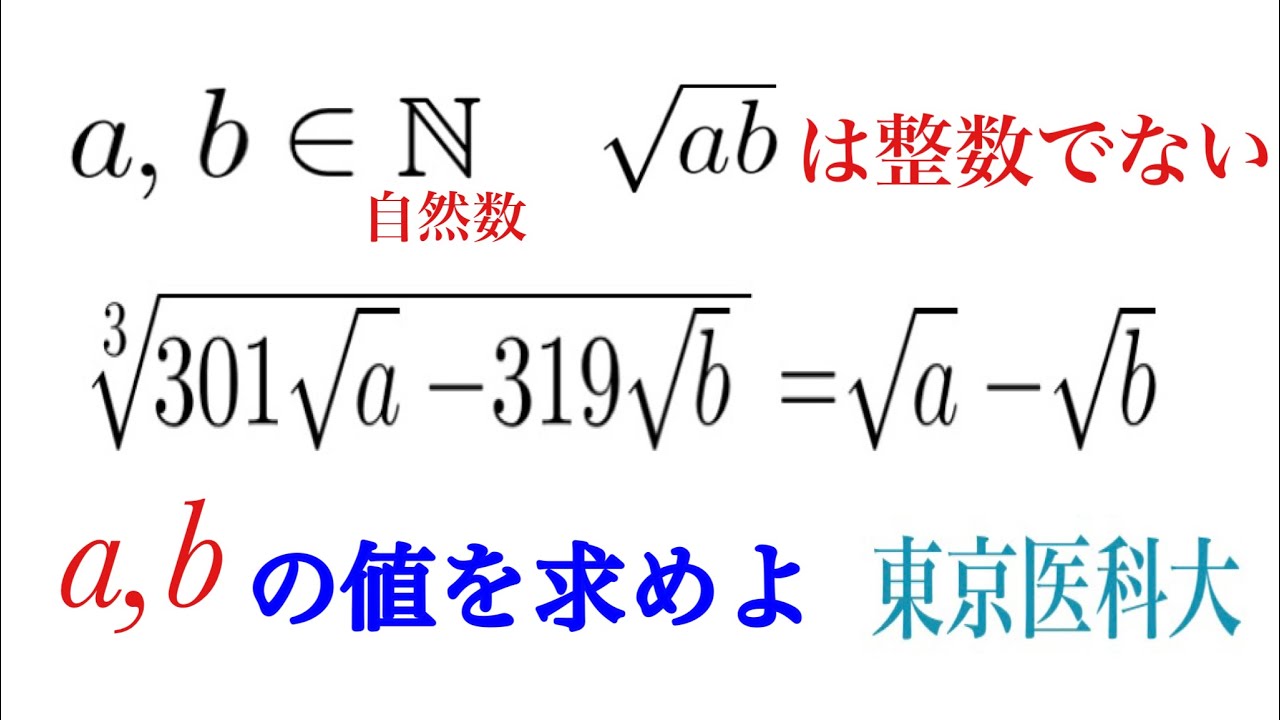
単元：
#数Ⅰ#数A#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#整数の性質#学校別大学入試過去問解説(数学)#数学(高校生)#東京医科大学#東京医科大学
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$a,b$は自然数であり、$\sqrt{ab}$は整数でないとき、
$\sqrt[3]{301\sqrt{a}-319\sqrt{b}}=\sqrt{a}-\sqrt{b}$
をみたす$a,b$を求めよ。
この動画を見る
$a,b$は自然数であり、$\sqrt{ab}$は整数でないとき、
$\sqrt[3]{301\sqrt{a}-319\sqrt{b}}=\sqrt{a}-\sqrt{b}$
をみたす$a,b$を求めよ。
筆算不要！！
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$\sqrt {999 \times 997 +1}$
この動画を見る
$\sqrt {999 \times 997 +1}$
工夫して解こうよ！平方根の計算
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$\frac{(\sqrt 3 + 1)^2}{\sqrt 2} + \frac{(\sqrt 6 - \sqrt 2 )^2}{2 \sqrt 2}$
滝高等学校
この動画を見る
$\frac{(\sqrt 3 + 1)^2}{\sqrt 2} + \frac{(\sqrt 6 - \sqrt 2 )^2}{2 \sqrt 2}$
滝高等学校
福田の数学〜慶應義塾大学2023年看護医療学部第２問(2)〜ルートが自然数になる条件
単元：
#数Ⅰ#数A#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#整数の性質#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\Large\boxed{2}$ (2)$n$を自然数とする。$\sqrt{\frac{200}{\sqrt n}}$が自然数となるような$n$をすべて求めると$n$=$\boxed{\ \ サ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{2}$ (2)$n$を自然数とする。$\sqrt{\frac{200}{\sqrt n}}$が自然数となるような$n$をすべて求めると$n$=$\boxed{\ \ サ\ \ }$である。
2023慶應義塾大学看護医療学部過去問
計算が面白い問題 大阪教育大附属池田
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#学校別大学入試過去問解説(数学)#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
18のすべての正の約数の正の平方根の和は$(1+\sqrt 2)x$という式で表される。
x=?
大阪教育大学附属高等学校平野校舎
この動画を見る
18のすべての正の約数の正の平方根の和は$(1+\sqrt 2)x$という式で表される。
x=?
大阪教育大学附属高等学校平野校舎
数と式 式の展開②【化学のタカシーがていねいに解説】
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
展開せよ
$(a+1)^3$ $(x+3y)^3$
$(2a-1)^3$ $(-3a+2b)^3$
展開せよ
$(a+5)(a^2-5a+25)$
$(3-a)(9+3a+a^2)$
$(2x+y)(4x^2-2xy+y^2)$
$(3a-2b)(9a^2+6ab+4b^2)$
計算せよ
$(x-1)(x-3)(x+1)(x+3)$ $(x+2)(x+5)(x-4)(x-1)$
$(a-b)(a+b)(a+b)(a+b)$ $(2x-y)^3(2x+y)^3$
$(a+b)^2(a-b)^2(a+ab+b)^2(a-ab+b)^2$
$(x+2)(x-2)(x^2+2x+4)(x^2-2x+4)$
$(a+b+c)^2+(a+b-c)^2+(b+c-a)^2+(c+a-b)^2$
この動画を見る
展開せよ
$(a+1)^3$ $(x+3y)^3$
$(2a-1)^3$ $(-3a+2b)^3$
展開せよ
$(a+5)(a^2-5a+25)$
$(3-a)(9+3a+a^2)$
$(2x+y)(4x^2-2xy+y^2)$
$(3a-2b)(9a^2+6ab+4b^2)$
計算せよ
$(x-1)(x-3)(x+1)(x+3)$ $(x+2)(x+5)(x-4)(x-1)$
$(a-b)(a+b)(a+b)(a+b)$ $(2x-y)^3(2x+y)^3$
$(a+b)^2(a-b)^2(a+ab+b)^2(a-ab+b)^2$
$(x+2)(x-2)(x^2+2x+4)(x^2-2x+4)$
$(a+b+c)^2+(a+b-c)^2+(b+c-a)^2+(c+a-b)^2$
数と式 式の展開①【化学のタカシーがていねいに解説】
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
[ ]内の文字について降べきの順に整理せよ
$ax^2+bx-x^4+ax^2-ab [x]$
$2x^2+y^2-3xy-2y^2+3y+4xy-x^2-2x-5 [y]$
$ax^3+a^2x-2x^2-a^3-3ax^3+4a^3 [a]$
$a^2b+b^3+abc-a^2c-ac^2+bc^2-ab^2+c^3 [a]$
ある多項式から$3x^2-xy+2y^2$を引くところ
を誤って加えたため，答えが$2x^2+xy-y^2$
となった。正しい答えを求めよ
次の式を展開した時の[ ]内の項の係数を
求めよ
$(5a^3-3a^2b+7ab^2-2b^3)(3a^2+2ab-3b^2)[a^2b^3][a^3b^2]$
$(x+2y-z)(3x+4y+2z)(-x+y-3z)[xy^2][xyz]$
この動画を見る
[ ]内の文字について降べきの順に整理せよ
$ax^2+bx-x^4+ax^2-ab [x]$
$2x^2+y^2-3xy-2y^2+3y+4xy-x^2-2x-5 [y]$
$ax^3+a^2x-2x^2-a^3-3ax^3+4a^3 [a]$
$a^2b+b^3+abc-a^2c-ac^2+bc^2-ab^2+c^3 [a]$
ある多項式から$3x^2-xy+2y^2$を引くところ
を誤って加えたため，答えが$2x^2+xy-y^2$
となった。正しい答えを求めよ
次の式を展開した時の[ ]内の項の係数を
求めよ
$(5a^3-3a^2b+7ab^2-2b^3)(3a^2+2ab-3b^2)[a^2b^3][a^3b^2]$
$(x+2y-z)(3x+4y+2z)(-x+y-3z)[xy^2][xyz]$
数と式 根号を含む計算【ホーン・フィールドがていねいに解説】
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
$\dfrac{\sqrt2}{\sqrt2-1}$の整数部分をa、小数部分をbとする。次の式の値を求めよ。
(1)$a$ (2)$b$ (3)$a+b+b^2$
次の各場合について、$\sqrt{x^2-10x+25}$をxの多項式で表せ。
(1)$x\geqq 5$ (2)$x\lt 5$
この動画を見る
$\dfrac{\sqrt2}{\sqrt2-1}$の整数部分をa、小数部分をbとする。次の式の値を求めよ。
(1)$a$ (2)$b$ (3)$a+b+b^2$
次の各場合について、$\sqrt{x^2-10x+25}$をxの多項式で表せ。
(1)$x\geqq 5$ (2)$x\lt 5$
ルートを外せ！！
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
ルートを外せ
$\sqrt {3^2} = $
$\sqrt {\pi ^2} = $
$\sqrt {(\pi -3)^2} = $
$\sqrt {(3 - \pi )^2} = $
この動画を見る
ルートを外せ
$\sqrt {3^2} = $
$\sqrt {\pi ^2} = $
$\sqrt {(\pi -3)^2} = $
$\sqrt {(3 - \pi )^2} = $
めずらしい？ √の計算 育英高校
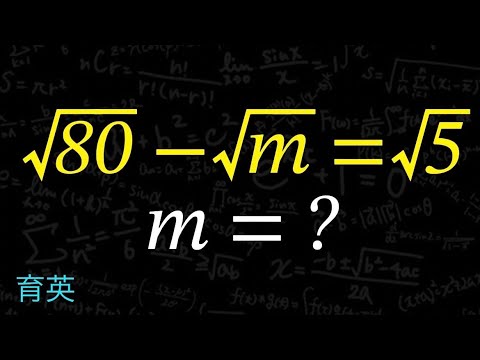
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$\sqrt{80} - \sqrt{m} = \sqrt{5}$
m=?
育英高等学校
この動画を見る
$\sqrt{80} - \sqrt{m} = \sqrt{5}$
m=?
育英高等学校
平方根の計算練習に、
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$a \sqrt b$の形に直す
$\sqrt {27} = $
$\sqrt {45} = $
$\sqrt {54} = $
$\sqrt {63} = $
$\sqrt {90} = $
この動画を見る
$a \sqrt b$の形に直す
$\sqrt {27} = $
$\sqrt {45} = $
$\sqrt {54} = $
$\sqrt {63} = $
$\sqrt {90} = $
平方根の複雑な計算を数楽に
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）
指導講師：
数学を数楽に
問題文全文(内容文)：
$(4 \sqrt2 + 4)(5 \sqrt 2 -5)^2$
この動画を見る
$(4 \sqrt2 + 4)(5 \sqrt 2 -5)^2$
中1生も高1生も大切な絶対値
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
絶対値が$\frac{13}{3}$以下である整数は何個？
神戸龍谷高等学校
この動画を見る
絶対値が$\frac{13}{3}$以下である整数は何個？
神戸龍谷高等学校
三乗根の計算
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
${}^3 \sqrt 3 +{}^3 \sqrt {-3}$
この動画を見る
${}^3 \sqrt 3 +{}^3 \sqrt {-3}$
記数法になじもう！これを見ればあなたもバルタン星人になれる！
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$0.252525……=\dfrac{1}{3}$
$0.161616……=\dfrac{2}{11}$
$0.77777……?$
$0.123_{(n)}=\dfrac{3}{13}_{(n)}$
nを求めよ.
この動画を見る
$0.252525……=\dfrac{1}{3}$
$0.161616……=\dfrac{2}{11}$
$0.77777……?$
$0.123_{(n)}=\dfrac{3}{13}_{(n)}$
nを求めよ.
真面目な数学の問題です。答えはスッキリ❗️
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
鈴木貫太郎
問題文全文(内容文)：
$0.252525･･････=\dfrac{1}{3}$
$0.161616･･････=\dfrac{2}{11}$
$0.77777･･････?$
この動画を見る
$0.252525･･････=\dfrac{1}{3}$
$0.161616･･････=\dfrac{2}{11}$
$0.77777･･････?$