数と式
数と式
福田のおもしろ数学244〜1次不等式が常に成り立つ条件
単元：
#数Ⅰ#数と式#一次不等式（不等式・絶対値のある方程式・不等式）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$0\lt m\lt3$であるすべての$m$に対して$2x-1\lt m(x-2)$が成り立つような$x$の範囲を求めよ。
この動画を見る
$0\lt m\lt3$であるすべての$m$に対して$2x-1\lt m(x-2)$が成り立つような$x$の範囲を求めよ。
平方根 式の値 立教新座
単元：
#数学(中学生)#中３数学#平方根#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$a \gt 0,b \gt 0で
a^{ 2 }=\dfrac{\sqrt{ 7 }+2}{\sqrt{ 2 }},b^{ 2 }=\dfrac{\sqrt{ 7 }-2}{\sqrt{ 2 }}のとき、
\dfrac{b}{a}-\dfrac{a}{b}=$？
この動画を見る
$a \gt 0,b \gt 0で
a^{ 2 }=\dfrac{\sqrt{ 7 }+2}{\sqrt{ 2 }},b^{ 2 }=\dfrac{\sqrt{ 7 }-2}{\sqrt{ 2 }}のとき、
\dfrac{b}{a}-\dfrac{a}{b}=$？
これできる？
単元：
#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
これできる？
※問題文は動画内参照
この動画を見る
これできる？
※問題文は動画内参照
#自治医科大学2024#式変形_21#元高校教員
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#式と証明#式の計算（整式・展開・因数分解）#整式の除法・分数式・二項定理#学校別大学入試過去問解説(数学)#数学(高校生)#自治医科大学
指導講師：
ますただ
問題文全文(内容文)：
$x^{\frac{1}{3}}+x^{-\frac{1}{3}}$のとき
$\displaystyle \frac{x+x^{-1}}{2}$の値を求めよ。
出典：自治医科大学 式変形問題
この動画を見る
$x^{\frac{1}{3}}+x^{-\frac{1}{3}}$のとき
$\displaystyle \frac{x+x^{-1}}{2}$の値を求めよ。
出典：自治医科大学 式変形問題
#福島大学2024#元高校教員
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#学校別大学入試過去問解説(数学)#数学(高校生)#福島大学
指導講師：
ますただ
問題文全文(内容文)：
$\sqrt{ 2023\times2025+1 }$の値を求めよ。
出典：2024年福島大学
この動画を見る
$\sqrt{ 2023\times2025+1 }$の値を求めよ。
出典：2024年福島大学
ポイントは実数 摂南大
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$x^2-6xy+10y^2-6y+9=0$
のときの$x,y$を求めよ。
$(ただしx,yは実数)$
この動画を見る
$x^2-6xy+10y^2-6y+9=0$
のときの$x,y$を求めよ。
$(ただしx,yは実数)$
ポイントは実数 摂南大
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$x^2-6xy+10y^2-6y+9=0$
$x=? y=?$
(ただし、$x,y$は実数）
この動画を見る
$x^2-6xy+10y^2-6y+9=0$
$x=? y=?$
(ただし、$x,y$は実数）
大学入試問題#901「基本だけど初手大事」 #電気通信大学(2024)
単元：
#数Ⅰ#数Ⅱ#大学入試過去問(数学)#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#微分法と積分法#学校別大学入試過去問解説(数学)#不定積分・定積分#数学(高校生)
指導講師：
ますただ
問題文全文(内容文)：
$\displaystyle \int_{0}^{4} \sqrt{ 2-\sqrt{ x} }$ $dx$
出典：2024年電気通信大学
この動画を見る
$\displaystyle \int_{0}^{4} \sqrt{ 2-\sqrt{ x} }$ $dx$
出典：2024年電気通信大学
福田の数学〜中央大学2024経済学部第1問(2)〜集合の要素の個数
単元：
#数Ⅰ#数A#大学入試過去問(数学)#数と式#集合と命題（集合・命題と条件・背理法）#整数の性質#約数・倍数・整数の割り算と余り・合同式#学校別大学入試過去問解説(数学)#中央大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$1$から$1000$までの整数全体の集合を$U$とする。$U$の部分集合$A,B$をそれぞれ$A=\{x|xは5の倍数\},B=\{x|xは7の倍数\}$とするとき、$\overline A \cap \overline B$の要素の個数$n(\overline A \cap \overline B)$を求めよ。
この動画を見る
$1$から$1000$までの整数全体の集合を$U$とする。$U$の部分集合$A,B$をそれぞれ$A=\{x|xは5の倍数\},B=\{x|xは7の倍数\}$とするとき、$\overline A \cap \overline B$の要素の個数$n(\overline A \cap \overline B)$を求めよ。
まず二乗したものを求める
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^2=2+\sqrt{3} \\
b^2=2-\sqrt{3}
\end{array}
\right.
\end{eqnarray}
$
のとき、$ab$の値を求めよ
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
a^2=2+\sqrt{3} \\
b^2=2-\sqrt{3}
\end{array}
\right.
\end{eqnarray}
$
のとき、$ab$の値を求めよ
中学生にはきついよ 因数分解 東京農大一
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算（整式・展開・因数分解）#学校別大学入試過去問解説(数学)#数学(高校生)#東京農工大学
指導講師：
数学を数楽に
問題文全文(内容文)：
因数分解せよ
$4a^4b^4-29a^2b^2+25$
この動画を見る
因数分解せよ
$4a^4b^4-29a^2b^2+25$
【高校入試では珍しい…！】二次方程式：函館ラ・サール高等学校～全国入試問題解法
単元：
#数学(中学生)#数と式#高校入試過去問(数学)#函館ラ・サール高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$kx^2-6x+1=0 の解の個数が1個となるようなkの値を2個求めなさい。$
この動画を見る
$kx^2-6x+1=0 の解の個数が1個となるようなkの値を2個求めなさい。$
√の中に8がいっぱい！！
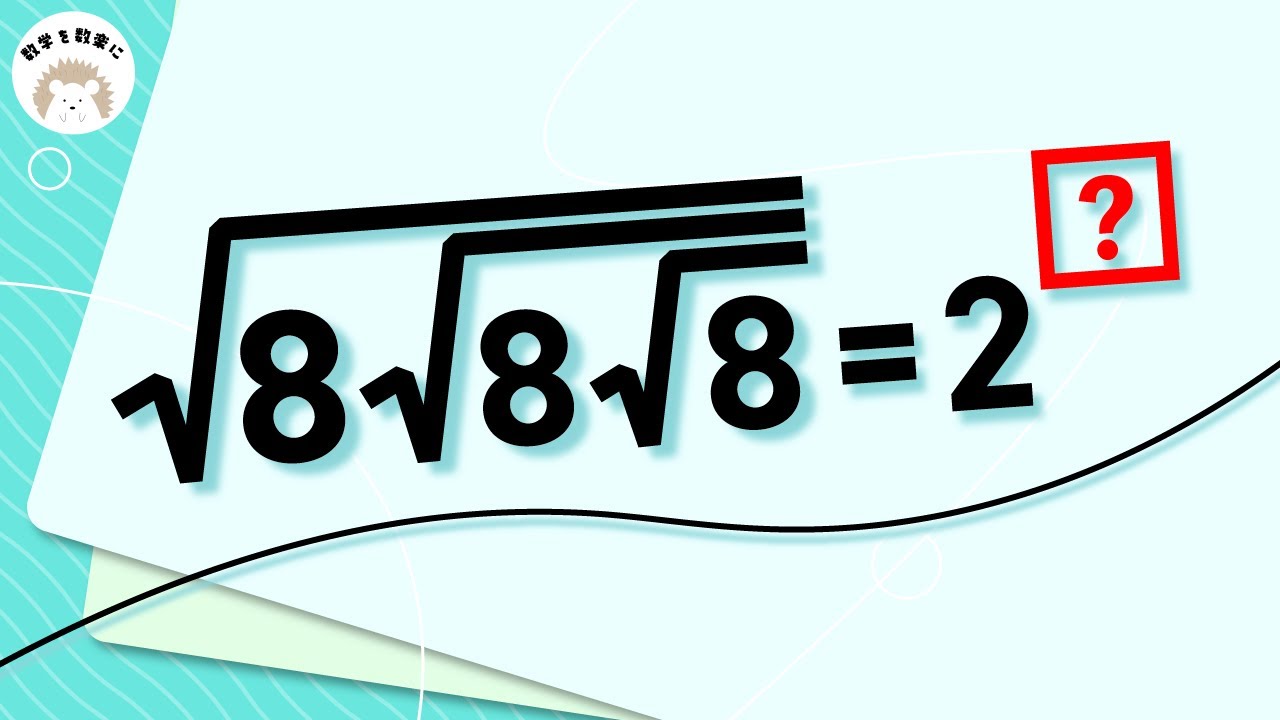
単元：
#数Ⅰ#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#指数関数と対数関数#指数関数
指導講師：
数学を数楽に
問題文全文(内容文)：
$\sqrt{8\sqrt{8\sqrt8}}=2$
この動画を見る
$\sqrt{8\sqrt{8\sqrt8}}=2$
福田のおもしろ数学210〜2つ対称式の条件から和を求める
単元：
#数Ⅰ#数学検定・数学甲子園・数学オリンピック等#数と式#式の計算（整式・展開・因数分解）#数学オリンピック#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
実数 $x, \, y$ が $(1+x)(1+y)(x+y)=2022, \, x^3+y^3=1933$ を満たすとき、$x+y=?$
この動画を見る
実数 $x, \, y$ が $(1+x)(1+y)(x+y)=2022, \, x^3+y^3=1933$ を満たすとき、$x+y=?$
最後まで油断するなよ因数分解
最後まで油断するなよ因数分解
factorization : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
単元：
#中３数学#式の計算（展開、因数分解）#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$(x^2 - 2x - 3)^2 + 13(x^2 - 2x -3) - 90 を因数分解せよ$
この動画を見る
$(x^2 - 2x - 3)^2 + 13(x^2 - 2x -3) - 90 を因数分解せよ$
大学入試問題#887「小問ではめんどいよー」 #兵庫医科大学(2010) #整式
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算（整式・展開・因数分解）#学校別大学入試過去問解説(数学)#数学(高校生)#兵庫医科大学
指導講師：
ますただ
問題文全文(内容文)：
$x^{2010}$を$x^4-1$で割った余りに$x=3$を代入した値を求めよ。
出典：2010年兵庫医科大学
この動画を見る
$x^{2010}$を$x^4-1$で割った余りに$x=3$を代入した値を求めよ。
出典：2010年兵庫医科大学
factorization : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
以下の式を因数分解せよ。
\[
(x^2 -2x -3 )^2 + 13(x^2 -2x -3) - 90
\]
この動画を見る
以下の式を因数分解せよ。
\[
(x^2 -2x -3 )^2 + 13(x^2 -2x -3) - 90
\]
【冷静に急いで…！】平方根：中央大学杉並高等学校～全国入試問題解法
単元：
#数学(中学生)#数と式#高校入試過去問(数学)#中央大学杉並高等学校
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$\sqrt{\sqrt{90-\sqrt{81}}+\sqrt{240 + \sqrt{256}}}$を計算しなさい
この動画を見る
$\sqrt{\sqrt{90-\sqrt{81}}+\sqrt{240 + \sqrt{256}}}$を計算しなさい
mathematical formula : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
単元：
#数学(中学生)#中３数学#式の計算（展開、因数分解）#数Ⅰ#数と式#数学(高校生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$(x+y)^2 = \frac{51+10 \sqrt{2}}{5}$
$x-y= \frac{1-5\sqrt{2}}{\sqrt{5}}$のとき$4xyの値を求めなさい。$
この動画を見る
$(x+y)^2 = \frac{51+10 \sqrt{2}}{5}$
$x-y= \frac{1-5\sqrt{2}}{\sqrt{5}}$のとき$4xyの値を求めなさい。$
x＋y🟰❓
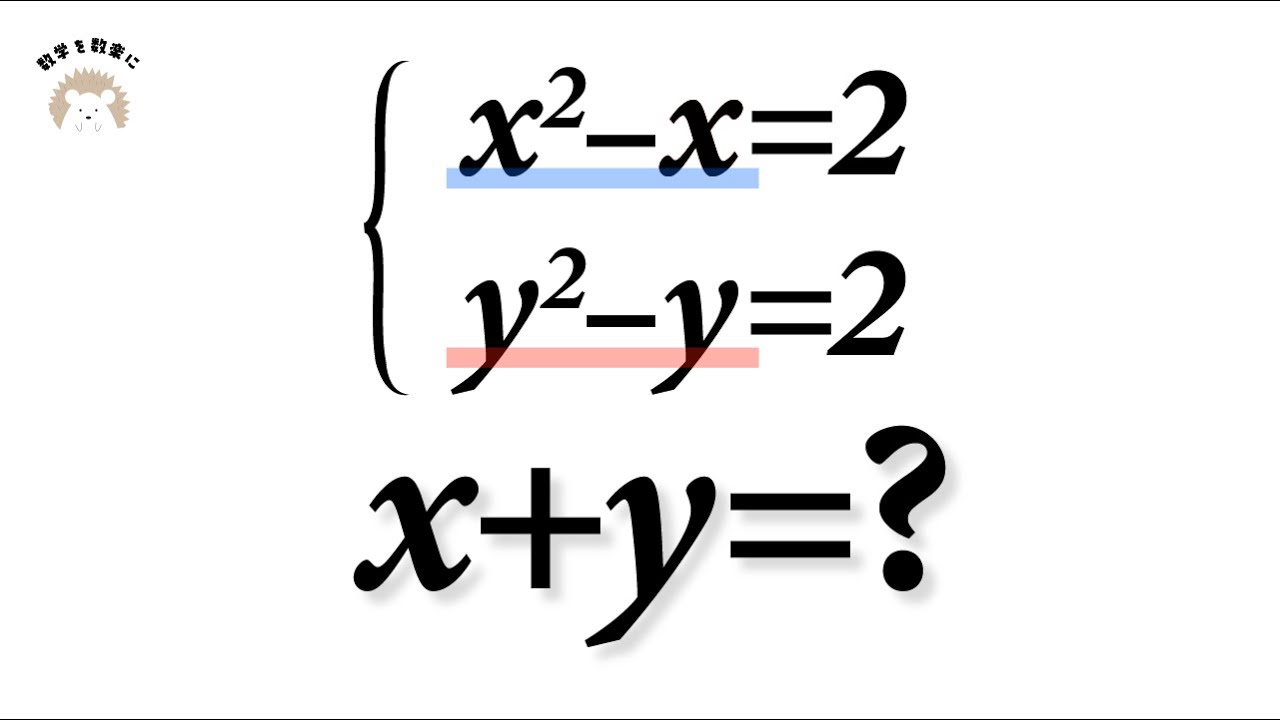
福田のおもしろ数学204〜値の計算
単元：
#数Ⅰ#数と式#式の計算（整式・展開・因数分解）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\sqrt{70\cdot71\cdot72\cdot73+1}$を計算してください。
この動画を見る
$\sqrt{70\cdot71\cdot72\cdot73+1}$を計算してください。
大学入試問題#883「コメントのしようがない」 #東京電機大学(2024) #方程式
単元：
#数Ⅰ#大学入試過去問(数学)#数と式#式の計算（整式・展開・因数分解）#学校別大学入試過去問解説(数学)#数学(高校生)#東京電機大学
指導講師：
ますただ
問題文全文(内容文)：
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2+x+1=y \\
y^2-3y+1=x
\end{array}
\right.
\end{eqnarray}$を解け
出典：2024年東京電機大学
この動画を見る
$\begin{eqnarray}
\left\{
\begin{array}{l}
x^2+x+1=y \\
y^2-3y+1=x
\end{array}
\right.
\end{eqnarray}$を解け
出典：2024年東京電機大学
平方根の計算
単元：
#数学(中学生)#中３数学#平方根#数Ⅰ#数と式#実数と平方根（循環小数・有理数・無理数・絶対値・平方根計算・2重根号）#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
√6 ×√24
この動画を見る
√6 ×√24
ごめんなさい
式の値
気づいた？
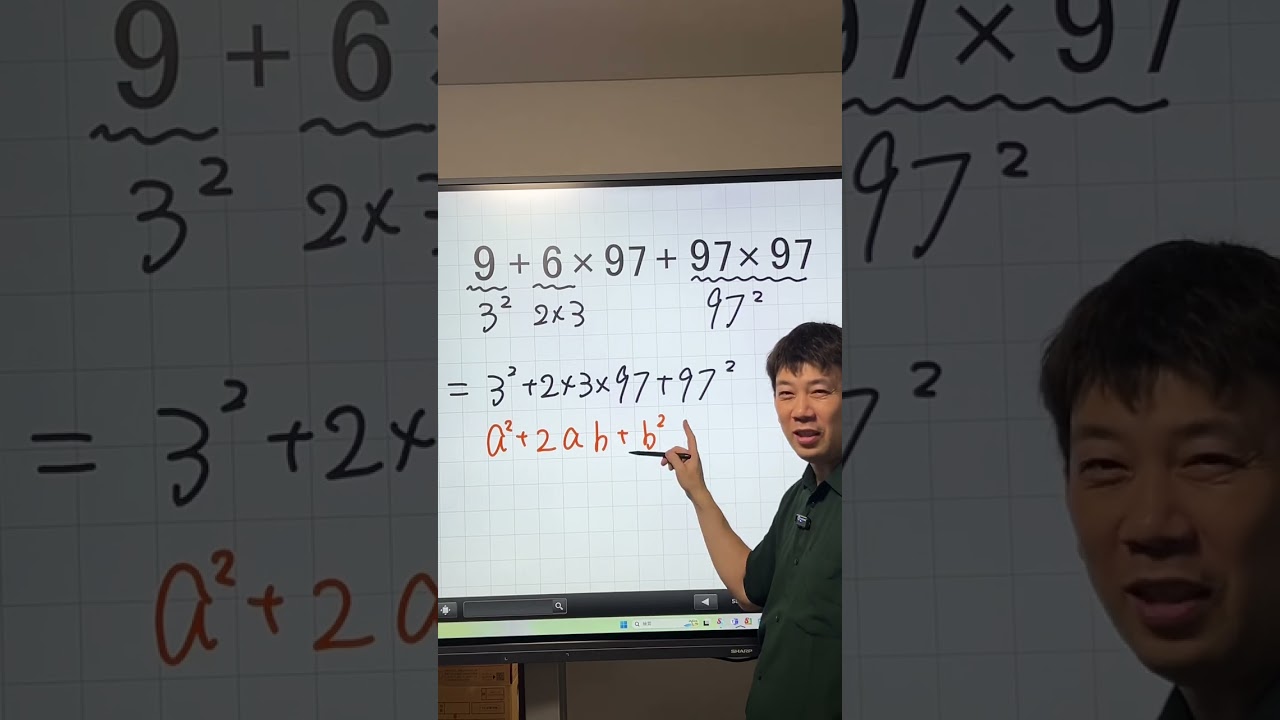
これなんで？ フルは↑
単元：
#数Ⅰ#数A#数Ⅱ#数と式#複素数と方程式#式の計算（整式・展開・因数分解）#整数の性質#約数・倍数・整数の割り算と余り・合同式#複素数
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
これなんで？ フルは↑
【問題文】20×20
この動画を見る
これなんで？ フルは↑
【問題文】20×20
「20+20=200」になる理由を解説
単元：
#数Ⅰ#数A#数Ⅱ#数と式#複素数と方程式#式の計算（整式・展開・因数分解）#整数の性質#約数・倍数・整数の割り算と余り・合同式#複素数#数学(高校生)
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
「20+20=200」になる理由を解説しています。
この動画を見る
「20+20=200」になる理由を解説しています。