 数Ⅰ
数Ⅰ
 数Ⅰ
数Ⅰ
福田のわかった数学〜高校1年生061〜三角形の形状決定問題(2)

単元:
#数Ⅰ#数Ⅱ#図形と計量#三角比への応用(正弦・余弦・面積)#三角関数#加法定理とその応用#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 三角形の形状決定(2)
次の等式が成り立つとき、$\triangle ABC$はどんな形の三角形か。
$\sin A\cos A=\sin B\cos B$
この動画を見る
数学$\textrm{I}$ 三角形の形状決定(2)
次の等式が成り立つとき、$\triangle ABC$はどんな形の三角形か。
$\sin A\cos A=\sin B\cos B$
立教大 整式の剰余

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$x^{2002}$を$x^4-1$で割った余りを求めよ.
立教大過去問
この動画を見る
$x^{2002}$を$x^4-1$で割った余りを求めよ.
立教大過去問
【数Ⅰ】2次方程式の解の配置問題【問題文を図にしよう】
単元:
#数Ⅰ#2次関数#2次方程式と2次不等式#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
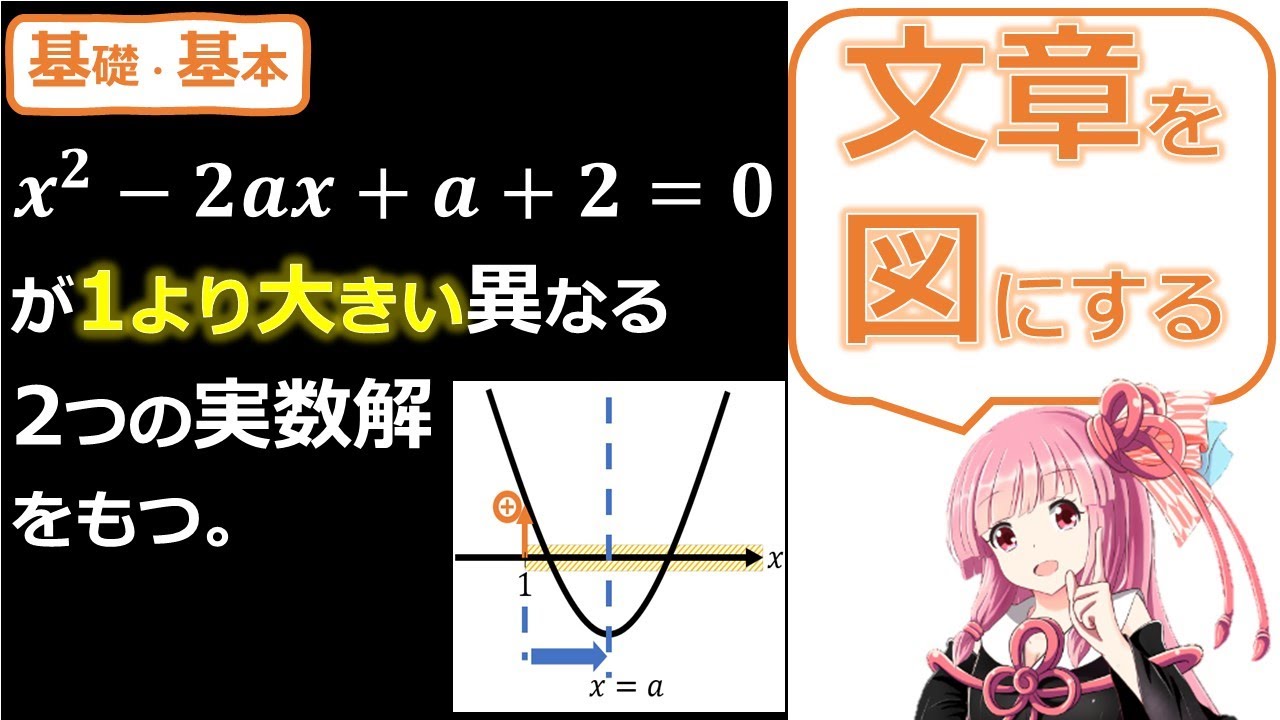
$ 2次方程式x^2-2ax+a+2=0の異なる2つの実数解が以下の条件を満たすとき定数aの値の範囲を求めよ.
(1)ともに1より大きい.
(2)一方が1より小さく,他方が1より大きい.$
この動画を見る
$ 2次方程式x^2-2ax+a+2=0の異なる2つの実数解が以下の条件を満たすとき定数aの値の範囲を求めよ.
(1)ともに1より大きい.
(2)一方が1より小さく,他方が1より大きい.$
福田の数学〜明治大学2021年理工学部第1問(1)〜2次方程式が整数を解にもつ条件

単元:
#数Ⅰ#数A#数Ⅱ#2次関数#複素数と方程式#2次方程式と2次不等式#整数の性質#約数・倍数・整数の割り算と余り・合同式#解と判別式・解と係数の関係#数学(高校生)#大学入試解答速報#数学#明治大学
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(1)$a$と$b$を正の整数とし、$f(x)=ax^2-bx+4$とおく。2次方程式$f(x)=0$は
異なる2つの実数解をもつとする。
$(\textrm{a})$2次方程式$f(x)=0$の2つの解がともに整数であるとき
$\left\{
\begin{array}{1}
a=1 \\
b=\boxed{\ \ ア\ \ }
\end{array}
\right.$
または
$\left\{
\begin{array}{1}
a=\boxed{\ \ イ\ \ }\\
b=\boxed{\ \ ウ\ \ }
\end{array}
\right.\\$
である。
$(\textrm{b})b=7$とする。2次方程式$f(x)=0$の2つの解のうち一方が整数であるとき、
$a=\boxed{\ \ エ\ \ }$であり、$f(x)=0$の2つの解は
$x=\boxed{\ \ エ\ \ },\ \frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}$
である。
2021明治大学理工学部過去問
この動画を見る
${\Large\boxed{1}}$(1)$a$と$b$を正の整数とし、$f(x)=ax^2-bx+4$とおく。2次方程式$f(x)=0$は
異なる2つの実数解をもつとする。
$(\textrm{a})$2次方程式$f(x)=0$の2つの解がともに整数であるとき
$\left\{
\begin{array}{1}
a=1 \\
b=\boxed{\ \ ア\ \ }
\end{array}
\right.$
または
$\left\{
\begin{array}{1}
a=\boxed{\ \ イ\ \ }\\
b=\boxed{\ \ ウ\ \ }
\end{array}
\right.\\$
である。
$(\textrm{b})b=7$とする。2次方程式$f(x)=0$の2つの解のうち一方が整数であるとき、
$a=\boxed{\ \ エ\ \ }$であり、$f(x)=0$の2つの解は
$x=\boxed{\ \ エ\ \ },\ \frac{\boxed{\ \ カ\ \ }}{\boxed{\ \ キ\ \ }}$
である。
2021明治大学理工学部過去問
【手元動画】数学IA 図形と計量の攻略法

単元:
#数Ⅰ#図形と計量#数学(高校生)
指導講師:
カサニマロ【べんとう・ふきのとうの授業動画】
問題文全文(内容文):
$\triangle ABC$において、$BC=2\sqrt{ 2 }$とする。
$\angle ACB$の二等分線と辺$AB$の交点を$D$とし、$CD=\sqrt{ 2 }, \cos \angle BCD=\displaystyle \frac{3}{4}$とする。
このとき、$BD=$[ア]であり$\sin \angle ADC=\displaystyle \frac{[イウ]}{[エ]}$である。
$\displaystyle \frac{AC}{AD}=\sqrt{ オ }$であるから$AD=[カ]$である。
$\triangle ABC$の外接円の半径は$\displaystyle \frac{キ\sqrt{ ク }}{ケ}$である
この動画を見る
$\triangle ABC$において、$BC=2\sqrt{ 2 }$とする。
$\angle ACB$の二等分線と辺$AB$の交点を$D$とし、$CD=\sqrt{ 2 }, \cos \angle BCD=\displaystyle \frac{3}{4}$とする。
このとき、$BD=$[ア]であり$\sin \angle ADC=\displaystyle \frac{[イウ]}{[エ]}$である。
$\displaystyle \frac{AC}{AD}=\sqrt{ オ }$であるから$AD=[カ]$である。
$\triangle ABC$の外接円の半径は$\displaystyle \frac{キ\sqrt{ ク }}{ケ}$である
福田のわかった数学〜高校2年生060〜対称式と領域(2)

単元:
#数Ⅰ#数Ⅱ#2次関数#2次方程式と2次不等式#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$ 対称式と領域(2)
実数$x,\ y$が$x^2+xy+y^2 \leqq 1$を
満たしながら動くとき
$xy+2(x+y)$
の最大値、最小値を求めよ。
この動画を見る
数学$\textrm{II}$ 対称式と領域(2)
実数$x,\ y$が$x^2+xy+y^2 \leqq 1$を
満たしながら動くとき
$xy+2(x+y)$
の最大値、最小値を求めよ。
どっちがでかい?お願い⁉️気づいて

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
どちらが大きいか?
$8^{3\sqrt9}$ vs $81$
この動画を見る
どちらが大きいか?
$8^{3\sqrt9}$ vs $81$
一発でできる!二重根号のはずし方

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
二重根号のはずし方に関して解説していきます.
この動画を見る
二重根号のはずし方に関して解説していきます.
福田のわかった数学〜高校1年生060〜三角形の形状決定問題(1)

単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$三角形の形状決定(1)
次の等式が成り立つとき、$\triangle ABC$はどんな三角形か。
$a^2+b^2+c^2=bc(\frac{1}{2}+\cos A)+ca(\frac{1}{2}+\cos B)+ab(\frac{1}{2}+\cos C)$
この動画を見る
数学$\textrm{I}$三角形の形状決定(1)
次の等式が成り立つとき、$\triangle ABC$はどんな三角形か。
$a^2+b^2+c^2=bc(\frac{1}{2}+\cos A)+ca(\frac{1}{2}+\cos B)+ab(\frac{1}{2}+\cos C)$
頑張れば中学生にも解ける問題

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$ a=\sqrt{\dfrac{1!2!3!・・・・・・25!26!}{n}}$が自然数となる最小の自然数$n$である.
そのとき,$a$の末尾に$0$は何個並ぶか.
この動画を見る
$ a=\sqrt{\dfrac{1!2!3!・・・・・・25!26!}{n}}$が自然数となる最小の自然数$n$である.
そのとき,$a$の末尾に$0$は何個並ぶか.
福田の数学〜明治大学2021年全学部統一入試Ⅲ第2問(2)〜2次方程式の解が同一円周上にある条件

単元:
#数Ⅱ#2次関数#図形の性質#複素数平面#2次方程式と2次不等式#周角と円に内接する四角形・円と接線・接弦定理#複素数平面#数学(高校生)#大学入試解答速報#数学#明治大学#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$(2)方程式$x^2+x+1=0$の2つの解を$\alpha,\ \beta$とする。またbを実数として、
方程式$x^2+x+1=0$の2つの解を$\gamma,\ \delta$とする。複素数平面上で、4点$A(\alpha),$
$B(\beta),C(\gamma),D(\delta)$が同じ円上にあるとき、bの値は$±\frac{\sqrt{\boxed{\ \ キ\ \ }}}{\boxed{\ \ ク\ \ }}$となる。
2021明治大学全統過去問
この動画を見る
${\Large\boxed{2}}$(2)方程式$x^2+x+1=0$の2つの解を$\alpha,\ \beta$とする。またbを実数として、
方程式$x^2+x+1=0$の2つの解を$\gamma,\ \delta$とする。複素数平面上で、4点$A(\alpha),$
$B(\beta),C(\gamma),D(\delta)$が同じ円上にあるとき、bの値は$±\frac{\sqrt{\boxed{\ \ キ\ \ }}}{\boxed{\ \ ク\ \ }}$となる。
2021明治大学全統過去問
福田のわかった数学〜高校2年生059〜対称式と領域(1)

単元:
#数Ⅰ#数Ⅱ#2次関数#2次方程式と2次不等式#図形と方程式#軌跡と領域#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{II}$対称式と領域(1)
実数$x,\ yがx^2+y^2 \leqq 1$を
満たしながら動くとき、
次の点の存在範囲を図示せよ。
(1)$P(x+y,\ x-y) (2)Q(x+y,\ xy)$
この動画を見る
数学$\textrm{II}$対称式と領域(1)
実数$x,\ yがx^2+y^2 \leqq 1$を
満たしながら動くとき、
次の点の存在範囲を図示せよ。
(1)$P(x+y,\ x-y) (2)Q(x+y,\ xy)$
福田の数学〜明治大学2021年全学部統一入試Ⅲ第2問(1)〜楕円と複素数平面

単元:
#平面上の曲線#複素数平面#図形と計量#三角比(三角比・拡張・相互関係・単位円)#2次曲線#複素数平面#大学入試解答速報#数学#明治大学#数C
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$(1)座標平面において、点$(-1,\ 0)$からの距離と点$(1,\ 0)$からの距離の和が4
である点は方程式$\frac{x^2}{\boxed{\ \ ア\ \ }}+\frac{y^2}{\boxed{\ \ イ\ \ }}=1$で表される曲線C上にある。点$(x,\ y)$
が曲線C上を動くとき、点$(x,\ y)$と点$(-1,\ 0)$の距離をdとおけば、dの最小値
は$\boxed{\ \ ウ\ \ }$、最大値は$\boxed{\ \ エ\ \ }$となる。複素数$z$が$|z|+|z-4|=8$を満たすとき、
$|z|$のとりうる範囲は$\boxed{\ \ オ\ \ } \leqq |z| \leqq \boxed{\ \ カ\ \ }$である。
2021明治大学全統過去問
この動画を見る
${\Large\boxed{2}}$(1)座標平面において、点$(-1,\ 0)$からの距離と点$(1,\ 0)$からの距離の和が4
である点は方程式$\frac{x^2}{\boxed{\ \ ア\ \ }}+\frac{y^2}{\boxed{\ \ イ\ \ }}=1$で表される曲線C上にある。点$(x,\ y)$
が曲線C上を動くとき、点$(x,\ y)$と点$(-1,\ 0)$の距離をdとおけば、dの最小値
は$\boxed{\ \ ウ\ \ }$、最大値は$\boxed{\ \ エ\ \ }$となる。複素数$z$が$|z|+|z-4|=8$を満たすとき、
$|z|$のとりうる範囲は$\boxed{\ \ オ\ \ } \leqq |z| \leqq \boxed{\ \ カ\ \ }$である。
2021明治大学全統過去問
福田のわかった数学〜高校1年生059〜図形の計量(10)正四面体の各辺に接する球の半径

単元:
#数A#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#内心・外心・重心とチェバ・メネラウス#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 図形の計量(10)
1辺の長さがaの正四面体の全ての辺に接する球の半径を求めよ。
この動画を見る
数学$\textrm{I}$ 図形の計量(10)
1辺の長さがaの正四面体の全ての辺に接する球の半径を求めよ。
【数Ⅰ】区間が動く2次関数の最大最小【丁寧に場合分け】

単元:
#数Ⅰ#2次関数#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$ aを定数とする.a \leqq x \leqq a+2における関数f(x)=x^2-2x+4の最大値および最小値を求めよ.$
この動画を見る
$ aを定数とする.a \leqq x \leqq a+2における関数f(x)=x^2-2x+4の最大値および最小値を求めよ.$
高校範囲?と思わせる慶應義塾高校の問題

単元:
#数学(中学生)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$a+b+c= \frac{1}{3}$ , $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=1$のとき
(a-1)(b-1)(c-1)=
慶應義塾高等学校
この動画を見る
$a+b+c= \frac{1}{3}$ , $\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=1$のとき
(a-1)(b-1)(c-1)=
慶應義塾高等学校
【数Ⅰ】軸が動く2次関数の最大最小【図を動かしながら場合分け】

単元:
#数Ⅰ#2次関数#2次関数とグラフ#数学(高校生)
指導講師:
めいちゃんねる
問題文全文(内容文):
$ y=x^2-4ax+a(0 \leqq x \leqq 2)
の最小値および最大値を求めよ.$
この動画を見る
$ y=x^2-4ax+a(0 \leqq x \leqq 2)
の最小値および最大値を求めよ.$
長方形と半円 3通りで解説しました
単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比(三角比・拡張・相互関係・単位円)#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
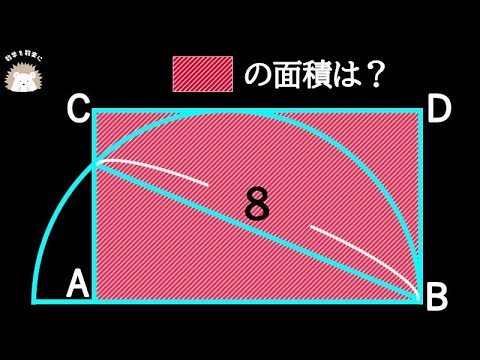
長方形の面積=?
*図は動画内参照
この動画を見る
長方形の面積=?
*図は動画内参照
福田の数学〜明治大学2021年全学部統一入試IⅡAB第2問〜2つのグラフの共有点の個数と面積

単元:
#数Ⅰ#数Ⅱ#2次関数#2次関数とグラフ#微分法と積分法#数学(高校生)#大学入試解答速報#数学#明治大学
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{2}}$$a,k$を実数とし、xの関数$f(x),\ g(x)$を次のようにする。
$f(x)=x^3-ax, g(x)=|x|+k$
(1)$a=4,\ k=0$のとき、曲線$y=f(x)$と$y=g(x)$は3個の異なる共有点をもつ。
それぞれの交点のx座標は$-\sqrt{\boxed{\ \ ア\ \ }},\ 0,\ \sqrt{\boxed{\ \ イ\ \ }}$である。
(2)$k=0$のとき、曲線$y=f(x)$と$y=g(x)$がちょうど2個の異なる共有点をもつ
aの範囲は$\boxed{\ \ ウ\ \ }$かつ$\boxed{\ \ エ\ \ }$である。
(3)$a=4$のとき、曲線$y=f(x)$と$y=g(x)$が3個の異なる共有点をもつkの範囲は
$-\frac{\boxed{\ \ オカ\ \ }\sqrt{\boxed{\ \ キク\ \ }}}{\boxed{\ \ ケ\ \ }} \lt k \lt \boxed{\ \ コ\ \ }$である。
(4)$a=4,\ k=\boxed{\ \ コ\ \ }$のとき、曲線$y=f(x)$と$y=g(x)$の共有点のx座標は$-\boxed{\ \ サ\ \ }$
と$\boxed{\ \ シ\ \ }+\sqrt{\boxed{\ \ ス\ \ }}$であり、$y=f(x)$と$y=g(x)$で囲まれる図形の面積は
$\boxed{\ \ セ\ \ }+\boxed{\ \ ソ\ \ }\sqrt{\boxed{\ \ タ\ \ }}$である。
$\boxed{\ \ ウ\ \ }$の解答群
$⓪-2 \lt a ①-2 \leqq a ②-1 \lt a ③-1 \leqq a ④0 \lt a$
$⑤0 \leqq a ⑥1 \lt a ⑦1 \leqq a ⑧2 \lt a ⑨2 \leqq a$
$\boxed{\ \ エ\ \ }$の解答群
$⓪a \lt -2 ①a \leqq -2 ②a \lt -1 ③a \leqq -1 ④a \lt 0$
$⑤a \leqq 0 ⑥a \lt 1 ⑦a \leqq 1 ⑧a \lt 2 ⑨a \leqq 2$
2021明治大学全統過去問
この動画を見る
${\Large\boxed{2}}$$a,k$を実数とし、xの関数$f(x),\ g(x)$を次のようにする。
$f(x)=x^3-ax, g(x)=|x|+k$
(1)$a=4,\ k=0$のとき、曲線$y=f(x)$と$y=g(x)$は3個の異なる共有点をもつ。
それぞれの交点のx座標は$-\sqrt{\boxed{\ \ ア\ \ }},\ 0,\ \sqrt{\boxed{\ \ イ\ \ }}$である。
(2)$k=0$のとき、曲線$y=f(x)$と$y=g(x)$がちょうど2個の異なる共有点をもつ
aの範囲は$\boxed{\ \ ウ\ \ }$かつ$\boxed{\ \ エ\ \ }$である。
(3)$a=4$のとき、曲線$y=f(x)$と$y=g(x)$が3個の異なる共有点をもつkの範囲は
$-\frac{\boxed{\ \ オカ\ \ }\sqrt{\boxed{\ \ キク\ \ }}}{\boxed{\ \ ケ\ \ }} \lt k \lt \boxed{\ \ コ\ \ }$である。
(4)$a=4,\ k=\boxed{\ \ コ\ \ }$のとき、曲線$y=f(x)$と$y=g(x)$の共有点のx座標は$-\boxed{\ \ サ\ \ }$
と$\boxed{\ \ シ\ \ }+\sqrt{\boxed{\ \ ス\ \ }}$であり、$y=f(x)$と$y=g(x)$で囲まれる図形の面積は
$\boxed{\ \ セ\ \ }+\boxed{\ \ ソ\ \ }\sqrt{\boxed{\ \ タ\ \ }}$である。
$\boxed{\ \ ウ\ \ }$の解答群
$⓪-2 \lt a ①-2 \leqq a ②-1 \lt a ③-1 \leqq a ④0 \lt a$
$⑤0 \leqq a ⑥1 \lt a ⑦1 \leqq a ⑧2 \lt a ⑨2 \leqq a$
$\boxed{\ \ エ\ \ }$の解答群
$⓪a \lt -2 ①a \leqq -2 ②a \lt -1 ③a \leqq -1 ④a \lt 0$
$⑤a \leqq 0 ⑥a \lt 1 ⑦a \leqq 1 ⑧a \lt 2 ⑨a \leqq 2$
2021明治大学全統過去問
福田のわかった数学〜高校1年生058〜図形の計量(8)正四面体の外接球の半径

単元:
#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 図形の計量(9)
1辺の長さがaである正四面体の各頂点を通る外接球の半径を求めよ。
この動画を見る
数学$\textrm{I}$ 図形の計量(9)
1辺の長さがaである正四面体の各頂点を通る外接球の半径を求めよ。
22.5°
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比(三角比・拡張・相互関係・単位円)#平面図形#角度と面積#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
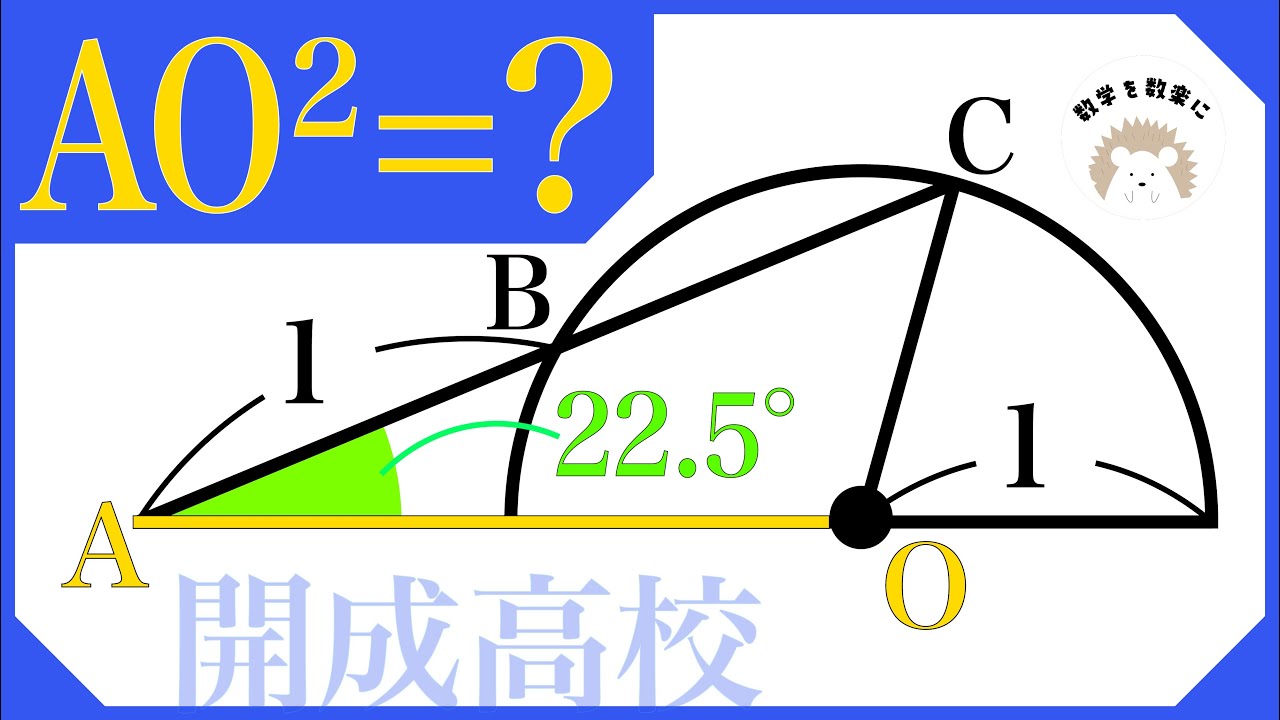
$AO^2 =?$
*図は動画内参照
開成高等学校
この動画を見る
$AO^2 =?$
*図は動画内参照
開成高等学校
福田の数学〜明治大学2021年全学部統一入試IⅡAB第1問(3)〜九九の表の平均と分散

単元:
#数Ⅰ#大学入試過去問(数学)#データの分析#データの分析#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
${\Large\boxed{1}}$(3)九九の表(1の段から9の段まで)に現れる81個の数の平均値$\boxed{\ \ シス\ \ }$であり、
分散は小数第一位を四捨五入して整数で求めると$\boxed{\ \ セソタ\ \ }$である。
2021明治大学全統過去問
この動画を見る
${\Large\boxed{1}}$(3)九九の表(1の段から9の段まで)に現れる81個の数の平均値$\boxed{\ \ シス\ \ }$であり、
分散は小数第一位を四捨五入して整数で求めると$\boxed{\ \ セソタ\ \ }$である。
2021明治大学全統過去問
ざ・挟み撃ち

単元:
#数Ⅰ#数と式#実数と平方根(循環小数・有理数・無理数・絶対値・平方根計算・2重根号)#数学(高校生)
指導講師:
鈴木貫太郎
問題文全文(内容文):
$\dfrac{1}{\sqrt{n^4+1}}+\dfrac{2}{\sqrt{n^4+2}}+・・・・・・+\dfrac{n}{\sqrt{n^4+n}}$
$\displaystyle \lim_{n\to \infty} \displaystyle \sum_{k=1}^{n}\dfrac{k}{\sqrt{n^4+k}}$
$a_n=\displaystyle \sum_{k=1}^n \dfrac{n}{\sqrt{k}}$
$b_n=\displaystyle \sum_{k=1}^n \dfrac{1}{\sqrt{2k+1}}$
$\displaystyle \lim_{n\to \infty} a_n,\displaystyle \lim_{n\to \infty}\dfrac{bn}{an}$を求めよ.
東大1990過去問
この動画を見る
$\dfrac{1}{\sqrt{n^4+1}}+\dfrac{2}{\sqrt{n^4+2}}+・・・・・・+\dfrac{n}{\sqrt{n^4+n}}$
$\displaystyle \lim_{n\to \infty} \displaystyle \sum_{k=1}^{n}\dfrac{k}{\sqrt{n^4+k}}$
$a_n=\displaystyle \sum_{k=1}^n \dfrac{n}{\sqrt{k}}$
$b_n=\displaystyle \sum_{k=1}^n \dfrac{1}{\sqrt{2k+1}}$
$\displaystyle \lim_{n\to \infty} a_n,\displaystyle \lim_{n\to \infty}\dfrac{bn}{an}$を求めよ.
東大1990過去問
【裏技】こんな因数分解あり?

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
$x^2-24x+60$ を因数分解せよ
因数分解の解き方解説動画です
この動画を見る
$x^2-24x+60$ を因数分解せよ
因数分解の解き方解説動画です
福田のわかった数学〜高校1年生057〜図形の計量(8)正四面体の内接球の半径

単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 図形の計量(8)
1辺の長さがaの正四面体の各面に接する内接球の半径を求めよ。
この動画を見る
数学$\textrm{I}$ 図形の計量(8)
1辺の長さがaの正四面体の各面に接する内接球の半径を求めよ。
因数分解の全パターン③【高校数学ⅠA】を宇宙一わかりやすく

単元:
#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
ハクシ高校【数学科】良問演習チャンネル
問題文全文(内容文):
次の式を因数分解せよ。
(1)$2x^2-10xy-48y^2$
(2)$a^3+27b^3$
(3)$x^3+3x^2+3x+1$
(4)$(x^2-3x)(x^2-3x-2)-8$
(5)$xy-x-y+1$
(6)$2a^2b-3ab+a-2b-2$
(7)$x^2+5xy+5x+6y^2+11y+4$
(8)$2x^2-3xy-2y^2+x+3y-1$
(9)$x^4-5x^2+4$
(10)$x^4+x^2+1$
(11)$x^4-6x^2+1$
(12)$(x+1)(x+3)(x+5)(x+7)+15$
(13)$(a+b)c^2+(b+c)a^2+(c+a)b^2+2abc$
(14)$x^3+y^3+z^3-3xyz$
この動画を見る
次の式を因数分解せよ。
(1)$2x^2-10xy-48y^2$
(2)$a^3+27b^3$
(3)$x^3+3x^2+3x+1$
(4)$(x^2-3x)(x^2-3x-2)-8$
(5)$xy-x-y+1$
(6)$2a^2b-3ab+a-2b-2$
(7)$x^2+5xy+5x+6y^2+11y+4$
(8)$2x^2-3xy-2y^2+x+3y-1$
(9)$x^4-5x^2+4$
(10)$x^4+x^2+1$
(11)$x^4-6x^2+1$
(12)$(x+1)(x+3)(x+5)(x+7)+15$
(13)$(a+b)c^2+(b+c)a^2+(c+a)b^2+2abc$
(14)$x^3+y^3+z^3-3xyz$
別に積分しろとは言ってません。(広陵(改))
単元:
#数学(中学生)#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
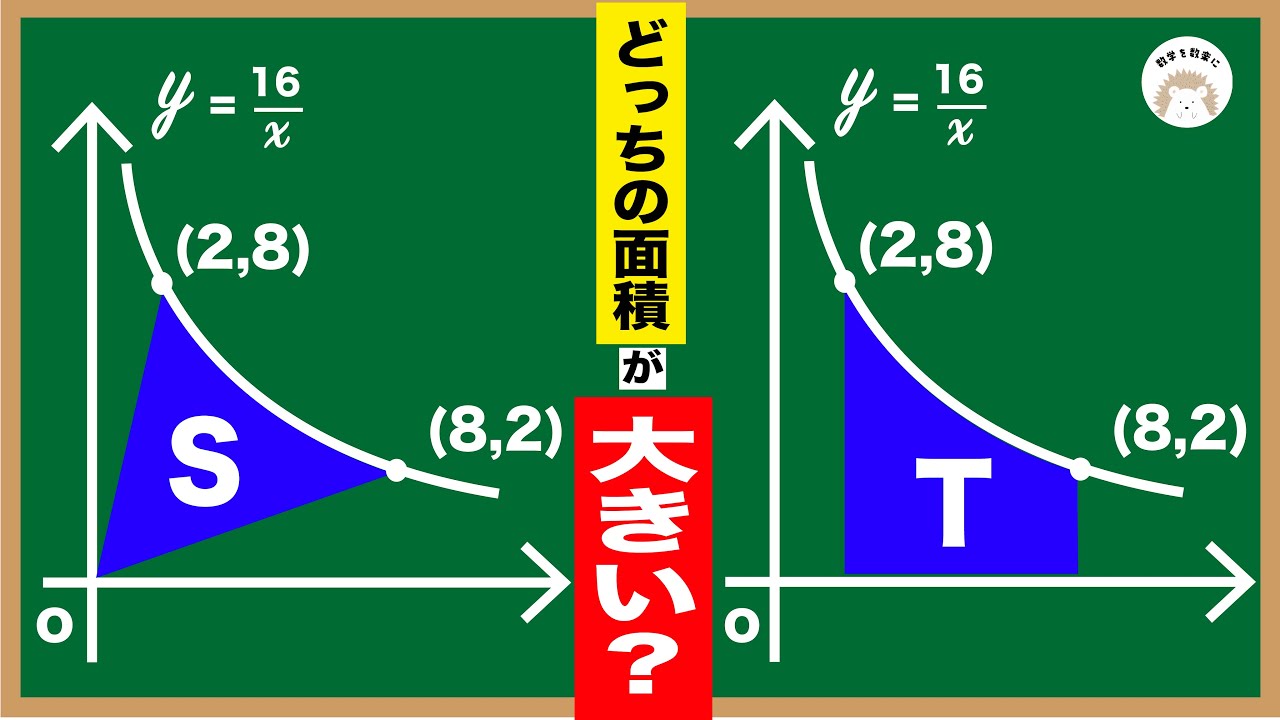
SとTどっちの面積が大きい?
*図は動画内参照
広陵高等学校
この動画を見る
SとTどっちの面積が大きい?
*図は動画内参照
広陵高等学校
【中学数学】因数分解のテクニック~マル秘必殺技~ 3-3【中3数学】

単元:
#数学(中学生)#中3数学#式の計算(展開、因数分解)#数Ⅰ#数と式#式の計算(整式・展開・因数分解)#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
次の式を因数分解せよ
$x^2-24x+60$
この動画を見る
次の式を因数分解せよ
$x^2-24x+60$
参りました。。。気付けば一瞬でした
福田のわかった数学〜高校1年生056〜図形の計量(7)等面四面体の体積

単元:
#数Ⅰ#図形と計量#三角比への応用(正弦・余弦・面積)#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
数学$\textrm{I}$ 図形の計量(7)
4つの面のどれも3辺の長さが
5,6,7の三角形である四面体
(等面四面体)の体積を求めよ。
この動画を見る
数学$\textrm{I}$ 図形の計量(7)
4つの面のどれも3辺の長さが
5,6,7の三角形である四面体
(等面四面体)の体積を求めよ。
