 周角と円に内接する四角形・円と接線・接弦定理
周角と円に内接する四角形・円と接線・接弦定理
 周角と円に内接する四角形・円と接線・接弦定理
周角と円に内接する四角形・円と接線・接弦定理
内接円の半径 広陵(広島県)
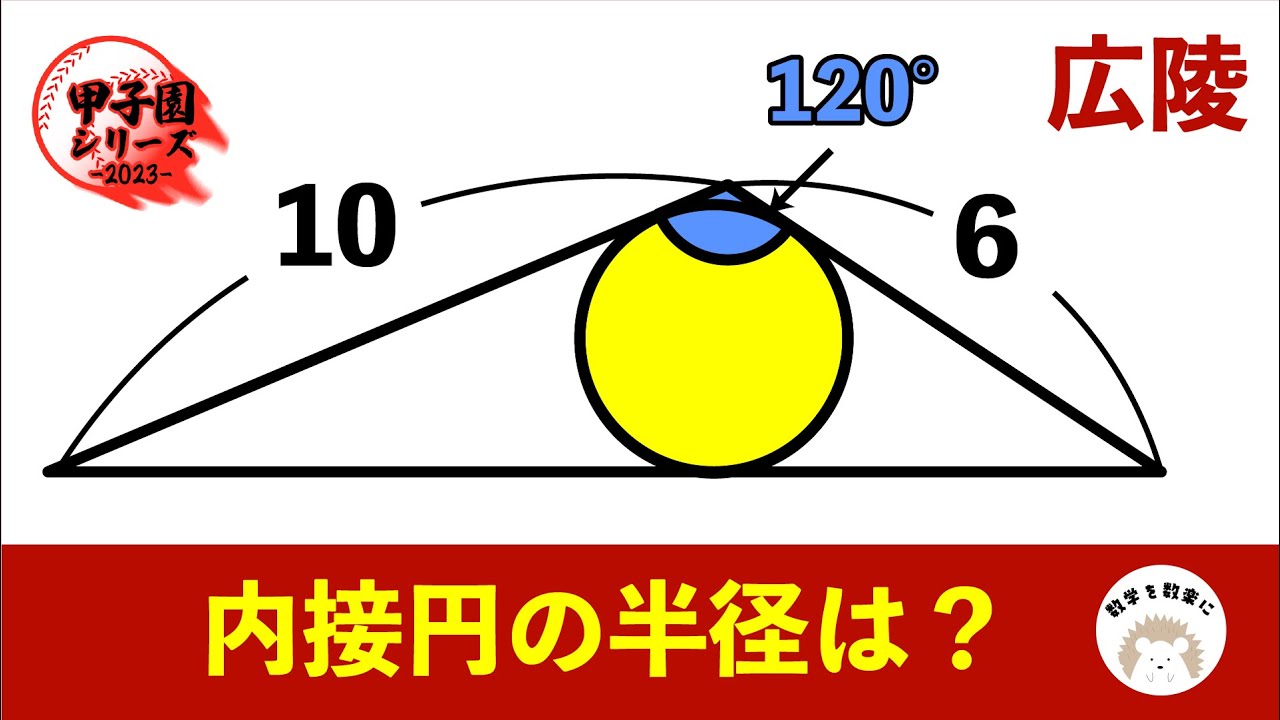
パックン 宇部鴻城(山口)

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
斜線部の面積=40π
小さい円の半径=?
*図は動画内参照
宇部鴻城高等学校
この動画を見る
斜線部の面積=40π
小さい円の半径=?
*図は動画内参照
宇部鴻城高等学校
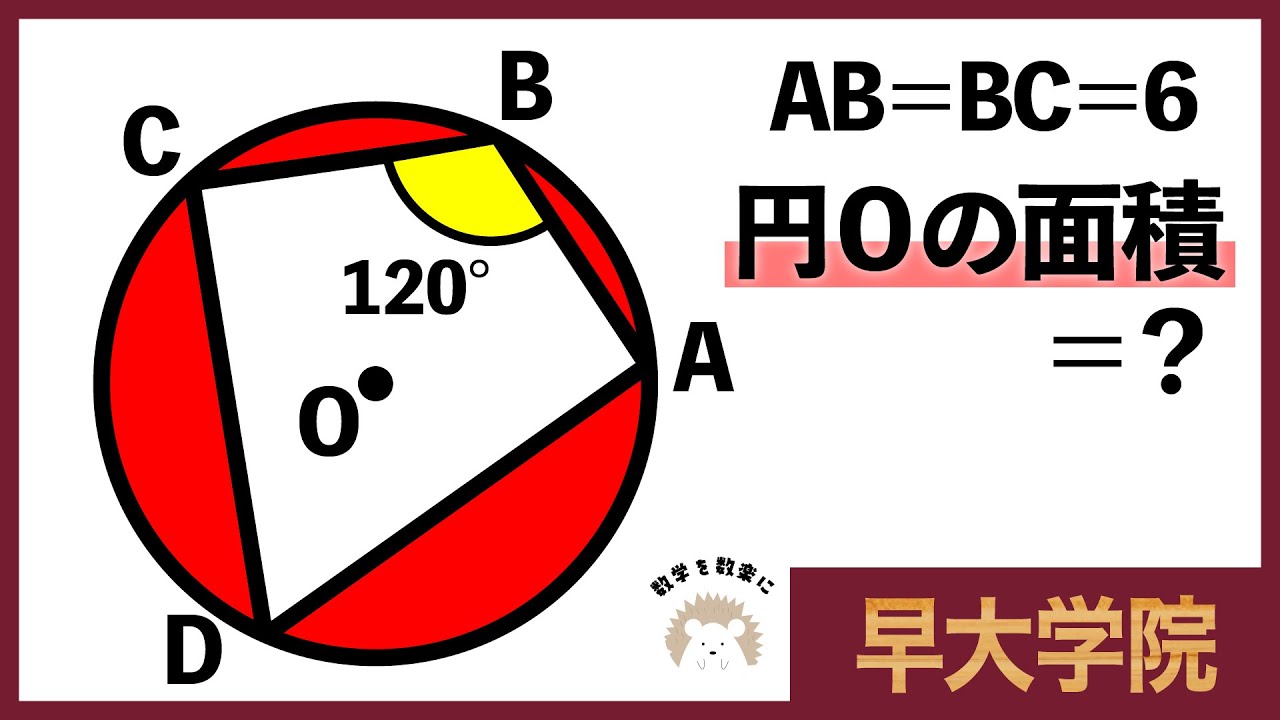
引けるかな?気づけるかな?円の面積 早稲田高等学院
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
AB=BC=6
円Oの面積=?
*図は動画内参照
早稲田大学 高等学院
この動画を見る
AB=BC=6
円Oの面積=?
*図は動画内参照
早稲田大学 高等学院
気付けば一瞬!!正方形と円

単元:
#数Ⅰ#数A#図形の性質#図形と計量#三角比(三角比・拡張・相互関係・単位円)#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
△BODの面積は?
*図は動画内参照
この動画を見る
△BODの面積は?
*図は動画内参照
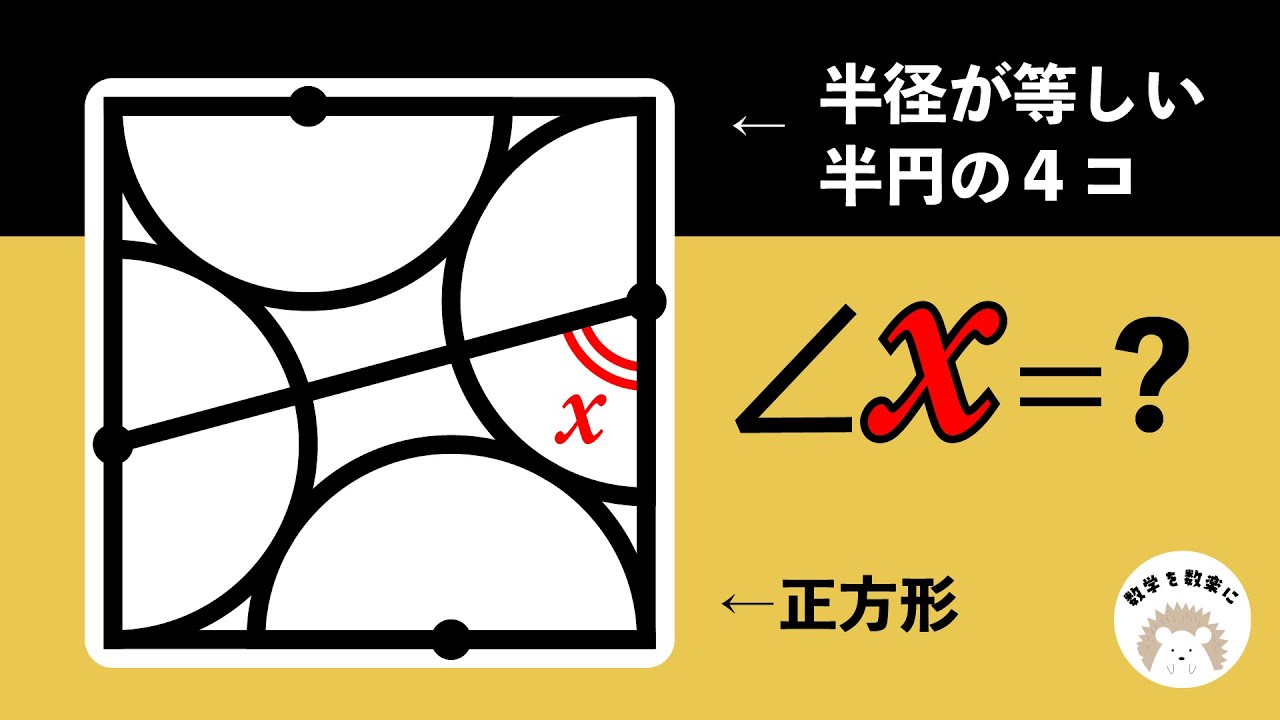
正方形と接する4つの半円
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
半径が等しい半円の4コ
$\angle AED =?$
*図は動画内参照
この動画を見る
半径が等しい半円の4コ
$\angle AED =?$
*図は動画内参照
補助線引けるかな?
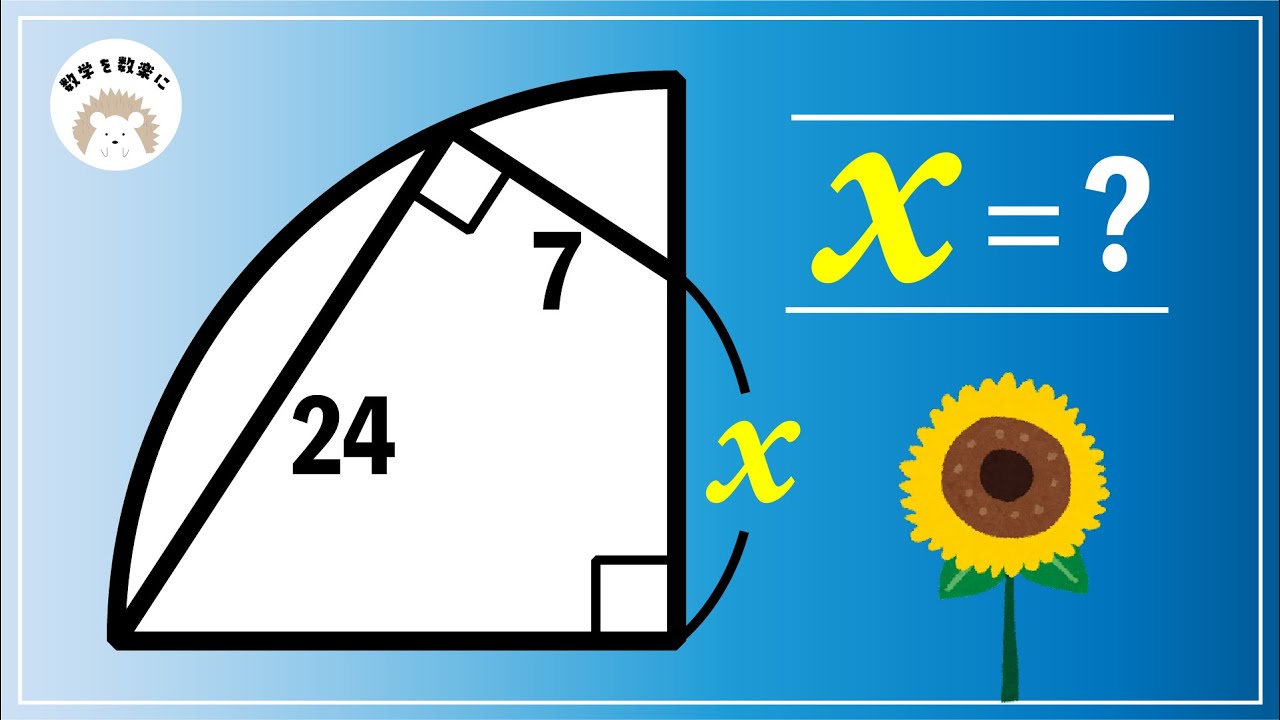
ベン図おかしくね?

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
ベン図に違和感を持つ人に対しての動画に関して解説していきます.
この動画を見る
ベン図に違和感を持つ人に対しての動画に関して解説していきます.
円錐の展開図から体積を求める(高校受験数学)

大学生が解けない小学生の問題
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理
指導講師:
【楽しい授業動画】あきとんとん
問題文全文(内容文):
大学生が解けない小学生の問題を解説していきいます.
この動画を見る
大学生が解けない小学生の問題を解説していきいます.
図形の性質 円の位置関係【TAKAHASHI名人がていねいに解説】

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
空間内の異なる2つの直線$ℓ 、m$ と異なる2つの平面$\alpha,\beta$について,
次の記述は常に正しいか。
(1) $\ell⊥\alpha、m⊥\alpha$ならば、$ℓ⊥m$である。
(2) $\ell ⊥\alpha、m⊥\alpha$ならば、$\alpha //\beta$である。
(3) $\ell //\alpha、m//\alpha$ならば、$\ell //m$である。
(4) $\ell //\alpha、m⊥\alpha$ならば、$\ell$と並行で$m$と垂直な直線がある。
正六角柱を底面に
平行でない1つの平面で切ったものである。
六角形$ABCDEF$ について,
辺$AB$ と平行な辺を答えよ。
立方体について、次の問いに答えよ。
(1) 辺$BF$ と垂直な面をすべて答えよ。
(2) 平面 $BFHD$ と平行な辺をすべて答えよ。
(3) この立方体に,平行な位置関係にある面は何組あるか。
(4) 平面$ABGH$と垂直な面をすべて答えよ。
この動画を見る
空間内の異なる2つの直線$ℓ 、m$ と異なる2つの平面$\alpha,\beta$について,
次の記述は常に正しいか。
(1) $\ell⊥\alpha、m⊥\alpha$ならば、$ℓ⊥m$である。
(2) $\ell ⊥\alpha、m⊥\alpha$ならば、$\alpha //\beta$である。
(3) $\ell //\alpha、m//\alpha$ならば、$\ell //m$である。
(4) $\ell //\alpha、m⊥\alpha$ならば、$\ell$と並行で$m$と垂直な直線がある。
正六角柱を底面に
平行でない1つの平面で切ったものである。
六角形$ABCDEF$ について,
辺$AB$ と平行な辺を答えよ。
立方体について、次の問いに答えよ。
(1) 辺$BF$ と垂直な面をすべて答えよ。
(2) 平面 $BFHD$ と平行な辺をすべて答えよ。
(3) この立方体に,平行な位置関係にある面は何組あるか。
(4) 平面$ABGH$と垂直な面をすべて答えよ。
図形の性質 円の位置関係【TAKAHASHI名人がていねいに解説】

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
図のように,数直線上の原点を中心とする半径3の円Oと、
この数直線上を動く点Pを中心とする半径2の円Pがある。
Pの座標をtとするとき,次の件を満たすとの値,またはtの値の範囲を求めよ。
(1) 2円O,Pの共通接線が4本引ける。
(2) 2円O,Pの共有点が1個である。
(3) 2円O,Pの共通接線が、座標が6である数直線上の点Aを通る。
図のように,半径3の外接する2円A, B
が、半径8の円Oに内接している。2円A, B
に外接し,円Oに内接する円Cの半径を求めよ。
この動画を見る
図のように,数直線上の原点を中心とする半径3の円Oと、
この数直線上を動く点Pを中心とする半径2の円Pがある。
Pの座標をtとするとき,次の件を満たすとの値,またはtの値の範囲を求めよ。
(1) 2円O,Pの共通接線が4本引ける。
(2) 2円O,Pの共有点が1個である。
(3) 2円O,Pの共通接線が、座標が6である数直線上の点Aを通る。
図のように,半径3の外接する2円A, B
が、半径8の円Oに内接している。2円A, B
に外接し,円Oに内接する円Cの半径を求めよ。
福田の数学〜九州大学2023年文系第2問〜2直線のなす角と外接円の半径

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#微分法と積分法#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#数学(高校生)#九州大学
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ xy平面上の曲線C:$y$=$x^3$-$x$ を考える。変数$t$>0に対して、曲線C上の点A($t$, $t^3$-$t$)における接線を$l$とする。直線$l$と直線$y$=-$x$の交点をB、三角形OABの外接円の中心をPとする。以下の問いに答えよ。
(1)点Bの座標を$t$を用いて表せ。
(2)θ=$\angle$OBAとする。$\sin^2\theta$を$t$を用いて表せ。
(3)$f(t)$=$\frac{OP}{OA}$とする。$t$>0のとき、$f(t)$を最小にする$t$の値と$f(t)$の最小値を求めよ。
2023九州大学文系過去問
この動画を見る
$\Large\boxed{2}$ xy平面上の曲線C:$y$=$x^3$-$x$ を考える。変数$t$>0に対して、曲線C上の点A($t$, $t^3$-$t$)における接線を$l$とする。直線$l$と直線$y$=-$x$の交点をB、三角形OABの外接円の中心をPとする。以下の問いに答えよ。
(1)点Bの座標を$t$を用いて表せ。
(2)θ=$\angle$OBAとする。$\sin^2\theta$を$t$を用いて表せ。
(3)$f(t)$=$\frac{OP}{OA}$とする。$t$>0のとき、$f(t)$を最小にする$t$の値と$f(t)$の最小値を求めよ。
2023九州大学文系過去問
葉っぱの面積
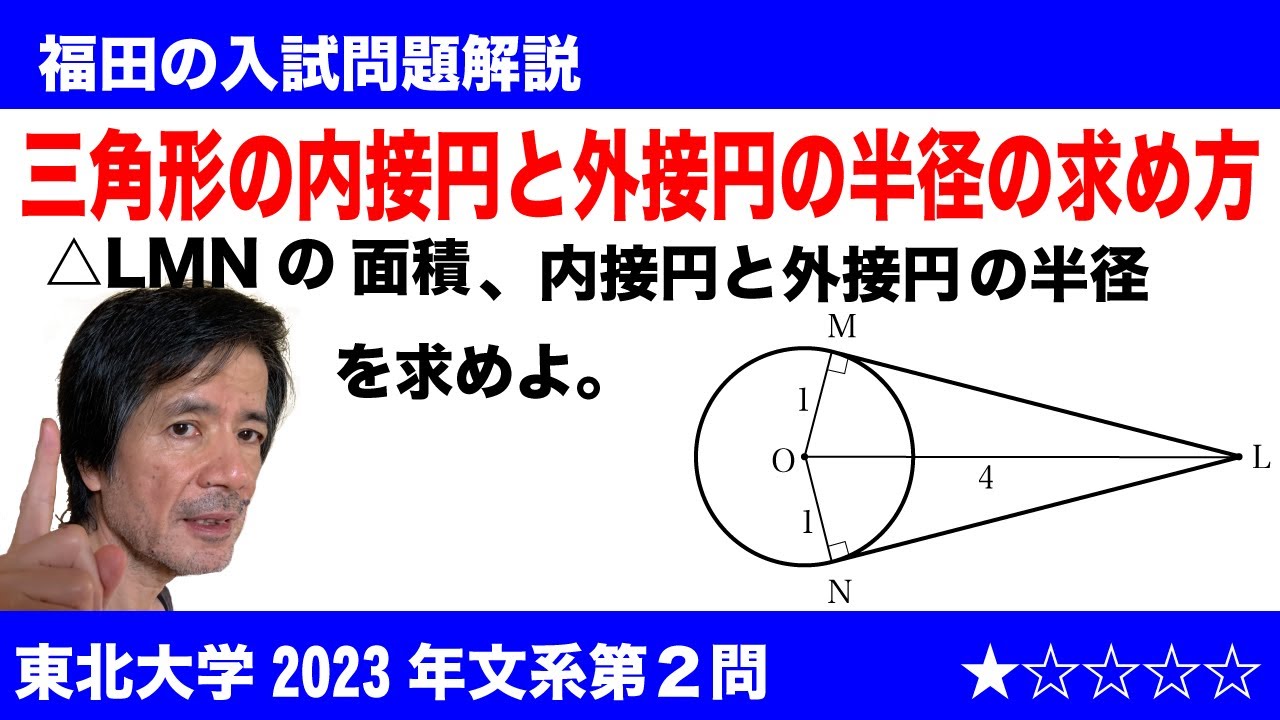
福田の数学〜東北大学2023年文系第1問〜三角形の面積と内接円と外接円の半径
単元:
#数Ⅰ#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#図形と計量#三角比への応用(正弦・余弦・面積)#三角形の辺の比(内分・外分・二等分線)#周角と円に内接する四角形・円と接線・接弦定理#三角関数#学校別大学入試過去問解説(数学)#東北大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{2}$ 平面上の半径1の円Cの中心Oから距離4だけ離れた点Lをとる。点Lを通る円Cの2本の接線と円Cの接点をそれぞれM、Nとする。以下の問いに答えよ。
(1)三角形LMNの面積を求めよ。
(2)三角形LMNの内接円の半径をrと、三角形LMNの外接円の半径Rをそれぞれ求めよ。
2023東北大学文系過去問
この動画を見る
$\Large\boxed{2}$ 平面上の半径1の円Cの中心Oから距離4だけ離れた点Lをとる。点Lを通る円Cの2本の接線と円Cの接点をそれぞれM、Nとする。以下の問いに答えよ。
(1)三角形LMNの面積を求めよ。
(2)三角形LMNの内接円の半径をrと、三角形LMNの外接円の半径Rをそれぞれ求めよ。
2023東北大学文系過去問
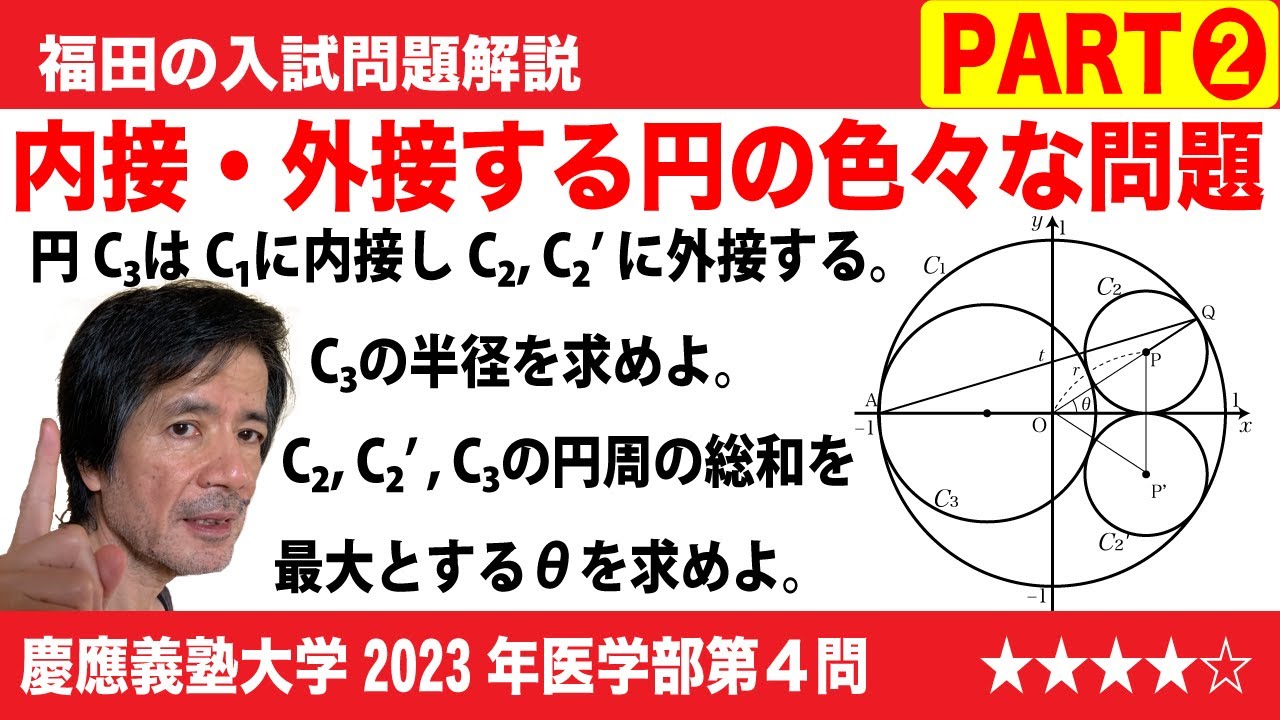
福田の数学〜慶應義塾大学2023年医学部第4問PART2〜円に内接する円の性質
単元:
#数A#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#微分とその応用#関数の変化(グラフ・最大最小・方程式・不等式)#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数Ⅲ
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
福田の数学〜慶應義塾大学2023年医学部第4問PART1〜円に内接する円の性質
単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#複素数平面#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#円と方程式#微分とその応用#複素数平面#図形への応用#微分法#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)#数C#数Ⅲ
指導講師:
福田次郎
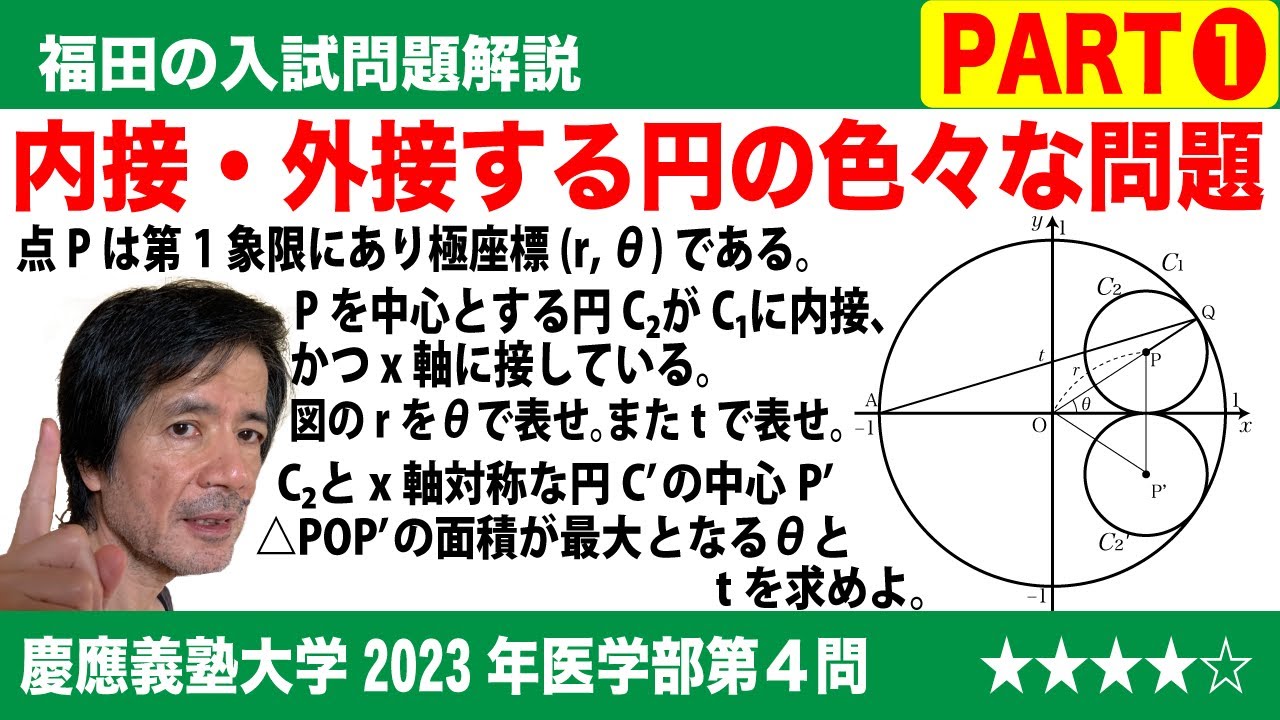
問題文全文(内容文):
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
この動画を見る
$\Large\boxed{4}$ 座標平面において原点Oを中心とする半径1の円を$C_1$とし、$C_1$の内部にある第1象限の点Pの極座標を(r, θ)とする。さらに点Pを中心とする円$C_2$が$C_1$上の点Qにおいて$C_1$に内接し、x軸上の点Rにおいてx軸に接しているとする。
また、極座標が(1, π)である$C_1$上の点をAとし、直線AQのy切片をtとする。
(1)rをθの式で表すとr=$\boxed{\ \ あ\ \ }$となり、tの式で表すとr=$\boxed{\ \ い\ \ }$となる。
(2)円$C_2$と同じ半径をもち、x軸に関して円$C_2$と対称な位置にある円$C'_2$の中心P'とする。三角形POP'の面積はθ=$\boxed{\ \ う\ \ }$のとき最大値$\boxed{\ \ え\ \ }$をとる。θ=$\boxed{\ \ う\ \ }$は条件t=$\boxed{\ \ お\ \ }$と同値である。
(3)円$C_1$に内接し、円$C_2$と$C'_2$の両方に外接する円のうち大きい方を$C_3$とする。円$C_3$の半径bをtの式で表すとb=$\boxed{\ \ か\ \ }$となる。
(4)3つの円$C_2$, $C'_2$, $C_3$の周の長さの和はθ=$\boxed{\ \ き\ \ }$の最大値$\boxed{\ \ く\ \ }$をとる。
2023慶應義塾大学看護医療学部過去問
視聴者さんからの出題

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\stackrel{\huge\frown}{AP}$+$\stackrel{\huge\frown}{BQ}$ =?
*図は動画内参照
この動画を見る
$\stackrel{\huge\frown}{AP}$+$\stackrel{\huge\frown}{BQ}$ =?
*図は動画内参照
図形と計量 円に内接する四角形の面積【烈's study!がていねいに解説】
単元:
#数Ⅰ#数A#図形の性質#図形と計量#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
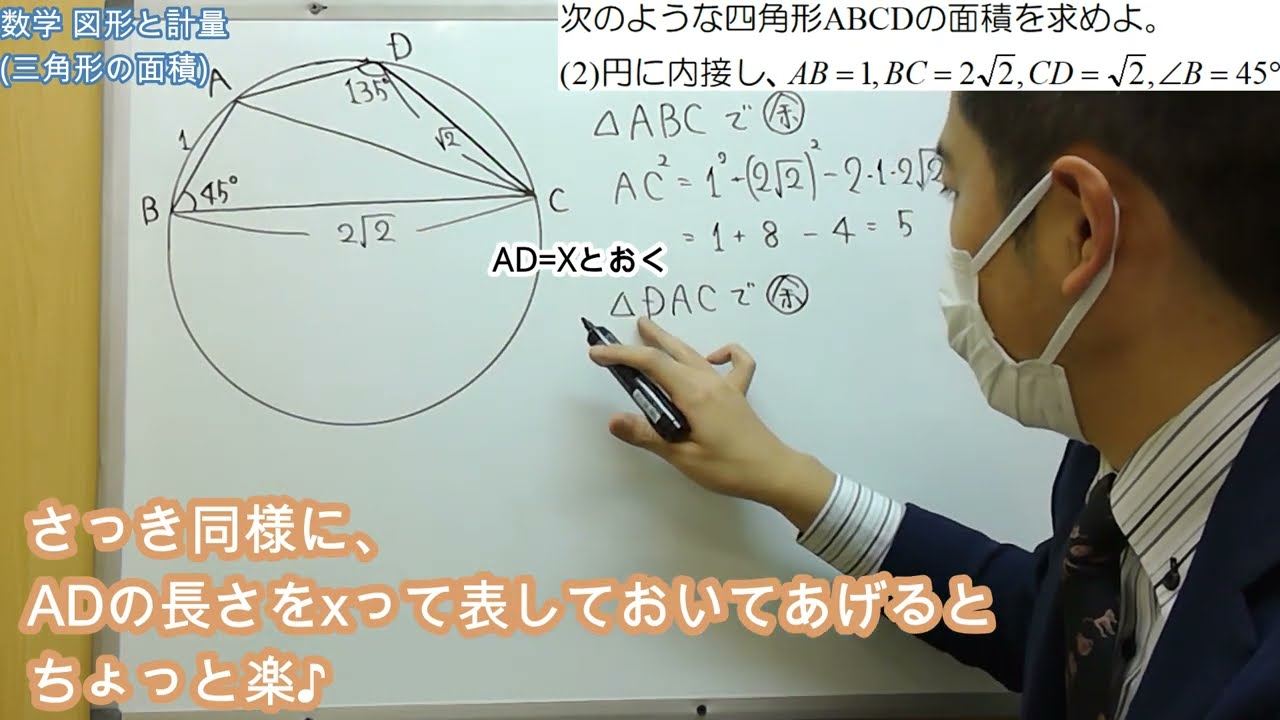
次のような四角形ABCDの面積を求めよ。
(1)円に内接し、$AB=4、BC=3、CD=1、\angle B=60°$
(2)円に内接し、$AB=1、BC=2\sqrt2、CD=\sqrt2、\angle B=45°$
この動画を見る
次のような四角形ABCDの面積を求めよ。
(1)円に内接し、$AB=4、BC=3、CD=1、\angle B=60°$
(2)円に内接し、$AB=1、BC=2\sqrt2、CD=\sqrt2、\angle B=45°$
図形と計量 四角形の面積【烈's study!がていねいに解説】

単元:
#数Ⅰ#数A#図形の性質#図形と計量#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
理数個別チャンネル
問題文全文(内容文):
次のような四角形ABCDの面積を求めよ。
(1)$\angle A=135°,\angle C=45°,AB=1,BC=3,CD=\sqrt2,DA=\sqrt2$
(2)$\angle B=120°,AB=3,BC=5,CD=5,DA=4$
この動画を見る
次のような四角形ABCDの面積を求めよ。
(1)$\angle A=135°,\angle C=45°,AB=1,BC=3,CD=\sqrt2,DA=\sqrt2$
(2)$\angle B=120°,AB=3,BC=5,CD=5,DA=4$
福田の数学〜慶應義塾大学2023年薬学部第1問(2)〜折れ線の最小と内接円の半径

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#三角関数#点と直線#加法定理とその応用#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{1}$ (2)aは正の定数とする。原点をOとするxy平面上に直線l:y=$\frac{2}{3}$xと2点A(0,a), B(17,20)がある。直線l上にとった動点Pと2点A,Bそれぞれを線分で結び、2つの線分の長さの和AP+BPが最小となったとき、$\angle APO$=45°であった。AP+BPが最小であるとき、直線BPを表す方程式はy=$\boxed{\ \ ウ\ \ }$であり、三角形ABPの内接円の半径は$\boxed{\ \ エ\ \ }$である。
2023慶應義塾大学薬学部過去問
この動画を見る
$\Large\boxed{1}$ (2)aは正の定数とする。原点をOとするxy平面上に直線l:y=$\frac{2}{3}$xと2点A(0,a), B(17,20)がある。直線l上にとった動点Pと2点A,Bそれぞれを線分で結び、2つの線分の長さの和AP+BPが最小となったとき、$\angle APO$=45°であった。AP+BPが最小であるとき、直線BPを表す方程式はy=$\boxed{\ \ ウ\ \ }$であり、三角形ABPの内接円の半径は$\boxed{\ \ エ\ \ }$である。
2023慶應義塾大学薬学部過去問
正方形と円
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
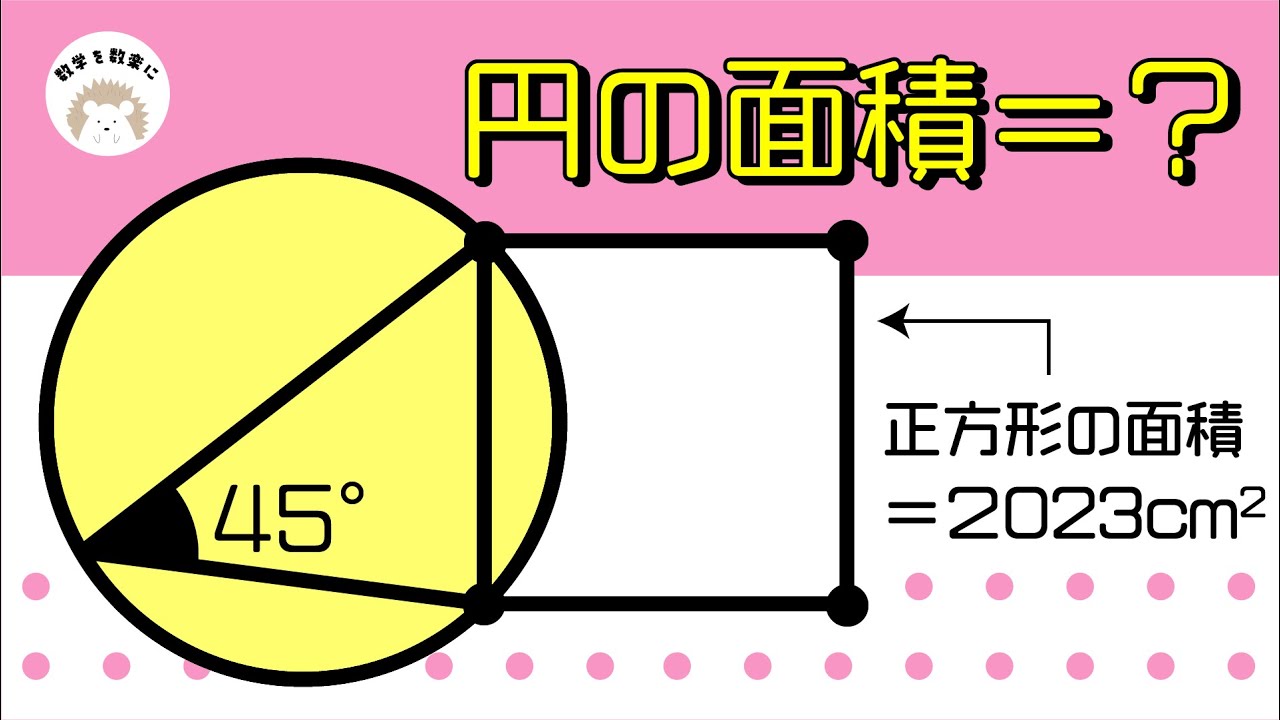
正方形の面積= 2023㎠
円の面積=?
*図は動画内参照
この動画を見る
正方形の面積= 2023㎠
円の面積=?
*図は動画内参照
気付けば一瞬!?
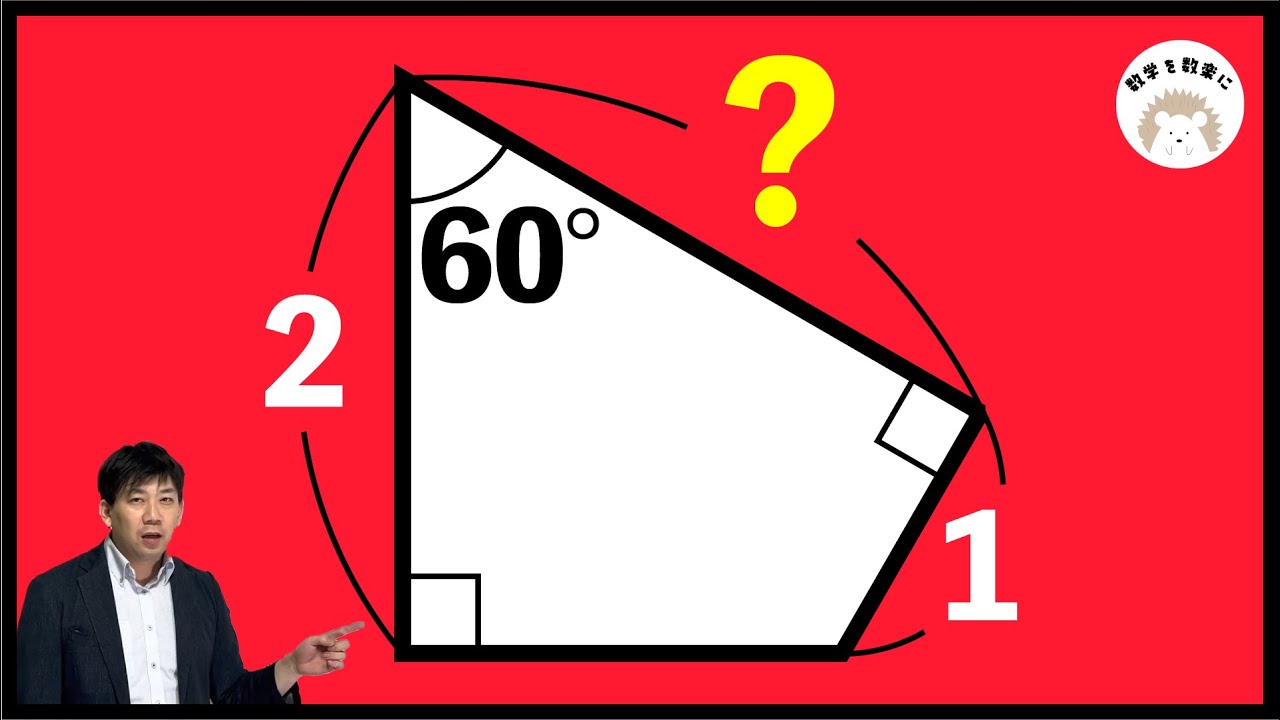
円と正方形 良問です たくさんの別解はコメント欄に いつもありがとうございます。

福田の数学〜京都大学2023年文系第3問〜半径1の円に内接する正五角形の一辺の長さの計量

単元:
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比(三角比・拡張・相互関係・単位円)#三角比への応用(正弦・余弦・面積)#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#京都大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$(1)$\cos 2\theta$と$\cos 3\theta$を$\cos\theta$の式として表せ。
(2)半径1の円に内接する正五角形の一辺の長さが1.15より大きいな否かを理由をつけて判定せよ。
2023京都大学文系過去問
この動画を見る
$\Large\boxed{3}$(1)$\cos 2\theta$と$\cos 3\theta$を$\cos\theta$の式として表せ。
(2)半径1の円に内接する正五角形の一辺の長さが1.15より大きいな否かを理由をつけて判定せよ。
2023京都大学文系過去問
ブーメランの角 明光学院

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle x =?$
*図は動画内参照
明光学院高等学校2023
この動画を見る
$\angle x =?$
*図は動画内参照
明光学院高等学校2023
2023高校入試解説42問目 内接円の半径の比 開成高校(改)
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
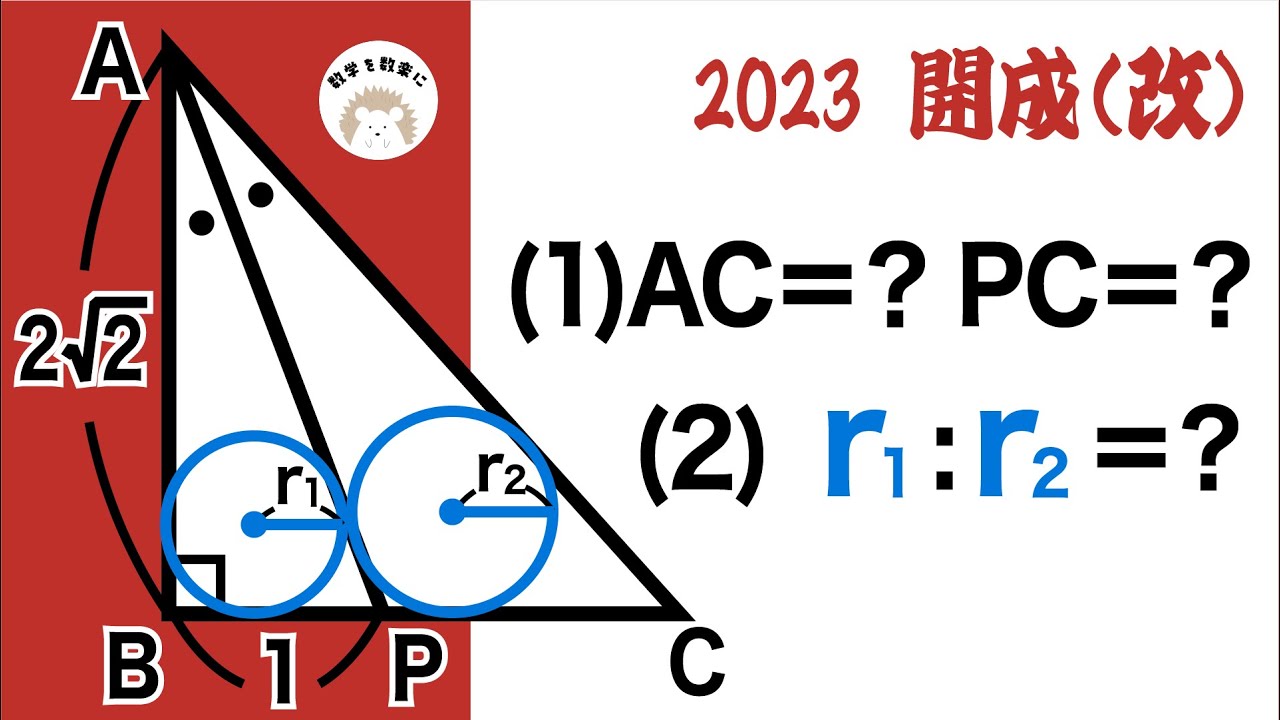
(1)$AC=? PC =?$
(2)$r_1:r_2 =?$
*図は動画内参照
2023 開成高等学校(改)
この動画を見る
(1)$AC=? PC =?$
(2)$r_1:r_2 =?$
*図は動画内参照
2023 開成高等学校(改)
2023高校入試解説36問目 正八角形の外接円の面積=❓ 中大杉並

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
正八角形の面積=?
円の面積=?
*図は動画内参照
2023中央大学杉並高等学校(改)
この動画を見る
正八角形の面積=?
円の面積=?
*図は動画内参照
2023中央大学杉並高等学校(改)
この長さを求める 国立高専←漢字間違えてしまいました。
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)
指導講師:
数学を数楽に
問題文全文(内容文):
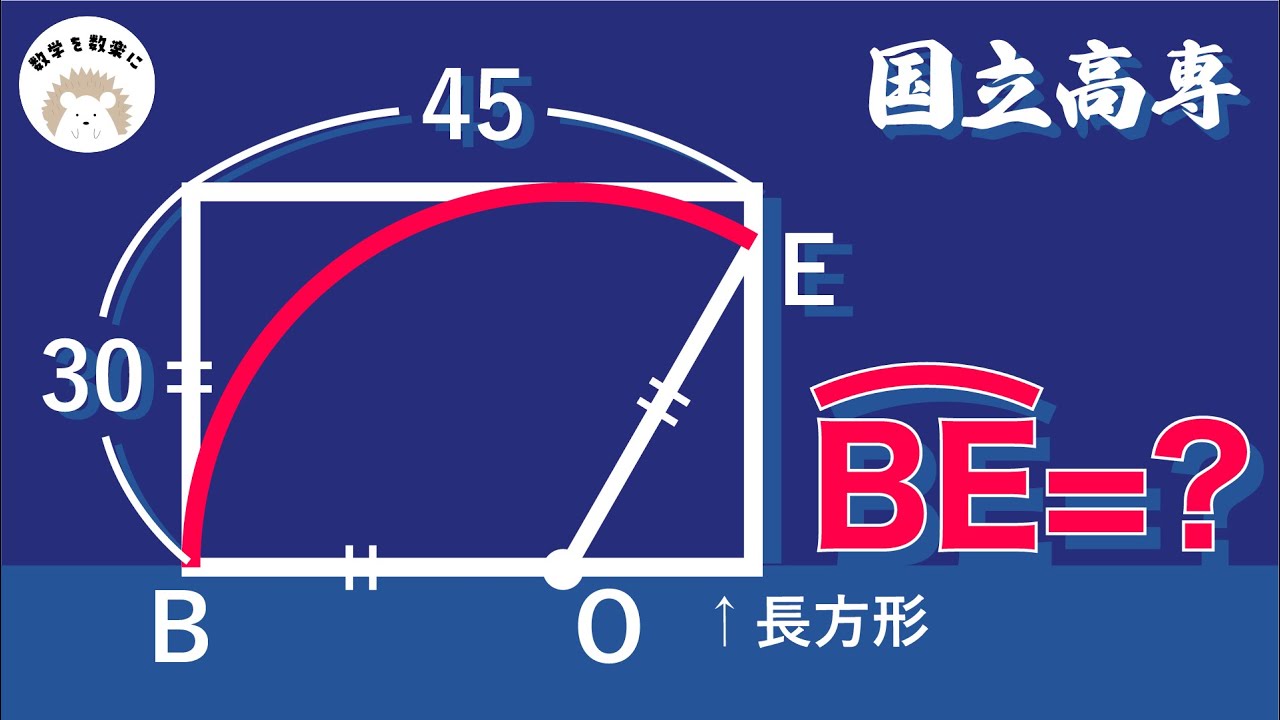
$\stackrel{\huge\frown}{BE}$=?
*図は動画内参照
国立高専
この動画を見る
$\stackrel{\huge\frown}{BE}$=?
*図は動画内参照
国立高専
【高校数学】裏技!円に内接する四角形の面積の求め方! #Shorts
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文):
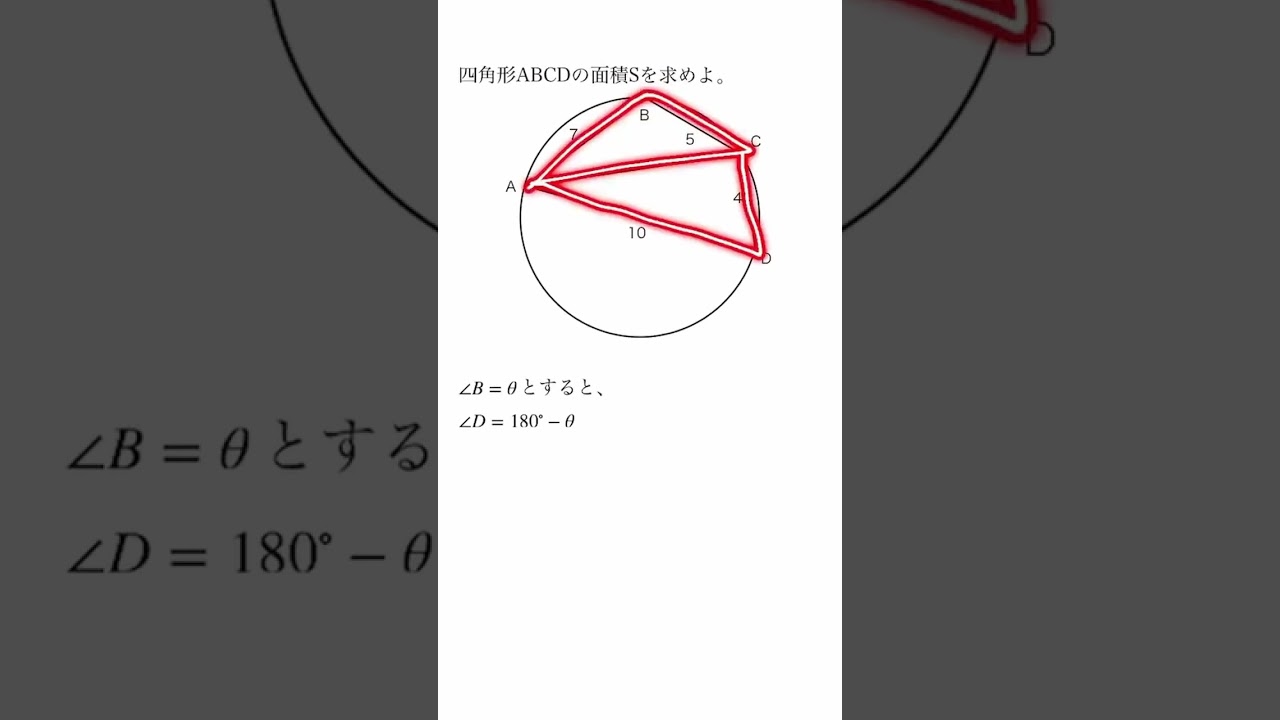
四角形$ABCD$の面積$S$を求めよ。
この動画を見る
四角形$ABCD$の面積$S$を求めよ。
福田の1.5倍速演習〜合格する重要問題100〜慶應義塾大学2020年度総合政策学部第3問〜半円に接する5つの円

単元:
#数A#大学入試過去問(数学)#図形の性質#三平方の定理#周角と円に内接する四角形・円と接線・接弦定理#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large\boxed{3}$ 図のように(※動画参照)半円の中に、半径1の4つの円A, B, C, Dと、別の半径の円Eがあり、次のように接している。円Aは半円の円弧と直径と円Bに接し、円Bは半円の円弧と円A, C, Eに接し、円Cは半円の円弧と円B, D, Eに接し、円Dは半円の円弧と直径と円Cに接している。また、円Eじゃ半円の直径と円B, Cに接している。
このとき、半円の半径は
$\boxed{\ \ アイ\ \ }+\sqrt{\boxed{\ \ ウエ\ \ }+\boxed{\ \ オカ\ \ }\sqrt{\boxed{\ \ キク\ \ }}}$
であり、円Eの半径は
$\frac{\boxed{\ \ ケコ\ \ }+\sqrt{\boxed{\ \ サシ\ \ }}}{\boxed{\ \ スセ\ \ }}$
である。
2020慶應義塾大学総合政策学部過去問
この動画を見る
$\Large\boxed{3}$ 図のように(※動画参照)半円の中に、半径1の4つの円A, B, C, Dと、別の半径の円Eがあり、次のように接している。円Aは半円の円弧と直径と円Bに接し、円Bは半円の円弧と円A, C, Eに接し、円Cは半円の円弧と円B, D, Eに接し、円Dは半円の円弧と直径と円Cに接している。また、円Eじゃ半円の直径と円B, Cに接している。
このとき、半円の半径は
$\boxed{\ \ アイ\ \ }+\sqrt{\boxed{\ \ ウエ\ \ }+\boxed{\ \ オカ\ \ }\sqrt{\boxed{\ \ キク\ \ }}}$
であり、円Eの半径は
$\frac{\boxed{\ \ ケコ\ \ }+\sqrt{\boxed{\ \ サシ\ \ }}}{\boxed{\ \ スセ\ \ }}$
である。
2020慶應義塾大学総合政策学部過去問
