周角と円に内接する四角形・円と接線・接弦定理
周角と円に内接する四角形・円と接線・接弦定理
 周角と円に内接する四角形・円と接線・接弦定理
周角と円に内接する四角形・円と接線・接弦定理
福田の数学〜2023年共通テスト速報〜数学IIB第2問微分積分〜円錐に内接する円柱の体積の最大と桜の開花予想

単元:
#数A#数Ⅱ#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#微分法と積分法#不定積分・定積分#面積、体積#数学(高校生)#大学入試解答速報#数学#共通テスト
指導講師:
福田次郎
問題文全文(内容文):
第2問
[1](1)kを正の定数とし、次の3次関数を考える。
$f(x)=x^2(k-x)$
y=f(x)のグラフとx軸との共有点の座標は(0, 0)と($\boxed{\boxed{\ \ ア\ \ }}$, 0)である。
f(x)の導関数f'(x)は
f'(x)=$\boxed{\ \ イウ\ \ }x^2+\boxed{\ \ エ\ \ }kx$
である。
x=$\boxed{\boxed{\ \ オ\ \ }}$のとき、f(x)は極小値$\boxed{\boxed{\ \ カ\ \ }}$をとる。
x=$\boxed{\boxed{\ \ キ\ \ }}$のとき、f(x)は極大値$\boxed{\boxed{\ \ ク\ \ }}$をとる。
また、0<x<kの範囲においてx=$\boxed{\boxed{\ \ キ\ \ }}$のときf(x)は最大となることがわかる。
$\boxed{\boxed{\ \ ア\ \ }}$, $\boxed{\boxed{\ \ オ\ \ }}$~$\boxed{\boxed{\ \ ク\ \ }}$ の解答群(同じものを繰り返し選んでもよい。)
⓪0 ①$\frac{1}{3}k$ ②$\frac{1}{2}k$ ③$\frac{2}{3}k$
④k ⑤$\frac{3}{2}k$ ⑥$-4k^2$ ⑦$\frac{1}{8}k^2$
⑧$\frac{2}{27}k^3$ ⑨$\frac{4}{27}k^3$ ⓐ$\frac{4}{9}k^3$ ⓑ$4k^3$
(2)後の図のように底面が半径9の円で高さが15の円錐に内接する円柱を考える。円柱の底面の半径と体積をそれぞれx, Vとする。Vをxの式で表すと
V=$\frac{\boxed{\ \ ケ\ \ }}{\boxed{\ \ コ\ \ }}\pi x^2(\boxed{\ \ サ\ \ }-x)$(0<x<9)
である。(1)の考察より、x=$\boxed{\ \ シ\ \ }$のときVは最大となることがわかる。Vの最大値は$\boxed{\ \ スセソ\ \ }\pi$である。
[2](1)定積分$\displaystyle\int_0^{30}(\frac{1}{5}x+3)dx$の値は$\boxed{\ \ タチツ\ \ }$である。
また、関数$\displaystyle\frac{1}{100}x^2-\frac{1}{6}x+5$の不定積分は
$\displaystyle\int(\frac{1}{100}x^2-\frac{1}{6}x+5)dx$=$\displaystyle\frac{1}{\boxed{\ \ テトナ\ \ }}x^3-\frac{1}{\boxed{\ \ ニヌ\ \ }}x^2+\boxed{\ \ ネ\ \ }x+C$である。ただし、Cは積分定数とする。
(2)ある地域では、毎年3月頃「ソメイヨシノ(桜の種類)の開花予想日」が話題になる。太郎さんと花子さんは、開花日時を予想する方法の一つに、2月に入ってからの気温を時間の関数とみて、その関数を積分した値をもとにする方法があることを知った。ソメイヨシノの開花日時を予想するために、二人は図1の6時間ごとの気温の折れ線グラフを見ながら、次のように考えることにした。(※図1は動画参照)
xの値の範囲を0以上の実数全体として、2月1日午前0時から24x時間経った時点をx日後とする。(例えば、10.3日後は2月11日午前7時12分を表す。)また、x日後の気温をy℃とする。このとき、yはxの関数であり、これをy=f(x)とおく。ただし、yは負にはならないものとする。
気温を表す関数f(x)を用いて二人はソメイヨシノの開花日時を次の設定で考えることにした。
設定:正の実数tに対して、f(x)を0からtまで積分した値をS(t)とする。すなわち、S(t)=$\displaystyle\int_0^tf(x)dx$とする。このS(t)が400に到達したとき、ソメイヨシノが開花する。
設定のもと、太郎さんは気温を表す関数y=f(x)のグラフを図2(※動画参照)のように直線とみなしてソメイヨシノの開花日時を考えることにした。
(i)太郎さんは
$f(x)=\displaystyle\frac{1}{5}x+3$ (x ≧0)
として考えた。このとき、ソメイヨシノの開花日時は2月に入ってから$\boxed{\boxed{\ \ ノ\ \ }}$となる。
$\boxed{\boxed{\ \ ノ\ \ }}$の解答群
⓪30日後 ①35日後 ②40日後
③45日後 ④50日後 ⑤55日後
⑥60日後 ⑦65日後
(ii)太郎さんと花子さんは、2月に入ってから30日後以降の気温について話をしている。
太郎:1次関数を用いてソメイヨシノの開花日時を求めてみたよ。
花子:気温の上がり方から考えて、2月に入ってから30日後以降の気温を表す関数が2次関数の場合も考えて見ようか。
花子さんは気温を表す関数f(x)を、0≦x≦30のときは太郎さんと同じように
f(x)=$\frac{1}{5}x+3$ ...①
とし、x≧30のときは
f(x)=$\frac{1}{100}x^2-\frac{1}{6}x+5$ ...②
として考えた。なお、x=30のとき①の右辺の値と②の右辺の値は一致する。花子さんの考えた式を用いて、ソメイヨシノの開花日時を考えよう。(1)より
$\displaystyle\int_0^{30}(\frac{1}{5}x+3)dx$=$\boxed{\ \ タチツ\ \ }$
であり
$\displaystyle\int_{30}^{40}(\frac{1}{100}x^2-\frac{1}{6}x+5)dx$=115
となることがわかる。
また、x ≧30の範囲においてf(x)は増加する。よって
$\displaystyle\int_{30}^{40}f(x)dx$ $\boxed{\boxed{\ \ ハ\ \ }}$ $\displaystyle\int_{40}^{50}f(x)dx$
であることがわかる。以上より、ソメイヨシノの開花日時は2月に入ってから$\boxed{\boxed{\ \ ヒ\ \ }}$となる。
2023共通テスト過去問
この動画を見る
第2問
[1](1)kを正の定数とし、次の3次関数を考える。
$f(x)=x^2(k-x)$
y=f(x)のグラフとx軸との共有点の座標は(0, 0)と($\boxed{\boxed{\ \ ア\ \ }}$, 0)である。
f(x)の導関数f'(x)は
f'(x)=$\boxed{\ \ イウ\ \ }x^2+\boxed{\ \ エ\ \ }kx$
である。
x=$\boxed{\boxed{\ \ オ\ \ }}$のとき、f(x)は極小値$\boxed{\boxed{\ \ カ\ \ }}$をとる。
x=$\boxed{\boxed{\ \ キ\ \ }}$のとき、f(x)は極大値$\boxed{\boxed{\ \ ク\ \ }}$をとる。
また、0<x<kの範囲においてx=$\boxed{\boxed{\ \ キ\ \ }}$のときf(x)は最大となることがわかる。
$\boxed{\boxed{\ \ ア\ \ }}$, $\boxed{\boxed{\ \ オ\ \ }}$~$\boxed{\boxed{\ \ ク\ \ }}$ の解答群(同じものを繰り返し選んでもよい。)
⓪0 ①$\frac{1}{3}k$ ②$\frac{1}{2}k$ ③$\frac{2}{3}k$
④k ⑤$\frac{3}{2}k$ ⑥$-4k^2$ ⑦$\frac{1}{8}k^2$
⑧$\frac{2}{27}k^3$ ⑨$\frac{4}{27}k^3$ ⓐ$\frac{4}{9}k^3$ ⓑ$4k^3$
(2)後の図のように底面が半径9の円で高さが15の円錐に内接する円柱を考える。円柱の底面の半径と体積をそれぞれx, Vとする。Vをxの式で表すと
V=$\frac{\boxed{\ \ ケ\ \ }}{\boxed{\ \ コ\ \ }}\pi x^2(\boxed{\ \ サ\ \ }-x)$(0<x<9)
である。(1)の考察より、x=$\boxed{\ \ シ\ \ }$のときVは最大となることがわかる。Vの最大値は$\boxed{\ \ スセソ\ \ }\pi$である。
[2](1)定積分$\displaystyle\int_0^{30}(\frac{1}{5}x+3)dx$の値は$\boxed{\ \ タチツ\ \ }$である。
また、関数$\displaystyle\frac{1}{100}x^2-\frac{1}{6}x+5$の不定積分は
$\displaystyle\int(\frac{1}{100}x^2-\frac{1}{6}x+5)dx$=$\displaystyle\frac{1}{\boxed{\ \ テトナ\ \ }}x^3-\frac{1}{\boxed{\ \ ニヌ\ \ }}x^2+\boxed{\ \ ネ\ \ }x+C$である。ただし、Cは積分定数とする。
(2)ある地域では、毎年3月頃「ソメイヨシノ(桜の種類)の開花予想日」が話題になる。太郎さんと花子さんは、開花日時を予想する方法の一つに、2月に入ってからの気温を時間の関数とみて、その関数を積分した値をもとにする方法があることを知った。ソメイヨシノの開花日時を予想するために、二人は図1の6時間ごとの気温の折れ線グラフを見ながら、次のように考えることにした。(※図1は動画参照)
xの値の範囲を0以上の実数全体として、2月1日午前0時から24x時間経った時点をx日後とする。(例えば、10.3日後は2月11日午前7時12分を表す。)また、x日後の気温をy℃とする。このとき、yはxの関数であり、これをy=f(x)とおく。ただし、yは負にはならないものとする。
気温を表す関数f(x)を用いて二人はソメイヨシノの開花日時を次の設定で考えることにした。
設定:正の実数tに対して、f(x)を0からtまで積分した値をS(t)とする。すなわち、S(t)=$\displaystyle\int_0^tf(x)dx$とする。このS(t)が400に到達したとき、ソメイヨシノが開花する。
設定のもと、太郎さんは気温を表す関数y=f(x)のグラフを図2(※動画参照)のように直線とみなしてソメイヨシノの開花日時を考えることにした。
(i)太郎さんは
$f(x)=\displaystyle\frac{1}{5}x+3$ (x ≧0)
として考えた。このとき、ソメイヨシノの開花日時は2月に入ってから$\boxed{\boxed{\ \ ノ\ \ }}$となる。
$\boxed{\boxed{\ \ ノ\ \ }}$の解答群
⓪30日後 ①35日後 ②40日後
③45日後 ④50日後 ⑤55日後
⑥60日後 ⑦65日後
(ii)太郎さんと花子さんは、2月に入ってから30日後以降の気温について話をしている。
太郎:1次関数を用いてソメイヨシノの開花日時を求めてみたよ。
花子:気温の上がり方から考えて、2月に入ってから30日後以降の気温を表す関数が2次関数の場合も考えて見ようか。
花子さんは気温を表す関数f(x)を、0≦x≦30のときは太郎さんと同じように
f(x)=$\frac{1}{5}x+3$ ...①
とし、x≧30のときは
f(x)=$\frac{1}{100}x^2-\frac{1}{6}x+5$ ...②
として考えた。なお、x=30のとき①の右辺の値と②の右辺の値は一致する。花子さんの考えた式を用いて、ソメイヨシノの開花日時を考えよう。(1)より
$\displaystyle\int_0^{30}(\frac{1}{5}x+3)dx$=$\boxed{\ \ タチツ\ \ }$
であり
$\displaystyle\int_{30}^{40}(\frac{1}{100}x^2-\frac{1}{6}x+5)dx$=115
となることがわかる。
また、x ≧30の範囲においてf(x)は増加する。よって
$\displaystyle\int_{30}^{40}f(x)dx$ $\boxed{\boxed{\ \ ハ\ \ }}$ $\displaystyle\int_{40}^{50}f(x)dx$
であることがわかる。以上より、ソメイヨシノの開花日時は2月に入ってから$\boxed{\boxed{\ \ ヒ\ \ }}$となる。
2023共通テスト過去問
2023高校入試解説17問目 3つの内接円 渋谷教育学園幕張
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
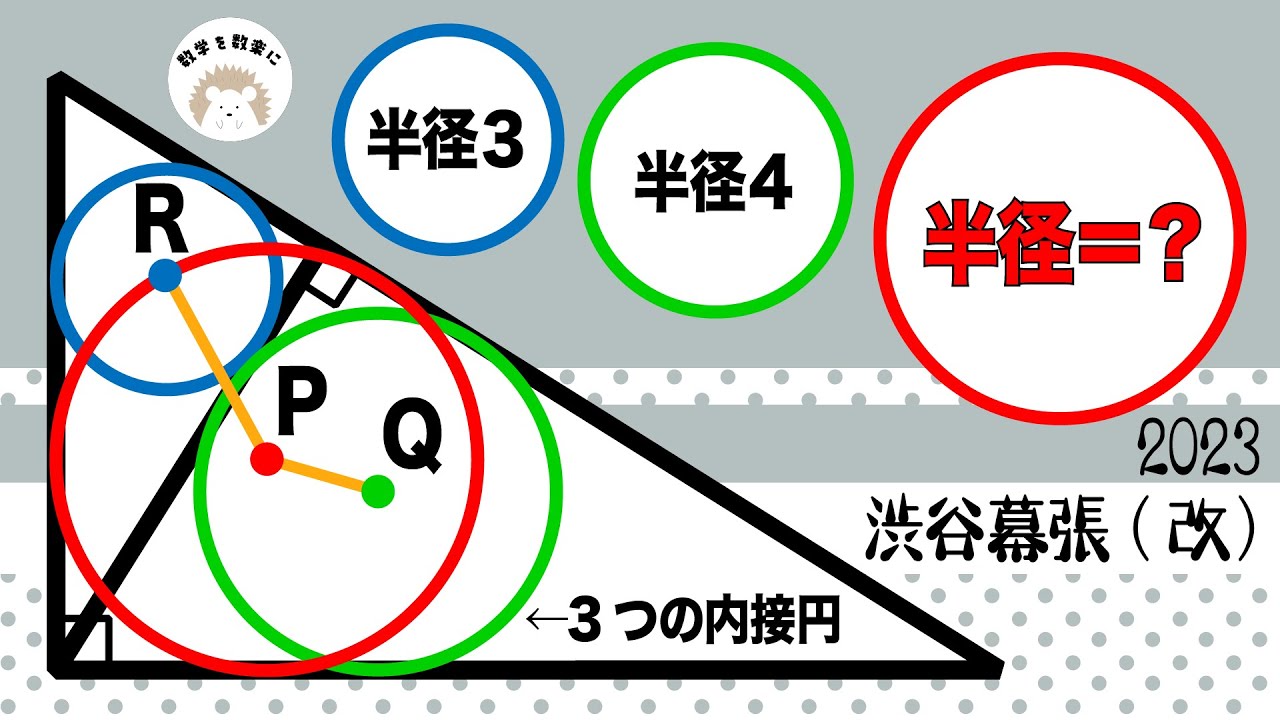
青○:半径3
緑○:半径4
赤○:半径=?
*図は動画内参照
2023渋谷教育学園幕張高等学校(改)
この動画を見る
青○:半径3
緑○:半径4
赤○:半径=?
*図は動画内参照
2023渋谷教育学園幕張高等学校(改)
2023高校入試解説12問目 台形と半円 解き方2通り 日大習志野(改)

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$AD=\frac{9}{4}$
半円Oの面積=?
*図は動画内参照
2023日本大学習志野高等学校
この動画を見る
$AD=\frac{9}{4}$
半円Oの面積=?
*図は動画内参照
2023日本大学習志野高等学校
福田の1.5倍速演習〜合格する重要問題059〜慶應義塾大学2019年度薬学部第1問(7)〜球に内接する四角錐の体積の最大値

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{1}}$ (7)正四角錐ABCDEの全ての頂点は半径3の球面上にある。
この正四角錐の体積Vの最大値は$\boxed{\ \ ソ\ \ }$である。
2019慶應義塾大学薬学部過去問
この動画を見る
$\Large{\boxed{1}}$ (7)正四角錐ABCDEの全ての頂点は半径3の球面上にある。
この正四角錐の体積Vの最大値は$\boxed{\ \ ソ\ \ }$である。
2019慶應義塾大学薬学部過去問
福田の1.5倍速演習〜合格する重要問題058〜慶應義塾大学2019年度環境情報学部第5問〜正方形の中の内接外接する円の半径

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#円と方程式#学校別大学入試過去問解説(数学)#慶應義塾大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$\Large{\boxed{5}}$ 図のように(※動画参照)、1つの正方形の中に、半径の異なる3種類の円が合計10個配置されている。
円$A_1$と$A_2$は半径が同じRで、それぞれ図のように正方形の2辺に内接している。
円$B_1,B_2,B_3,B_4,B_5,B_6$は半径が同じrで、円$B_1$と$B_2$は接し、
図のように両方とも円$A_1$に内接し円$A_2$に外接している。円$B_3$と$B_4$は接し、図のように両方とも円$A_1$と円$A_2$に内接している。円$B_5$と$B_6$は接し、
図のように両方とも円$A_1$に外接し円$A_2$に内接している。
円$C_1$と$C_2$は半径が同じ$r'$で、それぞれ図のように正方形の2辺に内接し、円$A_1$と$A_2$に外接している。なお、円$B_1,B_2,B_5,B_6$は正方形の辺に接していない。
このとき、正方形の1辺の長さをsとすると
$\left\{\begin{array}{1}
R=\displaystyle\frac{\boxed{\ \ アイ\ \ }}{\boxed{\ \ ウエ\ \ }}r \\
s=\left(\boxed{\ \ オカ\ \ }\sqrt{R}+\boxed{\ \ キク\ \ }\sqrt{r'}\right)^{\boxed{ケコ}}\\
r'=\frac{\boxed{\ \ サシ\ \ }+\displaystyle\sqrt{10}+\boxed{\ \ スセ\ \ }\sqrt{\boxed{\ \ ソタ\ \ }+\displaystyle5\sqrt{10}}}{\boxed{\ \ チツ\ \ }}r\\
\end{array}\right.$
である。
2019慶應義塾大学環境情報学部過去問
この動画を見る
$\Large{\boxed{5}}$ 図のように(※動画参照)、1つの正方形の中に、半径の異なる3種類の円が合計10個配置されている。
円$A_1$と$A_2$は半径が同じRで、それぞれ図のように正方形の2辺に内接している。
円$B_1,B_2,B_3,B_4,B_5,B_6$は半径が同じrで、円$B_1$と$B_2$は接し、
図のように両方とも円$A_1$に内接し円$A_2$に外接している。円$B_3$と$B_4$は接し、図のように両方とも円$A_1$と円$A_2$に内接している。円$B_5$と$B_6$は接し、
図のように両方とも円$A_1$に外接し円$A_2$に内接している。
円$C_1$と$C_2$は半径が同じ$r'$で、それぞれ図のように正方形の2辺に内接し、円$A_1$と$A_2$に外接している。なお、円$B_1,B_2,B_5,B_6$は正方形の辺に接していない。
このとき、正方形の1辺の長さをsとすると
$\left\{\begin{array}{1}
R=\displaystyle\frac{\boxed{\ \ アイ\ \ }}{\boxed{\ \ ウエ\ \ }}r \\
s=\left(\boxed{\ \ オカ\ \ }\sqrt{R}+\boxed{\ \ キク\ \ }\sqrt{r'}\right)^{\boxed{ケコ}}\\
r'=\frac{\boxed{\ \ サシ\ \ }+\displaystyle\sqrt{10}+\boxed{\ \ スセ\ \ }\sqrt{\boxed{\ \ ソタ\ \ }+\displaystyle5\sqrt{10}}}{\boxed{\ \ チツ\ \ }}r\\
\end{array}\right.$
である。
2019慶應義塾大学環境情報学部過去問
球が出てきただけでビビるなよ。海城高校
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
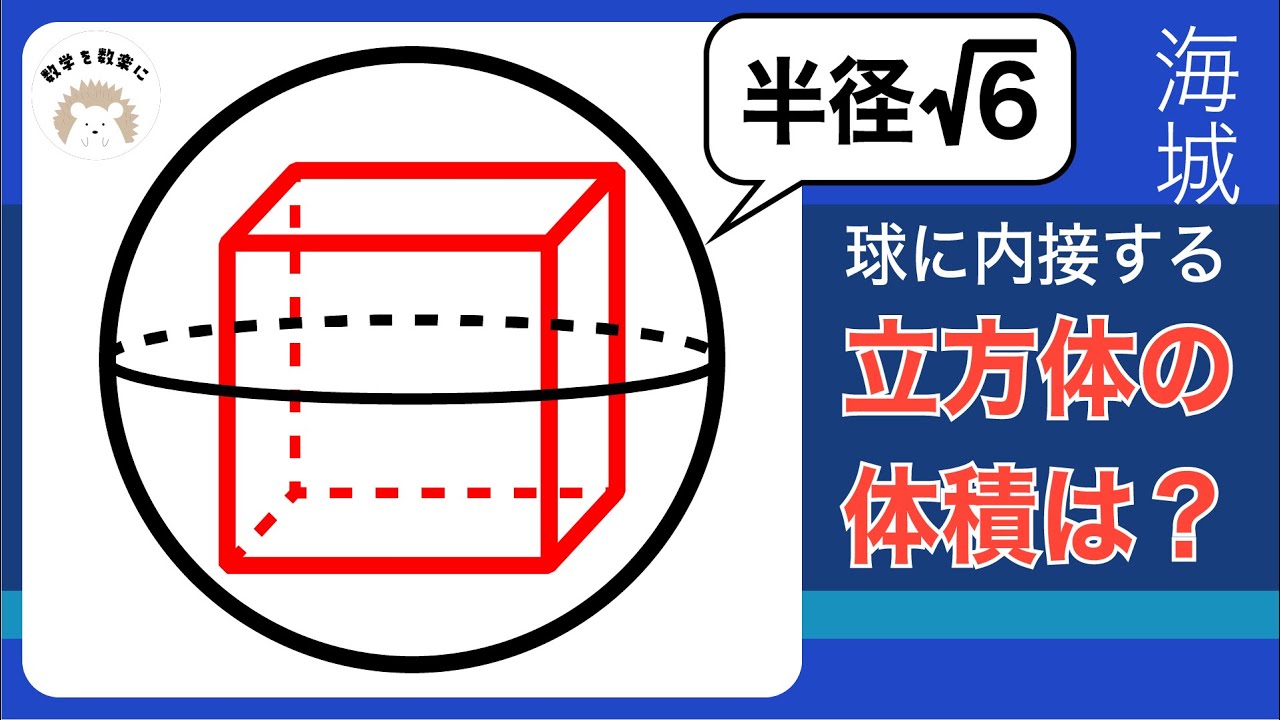
半径$\sqrt 6$の球に内接する立方体の体積=?
*図は動画内参照
海城高等学校
この動画を見る
半径$\sqrt 6$の球に内接する立方体の体積=?
*図は動画内参照
海城高等学校
斜線部分の面積を求めよ 洛南高校
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
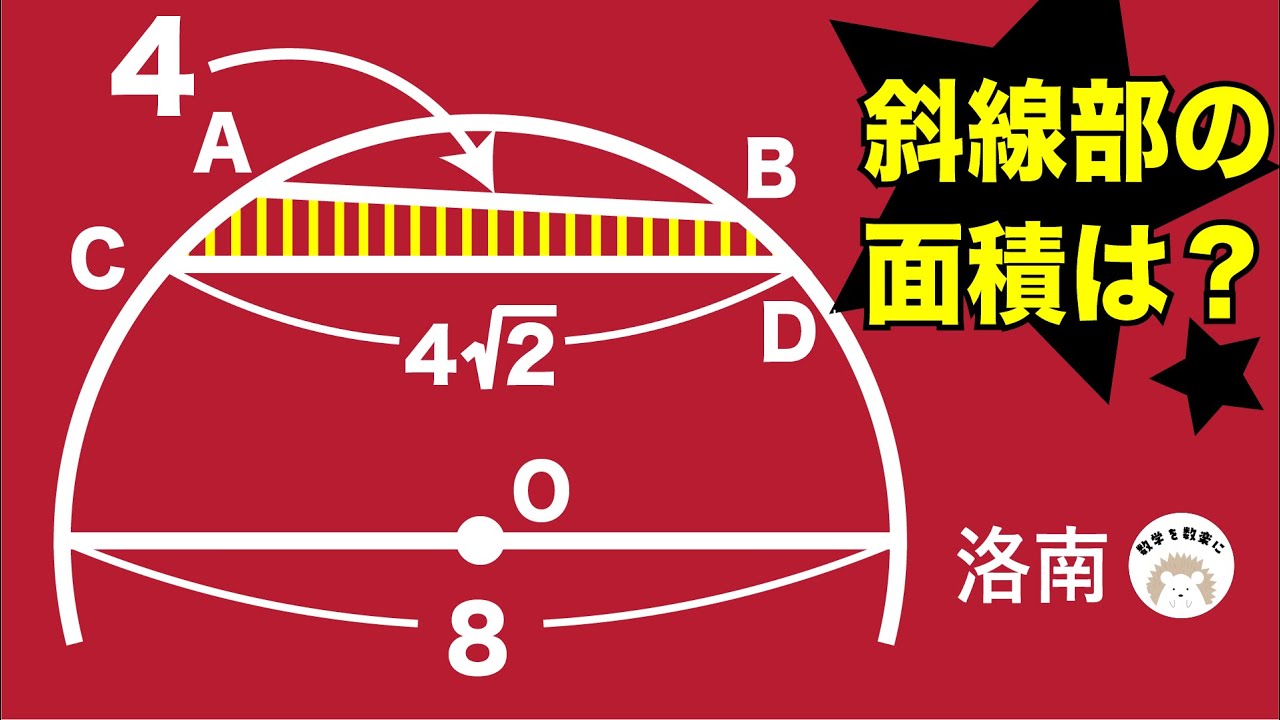
斜線部の面積を求めよ。
洛南高等学校
この動画を見る
斜線部の面積を求めよ。
洛南高等学校
気付けば、そして知っていれば一瞬!!円
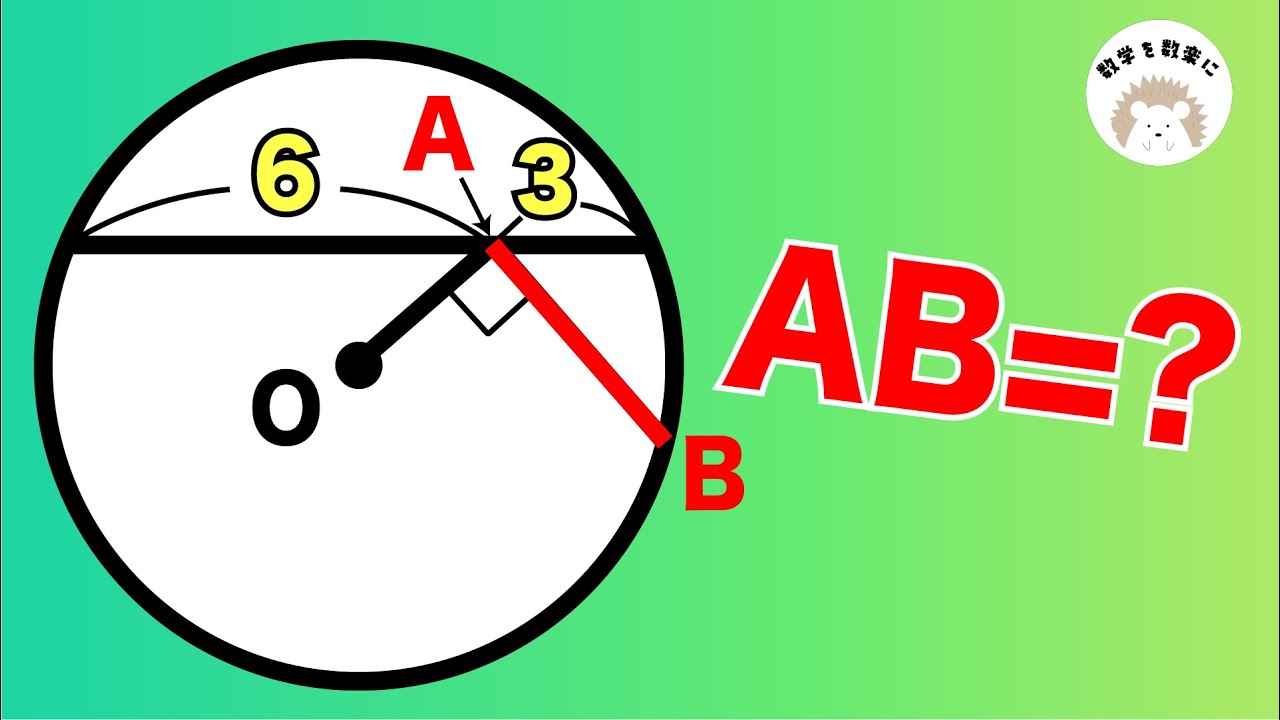
気付けば一瞬!!円と正方形
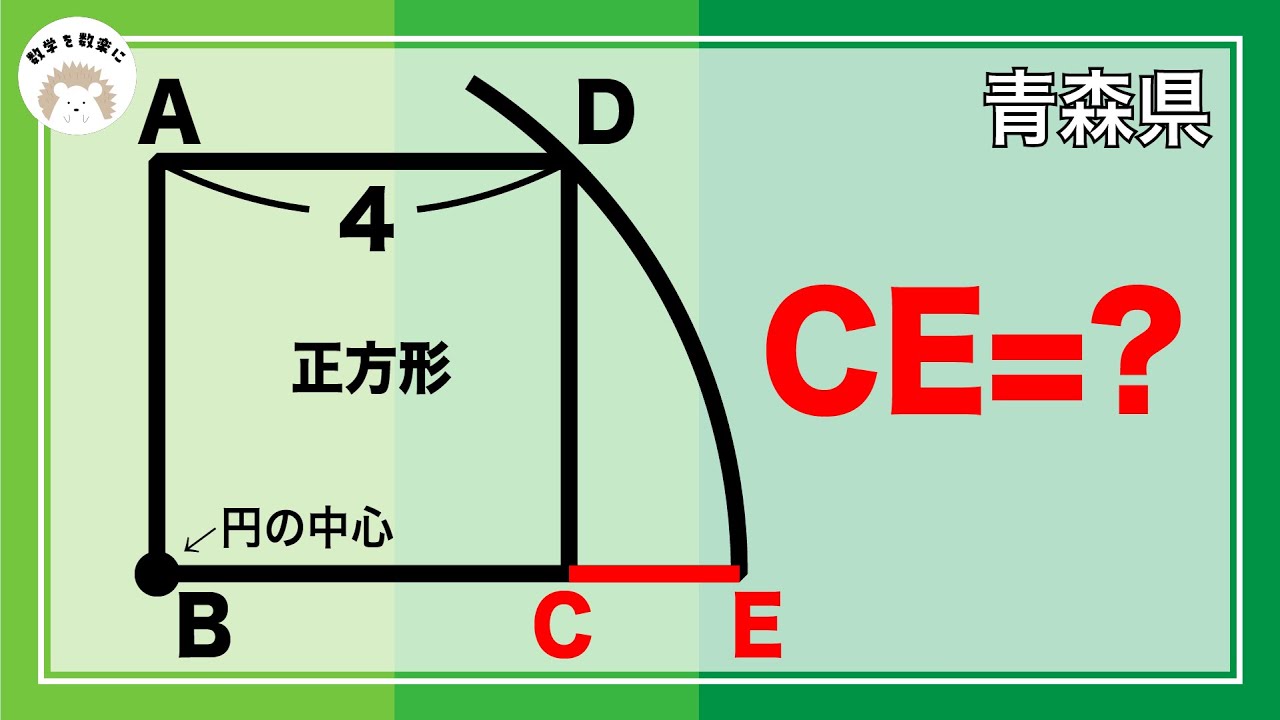
円と長方形
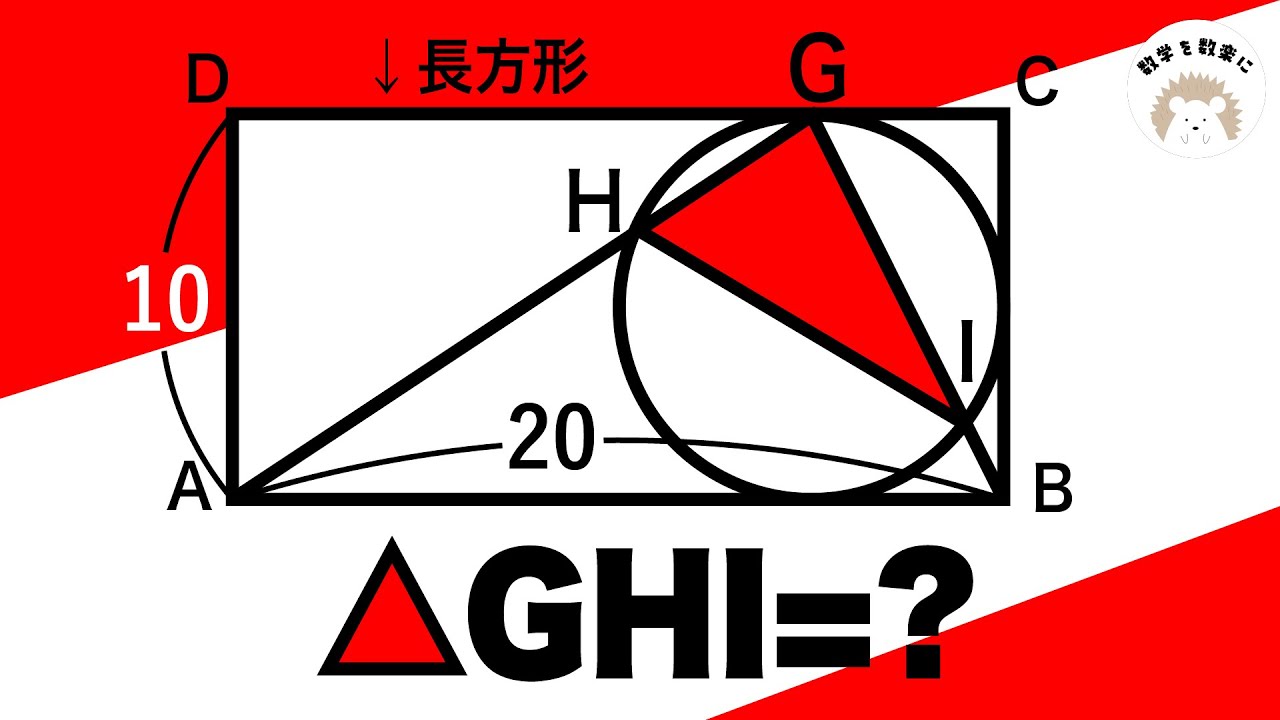
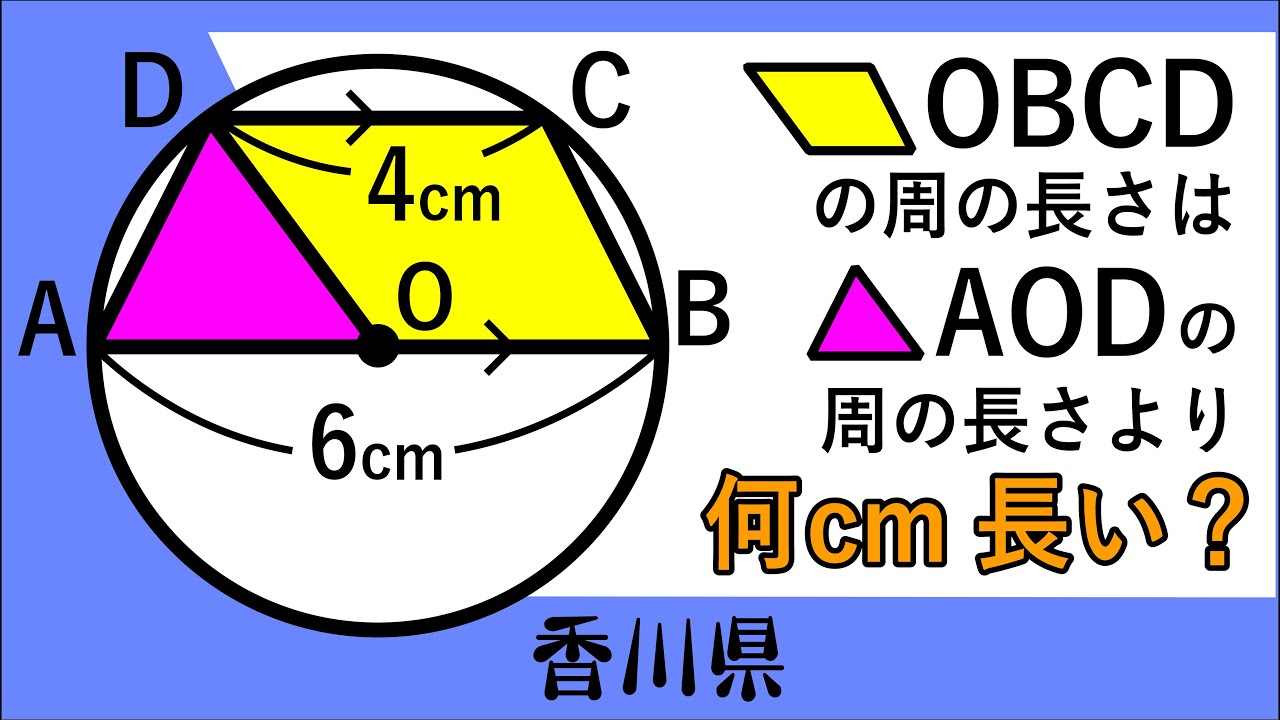
気づけば一瞬!!円に内接する台形 香川県
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
四角形OBCDの周の長さは△AODの周の長さより何㎝長い?
*図は動画内参照
香川県
この動画を見る
四角形OBCDの周の長さは△AODの周の長さより何㎝長い?
*図は動画内参照
香川県
面積が最小となるとき
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#平面図形#角度と面積#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
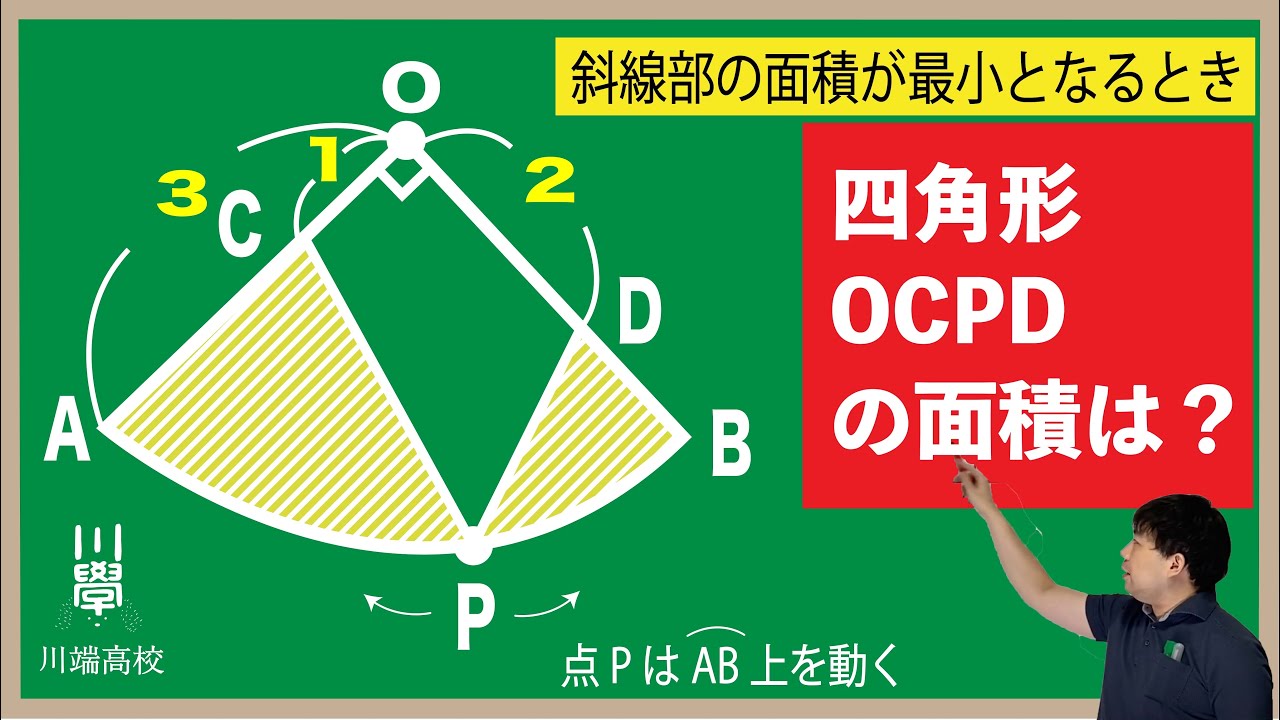
点Pは$\stackrel{\huge\frown}{AB}$上を動く
斜線部の面積が最小となるとき四角形OCPDの面積は?
*図は動画内参照
川端高校
この動画を見る
点Pは$\stackrel{\huge\frown}{AB}$上を動く
斜線部の面積が最小となるとき四角形OCPDの面積は?
*図は動画内参照
川端高校
円と台形
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
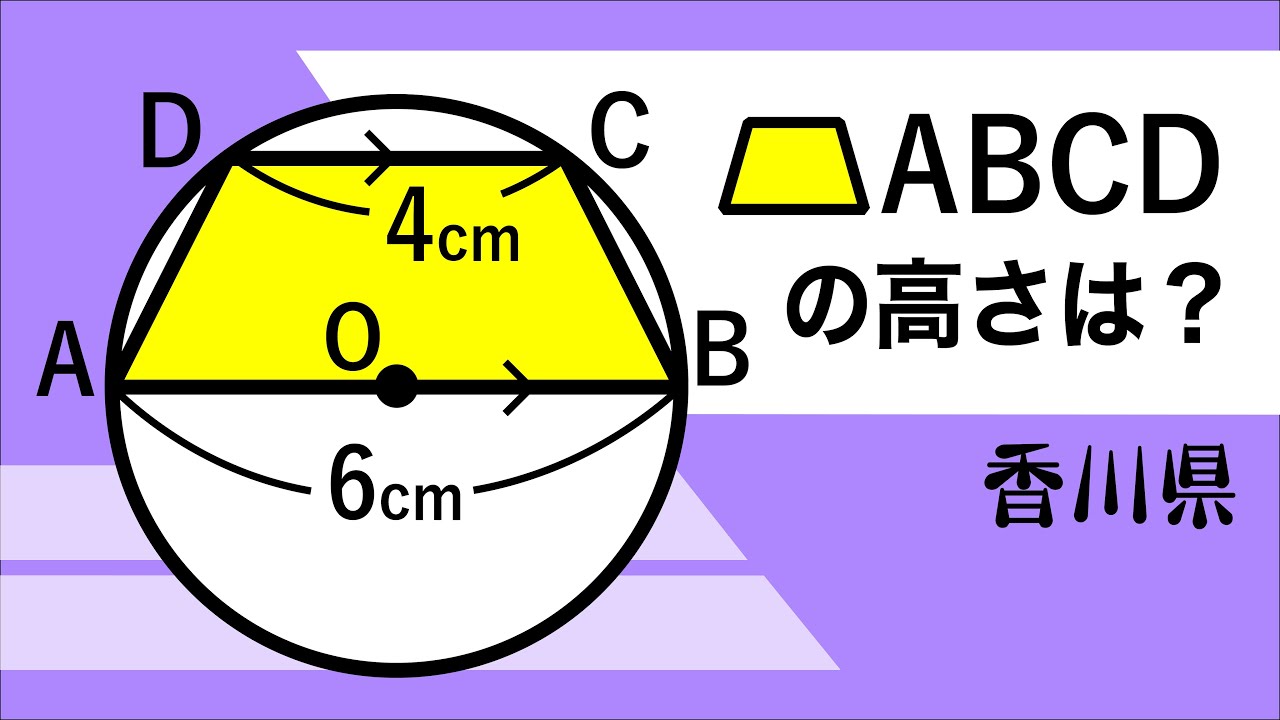
台形ABCDの高さは?
*図は動画内参照
香川県
この動画を見る
台形ABCDの高さは?
*図は動画内参照
香川県
座標平面 円と接線 中央大杉並
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
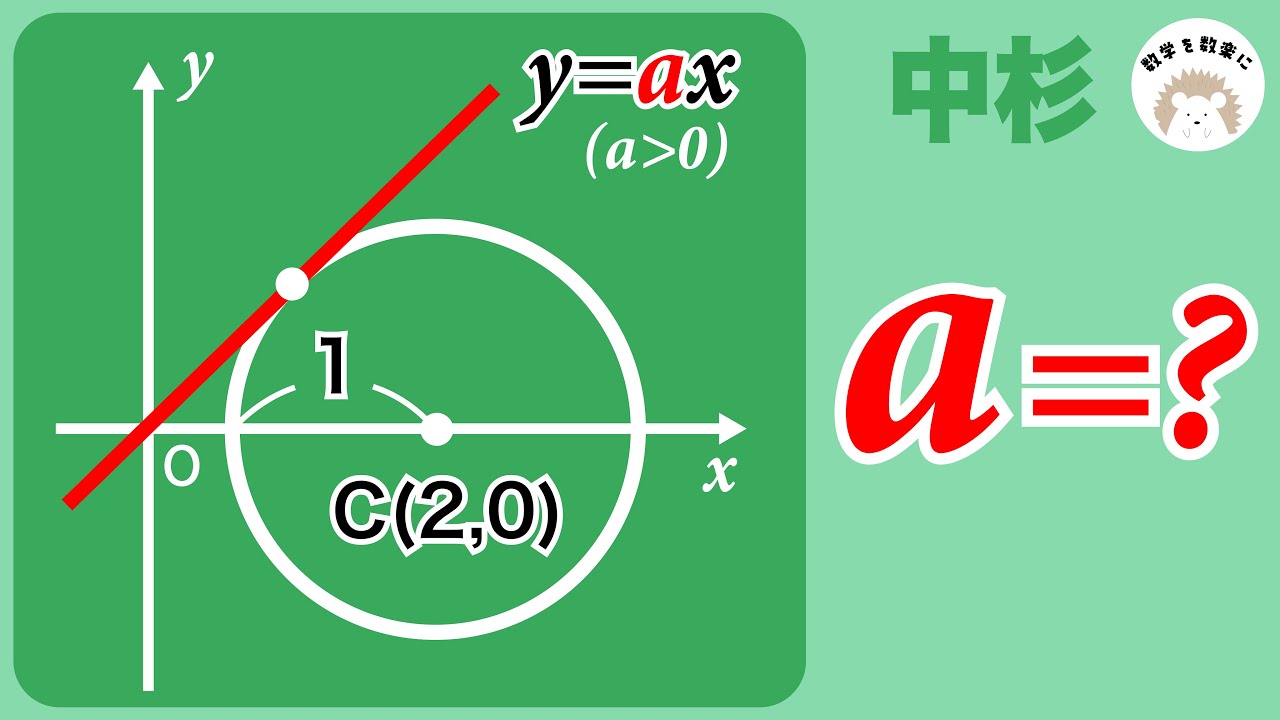
y=ax
a=?
*図は動画内参照
中央大学杉並高等学校
この動画を見る
y=ax
a=?
*図は動画内参照
中央大学杉並高等学校
長方形と円 愛知県

単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
長方形ABCDの面積=?
*図は動画内参照
愛知県
この動画を見る
長方形ABCDの面積=?
*図は動画内参照
愛知県
平行四辺形と円 東大寺学園
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
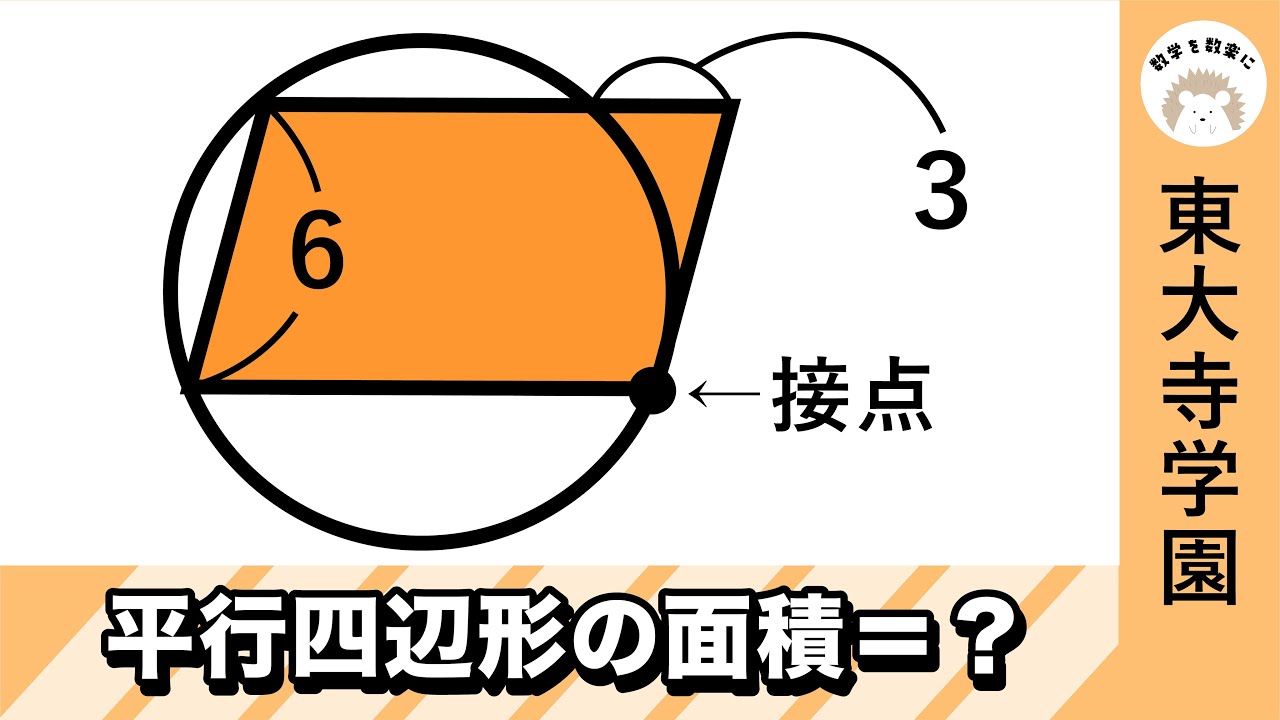
平行四辺形の面積=?
*図は動画内参照
東大寺学園高等学校
この動画を見る
平行四辺形の面積=?
*図は動画内参照
東大寺学園高等学校
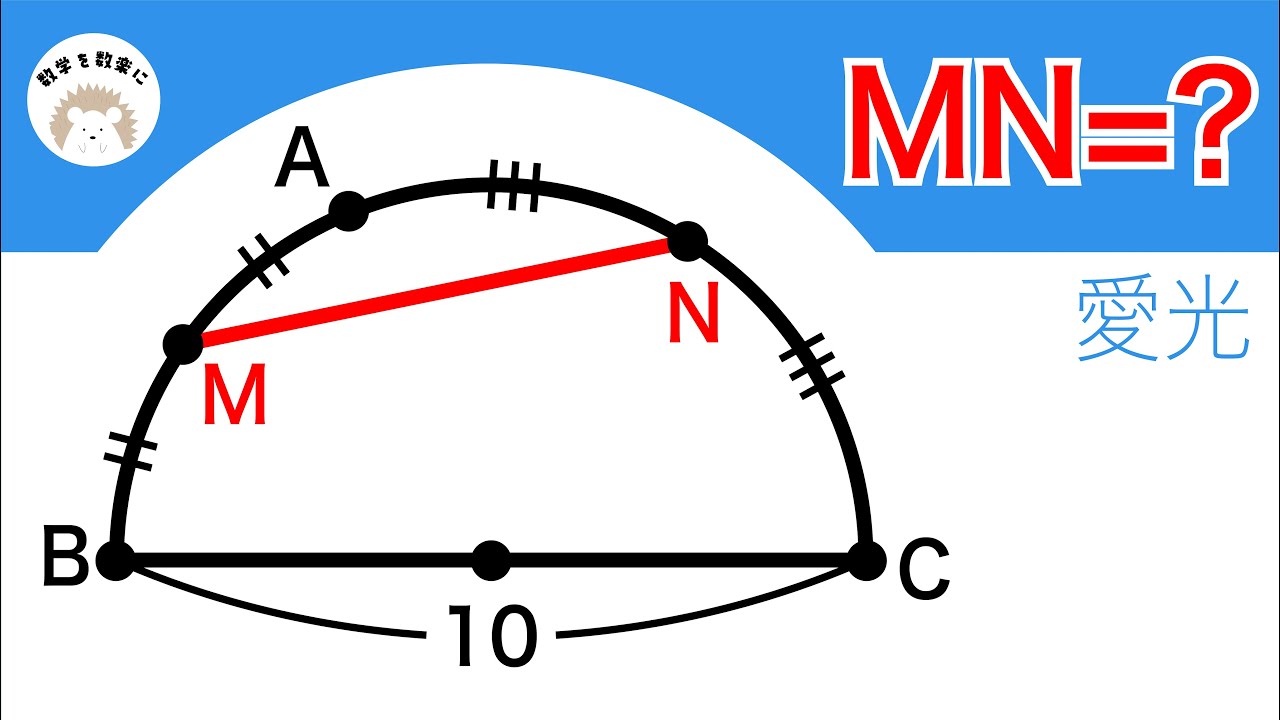
半円 愛光高校
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
MN=?
*図は動画内参照
愛光学園
この動画を見る
MN=?
*図は動画内参照
愛光学園
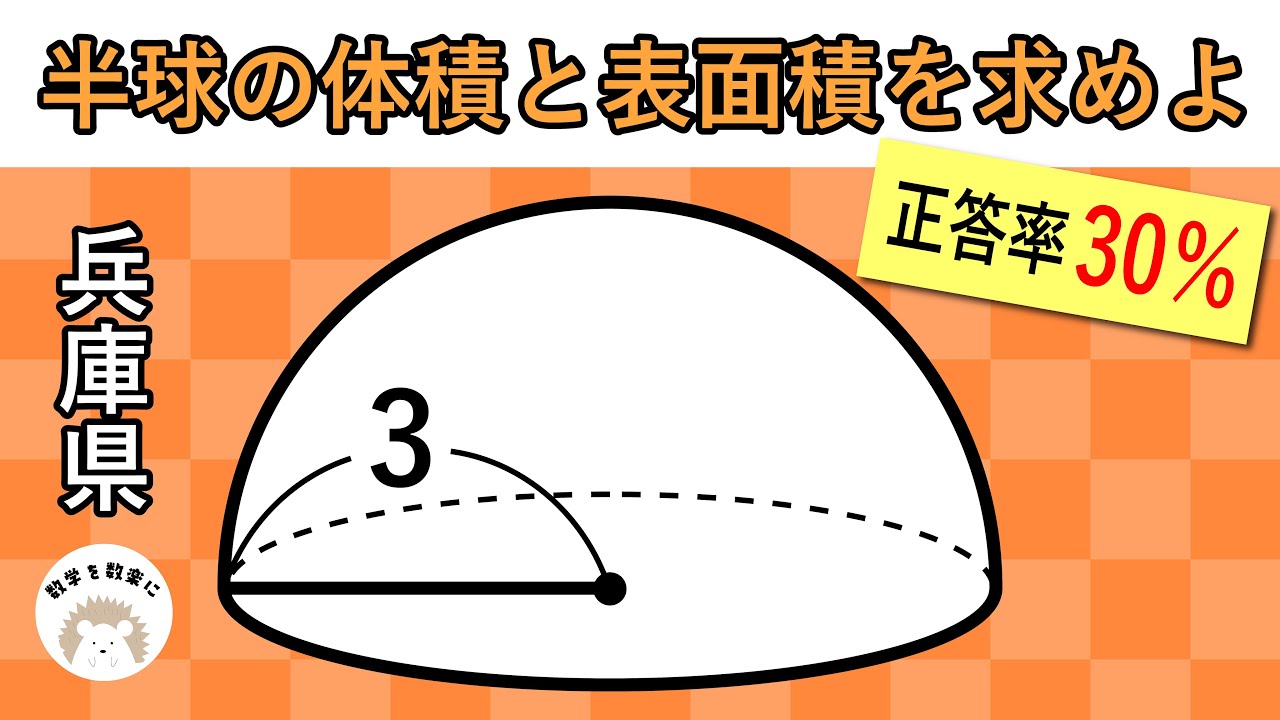
意外に間違えている。。半球の体積 表面積 兵庫県
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#立体図形#体積・表面積・回転体・水量・変化のグラフ
指導講師:
数学を数楽に
問題文全文(内容文):
半球の体積と表面積を求めよ
*図は動画内参照
兵庫県
この動画を見る
半球の体積と表面積を求めよ
*図は動画内参照
兵庫県
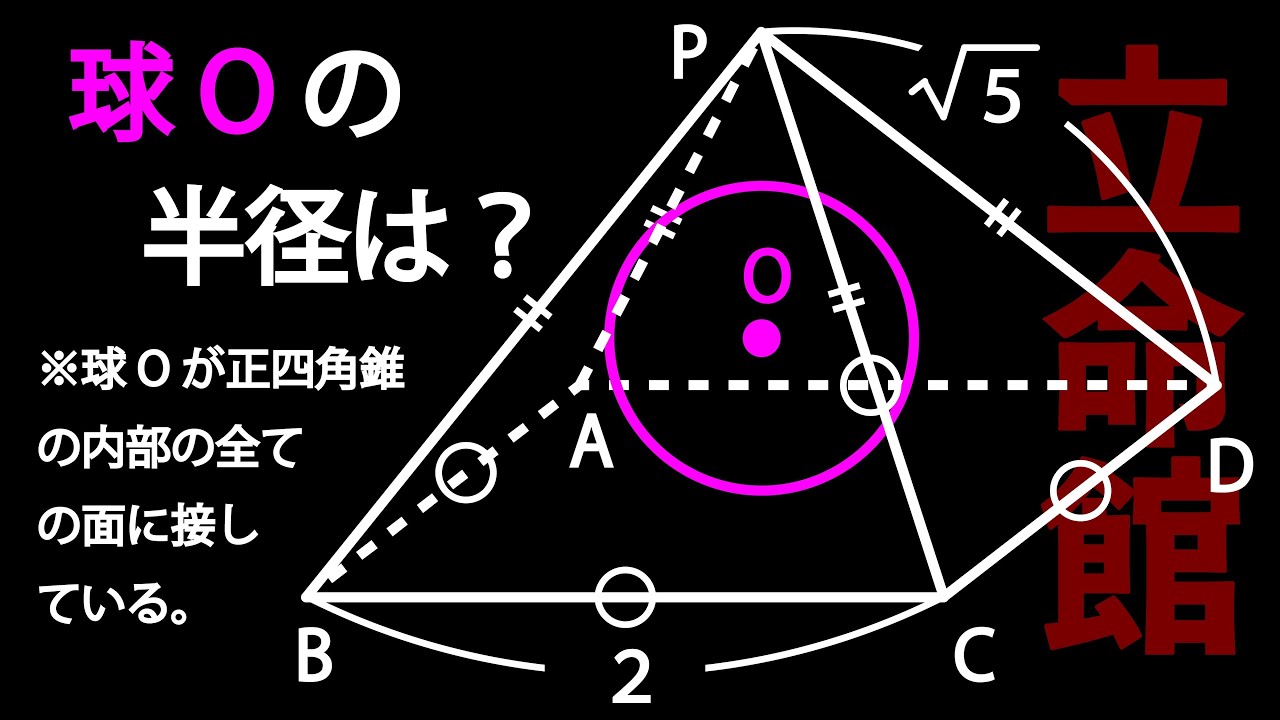
ビビったら負け 正四角錐の内接球の半径 立命館高校
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
球Oの半径は?
*球Oが正四角錐の内部の全ての面に接している。
*図は動画内参照
立命館高等学校
この動画を見る
球Oの半径は?
*球Oが正四角錐の内部の全ての面に接している。
*図は動画内参照
立命館高等学校
福田の数学〜立教大学2022年経済学部第3問〜放物線と円と直線で囲まれた面積

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#図形と方程式#微分法と積分法#円と方程式#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#立教大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
Oを原点とする座標平面上の放物線$C:y=x^2$とC上の点P$(\frac{\sqrt3}{2}, \ \frac{3}{4})$がある。
PにおけるCの接線をlとし、また、Pを通りlと直交する直線をmとする。
さらに、mとx軸の交点をQとする。このとき、次の問いに答えよ。
(1)mの方程式を$y=px+q$とするとき、定数p,qの値を求めよ。
(2)Qの座標を$(a,\ 0)$とするとき、aの値を求めよ。
(3)Qを中心とする半径rの円Dがlとただ1つの共有点を持つとき、rの値を求めよ。
(4)(1)で定めたp,qの値に対して、次の連立不等式の表す領域の面積S_1を求めよ。
$x \geqq 0,\ \ \ y \geqq 0,\ \ \ y \leqq px+q,\ \ \ y \leqq x^2$
(5)(2)で定めたaの値と(3)で定めたrの値に対して、次の連立不等式の表す領域
の面積S_2を求めよ。
$0 \leqq x \leqq \frac{\sqrt3}{2},\ \ \ y \geqq 0,\ \ \ y \leqq x^2,\ \ \ (x-a)^2+y^2 \geqq r^2$
2022立教学部経済学部過去問
この動画を見る
Oを原点とする座標平面上の放物線$C:y=x^2$とC上の点P$(\frac{\sqrt3}{2}, \ \frac{3}{4})$がある。
PにおけるCの接線をlとし、また、Pを通りlと直交する直線をmとする。
さらに、mとx軸の交点をQとする。このとき、次の問いに答えよ。
(1)mの方程式を$y=px+q$とするとき、定数p,qの値を求めよ。
(2)Qの座標を$(a,\ 0)$とするとき、aの値を求めよ。
(3)Qを中心とする半径rの円Dがlとただ1つの共有点を持つとき、rの値を求めよ。
(4)(1)で定めたp,qの値に対して、次の連立不等式の表す領域の面積S_1を求めよ。
$x \geqq 0,\ \ \ y \geqq 0,\ \ \ y \leqq px+q,\ \ \ y \leqq x^2$
(5)(2)で定めたaの値と(3)で定めたrの値に対して、次の連立不等式の表す領域
の面積S_2を求めよ。
$0 \leqq x \leqq \frac{\sqrt3}{2},\ \ \ y \geqq 0,\ \ \ y \leqq x^2,\ \ \ (x-a)^2+y^2 \geqq r^2$
2022立教学部経済学部過去問
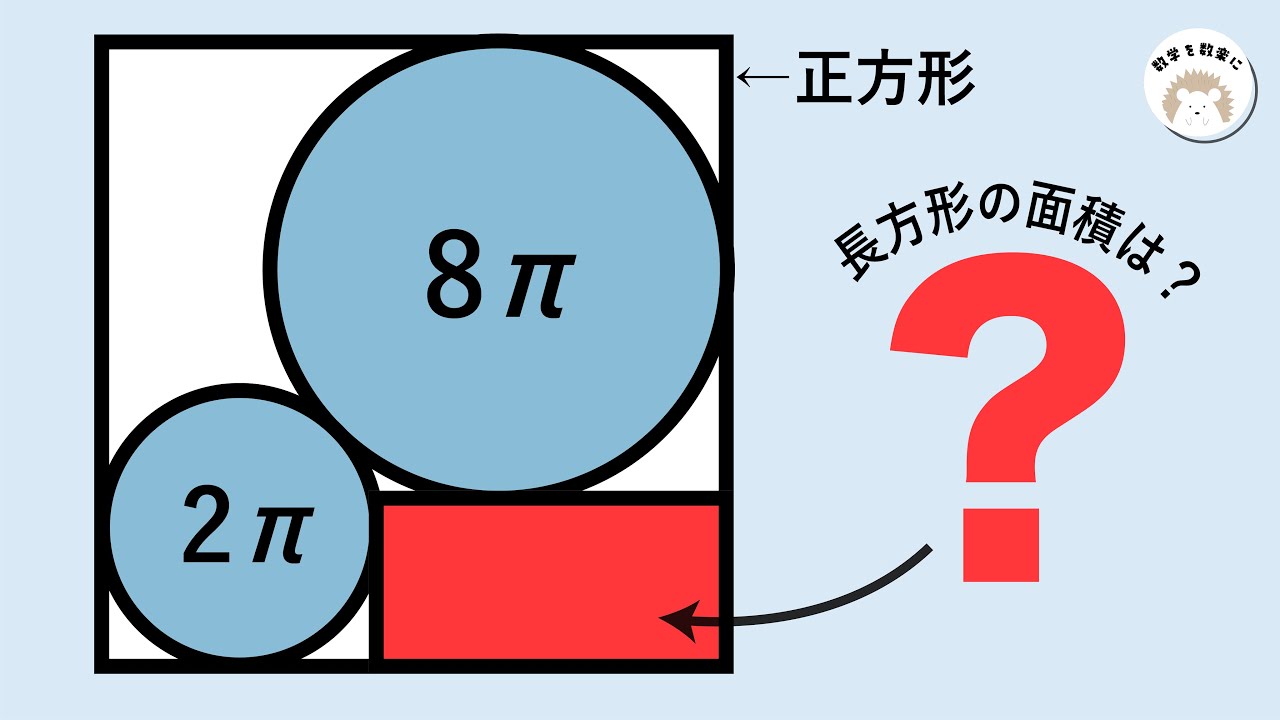
2つの円と正方形
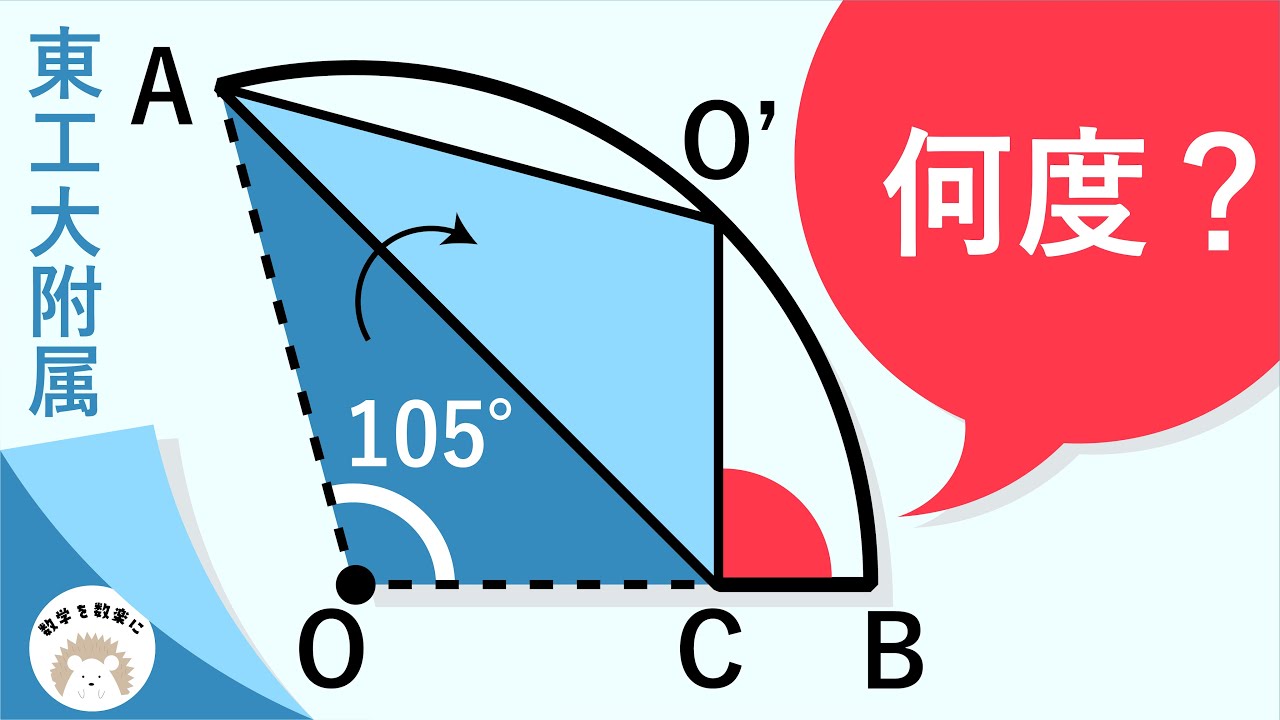
おうぎ形の折り返し 東工大附属
単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
何度?
*図は動画内参照
東京工業大学附属科学技術高等学校
この動画を見る
何度?
*図は動画内参照
東京工業大学附属科学技術高等学校
円周角 広島県

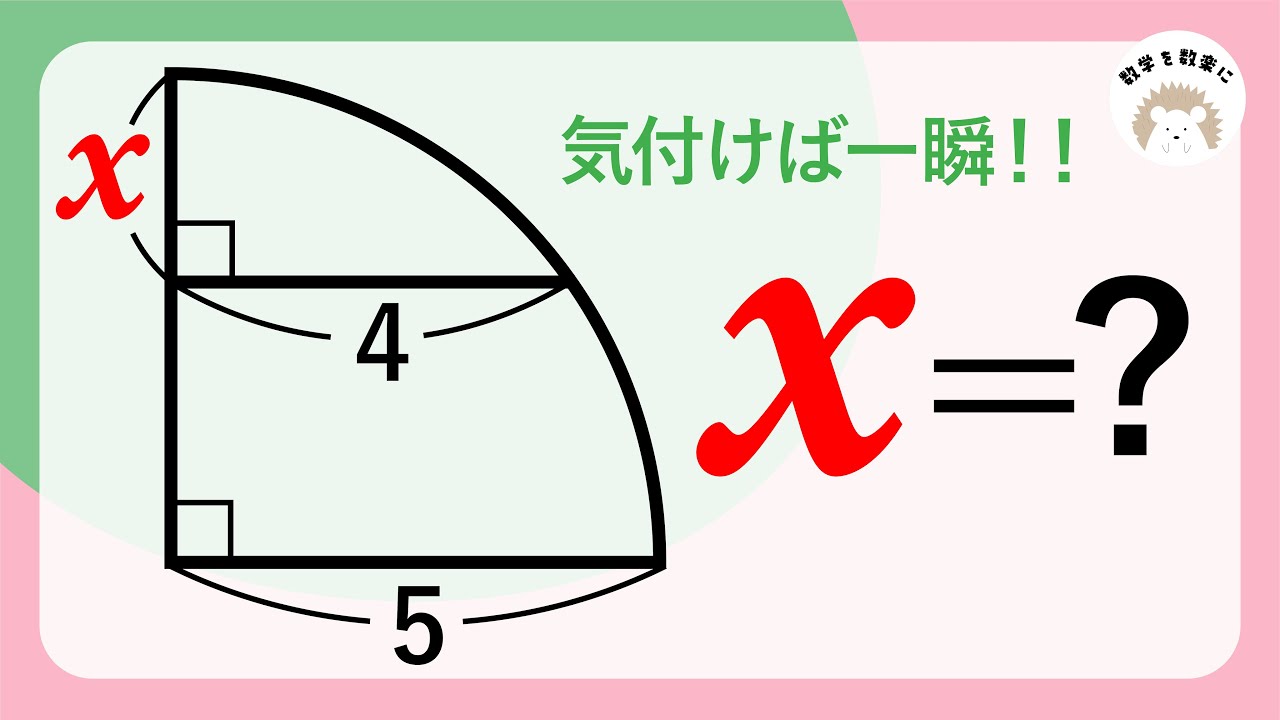
気付けば一瞬!! 4分の1円
福田の数学〜明治大学2022年全学部統一入試12AB第3問〜漸化式の図形への応用

単元:
#大学入試過去問(数学)#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数列#漸化式#学校別大学入試過去問解説(数学)#明治大学#数学(高校生)#数B
指導講師:
福田次郎
問題文全文(内容文):
(1)三角形$ABC$の内接円が辺$AB$と接する点をPとし、
辺$BC$と接する点を$Q$とし、辺$CA$と接する点をRとする。
$\angle A$の大きさを$θ$とすると、$\angle APR=\boxed{ア}$であり、
$\angle PQR=\boxed{ア}$である。
$\boxed{ア}$の解答群
$⓪0 ①\frac{\pi}{2} ②θ ③\frac{θ}{2} ④\frac{\pi}{2}-θ ⑤\frac{\pi-θ}{2}$
$⑥\pi-\frac{θ}{2} ⑦\pi-θ ⑧\frac{\pi-3θ}{2} ⑨\frac{\pi}{2}-3θ$
(2)三角形$T_1$の3つの角のうち、角の大きさが最小のものは$\frac{\pi}{6}$で、
最大のものは$\frac{\pi}{2}$であるとする。
$n=1,\ 2,\ 3,\ ...$について、三角形$T_n$の内接円を$O_n$とし、
$T_n$と$O_n$とが接する3つの点を頂点とするような三角形を$T_{n+1}$とする。
このとき、三角形$T_2$の3つの角のうち、
角の大きさが最小のものは$\frac{\pi}{\boxed{イ}}$で、
最大のものは$\frac{\boxed{ウ}\ \pi}{\boxed{エオ}}$である。
$n=1,\ 2,\ 3,\ ...$について、三角形$T_n$の3つの角のうち、
角の大きさが最小のものを$a_n$とし、最大のものを$b_n$とする。三角形$T_{n+1}$について、
$a_{n+1}=\boxed{カ},\ \ \ b_{n+1}=\boxed{キ}$
と表せる。この式より
$a_n+b_n=\frac{\boxed{ク}}{\boxed{ケ}}\pi,$
$b_n-a_n=\frac{\pi}{\boxed{コ}・\boxed{サ}^{n-1}}$
であり、$a_n=\frac{\pi}{\boxed{シ}}(1-\frac{1}{\boxed{ス}^n}) $である。
$\boxed{カ}、\boxed{キ}$の解答群
$⓪\frac{a_n}{2} ①\frac{b_n}{2} ②\frac{\pi}{2}-a_n ③\frac{\pi}{2}-b_n ④\frac{\pi-a_n}{2}$
$⑤\frac{\pi-b_n}{2} ⑥\pi-\frac{a_n}{2} ⑦\pi-\frac{b_n}{2} ⑧\pi-a_n ⑨\pi-b_n$
2022明治大学全統過去問
この動画を見る
(1)三角形$ABC$の内接円が辺$AB$と接する点をPとし、
辺$BC$と接する点を$Q$とし、辺$CA$と接する点をRとする。
$\angle A$の大きさを$θ$とすると、$\angle APR=\boxed{ア}$であり、
$\angle PQR=\boxed{ア}$である。
$\boxed{ア}$の解答群
$⓪0 ①\frac{\pi}{2} ②θ ③\frac{θ}{2} ④\frac{\pi}{2}-θ ⑤\frac{\pi-θ}{2}$
$⑥\pi-\frac{θ}{2} ⑦\pi-θ ⑧\frac{\pi-3θ}{2} ⑨\frac{\pi}{2}-3θ$
(2)三角形$T_1$の3つの角のうち、角の大きさが最小のものは$\frac{\pi}{6}$で、
最大のものは$\frac{\pi}{2}$であるとする。
$n=1,\ 2,\ 3,\ ...$について、三角形$T_n$の内接円を$O_n$とし、
$T_n$と$O_n$とが接する3つの点を頂点とするような三角形を$T_{n+1}$とする。
このとき、三角形$T_2$の3つの角のうち、
角の大きさが最小のものは$\frac{\pi}{\boxed{イ}}$で、
最大のものは$\frac{\boxed{ウ}\ \pi}{\boxed{エオ}}$である。
$n=1,\ 2,\ 3,\ ...$について、三角形$T_n$の3つの角のうち、
角の大きさが最小のものを$a_n$とし、最大のものを$b_n$とする。三角形$T_{n+1}$について、
$a_{n+1}=\boxed{カ},\ \ \ b_{n+1}=\boxed{キ}$
と表せる。この式より
$a_n+b_n=\frac{\boxed{ク}}{\boxed{ケ}}\pi,$
$b_n-a_n=\frac{\pi}{\boxed{コ}・\boxed{サ}^{n-1}}$
であり、$a_n=\frac{\pi}{\boxed{シ}}(1-\frac{1}{\boxed{ス}^n}) $である。
$\boxed{カ}、\boxed{キ}$の解答群
$⓪\frac{a_n}{2} ①\frac{b_n}{2} ②\frac{\pi}{2}-a_n ③\frac{\pi}{2}-b_n ④\frac{\pi-a_n}{2}$
$⑤\frac{\pi-b_n}{2} ⑥\pi-\frac{a_n}{2} ⑦\pi-\frac{b_n}{2} ⑧\pi-a_n ⑨\pi-b_n$
2022明治大学全統過去問
仙台育英 正四面体の内接球の半径

単元:
#数学(中学生)#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#高校入試過去問(数学)#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
内接球の半径=?
*図は動画内参照
仙台育英学園高等学校
この動画を見る
内接球の半径=?
*図は動画内参照
仙台育英学園高等学校
福田の数学〜早稲田大学2022年社会科学部第2問〜平面幾何と3次関数の増減

単元:
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#内心・外心・重心とチェバ・メネラウス#周角と円に内接する四角形・円と接線・接弦定理#指数関数と対数関数#微分法と積分法#指数関数#接線と増減表・最大値・最小値#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師:
福田次郎
問題文全文(内容文):
$AB=AC=1,\ BC=a$の二等辺三角形$ABC$の内接円を$I$、外接円を$O$とする。
ただし、$0 \lt a \lt \sqrt2$ である。また、三角形$ABC$と円$I$の3つの接点を頂点とする
三角形を$T$、3点$A,\ B,\ C$で円$O$に外接する三角形を$U$とする。次の問いに答えよ。
(1)三角形$T$の、$BC$に平行な辺の長さ$t$を$a$で表せ。
(2)三角形$U$の、$BC$に平行な辺の長さ$u$を$a$で表せ。
(3)$\frac{t}{u}=p$とする。$p$が最大となる$a$の値と、そのときの$p$の値を求めよ。
2022早稲田大学社会科学部過去問
この動画を見る
$AB=AC=1,\ BC=a$の二等辺三角形$ABC$の内接円を$I$、外接円を$O$とする。
ただし、$0 \lt a \lt \sqrt2$ である。また、三角形$ABC$と円$I$の3つの接点を頂点とする
三角形を$T$、3点$A,\ B,\ C$で円$O$に外接する三角形を$U$とする。次の問いに答えよ。
(1)三角形$T$の、$BC$に平行な辺の長さ$t$を$a$で表せ。
(2)三角形$U$の、$BC$に平行な辺の長さ$u$を$a$で表せ。
(3)$\frac{t}{u}=p$とする。$p$が最大となる$a$の値と、そのときの$p$の値を求めよ。
2022早稲田大学社会科学部過去問
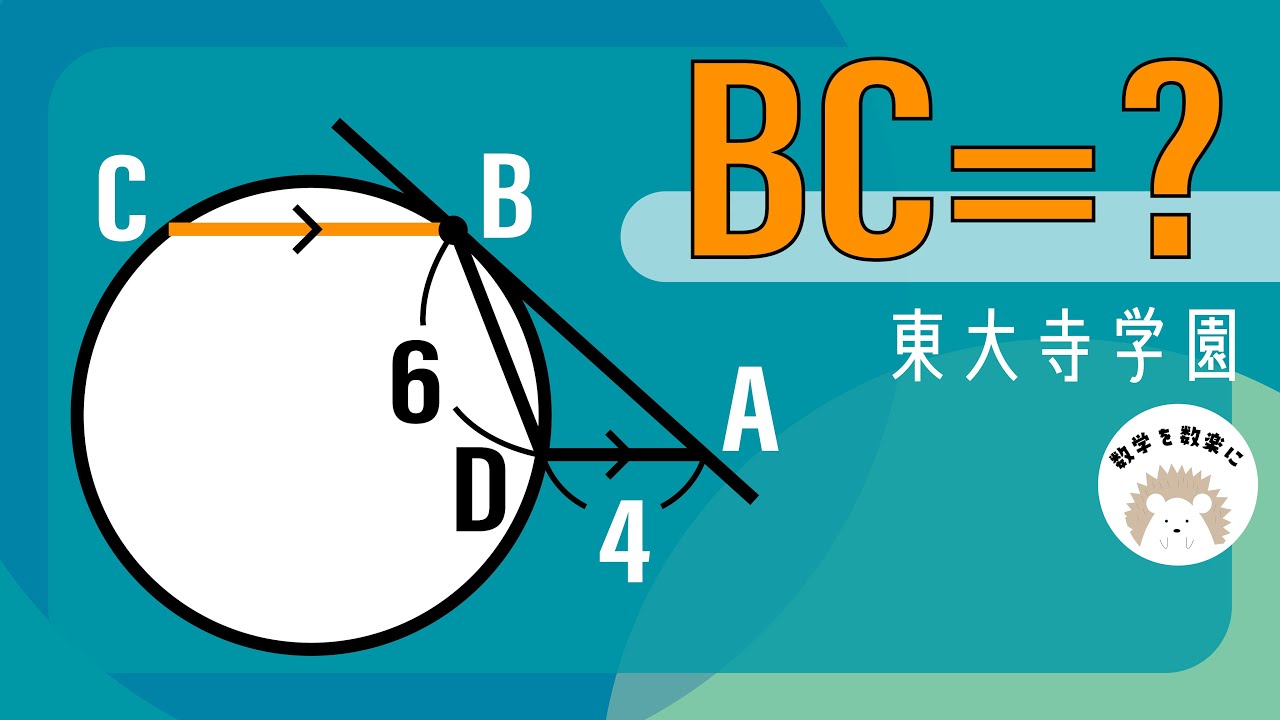
接線といったら〇〇定理
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
BC=?
*図は動画内参照
東大寺学園高等学校
この動画を見る
BC=?
*図は動画内参照
東大寺学園高等学校
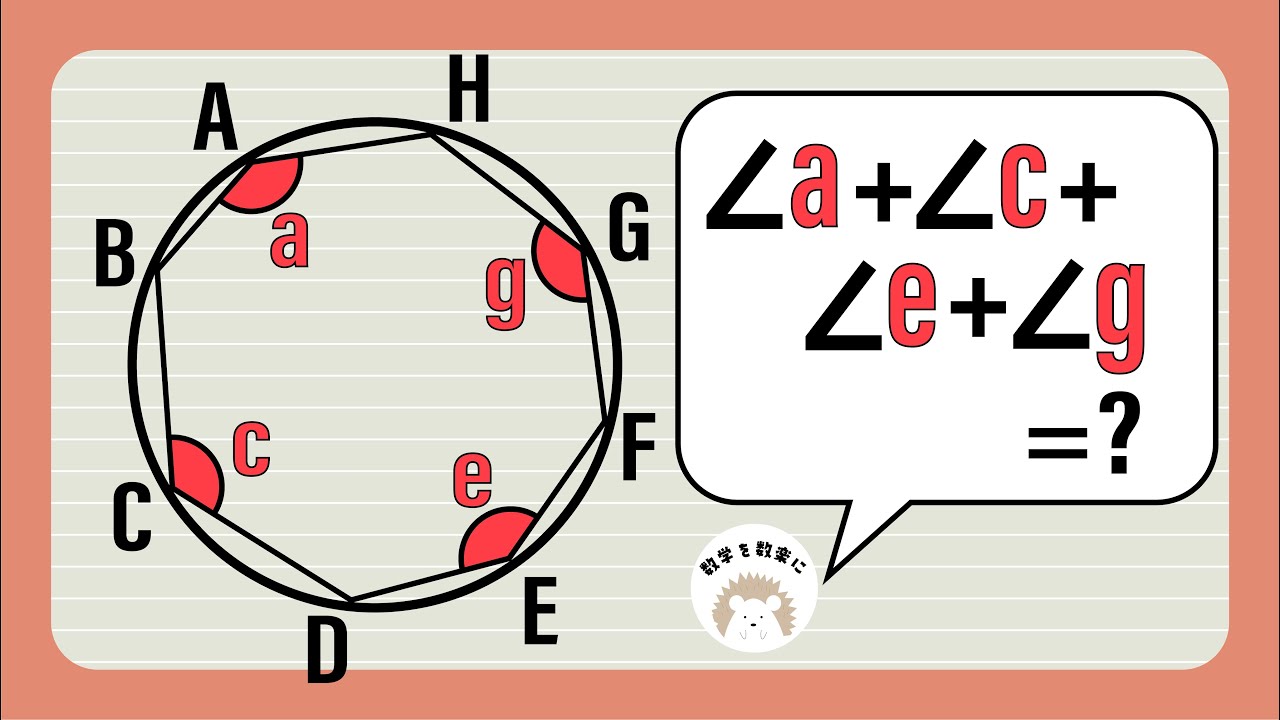
円と八角形と角の和
単元:
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師:
数学を数楽に
問題文全文(内容文):
$\angle a + \angle c + \angle e + \angle g = ?$
*図は動画内参照
この動画を見る
$\angle a + \angle c + \angle e + \angle g = ?$
*図は動画内参照
補助線引ける? 正方形と半円