図形の性質
図形の性質
【数A】【図形の性質】チェバメネラウス ※問題文は概要欄
単元：
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形の性質#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
(1)：△ABCの辺AB、AC上に、それぞれ頂点と異なる点D、Eを取る時、等式【△ADE/△ABC】＝【AD/AB】×【AE/AC】が成り立つことを証明せよ。
(2)：△ABCの辺BCを２：３、辺CAを３：１、辺ABを１：２に内分する点をそれぞれD、E、Fとする時、次の値を求めよ。
(ア)△AFE/△ABC (イ)△DEF/△ABC
△ABCの辺ABを２：３に内分する点をR、辺ACを５：６に内分する点をQとする。線分BQと線分CRの交点をOとする。直線AOと辺BCの交点をPとする。
(1)BP：PCを求めよ。 (2)△OBC：△ABCを求めよ。
△ABCの辺ABを２：１に内分する点をD、辺ACを３：１に内分する点をEとする。直線DEとBCの交点をPとする。
(1)BP：PCを求めよ。 (2)DP：PEを求めよ。
この動画を見る
(1)：△ABCの辺AB、AC上に、それぞれ頂点と異なる点D、Eを取る時、等式【△ADE/△ABC】＝【AD/AB】×【AE/AC】が成り立つことを証明せよ。
(2)：△ABCの辺BCを２：３、辺CAを３：１、辺ABを１：２に内分する点をそれぞれD、E、Fとする時、次の値を求めよ。
(ア)△AFE/△ABC (イ)△DEF/△ABC
△ABCの辺ABを２：３に内分する点をR、辺ACを５：６に内分する点をQとする。線分BQと線分CRの交点をOとする。直線AOと辺BCの交点をPとする。
(1)BP：PCを求めよ。 (2)△OBC：△ABCを求めよ。
△ABCの辺ABを２：１に内分する点をD、辺ACを３：１に内分する点をEとする。直線DEとBCの交点をPとする。
(1)BP：PCを求めよ。 (2)DP：PEを求めよ。
【数A】【図形の性質】図形の性質の基本2 ※問題文は概要欄
単元：
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形の性質#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
三角形ABCの内心をIとし、3辺BC、CA、ABに関してIと対称な点をそれぞれP,Q,Rとする。Iは三角形PQRについてどのような点か？
三角形ABCの内心をI、角Aの内部の傍心をＩ₁とする時、次の問いに答えよ。
（１）角ＩＢＩ₁の大きさを求めよ。
（２）三角形ＡＢＣの外接円は線分ＩＩ₁を二等分することを証明せよ。
ＡＢ＝ＡＣである二等辺三角形ＡＢＣの頂点Ａから辺ＢＣに下ろした垂線をＡＤとする。
角Ｂの内部の傍接円ＩＢの半径はＡＤに等しいことを証明せよ。
この動画を見る
三角形ABCの内心をIとし、3辺BC、CA、ABに関してIと対称な点をそれぞれP,Q,Rとする。Iは三角形PQRについてどのような点か？
三角形ABCの内心をI、角Aの内部の傍心をＩ₁とする時、次の問いに答えよ。
（１）角ＩＢＩ₁の大きさを求めよ。
（２）三角形ＡＢＣの外接円は線分ＩＩ₁を二等分することを証明せよ。
ＡＢ＝ＡＣである二等辺三角形ＡＢＣの頂点Ａから辺ＢＣに下ろした垂線をＡＤとする。
角Ｂの内部の傍接円ＩＢの半径はＡＤに等しいことを証明せよ。
【数A】【図形の性質】図形の性質の基本1 ※問題文は概要欄
単元：
#数A#図形の性質#内心・外心・重心とチェバ・メネラウス#数学(高校生)
教材：
#4S数学#4S数学Ⅰ＋AのB問題解説（新課程2022年以降）#図形の性質#中高教材
指導講師：
理数個別チャンネル
問題文全文(内容文)：
外心と内心が一致する三角形は正三角形である。このことを証明せよ。
図の三角形ABCは角B＝90度の直角三角形であり、3点D、E、Fは三角形ABCの外心・内心・重心のいずれかであるとする。このとき、三角形ABCの外心・内心・重心は3点D、E、Fのいずれであるか？
三角形ABCにおいて、AB＝AC＝3、BC＝2である。三角形ABCの重心をG、内心をIとするとき、線分GIの長さを求めよ。
図において、点Hは三角形ABCの垂心である。角α、βを求めよ。
この動画を見る
外心と内心が一致する三角形は正三角形である。このことを証明せよ。
図の三角形ABCは角B＝90度の直角三角形であり、3点D、E、Fは三角形ABCの外心・内心・重心のいずれかであるとする。このとき、三角形ABCの外心・内心・重心は3点D、E、Fのいずれであるか？
三角形ABCにおいて、AB＝AC＝3、BC＝2である。三角形ABCの重心をG、内心をIとするとき、線分GIの長さを求めよ。
図において、点Hは三角形ABCの垂心である。角α、βを求めよ。
shape problems : Shirotan's cute kawaii math show #Math #exam #questions #brainteasers #study
単元：
#数Ⅰ#数A#図形の性質#数学(高校生)
指導講師：
高校入試から見た数学の世界「全部入試問題」by しろたん
問題文全文(内容文)：
$\angle{B}=45^{ \circ }$
$\angle{C}=15^{ \circ }$
$AC=2\sqrt{3}+2 \triangle{ABC}の面積を求めなさい$
この動画を見る
$\angle{B}=45^{ \circ }$
$\angle{C}=15^{ \circ }$
$AC=2\sqrt{3}+2 \triangle{ABC}の面積を求めなさい$
角の二度分線
高校1年生から早稲田に挑戦！三角比の難問！【早稲田大学】【数学 入試問題】
単元：
#数Ⅰ#数A#大学入試過去問(数学)#図形の性質#図形と計量#三角比（三角比・拡張・相互関係・単位円）#三角比への応用（正弦・余弦・面積）#学校別大学入試過去問解説(数学)#早稲田大学#数学(高校生)
指導講師：
数学・算数の楽しさを思い出した / Ken
問題文全文(内容文)：
m,nを正の整数とする。半径1の円に内接する△ABCが
sinA=m/17,sinB=n/17,sin²C=sin²A+sin²B
を満たすとき△ABCの内接円の半径を求めよ。
この動画を見る
m,nを正の整数とする。半径1の円に内接する△ABCが
sinA=m/17,sinB=n/17,sin²C=sin²A+sin²B
を満たすとき△ABCの内接円の半径を求めよ。
福田のおもしろ数学330〜三角形の成立条件と条件を満たす三角形の個数
単元：
#数A#図形の性質#整数の性質#三角形の辺の比（内分・外分・二等分線）#約数・倍数・整数の割り算と余り・合同式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
自然数$n\geqq 3$に対して$f(n)$を各辺の長さが整数かつ周の長さが$n$である三角形の個数で定義する。
（例えば$f(3)=1,f(4)=0,f(7)=2$である）
$f(1999)\geq f(1966),f(2000)=f(1997)$を示せ。
この動画を見る
自然数$n\geqq 3$に対して$f(n)$を各辺の長さが整数かつ周の長さが$n$である三角形の個数で定義する。
（例えば$f(3)=1,f(4)=0,f(7)=2$である）
$f(1999)\geq f(1966),f(2000)=f(1997)$を示せ。
福田のおもしろ数学326〜三角形の内接円の半径
単元：
#数A#図形の性質#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
図のように半径34の円が8個、△ABCの辺BCに接しながら一列に外接しながら並んでいる。両端の円はそれぞれ辺AB、ACに接する。同じように半径1の円を並べると2022個並んだ。このとき、△ABCの内接円の半径を求めよ。
この動画を見る
図のように半径34の円が8個、△ABCの辺BCに接しながら一列に外接しながら並んでいる。両端の円はそれぞれ辺AB、ACに接する。同じように半径1の円を並べると2022個並んだ。このとき、△ABCの内接円の半径を求めよ。
福田のおもしろ数学322〜有限個の点の集合の性質
単元：
#数A#図形の性質
指導講師：
福田次郎
問題文全文(内容文)：
「どの3点A,B,Cを選んでも、△ABCの面積は1未満である」
という性質を持つ平面上の有限個の点がある。
これらすべての点を、周および内部に含むような、面積4未満の三角形が存在することを証明せよ。
この動画を見る
「どの3点A,B,Cを選んでも、△ABCの面積は1未満である」
という性質を持つ平面上の有限個の点がある。
これらすべての点を、周および内部に含むような、面積4未満の三角形が存在することを証明せよ。
福田のおもしろ数学312〜三角形の内角と辺の長さに成り立つ不等式の証明
単元：
#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\triangle $ABCにおいて$60 \leqq \frac{aA+bB+cC}{a+b+c} \lt 90$が成り立つことを証明してください。ただし、A,B,Cは度数法で表されているものとする。
この動画を見る
$\triangle $ABCにおいて$60 \leqq \frac{aA+bB+cC}{a+b+c} \lt 90$が成り立つことを証明してください。ただし、A,B,Cは度数法で表されているものとする。
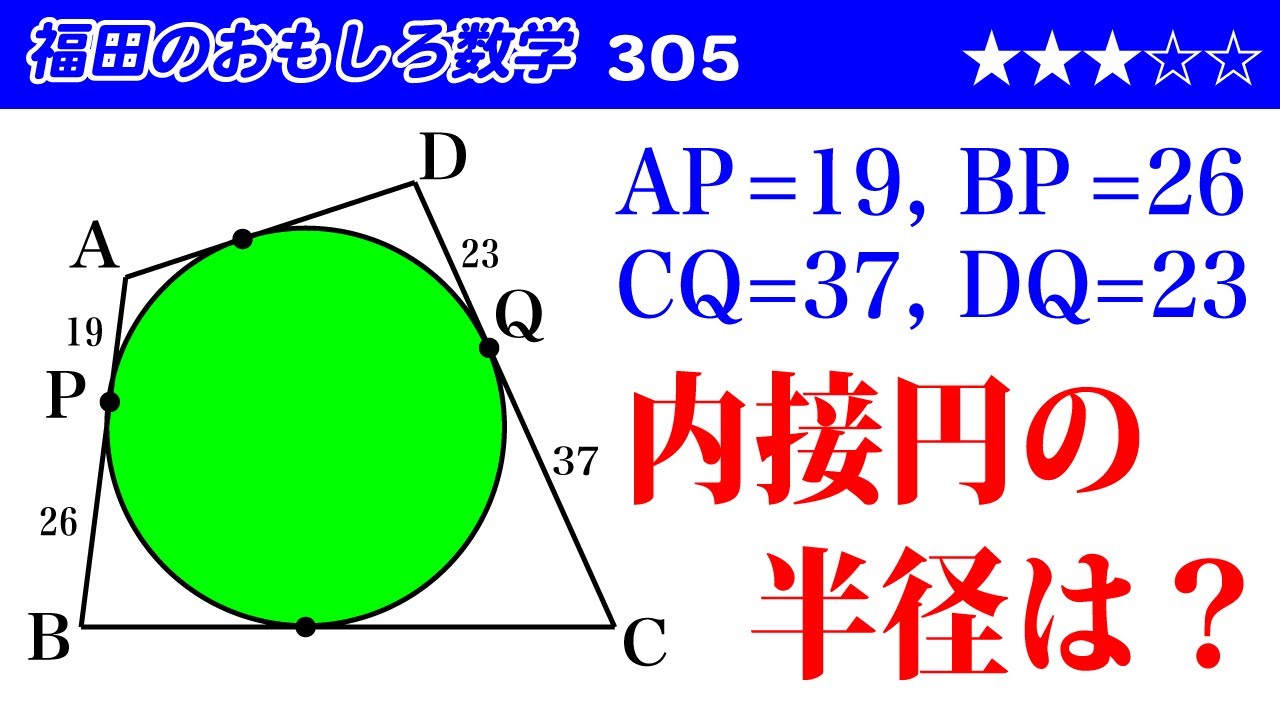
福田のおもしろ数学305〜四角形に内接する円の半径
単元：
#数Ⅰ#数A#図形の性質#図形と計量#三角比への応用（正弦・余弦・面積）#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
図は動画参照
$AP=19,BP=26,CQ=37,DQ=23$
内接円の半径は？
この動画を見る
図は動画参照
$AP=19,BP=26,CQ=37,DQ=23$
内接円の半径は？
福田の数学〜早稲田大学2024教育学部第1問(3)〜対称軸を2本もつ多角形
単元：
#数A#図形の性質#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$xy$ 平面上の多角形で、$x$ 軸はこの多角形の対称軸であり、直線 $y=\frac{\sqrt{3}}{3} x$ もこの多角形の対称軸であるものを考える。このような多角形の辺の数の最小値を求めよ。
この動画を見る
$xy$ 平面上の多角形で、$x$ 軸はこの多角形の対称軸であり、直線 $y=\frac{\sqrt{3}}{3} x$ もこの多角形の対称軸であるものを考える。このような多角形の辺の数の最小値を求めよ。
福田のおもしろ数学298〜幾何の問題2つの長方形
単元：
#数A#図形の性質#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$\mathrm{A,D,H,G}$ が同一円周上にあるとき、$\mathrm{CE}$ の長さを求めよ。（図は動画内参照）
この動画を見る
$\mathrm{A,D,H,G}$ が同一円周上にあるとき、$\mathrm{CE}$ の長さを求めよ。（図は動画内参照）
福田の数学〜早稲田大学2024教育学部第1問(2)〜空間で格子点を頂点とする正六角形の一辺の長さの最小値
単元：
#数A#図形の性質#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
$x$ 座標、$y$ 座標、$z$ 座標がすべて整数であるような $xyz$ 空間の点を格子点と呼ぶ。頂点がすべて格子点であるような $xyz$ 空間内の正 $6$ 角形の $1$ 辺の長さの最小値を求めよ。
この動画を見る
$x$ 座標、$y$ 座標、$z$ 座標がすべて整数であるような $xyz$ 空間の点を格子点と呼ぶ。頂点がすべて格子点であるような $xyz$ 空間内の正 $6$ 角形の $1$ 辺の長さの最小値を求めよ。
〇〇きの定理で解説！！
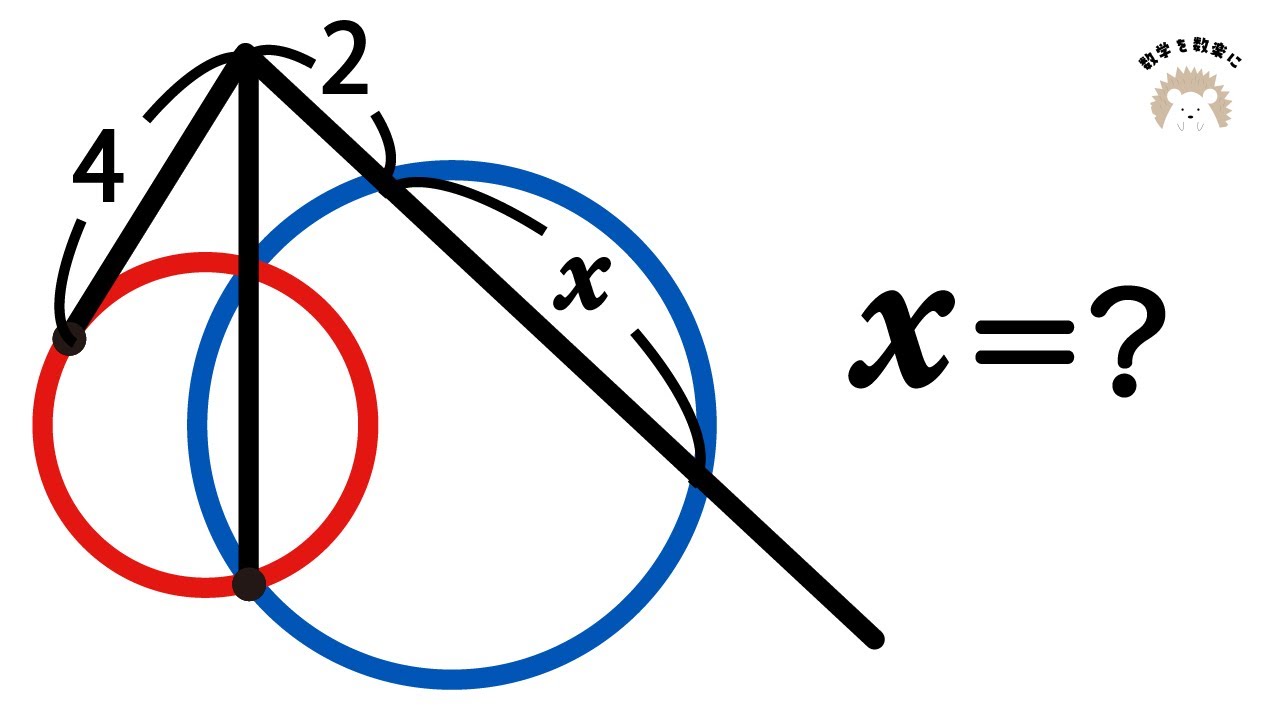
〇〇きの定理で解説！！
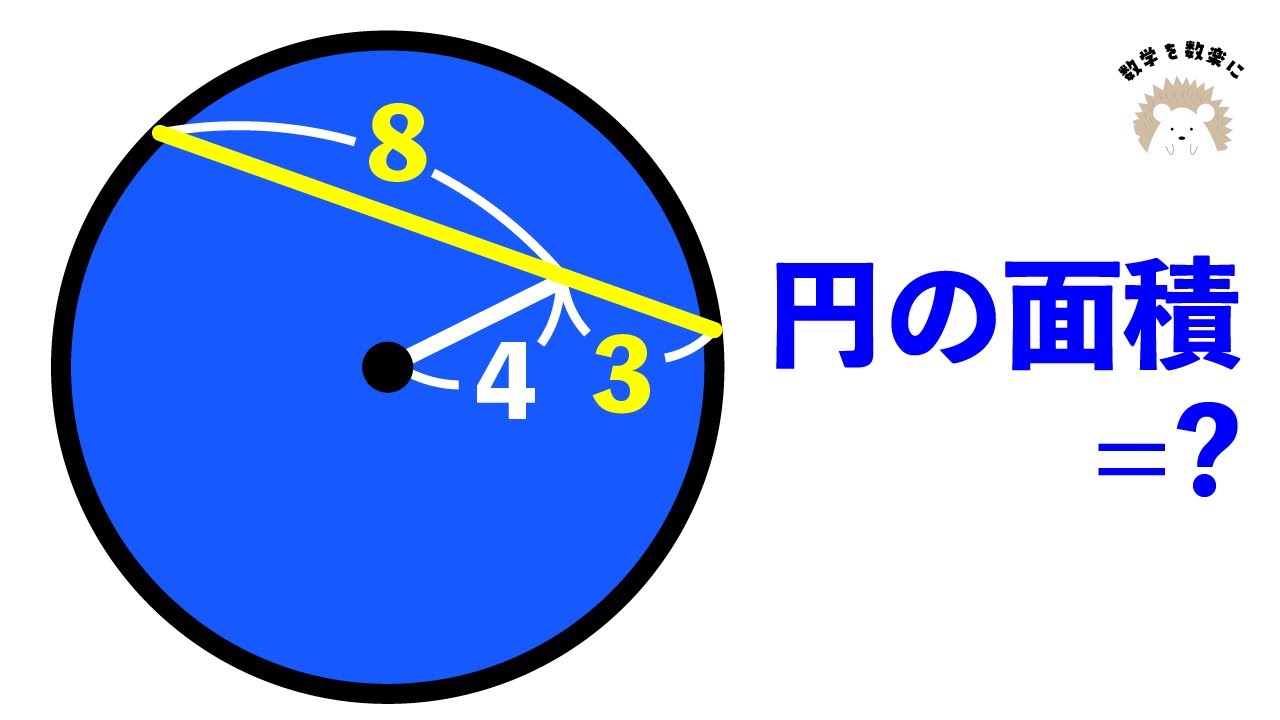
知っていればほぼ一瞬！！円の面積🟰❓
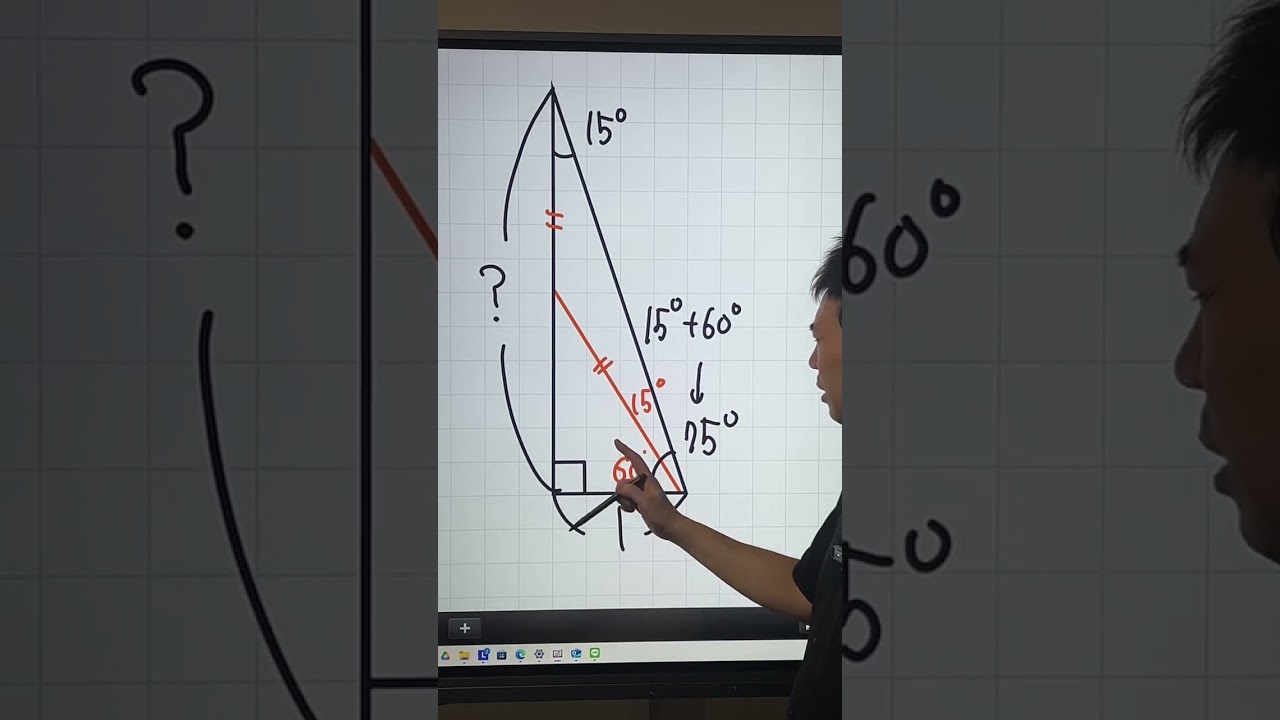
15°75°90°の直角三角形
福田のおもしろ数学225〜楕円と直線の交点を使った線分の長さの積の最小値
単元：
#数A#図形の性質#平面上の曲線#方べきの定理と２つの円の関係#2次曲線#数学(高校生)#数C
指導講師：
福田次郎
問題文全文(内容文)：
点 $\mathrm{P}(2,1)$ を通る直線が楕円 $\displaystyle \frac{x^2}{2}+\frac{y^2}{3}=1$ と異なる2点 $\mathrm{Q}, \, \mathrm{R}$ で交わっている。$\mathrm{PQ} \cdot \mathrm{PR}$ の最小値を求めよ。
この動画を見る
点 $\mathrm{P}(2,1)$ を通る直線が楕円 $\displaystyle \frac{x^2}{2}+\frac{y^2}{3}=1$ と異なる2点 $\mathrm{Q}, \, \mathrm{R}$ で交わっている。$\mathrm{PQ} \cdot \mathrm{PR}$ の最小値を求めよ。
直角三角形の中に直角
単元：
#数学(中学生)#中１数学#数A#図形の性質#三角形の辺の比（内分・外分・二等分線）#平面図形#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
次の図のxを求めよ。
（図は動画参照）
この動画を見る
次の図のxを求めよ。
（図は動画参照）
傍接円の半径 難関高校受験者必見！！
引けるか！？補助線
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
数学を数楽に
問題文全文(内容文)：
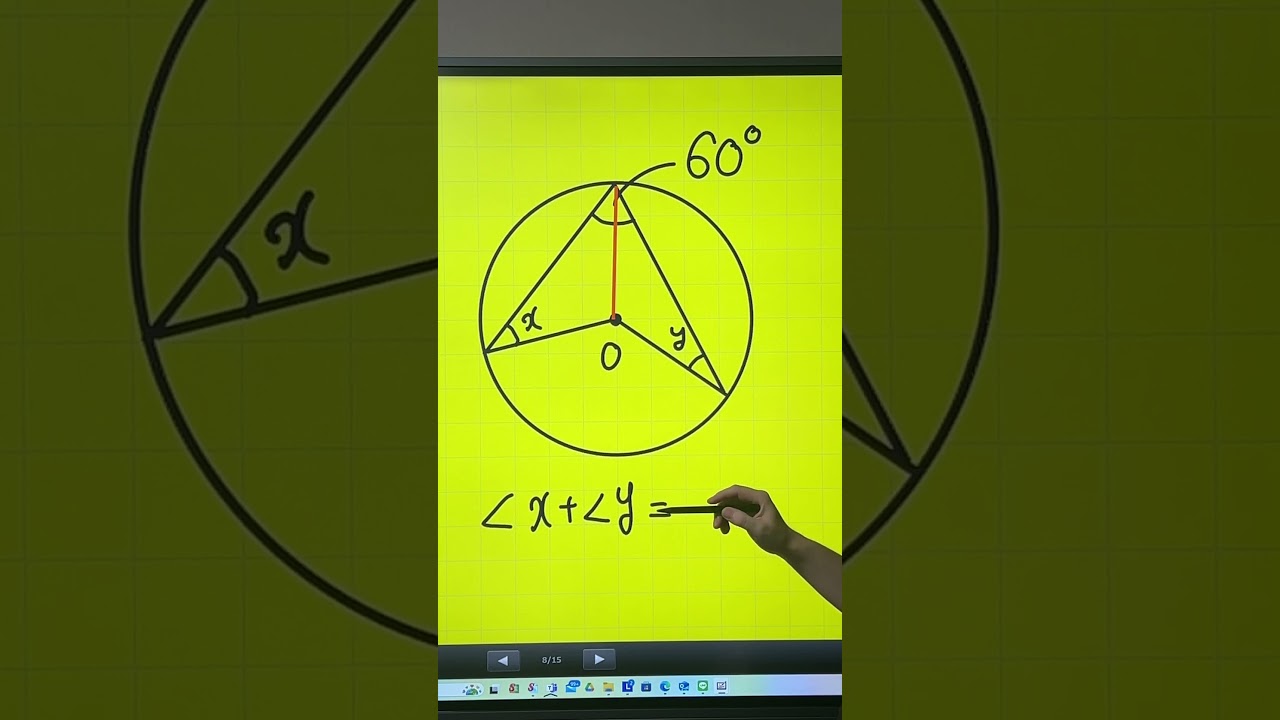
次の角度を求めよ（図は動画参照）
$\angle x+\angle y=$
この動画を見る
次の角度を求めよ（図は動画参照）
$\angle x+\angle y=$
福田の数学〜千葉大学2024年文系第1問〜三角形の成立条件と対数
単元：
#数A#数Ⅱ#大学入試過去問(数学)#図形の性質#三角形の辺の比（内分・外分・二等分線）#指数関数と対数関数#対数関数#千葉大学#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
(1) 3辺の長さが$2,5,a$である三角形が存在するような、$a$の値の範囲を求めよ。
(2) 3辺の長さが$\log_{10}(5x),\log_{10}(x+10),\log_{10}3$である三角形が存在するような、$x$の値の範囲を求めよ。
(3) ある二等辺三角形の3辺の長さが$\log_{10}(5x),\log_{10}(x+10),\log_{10}3$であるとき、$x$の値を求めよ。
この動画を見る
(1) 3辺の長さが$2,5,a$である三角形が存在するような、$a$の値の範囲を求めよ。
(2) 3辺の長さが$\log_{10}(5x),\log_{10}(x+10),\log_{10}3$である三角形が存在するような、$x$の値の範囲を求めよ。
(3) ある二等辺三角形の3辺の長さが$\log_{10}(5x),\log_{10}(x+10),\log_{10}3$であるとき、$x$の値を求めよ。
【保存版】相加平均・相乗平均の覚え方
単元：
#数Ⅱ#図形の性質#式と証明#周角と円に内接する四角形・円と接線・接弦定理#恒等式・等式・不等式の証明#その他#数学(高校生)#参考書紹介
指導講師：
【楽しい授業動画】あきとんとん
問題文全文(内容文)：
【保存版】相加平均・相乗平均の覚え方
※問題は動画内参照
この動画を見る
【保存版】相加平均・相乗平均の覚え方
※問題は動画内参照
三角形の重心 一点で交わるのはなぜ？
内心 内角の二等分線が一点で交わるのはなぜ？
【高校数学】円と直線が接するときの２パターンの考え方【数学のコツ】
単元：
#数A#図形の性質#周角と円に内接する四角形・円と接線・接弦定理#数学(高校生)
指導講師：
理数個別チャンネル
問題文全文(内容文)：
次の円と直線が接するときの$k$の値と接点の座標を求めよ。
$x^2+y^2=4, y=x+k$
この動画を見る
次の円と直線が接するときの$k$の値と接点の座標を求めよ。
$x^2+y^2=4, y=x+k$
これなに？
福田のおもしろ数学148〜円の面積
単元：
#数A#数Ⅱ#図形の性質#図形と方程式#数学(高校生)
指導講師：
福田次郎
問題文全文(内容文)：
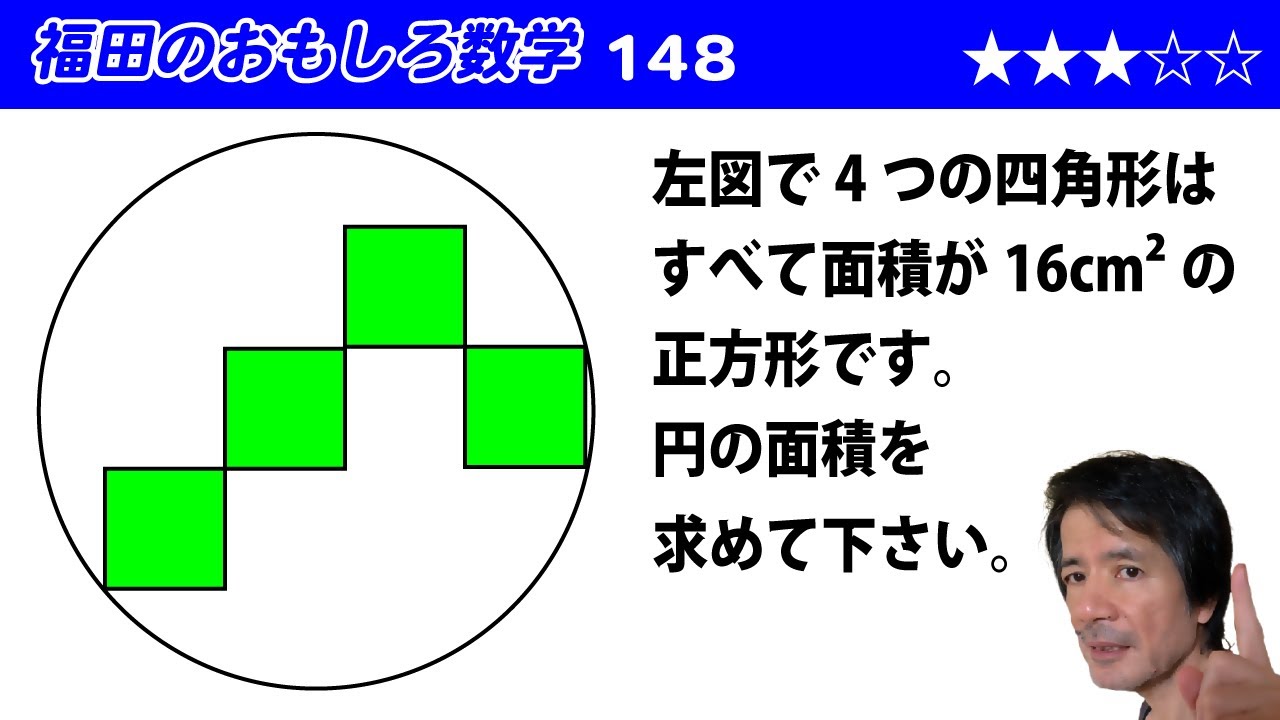
左図(※動画参照)で4つの四角形はすべて面積が$16 \textrm{cm}^2$の正方形です。
円の面積を求めて下さい。
この動画を見る
左図(※動画参照)で4つの四角形はすべて面積が$16 \textrm{cm}^2$の正方形です。
円の面積を求めて下さい。
接線の長さ
